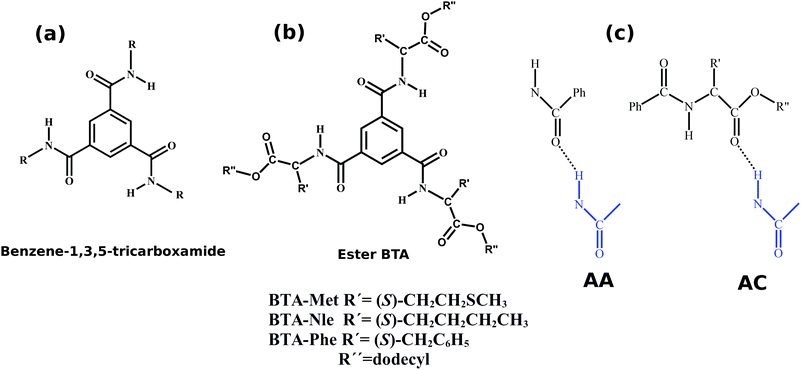
Understanding the self-assembly of amino ester-based benzene-1,3,5-tricarboxamides using molecular dynamics simulations†
Karteek K.
Bejagam
a,
Richard C.
Remsing
b,
Michael L.
Klein
b and
Sundaram
Balasubramanian
*a
aChemistry and Physics of Materials Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore 560 064, India. E-mail: bala@jncasr.ac.in
bInstitute for Computational Molecular Science, Temple University, Philadelphia, PA 19122, USA
First published on 24th November 2016
Abstract
Amino ester-based benzene-1,3,5-tricarboxamides (BTAs) are widely studied experimentally for their facile self-assembly, which leads to strong three-fold hydrogen bonded supramolecular polymers. Understanding the supramolecular assembly of these BTAs is complicated by the presence of two types of dimers, based on the nature of the intermolecular hydrogen bonding pattern: amide–amide (AA) and amide–carboxylate (AC). AA dimers form three hydrogen bonds between the two molecules, are typical of BTA stacks, and act as a basic building block of assembly. In contrast, AC hydrogen bonding results in six hydrogen bonds between two molecules, and this face-to-face orientation results in a dimer that is more stable than the AA one, however, unfavorable for further assembly. We perform atomistic molecular dynamics (MD) simulations of three derivatives of BTA in order to rationalize the large body of experimental data for these systems, specifically the relative stabilities of AA and AC dimers and oligomers. We find that at zero Kelvin, the AC dimer is more stable than the AA dimer by roughly 20 kcal mol−1. MD simulations of three BTA derivatives (BTA-Met, BTA-Nle, and BTA-Phe) under realistic conditions show that BTA-Met and BTA-Phe can aggregate to form longer assemblies via additional stabilization offered by weak CH⋯S and CH⋯π hydrogen bonds, respectively. However, the aggregation of BTA-Nle, which is devoid of such functionalities, is limited to that of a dimer. We then employ umbrella sampling to show that oligomers of BTA-Met and BTA-Phe are stable over those of dimers and demonstrate that this results from such weak interactions.
1 Introduction
Benzene-1,3,5-tricarboxamide (commonly known as BTA) and its derivatives have been widely studied for their facile self-assembly which leads to strong, three-fold hydrogen bonded supramolecular polymers.1–4 The molecular structure of BTA is shown in Fig. 1. The mechanism of self-assembly and the structure of aggregates are highly sensitive to the nature of the substituents. For aliphatic chains at R, BTAs self-assemble in a cooperative fashion5 (i.e., nucleation and growth stages), while for R = 3,3′-diamino-2,2′-bipyridine, they self-assemble via an isodesmic pathway6 (association constant is independent of oligomer size). The pattern of the hydrogen bonding network determines the mechanism of self-assembly; to a first approximation, intermolecular hydrogen bonding leads to cooperative assembly5 while intramolecular hydrogen bonding favors isodesmic routes.6 Furthermore, the length of the alkyl tail affects the molecular packing in crystal structures.7,8 Partial fluorination of peripheral alkyl tails has been demonstrated to break the symmetry of achiral BTAs.9 These studies display an influence of various substituents on the self-assembled structures in both solution and solid states.In the present article, the self-assembly of BTA molecules appended with amino ester-based moieties have been investigated. BTA with such carboxymethyl peripheral groups crystallizes in a face-to-face dimer fashion with six hydrogen bonds.10 In a recent work, Desmarchelier et al. reported the synthesis of three amino ester-based BTAs and the exploration of the effect of three substituents (Met, Nle, and Phe, see Fig. 1) on the self-assembled structures, as a function of both concentration and temperature.11 Formation of either one-dimensional long aggregates or dimers was seen to be dependent on the substituent. At ambient conditions, BTA-Met and BTA-Phe self-assemble into long one-dimensional stacks, with a specific helical handedness, while the self-assembly of BTA-Nle does not proceed beyond a dimer. “Sergeants-and-Soldiers” experiments too were performed by introducing small concentrations of amino ester-BTAs (sergeants) into a solution of alkyl BTAs (soldiers). While the pure alkyl BTA solution had equal amounts of left and right handed supramolecular stacks, the introduction of a few molecules of ester-BTAs led to the enrichment (chiral amplification) of stacks of a preferred handedness.
The present molecular dynamics simulation study aims at obtaining a microscopic understanding of the role of substituents in stabilizing either the long assemblies or dimers; the structure of the dimeric species in solution is also proposed. We also elucidate the free energy difference between two variants of dimers and address the favourable interactions responsible for the stability of long assemblies. Umbrella sampling simulations to determine the relative FE differences between oligomers and dimers are also presented. We further demonstrate the facile formation of long oligomers for the Met compound and a decreased affinity for oligomer formation for the Phe compound, while the growth of the Nle compound is limited just to a dimer.
2 Computational details
Classical Molecular Dynamics (MD) simulations were performed using the LAMMPS12 package. All-atom, fully flexible DREIDING13 parameters combined with Gasteiger partial charges14 on the atomic sites were employed to model the supramolecules. Solvent molecules were modelled through an united atom approach using a TraPPE force field.15 Cross interactions between the solute and solvent molecules were handled by DREIDING's mixing rules. Real space interactions were truncated at 12 Å and long range corrections to energy and pressure were included. Long range Coulombic interactions were handled using the particle–particle particle-mesh (PPPM) method. Three-dimensional periodic boundary conditions were applied. Equations of motions were integrated using the velocity-Verlet algorithm with a time-step of 0.5 fs. Simulations were carried out in the isothermal–isobaric (NPT) ensemble. Temperature and pressure control were achieved by the Nosé–Hoover thermostat16,17 and barostat with coupling constants of 1 ps. 1–4 interactions were treated with full-scaling. Snapshots were visualized and rendered using VMD.18 Details of the simulated systems are given in Table S5 (ESI†). Criteria adopted to determine amide–amide (AA) and amide–carboxylate (AC) hydrogen bonds,19 and CH⋯S and CH⋯π weak hydrogen bonds20,21 are listed in Table 1.Quantum chemical calculations were performed using both Gaussian0922 and CP2K23 softwares. In Gaussian09, optimizations of two dimer variants have been carried out at B3LYP/6-31g(d,p) level of theory. In CP2K calculations, all valence electrons were treated in a mixed basis with an energy cutoff of 280 Ry. The short range basis of triple-ζ single polarization (TZVP) was used. Effect of core electrons and nuclei were handled by Goedecker–Teter–Hutter (GTH)24 pseudo-potentials. The exchange and correlation interactions were treated using the Perdew–Burke–Ernzerhof (PBE)25 functional. Empirical van der Waals terms were accounted using the DFT-D326 approach developed by Grimme.
Apart from unbiased MD simulations, free energy calculations have been performed using the colvars module27 implemented in the LAMMPS12 package. Umbrella Sampling (US)28 was employed to estimate the relative free energies between two states. UWHAM29,30 was used to obtain the free energies along the reaction coordinate (RC). We estimate the error in the calculation of free energy profiles to be about 1 kcal mol−1.
3 Results and discussion
3.1 Energy differences between the two dimers
Amino ester-based BTAs considered here can dimerize into two different forms with differing hydrogen bonding patterns; the NH of the amide group can hydrogen bond with the oxygen of either the amide (AA) or of the carboxylate (AC) group of another molecule, as shown in Fig. 2. In an AA dimer, three hydrogen bonds (H-bonds) are formed between the amide ‘NH’ of one molecule and the amide ‘O’ of another molecule. This dimer possesses free hydrogen bonding sites which can be exploited to extend it further to larger oligomers. The hydrogen bonding network in an AA dimer is similar to that in traditional alkyl BTAs;31 thus, an AA dimer acts as a basic building block for a long assembly. On the other hand, in an AC dimer, hydrogen bonds are formed between the amide ‘NH’ of one molecule and the carboxylate ‘O’ of another molecule, and vice versa, as shown in Fig. 2. Face-to-face dimerization of two molecules in such an AC dimer leads to the formation of six hydrogen bonds, leaving no free hydrogen bonding sites. Such a dimer cannot be further extended to an oligomer.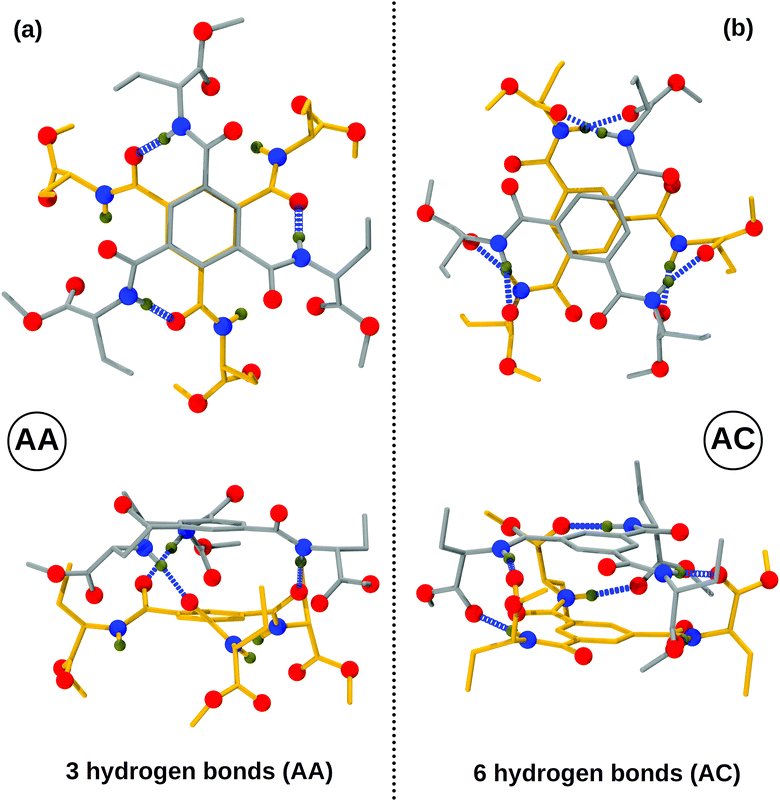 | ||
| Fig. 2 Top and side views of both types of dimers with R′ = CH2CH3 and R′′ = CH3. (a) Amide–amide (AA) dimer and (b) amide–carboxylate (AC) dimer. Color scheme: carbon (molecule 1)-gray; carbon (molecule 2)-yellow; oxygen-red; nitrogen-blue; hydrogen-tan; non-polar hydrogens are not shown for clarity. Also see Fig. S8 (ESI†). | ||
Energy differences between the two variants of dimers for R′ = CH2CH3 and R′′ = CH3 have been determined using both quantum chemical calculations and empirical force fields at zero Kelvin and these are provided in Table 2. Clearly, the AC dimer is more stable than the corresponding AA dimer, independent of the level of theory. The energy difference between the two dimer types arise due to: (i) differing number of hydrogen bonds and (ii) dihedral penalty: in an AC dimer, the ‘NH’ group hydrogen bonds with the carboxylate oxygen of another molecule within the plane of the former's benzene ring; thus, the amide group has no need to rotate about the benzene plane (see Fig. 2). On the other hand, in an AA dimer, the amide group rotates about the benzene plane so as to form hydrogen bonds. As a result, a dihedral penalty of 0.25 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 is associated for each such dihedral in the AA configuration.
31 is associated for each such dihedral in the AA configuration.
| Method | ΔE = EAA − EAC |
|---|---|
| DREIDING | 20.7 |
| B3LYP/6-31g(d,p) | 12.5 |
| PBE-D3 | 27.9 |
In summary, the AC dimer is more stable than the AA dimer both by way of forming more hydrogen bonds and also by not incurring the dihedral penalty in doing so.
3.2 Favourable interactions in an assembly
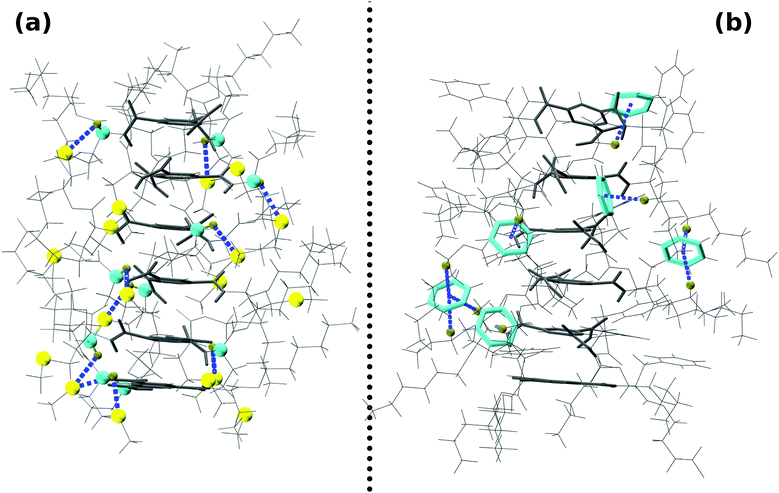
Desmarchelier et al. observed the formation of long assemblies for BTA-Met and BTA-Phe in cyclohexane solvent at ambient conditions, but not so in the case of BTA-Nle.11 The discussion above showed that BTA molecules can aggregate to form long stacks only via the AA hydrogen bonding pattern. Thus, although an AC dimer is favoured over the corresponding AA dimer by a large extent, albeit in gas phase, there must be some additional stability accruing in an oligomer which overcomes the energy difference between the two dimer types. Thus, to understand the stability of an oligomer, a hexamer of BTA-Met and BTA-Phe each were geometry optimized at the PBE-D3 level of theory using CP2K23 and the optimized geometries are shown in Fig. 3. In these calculations, R′′ was truncated to hexyl instead of the dodecyl used in experiments,11 to decrease the computational cost. In the case of BTA-Met, sulfur forms weak hydrogen bonds with the CH of the alkyl tails. A total of ten CH⋯S hydrogen bonds were observed in a hexamer of BTA-Met. Similarly, in a hexamer of BTA-Phe, the phenyl rings were observed to participate in weak CH⋯π hydrogen bonds. Thus, CH⋯S20,32,33 and CH⋯π20,34–36 hydrogen bonds likely stabilize the longer assemblies of BTA-Met and BTA-Phe, respectively. However, such specific interactions are not available in BTA-Nle molecules, and thus their self-assembly is just limited to dimers. Additionally, oligomers of BTA-Met and BTA-Phe are stabilized via 1–3 interactions. In the present context, 1–3 interactions refer to the stabilization offered by the interaction between two molecules in an oligomer separated by just one molecule. For example, in a hexamer, 1–3 interactions refer to interactions between 1–3, 2–4, 3–5, and 4–6 pairs, where these indices refer to the positions of the molecules starting from one end of the oligomer.An oligomer of size n contains 3(n − 1) AA hydrogen bonds, while equivalently, n such molecules can form n/2 AC dimers, each possessing 6 AC hydrogen bonds. Therefore, an oligomer possesses 3(n − 1) AA H-bonds while the corresponding AC dimers can have 3n AC H-bonds. Although the former contains three fewer hydrogen bonds, 1–3 interactions can contribute significantly towards its stabilization. As mentioned earlier, the oligomers of BTA-Met and BTA-Phe are further stabilized by CH⋯S and CH⋯π interactions respectively.
Zero Kelvin, gas-phase, optimized structures of BTA-Met and BTA-Phe demonstrate the existence of weak CH⋯S and CH⋯π hydrogen bonds, respectively. However, it remains to be seen if these interactions are maintained in the solution phase at finite temperature, the solvent being cyclohexane. Pre-formed hexamers of BTA-Met and BTA-Phe with R′′ = dodecyl were soaked in explicit cyclohexane solvent and MD simulations were carried out at 298.15 K. Configurations were saved every 2.5 ps for post-processing and visualization. The distance between the core benzene ring and the last carbon of all the three dodecyl tails of the central two molecules of the hexamer was determined. The distribution of the distances for BTA-Met and BTA-Phe are shown in Fig. S4 (ESI†) from which we obtain the cross-sectional radii of BTA-Met and BTA-Phe to be 17.8 Å and 18.0 Å respectively which are quite comparable to the experimental values of 16.0 Å and 16.5 Å respectively.11 All the amide–amide (AA) hydrogen bonds were found to be intact throughout the simulations which implies that the force field parameters adopted here represent the system reasonably well. The distribution of the number of CH⋯S and CH⋯π hydrogen bonds in the BTA-Met and BTA-Phe systems respectively are shown in Fig. 4. In addition, the average 1–3 interactions in a hexamer of BTA-Met and BTA-Phe in solution were −52 kcal mol−1 and −58 kcal mol−1 respectively. The persistence of such interactions (weak hydrogen bonds and 1–3 interactions) at ambient conditions strongly suggests the stabilization of oligomeric structures over their dimeric species.
 | ||
| Fig. 4 Distribution of the number of CH⋯S and CH⋯π weak hydrogen bonds in a hexamer of BTA-Met and BTA-Phe, respectively. Simulations have been performed in cyclohexane solvent at 298.15 K. | ||
3.3 Stability of dimers at finite temperature
Having understood the stability of long oligomers of BTA-Met and BTA-Phe, we revert our attention back to the two types of dimers: AA and AC. We would like to elucidate the relative stability of the two variants of dimers for all the three substituents (Met, Nle, Phe) at finite temperature in explicit cyclohexane solvent. Towards this aim, for each derivative, simulations were performed starting with either the AC or AA dimer configuration soaked in a well-equilibrated cyclohexane solvent for 20 ns. These simulations were carried out at two temperatures 298.15 K and 350 K in the isothermal–isobaric (NPT) ensemble. Trajectories for analysis were 30 ns in duration. The number of AA and AC hydrogen bonds as a function of time in these simulations are plotted in Fig. S5 and S6 (ESI†). The mean values of the number of hydrogen bonds are provided in Table 3.| System | Dimer type | Temperature | |||
|---|---|---|---|---|---|
| 298.15 K | 350 K | ||||
| AA HBs | AC HBs | AA HBs | AC HBs | ||
| BTA-Met | AC | 0.2 ± 0.2 | 5.5 ± 0.4 | 0.6 ± 0.3 | 4.5 ± 0.3 |
| BTA-Nle | AC | 0.1 ± 0.3 | 5.7 ± 0.4 | 0.9 ± 0.2 | 4.5 ± 0.3 |
| BTA-Phe | AC | 0 ± 0 | 5.9 ± 0.0 | 1.1 ± 0.7 | 3.8 ± 0.4 |
| BTA-Met | AA | 2.9 ± 0.1 | 1.6 ± 0.1 | 0.6 ± 0.1 | 4.8 ± 0.3 |
| BTA-Nle | AA | 2.2 ± 0.6 | 2.3 ± 1.1 | 0.9 ± 0.6 | 4.1 ± 0.9 |
| BTA-Phe | AA | 2.3 ± 0.5 | 2.4 ± 0.9 | 1.3 ± 0.7 | 3.2 ± 0.4 |
| BTA-Met | AC* | 0.6 ± 0.3 | 5.1 ± 0.3 | — | — |
| BTA-Nle | AC* | 0.0 ± 0.0 | 4.1 ± 0.1 | — | — |
| BTA-Phe | AC* | 2.0 ± 0.0 | 3.2 ± 0.5 | — | — |
At 298.15 K, the AC dimer is the most stable configuration, while at 350 K, the dimer possesses a mixture of AA and AC H-bonds (total number of H-bonds being six or more). In order to verify if the room temperature results are due to inadequate sampling, configurations obtained from the simulations of the AC dimer at 350 K (possessing a mixture of AA and AC H-bonds) were cooled to 298.15 K over a duration of 2.5 ns. MD simulations initiated from such configurations, were run for 50 ns at 298.15 K (see Fig. S7, ESI†). The number of AC H-bonds are seen to increase, however, the dimer does not completely convert to an AC type (see Fig. S7, ESI† and Table 3) within the time-scales accessible here. This suggests that the AC dimer is the most stable configuration at ambient conditions.
3.4 Free energy simulations
| System | ΔGACAA | ΔG2AA4AA | ΔG2AC4AA |
|---|---|---|---|
| BTA-Met | 8.4 | 17.8 | 1.0 |
| BTA-Nle | 15.4 | 10.7 | −20.1 |
| BTA-Phe | 15.1 | 14.0 | −16.2 |
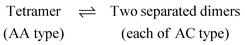 | (1) |
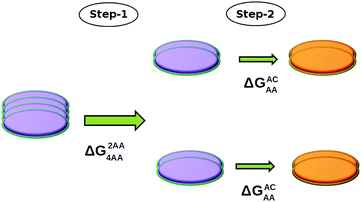
This FE difference (ΔG2AC4AA) between a tetramer (4AA) and its two AC dimers (2AC) can be calculated in two steps, as follows:
(i) Two dimers that belong to a tetramer are pulled apart in such a way that the configurations of the resulting dimers are unaltered i.e., each dimer resembles an AA dimer throughout the pulling process. Let us call the free energy associated with this step as ΔG2AA4AA.
(ii) Each AA dimer is subsequently converted into an AC dimer, and the free energy change (ΔGACAA) associated with this step is the negative of ΔGAAAC which has already been determined (see Fig. 5).
Using the above two steps, the free energy difference between an AA tetramer and two AC dimers (ΔG2AC4AA) can be easily determined as ΔG2AA4AA − 2 × ΔGACAA. A scheme of this procedure is shown in Fig. 6.
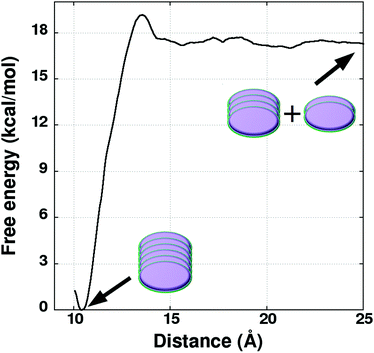
Following the scheme provided in Fig. 6, US simulations have been performed to determine the FE change between a system consisting of two independent dimers (in AA fashion) and a tetramer in cyclohexane solvent at 298.15 K. The distance between the center of mass of the two dimers was employed as a reaction coordinate. US simulations have been carried out over 30 windows for optimum overlap of probability distributions, spanning the RC value from 7.0 Å to 21.5 Å (see Fig. S12, ESI†). The geometry of the two pairs of molecules constituting the tetramer was restrained to a RMSD value of 1.3 Å (with respect to the AA dimer). This value was chosen based on fluctuations in the configurations exhibited by the pairs in the unbiased tetramer simulations (see Fig. S13, ESI†).38 Free energy profiles were obtained using UWHAM.29,30 The profiles are displayed in Fig. 7 and ΔG values determined as the difference between the free energy at the minimum and at 21.5 Å are provided in Table 4. The free energy profiles shown in Fig. 7 exhibit oscillations at a RC value of 10 Å. The dip in free energy at that distance is due to more negative potential energy, caused by a reorientation of the separating dimers (see Fig. S14, ESI†). The dimers were nearly parallel to each other until 7–8 Å but become almost perpendicular at around 10 Å leading to increased interaction between them which causes the dip in the free energy profile.
 | ||
| Fig. 7 Free energy profiles associated with pulling the two dimers apart from a tetramer. Geometry of each dimer is constrained with a RMSD variable. Simulations are carried out at 298.15 K in explicit cyclohexane solvent. The oscillations in the free energy profiles are due to the reorientation of dimers during their separation (see Fig. S14, ESI†). | ||
The free energy difference between a tetramer and two AC dimers (ΔG2AC4AA) was determined for all the three derivatives at 298.15 K. For BTA-Met, the tetramer is more stable than the two AC dimers by 1.0 kcal mol−1. In contrast, the two AC dimers of BTA-Nle are more stable than a tetramer by 20.1 kcal mol−1. The stabilities of either an oligomer (for BTA-Met) or of a dimer (for BTA-Nle) is consistent with experimental observations.11 However, in the case of BTA-Phe, the configuration of two independent AC dimers was found to be more stable than a tetramer (the difference being −16.2 kcal mol−1), while the opposite is found in experiments.11 This can be understood as follows: there exists an additional stability imparted to the oligomers of BTA-Met and BTA-Phe due to CH⋯S and CH⋯π hydrogen bonds, respectively, as well as due to 1–3 interactions. Therefore, the free energy balance between the oligomer and the corresponding AC dimers should shift towards the formation of an oligomer with increase in oligomer size. Hence the free energy difference of 1.0 kcal mol−1 and −16.2 kcal mol−1 for BTA-Met and BTA-Phe, respectively increases (i.e., becomes more positive) with increasing oligomer size-favouring the oligomer formation. In the case of BTA-Phe, the AA tetramer is less stable than the configuration of two independent dimers by 16.2 kcal mol−1. As the CH⋯π interaction is weak, BTA-Phe may require an oligomer much larger than a tetramer for the reversal in stability. Thus, we explored the free energy of its hexamer to understand if the balance tilts towards oligomerization.
Free energy difference between a hexamer and three AC dimers. Umbrella sampling simulations were performed to estimate the free energy difference between a hexamer with AA hydrogen bonding and three AC dimers (ΔG3AC6AA), for BTA-Phe.
 | (2) |
As before, a tetramer and an AA dimer were separated from a hexamer to quantify the free energy difference (ΔG4AA+AA6AA) in the first step. The geometry of a tetramer and of a dimer constituting the hexamer were restrained to a RMSD value of 1.3 Å. The distance between the center of mass of the tetramer and center of mass of the dimer was chosen to be the reaction coordinate. Two styles ‘distanceZ’ and ‘distanceXY’ of the colvars module were used to determine the free profiles. ‘DistanceZ’ style was employed to determine the free energy profile along the reaction coordinate. ‘DistanceXY’ was used to restrain the dimer coaxially along the tetramer. A schematic description of distanceZ and distanceXY is given in Fig. S15 (ESI†). Umbrella sampling simulations were performed in 30 windows spanning from 10.5 Å to 25.0 Å. The overlap of probability distributions along the RC is displayed in Fig. S18 (ESI†). The profile is shown in Fig. 8 with ΔG4AA+AA6AA being 17.3 kcal mol−1. Using a Born-Haber cycle approach, the free energy difference between a hexamer and its three AC dimers can be estimated as shown in Fig. S19 (ESI†) and evaluated as
| ΔG3AC6AA = ΔG4AA+AA6AA + ΔG2AA4AA − 3 × ΔGACAA |
Substituting the values in the above expression, we obtain ΔG3AC6AA to be −14 kcal mol−1. Although the value favours the formation of three AC dimers over a hexamer, the difference in free energy of the oligomer and its AC dimers decreased by just 2 kcal mol−1 (from tetramer to hexamer). This could point to limitations in the force field for this molecule as well which may require further refinement. Furthermore, experiments11 performed at 293 K reveal that the critical concentrations for the formation of long assemblies of BTA-Met and BTA-Phe were 0.28 mM and 0.44 mM respectively. Thus, in the case of BTA-Phe, the formation of an oligomer requires higher concentration compared to that of BTA-Met. Our results on relative free energy differences may not be inconsistent with these experimental observations.
4 Conclusions
In amino ester-based benzene-1,3,5-tricarboxamide, two variants of dimer configurations are possible which are differentiated based on their hydrogen bonding patterns. An AA dimer is one in which hydrogen bonds are formed between amide groups, similar to typical alkyl-derivatized BTA stacks.31 In contrast, an AC dimer is formed via hydrogen bonds between amide and carboxylate groups. The latter is more stable than the AA dimer by ≈20 kcal mol−1 at zero Kelvin, for molecules in the gas phase, with short tails. The face-to-face dimerization of two molecules leads to the formation of an AC dimer, which precludes further elongation to form oligomers. Thus, only pairs of molecules with amide–amide hydrogen bonding can propagate further to an oligomer.Following recent experiments,11 the self-assembly of three derivatives of amino ester BTA (Met, Nle, Phe) have been studied in cyclohexane at finite temperature using atomistic MD simulations. Assemblies of BTA-Met and BTA-Phe are seen to be stabilized by weak CH⋯S and CH⋯π hydrogen bonds, respectively. Also, the structure of a dimer of these molecules at 298.15 K is different from that at 350 K. At higher temperatures, the dimers possess a mixture of AA and AC hydrogen bonding types, whereas at ambient conditions, they consist of only AC H-bonds.
Umbrella sampling simulations have been performed to quantify the free energy difference between these two dimer variants. Additionally, such simulations have also been carried out to estimate the free energy difference between an oligomer and its corresponding stable dimers (AC ones). The present results convincingly show the thermodynamic stability of long oligomers of BTA-Met and BTA-Phe and of only dimers of BTA-Nle. The study uncovers the structural and thermodynamic aspects of amino ester-based BTAs for the three substituents. The approach presented here can guide experimentalists in the choice of substituents to control self-assembled structures. It would be interesting to study both the chiral amplification imparted by amino ester-BTAs to alkyl BTAs as well as the influence of partial fluorination of the tails on chirality through MD simulations. These would constitute our future investigations.
Acknowledgements
KKB thanks CSIR, India for a senior research fellowship. RCR acknowledges an APS-IUSSTF Physics Post-doc Visitation Program award.Notes and references
- I. Danila, F. Riobé, F. Piron, J. Puigmartí-Luis, J. D. Wallis, M. Linares, H. Ågren, D. Beljonne, D. B. Amabilino and N. Avarvari, J. Am. Chem. Soc., 2011, 133, 8344–8353 CrossRef CAS PubMed.
- P. Brocorens, M. Linares, C. Guyard-Duhayon, R. Guillot, B. Andrioletti, D. Suhr, B. Isare, R. Lazzaroni and L. Bouteiller, J. Phys. Chem. B, 2013, 117, 5379–5386 CrossRef CAS PubMed.
- S. Cantekin, T. F. A. de Greef and A. R. A. Palmans, Chem. Soc. Rev., 2012, 41, 6125–6137 RSC.
- S. H. Jung, J. Jeon, H. Kim, J. Jaworski and J. H. Jung, J. Am. Chem. Soc., 2014, 136, 6446–6452 CrossRef CAS PubMed.
- P. J. M. Stals, M. M. J. Smulders, R. Martín-Rapún, A. R. A. Palmans and E. W. Meijer, Chem. – Eur. J., 2009, 15, 2071–2080 CrossRef CAS PubMed.
- T. Metzroth, A. Hoffmann, R. Martin-Rapun, M. M. J. Smulders, K. Pieterse, A. R. A. Palmans, J. A. J. M. Vekemans, E. W. Meijer, H. W. Spiess and J. Gauss, Chem. Sci., 2011, 2, 69–76 RSC.
- K. Hanabusa, C. Koto, M. Kimura, H. Shirai and A. Kakehi, Chem. Lett., 1997, 429–430 CrossRef CAS.
- C. A. Jiménez, J. B. Belmar, L. Ortíz, P. Hidalgo, O. Fabelo, J. Pasán and C. Ruiz-Pérez, Cryst. Growth Des., 2009, 9, 4987–4989 Search PubMed.
- P. J. M. Stals, P. A. Korevaar, M. A. J. Gillissen, T. F. A. de Greef, C. F. C. Fitié, R. P. Sijbesma, A. R. A. Palmans and E. W. Meijer, Angew. Chem., Int. Ed., 2012, 51, 11297–11301 CrossRef CAS PubMed.
- B. Gong, C. Zheng and Y. Yan, J. Chem. Crystallogr., 1999, 29, 649–652 CrossRef CAS.
- A. Desmarchelier, M. Raynal, P. Brocorens, N. Vanthuyne and L. Bouteiller, Chem. Commun., 2015, 51, 7397–7400 RSC.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- J. Gasteiger and M. Marsili, Tetrahedron, 1980, 36, 3219–3228 CrossRef CAS.
- S. J. Keasler, S. M. Charan, C. D. Wick, I. G. Economou and J. I. Siepmann, J. Phys. Chem. B, 2012, 116, 11234–11246 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- C. Kulkarni, S. K. Reddy, S. J. George and S. Balasubramanian, Chem. Phys. Lett., 2011, 515, 226–230 CrossRef CAS.
- S. K. Panigrahi and G. R. Desiraju, Proteins: Struct., Funct., Bioinf., 2007, 67, 128–141 CrossRef CAS PubMed.
- P. Zhou, F. Tian, F. Lv and Z. Shang, Proteins: Struct., Funct., Bioinf., 2009, 76, 151–163 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CrossRef CAS.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- G. Fiorin, M. L. Klein and J. Hénin, Mol. Phys., 2013, 111, 3345–3362 CrossRef CAS.
- G. Torrie and J. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- Z. Tan, E. Gallicchio, M. Lapelosa and R. M. Levy, J. Chem. Phys., 2012, 136, 144102 CrossRef PubMed.
- Z. Tan and E. Gallicchio, UWHAM: unbinned weighted histogram analysis method, 2012 Search PubMed.
- K. K. Bejagam, G. Fiorin, M. L. Klein and S. Balasubramanian, J. Phys. Chem. B, 2014, 118, 5218–5228 CrossRef CAS PubMed.
- M. K. Krepps, S. Parkin and D. A. Atwood, Cryst. Growth Des., 2001, 1, 291–297 CAS.
- L. M. Gregoret, S. D. Rader, R. J. Fletterick and F. E. Cohen, Proteins: Struct., Funct., Bioinf., 1991, 9, 99–107 CrossRef CAS PubMed.
- M. Brandl, M. S. Weiss, A. Jabs, J. Sühnel and R. Hilgenfeld, J. Mol. Biol., 2001, 307, 357–377 CrossRef CAS PubMed.
- M. Harigai, M. Kataoka and Y. Imamoto, J. Am. Chem. Soc., 2006, 128, 10646–10647 CrossRef CAS PubMed.
- M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873–13900 RSC.
- To restrain along the diagonal, high force constant was needed especially at (2.5,2.5).
- We have also carried out simulations with a restraint value of 1.5 Å. There is not much change in the free energy difference for a dimer restrained with either 1.3 Å or 1.5 Å (see Fig. S16 and S17, ESI†).
Footnote |
| † Electronic supplementary information (ESI) available: Additional simulation details are listed. Reference structures used for restraining the oligomer geometry are given. More details on free energy simulations are discussed. See DOI: 10.1039/c6cp06742e |
| This journal is © the Owner Societies 2017 |