New insights into mammalian signaling pathways using microfluidic pulsatile inputs and mathematical modeling

Abstract

Temporally modulated input mimics physiology. This chemical communication strategy filters the biochemical noise through entrainment and phase-locking. Under laboratory conditions, it also expands the observability space for downstream responses. A combined approach involving microfluidic pulsatile stimulation and mathematical modeling has led to deciphering of hidden/unknown temporal motifs in several mammalian signaling pathways and has provided mechanistic insights, including how these motifs combine to form distinct band-pass filters and govern fate regulation under dynamic microenvironment. This approach can be utilized to understand signaling circuit architectures and to gain mechanistic insights for several other signaling systems. Potential applications include synthetic biology and biotechnology, in developing pharmaceutical interventions, and in developing lab-on-chip models.

---

M. Sumit

Madhuresh Sumit recieved his BS from Indian Institute of Science Education and Research (IISER) Pune India, and MS (Chemical Engineering) from the University of Michigan. His research interest lies in understanding cell signaling pathways using combined experimental and mathematical modeling approach. He did his PhD dissertation research jointly in the micro/nano/molecular biotechnology lab and laboratory for quantitative signaling and multi-scale modeling at the University of Michigan, where he worked on information processing under physiological pulsatile stimulation in a G-protein coupled signaling pathway. He is currently a postdoctoral fellow at Pfizer under Pfizer-MIT initiative program.

S. Takayama

Shuichi Takayama's research interests (BS & MS from the University of Tokyo, PhD from the Scripps Research Institute) started with organic synthesis. Subsequently he pursued postdoctoral studies in bioengineered microsystems at Harvard University as a Leukemia and Lymphoma Society Fellow. He is currently Professor at the University of Michigan in the Biomedical Engineering Department and Macromolecular Science and Engineering Program. Research topics include microfluidic models of the body such as the oviduct, lung, gut, and cancer metastasis. He also develops aqueous two phase system micropatterning technologies, studies timing and rhythms of cell signaling, constructs self-switching fluidic circuits, and performs nanofluidic single strand chromatin analysis.

J. J. Linderman

Jennifer Linderman is a professor of chemical engineering and of biomedical engineering at the University of Michigan, a fellow of AIMBE, and Director of the University of Michigan ADVANCE Program. She received her BS degree from the University of Rochester, and her MSE and PhD degrees from the University of Pennsylvania. Her research interests are in systems biology, computational biology, immunology, tuberculosis, cell signaling and cell migration.

---

Insight, innovation, integration

A major challenge in investigating cellular signaling pathways is to develop platforms that can provide quantitative and mechanistic insights. Here, we focus on using pulsatile inputs of ligand delivered via microfluidics. A combined approach of microfluidics and mathematical modeling provides a unique platform that is capable of mimicking the dynamic cellular microenvironment, achieving synchronized responses, making quantitative predictions, and providing mechanistic insights. This approach has recently been applied successfully to several mammalian (as well as non-mammalian) signaling pathways to elucidate signaling circuit architectures and/or gain mechanistic insights into temporal signal processing. We review the advantages of this approach over conventional methods, discuss the new insights gained for several mammalian signaling pathways, and speculate future applications. In particular, an increased understanding of temporal processing of signals might be exploited for biotechnological and pharmaceutical applications.

Introduction

Signaling pathways transmit specific information from a cell's external microenvironment to downstream effectors to bring about physiological or phenotypic changes. Often, the microenvironment presents dynamic inputs and cells must be able to discern these to their advantage. Conventional methods to investigate these pathways, such as exposing cells to step changes in ligand concentration, can fail to provide a systems-level quantitative understanding of signal circuit architecture and its physiological implications under dynamic inputs. Additionally, these signaling pathways are often non-linear and function on wide range of time scales. Therefore, to fully characterize them requires probing at different frequencies. Investigation of cellular networks using pulsatile stimulation and mathematical modeling can provide new insights into signalling pathways.

Broadly speaking, this approach has three advantages. First, pulsatile stimulation may mimic physiology and thus provide relevant insights. Second, pulsatile stimulation synchronizes responses at the single cell level via phase-locking or entrainment, thus reducing noise in the read-out. Third, pulsatile stimulation can provide mechanistic insights into the consequences of temporally varying inputs. These insights can be helpful in dissecting circuit architecture, in discerning temporal encoding and decoding, in understanding fate regulation, and in illuminating emergent behavior. Pulsatile stimulation along with mathematical modeling has been used successfully in dissecting several such temporal mechanisms, providing a new direction for the field. Here, we describe how this approach has been useful in investigating a few of these signaling pathways, and has contributed to deciphering hidden or unknown signaling motifs or delineating mechanisms, focusing on the mammalian signaling pathways. We also discuss its prospects in uncovering hidden or unknown motifs in other signaling systems, and other potential applications in synthetic biology, biotechnology and lab-on-chip model systems.

Dynamic microenvironment expands the observability space

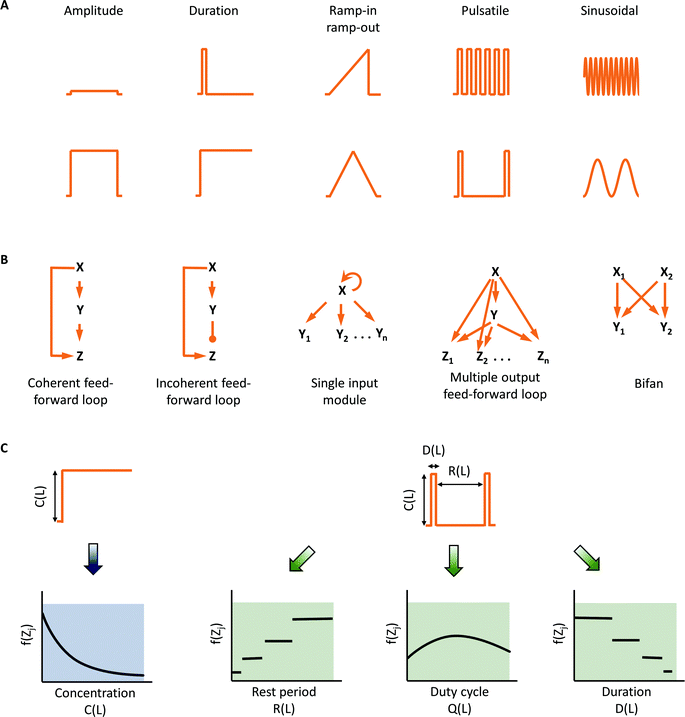
The microenvironment surrounding cells in tissues of a multi-cellular organism can change rapidly due to various metabolic and signalling processes.^1,2 In general, these dynamic patterns include changes in amplitude, duration of stimulation, gradients, or periodicity of input signal (Fig. 1A). We can exploit a cell's ability to discern these dynamics in our experiments, and use information gathered to help understand signaling circuit architecture³ (Fig. 1B). The central hypothesis for such investigation is that cells are able to discern time-varying inputs and have evolved to take advantage of temporal information available in their microenvironment. Cells may utilize these dynamics to make appropriate decisions.

Fig. 1 Dynamic microenvironments expand observability space to facilitate investigation of complex network structures. (A) Dynamic signaling input patterns observed in biological systems including modulation in amplitude, duration, gradient, pulse frequency, and sinusoidal rhythms. (B) Examples of network motifs present in transcription networks that can sense temporal inputs. (C) Temporal modulation expands the observability space by providing additional input–output responses and aids in distinguishing different network motifs.

Understanding complex signaling pathways primarily depends on robust discernment of signaling circuit architecture. This requires comparing and evaluating multiple response features. One could look at every signaling node as a read-out, but this has practical limitations. However, we can think of an “observability space” that comprises non-redundant and informative read-outs in the space-time domain that can be created by temporally varying inputs. In this observability space, rather than evaluating responses at each signaling node, we can alternatively evaluate responses at fewer signaling nodes, but with several temporally varying inputs. Most commonly, responses are measured for step changes in the input only, and therefore, the observability space is quite narrow. To expand the observability space, temporally varying stimulations such as pulsatile stimulation with input parameters of duration of stimulation, rest period between the stimulations and duty cycle ratio can be used (Fig. 1C). The space can be further expanded by introducing distinct temporal patterns such as gradients, ramp-in and ramp-out. Thus, the same read-out can be measured dynamically for several input conditions. This expansion of observability space can play an essential role in weeding out non-conforming circuit architectures,⁴ as well as in gaining mechanistic insights into how temporal information is processed in a particular signaling circuit.

Advantages of microfluidics and pulsatile stimulation

Signaling circuit investigations at the single cell level with pulsed stimulation requires delivery of time-dependent ligand or drug molecule input. Large fluid volumes in macroscale systems prevent rapid changes in concentrations, thus making these systems inaccurate and low throughput. To this end, microfluidic devices have recently been designed and developed that can handle microliter and sub-microliter volumes of fluids, and can precisely mimic and manipulate the cellular microenvironment in both timescales as well as length scales.^5–7 Advantages of microfluidics and pulsatile stimulation can be broadly classified into (but not limited to) the following:

Mimicking physiology

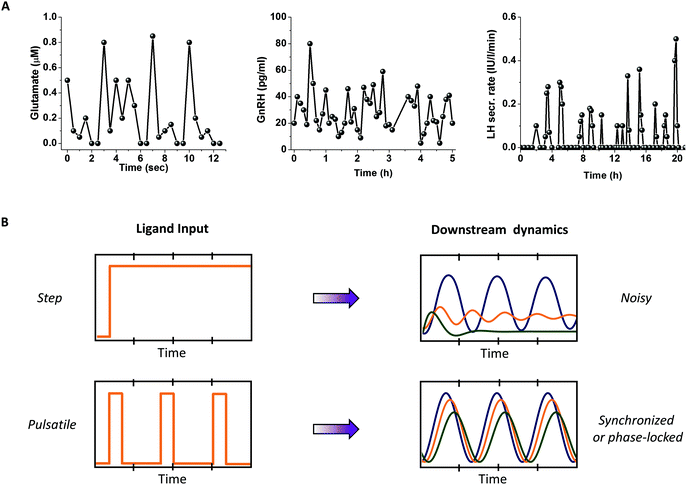
Several physiologically relevant stimuli, including neurotransmitters, metabolic enzymes, hormones, and growth factors, are released in pulsatile bursts (Fig. 2A).^8–12 Time scales for these bursts vary widely from milliseconds to several hours. Consequently, downstream activation of effector molecules may vary significantly for time varying inputs as compared to step changes.^1,13,14 Microfluidics allows the study of cells under controlled fluid flow, in particular, under controlled ligand stimulation.^5,15 Complex time varying patterns of ligands such as pulsatile bursts can be delivered with high temporal resolution using microfluidic devices, thus mimicking the dynamic physiological microenvironment in a controlled fashion.

Fig. 2 Advantages of pulsatile stimulation over conventional methods. (A) Mimics physiology: pulsatile stimulation can mimic several time-varying ligand secretions that are physiologically more relevant, such as glutamate, Gonadotropin releasing hormone (GnRH) and Luteinizing Hormone (LH) are all known to be secreted in pulsatile fashion. Data adapted from several sources referenced at appropriate place in the text. (B) Synchronizes response through phase-locking/entrainment: pulsatile stimulation results in phase-locking or entrainment in several non-linear systems thus filters out the temporal variations because of biochemical noise or cell-to-cell variability.

Controlled and synchronized responses

In vitro cultures show significant cell-to-cell variability.^16–18 Under step stimulation of a signaling pathway, cells tend to vary widely in their responses.^19–21 While some cells exhibit oscillatory responses, others may exhibit peak-and-plateau, single spike or no response. Biochemical noise, also known as cell-to-cell variability or extrinsic noise, is believed to contribute to this wide range of responses, making it difficult to interpret signal pathway dynamics. However, under external periodic stimulation, signaling systems may exhibit synchronized or phase locked responses⁴ that are easier to interpret and quantify (Fig. 2B).

Gaining mechanistic insights

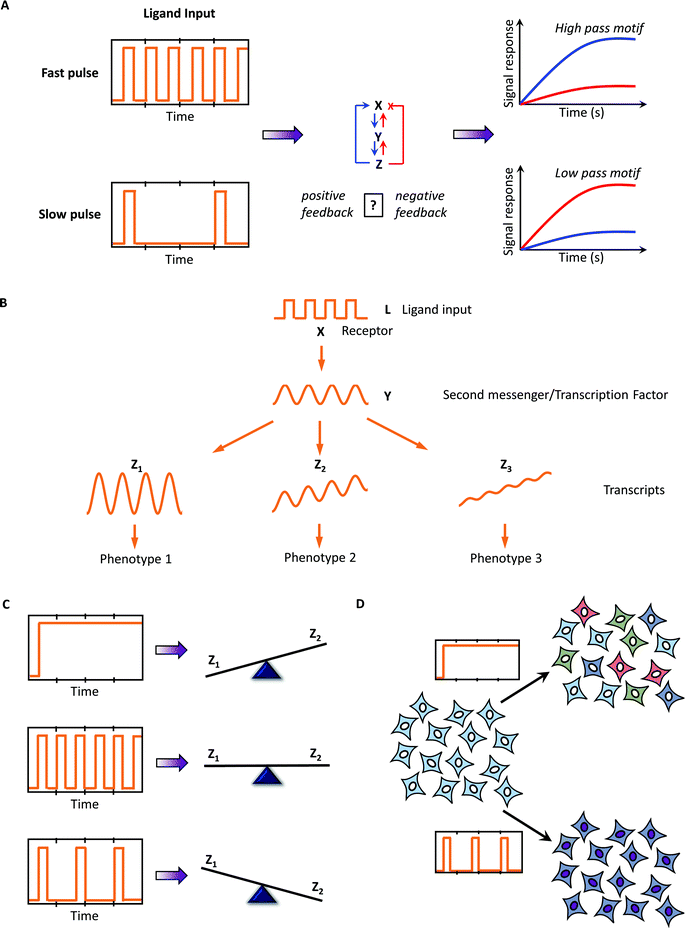
Pulsatile microfluidics also provides several mechanistic insights about the signaling system, including:

Dissecting circuit architectures. Signaling circuits often have their own time scales of responding to a stimulus that depends on the circuit architecture of the motifs that constitute the pathway. Variation in stimulation parameters such as duration of stimulation or rest period between the stimulations may reveal whether a particular pathway prefers rapid (high pass) or slow (low pass) stimulation to elicit optimum response (Fig. 3A). A retrospective approach using such frequency response analysis provides insights into the constituent motifs that may be present in the signaling pathway.

Fig. 3 Mechanistic insights provided by pulsatile stimulation and mathematical modeling. (A) Several circuit architectures can be dissected through frequency response analysis; (B) temporal encoding/decoding of the downstream response can be uniquely discerned using this approach. (C) Pulsatile stimulation may also lead to distinct downstream responses, thus regulating different fates through the same input. (D) Using microfluidics to study behavior of entrained/phase-locked cells also provides a platform to study collective population behavior often observed physiologically.

Discerning temporal encoding and decoding. Ligand stimulation often leads to signaling via second messengers. These second messengers often encode temporal information that leads to distinct downstream responses depending on how signals from the second messengers are integrated downstream. Thus, the same oscillation in a second messenger or a transcription factor may result in complete integration, or partial integration or even no integration downstream, which may result in three distinct phenotypic responses (Fig. 3B). Pulsatile stimulation provides a platform to quantify how a particular pulsed signal is processed downstream, and thus provides mechanistic insights into the temporal encoding and decoding of a particular signaling pathway.

Fate regulation. Several studies have shown that transcription factor activation and gene transcription vary significantly between step changes and pulsatile stimulation.^1,13,14,22 The dynamics of activation and deactivation of transcription factors, or nuclear translocation and back-translocation, may determine whether a continuous or a pulsatile stimulation leads to higher activity. Consequently, for two distinct transcription factors (say Z1 and Z2), the amount of activation may differ for different temporal inputs. This may lead to several combinations of gene activation, consequently determining the fate of the physiological/phenotypic response (Fig. 3C) and underscoring the importance of understanding how dynamic stimulation of cells may control physiological responses and cell fate.

Emergent population behaviour. Pulsatile microfluidics can also be used as a tool for externally phase locking or synchronizing a cell population to study emergent population behaviour in vitro (Fig. 3D). Several physiological phenomena, such as hormonal secretion and heart contractions, are rhythmic or oscillatory at the tissue/organ scale. Such rhythmic activities indicate synchronization of millions of cells.^23,24 Microfluidics allows mimicking these tissue scale conditions in an in vitro system. These features have also been explored to develop organ-on-chip and human-on-chip systems.^25–27

Mathematical modeling of signaling pathways

Mathematical and computational modeling has been used extensively to describe and make predictions for dynamical systems in biology, including predator–prey dynamics,^28,29 microbial growth,³⁰ embryonic morphogenesis,³¹ cell cycle dynamics³² and cell signaling pathways.^33,34 Investigation of biochemical pathways is aided by quantitative model predictions that can be tested experimentally, with insights feeding back to improve the models. These models can be deterministic, e.g. described by ordinary or partial differential equations (ODEs and PDEs, respectively), or stochastic, e.g. described by dynamic Monte Carlo methods. Combinations of deterministic and stochastic modeling are also used,³⁵ as well as newer approaches such as Bayesian networks. Appropriate selection of a modeling approach depends on the information available and questions of interest. For modeling signaling pathways, the availability of experimentally determined kinetic parameters and the capability of getting time-dependent or space-dependent read-outs are important, especially when developing a detailed ODE or PDE model of a signaling pathway. Signaling events that involve discrete and random waiting times (such as binding of a transcription factor to a gene sequence or low copy numbers of signaling molecules interacting with each other), or processes where the continuum assumption is not valid, are best described by stochastic processes. Because parameter values in models are seldom known with certainty, uncertainty and sensitivity analyses are an important aspect of mathematical and computational modeling.^36–38 Techniques to efficiently sample the parameter space and to determine the correlation of the signaling response with each of the parameter varied are helpful.^39,40

With the advent of time-lapse microscopy with high spatio-temporal resolution, it has been possible to measure time traces of signaling components at the single cell scale. However, as discussed earlier, in vitro cultures are prone to cell-to-cell variability. Thus, the single cell traces obtained experimentally are often noisy and it is difficult to interpret the signaling dynamics. For this reason, mathematical and computational models at the single cell scale may also incorporate cell-to-cell variability (commonly termed “extrinsic noise”) by choosing initial values of the signaling components from a statistical distribution.⁴¹ To interpret single cell data, information theoretic analysis has recently been utilized to estimate the noise and information components in the signal.^19,20 Next, we show how the combined approach of pulsatile stimulation and mathematical analysis have led to critical insights for signalling pathways.

Examples of signaling pathways investigated

Investigation of cellular signaling pathways with dynamic inputs using microfluidics is a research area that has grown significantly in the recent years. Several mammalian^{1,4,13,14,21,23,24,35,42–46} as well as non-mammalian systems including bacteria,^47–49 amoeba,⁵⁰ yeast,^51,52 and nematodes^22,53 have been investigated. Here we discuss in detail a few recent examples from mammalian signaling pathways, but also mention briefly examples from non-mammalian systems.

GPCR signaling

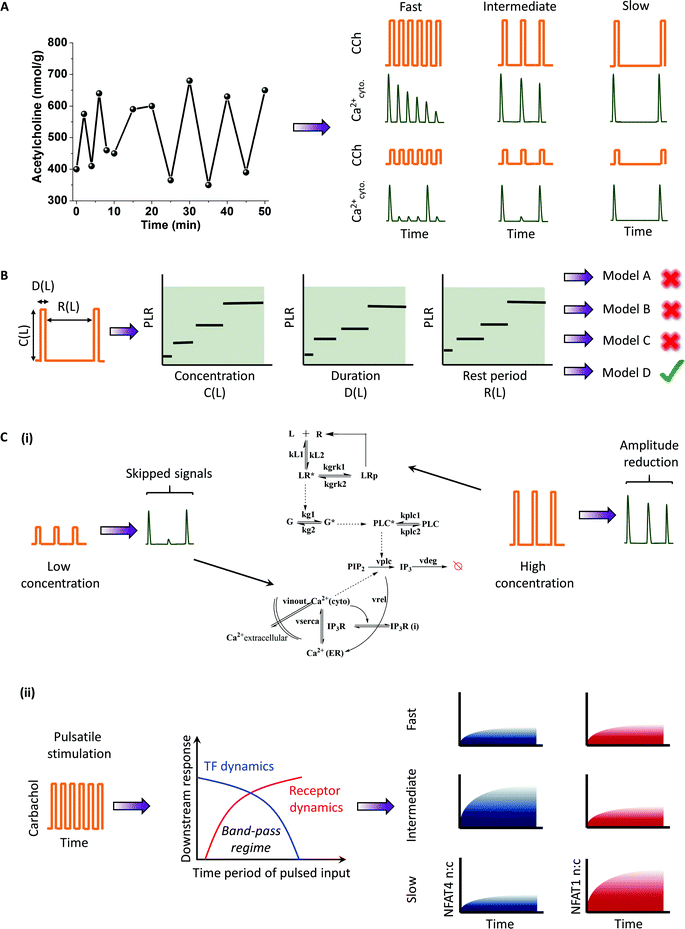
G-Protein Coupled Receptors (GPCR) primarily signal through G-protein coupling, resulting in various downstream signaling events through second messengers such as cytoplasmic calcium and ATP. These second messengers have oscillatory dynamics because of positive and negative feedback.^9,54 The receptor itself may undergo dynamic uncoupling leading to oscillatory dynamics of G-protein activation.⁵⁵ The oscillatory calcium response is widely studied to understand the temporal encoding of calcium-induced transcription factors.^56–59 Several GPCR ligands are released in pulsatile bursts under physiological conditions, including glutamate⁸ (millisecond to a few second scale) and GnRH¹² (Gonadotropin releasing hormone) (a few hours) (Fig. 2A). One such example is a neurotransmitter, acetylcholine, an agonist for the cholinergic muscarinic M3 receptor. Acetylcholine has been observed to be released in pulsatile fashion¹⁰ (Fig. 4A). To understand its physiological relevance and to elucidate signaling circuit architecture, we used pulsatile stimulation of HEK 293 cells stably expressing M3 receptor with carbachol (CCh), a chemical analog of acetylcholine.^4,42 Upon pulsed CCh stimulations, cells exhibit responses phase-locked with the input pulse (Fig. 4A).

Fig. 4 Application of pulsatile stimulation and mathematical modeling in GPCR-calcium signaling. (A) Mimics physiology: acetylcholine, the natural agonist of muscarinic M3 receptor (a GPCR), is a neurotransmitter that is released in pulsatile manner. Carbachol, a chemical analog of acetylcholine, is delivered in a similar frequency regime to elicit downstream calcium responses. (B) Phase-locked calcium signal downstream of ligand-induced GPCR signaling expands the number of observables. The expanded space is utilized to identify appropriate signaling motifs that could best explain the experimental results. (C) (i) Pulsed stimulation can also be utilized to identify pathway recovery properties. (ii) The circuit architecture of GPCR-signaling thus identified predicts a band-pass filter for the temporal ligand inputs. Pulsatile stimulation can select for two different NFAT isoforms depending on their band-pass regime.

We define the phase locking ratio (PLR), a measure of response fidelity, as the ratio of number of calcium responses (above a threshold value) to the number of input ligand pulse. We showed that the PLR changes with the stimulation parameters concentration (C), duration (D) and rest period (R). The phase-locking analysis provided an expanded observability space to compare several models and examine the differences in activation and recovery properties between the models, not possible with conventional methods. Utilizing these results, we compared several existing models with distinct signaling motifs (positive and negative feedbacks) to discover the circuit architecture that best explained the experimental data (Fig. 4B). The analysis also revealed the importance of basal levels of Phospholipase C (PLC) in generating subthreshold peaks. Pulsatile stimulation was also utilized to understand the pathway recovery properties in multiple concentration regimes.⁴³ In particular, we found that the reduction in phase-locking at low values of C and D and the reduction in signal amplitude at high values of C and D for a fixed R can identify the recovery properties of cytoplasmic calcium and receptor phosphorylation respectively (Fig. 4C(i)). Pathway recovery properties were utilized to improve the GPCR-calcium model by incorporating a receptor phosphorylation module (a regulatory motif).

To gain mechanistic insights into the downstream signal regulation, we utilized pulsatile stimulation of HEK293 cells stably expressing M3 receptors to generate synchronized calcium oscillations of varying frequencies (fast (R = 24 s), intermediate (R = 72 s) and slow (R = 144 s)).¹³ Using two downstream readouts – cytoplasmic calcium and calcium induced NFAT (nuclear factor of activated T-Lymphocytes) nuclear translocation, we investigated the response dynamics under frequency and amplitude-modulated signals (Fig. 4C(ii)). Although the rapid oscillation of cytoplasmic calcium induced artificially using patch-clamp has been shown to maximize the downstream transcription factor activation,^22,56,59 under a more physiological condition, fast pulsing led to rapid desensitization of the receptors, thus preventing a sustained calcium oscillation, and in turn was unable to maximize the NFAT translocation. A slow stimulation did resolve the issue with receptor desensitization but was unable to provide sufficient calcium flux for retaining activated NFAT4 in the nucleus. Consequently, an intermediate frequency window for receptor stimulation optimized the NFAT4 translocation, analogous to the engineering concept of band-pass processing of signals (Fig. 4C). Band-pass processing in this GPCR system is a combined effect of low-pass filtering by the receptor, and high-pass filtering by the calcium induced NFAT motif and these parameters determine the band-pass window. To further validate this, we measured the band-pass window for another isoform of NFAT (NFAT1), known to have a relatively slower kinetics,⁶⁰ and showed that the band-pass regime shifts to slower stimulation frequencies (Fig. 4C(ii)). Our analysis suggests that pulsatile stimulations may encode for different timings optimized for the activation of distinct downstream signals such as transcription factor activation.

NFκB signaling

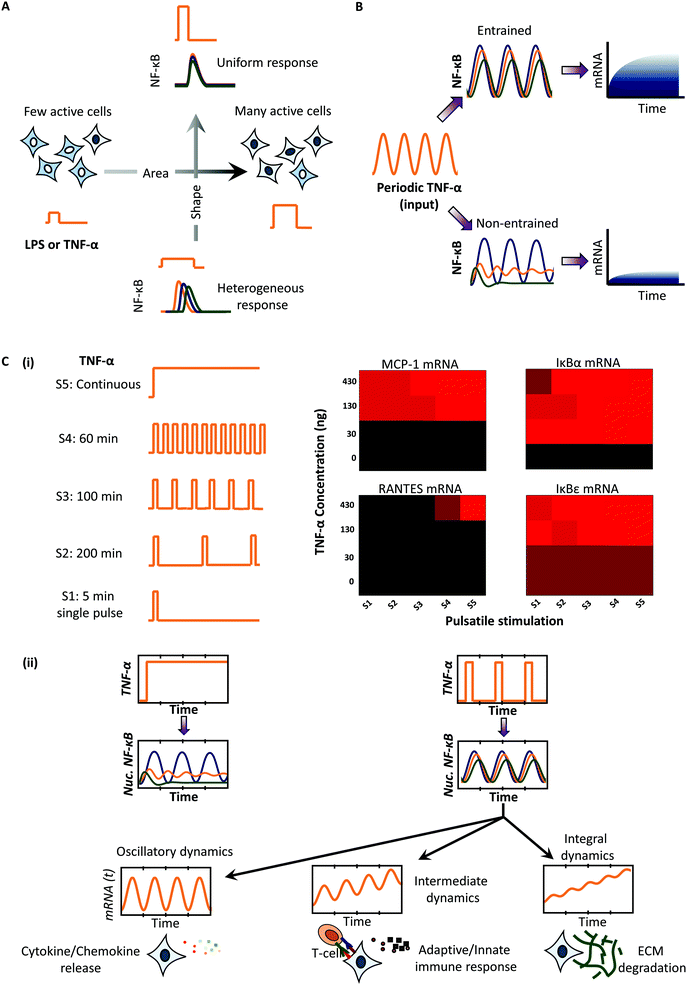
In mammalian systems, NFκB (nuclear factor κB) signaling is by far the pathway most studied using microfluidics and mathematical modeling. The intrinsic oscillatory dynamics of the pathway are on the time scale of minutes to hours and can be conveniently investigated for frequency modulated signaling.^{21,35,44–46} Tumor Necrosis Factor-α (TNF-α) is an inflammatory signal that activates NFκB and induces its nuclear translocation via phosphorylation of the upstream IKKs kinases.⁶¹ TNF-α is secreted in pulsatile bursts by cells neighbouring to the T-cells, thus making the study using pulsatile microfluidics physiologically relevant.⁴⁶ Kellogg et al. showed that pulsatile stimulation provides an opportunity to control the activation probability and heterogeneity of response at the single cell level.⁴⁴ Using pulses with varying concentration (C) and duration (D), they showed that the shape of stimulation keeping C*D constant determines the heterogeneity of the response, whereas the area of the stimulation (C*D) determines the fraction of cells actively responding to the stimulation (Fig. 5A). Thus, using an appropriate concentration and duration of stimulation, cells may be synchronized for NF-κB responses despite existing heterogeneity in the system. The heterogeneity may result from cell-to-cell variability (extrinsic noise) and inherent stochasticity associated with biochemical reactions that is present in the time series of single cells (intrinsic noise). The effects of noise were investigated in LPS-induced NF-κB signaling to show that noise contributes to the broadening of the entrainment window for saw-tooth waveforms of pulsatile stimulation.⁴⁵ They further showed that entrained cells produce significantly higher transcripts as compared to non-entrained cells (Fig. 5B).

Fig. 5 Application of pulsatile stimulation and mathematical modeling in NFκB signaling. (A) Short pulses of TNF-alpha mimic physiological TNF-alpha release bursts. These pulsed input are controlled for area and shape to determine the fraction of actively responding cells and heterogeneity of the downstream NFκB response. (B) Pulsatile input phase-locks/synchronizes the NFκB response. Entrainment facilitated by cell-to-cell variability and stochastic noise results in enhanced amount of mRNA production. (C) (i) Stimulation with various TNF-alpha temporal patterns show differential sensitivities of mRNA transcripts. (ii) Genome-wide transcriptome analysis of entrained cells shows that the signals downstream of NFκB may integrate the upstream signals in three distinct ways depending on the rate constants for mRNA degradation, thus brining distinct fate regulations.

Pulsatile stimulation of NF-κB pathway has also been utilized to gain mechanistic insights about the pathway. Ashall et al.⁴⁶ utilized pulsatile stimulation of TNF-α to show that a minimum ‘reset time’ is needed for complete recovery of NFκB amplitude peak. They found that the dampening is contributed not only by the negative feedback from NFκB-induced IκB expression, but also from A20 expression that inhibits the activation of an intermediate kinase, IKK-α. Thus, they utilized pulsing to figure out a hidden regulatory motif that was unknown prior to their investigation. Cells utilize pulsatile stimulation to determine the timing and specificity of NFκB dependent transcription. In particular, they showed that the four NFκB dependent transcripts viz. RANTES, IκBε, IκBα and MCP-1 are expressed in distinct fashion for the various TNF-α pulsatile stimulation patterns (Fig. 5C(i)). These results suggest selective high pass filtering of downstream signal activation, similar to calcium-NFAT signaling in the absence of receptor regulatory kinetics.¹³ Thus, oscillatory signals are integrated at different paces downstream, resulting in distinct sets of transcriptional activation and fate regulation.

Recently, Zambrano et al.²¹ utilized pulsatile stimulation of GFP-p65 knock-in MEF cell populations with TNF-α to obtain synchronous NFκB dynamics for studying genome-wide transcriptional output. They showed that TNF-α induced NFκB signaling behaves like a damped oscillator, with no memory/entrainment, and simply follows the input signal dynamics. These conclusions are in contrast with what was observed earlier⁴⁵ and suggest that the observed entrainment may be a signaling circuit effect. The genome-wide analysis of transcripts revealed that transcriptional dynamics downstream of NFκB dynamics results into three distinct ways of signal integration depending on the rate of mRNA degradation (Fig. 5C(ii)). These results along with those from Ashall et al.⁴⁶ support our speculation that downstream signaling processes in several other signaling pathways follow distinct high-pass filters depending upon different rates of signal integration.

Taken together, pulsatile microfluidics and mathematical modeling of NFκB signaling revealed hidden negative feedback mechanisms, factors that are essential in getting synchronised and entrained response, as well as elucidated the downstream implications of temporally varying signals. Importantly, conventional stimulation, using step changes in the ligand concentration, would not have allowed these findings.

ERK signaling

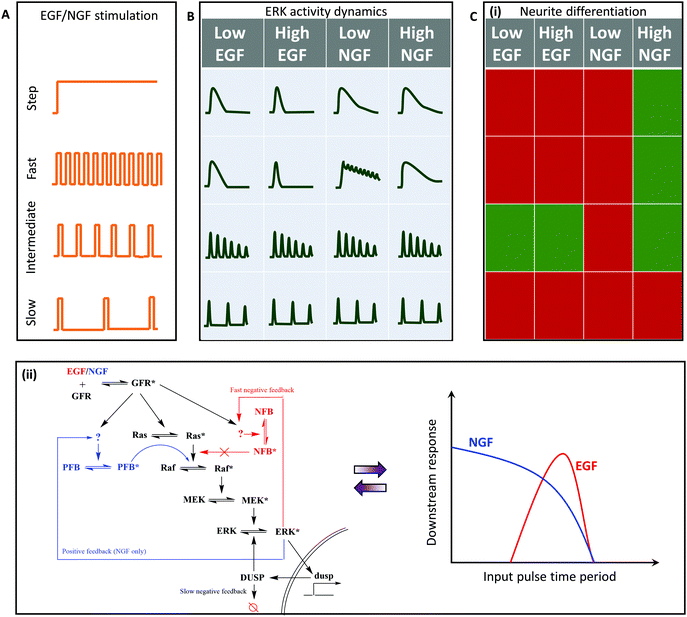
Extracellular-regulated kinase (ERK) signaling plays an important role in cell fate regulation, including differentiation and cell proliferation. Stimulation by growth factors (GFs) like EGF (epidermal) and NGF (nerve) leads to the activation of GF receptors that activate a Ras-GTPase. This triggers the MAP kinase cascade that results in ERK activation.^62,63 The ligands EGF and NGF are known to have distinct ERK activation dynamics that lead to proliferation and differentiation, respectively.^62,63 Similar to NF-κB and GPCR-calcium signaling, continuous stimulation of GFs leads to heterogeneous downstream ERK activation, thus complicating our understanding of the circuit architecture that differentiates the two input ligands. Although details about the dynamics of release of these growth factors are yet unknown, Ryu et al.¹⁴ utilized pulsatile stimulation to investigate this pathway in PC-12 cells for neurite growth (differentiation) (Fig. 6A). Pulsed inputs generated synchronized homogenous ERK signaling. However, the phase locked responses differed for fast GF stimulation in case of EGF and NGF, suggesting that the two may have different kinetics and mechanisms of regulating the signal despite acting on the same signaling pathway (Fig. 6B).

Fig. 6 Application of pulsatile stimulation and mathematical modeling in ERK signaling. (A) Temporal variations in growth factor (GF) release remains unexplored, but it can still be utilized to study GF-induced ERK signaling and neurite differentiation. (B) Step stimulation leads to peak-and-plateau type ERK response. Fast pulsatile stimulation is capable of discerning differences in the ERK activation elicited by the two GFs, viz. epidermal (EGF) and nerve (NGF) growth factors. (C) (i) Temporally modulated growth factor stimulations, EGF and NGF, lead to distinct fates of neurite differentiation based on temporal regimes. Red represents no significant differentiation, while green represents the cells differentiated significantly. (ii) Experimental and mathematical analysis suggests existence of two distinct regulatory pathways for EGF (red) and NGF (blue). GF mediated differentiation can be interpreted as two different band-pass regimes for EGF (red) and NGF (blue).

Pulsatile stimulation of the ERK signaling pathways also provided several mechanistic insights. Sustained EGF stimulation led to an undifferentiated state while sustained NGF stimulation led to a differentiated state. Pulsatile stimulation of high concentration NGF also led to a differentiated state, except for slow stimulations (D = 3 min, R = 60 min) (Fig. 6C(i)). Since low NGF concentrations did not induce differentiation, they inferred that high NGF concentrations are required to trigger the pathways involved in differentiation other than ERK activation. Both low and high concentrations of EGF under intermediate pulsing (D = 3 min, R = 10 min–20 min) led to significant neurite growth and differentiation, similar to our results on NFAT activation,¹³ suggesting the existence of band-pass processing. In summary, this study revealed how MAPK network structures differ for the two input ligands to provide an explanation for the differential cell fates induced by the two GFs and how EGF can be used for differentiation under pulsatile conditions.

The results from Ryu et al. also suggest that the two GFs generate different band-pass windows for the ERK signaling and subsequent differentiation pathway, consistent with our earlier findings in GPCR-calcium-NFAT signaling.¹³ While the EGF acts in a narrow intermediate regime window (R = 10 min–20 min), NGF acts in a much wider window, almost as a high pass filter, suggesting that EGF signaling comprises of additional low pass filter along with the downstream high pass amplification (Fig. 6C(ii)). This is consistent with the findings of Ryu et al., which suggests that EGF induces a fast negative feedback through the channels yet unknown. Additionally, the high pass filtering properties of NGF that works only with high dosage can be attributed to a positive feedback speculated to be present in the NGF signaling network, but not in the EGF signaling network. Gaining these valuable insights to determine the precise molecular circuitry was possible only because of using pulsed signals that bypassed cellular heterogeneity to probe specific network properties.

TGF-β signaling

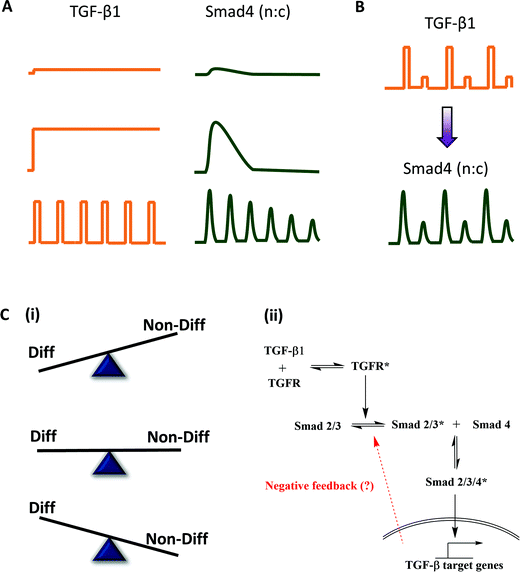
Transforming growth factor β (TGF-β) is a well-known mammalian morphogen that conveys positional information and determines cell fate during embryonic development.⁶⁴ TGF-β mediated signaling involves phosphorylation of a receptor-activated Smad (R-Smad) upon its binding to the TGF-β receptor. The phosphorylated R-Smad undergoes nuclear translocation, acts as a transcription factor and brings about transcriptional changes. These morphogen levels are not static and may present a dynamic (oscillatory or pulsatile) micro-environment to the developing embryo,^65,66 thus suggesting physiological relevance of investigating the pathway with pulsatile inputs. To understand the implication of temporal encoding of such dynamic morphogenic signals in embryonic patterning, Sorre et al.¹ probed C2C12 cells using GFP-Smad4 fusion protein in a microfluidic cell culture device and live cell imaging. TGF-β stimulation leads to nuclear translocation of Smad4-GFP under various temporal inputs (Fig. 7A). Results from synchronized phase locked response with alternate high and low TGF-β stimulation suggests that Smad4 activation has no memory of stimulation (Fig. 7B), similar to the observations of Zambrano et al.²¹ for NFκB signaling.

Fig. 7 Application of pulsatile stimulation and mathematical modeling in TGF-β signaling. (A) TGF-β signaling in embryonic development has been observed to be dynamic rather than static. Pulsed stimulations result in damped oscillations while step stimulation only gives a peak and plateau response. (B and C) TGF-β signaling leads to nuclear translocation of Smad4, but exact pathway mechanisms are still debated. (B) Temporally varying inputs show no memory of stimulation and adapts to the external pulsing. (C) (i) Pulsatile stimulation is more efficient is preventing differentiation of myocytes as compared to step changes in ligand concentration. (ii) Dampening of Smad4 oscillations upon rapid TGF stimulation and existence of refractory period for signal recovery suggests existence of negative feedback that guides an adaptive mechanism of embryonic development.

Pulsatile TGF-β stimulation also provided several mechanistic insights about the pathway and about embryonic development pattern formation. While step changes in TGF-β concentration led to partial prevention of differentiation of myoblasts to form myotubes, pulsatile TGF-β stimulation was more potent in preventing differentiation (Fig. 7C(i)). They also determined that there is a minimum reset time for Smad4 amplitude recovery during pulsatile stimulation, similar to the observation of Ashall et al.⁴⁶ in the NFκB signaling, and Jovic et al.⁴³ in the GPCR signaling. This suggested that there must exist a negative feedback motif (they called it ‘adaptive mechanism’), which was yet unknown (Fig. 7C(ii)). A detailed mathematical model analysis revealed that the adaptive mechanism leads to a more robust pattern formation in the embryonic development, as compared to the linear model without any negative feedback. The existence of negative feedback and lowering of Smad4 amplitude upon rapid stimulation also suggests that the system works in a band-pass manner similar to GPCR-mediated NFAT translocation¹³ and EGF mediated differentiation.¹⁴ Thus, a possible implication of band-pass filtering in signaling is to weed out the high-pass noise during embryonic development while utilizing the negative feedback for robust pattern formation under dynamic microenvironments.

Insulin (RTK) signaling

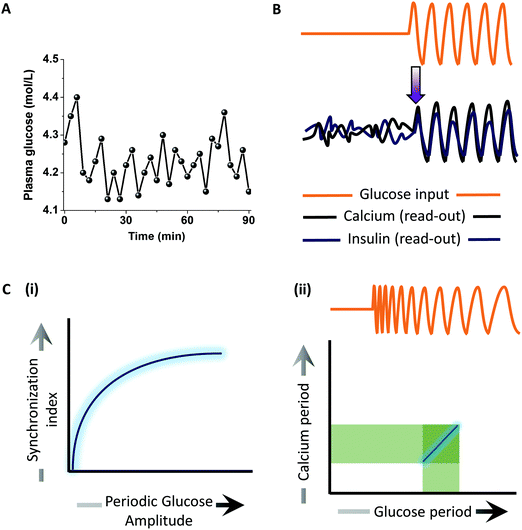
Understanding synchronized cell behaviour at the tissue scale is fundamental to physiology. One such example is insulin secretion from the islets of Langerhans that are mainly composed of pancreatic β-cells. It has been known that the glucose levels in blood plasma oscillate over time⁶⁷ (Fig. 8A). Upon elevated glucose levels, the rate of glycolysis and consequently the ATP concentration increases in the β-cells, thus blocking potassium channels and opening up calcium channels. Positive feedback from calcium (calcium induced calcium release) raises its level and leads to the secretion of insulin granules via exocytosis. Not only is sugar metabolism oscillatory, but so is insulin secretion, both having a period of ∼5 min. How these islets synchronize to generate oscillations in the insulin secretion has remained largely unknown. Dhumpa et al.²⁴ used a microfluidic device to investigate how step and oscillatory glucose input synchronizes the insulin secretion. They showed that under step elevation of the glucose level, the calcium and insulin read-outs in the islet remained uncorrelated with no entrainment. In contrast, oscillatory glucose input led to oscillations in the calcium as well as insulin secretion in an entrained fashion (Fig. 8B). The synchronization index increased with increasing periodic glucose amplitude (Fig. 8C(i)). Mathematical modeling of the system revealed that an insulin-dependent negative feedback action of the liver on glucose level leads to synchronized oscillations in the islets. In a more recent work,²³ they determined the synchronization window by using a chirped waveform of glucose stimulation to find that the strongest resonance between the glucose input and calcium oscillations was within 2 min of the natural period of oscillation (∼5 min) (Fig. 8C(ii)). These studies reveal how feedback mechanisms may induce synchronized oscillations at the tissue scale to give rise to emergent behaviours.

Fig. 8 Application of pulsatile stimulation and mathematical modeling in insulin signaling. (A) Plasma glucose levels have been observed to have oscillatory dynamics. (B) Calcium and insulin secretion show entrainment to synchronize at the tissue scale upon periodic glucose stimulation, providing insights into a possible negative feedback in glucose–insulin metabolism. (C) (i) Extent of synchronization increases with increase in periodic glucose amplitude. (ii) The entrainment window for calcium oscillation upon periodic glucose exposure is confined ∼2 min from the natural oscillation frequency found physiologically.

Examples from non-mammalian systems

Several non-mammalian systems have also been investigated through temporal modulation of input signals using microfluidics and mathematical modeling to elucidate specific signaling features. One of the pioneering works in the field was the investigation of osmoregulation in Saccharomyces cerevisiae using periodic stimulation of NaCl.⁶⁸ This work illustrated using pulsatile stimulation to dissect circuit architectures such as negative feedback. A synthetic oscillatory network inducible with arabinose has been studied in the bacterial system using oscillatory arabinose input to quantitatively understand the entrainment of biological clocks.⁴⁹ These bacterial oscillators displayed a wide range of tunable frequencies and higher-order resonance. Computational simulation of this system indicated that the entrainment robustness of biological clocks may be attributed to the presence of a positive-feedback loop. Thus, a hidden or unknown motif could be unravelled by simply interrogating the system with pulsatile inputs.

In another work, a social amoeba, Dictyostelium discoideim, was studied to understand its coordinated and synchronized cAMP oscillations at population scale under starving conditions.⁵⁰ Using pulsatile microfluidic stimulations and mathematical modelling, they showed that the intracellular noise (stochastic heterogeneity) is the key driver of the population level behavior and that the biochemical noise (cell-to-cell variability) alone was unable to reproduce the results.

Hao et al.⁵¹ studied how transcription factors (TFs) process dynamic input to generate diverse range of dynamic responses. Using yeast (Saccharomyces cerevisiae) as their model system, they showed that the stress-responsive TF Msn2 is able to distinguish various dynamic stress inputs based on upstream kinetics and may process it differently as a tracker, as a filter or as a signal integrator. In a more recent work, another group showed that the oscillatory stress stimulation in yeast cells results in an intermediate frequency regime for which the growth is slowed down significantly.⁵² These observations strengthen our argument that band-pass processing of temporal information must be existing in a wide variety of signaling pathways. While they attribute this regime to be non-natural and interpret this as a hidden sensitivity of cellular regulatory networks, the regime ∼8 min period for which the MAPK activation is maximized may have some physiological relevance that is yet unknown.

Another model system studied widely with microfluidics is a nematode (Caenorhabditis elegans). Tomida et al.²² measured calcium and MAPK activity in sensory neurons of C. elegans under pulsatile stimulation of changes in NaCl concentration. The study showed that the stimulation parameters (C, D and R) determine the extent of MAPK-1 activation in a non-linear fashion attributed to the calcium dynamics which showed dampening at rapid stimulations. Although not proven mathematically, we speculate that these results are similar to the concept of band-pass filter¹³ (Fig. 4C).

Insights and perspectives

Investigation of cellular signaling dynamics using microfluidics and mathematical/computational modeling allows unique advantages in dissecting signaling circuitry by utilizing a wide observability space while bypassing response heterogeneity.

Multi-tasking through temporal compartmentalization

Components of signal transduction pathways are often involved in multiple signalling pathways, and can perhaps be thought to “multi-task”. One of the best examples is the second messenger calcium. It is essential to understand how these components elicit some downstream signals but not others. One way these signalling components evolved for multi-tasking is through the compartmentalization of space, and spatial compartmentalization to facilitate complex tasks such as photosynthesis and aerobic respiration have been well-studied. Compartmentalization within the temporal regime is less understood. In the examples discussed in previous section, we found that cells prefer timings that are “just right” – not too fast, not too slow. Analogous to compartmentalization of space, we may conceptualize time to be compartmentalized as well. In different ‘temporal compartments’ the same signalling molecule may be involved in different tasks. Recent findings about optimum frequency regimes wherein a signaling molecule may be able to activate two distinct downstream responses in two different ‘temporal compartments’ support this hypothesis.¹³

Selectivity amidst heterogeneity

A fundamental problem in biology is to understand how selectivity is achieved in a cell population. In case of spatial selectivity (such as cell fate determination during embryonic development), several experimental and mathematical insights are available.⁶⁹ However, mechanisms for temporal selectivity, wherein timing alone may be able to segregate responsive and non-responsive cells, remains largely unknown. Pulsatile stimulations can be utilized to test if a sub-population of cells select a particular response that is distinct from the others. Modeling biochemical variability along with pulsed stimulation may lead to additional insights into how cellular sub-populations can be selectively activated or deactivated.

Modular signaling through combinatorics

An important inference from the pulsing of signaling pathways is band-pass processing, wherein the optimum frequency regimes differ for different upstream and downstream motifs. With advancements in synthetic biology, in the near future it will be possible to generate cell lines with various combinations of upstream and downstream modules that have unique band-pass regimes. One such example existing in nature is the metabotropic glutamate receptors. Two of the metabotropic glutamate receptors, mGlu1 and mGlu5, have been shown to have distinct functional roles.^70–75 While the mechanism through which they signal appears the same, they do possess distinct receptor regulation kinetics.⁷¹ Upon stimulation, mGlu1 receptor desensitizes rapidly and recovers slowly, leading to single peak-and-plateau type calcium response. In contrast, mGlu5 receptor is phosphorylated and dephosphorylated rapidly (known as “dynamic uncoupling”),⁵⁵ resulting in robust calcium oscillations. Thus, these two receptor subtypes may have different band-pass regimes, and they might be sensitive to distinct temporal stimulation patterns. This might be the reason why these two sub-types have functionally different roles. It would be interesting to explore several other combinatorics as to how they may lead to distinct physiological responses simple based on distinct upstream and downstream kinetics.

Recent studies in neuroscience and immunology suggest links between neural reflexes and immune responses.^76,77 Even our previous study suggests that neurotransmitters such as acetylcholine can induce NFAT activation.¹³ The band-pass analysis also predicts that at a longer (and rather more sustained) rest periods, calcium oscillations may elicit NFκB response.⁷⁸ Both NFAT and NFκB play crucial roles in immune response. It would be interesting to explore how different rest periods (and different agonists) may elicit immune response upon pulsatile stimulation of cells. This study will not only provide scientific insights into mechanisms of immune response, but also aid development of relevant and more potent therapeutics.

Synthetic biology applications such as coherent cellular responses or ‘cellular lasers’

Results from pulsatile stimulation of cells have demonstrated that phase-locked responses under a particular stimulation frequency window lead to maximum downstream response.^13,45,52 Moreover, recent findings suggest that for most of the cell signaling pathways, incoherent response may be due to cell-to-cell variability or biochemical noise.^19,20,45 Taking these two results together, we hypothesize that by minimizing cell-to-cell variability using genetic tools and stimulating cells in pulsatile fashion using automated microfluidic oscillators, we should be able to get coherent downstream response in a cell population, analogous to the concept of lasers in optics. ‘Cellular lasers’ would greatly enhance desired output in biotechnology-related applications.

Conclusions

Immense opportunities lie in investigating signaling pathways where external fluctuations and dynamics in the microenvironment may be playing a critical role. The advantage of utilizing microfluidic pulsatile stimulation and mathematical modeling lies in mimicking physiology, synchronizing heterogeneous single-cell responses and gaining several mechanistic insights about the pathway. We show that this approach has been utilized successfully to investigate several major mammalian signaling pathways, and has provided a deeper understanding about the signaling circuitries. We also speculate that this approach will be helpful in understanding several other signaling mechanisms, and it also has potential for applications in pharmacology, and synthetic biology. With the advancements in microfabrication technology^79–83 and mathematical modeling, we speculate that investigating signaling pathways with this approach will provide better understanding of such pathways and also lead to several biomedical applications. Advanced mathematical approaches such as multi-scale modeling and agent-based modeling will further push the investigation at systems scale.^84,85 Tools such as optogenetics⁸⁶ and high resolution imaging will expand the investigation from temporal modulation to spatiotemporal modulation.^87,88 These advancements could lead to several synthetic biology applications such as on-chip (in vitro) tissue scale fate-regulation. Taken together, this approach has created a new paradigm for the investigation of cell signaling pathways.

Acknowledgements

We thank NIH (GM096040) for funding. We also thank Dr Andreja Jovic for suggestions.

Notes and references

1. B. Sorre, A. Warmflash, A. H. Brivanlou and E. Siggia, Dev. Cell, 2014, 30, 334–342.
2. L. Ashall, C. A. Horton, D. E. Nelson, P. Paszek, C. V. Harper, K. Sillitoe, S. Ryan, D. G. Spiller, J. F. Unitt, D. S. Broomhead, D. B. Kell, D. A. Rand, V. Sée and M. R. H. White, Science, 2009, 324, 242–246.
3. U. Alon, An Introduction to Systems Biology: Design Principles of Biological Circuits, Hall/CRC, 2007.
4. A. Jovic, B. Howell, M. Cote, S. M. Wade, K. Mehta, A. Miyawaki, R. R. Neubig, J. J. Linderman and S. Takayama, PLoS Comput. Biol., 2010, 6, e1001040.
5. T. A. Duncombe, A. M. Tentori and A. E. Herr, Nat. Rev. Mol. Cell Biol., 2015, 16, 554–567.
6. W. Gu, X. Zhu, N. Futai, B. S. Cho and S. Takayama, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 15861–15866.
7. B. Mosadegh, C.-H. Kuo, Y.-C. Tung, Y.-S. Torisawa, T. Bersano-Begey, H. Tavana and S. Takayama, Nat. Phys., 2010, 6, 433–437.
8. M. De Pittà, M. Goldberg, V. Volman, H. Berry and E. Ben-Jacob, J. Biol. Phys., 2009, 35, 383–411.
9. O. Dyachok, Y. Isakov, J. Sagetorp and A. Tengholm, Nature, 2006, 439, 349–352.
10. Y. Dunant, P. Jirounek, M. Israël, B. Lesbats and R. Manaranche, Nature, 1974, 252, 485–486.
11. M. Bergendahl, J. A. Aloi, A. Iranmanesh, T. M. Mulligan, J. D. Veldhuis, M. Bergendahl, J. A. Aloi, A. L. I. Iranmanesh, T. M. Mulligan and J. D. Veldhuis, J. Endocrinol. Metab., 1998, 83, 1967–1975.
12. P. E. Chappell, R. S. White and P. L. Mellon, J. Neurosci., 2003, 23, 11202–11213.
13. M. Sumit, R. R. Neubig, S. Takayama and J. J. Linderman, Integr. Biol., 2015, 7, 1378–1386.
14. H. Ryu, M. Chung, M. Dobrzyński, D. Fey, Y. Blum, S. S. Lee, M. Peter, B. N. Kholodenko, N. L. Jeon and O. Pertz, Mol. Syst. Biol., 2015, 11, 838.
15. M. G. Roper, Anal. Chem., 2016, 88, 381–394.
16. B. Snijder and L. Pelkmans, Nat. Rev. Mol. Cell Biol., 2011, 12, 119–125.
17. J. E. Ladbury and S. T. Arold, Trends Biochem. Sci., 2012, 37, 173–178.
18. J. J. Hughey, M. V. Gutschow, B. T. Bajar and M. W. Covert, Mol. Biol. Cell, 2014, 26, 583–590.
19. J. Selimkhanov, B. Taylor, J. Yao, A. Pilko, J. Albeck, A. Hoffmann, L. Tsimring and R. Wollman, Science, 2014, 346, 1370–1373.
20. R. Cheong, A. Rhee, C. J. Wang, I. Nemenman and A. Levchenko, Science, 2011, 334, 354–358.
21. S. Zambrano, I. De Toma, A. Piffer, M. E. Bianchi and A. Agresti, eLife, 2016, 5, e09100.
22. T. Tomida, S. Oda, M. Takekawa, Y. Iino and H. Saito, Sci. Signaling, 2012, 5, ra76.
23. R. Dhumpa, T. M. Truong, X. Wang and M. G. Roper, Integr. Biol., 2015, 7, 1061–1067.
24. R. Dhumpa, T. M. Truong, X. Wang, R. Bertram and M. G. Roper, Biophys. J., 2014, 106, 2275–2282.
25. C. Moraes, J. M. Labuz, B. M. Leung, M. Inoue, T.-H. Chun and S. Takayama, Integr. Biol., 2013, 5, 1149–1161.
26. S. N. Bhatia and D. E. Ingber, Nat. Biotechnol., 2014, 32, 760–772.
27. K. Yum, S. G. Hong, K. E. Healy and L. P. Lee, Biotechnol. J., 2014, 9, 16–27.
28. A. J. Lotka, Elements of Physical Biology, Williams Wilkins Co., 1925, 435.
29. V. Volterra, Mem. Accad. Lincei, 1926, 6, 31–113.
30. J. Monod, Annu. Rev. Med., 1949, 3, 371–394.
31. A. M. Turing, Philos. Trans. R. Soc., B, 1952, 237, 37–72.
32. J. C. Sible and J. J. Tyson, Methods, 2007, 41, 238–247.
33. J. J. Linderman, J. Biol. Chem., 2009, 284, 5427–5431.
34. B. B. Aldridge, J. M. Burke, D. A. Lauffenburger and P. K. Sorger, Nat. Cell Biol., 2006, 8, 1195–1203.
35. S. Tay, J. J. Hughey, T. K. Lee, T. Lipniacki, S. R. Quake and M. W. Covert, Nature, 2010, 466, 267–271.
36. S. Marino, I. B. Hogue, C. J. Ray and D. E. Kirschner, J. Theor. Biol., 2008, 254, 178–196.
37. D. E. Zak, J. Stelling and F. J. Doyle, Comput. Chem. Eng., 2005, 29, 663–673.
38. A. Saltelli, S. Tarantola, F. Campolongo and M. Ratto, Sensitivity Analysis in Practice, John Wiley & Sons, Ltd, Chichester, UK, 2002.
39. S. M. Blower and H. Dowlatabadi, Int. Stat. Rev., 1994, 62, 229–243.
40. A. Saltelli, S. Tarantola, F. Campolongo and M. Ratto, Sensitivity Analysis in Practice, John Wiley & Sons, Ltd, Chichester, UK, 2002.
41. P. A. Mahama and J. J. Linderman, Biotechnol. Prog., 1994, 10, 45–54.
42. A. Jovic, S. M. Wade, A. Miyawaki, R. R. Neubig, J. J. Linderman and S. Takayama, Mol. Biosyst., 2011, 7, 2238–2244.
43. A. Jovic, S. M. Wade, R. R. Neubig, J. J. Linderman and S. Takayama, Integr. Biol., 2013, 5, 932–939.
44. R. A. Kellogg, C. Tian, T. Lipniacki, S. R. Quake and S. Tay, eLife, 2015, 4, 1–26.
45. R. A. Kellogg and S. Tay, Cell, 2015, 160, 381–392.
46. L. Ashall, C. A. Horton, D. E. Nelson, P. Paszek, C. V. Harper, K. Sillitoe, S. Ryan, D. G. Spiller, J. F. Unitt, D. S. Broomhead, D. B. Kell, D. A. Rand, V. Sée and M. R. H. White, Science, 2009, 324, 242–246.
47. A. Prindle, J. Selimkhanov, H. Li, I. Razinkov, L. S. Tsimring and J. Hasty, Nature, 2014, 508, 387–391.
48. L. Tsimring, J. Hasty, T. Danino, O. Mondrago, O. Mondragón-Palomino, L. Tsimring and J. Hasty, Nature, 2010, 463, 326–330.
49. O. Mondragón-Palomino, T. Danino, J. Selimkhanov, L. Tsimring and J. Hasty, Science, 2011, 333, 1315–1319.
50. A. E. Sgro, D. J. Schwab, J. Noorbakhsh, T. Mestler, P. Mehta and T. Gregor, Mol. Syst. Biol., 2015, 11, 779.
51. N. Hao, B. A. Budnik, J. Gunawardena and E. K. O’Shea, Science, 2013, 339, 460–464.
52. A. Mitchell, P. Wei and W. A. Lim, Science, 2015, 350, 1379–1383.
53. S. Kato, Y. Xu, C. E. Cho, L. F. Abbott and C. I. Bargmann, Neuron, 2014, 81, 616–628.
54. A. Politi, L. D. Gaspers, A. P. Thomas and T. Höfer, Biophys. J., 2006, 90, 3120–3133.
55. G. Dupont, E. F. L. Lokenye and R. A. J. Challiss, Biochimie, 2011, 93, 2132–2138.
56. R. E. Dolmetsch, R. S. Lewis, C. C. Goodnow and J. I. Healy, Nature, 1997, 386, 855–858.
57. T. Tomida, K. Hirose, A. Takizawa, F. Shibasaki and M. Iino, EMBO J., 2003, 22, 3825–3832.
58. W. Li, J. Llopis, M. Whitney, G. Zlokarnik and R. Y. Tsien, Nature, 1998, 392, 936–941.
59. R. E. Dolmetsch, K. Xu and R. S. Lewis, Nature, 1998, 392, 933–936.
60. N. Yissachar, T. S. Fischler, A. A. Cohen, S. Reich-zeliger, D. Russ, E. Shifrut and Z. Porat, Mol. Cell, 2013, 49, 322–330.
61. A. Hoffmann, A. Levchenko, M. L. Scott and D. Baltimore, Science, 2002, 298, 1241–1245.
62. R. Avraham and Y. Yarden, Nat. Rev. Mol. Cell Biol., 2011, 12, 104–117.
63. C. J. Marshall, Cell, 1995, 80, 179–185.
64. J. Massagué, Nat. Rev. Mol. Cell Biol., 2012, 13, 616–630.
65. A. Warmflash, Q. Zhang, B. Sorre, A. Vonica, E. D. Siggia and A. H. Brivanlou, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E1947–E1956.
66. A. Aulehla and O. Pourquié, Cold Spring Harbor Perspect. Biol., 2010, 2, a000869.
67. D. A. Lang, D. R. Matthews, J. Peto and R. C. Turner, N. Engl. J. Med., 1979, 301, 1023–1027.
68. J. T. Mettetal, D. Muzzey, C. Gómez-Uribe and A. van Oudenaarden, Science, 2008, 319, 482–484.
69. B. N. Kholodenko, Nat. Rev. Mol. Cell Biol., 2006, 7, 165–176.
70. J. Kotlinska and M. Bochenski, Eur. J. Pharmacol., 2007, 558, 113–118.
71. S. J. Bradley and R. A. J. Challiss, Biochem. Pharmacol., 2012, 84, 249–259.
72. G. Mannaioni, M. J. Marino, O. Valenti, S. F. Traynelis and P. J. Conn, J. Neurosci., 2001, 21, 5925–5934.
73. H. Sun and V. Neugebauer, J. Neurophysiol., 2011, 106, 960–973.
74. M. Pietraszek, A. Gravius, D. Schäfer, T. Weil, D. Trifanova and W. Danysz, Neuropharmacology, 2005, 49, 73–85.
75. P. Gubellini, E. Saulle, D. Centonze, C. Costa, D. Tropepi, G. Bernardi, F. Conquet and P. Calabresi, Neuropharmacology, 2003, 44, 8–16.
76. F. M. Abboud, S. C. Harwani and M. W. Chapleau, Hypertension, 2012, 59, 755–762.
77. E. M. Sternberg, Nat. Rev. Immunol., 2006, 6, 318–328.
78. Z. P. Xu, Y. Song, K. Yang, W. Zhou, L. N. Hou, L. Zhu, H. Z. Chen and Y. Y. Cui, Inflammation Res., 2014, 63, 463–473.
79. D. Kilinc, J. Schwab, S. Rampini, O. W. Ikpekha, A. Thampi, A. Blasiak, P. Li, R. Schwamborn, W. Kolch, D. Matallanas and G. U. Lee, Integr. Biol., 2015, 39–49.
80. C. Siltanen, M. Yaghoobi, A. Haque, J. You, J. Lowen, M. Soleimani and A. Revzin, Acta Biomater., 2016, 1–8.
81. A. S. Hansen, N. Hao and E. K. O. Shea, Nat. Protoc., 2015, 10, 1181–1197.
82. T. Frank and S. Tay, Lab Chip, 2015, 15, 2192–2200.
83. L. He, A. Kniss, A. San-Miguel, T. Rouse, M. L. Kemp and H. Lu, Lab Chip, 2015, 15, 1497–1507.
84. N. A. Cilfone, D. E. Kirschner and J. J. Linderman, Cell. Mol. Bioeng., 2015, 8, 119–136.
85. M. Behar, D. Barken, S. L. Werner and A. Hoffmann, Cell, 2013, 155, 448–461.
86. J. E. Toettcher, O. D. Weiner and W. A. Lim, Cell, 2013, 155, 1422–1434.
87. A. Warmflash, B. Sorre, F. Etoc, E. D. Siggia and A. H. Brivanlou, Nat. Methods, 2014, 11, 847–854.
88. P. Kar and A. B. Parekh, Mol. Cell, 2015, 58, 232–243.

---