Determination of the isotopic composition of micrometric uranium particles by UV femtosecond laser ablation coupled with sector-field single-collector ICP-MS
A.
Donard
ab,
F.
Pointurier
*b,
A.-C.
Pottin
b,
A.
Hubert
b and
C.
Pécheyran
a
aIPREM, Université de Pau et des Pays de l'Adour, UMR 5254, Hélioparc Pau-Pyrénées, 2 Avenue du Président Angot, 64053 Pau, France. E-mail: Christophe.pecheyran@univ-pau.fr; Fax: +33 559 407 781; Tel: +33 559 407 757
bCEA, DAM, DIF, F-91297 Arpajon, France. E-mail: fabien.pointurier@cea.fr; Fax: +33 1 69 26 70 65; Tel: +33 1 69 26 49 17
First published on 4th October 2016
Abstract
In this article, the coupling of a UV-fs-LA system with a sector-field ICP-MS for isotopic analysis of individual sub micrometric and micrometric uranium particles, especially for the measurement of minor isotopes (234U and 236U), is discussed. Ablation of uranium particles results in short (a few seconds) and highly noisy signals with sudden and extremely brief (<1 ms) increases in intensity (referred to as ‘spikes’), making the precise determination of isotope ratios very challenging. Uranium particles were located beforehand by means of suitable techniques. Three isotope ratio calculation methods are evaluated. The influence of signal spikes on the accuracy and precision of the isotope ratios is discussed. Thanks to the implementation of a ‘spike rejection filter’, the measurement of uranium isotope ratios in particles from an isotopically certified reference material (NBS U010) is greatly improved. Measured ratios are in acceptable agreement with the reference values although a systematic bias was observed. Limits of detection of a few tens of attograms for minor isotopes are achieved. Isotopic mapping in the area around the initial ablation crater allows the observation of the deposition of debris. No isotope ratio bias is observed when analyzing uranium particles mixed with lead particles, showing that no significant lead-based polyatomic interference is produced. Results, including minor isotope ratios, obtained with particles of sizes from 0.3 to 1.5 μm sampled in a nuclear facility, are in good agreement with the values obtained by another well-established method for such analysis.
Introduction
“Environmental sample” analysis has become an important safeguarding tool since the discovery of Iraq's nuclear program in the 90s.1 Isotopic composition of uranium particles collected on cotton clothes wiped over surfaces in nuclear facilities (walls, instruments, furniture…) by IAEA inspectors is analysed by a handful of highly specialized laboratories and compared with the results expected from the facility operators' declaration within the frame of the non-proliferation treaty.2 A very low proportion of the dust sampled by inspectors consists of uranium particles which come from the nuclear material used in the facility. The so-called ‘particle analysis’ consists of analysing each particle separately to determine their individual uranium and/or plutonium isotopic composition. This allows distinguishing between civilian and, potentially, military use of the corresponding bulk material.However, in a cotton cloth sample, referred to as the ‘swipe sample’, particles coming from an undeclared material might be present at extremely low concentrations among environmental dust and particles from declared nuclear material. Because of the extremely small size of the collected uranium particles (typically varying from a few nanometers to a few micrometers), very sensitive analytical methods must be used. Nowadays, two particle analysis techniques are routinely used to characterize uranium isotopic composition: Fission Track Thermal Ionization Mass Spectrometry (FT-TIMS)3,4 and Secondary Ionization Mass Spectrometry (SIMS).5,6 However, these techniques present certain limitations: FT-TIMS has a very low ionization efficiency which prevents the analysis of small (≪1 μm) particles. In addition, certain steps of the analytical procedure are tedious and time-consuming, for instance the irradiation and the consecutive cooling of the samples, the micro-sampling of the selected particles for deposition onto the TIMS filament, etc.7 SIMS analysis is faster, but measurement of minor uranium isotopes 234U, 236U and even 235U can be affected by polyatomic interference leading to false detection of these isotopes and to overestimated isotopic ratios.8
Laser ablation coupled with inductively coupled plasma mass spectrometry (LA-ICP-MS) has been proven to be a possible alternative to determine the isotopic composition of uranium particles.9 The analysis can be performed directly on the particles once deposited onto an appropriate substrate as this technique has a spatial resolution of a few micrometres depending on the laser beam size. Because no micro-sampling is needed the sample preparation time is reduced compared to the SIMS technique; analysis of single particles is performed rapidly (within a minute). The high sensitivity of the ICP-MS in combination with the fast introduction of the material has the effect of producing a high signal to noise ratio, which leads to low limits of detection. However, for real μm-sized particles scarcely deposited on substrates, it is necessary to locate uranium particles by using external techniques prior to the analysis.
The LA-ICP-MS technique has already been applied to uranium particle analysis.10 Without any pre-localization, a few authors have managed to measure isotopic ratios in particles made of uranium certified reference materials (CRMs), either by performing scan ablation11 or by targeting particles large enough to be visible with the optical system of the laser ablation device (at least several μm).12,13 Pointurier et al.10 described the use of LA-ICP-MS with a quadrupole-based ICP-MS (ICP-QMS) and a nanosecond laser ablation system (ns-LA) to measure the 235U/238U in particles of an IAEA swipe sample using precise localization techniques such as the fission track (FT) technique and scanning electron microscopy (SEM) equipped with an energy dispersive X-ray detector (EDX). The 235U/238U isotopic ratios measured by LA-ICP-QMS in sub-micrometric particles were in good agreement with values previously measured with the FT-TIMS technique10 and with both the FT-TIMS and SIMS techniques.9 The accuracy of measurement of 235U/238U by ns-LA-ICP-QMS was comparable to those of the well-established particle analysis techniques. However, the reproducibility of ns-LA-ICP-QMS achievable on particles of known isotopic composition was poorer than for the FT-TIMS and SIMS (RSD of 7% for ns-LA-ICP-QMS, versus 4.5% for FT-TIMS, and 3% for SIMS). Other limitations have been noticed by Hubert et al.14 who proved that ablation of particles could lead to significant (a few percent of the initial mass of the ablated particle) surface contamination around the ablation crater due to deposition of ablation debris even when using a femtosecond laser.
However, to our knowledge, no minor isotopes (234U, 236U) have yet been measured in sub-micrometric particles. Varga et al.13 investigated the uranium composition of several relatively large uranium oxide particles (∼10 μm) of different 235U enrichments. 234U/238U ratios in natural uranium (NU) and depleted uranium (DU) measured by LA-ICP-MS were systematically higher than the ratios measured with the same ICP-MS after sample dissolution. The agreement was better when the authors used a higher mass resolution (R = 4000).
In this study we evaluated the performance of a single collector double focusing sector-field ICP-MS (ICP-SFMS) coupled with a UV femtosecond laser (fs-LA). Study of sub-micrometric and micrometric sized particle analysis in terms of the detection limit, accuracy, precision and detection capability of minor uranium isotopes was carried out. Special attention was also paid to signal processing. Spike removal and three methods for isotope ratio calculation were evaluated and discussed. Deposit of ablation debris in the vicinity of the ablated area and polyatomic interferences likely to occur when lead containing particles are mixed with uranium particles were studied. Results from CRMs and real-life cotton swipe uranium particle samples are presented with regard to 234U/238U, 235U/238U and 236U/238U. These results are discussed and compared to those obtained with the FT-TIMS technique.
Materials and methods
Sample preparation
Uranium particles used in this study were extracted from the isotopic CRM NBS U010, NBS U950A (NBL, Argonne, Illinois, USA), and from real-life swipe samples. Both NBS reference materials are in the form of highly purified U3O8 powder, from which particles were sampled and deposited on appropriate substrates. To evaluate the influence of lead interference due to polyatomic species including Pb on U minor isotopes, NBS U950A particles, whose isotopic composition is very similar to that of NU,15 were mixed with lead particles. Lead particles were collected by wiping a cotton cloth on a lead brick; Pb particles were then extracted by means of an ultrasonic bath and mixed in ethanol with NBS U950A particles. The isotopic composition of uranium particles from an IAEA swipe field sample (#21954-11-01) previously analysed by FT-TIMS and ns-LA-ICP-QMS10 was characterised. Particles were also extracted from the cotton cloth by means of an ultrasonic ethanol bath.The specific procedure designed for FT-TIMS deposition was applied to all the analysed particles. Particles were dispersed in a mixture of collodion (4% nitrocellulose in ether-alcohol media, Merck) and ethanol; a drop was then deposited on a polycarbonate disk. After solvent evaporation, particles were fixed onto the disk by a thin layer of collodion.
Localisation of uranium particles on the polycarbonate disk was performed with two techniques. NBS U010 and NBS U950A particles were detected using a SEM/EDX equipped with GSR software (Phillips-FEI ‘XL30 ESEM’, Eindhoven, The Netherlands) while particles from the IAEA sample were localised by observation of fission tracks obtained after irradiation in a nuclear reactor (∼1015 thermal neutrons per cm2, Orphée reactor, Saclay, France). In both cases correspondence between the coordinates of the particles in the device used to locate them (SEM or optical microscope used for observation of the fission tracks) and in the ablation cell was determined using a 2-point algorithm with landmarks (tiny holes previously formed by pushing a tip through the deposition disk and the corresponding fission track detector disk). Both techniques are described with more details elsewhere.10
Fission track localizations were performed on IAEA particles. The number of observed fission tracks is related to the number of 235U fissile atoms, and therefore to the equivalent diameter of the particle (assuming a spherical particle and a given density), according to the following equation:
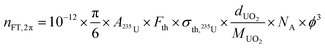 | (1) |
LA-ICPMS instrumentation
A fs-UV LA system (Lambda 3, Nexeya/Amplitude Systèmes, Bordeaux, France) and an ICP-SFMS Element XR (ThermoFisher Scientific, Bremen, Germany) fitted with the jet interface were used. The laser was fitted with a diode-pumped Yb:KGW crystal laser source (HP2, Amplitude Systèmes, Pessac, France). A harmonic generator directly located after the laser source allowed the user to choose from three wavelengths: 1030 nm (fundamental), 515 nm (2nd harmonic) and 257 nm (4th harmonic). The pros and cons of fs-laser ablation for particle analysis were already discussed by Hubert et al.14 An advantage over ns-laser is expected as fs-ablation reportedly produces thinner aerosols than ns-ablation, which has a positive effect on isotopic measurements. For this study, only the UV 257 nm wavelength was used as it was the only one available at the time of the experiments. The pulse duration was less than 400 fs at this wavelength. The laser source can operate within a wide range of repetition rates (1 Hz to 100 kHz) and energy ranging from 2 mJ per pulse below 1 kHz to 0.08 mJ at 100 kHz. Complex trajectories can be realized by moving the laser beam across the surface of the sample using the movement of galvanometric scanners combined with a high repetition rate. A low mass resolution of 300 was chosen on the ICP-SFMS to ensure the highest ion transmission in order to have the best probability of measuring minor uranium isotopes (234U and 236U). Ablation fragments were carried to the mass spectrometer by a helium flux (600 mL min−1). Addition of nitrogen into the plasma has been proven to enhance sensitivity in the high mass range;16–18 hence 10 mL min−1 was added to the helium flow. Measurements were performed under dry plasma conditions. The coupling was tuned on a daily basis in order to achieve the best compromise in terms of sensitivity, accuracy, atomization efficiency and reproducibility. Particle ablation resulted in a short transient signal. Measuring such a signal with a single collector ICP-MS is a challenge and multiple-collector ICP-MS is more suitable for this. However, the ICP-SF-MS used in the study is the only one available which has sufficient sensitivity for measuring U minor isotopes in sub-μm sized particles.Hence a small measurement time per isotope was required to define a sufficient number of individual measurements for each isotope in order to be as representative as possible of the transient ablation signal and to prevent a skew effect. Thus 234U, 235U, 236U, 238U, 238U1H were recorded with a measurement time per isotope of 2 ms within each measurement cycle for all isotopes except 238U whose signal intensity on some occasions exceeded the upper threshold of the analog counting mode and was then detected in the Faraday cup. When the Faraday cup is used a longer measurement time must be set to meet the instrument's requirements. A given isotope must be defined by at least 5 samples per peak to be measured on a Faraday cup (for Element XR, samples per peak refers to the number of points that defines the peak scanned around the m/z for each isotope). 238U was then recorded with a time measurement of 5 ms. Laser and ICP-SFMS parameters are shown in Table 1.
| Laser | HP2, Yb:KGW |
|---|---|
| Wavelength | 257 nm |
| Pulse duration | 360 fs |
| Repetition rate | 1000 Hz |
| Scanner speed | 1 mm s−1 |
| ICPMS | Element XR, jet interface | |
|---|---|---|
| RF power | 1200 W | |
| Cooling gas flow rate | 15 L min−1 | |
| Auxiliary gas flow rate | 1.10 L min−1 | |
| Nebulizer gas flow rate | 0.7 L min−1 | |
| Resolution | 300 | |
| Scan type | EScan | |
| Measured isotope | 234U, 235U, 236U, 238U1H | 238U |
| Sample per peak | 60 | 60 |
| Mass window | 4% | 9% |
| Setting time | 1 ms | 1 ms |
| Sample time | 1 ms | 1 ms |
Dead time was measured according to the method described by Russ19 and automatically corrected by the Element XR software. Detector cross-calibration was checked twice a day using the appropriate sequence of the Element Software. In addition, the fs-LA-ICP-MS coupling was tuned daily to ensure robust and stable ICP conditions; the Ar carrier gas flow rate, torch position and power were adjusted so that the U/Th ratio was close to 1 ± 0.02 when ablating SRM NIST 612 glass.
Ablation scheme
Most of the particles analyzed in this study are sub-micrometric, and are not visible with the optical microscope of the laser ablation system. The precision of the 2-point algorithm used to translate the coordinates from the localization method chosen (either FT or SEM/EDX) to the laser optic system is ±15 μm. To ensure that the targeted particle is ablated, an ablation area is defined as a 50 μm × 50 μm square around the theoretical position of the particle. Using the galvanometric scanner device, ablation was performed corresponding to 50 segments of 50 μm, 1 μm apart. Under our laser conditions (scanner of 1 mm s−1 and repetition rate of 1 kHz), the ablation was complete in 2.5 s.To study deposits of debris resulting from the ablation of a particle, LA-ICP-MS imaging was performed around the ablated crater. In this case, the resulting ablated area was a square of 400 μm × 400 μm centered on the previously ablated crater. The square was composed of 10 lines each 40 μm wide and 400 μm in length. Only 235U was recorded with a dwell time of 0.5 s. Therefore, the spatial resolution was 12.5 μm × 40 μm.
Data evaluation
Signal intensities were recorded in the time-resolved analysis mode. Blank corrections were calculated point by point by subtraction of the average signal recorded during the 20 s prior to ablation.236U was corrected for 235U hydride formation and peak tailing assumed to be equal to the 238U1H/238U ratio:
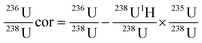 | (2) |
Three data processing approaches were compared for the calculation of the isotopic ratios 234U/238U, 235U/238U and 236U/238U.
(1) Weighted integration (WI). Each point of the integration was weighted by the sum of the count rates measured for both isotopes. The average isotope ratio ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) is calculated according to the formula:
is calculated according to the formula:
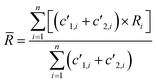 | (3) |
The uncertainty of the measurement (which corresponds to the internal precision) is estimated from the standard deviation of the individual ratios obtained for each repetition, weighted by the sum of the count rates measured for the corresponding repetition:
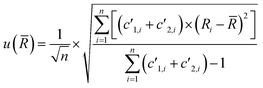 | (4) |
(2) Total Integration (TI): isotopic ratios are calculated by dividing the sum of the measured number of counts for the first isotope by the sum of the measured number of counts for the second isotope. For a given isotope, the measured signal is taken into account only if it is higher than 1% of the maximum signal measured for the whole ablation peak. Therefore, the average isotopic ratio is defined by:
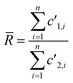 | (5) |
(3) Linear regression slope (LRS): this method is based on the method developed by Fietzke20 and is applied to isotopic measurement.21,22 LRS has been proven to be a reliable method to calculate isotopic ratios and has been used by Kappel et al.11 Isotope ratios are calculated by estimating the mean slope of a linear regression using the “least squares method”.
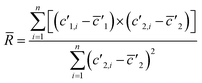 | (6) |
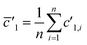 and
and 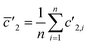 .
.
Results and discussion
Effect of the deposition process
After the deposition process, NBS particles were more or less fragmented and appeared as agglomerates of several smaller (sub μm) particles (see Fig. 1). However, all fragments observed in the same area belong to the same initial particle and have the same isotopic composition. Sizes of the agglomerates ranged between 2 and 10 μm. Therefore, the exact quantity of uranium in agglomerates cannot be known with certainty. Nevertheless, it can be reasonably assumed that sizes of these ‘particles’ are typically a few μm.To take into account the possible disaggregation of the particles and the error in the relocation process, ablated areas are rather large (50 μm × 50 μm) with respect to the particle's initial sizes. Therefore, for ‘real-life’ samples, it cannot be ruled out that very small – maybe nanometre-sized – particles are present in the analysed area of a given particle. However, the other well-established techniques for particle analyses (i.e. SIMS and fission tracks – TIMS) employed for years for analysing particles sampled by IAEA inspectors are based on the same preparation process and have also analysed areas larger than the expected dimensions of the uranium particles. However, partial or complete disaggregation of particles is not a major problem as long as fragments remain in a limited area, which is included in the analysed area; isotopic mixing is sometimes observed whatever the measurement technique. So, this limitation accounts for all ‘particle analysis’ techniques, and not specifically for laser ablation – ICP-MS.
Limits of detection
LA-ICP-MS analyses were performed with the same analytical conditions for ‘blank disks’ (with only the collodion coating deposited onto the polycarbonate disk) to estimate the limits of detection of the method. Measured signals were close to the baseline signal recorded before ablation. Signals integrated over 10 s (i.e. the integration time for the ablation of a uranium particle) were between 0 and 20 counts. With less than 70 counts, estimation of the limits of detection is based on Poisson statistics.23 Limits of detection were calculated according to the formula given by the IUPAC: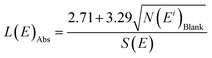 | (7) |
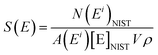 | (8) |
| 234U | 235U | 236U | 238U | |
|---|---|---|---|---|
| N(Ei)Blank | 0.5 | 0.5 | 0.1 | 10 |
| N(Ei)NIST 610 | 1.6 × 102 | 2.3 × 104 | 5.2 × 102 | 4.5 × 107 |
| L(E)Abs(ag) | 46 | 75 | 43 | 40 |
| Abundance in NIST 610 | 9.9 × 10−6 | 2.3 × 10−3 | 4.3 × 10−5 | 0.998 |
Deposition of ablation debris around the crater
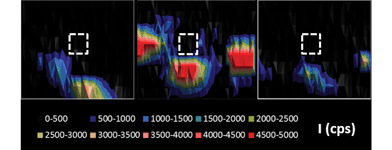
Particles are ablated directly on the polycarbonate disk where particles are embedded into the collodion coating. However, Hubert et al.14 observed evidence of debris of the ablated particle around the ablated zone when using IR femtosecond laser ablation. This implies a risk of contamination if the distance between particles of interest is too short. Mapping of fragments of uranium particles in the surrounding ablated zones (LA-ICP-MS imaging) was performed in this study after uranium particle ablation. The use of an ICP-SFMS, which gives higher sensitivity than the quadrupole used in the previous study,14 allowed the detection of smaller deposition debris. The 235U signals were recorded both during the ablation of the particle and during the “imaging” of the surrounding area of the crater to estimate the remaining amount of uranium deposited around the crater. Three particles were studied. The percentage of the signal obtained around the crater with respect to the initial particle signal ranged from 0.4% to 3.5%. Fig. 2 shows the typical signal distribution of uranium around the crater after ablation. Results are in good agreement with those obtained by Hubert et al.14 even if different laser ablation devices and ICP-MS were used: the same order of magnitude for the fraction of deposited uranium, and no systematic tendency in the fall out (for instance a preferential direction for the deposition) could be defined. It is worth noting that in this study we used a UV-fs laser whereas Hubert et al. used an IR-fs laser. Depending on the size of the particles analyzed, contamination can induce a bias in the isotopic ratio measured if particles present several isotopic compositions in the sample. To prevent any contamination, the operator has to analyze particles which are sufficiently separated from each other (at least 200 μm). The precision of the algorithm used to re-localize the particle with the optical system of the laser could be improved (for example by using a 3-point algorithm) to reduce the size of the ablated area. By reducing the size of the ablated area, the probability of analyzing debris of a previous ablation with the particle decreases.Signal processing
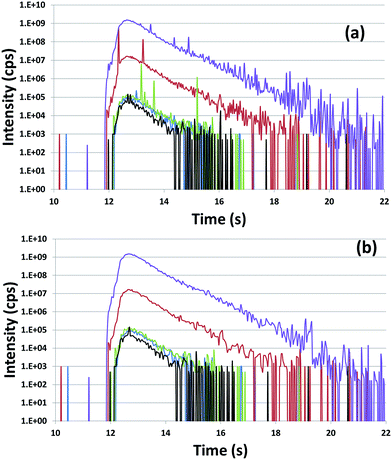
To verify the performance of the method and discuss the calculation methods, particles extracted from the NBS U010 CRM were analyzed. In this case, particles were localized by SEM/EDX. An example of isotopic signals recorded for the ablation of an NBS U010 particle is displayed in Fig. 3. For each isotope, the registered signals show several sudden and extremely short increases of intensity called “spikes” which are generally observed for a single isotope within a measurement cycle. To study the influence of the spikes on the isotopic ratios measured, a “spike rejection filter” (SRF) was applied to the raw data using a VBA macro (Microsoft “Excel”™). Spikes are defined and rejected as follows: a, b, c are successive measurement points (counts rates), if b > 1.1 × a and b > 1.1 × c, then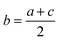 .
.
Isotopic ratios measured with and without applying the SRF for the analysis of NBS U010 particles are compared in Table 3. To simplify the table only the results obtained with WI and LRS calculation methods are given. For NBS U010, suppression of the spikes significantly improves the accuracy, for both the internal and external precision of all isotope ratios for both calculation methods. The origin of the spikes might be related to the detection of larger ablation fragments or to a higher density of ablation fragments during the counting time for a given isotope. Actually, the ablation of a micrometric particle by a femtosecond laser UV produces very small ablation fragments (with size typically in the nanometer range) that are transported to the ICP where they are atomized-ionized prior to introduction into the mass spectrometer.25 The ion cloud formed after the atomization–ionization of a given ablation fragment is measured by the detector for a few hundreds of microseconds. As the ICP-SFMS used in this study is a mono-collector instrument, isotopes are recorded sequentially. Because the time of measurement per isotope (2 ms and 5 ms) is longer than the time of detection of particles, the signal measured for a given isotope is not correlated with the signal measured for the other isotopes. Hence, the arrival of a large ablation fragment is too brief to be recorded for more than one isotope: the corresponding high signal is detected for one isotope only, which irremediably biases the isotope ratios measured within a measurement cycle. The internal precision which, in both calculation methods, is based on the standard deviation of the isotope ratio within a measurement cycle is also affected by these spikes. Therefore, for the other results presented in this publication, SRF was applied.
| 234U/238U (×10−5) | 235U/238U (×10−2) | 236U/238U (×10−5) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Without SRF | With SRF | Without SRF | With SRF | Without SRF | With SRF | |||||||
| WI | LRS | WI | LRS | WI | LRS | WI | LRS | WI | LRS | WI | LRS | |
| Certified ratio | 5.5 | 1.0 | 6.9 | |||||||||
| Measured average isotope ratio | 8.3 | 8.5 | 5.7 | 5.6 | 1.7 | 1.1 | 1.0 | 1.0 | 9.7 | 8.7 | 7.3 | 7.2 |
| External precision (absolute/relative) | 3.9/48% | 7.2/85% | 0.6/10% | 0.7/13% | 1.5/91% | 0.3/26% | 0.04/4% | 0.06/5% | 1.8/19% | 2.4/27% | 0.7/10% | 0.9/13% |
| Average internal precision (absolute/relative) | 2.7/32% | 0.7/8% | 0.3/4% | 0.1/2% | 1.3/32% | 0.1/12% | 0.02/1% | 0.01/1% | 2.8/29% | 0.7/8% | 0.3/5% | 0.1/1% |
| Relative error with respect to the certified ratio | 52% | 56% | 5% | 3% | 67% | 10% | 1% | 1% | 40% | 26% | 7% | 4% |
To compare the three data processing approaches previously defined, isotope ratios and their related precision and accuracy obtained from 16 particles of NBS U010 are presented in Table 4.
| 234U/238U (×10−5) | 235U/238U (×10−2) | 236U/238U (×10−5) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| WI | TI | LRS | WI | TI | LRS | WI | TI | LRS | |
| Certified ratio | 5.5 | 1.0 | 6.9 | ||||||
| Average isotope ratio | 5.7 | 6.1 | 5.6 | 1.0 | 1.0 | 1.0 | 7.3 | 7.5 | 7.2 |
| External precision (SD/RSD) | 0.6/10% | 0.7/12% | 0.7/13% | 0.4/4% | 0.4/4% | 0.5/5% | 0.7/10% | 0.7/10% | 0.8/12% |
| Average internal precision (absolute/relative) | 0.3/4% | — | 0.2/2% | 0.02/1% | — | 0.01/1% | 0.3/5% | — | 0.1/1% |
| Relative error with respect to the certified ratio | 5% | 11% | 3% | 1% | 1% | 1% | 7% | 9% | 4% |
According to these results, the calculation methods giving more importance to the highest intensity points (WI and LRS) lead to more accurate results. For both methods, relative errors of all isotope ratios 234U/238U, 235U/238U and 236U/238U with respect to the certified values are below 7% for all ratios and close to 1% for the 235U/238U ratios.
Slight biases were observed with regard to reference values for all three isotope ratios. It should be mentioned that these biases are not due to the sequential nature of the data acquisition (data points of the different isotopes are systematically shifted by a few ms), as the authors found no significant differences when interpolating data points to correct for the time shift. Besides, these deviations from reference values are too large to be explained by the mass bias phenomenon, which leads to deviation lower than 1% with this instrument (analysis of liquid samples). However, these biases are apparently associated with the very high 238U count rates recorded for some particles. Fig. 4 displays each isotope ratio measured for the 16 NBS U010 particles according to the maximum count rate measured for the 238U signal. To simplify the graphs, only results from one calculation method (LRS) are presented. A similar tendency was observed for the WI method. All measured isotope ratios (234U/238U, 235U/238U and 236U/238U) follow roughly the same trend, increasing with the 238U signal count rate. Only two particles presenting the highest 238U maximum count rate (exceeding the analog detector capacity of 5 × 109 cps and consequently recorded with the Faraday cup) depart from the trend when considering 235U/238U. A similar effect has already been discussed in the literature.18 Aramendía et al.18 compared lead isotope ratios measured in the certified reference material BCR 126A by LA-ICP-MS (with two ICP-MS with sequential detection: a quadrupole based ICPMS X-series II and a sector-field ICP-MS Element XR). They observed similar results, i.e. the increase in the count rates producing biased isotope ratios. The more the isotope ratios deviate from unity the stronger they are affected by the highest count rates. They observed similar behavior when a liquid certified reference material (NIST 981) was analyzed by classical nebulization with the same instruments, which rules out a potential “plasma loading” effect specific to LA-ICP-MS. They concluded that the deviation of the counting efficiency of the detectors (both secondary electron multipliers) for higher count rates in the analog mode was responsible for this bias, as previously observed in the literature.26 In our study, we used the same ICP-MS and hence the same kind of detector, as Aramandia et al. So, the positive bias in the isotope ratios measured in this study for all particles where maximum count rates were higher than ∼2 × 108 cps can be explained by systematic underestimation of the highest 238U count rates (which are not regarded as ‘spikes’ and, consequently, are not removed by the SRF). The linearity of the analogic mode of the detector should be tested with highly concentrated uranium solutions (for instance natural uranium) in the continuous injection mode and in a ‘discontinuous’ injection mode so as to mimic the discrete arrivals of ablation fragments.
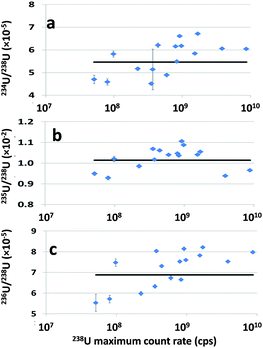 | ||
| Fig. 4 234U/238U (a), 235U/238U (b) and 236U/238U (c) measured for the ablation of 16 NBS U010 particles versus the 238U maximum count rate (cps). Lines in black represent the certified values. | ||
Effect of lead-based polyatomic interference on minor U isotopes
Lead-based interference is a great concern in the particle analysis of safeguard samples, especially for the SIMS technique through the formation of PbCO+ species, because particulate matter sampled in nuclear facilities may contain numerous lead particles as lead is widely used in the nuclear industry because of its property of radiation protection. Therefore, as lead-containing particles may be present in the ablated area along with the located uranium particle, the formation and potential influence on uranium isotope measurements of lead-based polyatomic interference was studied. To conduct this experiment, three different sample disks were prepared according to the protocol described above: a disk containing particles of NBS U950A with an isotopic composition close to NU (disk ‘U’), a disk containing a mixture of NBS U950A and lead particles collected on a lead brick (disk ‘U–Pb’) and a disk containing only lead particles (disk ‘Pb’). All Pb and U particles (larger than 0.7 μm) were located beforehand by SEM, to ascertain that both kinds of particles are present in the analyzed area. Firstly, count rates of lead and uranium isotopes were recorded during the ablation of lead particles on the ‘Pb’ disk. Sizes of the lead particles were found to range between 1 and 20 μm (according to SEM/EDX). Significant signals at m/z of 234U and 238U were detected during the ablation of a few lead particles. The average isotopic ratios 234U/208Pb and 238U/208Pb were respectively 4 × 10−4 and 3 × 10−6, corresponding to numbers of integrated counts ranging from 27 to 183 counts for 234U and from 1 to 10 counts for 238U. The main potential lead-based polyatomic interferences at m/z of 234U and 238U are 206Pb14N2, 204Pb14N16O and 207Pb31P, 206Pb32S, 204Pb34S respectively. So, the risk of overestimating the 234U/238U ratio when Pb particles are present must be considered. 234U/238U ratios measured during the ablation of uranium particles on disks ‘U’ and ‘U–Pb’ were calculated with the WI method and compared (see Fig. 5). As uranium and lead particles were randomly distributed, the quantity of lead ablated on the ‘U–Pb’ disk varied for each ablation. Pb/U ratios were found to range between 0.05 and 2 (10 ablations, ‘U–Pb’ disk).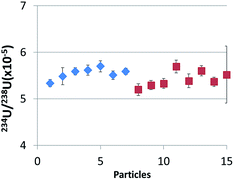 | ||
| Fig. 5 234U/238U ratios measured by LA-ICP-MS for uranium particles in the disk ‘U–Pb’ (uranium particles mix with lead particles, blue diamonds) and ‘U’ (only uranium particles, red squares). | ||
The average isotope ratios (234U/238U ± SD) measured by LA-ICP-MS of uranium particles on disks ‘U’ and ‘U–Pb’ were (5.4 ± 0.3) × 10−5 and (5.5 ± 0.1) × 10−5. These ratios present no significant difference as a result of very limited Pb-based interference. However, the analyzed particles were relatively large (between 3.5 and 6.5 μm according to signal intensities, assuming a spherical shape and UO2 density) and, as a consequence, 234U intensities are relatively high (at least 650 integrated counts). Although, compared to the experiment of Varga et al.,13 for the equivalent particle size, our analytical conditions were more favorable for the observation of Pb-based interference as uranium particles were surrounded by lead particles, no bias in the isotopic ratios was observed. However, smaller uranium particles would probably be more vulnerable to poly-atomic interference and further experiments with sub-micrometric particles should be carried out in the future.
Application to a real-life swipe sample
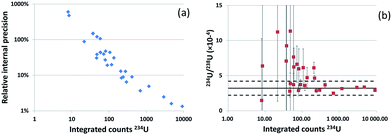
The method developed was applied to particles extracted from an IAEA swipe sample (#21954-11-01). Particles from the same sample had previously been analyzed by FT-TIMS and LA-ICP-MS (nanosecond LA device and quadrupole-based ICP-MS).10 Two isotope compositions were detected: low enriched uranium (LEU) and natural uranium (NU). Only 235U and 238U isotopes were measured by ns-LA-ICP-QMS as the sensitivity of the ns-LA-ICP-QMS was insufficient for 234U and 236U. In this study uranium particles from this swipe sample were analyzed by fs-UV-LA-ICP-SFMS. Localization of the particles was performed using fission tracks. Numbers of tracks were counted to estimate the size of the ablated particles. Assuming that the particles are made of UO2, particle equivalent diameters range from 0.3 to 1.6 μm (average: 0.70 μm). WI and LRS methods were applied. All results are gathered in Table 5. 235U/238U ratios were successfully measured in all analyzed particles. Only one particle could be identified as NU, all the others being LEU particles. On average, 235U/238U ratios measured by LA-ICP-MS and calculated using WI and LRS are in good agreement with TIMS results, with a limited relative difference which is comprised within the uncertainties of the TIMS results. It should be noted that the analyzed sample is not a reference material, and is not even a homogeneous sample (as ‘particle analysis’ is a destructive method, particles belonging to the same isotopic category, i.e. NU and LEU, measured by both LA-ICP-MS and TIMS techniques are certainly not identical). This may explain the small differences between the LA-ICP-MS and TIMS results. The 234U/238U ratios were successfully measured in all particles, and the 236U/238U ratios in 16 particles out of 27 (for the other particles, count rates at the m/z ratio of 236U were below the detection limit). However, both isotope ratios were highly dispersed (relative internal precisions between 49% and 56% depending on the calculation method for 234U/238U and between 44% and 90% for 236U/238U). It should be noted that masses of minor isotopes are extremely low, in the order of a few femtograms or below. To study the effect of the size of the particle on the results, the internal precision and the relative difference with TIMS results were plotted according to the number of counts integrated for the 234U signal (Fig. 6). Only the results for the WI calculation method are displayed (results from LRS showed the same trend).| 234U/238U (×10−4) | 235U/238U (×10−2) | 236U/238U (×10−5) | |||||
|---|---|---|---|---|---|---|---|
| WI | LRS | WI | LRS | WI | LRS | ||
| LEU | Isotope ratio measured by TIMS (absolute internal precision) | 3.2 (±1.0) | 3.3 (±0.4) | Not detected | |||
| Measured average isotope ratio | 5.1 | 4.1 | 3.2 | 2.8 | 2.0 | 2.1 | |
| External precision (SD/RSD) | 2.5/49% | 2.3/56% | 0.4/13% | 0.5/17% | 0.9/44% | 1.9/90% | |
| Average internal precision (absolute/relative) | 4.0/57% | 0.6/12% | 0.2/7% | 0.1/4% | 5.7/277% | 0.5/22% | |
| Relative difference with TIMS average value | 62% | 29% | −1% | −13% | — | — | |
| NU | Isotope ratio measured by TIMS (absolute internal precision) | 0.5 (±0.2) | 0.9 (±0.1) | Not detected | |||
| Measured average isotope ratio | 0.51 | 0.46 | 0.70 | 0.70 | 0.59 | 0.64 | |
| External precision (SD/RSD) | — | — | — | — | — | — | |
| Average internal precision (absolute/relative) | 0.07/13% | 0.01/3% | 0.01/1% | 0.01/1% | 0.3/49% | 0.05/8% | |
| Relative difference with TIMS average value | −2% | −13% | −18% | −18% | — | — | |
For higher 234U integrated counts, the internal precision is improved and the isotope ratio is in better agreement with TIMS values. Particles presenting 234U signal above 250 counts provided 234U/238U isotope ratios within the uncertainties of the TIMS measured values and an internal precision below 10%. This corresponds to particles with equivalent diameters above 0.5 μm.
For 236U/238U ratios the numbers of integrated counts for 236U (6 to 198 counts) were smaller than those for 234U. By choosing appropriate selection criteria (50 integrated counts for 236U), an acceptable (lower than 20%) internal precision was obtained (18% and 8% for WI and LRS respectively) for particles where more than 50 counts were obtained for 236U. However, internal precision was higher than for the 234U/238U ratios, and the isotopic ratios were more dispersed (relative internal precisions between 46% and 58% for WI and LRS respectively) than for the 234U/238U ratios. 236U was not detected by TIMS; hence no relative difference could be calculated.
Lastly, one can argue that this method would lack specificity as in the case of a mixture of particles since only a random number of particles can be analysed and a specific particle cannot be allocated individually. However, this is also true for the fission tracks – TIMS technique, which has been however successfully employed since many years for ‘particle analyses’ (the majority of the safeguard samples are presently always analysed with this technique).
The situation is different with modern SIMS instruments that are now equipped with automated software which performs an isotopic screening of the deposition disk: although many false detections may occur (because of polyatomic interferences) all uranium particles (at least the ones which are large enough) are detected and a limited number of these particles can be selected for precise isotopic analysis (micro-beam mode of the SIMS).
It should also be mentioned that, like with the other two methods used for particle analysis (fission tracks – TIMS and SIMS), only a finite number of particles are analysed. The goal of ‘particle analysis’ is to measure as precisely as possible the isotopic composition of a representative, statistically significant number of uranium particles. To improve the confidence in the detected uranium isotopic compositions in a sample, a larger number of particles must be analysed. However, precise isotopic analysis is time consuming so that at most 20 to 30 particles are usually analysed per sample, either by fission tracks – TIMS or SIMS (provided the sample contains sufficient uranium particles). One of the major advantages of LA-ICP-MS over the other techniques is that the analysis is faster (typically a few tens of seconds per analysis) once the material to analyse has been localized. This represents a significant gain of time compared to TIMS where the particles need in addition to be manipulated one by one. Therefore, a larger number of particles can be analysed by LA-ICP-MS than by TIMS and SIMS within a day.
Estimation of the overall uncertainty
From the results gathered in Table 4, it appears that average ‘internal precisions’ measured for each particle are clearly lower than the ‘external precisions’ calculated as the standard deviations of the results obtained by analyzing a set of particles from the same standard material (here the NBS U010 CRM) which are expected to have all the same isotopic composition. The ‘internal precisions’ obviously do not account for various biases which lead to relatively large dispersions of the isotopic ratios for particles of the same material. Most of these biases certainly arise from the nature of the signals produced by the measurement of an individual ablation fragment. Actually, these signals are very short (shorter than the dwell times of 2 ms or 5 ms used with the instrument) and their intensity varies over several orders of magnitude, reaching very high count rates, so that several acquisition modes (ion counting in the pulse counting mode or in the analog mode, Faraday cup) with different behaviors toward highly transient signals are involved. However, the ‘external precisions’ reported in Table 4 certainly take into account both the ‘internal precision’ and the various biases due to the detector (dead time, non-linearity) as particles with a very large range of 238U count rates were analyzed (see Fig. 4). Biases produced by the highest 238U count rates can hardly be estimated because of the large dispersion of the individual results.Signals for blanks are clearly negligible as, when the analysis is performed on a ‘blank disk’ (only polycarbonate and collodion), only a very low intensity signal at the mass to charge ratio of 238U is recorded. No signals are detectable at the mass to charge ratios of other uranium isotopes. Similarly, memory effect and effect of polyatomic interferences are neglected. In this study, results were not corrected from mass bias. Mass bias correction can be estimated from measurements of standard solutions, assuming that mass bias is the same in the laser ablation mode as in the liquid nebulization introduction mode. Measurements show that mass bias leads at most to a relative deviation of ∼0.6% of the 235U/238U ratios (and so of ∼0.8% of the 234U/238U ratios and of ∼0.4% of the 236U/238U ratios).
So, the global contributions of the precision and of the bias due to the detector, experimentally determined and given as ‘external precisions’ in Table 4, are obviously the major source of uncertainty for all isotope ratios. As a consequence, global standard-uncertainties of the method can be reduced to the ‘external precisions’ reported in Table 4i.e. ∼5% for the 235U/238U ratio and ∼12% for the 234U/238U and 236U/238U ratios.
Conclusions
The results of this study show that the coupling of an fs-UV-LA device with an ICP-SFMS enables the measurement of all isotope ratios (234U/238U, 235U/238U and 236U/238U) in single uranium micrometric and sub-micrometric particles after localization of the particles by means of suitable methods (SEM or fission tracks). The high sensitivity of the ICP-SFMS enhanced by the ‘Jet Interface’ provides detection limits in the range of a few tens of attograms for all uranium isotopes. Several possible limitations of this technique for application to analysis of particles extracted from “real-life” samples were studied and discussed. By performing ‘imaging LA-ICP-MS’ around craters resulting from particle ablation, random deposition of particle debris representing between 0.4% and 3.5% of the mass of the initially ablated particle was observed in the surrounding area. To prevent any contaminations that could lead to isotopic ratio bias (if particles with different isotopic compositions are present in the sample), the analysed particles must be separated, after deposition on polycarbonate disks, by at least 200 μm. The presence of “spikes” in the recorded signals is also a limitation for the accuracy and precision of the measurement of isotopic ratios in single particles. The duration of the signal produced by the analysis of single ablation fragments that comprised the aerosol is less than the time of measurement per isotope (‘dwell time’), thus, signals recorded for each isotope during a measurement cycle are not correlated with each other. Spikes that correspond to the arrival of large ablation fragments or of a high density of ablation fragments are not registered for all isotopes with a single collector instrument. This leads to biases in the isotope ratios and to limited precision. Implementation of a spike rejection filter greatly improves both accuracy and precision in all isotope ratios although systematic biases with respect to certified ratios in particles from a certified reference material (NBS U010) are always observed. The remaining biases may be due to deviation from the linearity of the analog mode of the detector for high count rates (higher than 108 cps) for the most abundant isotope (238U) which are not eliminated by the spike rejection filter. Three methods of calculation of the isotope ratios were compared. Weighed integration and linear regression slope methods give the best agreement with the certified isotopic composition of NBS U010 standard despite the deviation possibly linked to the use of the analog acquisition mode of the detector. Biases from the certified ratios were 5% and 3% for 234U/238U, 1.4% and 0.7% for 235U/238U, and 7% and 4% for 236U/238U for the WI and LRS methods respectively. It should be noted that LRS has the advantage of taking 100% of the signal, whereas WI rejects 1% of the signal.Lead particles around micrometric uranium particles did not produce a significant level of lead-based polyatomic species. Therefore, no bias in the 234U/238U ratios was observed. It should be noted that smaller, sub-micrometric, uranium particles might be affected by this lead-based interference. Finally, major and, for the first time, minor isotopes of uranium particles extracted from a real-life swipe sample were successfully measured in individual sub-micrometric particles. Moreover, 234U/238U and 235U/238U ratios were consistent with the values measured by TIMS for all analysed particles. 236U was not detected by TIMS. Acceptable relative precision (less than 20%) was obtained for minor isotope ratios (234U/238U and 236U/238U) for particles with a diameter larger than 0.5 μm. Thus, the LA-ICP-MS technique presents advantages for the so-called ‘particle analysis’ but faces instrumental limitations when using a single-collector instrument. This limitation might be eliminated by using a multi-collector ICP-MS, for which all isotopic signals are registered simultaneously.
Acknowledgements
The authors would like to thank Olivier Marie (CEA) for providing SEM images and location of uranium and lead particles by SEM. Region Aquitaine and Feders are also thanked for instrument funding.Notes and references
- D. Donohue, J. Alloys Compd., 1998, 271–273, 11–18 CrossRef CAS.
- D. L. Donohue, Anal. Chem., 2002, 74, 28A–35A CrossRef CAS.
- M. Kraiem, S. Richter, H. Kühn, E. a. Stefaniak, G. Kerckhove, J. Truyens and Y. Aregbe, Anal. Chem., 2011, 83, 3011–3016 CrossRef CAS PubMed.
- Y. Chen, Y. Shen, Z.-Y. Chang, Y.-G. Zhao, S.-L. Guo, J.-Y. Cui and Y. Liu, Radiat. Meas., 2013, 50, 43–45 CrossRef CAS.
- Y. Ranebo, P. M. L. Hedberg, M. J. Whitehouse, K. Ingeneri and S. Littmann, J. Anal. At. Spectrom., 2009, 24, 277–287 RSC.
- G. Tamborini, M. Betti, V. Forcina, T. Hiernaut, B. Giovannone and L. Koch, Spectrochim. Acta, Part B, 1998, 53, 1289–1302 CrossRef.
- M. Kraiem, K. Mayer, T. Gouder, A. Seibert, T. Wiss and J.-P. Hiernaut, J. Anal. At. Spectrom., 2010, 25, 1138–1144 RSC.
- F. Esaka, K. T. Esaka, C. G. Lee, M. Magara, S. Sakurai, S. Usuda and K. Watanabe, Talanta, 2007, 71, 1011–1015 CrossRef CAS PubMed.
- F. Pointurier, A. Hubert and A.-C. Pottin, J. Radioanal. Nucl. Chem., 2012, 296, 609–616 CrossRef.
- F. Pointurier, A. C. Pottin and A. Hubert, Anal. Chem., 2011, 83, 7841–7848 CrossRef CAS PubMed.
- S. Kappel, S. F. Boulyga, L. Dorta, D. Günther, B. Hattendorf, D. Koffler, G. Laaha, F. Leisch and T. Prohaska, Anal. Bioanal. Chem., 2013, 405, 2943–2955 CrossRef CAS PubMed.
- S. Kappel, S. F. Boulyga and T. Prohaska, J. Environ. Radioact., 2012, 113, 8–15 CrossRef CAS PubMed.
- Z. Varga, Anal. Chim. Acta, 2008, 625, 1–7 CrossRef CAS PubMed.
- A. Hubert, F. Claverie, C. Pécheyran and F. Pointurier, Spectrochim. Acta, Part B, 2014, 93, 52–60 CrossRef CAS.
- Y. Nir-El, Appl. Radiat. Isot., 2000, 52, 753–757 CrossRef CAS PubMed.
- T. Hirata and R. W. Nesbitt, Geochim. Cosmochim. Acta, 1995, 59, 2491–2500 CrossRef CAS.
- S. A. Crowe, B. J. Fryer, I. M. Samson and J. E. Gagnon, J. Anal. At. Spectrom., 2003, 18, 1331–1338 RSC.
- M. Aramendía, M. Resano and F. Vanhaecke, J. Anal. At. Spectrom., 2010, 25, 390–404 RSC.
- G. P. Russ III, Application of inductively coupled plasma mass spectrometer, Blackie, Glasgow, 1989 Search PubMed.
- J. Fietzke, V. Liebetrau, D. Günther, K. Gürs, K. Hametner, K. Zumholz, T. H. Hansteen and A. Eisenhauer, J. Anal. At. Spectrom., 2008, 23, 955–961 RSC.
- V. N. Epov, S. Berail, M. Jimenez-Moreno, V. Perrot, C. Pecheyran, D. Amouroux and O. F. X. Donard, Anal. Chem., 2010, 82, 5652–5662 CrossRef CAS PubMed.
- A. Gourgiotis, S. Bérail, P. Louvat, H. Isnard, J. Moureau, A. Nonell, G. Manhès, J.-L. Birck, J. Gaillardet, C. Pécheyran, F. Chartier and O. F. X. Donard, J. Anal. At. Spectrom., 2014, 29, 1607–1617 RSC.
- M. Tanner and D. Günther, Anal. Chim. Acta, 2009, 633, 19–28 CrossRef CAS PubMed.
- A. M. Duffin, G. L. Hart, R. C. Hanlen and G. C. Eiden, J. Radioanal. Nucl. Chem., 2013, 296, 1031–1036 CrossRef CAS.
- R. Glaus, R. Kaegi, F. Krumeich and D. Günther, Spectrochim. Acta, Part B, 2010, 65, 812–822 CrossRef.
- K. J. R. Rosman, W. Lycke, R. Damen, R. Werz, F. Hendrickx, P. De Bievre and L. Traas, Int. J. Mass Spectrom. Ion Processes, 1987, 79, 61–71 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |