U–Pb age determination for zircons using laser ablation-ICP-mass spectrometry equipped with six multiple-ion counting detectors†
Kentaro
Hattori
a,
Shuhei
Sakata
b,
Michitaka
Tanaka
a,
Yuji
Orihashi
c and
Takafumi
Hirata
*ad
aGraduate School of Science, Kyoto University, Kitashirakawa Oiwakecho, Sakyo-ku, Kyoto 606-8502, Japan
bDepartment of Chemistry, Gakushuin University, Mejiro 1-5-1, Toshima-ku, Tokyo 171-8588, Japan
cEarthquake Research Institute, The Univ. Tokyo, Yayoi 1-1-1, Tokyo 113-0032, Japan
dGeochemistry Research Center, Graduate School of Science, The University of Tokyo, Hongo, Tokyo, 113-0033, Japan. E-mail: hrt1@eqchem.s.u-tokyo.ac.jp; Tel: +81-35841-4621
First published on 20th October 2016
Abstract
Precise zircon U–Pb age determinations have been made on Plešovice zircon using laser ablation-multiple ion counting-inductively coupled plasma-mass spectrometry (LA-MIC-ICP-MS). To achieve high precision and high spatial resolution age determination, multiple ion counting using six electron multipliers was employed. The intensities of Hg–Pb–U isotope (202Hg, 204(Hg + Pb), 206Pb, 207Pb, 208Pb, and 238U) signals were monitored simultaneously without mass scanning. In static acquisition mode, the resultant 238U–206Pb concordia age for Plešovice was 336.3 ± 1.9 Ma, demonstrating improved precision over that achieved using a magnetic sector-based single-collector-ICP-MS, which was 340.3 ± 3.5 Ma for Plešovice. A high duty cycle can be achieved, along with a short integration time or a small sample volume for analysis, allowing high spatial resolution. More importantly, downhole fractionation can be reduced with a shallow ablation pit. To take full advantage of the setup, a one-second LA analysis (8 laser shots with an 8 Hz repetition rate) was adopted for U–Pb age determination. The resultant concordia age for Plešovice was 339.5 ± 6.7 Ma, demonstrating that the repeatability and laboratory bias precision of the resultant age data were comparable to conventional ablation with a single-collector-ICP-MS. The depths and crater diameters of the ablation pits were, respectively, about >1 μm and 25 μm. The data presented herein demonstrate clearly that multiple ion counting-ICP-MS can become a fast and user-friendly tool for use in U–Pb zircon geochronology.
Introduction
Zircon has been widely used to decode both the geochemical and geochronological backgrounds of samples.1,2 Conventional bulk dating using isotope dilution thermal ionization mass spectrometry (ID-TIMS) has been widely used.3–8 It is widely recognized that the U–Th–Pb isotopic data obtained using the TIMS technique can become the benchmark data for most of the calibration protocols used in many analytical techniques. Along with this benefit, it is true that some zircon grains can have complex textures or heterogeneous distribution of U–Pb isotopes. Schmitt et al. reported that the U–Th–Pb age determined from an overgrown thin layer of a zircon crystal was significantly less than that determined from the core of the zircon.9 This result is explainable either by the secondary growth of the rim through a magmatic process, or by the delay of the start of a U–Th–Pb chronometer attributable to the isotopic diffusion caused by decompression or by rapid cooling in the host magma.9,10 This explanation suggests that the chronological data obtained from the in situ or thin-outer layer can provide information related to conditions of a magma chamber or the chronological constraints on the magmatic processes. In fact, many pioneering studies have revealed that an in situ U–Th–Pb isotopic analysis can provide reliable chronological information. Another analytical problem associated with the TIMS technique is that the technique requires both high analytical skills and longer analysis time. Recent applications have demonstrated that an age histogram based on large amounts of zircon U–Pb age data provides key information related to the geological settings of the sample.11,12 To achieve this, a U–Pb isotopic analysis can be conducted by the application of a probing technique such as secondary ion mass spectrometry (SIMS),13–16 or ICP-MS along with laser ablation sampling (LA-ICP-MS).17–19This study used LA-ICP-MS combined with a multiple-collector system setup to improve the precision and the spatial resolution of the in situ U–Pb isotopic analysis. Using the multiple collector system setup, the analytical precision of the isotope ratio measurements can be improved even from very unstable or transient signals.20–22 However, it is noteworthy that, even with the multiple collector system, the resulting precision and accuracy of isotope ratio measurements can be degraded under the large contribution of signal spikes. The contribution of the signal spikes, which are widely found in signal intensity profiles obtained using the LA sampling technique, can be an important source of analytical errors.23–25 In fact, the resulting precision in the isotope ratio measurements achieved by the LA technique is generally poorer than that achieved using the solution introduction technique. This poor precision can be attributed to the slow response of the Faraday amplifiers.8,26–28
To minimize the contribution of the unstable signal intensity profile, a signal smoothing device is applicable to obtain further precise isotope data.29 Despite marked success in achieving high precision in isotope ratio measurements, the application of multiple-Faraday collectors can be retarded by the lower sensitivity of the collectors. To achieve further high spatial resolution of the analysis, the MC-ICP-MS system equipped with a multiple ion counting system is expected to be an effective approach. Johnston et al. reported precise in situ U–Pb isotopic ratio data obtained using a multiple-ion counting system applied to the ICP-MS technique.30 Bühn et al. reported precise U–Pb isotopic data using the multiple-ion counting system.31 Despite considerable success in achieving higher precision in the Pb isotopic ratio measurements, the depths of the resulting ablation pits were 4–40 μm, suggesting a restricted analytical capability of LA-ICP-MS in U–Pb dating from the outer thin-layer region.
Recently, precise U–Pb isotopic ratio data from zircons using MC-ICP-MS equipped with multiple Faraday cups have been reported.27,28 To enhance the Faraday detector sensitivity, a 1012 ohm resistor, rather than a conventional 1011 ohm resistor, was used to measure the U–Pb isotopic ratios.8 Because of the slow response of Faraday amplifiers, the ion signal stability is a key factor in realizing precise isotopic ratio measurements using the 1012 ohm resistor. To achieve higher stability, a large ablation pit (30 μm diameter, 20 μm depth) for U–Pb isotopic analysis was adopted.27 Despite better precision of the Pb/U isotope ratio measurements, the analytical capability of this technique for U–Pb dating for small zircon grains is expected to be limited mainly by deeper ablation pits, which can enhance the risk of laser ablation of secondary inclusions, and by the large contribution of down-hole fractionation. With the larger aspect ratio craters, the measured Pb/U ratios can be susceptible to down-hole fractionation (i.e., time-dependent and matrix-dependent). Therefore, careful correction must be applied to obtain reliable U–Pb age determinations. Cottle et al. reported precise U–Pb isotopic ratio data from zircon using one-shot LA.19 The resulting ablation pit depth is as little as 1 μm. Therefore, high-resolution depth profiling can be achieved. This method has a high spatial resolution in depth but a low spatial resolution in diameter. For this study, to improve the high spatial resolution of U–Pb dating, a multiple ion counting-ICP-MS technique using six high-gain electron multipliers (MIC-ICP-MS) was used to achieve both high-precision U–Pb isotope ratio measurements and improved spatial resolution.
Experimental
ICP-MS and laser
The MIC-ICP-MS instrument used for this study was a multiple collector ICP-MS (Nu Plasma II; Nu Instruments Ltd., Wrexham, UK). Six full-size electron multipliers were used for the simultaneous detection of ion signals: 202Hg, 204(Hg + Pb), 206Pb, 207Pb, 208Pb, and 238U. The type of multipliers used for this study was an ETP discrete dynode electron multiplier (ETP model 14144; SGE Analytical Sciences/Trajan Scientific Australia Pty. Ltd., Australia). Ion-counting mode was used throughout this study.For comparison, a U–Pb isotope analysis was conducted in a single-collector-ICP-MS system. The ICP-MS instrument used for this study (Nu AttoM High-Resolution ICP-MS; Nu Instruments Ltd., Wrexham, UK) supported electrostatic scanning to monitor 202Hg, 204(Hg + Pb), 206Pb, 207Pb, 208Pb, and 238U signals.
The LA systems used for this study were the ESI NWR femto (ESI New Wave Research Inc., Oregon, USA) and the ESI NWR193 for one second ablation. A two-volume cell (TV1) was used throughout this study. Fluence is a key factor related to the minimization of the elemental fractionation during laser ablation.32 Lower fluence and lower repetition rates were useful for reducing elemental fractionation in the Pb/U ratio measurements. Moreover, down-hole fractionation can be minimized with the laser ablation with shallower crater depth. In this study, a fluence of about 2.0 J cm−2, a repetition rate of 8 Hz, and 20 laser shots were used. An ablation pit size of 25 μm was used for all analyses. To reduce the Hg background, a charcoal filter was applied to the Ar carrier gas.32,33 Commercially available charcoal granules designed specifically for Hg adsorption were packed in the filter (Shirasagi No. 4, Activated Carbon; Japan Envirochemicals Ltd., Osaka, Japan).
After the samples were set into the LA cell, He gas was flushed into the sample cell for at least 2 h. This step is extremely important for stabilizing UO+/U+ and mass fractionation factors for U–Pb isotopes. Before the U–Pb isotopic analysis, one-shot cleaning was used to remove the possible surface contamination of analytes through mineral separation, mounting, and polishing procedures.34
The ICP-MS operational settings were optimized by maximizing the 238U signal obtained from LA using National Institute of Standards and Technology Standard Reference Materials (NIST SRM) 612. After the optimization of the torch position and ion lens setting, the flow rate of the He carrier gas was adjusted to lower the ThO+/Th+ ratio to around 0.2% or less. This step is critically important for achieving a lower UO production rate for Pb/U ratio measurement by decreasing UO+ and increasing U+.
Because of the large contribution of signal spikes, the signal intensity profile obtained in the first 1 s was not used for calculations. The details of the instrumentation and operational settings are presented in Table 1 (20-shot dating).
| Laser ablation system | |
| Make, model & type | ESI/New Wave Research, NWR femto |
| Ablation cell | Two volume cell |
| Laser wavelength (nm) | 260 nm |
| Pulse width (ns) | <130 fs |
| Fluence (J cm−2) | 2.0 J cm−2 |
| Repetition rate (Hz) | 8 Hz |
| Ablation duration (s) | 2.5 s |
| Spot diameter (μm) | 25 μm |
| Sampling mode | Static spot ablation |
| Carrier gas | He in the cell, Ar make-up gas combined using a T-piece along the sample transport line to the torch |
| Cell carrier gas flow (L min−1) | 0.60 L min−1 |
| ICP-MS Instrument (Multiple collector-ICP-mass spectrometer) | |
| Make, model & type | Nu Instruments, Nu Plasmall HR-MC-ICP-MS |
| Sample introduction | Ablation aerosol |
| RF power (W) | 1300 W |
| Make-up gas flow (L min−1) | 0.70 L min−1 |
| Detection system | Mixed Faraday-multiple ion counting array |
| Monitored isotopes | 202Hg, 204(Hg + Pb), 206Pb, 207Pb, 208Pb, 232Th, 238U |
| Integration time per peak times (ms) | 200 ms for each isotope |
| Total integration time per reading (s) | 3 s |
| Detector | Six full size multipliers (IC) and one Faraday cup (H): IC0 for 208Pb, IC1 for 207Pb, IC2 for 206Pb, IC3 for 204(Hg + Pb), IC4 for 202Hg, IC5 for 238U and H8 for 232Th |
| IC dead time (ns) | 17.4, 22.1, 10.4, 12.6, 12.6 & 9.1 ns IC0, IC1, IC2, IC3, IC4 & IC5 resp. |
| ICP-MS Instrument (Single collector-ICP-mass spectrometer) | |
| Make, model & type | Nu Instruments, NuPlasma AttoM ICP-MS |
| Sample introduction | Ablation aerosol |
| RF power (W) | 1300 W |
| Make-up gas flow (L min−1) | 0.70 L min−1 |
| Detection system | Ion counting mode and ion-attenuated mode |
| Monitored isotopes | 202Hg, 204(Hg + Pb), 206Pb, 207Pb, 208Pb, 232Th, 238U |
| Integration time per peak times (ms) | 1 ms for each isotope |
| Total integration time per reading (s) | 5 s |
| Detector | One full size multiplier (IC): 202Hg, 204(Hg + Pb), 206Pb, 207Pb, 208Pb, 232Th and 238U |
| IC dead time (ns) | 12.2 ns for IC |
| Data processing | |
| Gas blank | 30 s on-peak zero subtracted |
| Calibration strategy | 91500 and NIST SRM 610 used as primary reference material |
| Data processing package used | Spreadsheet for data normalization, uncertainty propagation and age calculation |
| Common-Pb correction | No common-Pb correction applied to the data |
| Uncertainty level & propagation | Both the repeatability of the ratio measurements and counting statistics of the measured isotope signals were propagated35 |
| Normalization | 206Pb/238U = 0.17917 (zircon 91500)36 |
| 207Pb/206Pb = 0.9096 (NIST SRM 610)37 | |
| 238U/235U = 137.818 (zircon 91500)38 | |
| 238U/235U = 137.803 (Plešovice)38 | |
Dead time correction of the ion counters
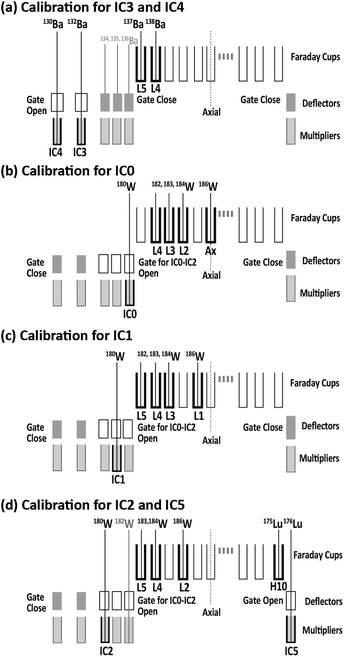
The dead time for each ion counter was ascertained by monitoring the counting losses of Ba, Lu, and W ion signals obtained through solution nebulization. Isotopic ratios (132Ba/137Ba, 130Ba/137Ba, 176Lu/175Lu, and 180W/182W) were measured using a combination of electron multipliers and Faraday collectors.Fig. 1 presents the collector arrangement for ion counting system measurements. To measure the dead time values for IC0, IC1, and IC2, the deviations in 180W(IC0, IC1, and IC2)/182W(Faraday) ratios were monitored by introducing W standard solutions of various concentrations. To measure the dead time values for IC3 and IC4, the deviations in 132Ba(IC3)/137Ba(Faraday) and 130Ba(IC4)/137Ba(Faraday) ratios were monitored by introducing the Ba solution. Finally, the dead time for IC5 was calculated according to changes in the 176Lu(IC5)/175Lu(Faraday) ratios through the introduction of the Lu solution. The dead time of the ion counting system was determined by analyzing the regression of the data points based on a non-paralyzed type of dead time correction.39 The resulting dead time values for the five ion-counting systems were 17.4 ± 1.2 ns for IC0, 22.1 ± 0.4 ns for IC1, 10.4 ± 0.9 ns for IC2, 12.6 ± 1.7 ns for IC3, 12.6 ± 0.9 ns for IC4, and 9.1 ± 0.5 ns for IC5 (uncertainties are 2SD calculated based on the sum of total deviations for each data point from the regression lines). Based on the format of Horstwood et al., these dead times are presented in Table 1.40
Data reduction
Instrumental mass bias, including the effect of oxide/metal ion yield of UO+/U+ on 206Pb/238U, was corrected externally by normalizing 206Pb/238U as 0.17917 for the Nancy standard zircon (Nancy 91500).36 The gains of the multipliers and mass biases on the 207Pb/206Pb for the 207Pb/206Pb ratio measurements (IC1/IC2) were calibrated externally by monitoring the 207Pb/206Pb ratio through the laser ablation of NIST SRM 610 (207Pb/206Pb = 0.9096).37 Data acquisitions for all primary reference materials and samples were conducted under identical analytical conditions.The analytical session included one gas blank measurement for 30 s, three-time-repeated U–Pb isotope analyses for NIST SRM 610 and Nancy 91500 zircons, and 15-time repeated U–Pb analyses from 15 spots on the same zircon grain. The signals obtained from laser ablation were integrated. The averaged 206Pb/238U and 207Pb/206Pb of Nancy 91500 zircon and NIST SRM 610 were used for both gain calibration between ion counters and the correction of Pb/U and Pb/Pb fractionation during laser ablation. The background counts were calculated by averaging two gas blank counts obtained before and after the measurements of the Nancy 91500 zircon. In addition, a blank subtraction correction was conducted by interpolating the two averaged background counts. In this study, the signal intensity of 235U in Nancy 91500 zircons was calculated based on the signal intensity of 238U by normalizing the 238U/235U ratio as 137.818.38 Uncertainties from the Pb/U and Pb/Pb isotopic ratio measurements for the primary reference material and the counting statistics for each analyte were used to estimate the overall uncertainties for the resulting age data. We used the equations of Sakata et al. to calculate error propagation in the 206Pb/238U and 207Pb/235U ratios.35 The U–Pb concordia age was calculated using the Isoplot 3.75 program of Ludwig.41
Results and discussion
Mid-term stability of the ion counter
To evaluate the mid-term stability of the multiple ion counting system, the 206Pb (IC2)/238U (IC5) ratio was monitored for 1000 min, or approximately 17 h. The 206Pb/238U ratio was obtained every 10 min using laser ablation of Nancy 91500. The resultant 206Pb and 238U signals were integrated for 10 s. The 206Pb/238U ratios obtained using single collector-ICP-MS and MIC-ICP-MS are shown against the elapsed time (Fig. 2). No correction for the mass bias factor was made for either the single-collector-ICP-MS or MIC-ICP-MS measurements. With the single-collector-ICP-MS, the overall changes in the measured 206Pb/238U ratios were 6%. This change is almost comparable to the uncertainties in the 206Pb/238U measurements. For MIC-ICP-MS, the variation of the individual 206Pb/238U measurement is remarkably smaller than that found in the single collector instrument. Despite this, the 206Pb/238U ratio increased systematically to 5% through the analysis sequence. The observations indicate that the improved repeatability in multiple ion counting revealed a mid-term drift of Pb/U perhaps because of instrumental drift. Systematic drift in UO+/U+ yield and mass fractionation in Pb isotopes were reported by Kimura et al. using multiple Faraday-ICP-MS.28 This study confirmed the drift even with the low UO+/U+ setting. Based on the data obtained here, the calibration of the Pb/U ratio should be conducted every 1–2 h to minimize the contribution from these factors.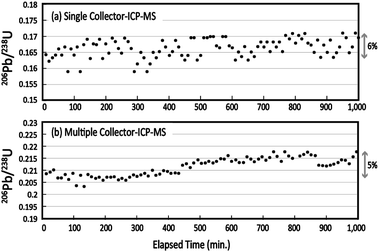 | ||
| Fig. 2 Medium-term stability in the measured 206Pb/238U ratio obtained by (a) single collector-ICP-MS and (b) multiple collector-ICP-MS. | ||
U–Pb age determination using 20-shot laser ablation
In this study, the U–Pb ages were obtained for a zircon material. This material is Plešovice zircon collected from metamorphic rocks in the Bohemian Massif (Plešovice, Czech Republic).42 The 238U–206Pb age was 337.13 ± 0.37 Ma (weighted average), as determined by ID–TIMS.42The U–Pb isotopic data obtained using the single-collector-ICP-MS, combined with the femtosecond laser ablation system, are depicted in Fig. 3(a). All the U–Pb isotopic data were obtained from identical grains for Plešovice throughout this study. Despite the slight scattering of the resultant U–Pb isotopic data, the measured 206Pb/238U and 207Pb/235U ratios fell close to the concordia curve. The resultant concordia age was 340.3 ± 3.5 Ma (RSD = 1.0%, n = 15, MSWD = 2.2) for Plešovice. The U–Pb isotopic data obtained by MIC-ICP-MS using the multiple ion counting system are shown on the concordia diagram (Fig. 3(b)). The measured concordia age was 336.3 ± 1.9 Ma (RSD = 0.6%, n = 15, MSWD = 0.35) for Plešovice. The resultant uncertainties in the 206Pb/238U and 207Pb/235U ratio measurements are significantly smaller than those found in the U–Pb isotopic data obtained using the single-collector-ICP-MS. The measured concordia age for Plešovice shows excellent agreement with age data obtained both by present single-collector-ICP-MS analysis (340.3 ± 3.5 Ma) and the reported ID-TIMS (337.13 ± 0.37 Ma). The U–Pb age data for Plešovice clearly demonstrate the feasibility of both the system setup and the calibration protocol adopted for this study.
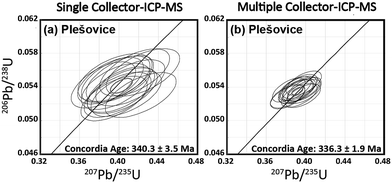 | ||
| Fig. 3 Plot of 206Pb/238U versus207Pb/235U ratios (concordia diagram) for Plešovice zircon obtained by the femtosecond LA-ICP-MS technique. | ||
The spatial resolution achieved in this study was 25 μm in diameter and >1 μm in depth, whereas Cottle et al. used the condition of 35 μm diameter and 0.13 μm depth.43 Along with the lower spatial resolution achieved here, the precision of the weighted mean 238U–206Pb age (0.5%, 2SE, MSWD = 0.06) was significantly better than that obtained by Cottle et al. (0.9%, 2SE, MSWD = 1.3).43 This lower precision by Cottle et al.43 is attributable mainly to the slow response of the Faraday amplifier used for monitoring 238U. For better analytical precision and high spatial resolution, the multiple ion counting (MIC) system setup can become another flexible approach for in situ U–Pb isotope ratio measurements.
U–Pb age determination using 1 s laser ablation
The aspect ratio of depth against diameter of a crater formed by LA is an important parameter to control elemental fractionation during the LA.44 Therefore, when longer LA is employed, the crater can have a higher aspect ratio, which introduces uncertainties in the Pb/U ratio measurement. In contrast, the fewer laser shots in the U–Pb isotope ratio measurement improve the spatial resolution and reduce the elemental fractionation during the analysis. Moreover, the U–Pb isotope analysis from the shallower ablation pit can provide key information related to U–Pb ages for the outer thin layers of the zircon grains.9 We have tried to obtain U–Pb age data with a smaller laser shot number. In this study, a total LA time of 1 s was employed to obtain the U–Pb isotope ratio data from 15 spots on a single grain of Plešovice; the total number of laser shots, 8, corresponds to the repetition rate of 8 Hz. To achieve very thin layer sampling, an ArF Excimer laser (NWR Ex ESI Portland, US), operating at a wavelength of DUV 193 nm, was used in this measurement. For 206Pb and 207Pb, we used Daly detectors instead of multipliers. The details of instrumentation and operational settings are presented in Table 2 (1 s dating).| Laser ablation system | |
| Make, model & type | ESI/New Wave Research, NWR Ex |
| Ablation cell | Two volume cell |
| Laser wavelength (nm) | 193 nm |
| Pulse width (ns) | <4 ns |
| Fluence (J cm−2) | 1.5–1.6 J cm−2 |
| Repetition rate (Hz) | 8 Hz |
| Ablation duration (s) | 1 s |
| Spot diameter (μm) | 25 μm |
| Sampling mode | Static spot ablation |
| Carrier gas | He in the cell, Ar make-up gas combined using a T-piece along the sample transport line to the torch |
| Cell carrier gas flow (L min−1) | 0.53 L min−1 |
| ICP-MS Instrument | |
| Make, model & type | Nu Instruments, Nu Plasmall HR-MC-ICP-MS |
| Sample introduction | Ablation aerosol |
| RF power (W) | 1300 W |
| Make-up gas flow (L min−1) | 0.70 L min−1 |
| Detection system | Mixed Faraday-multiple ion counting array |
| Monitored isotopes | 202Hg, 204(Hg + Pb), 206Pb, 207Pb, 208Pb, 232Th, 238U |
| Integration time per peak times (ms) | 200 ms for each isotope |
| Total integration time per reading (s) | 3 s |
| Detector | Four full size multipliers (IC), two daly detectors (D) and one faraday cup (H): IC0 for 208Pb, D1 for 207Pb, D2 for 206Pb, IC3 for 204(Hg + Pb), IC4 for 202Hg, IC5 for 238U and H8 for 232Th |
| IC dead time (ns) | 15.8, 20.0, 8.6, 14.7, 18.9 & 20.0 ns IC0, D1, D2, IC3, IC4 & IC5 resp. |
With the signal smoothing device adopted in this study, the duration time was about 3 s. Because of the large contribution of signal spikes, the signal intensity profile obtained in the first 1 s was not used for additional calculations. After discarding the signals of the first 1 s as a preablation, a total of 3 s signals were used for calculations, suggesting that the overall duty cycle achieved in 1 s ablation was higher than 70%.
After U–Pb age determination using 1 s laser ablation, the diameter and depth of the resulting ablation pit were 25 μm and <1 μm, respectively, as estimated using a high-magnification microscope with 2000× magnification (Leica DVM5000 HD digital microscope; Leica Microsystems, Germany). The U–Pb isotope ratio values were calculated in the same manner as that used for 20-shot dating. The U–Pb isotope ratio data obtained with 1 s ablation is shown in the concordia diagram (Fig. 4). The resultant U–Pb concordia age for Plešovice is 339.5 ± 6.7 Ma (RSD = 2.0%, n = 15, MSWD = 0.65). This is consistent with both the data from the literature (337.13 ± 0.37 Ma)42 and those obtained from conventional continuous LA (336.3 ± 1.9 Ma; Fig. 3(b)). The resultant uncertainties obtained with 1 s ablation for Plešovice (RSD = 2.0%) are significantly poorer than the 0.6% achieved using conventional continuous LA (Fig. 3(b)). This poorer result is attributable to the large contribution of the counting statistics for 206Pb and 207Pb signals. Although the spatial resolution in depth is lower than that reported by Schmitt et al.,9 this method might decode some volcanic activity and be applicable to younger zircons. The precision of the U–Pb age determination achieved by 1 s LA was comparable to that obtained using the single collector-ICP-MS system combined with the continuous LA for 20-shot dating (Fig. 3(b)).
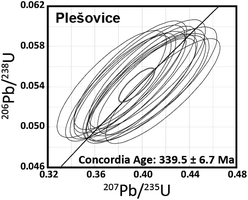 | ||
| Fig. 4 206Pb/238U and 207Pb/235U ratio data for Plešovice zircon obtained by the multiple ion counting-ICP-MS technique involving 1 s laser ablation using ArF excimer laser ablation. | ||
Conclusion
In this study, six U–Pb isotopes' signals, 202Hg, 204(Hg + Pb), 206Pb, 207Pb, 208Pb, and 238U, were obtained from the LA of zircon materials. These isotopes were measured simultaneously using a multiple ion counting system with six full-sized ion multipliers equipped on a magnetic sector-based ICP-MS. With the present multiple ion counting system, uncertainties in the U–Pb age determination showed significant improvements over those achieved using the single-collector system setup.The MC application remarkably intensified the overall duty cycle collection efficiency of the ion signals, which suggests that each isotope can be analyzed even under a shorter ablation time. In fact, a shorter ablation time (e.g., 1 s) can produce a shallower ablation pit depth. The precision of the U–Pb concordia age for Plešovice (RSD = 2.0%) was significantly poorer than that achieved using conventional continuous LA (RSD = 0.6%). With the shorter ablation time, signal intensities for the analyses are expected to become very small. Moreover, the smaller ion beam size produced by the shorter ablation time can induce a large contribution of the counting statistics originating from the small total number of analytes produced through the LA of a small sample volume. It is noteworthy that the uncertainty obtained from 1 s ablation is comparable to that achieved by the single collector-ICP-MS system setup combined with conventional continuous LA.
Acknowledgements
The authors thank Drs H. Iwano and T. Danhara (Kyoto Fission-Track Co. Ltd., Japan); Y. Kon (Agency for Industry and Scientific Technology); T. Iizuka (The University of Tokyo, Japan); R. W. Nesbitt and A. Milton (University of Southampton, UK); Ciaran O'Connor (ESI New Wave Research Inc., USA) and D. Günther (ETH Zurich, Switzerland) for offering valuable scientific advice. We are also grateful to anonymous reviewers. Critical comments given by the reviewers were highly valuable to improve the manuscript. This work was partly supported by a Grant-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science and Technology, Japan for TH (A26247094).References
- P. W. Hoskin and U. Schaltegger, Rev. Mineral. Geochem., 2003, 53(1), 27–62, DOI:10.2113/0530027.
- D. J. Cherniak and E. B. Watson, Rev. Mineral. Geochem., 2003, 53(1), 113–143, DOI:10.2113/0530113.
- T. E. Krogh, Geochim. Cosmochim. Acta, 1982, 46, 631–636, DOI:10.1016/0016-7037(82)90165-X.
- B. R. Schöne, J. Lega, K. W. Flessa, D. H. Goodwin and D. L. Dettman, Palaeogeogr., Palaeoclimatol., Palaeoecol., 2002, 184(1–2), 131–146, DOI:10.1016/S0031-0182(02)00252-3.
- B. Schoene, C. Latkoczy, U. Schaltegger and D. Günther, Geochim. Cosmochim. Acta, 2010, 74, 7144–7159, DOI:10.1016/j.gca.2010.09.016.
- B. Schoene, U. Schaltegger, P. Brack, C. Latkoczy, A. Stracke and D. Günther, Earth Planet. Sci. Lett., 2012, 355–356, 162–173, DOI:10.1016/j.epsl.2012.08.019.
- U. Schaltegger, A. K. Schmitt and M. S. A. Horstwood, Chem. Geol., 2015, 402, 89–110, DOI:10.1016/j.chemgeo.2015.02.028.
- A. von Quadt, J. –F. Wotzlaw, Y. Buret, S. J. E. Large, I. Peytcheva and A. Trinquier, J. Anal. At. Spectrom., 2016, 31, 658–665, 10.1039/C5JA00457H.
- A. K. Schmitt, D. F. Stockli, J. M. Lindsay, R. Robertson, M. Lovera and R. Kislitsyn, Earth Planet. Sci. Lett., 2010, 295, 91–103, DOI:10.1016/j.epsl.2010.03.028.
- J. Lowenstern, H. Persing, J. Wooden, M. Lanphere, J. Donnelly Nolan and T. Grove, Earth Planet. Sci. Lett., 2000, 183(1), 291–302, DOI:10.1016/S0012-821X(00)00273-9.
- S. Rino, T. Komiya, B. F. Windley, I. Katayama, A. Motoki and T. Hirata, Phys. Earth Planet. Inter., 2004, 146(1), 369–394, DOI:10.1016/j.gr.2008.01.001.
- U. Schaltegger, A. Schmitt and M. Horstwood, Chem. Geol., 2015, 402, 89–110, DOI:10.1016/j.chemgeo.2015.02.028.
- W. Compston, I. S. Williams and C. Meyer, J. Geophys. Res.: Solid Earth, 1984, 89, B525–B534, DOI:10.1029/JB089iS02p0B525.
- T. R. Ireland and F. Wlotzka, Earth Planet. Sci. Lett., 1992, 109(1), 1–10, DOI:10.1016/0012-821X(92)90069-8.
- S. A. Bowring and I. S. Williams, Contrib. Mineral. Petrol., 1999, 134(1), 3–16, DOI:10.1007/s004100050465.
- J. W. Goodge, P. Myrow, I. S. Williams and S. A. Bowring, J. Geol., 2002, 110(4), 393–406, DOI:10.1086/340629.
- T. Iizuka and T. Hirata, Chem. Geol., 2005, 220(1), 121–137, DOI:10.1016/j.chemgeo.2005.03.010.
- T. Iizuka, K. Horie, T. Komiya, S. Maruyama, T. Hirata, H. Hidaka and B. F. Windley, Geology, 2006, 34, 245–248, DOI:10.1130/G22124.1.
- J. Cottle, M. Horstwood and R. R. Parrish, J. Anal. At. Spectrom., 2009, 24(10), 1355–1363, 10.1039/B821899D.
- A. J. Walder, I. Platzner and P. A. Freedman, J. Anal. At. Spectrom., 1993, 8(1), 19–23, 10.1039/JA9930800019.
- M. F. Thirlwall and A. J. Walder, Chem. Geol., 1995, 122, 241–247, DOI:10.1016/0009-2541(95)00003-5.
- J. M. Cottle, A. J. Burrows, A. R. Kylander-Clark, P. A. Freedman and R. S. Cohen, J. Anal. At. Spectrom., 2013, 28(11), 1700–1706, 10.1039/C3JA50216C.
- D. Günther and C. A. Heinrich, J. Anal. At. Spectrom., 1999, 14(9), 1363–1368, 10.1039/A901648A.
- R. Russo, X. Mao, C. Liu and J. Gonzalez, J. Anal. At. Spectrom., 2004, 19(9), 1084–1089, 10.1039/B403368J.
- M. Guillong, A. von Quadt, S. Sakata, I. Peytcheva and O. Bachmann, J. Anal. At. Spectrom., 2014, 29, 963–970, 10.1039/C4JA00009A.
- T. Hirata, Y. Hayano and T. Ohno, J. Anal. At. Spectrom., 2003, 18(10), 1283–1288, 10.1039/B305127G.
- J. Kimura, Q. Chang, K. Itano, T. Iizuka, B. S. Vaglarov and K. Tani, J. Anal. At. Spectrom., 2015, 30(2), 494–505, 10.1039/C4JA00257A.
- J. Kimura, Q. Chang, N. Kanazawa, S. Sasaki and B. S. Vaglarov, J. Anal. At. Spectrom., 2016, 31(3), 790–800, 10.1039/C5JA00374A.
- A. Tunheng and T. Hirata, J. Anal. At. Spectrom., 2004, 19, 932–934, 10.1039/B402493A.
- S. Johnston, G. Gehrels, V. Valencia and J. Ruiz, Chem. Geol., 2009, 259(3), 218–229, DOI:10.1016/j.chemgeo.2008.11.004.
- B. Bühn, M. M. Pimentel, M. Matteini and E. L. Dantas, An. Acad. Bras. Cienc., 2009, 81(1), 99–114, DOI:10.1590/S0001-37652009000100011.
- T. Hirata and R. W. Nesbitt, Geochim. Cosmochim. Acta, 1995, 59(12), 2491–2500, 10.1039/B504153H.
- T. Hirata, T. Iizuka and Y. Orihashi, J. Anal. At. Spectrom., 2005, 20(8), 696–701, 10.1039/B504153H.
- T. Iizuka and T. Hirata, Geochem. J., 2004, 38, 229–241, DOI:10.1016/j.chemgeo.2005.03.010.
- S. Sakata, K. Hattori, H. Iwano, T. D. Yokoyama, T. Danhara and T. Hirata, Geostand. Geoanal. Res., 2014, 38(4), 409–420, DOI:10.1111/j.1751-908X.2014.00320.x.
- M. Wiedenbeck, P. Allé, F. Corfu, W. L. Griffin, M. Meier, F. Oberli, A. Von Quadt, J. C. Roddick and W. Spiegel, Geostand. Newsl., 1995, 19(1), 1–23, DOI:10.1111/j.1751-908X.1995.tb00147.x.
- A. J. Walder, I. D. Abell, I. Platzner and P. A. Freedman, Spectrochim. Acta, Part B, 1993, 48, 397–402, DOI:10.1016/0584-8547(93)80044-U.
- J. Hiess, D. J. Condon, M. McLean and S. R. Noble, Science, 2012, 335, 1610–1614, DOI:10.1126/science.1215507.
- L. M. Larsen and A. B. Kostinski, Meas. Sci. Technol., 2009, 20, 1–10, DOI:10.1088/0957-0233/20/9/095101.
- M. S. A. Horstwood, J. Košler, G. Gehrels, S. E. Jackson, N. M. McLean, C. Paton, N. J. Pearson, K. Sircombe, P. Sylvester, P. Vermeesch, J. F. Bowring, D. J. Condon and B. Schoene, Geostand. Geoanal. Res., 2016, 40, 311–332, DOI:10.1111/j.1751-908X.2016.00379.x.
- K. Ludwig, User's Manual for Isoplot 3.75: A geochronological toolkit for Microsoft Excel, Berkeley Geochronology Center Special Publication, 2012, vol. 5, p. 75 Search PubMed.
- J. Sláma, J. Košler, D. J. Condon, J. L. Crowley, A. Gerdes, J. M. Hanchar, M. S. A. Horstwood, G. A. Morris, L. Nasdala, N. Norberg, U. Schaltegger, B. Schoene, M. N. Tubrett and M. J. Whitehouse, Chem. Geol., 2008, 249(1), 1–35, DOI:10.1016/j.chemgeo.2007.11.005.
- J. M. Cottle, M. John, A. R. Kylander-Clark and J. C. Vrijmoed, Chem. Geol., 2012, 332, 136–147, DOI:10.1016/j.chemgeo.2012.09.035.
- I. Horn, R. L. Rudnick and W. F. McDonough, Chem. Geol., 2000, 164(3), 281–301, DOI:10.1016/S0009-2541(99)00168-0.
Footnote |
| † Electronic supplementary information (ESI) available: ESI data Table 1: U–Th–Pb isotopic data of Plešovice zircon obtained by single collector-ICP-MS shown in Fig. 3; Table 2: U–Th–Pb isotopic data of Plešovice zircon obtained by multiple collector-ICP-MS shown in Fig. 3; Table 3: U–Th–Pb isotopic data of Plešovice zircon obtained by multiple collector-ICP-MS shown in Fig. 4. These tables are based on the format of Horstwood et al. (2016). See DOI: 10.1039/c6ja00311g |
| This journal is © The Royal Society of Chemistry 2017 |