Tantalum isotope ratio measurements and isotope abundances determined by MC-ICP-MS using amplifiers equipped with 1010, 1012 and 1013 Ohm resistors
M.
Pfeifer
 *ab,
N. S.
Lloyd
c,
S. T. M.
Peters
d,
F.
Wombacher
ab,
B.-M.
Elfers
ab,
T.
Schulz
e and
C.
Münker
ab
*ab,
N. S.
Lloyd
c,
S. T. M.
Peters
d,
F.
Wombacher
ab,
B.-M.
Elfers
ab,
T.
Schulz
e and
C.
Münker
ab
aInstitut für Geologie und Mineralogie, Universität zu Köln, Zülpicher Str. 49b, 50674 Cologne, Germany. E-mail: m.pfeifer@uni-koeln.de
bSteinmann-Institut, Poppelsdorfer Schloss, Meckenheimer Allee 169, 53115 Bonn, Germany
cThermo Fisher Scientific, Hanna-Kunath-Str. 11, 28199 Bremen, Germany
dGeorg-August-Universität, Geowissenschaftliches Zentrum, Goldschmidtstrasse 1, 37077 Göttingen, Germany
eDepartment of Lithospheric Research, University Vienna, Althanstrasse 14, 1090 Vienna, Austria
First published on 21st November 2016
Abstract
Due to analytical difficulties related to the low abundance of 180Ta (about 0.012%), the absolute isotope composition of tantalum is not well known and possible natural variations in 180Ta/181Ta are so far unconstrained. Improved precision is required in order to evaluate the homogeneity of Ta isotope distributions among solar system materials and whether natural Ta stable isotope variations exist on Earth. Using a Neptune™ multicollector-inductively coupled plasma-mass spectrometry (MC-ICP-MS) system and different resistors in the Faraday cup amplifier feedback loops (a 1010 Ω for 181Ta; 1012 or newly developed 1013 Ω resistors for 180Ta and Hf interference monitor isotopes) now allows relative analyses of 180Ta/181Ta with an intermediate precision of ca. ±4ε (ε refers to one part in 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) using 25 to 100 ng Ta and thus even for sample sizes available from meteorites (e.g., 1 g). The 1013 Ω amplifier resistors proved to be of paramount importance for high-precision Ta isotope ratio measurements of low amounts of material. Tailing effects from the large 181Ta beam have previously been underestimated. A thorough assessment of this effect revealed a tailing contribution of ∼2.5% on the currently recommended IUPAC ratio. Potential systematic biases in the mass discrimination correction are assumed being of minor importance compared to an uncertainty of ∼0.4% achieved for the estimate of the “true” 180Ta/181Ta ratio. We propose a new 180Ta/181Ta isotope ratio of 0.00011705(41), equivalent to 181Ta/180Ta = 8543(30), yielding isotope abundances of 0.011704(41) % for 180Ta and 99.988296(41) % for 181Ta, and an absolute atomic weight for tantalum of 180.9478787(38) u (all uncertainties with k = 2).
000) using 25 to 100 ng Ta and thus even for sample sizes available from meteorites (e.g., 1 g). The 1013 Ω amplifier resistors proved to be of paramount importance for high-precision Ta isotope ratio measurements of low amounts of material. Tailing effects from the large 181Ta beam have previously been underestimated. A thorough assessment of this effect revealed a tailing contribution of ∼2.5% on the currently recommended IUPAC ratio. Potential systematic biases in the mass discrimination correction are assumed being of minor importance compared to an uncertainty of ∼0.4% achieved for the estimate of the “true” 180Ta/181Ta ratio. We propose a new 180Ta/181Ta isotope ratio of 0.00011705(41), equivalent to 181Ta/180Ta = 8543(30), yielding isotope abundances of 0.011704(41) % for 180Ta and 99.988296(41) % for 181Ta, and an absolute atomic weight for tantalum of 180.9478787(38) u (all uncertainties with k = 2).
1. Introduction
Tantalum is the rarest chemical element in the solar system. It consists of two isotopes with the major isotope 181Ta accounting for 99.98799(8) % of its molar abundance, according to current IUPAC recommendations.1 In contrast, the reported relative abundance of 180Ta equals only 0.01201(8) %,1 making 180Ta the rarest stable nuclide in the solar system, which is why 180Ta was not discovered until 1955.2 Furthermore, 180Ta is the only observationally stable isotope present as an excited nuclear isomer. In its ground state, 180Ta decays to 180Hf and 180W with a half-life of only 8 hours (e.g., ref. 3 and 4). The extreme difference in isotope abundances of a factor of more than 8000 makes the precise and accurate determination of Ta isotope ratios by mass spectrometry challenging. Using a multi-collector ICP-MS system (MC-ICP-MS), we partially overcome the large difference in isotope abundances by collecting a large ion beam for 181Ta in a Faraday cup with 1010 Ω resistor in the amplifier feedback loop (up to 5 × 10−9 A, equivalent to 500 V if common 1011 Ω resistors would be applied), while collecting the low abundance isotope 180Ta and isobaric interference monitors with Faraday amplifiers with high-Ohm resistors.The isotope composition of Ta is of particular interest because it may vary in extraterrestrial materials. For many elements technical advances in mass spectrometry over the past 15 years (e.g., ref. 5) made it possible to resolve small isotope anomalies at the sub-per mill level in solar system materials relative to Earth, e.g., Zr,6 Mo,7,8 Ru,9 Ba,10 Nd,11,12 or Sm.12 These so-called nucleosynthetic isotope anomalies give testimony to the early evolution of the solar system, such as thermal processing of presolar grains from other stars13,14 or later injection of material from nearby star explosions into the nascent solar system.15 Additionally, the Ta isotope compositions of natural samples may show variations due to mass-dependent, nuclear volume dependent or kinetic stable isotope fractionation during geological processes. Hence, sufficiently precise measurements protocols for Ta isotopes in order to identify such effects are required.
Previous Ta isotope analyses by MC-ICP-MS and thermal ionisation mass spectrometry (TIMS) employed Faraday collectors with 1011 Ω resistors in the amplifier feedback loop. The electronic noise contribution from this conventional setup can be reduced by about a factor of three by the use of recently developed amplifiers with 1012 Ω resistors.16,17 Amplifiers with 1012 Ω resistors are used in TIMS and MC-ICP-MS for three main purposes: (1) measurement of small sample sizes,16,18,19 (2) precise monitoring of interfering elements20–23 and (3) combined application with 1010, 1011, and 1012 Ω resistors to account for largely different ion beam intensities of one element.23–25 The advent of newly developed amplifiers equipped with 1013 Ω resistors further reduced physical limitations by, in theory, increasing the signal-to-noise ratio by a factor of √100 compared to an amplifier equipped with a 1011 Ω resistor.26–28 The precision of a 4 × 10−14 A ion current (equivalent to 4 mV with 1011 Ω resistors) on 143Nd was shown to improve by factors of 2 and 4 compared to 1012 and 1011 Ω amplifiers, respectively.26 At count rates above 2 × 104 cps (= 0.32 mV), 1013 Ω resistors even proved to be superior to secondary electron multipliers.26 Collectively, these technical improvements set the stage to search for small differences in Ta isotope ratios in geological and meteoritic materials.
So far, only Kimura et al.29 documented the applicability of amplifiers equipped with 1013 Ω resistors in MC-ICP-MS. Here, we also compare the performance of 1013 Ω resistors with that of 1012 amplifiers. We extend the application of 1013 Ω resistors to precise monitoring of strongly interfering elements and to measuring very low abundance isotopes that limit the precision of isotope ratio measurements. A protocol is presented here for high-precision Ta isotope ratio measurements, with an emphasis on the application to extraterrestrial samples of limited size. This protocol furthermore allows a re-evaluation of the terrestrial 180Ta/181Ta isotope ratio that is recommended by IUPAC (0.0001201(6) (ref. 3)) and by Weyer et al. (0.0001198(6) (ref. 30)). It was previously shown that abundance sensitivity plays a critical role in MC-ICP-MS for the determination of accurate isotope ratios for heavy elements.31 In fact, it was observed that 181Ta can induce significant peak tailing over up to 3 u distance from the centre.32 The two studies that previously presented Ta isotope data discuss this abundance sensitivity effect. While de Laeter and Bukilic3 neglected tailing effects, Weyer et al.30 identified abundance sensitivity as the limiting factor for accurate Ta isotope ratio measurements. The latter study consequently suggested a lowermost value for 180Ta/181Ta = 0.000115. In the present study, we evaluate the effect of varying pressure at the high-vacuum end of the instrument on the abundance sensitivity and measured isotope ratios. We then present an offline tailing correction, suggesting that the tailing of 181Ta on 180Ta has been underestimated in the past. A significantly lower 180Ta/181Ta isotope ratio and, therefore, a lower absolute isotope abundance of 180Ta are proposed.
2. Experimental
Measurements were conducted on a Thermo Scientific Neptune™ MC-ICP-MS instrument (upgraded with a Plus interface) at facilities at the joint Cologne-Bonn MC-ICP-MS laboratory, Germany, and on a Thermo Scientific Neptune Plus™ at Bremen, Germany, from February 2013 to March 2016. The data were obtained in 12 individual sessions consisting of 22 measurement sequences.2.1. General set-up and data evaluation
Traditionally, many users of mass spectrometers discuss ion beam intensities in voltages measured across the resistor, rather than ion currents. However, measured voltages change with the resistor value according to Ohm's law. In order to compare the signal intensities we report voltages as V*, meaning the signal intensity as if a 1011 Ω resistor were in use, which is in the same manner as the instrument software reports ion beam signal intensities. Both instruments were operated with a Jet interface (Jet sampler cone, X-skimmer cone, and On-Tool booster pump) and a Cetac ARIDUS II™ desolvating system. The PFA nebulisers provide uptake rates of ca. 100 μl min−1, using 0.56 M HNO3/0.24 M HF as measurement solution. Typical operating conditions are given in Table 1 for the instruments at Cologne-Bonn and Bremen with a single analysis comprising of 120 cycles of 4.2 s integration time or 60 cycles of 8.4 s integration time to account for settling delays of the high-Ohm resistors.| Cologne-Bonn | Bremen | |
|---|---|---|
| Operation power [W] | 1300 | 1300 |
| Sample gas flow rate [l min−1] | 0.9 | 0.6–0.8 |
| Auxiliary gas flow rate [l min−1] | 0.7 | 0.8 |
| Cooling gas flow rate [l min−1] | 15 | 16.3 |
| Fore vacuum pressure [mbar] | <5 × 10−3 | <1.3 × 10−3 |
| High vacuum pressure [mbar] | <1.5 × 10−7 | <3 × 10−7 |
| Analyser pressure [mbar] | 0.8–3.6 × 10−8 | 1.2–2.4 × 10−8 |
| Nebuliser | 100 μl min−1 MicroFlow PFA | 100 μl min−1 MicroFlow PFA |
| ARIDUS II™ sweep gas flow rate [Ar, l min−1] | 5.2 | 4–5 |
| ARIDUS II™ nitrogen gas flow rate [l min−1] | 0.05 | 0.05 |
Tantalum consumption for one measurement at Bremen was ∼25 ng leading to a 4.5 × 10−10 A ion current on 181Ta for a 30 ng g−1 standard solution (corresponds to 45 V*). At Cologne-Bonn, ion currents of around 2 × 10−9 A were achieved for a 100 ng g−1 solutions, consuming ∼90 ng Ta. This translates to 1600–1900 V* per μg g−1 Ta at both instruments. Mass bias correction was typically performed externally using doped Yb. For this purpose, the Alfa Aesar Specpure® plasma Yb standard solution (LOT 71-064667L) was admixed to the Ta solutions at a concentration of ca. 8 ng g−1, resulting in an ion current of ca. 6 × 10−11 A on the largest isotope 174Yb (isotope abundance of ∼32%). External mass bias correction based on Re isotopes (Alfa Aesar Specpure® LOT 71-071361B) was also tested (Section 2.2.). The Ta standard solution that was predominantly used during this project had previously been prepared from AMES Ta-metal at Münster.30 Additionally, the Alfa Aesar Specpure® Ta plasma standard solution (LOT 15024103) and Merck Certipur® Ta ICP standard solution (LOT HC56783956) were measured for comparison and to test for potential stable isotope fractionation during the industrial Ta purification process.
Gain calibration for the Faraday amplifier was performed using the software operated standard procedure where a 33.3 fA reference current (equal to 3.33 V*) is consecutively applied to all amplifiers, except for those equipped with 1013 Ω resistors as those would saturate at signals >0.5 V*. The 1013 Ω amplifier cross-calibration was then conducted using a protocol comparable to that described by Kimura et al.29 In this case, separate 30 minute measurements were made with a Nd solution (here: Merck Certipur® ICP standard solution LOT HC077146), first with the electronically calibrated 1011 Ω amplifiers with ca. 140 mV* on 148Nd using a 10 ng g−1 solution in wet plasma. The amplifiers connected to the Faraday cups that collect 145Nd, 148Nd, and 150Nd were then switched to 1013 Ω amplifiers, while keeping the 144Nd ion beam in a Faraday cup connected to a gain calibrated 1011 Ω amplifier. The tuning parameters were kept unchanged during the 20 minutes baseline measurement and the subsequent repeated measurement of the Nd standard. The gains for the 1013 Ω amplifiers were calculated from the results from the two measurements and were manually entered in the executive table of the instrument software. Hence, no assumptions about true isotope ratios and accuracy of mass discrimination laws needed to be made during this gain calibration procedure, as the 1013 resistor amplifier gains are calculated from the ratios in comparison to the same isotope ratios previously measured with gain corrected 1011 Ω resistors. The three isotopes of Nd measured here are of comparable abundance and make Nd an ideal element for cross calibration of up to three 1013 Ω amplifiers. Kimura et al. applied an inter-calibration approach by cycling the attached amplifiers to each Nd isotope and calculate the gains on the amplifiers with a solver function in Excel.29 Our approach could be simplified as the normalising isotope 144Nd was always measured with a previously gain corrected 1011 Ω resistor. Earlier work applied measurements of secondary standards to monitor the stability of the gain calibration. This is not necessary, as the amplifiers proved to be stable enough on timescales relevant for typical lengths of MC-ICP-MS analytical sessions.26
The typical repeatability (corresponds to internal precision in the geochemical literature) of the Nd measurements with 1013 Ω amplifiers is better than 80 ppm (2SE) for 148Nd/144Nd. Repeated measurements using this protocol yield an intermediate precision (corresponds to external reproducibility in geochemical publications) of better than 82 ppm for 148Nd/144Nd (2S.D., n = 10). The electronic cross calibration of the standard 1011 Ω amplifiers using a 33.3 fA reference current is typically reproducible to better than 16 ppm (2S.D.), which results in a combined uncertainty of the cross calibration of ca. 1ε (2S.D.), in accord with previously reported gain precision for 1013 Ω amplifiers.28 This uncertainty cancels out for measurements relative to a standard.
The baseline was measured prior to each measurement session with a deflected ion beam over 1000 cycles of 1.05 s each. Baseline measurements were always performed more than 30 minutes after the gain calibration to allow settling of our early model 1012 Ω resistors towards baseline levels. Low intensity 180Ta and the critical interference monitor 178Hf were collected in Faraday cups attached to amplifiers with 1012 Ω resistors at Cologne-Bonn and to amplifiers with 1013 Ω resistors at Bremen (Table 2). In order to improve the counting statistics and the signal to noise ratio for the low-abundance isotope 180Ta, large signals had to be measured for 181Ta, using an amplifier with a 1010 Ω resistor at Cologne-Bonn. Additional ion beams were collected with amplifiers with 1011 Ω resistors (Table 2). Typical signal voltages on 181Ta were 45 V* at Bremen and 150–200 V* at Cologne-Bonn to achieve sufficient precision with ca. 5 and 20 mV* on 180Ta, respectively.
| Configuration | L4 | L3 | L2 | L1 | C | H1 | H2 | H3 | H4 |
|---|---|---|---|---|---|---|---|---|---|
| Yb-Based mass bias correction | 171Yb | 172Yb | 173Yb | 174Yb, (174Hf) | 178Hf | 179Hf | 180 Ta, (180Hf), (180W) | 181 Ta | 183W |
| Amplifier Cologne-Bonn | 1011 | 1011 | 1011 | 1011 | 10 12 | 1011 | 10 12 | 10 10 | 1011 |
| Amplifier Bremen | 1011 | 1011 | 1011 | 1011 | 10 13 | 10 12 | 10 13 | 1011 | 10 12 |
| Re-Based mass bias correction | 178Hf | 179Hf | 180 Ta, (180Hf), (180W) | 181 Ta | 183W | 184W, (184Os) | 185Re | 187Re, (187Os) | 189Os |
| Amplifier Cologne Bonn | 10 12 | 1011 | 10 12 | 10 10 | 1011 | 1011 | 1011 | 1011 | 1011 |
For comparison, all data were processed offline and online. Instrumental mass bias was corrected externally based on the measured isotope composition of Yb between masses 171 and 174, using the exponential law (also known as Russell's law)33 and the Yb ratios recommended by Albalat et al.34 The latter data agreed better with our mass discrimination corrected data than the IUPAC recommended values from de Laeter and Bukilic.35 All Ta isotope data are reported relative either to 173Yb/171Yb = 1.12489 (Yb-based mass bias correction (ref. 34)) or 187Re/185Re = 1.67394 (Re-based mass bias correction (ref. 1)). Elemental isobaric interferences were corrected based on 180Hf/178Hf = 1.2863 and 180W/183W = 0.008304, which represent our long-term measured values.23 In particular the very large isobaric interference from 180Hf (relative abundance 35.08%) on 180Ta required careful correction, even in the case of the purest standard solutions. In terms of mass fractionation, elements of similar mass such as Yb, Hf, Ta, W, and Re transmitted through the mass spectrometer will be biased by very similar extents. Therefore, for the correction of 180Hf and 180W interferences on 180Ta, the literature 180Hf/178Hf and 180W/183W ratios23 were artificially biased using the exponential law and the fractionation factor determined from 173Yb/171Yb or 187Re/185Re. Regular tests with Hf-doped Ta standard solutions confirmed the robustness of the interference correction over time. The measured 178Hf/181Ta of the pure standard solutions were <1 × 10−6, i.e., below the threshold of 178Hf/181Ta = 8 × 10−6 at which the correction starts to introduce significant biases. The minor interference of 174Hf (∼0.16%) on 174Yb does not result in significant uncertainty propagation into the external mass bias correction, nor does it affect the absolute mass-bias corrected Ta isotope ratios, because Hf is virtually absent in the Ta standard solutions. The same applies for the interference of 187Os on 187Re if doped Re is used for external normalisation.
Measured data are partly presented as the deviation from a reference standard using the epsilon notation (parts per ten thousand):
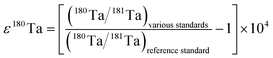 | (1) |
This notation is commonly preferred over absolute values because relative measurements achieve better precision than absolute analyses. This is mainly due to changes in the abundance sensitivity of the instrument, which result in a drift of the measured isotope ratios that is specific to each analytical session. This drift can be corrected by bracketing measurements with the adjacent standards or by mathematical regression through the data. Henceforth, the quoted values for intermediate precision correspond to the 2 times standard deviation of the measured Ta isotope ratios relative to a linear or sometimes polynomial fit through the data for standards of an analytical session.
2.2. Correction of instrumental mass discrimination
In inductively coupled plasma mass spectrometry, heavy isotopes are preferentially transmitted. For heavy elements like Ta, this mass bias typically increases heavy over light isotopes by about 1% u−1 (e.g., ref. 36). Addition of another element of similar mass, e.g., Yb to the Ta solutions, allows monitoring of changes in mass bias during the measurement session (e.g., ref. 37). This external mass discrimination correction often allows for more precise relative isotope ratio measurements and also improves the accuracy of the isotope ratio measurement. In detail, however, this correction depends on the accuracy of isotope composition assumed for the admixed element solution and suffers from differences in the mass bias behaviour between the two elements. These differences in mass bias behaviour between two elements depend on tuning parameters and cones and are commonly observed between measurement sessions.36,38 Here, the Ta isotope ratio data were corrected for instrumental mass discrimination based on the concurrent measurement of Yb and in some cases Re isotope ratios. As Yb has more than two isotopes, its isotope composition enables assessment of polyatomic interferences on specific isotopes. Furthermore, Yb-based mass bias correction allows the comparison of results that are calculated with different Yb isotope ratios.The mass bias corrected 180Ta/181Ta based on different Yb ratios are indistinguishable within repeatability (2SE). Neither, the use of conventional (as opposed to “Jet”) sampling cones, nor variations in Yb/Ta of the measurement solution affected the mass fractionation corrected Ta isotope ratios significantly. Altogether, Yb isotopes therefore seem to be robust monitors for the instrumental mass bias drift of Ta isotopes. To verify the accuracy of Yb-normalised data, we also tested the correction for the instrumental mass bias by using admixed Re. Rhenium exhibits advantages as well as disadvantages over Yb as a doping element for mass bias correction. On the one hand, Re allows for better Hf interference correction for up to 5 × 10−5 of 178Hf/181Ta, more than five times higher than possible using the Yb-doping protocol. This was also evident from somewhat smaller repeatability of single Ta measurements which may be a result of similar sampling of Re, Hf, and Ta ions from the plasma, as they all exhibit more similar first ionisation potentials compared to Yb. On the other hand, we observed that Re sometimes fails to provide an accurate external mass bias correction. This is assumed to stem from occasional isotope fractionation effects of Re inside the Aridus desolvating system, where Re seems to get lost through the membrane at higher temperatures, which then results in outliers in the Ta standard solution data. Similar observations were made for tungsten stable isotope analyses when using Re for external mass bias correction.39 With the exception of occasional outliers, the Re-normalised Ta isotope compositions overlap with the Yb-normalised data within intermediate precision (2S.D.). As the behaviour of Yb during measurements was more reliable compared to Re and the measured Ta standard solutions are pure enough in Hf, we preferred using Yb-normalisation to correct for instrumental mass bias.
Notably, all mass bias corrected 180Ta/181Ta ratios are approximately 30ε higher (corrected relative to 173Yb/171Yb) if the recently proposed Yb isotope abundances by Wang et al.40 are considered for the mass bias correction. We prefer the Yb isotope abundances reported by Albalat et al.,34 because use of the Yb isotope abundances by Wang et al.40 as a means for mass bias correction would lead to a mismatch between the Re- and Yb-normalised Ta isotope compositions (Section 3.4.). Furthermore, Albalat et al.34 give the Yb isotope composition of a plasma standard from Alfa Aesar, and we used a similar Yb standard solution in this study. Wang et al.40 compiled different standard solutions, which might display different isotope fractionation either by industrial processing or naturally, as there exists a stable Yb isotope variability of more than 0.5 per mil on Earth.34 A strong argument for the Albalat et al.34 data is consistency, yielding Ta ratios within 1ε after mass bias correction with different Yb ratios. In contrast, when using the Wang et al.40 data, 180Ta/181Ta ratios of the same measurement deviate by up to 20ε, depending on the Yb ratio used for normalisation. Despite the inconsistency in published Yb isotope data, other factors than mass discrimination correction, e.g., the correction of the 180Hf interference and especially the abundance sensitivity affect the accuracy of the Ta isotope ratio measured more prominently.
2.3. Abundance sensitivity in 180Ta/181Ta measurements
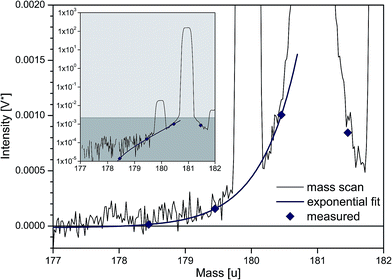
Accurate Ta isotope ratio measurements require an assessment of abundance sensitivity effects from 181Ta on the far rarer 180Ta.3,30 For the Neptune Plus MC-ICP-MS, the abundance sensitivity on 237U in the presence of a strong 238U beam is specified to be below 5 ppm.41 The abundance sensitivity at one u below 181Ta is typically between 1.9 to 3.1 ppm at both instruments at Cologne-Bonn and Bremen, which translates into an additional signal contribution onto 180Ta of approximately 2%. Tailing of 181Ta on the low-mass side can also affect the signals on 179Hf and 178Hf. We observed that interference monitor 178Hf was compromised at ion currents >2 × 10−9 A on 181Ta (= 200 V*). An upper limit of 200 V* on 181Ta was therefore set during the course of our study. Lower 181Ta beam intensities used at Bremen (<45 V*) did not result in significant tailing effects on 178Hf and potential error contributions on 180Ta/181Ta. Abundance sensitivity effects were also observed on the high-mass side of 181Ta. The tail contribution from 181Ta on the 180W interference monitor 183W is ca. 0.2 ppm and translates into an additional correction of 0.2ε on the Ta isotope ratio, if compared to correction with non-influenced 184W as interference monitor. This is well within the repeatability (2SE) of 180Ta/181Ta ratios and negligible within the framework of our study.In order to monitor the tail from 181Ta on adjacent masses, the mass set in the centre cup was increased by 0.5 u immediately before and after each sequence of measurements. The peak centre routine was only executed before the measurements to avoid observed shifts of several ε in measured Ta isotope ratios during the sequence due to a shifted tail caused by a changed mass calibration. The intensities on masses 178.45, 179.45 and 180.45 during aspiration of a high concentrated standard solution were recorded with 60 cycles of 4.2 s each and an empirical equation was fitted for the mass region from 177 to 180.7 (Fig. 1) in order to evaluate the tailing effect on full masses at 177.944, 178.946 and 179.947 u:
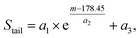 | (2) |
Typical values are a1 ≈ 3.5 × 10−6, a2 ≈ 0.44, and a3 ≈ 1 × 10−5 for abundance sensitivity measured at ca. 45 V on 181Ta for both instruments. The same exponential fit was previously applied to correct tailing from 140Ce on minor Ce isotopes in TIMS.42 The tailing of 181Ta calculated from eqn (2) fits the measured tail extremely well (Fig. 1). Typical drift of abundance sensitivity at mass 180 was below 0.3 ppm throughout an analytical session, corresponding to a maximum shift of 25ε in 180Ta/181Ta (discussed in Section 3.3.).
2.4. Terminology related to uncertainties
This study addresses two communities that use different vocabularies. In isotope geo- and cosmochemistry, data are usually presented relative to a standard, whereby it is commonly assumed that the standard measurements are affected by the same systematic biases as the sample measurements. The validity of the measurement is defined by variability observed in repeated measurements of standards or samples. The report of best estimates on absolute (true) isotope abundances requires a more thorough assessment of all random and systematic influences by applying the error approach in order to assign a realistic uncertainty to a measured quantity.Here, we adopt the terminology recommended by the Joint Committee for Guides in Metrology and listed in the International Vocabulary of Metrology (VIM)43 but occasionally include terms in brackets that are used in the geochemical community. We follow the recommendations from the Guide to Expression of Uncertainty in Measurement (GUM) of ISO/BIPM44 to present our best estimate of the absolute Ta isotope ratio and the corresponding isotope abundances in Chapter 3.4. Type A (random) and Type B (evaluated by non-statistical means) uncertainties are discussed and propagated as the quadratic sums to obtain the measurement uncertainty. The expanded uncertainty includes a coverage factor (k = 2).
The following terms are commonly used and accepted in geo- and cosmochemistry to report the validity of a measurement. The “(external) reproducibility” states the precision of a method reported as the relative variability of repeated standard (or sample) measurements, in standard deviations (usually with a coverage factor of k = 2). The appropriate term following VIM43 is “intermediate precision”, where the variability of repeated measurements is reported for the same instrument and method over an extended period of time. “Internal precision” as used in isotope geochemistry expresses the variability of a single measurement, e.g., 60 successive integrations for 8.4 s, usually as the experimental standard deviation of the mean (S.D./N−0.5) with a coverage factor k = 2 (often called “2 standard error”), in which S.D. is the standard deviation and N is the number of successive integrations (60 in the example above). The closest equivalent in metrology, repeatability, includes replicate measurements on the same or similar objects over a short period of time.
Here, we use repeatability to state the uncertainty of single measurements corresponding to 2SE (2 standard error = standard deviations of the mean with k = 2). Intermediate precision (external reproducibility), i.e., the standard deviation of the observations with k = 2 is indicated as 2S.D.
3. Results and discussions
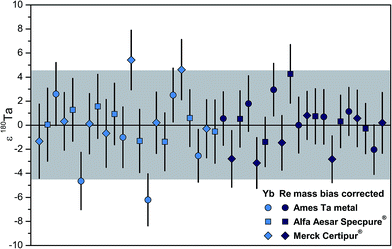
Below, the intermediate precision (in geochemistry: external reproducibility) of our method is evaluated. The Ta isotope compositions of the three different standard materials are compared. Then, the results that are based on the newly developed amplifiers with 1013 Ω resistors are compared with those obtained using amplifiers with 1012 Ω resistors. After discussing the effect of abundance sensitivity on the 180Ta/181Ta ratio, we propose new best estimates of absolute Ta isotope abundances.3.1. Intermediate precision and homogeneity of Ta standard solutions
The intermediate precision (external reproducibility) of Ta isotope ratios that were measured during an analytical session was calculated relative to a regression through the data of the respective session. The regression accounts for changes in abundance sensitivity of the instrument during a sequence (Fig. 2). Intermediate precision is reported as the variability of the standards in a session around the regression fit. Thus, it gives a minimum value from which a sample must deviate from the bracketing terrestrial standards to be resolved as anomalous. The typical intermediate precision (2 relative S.D.) for Yb corrected Ta isotope ratios at Bremen and Cologne-Bonn was ±4.4ε and ±4.0ε, respectively. The Re corrected data yielded an intermediate precision of ±4.1ε but occasionally showed outliers (defined as >3S.D. away from the mean of the data set, not included), making this procedure less reliable. The intermediate precision is typically a factor of ca. 1.5 to 2 higher than the typical repeatability (around ±2 to ±3.5ε, 2 relative SE). One possible reason could be scatter of interfering element signals, particularly of the monitoring mass 178Hf, that is not averaged out during a single measurement. The signal on 179Hf is apparently more stable than the signal on 178Hf, but this apparent stability reflects the larger tailing contribution from the 181Ta signal to 179Hf. Thus, when 179Hf is used to correct for the interference of isobaric 180Hf, the intermediate precision of 180Ta/181Ta is therefore worse, i.e., ca. ±8ε.All Ta standard solutions were measured with external mass bias correction relative to both Yb and Re. Notably, the measured standard solutions have indistinguishable interference and mass bias corrected 180Ta/181Ta (Fig. 2). These particular standards can therefore be used interchangeably for bracketing of natural samples. The different standard solutions define a common intermediate precision of ±4.5ε. We therefore suggest that the Ta isotope ratio that represents the natural one can be inferred from our suite of Ta standard solutions and that the Ta purification processes were not accompanied by resolvable isotope fractionation effects. The majority of this work is based on measurements of the AMES metal standard because it showed the lowest Hf impurity.
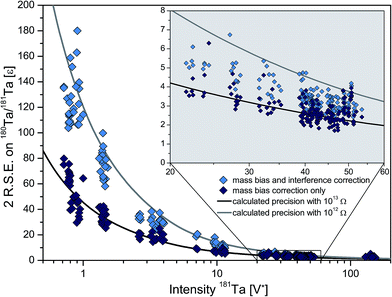
3.2. Low ion beam measurements using 1013 Ω resistor Faraday cup amplifiers
In order to evaluate the repeatability (internal precision in geochemistry) of the Ta isotope measurements with 1013 Ω resistors, we calculated the theoretically achievable in-run repeatability. The repeatability of measurements with Faraday cups is dependent on the sum of the shot noise, described by the Poisson distribution of ion detection, and the thermal Johnson–Nyquist noise of the amplifier resistor.5 The shot noise describes the stochastic nature of impinging charged particles on the detector. The absolute uncertainty that is caused by the shot noise can be calculated as the inverse square root of the number of particles N at mass i that reach the detector, and 1 mV* being equivalent to 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cps. This means that the relative contribution from shot noise is purely dependent on the intensity of the signal and decreases with higher intensity. The thermal noise of the amplifier that is coupled to the detector, in contrast, results from the agitation of charge carriers in an electrical circuit at non-zero temperature. This is the Johnson–Nyquist noise (ΔV) and is defined as
700 cps. This means that the relative contribution from shot noise is purely dependent on the intensity of the signal and decreases with higher intensity. The thermal noise of the amplifier that is coupled to the detector, in contrast, results from the agitation of charge carriers in an electrical circuit at non-zero temperature. This is the Johnson–Nyquist noise (ΔV) and is defined as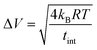 | (3) |
Fig. 3 shows the analytical repeatability of Ta isotope ratio data obtained with amplifiers with 1013 Ω resistors compared to the repeatability predicted by Poisson statistics combined with Johnson–Nyquist noise. Although there is an overall good agreement between the measured and calculated repeatability for the mass bias corrected isotope ratios, the isotope ratios that are additionally corrected for interfering 180Hf show a systematically higher in-run repeatability than the predicted repeatability, particularly at low signal intensity. The higher in-run repeatability for the interference corrected isotope ratios likely reflects noise propagation from the amplifier that is used to collect the interference monitor at mass 178. Notably, the use of an amplifier with 1013 Ω resistor clearly improves the signal-to-noise ratio on mass 178 and therefore reduces the noise propagation compared to the use of a 1012 Ω resistor. This pattern becomes evident by the comparison of the repeatability in Hf corrected and uncorrected data obtained with 1012 and 1013 Ω amplifiers at mass 178, at ca. 40 V* for 181Ta. While the correction for 180Hf interference leads to an increase by 2 to 3ε to about ±7 to ±8ε when a 1012 Ω amplifier was used to collect 178Hf (Cologne-Bonn), measurements at Bremen using the 1013 Ω amplifiers only yielded an increase in repeatability by ca. 1ε or less, which results in a repeatability of ±3 to ±3.5ε after interference corrections (2 relative SE). Together, the repeatability of Ta isotope measurements is thus limited by the noise contribution and counting statistics on both masses, 178 and 180, illustrating the advantage of the 1013 Ω amplifiers for precise Ta isotope ratio measurements.
In Fig. 3, scatter around the theoretically predicted values likely arise from differences in the response delay times between the 1011 Ω amplifier that is used to collect 181Ta and the 1013 Ω amplifiers. While 1011 Ω amplifiers process a signal within one second, higher resistivity amplifiers need around ten seconds to convert a detector signal into electronic readings. The same effect has previously been reported for signal drift with TIMS28 and is prominent at timescales of transient signals in laser ablation-MC-ICP-MS.29 With solution MC-ICP-MS, a drop in intensity, due to, e.g., nebuliser fluctuations, is directly processed by 1011 Ω amplifiers for high-abundance masses, while it takes one or two integration cycles on the low-abundance mass 180 with 1013 Ω amplifiers. On the cycle level, the measured data therefore may show spikes, followed by mirroring spikes in the opposite direction, when the signal is processed after the delay through the higher Ohm amplifiers. Higher integrations times of 16 s or more can minimise these effects or a correction might be applied as in laser ablation MC-ICP-MS.29 However, it is noteworthy that the intermediate precision is not affected, as long as the whole signal is integrated over a complete measurement run and no overall drift in signal intensities is present.
A major concern in TIMS work with new 1013 Ω amplifiers is the baseline stability over the course of an analytical session and during long-run measurements.18,19,26 Generally, the stability of higher Ohm resistors was shown to be suitable for long-run TIMS measurements, also for the new 1013 Ω resistor Faraday amplifiers.26 The baseline stability is of less concern for MC-ICP-MS measurements, as a run only takes 15 minutes including wash-out and uptake time. Any potential drift is therefore sufficiently covered by standard bracketing.
3.3. Effect of tailing on measured Ta ratios
The drift in Ta isotope ratios that was observed over several analytical sessions is related to the abundance sensitivity of the instrument. Changes in the instrumental vacuum directly translate into variable contributions of tailing effects on the measured intensity at mass 180, thus altering the measured 180Ta/181Ta. This effect is evident when comparing the non-tailing corrected but mass-bias and interference corrected Ta isotope ratios with the ion getter pump (IGP) pressure for the two analytical sessions with the largest drift in vacuum readings (Fig. 4). The IGP pressure represents the vacuum condition in the back-end of the mass spectrometer, where the flight tube and the detectors of the instrument are located. A clear correlation between the measured 180Ta/181Ta and IGP pressure highlights the influence of ion collisions with residual gas on the actual abundance sensitivity. Notably, extrapolations of these trends to zero IGP pressure result in higher 180Ta/181Ta ratios than the proposed absolute tailing corrected value (Fig. 4). This indicates that the 181Ta tail partially originates from collisions in the front part of the instrument. The drift in Ta isotope ratios relative to the IGP pressure is slightly less pronounced when 179Hf is used to correct for 180Hf interference than when 178Hf is used, because of tailing from 181Ta onto mass 179, which then additionally removes some of the tailing effect from 180Ta.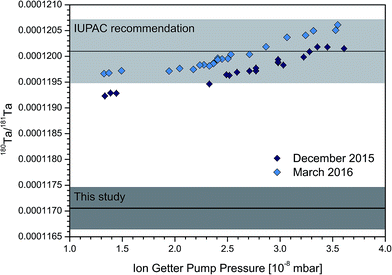 | ||
| Fig. 4 Measured 180Ta/181Ta ratios plotted against the ion getter pump pressure in 10−8 mbar during the two sessions with the largest drift at the Cologne-Bonn facilities. The dark shaded area shows the Ta isotope ratio proposed in this study, the light shaded area represents the presently accepted value.1,3 The individual in-run repeatability (2SE) is smaller than or equal in size to the symbols. Ion getter pump data are taken from the individual log files of each measurement. | ||
The analytical sessions that are illustrated in Fig. 4 show similar trends of increasing 180Ta/181Ta with IGP pressure, but also show an offset in 180Ta/181Ta relative to each other. This offset could be explained by different centre masses of the magnet or by different conditions in the low vacuum part of the mass spectrometer. To a smaller extent, pressure changes were also observed in earlier sessions but did not result in such a strong drift of measured 180Ta/181Ta ratios as exemplified in Fig. 4. During the two sessions at Cologne-Bonn illustrated in Fig. 4, a deteriorated skimmer cone was used that apparently caused a stronger pressure change in the analyser part of the instrument and consequently larger drift. In addition to the elevated maximum IGP pressure, the non-ideal cone geometry potentially changed the composition of the residual gas to a more argon-rich atmosphere. The larger mass of Ar atoms compared to, e.g., N2, could then lead to a comparably stronger deflection of ions.
The dependence of tailing effects on different ion beam intensities was tested to verify the reliability of standard-sample bracketing at different intensities. The abundance sensitivity remained the same in both instruments for ion currents between 2 × 10−10 and 2 × 10−9 A for 181Ta, corresponding to intensities from 20 to 200 V*. At such levels of ion currents, the tail contribution of 181Ta on the 180Ta signal displays a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correlation with the intensity of the 181Ta signal. Consequently, even improperly concentration-matched standards therefore would not induce systematic biases in standard-sample bracketing methods. Furthermore, this stability in abundance sensitivity ensures the applicability of our tailing correction protocol with two tail measurements bracketing a sequence. Also the relative contribution of the 181Ta tail on mass 179 with which the interference monitor 179Hf is collected correlates linearly with the 181Ta signal. At ion currents below 2 × 10−10 A, in contrast, the relative contribution of the 181Ta tail on lower masses is less pronounced, because it is within the scatter of the measured baseline. For such low intensities, the Ta concentrations of the bracketing standards need to closely match the concentration of the sample.
1 correlation with the intensity of the 181Ta signal. Consequently, even improperly concentration-matched standards therefore would not induce systematic biases in standard-sample bracketing methods. Furthermore, this stability in abundance sensitivity ensures the applicability of our tailing correction protocol with two tail measurements bracketing a sequence. Also the relative contribution of the 181Ta tail on mass 179 with which the interference monitor 179Hf is collected correlates linearly with the 181Ta signal. At ion currents below 2 × 10−10 A, in contrast, the relative contribution of the 181Ta tail on lower masses is less pronounced, because it is within the scatter of the measured baseline. For such low intensities, the Ta concentrations of the bracketing standards need to closely match the concentration of the sample.
In another test, we investigated the influence of mass resolution on the abundance sensitivity of the instrument while keeping cup positions and the major tuning parameters constant. Tailing effects are strongest in low resolution (LR) and continually decrease from medium resolution (MR) to high resolution (HR). In MR and HR modes, the abundance sensitivity of the instrument was ca. 1 ppm at one u below 181Ta compared to 2.5 ppm in LR. Hence, the measured mean Ta isotope ratio without tail correction decreases from 0.00012000(58) in LR to 0.00011845(4) in MR and to 0.00011838(3) in HR (uncertainty as intermediate precision in 2S.D.). The decreasing tailing effects with increasing mass resolution at least in part relate to the much lower IGP pressure of 0.6 to 1 × 10−8 mbar in MR and HR compared to 2 to 3.6 × 10−8 mbar in LR. However, the difference in IGP pressure alone cannot fully explain the difference in Ta isotope ratios between the different mass resolution modes, because 180Ta/181Ta ratios in MR and HR are significantly lower than LR data from earlier sessions at comparable IGP pressures. Possibly, the improved abundance sensitivity in MR and HR can be explained by two physical and geometrical effects. First, the smaller slits produce a narrower beam. This results in a larger distance from the edge of the beam to the neighbouring cup, compared to a wider beam in LR. Consequently, even when the tail exhibits the same geometry in all resolution modes, the tail is shifted towards the centre of the cup by exactly the distance with which the beam edge is shifted towards the central mass of 181Ta. Secondly, the smaller slit size in HR preferentially samples ions from an inner part of the ion beam. In the centre of the ion beam, the ion population is assumed to be more homogeneous in terms of its kinetic energy distribution. Therefore, ions with more dispersed kinetic energies in the outer section of the beam are blocked by the slit.
3.4. The absolute isotope composition of tantalum
The preparation of gravimetric solutions by mixtures of mono-isotopic tracers is considered as an approach to most accurately determine absolute isotope ratios (e.g., ref. 45). Such gravimetrically known isotope mixtures can be used to accurately correct for mass discrimination. In the case of Ta, however, a sufficiently pure 180Ta tracer is commercially not available.Only two recent studies have attempted to constrain the absolute isotope composition of Ta within the last 20 years.3,30 The values that are currently recommended by IUPAC are those by de Laeter and Bukilic3 who reported 180Ta/181Ta = 0.00012012(62) based on TIMS measurements. Weyer et al.,30 in contrast, reported 180Ta/181Ta = 0.00011980(60) based on MC-ICP-MS measurements (intermediate precision reported as 2S.D.). Both studies discuss the effects of abundance sensitivity on the measured 180Ta/181Ta ratios on the basis of a mass scan. However, in linear space, the tailing effect from 181Ta on 180Ta is difficult to detect. For this reason, de Laeter and Bukilic3 assumed that the accuracy of their measured 180Ta/181Ta ratios is unaffected by abundance sensitivity. In contrast, Weyer et al.30 expected tailing effects on 180Ta based on the observed peak tailing of a 238U beam. Based on this observation, after applying a baseline correction, they suggest the presence of a residual 181Ta tail of approximately 5 ppm on 180Ta, resulting in a ∼4% lower 180Ta/181Ta ratio than their measured value, i.e., by about 0.000115. Nevertheless, neither of these studies obtained precise measurements between the peaks to better quantify the exact tail contribution. Our half mass measurements reveal a 181Ta tail contribution of around 2.5% in the Neptune MC-ICP-MS at Bonn and Bremen on the 180Ta signal (Fig. 1). Consequently, the Ta isotope ratio of 0.00012012 on which the current IUPAC recommended isotope composition of Ta is based, is most likely an overestimation.
The importance of the tail correction in establishing the best estimate on the Ta isotope ratio is furthermore illustrated by the improvement in intermediate precision that is seen when data are corrected for abundance sensitivity effects. Our mean values of standard measurements that are mass-bias and interference corrected, but not abundance sensitivity corrected 180Ta/181Ta in 22 LR sequences range from 0.00011933(10) to 0.00012023(8), i.e., corresponding to 75ε difference (experimental standard deviations, k = 2). This range is substantially worse than the intermediate precision of 180Ta/181Ta measurements within the individual analytical sessions, which is typically <4.5ε after interference, mass-bias, and drift correction. If 180Ta/181Ta ratios are also corrected for abundance sensitivity, both the variability within sequences (by about 1ε) and the maximum spread in mean values of the individual sequences is reduced (in case of the two sequences with the most extreme Ta ratios before tailing correction to only 5ε).
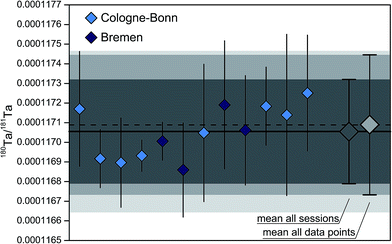
Based on an improved determination of the tail contribution on 180Ta, we propose here a new best estimate of the absolute 180Ta/181Ta isotope ratio of 0.00011705(41) (Fig. 4 and 5), which is equal to a 181Ta/180Ta of 8543(30) with expanded measurement uncertainty of k = 2. This value represents the mean of 12 analytical sessions over a 28 months period from two laboratories (Table 3), with 430 single measurements forming the basis of the data set. The arithmetic mean of the individual sessions is considered most appropriate for the determination of the absolute 180Ta/181Ta ratio. Different methods (i.e., Re and Yb based mass discrimination correction, different mass resolutions) and standard solutions were used in the same sessions for direct comparison. As no differences were resolved between different methods and Ta standard solutions the data was combined into mean values. The data selected were limited to measurements with a signal of more than 25 V* on 181Ta at Bremen and Cologne-Bonn, providing sufficient counting statistics and a stable tail contribution on 180Ta. One of 22 sequences obtained during the individual 12 sessions was rejected for the final evaluation due to an exceptionally large non-linear drift during the sequence, leading to values up to 5 standard deviations above the mean of the data set. Of the remaining 430 measurements, 16 measurements were rejected using a 2-sigma outlier criterion. These data has typically been obtained during sessions with relatively large drift that has possibly been insufficiently corrected with our linear offline tailing correction. The mean of the remaining single measurements is 0.00011709(36) and overlaps with the mean of the remaining sessions of 0.00011705(27) within the experimental standard deviation and k = 2 (in geochemistry 2S.D.). Importantly, the abundance sensitivity corrected data from all reported measurement sessions at Cologne-Bonn and Bremen overlap within their 2 standard deviation (Table 3 and Fig. 5). Also the use of different elements (Yb, Re) for mass bias correction results in absolute Ta isotope ratios that are indistinguishable from each other (Table 4).
| Session date | Facility | N | 180Ta/181Ta | 181Ta/180Ta | MB corr. | Standards | ||
|---|---|---|---|---|---|---|---|---|
| Mean | Uncertainty | Mean | Uncertainty | |||||
| a This session includes the MR and HR data. One Yb-based mass bias corrected sequence was rejected from the dataset because of unusual large drift in abundance sensitivity during this session (see text). | ||||||||
| 27.10.2013 | Cologne-Bonn | 25 | 0.00011717 | 0.00000015 | 8534.6 | 10.7 | Yb | AA |
| 21.12.2013 | Cologne-Bonn | 16 | 0.00011692 | 0.00000007 | 8553.0 | 5.4 | Yb | AA |
| 08.01.2014 | Cologne-Bonn | 23 | 0.00011690 | 0.00000011 | 8554.6 | 8.3 | Yb | AA |
| 10.05.2014 | Cologne-Bonn | 24 | 0.00011693 | 0.00000004 | 8552.0 | 2.9 | Yb | Ames |
| 05.06.2014 | Bremen | 20 | 0.00011701 | 0.00000005 | 8546.6 | 3.5 | Yb | Ames |
| 28.–30.07.2014 | Bremen | 30 | 0.00011686 | 0.00000012 | 8557.3 | 8.8 | Yb | Ames |
| 12.09.2014 | Cologne-Bonn | 22 | 0.00011705 | 0.00000017 | 8543.5 | 12.8 | Yb | Ames |
| 16.–19.03.2015 | Bremen | 72 | 0.00011719 | 0.00000016 | 8533.1 | 11.9 | Yb | Ames |
| 22.–24.06.2015 | Bremen | 67 | 0.00011706 | 0.00000014 | 8542.5 | 10.2 | Yb | Ames |
| 15.–16.09.2015 | Cologne-Bonn | 60 | 0.00011718 | 0.00000010 | 8533.6 | 7.3 | Yb, Re | Ames |
| 14.12.2015 | Cologne-Bonn | 18 | 0.00011714 | 0.00000021 | 8536.8 | 15.0 | Yb | AA, Ames |
| 29.02.–02.03.2016a | Cologne-Bonn | 40 | 0.00011725 | 0.00000015 | 8528.7 | 10.7 | Yb, Re | AA, Ames, Merck |
| This study | 180Ta/181Ta | Standard deviation | N | Standard deviation of the mean (k = 2) |
|---|---|---|---|---|
| a Compiled from Re- and Yb-based mass bias correction. b Compiled from all three Ta Std solutions. c Yb-Based mass bias correction applied to AMES and Alfa Aesar Ta standards. d Uncertainty as expanded measurement uncertainty or as stated in previous publications (k = 2). | ||||
| Mean sessions , | 0.00011705 | 0.00000013 | 12 | 0.00000008 |
| Mean all dataa,b | 0.00011709 | 0.00000018 | 414 | 0.00000002 |
| Mean data Bremenc | 0.00011708 | 0.00000018 | 181 | 0.00000003 |
| Mean data Cologne-Bonna,b | 0.00011710 | 0.00000018 | 233 | 0.00000002 |
| Alfa Aesar Specpure®a | 0.00011707 | 0.00000022 | 89 | 0.00000005 |
| Ames pure metala | 0.00011710 | 0.00000016 | 314 | 0.00000002 |
| Merck Certipur®a | 0.00011713 | 0.00000005 | 8 | 0.00000003 |
| Re mass bias correctedb | 0.00011716 | 0.00000008 | 58 | 0.00000002 |
| Yb mass bias correctedb | 0.00011708 | 0.00000019 | 356 | 0.00000002 |
| Medium resolutionc | 0.00011744 | 0.00000002 | 8 | 0.00000002 |
| High resolutionc | 0.00011739 | 0.00000002 | 8 | 0.00000002 |
The large number of data obtained with different methods and standards allows calculating the respective standard deviation of the mean for 180Ta/181Ta, which will then allow evaluating possible systematic effects between different methods (Table 4). The 180Ta/181Ta ratios measured in MR and HR (0.00011744(2), n = 8 and 0.00011739(2), n = 8) are outside the standard deviations of the mean (k = 2) of all data (180Ta/181Ta = 0.00011709(2), n = 414). It remains ambiguous whether these apparently higher 180Ta/181Ta ratios reflect the relatively small number of data that was obtained in MR and HR mode or relate to inaccuracies of tailing determinations in MR and HR mode, where the improved abundance sensitivity reduces the counting statistics and hence repeatability for the half mass measurements and impedes an sufficiently accurate empirical fit. Likewise, Re-based mass bias corrected Ta isotope ratios on average are slightly higher (180Ta/181Ta = 0.00011716(2), n = 58) than the mean of the Yb-based mass discrimination corrected data (180Ta/181Ta = 0.00011708(2), n = 356). This apparently high 180Ta/181Ta may also be an expression of the limited number of Re-corrected data, which were obtained over two analytical sessions at Cologne-Bonn only. The full variability seen in the rest of the Yb-corrected data over the course of the project is not represented by the Re values, thus confirming this assertion. However, slight systematic differences between the Yb and Re normalised data that are related to insufficient correction for the instrumental mass bias cannot be excluded. All other data obtained with different standards and methods are indistinguishable within their standard deviation of the mean (k = 2; 2SE in geochemistry). This indicates that differences in cup efficiency, gain correction between different sessions, and differences in isotope compositions of the standards (see Chapter 3.1.) are negligible within the uncertainty of our measurements.
These minor potential systematic effects describe above could indicate that the overall data set is not purely statistically controlled. While the MR and HR offset most likely is attributed to inaccuracies in the empirical tailing fit, the accuracy of the mass discrimination correction and the input is further considered. Nonetheless, the small absolute difference in Yb and Re normalised Ta isotope ratios of only 0.00000008 is well within the expanded measurement uncertainty (±0.00000041). If the recently proposed Yb isotope abundances by Wang et al.40 rather than those by Albalat et al.34 are used for correction of the instrumental mass bias, the mean 180Ta/181Ta of the Yb-corrected data shifts further downwards by approximately 25 to 30ε (0.25–0.3%), which is similar to the random measurement uncertainty (k = 2) of the 180Ta/181Ta ratio. The Re isotope composition used in this work and recommended by IUPAC is based on a publication by Gramlich et al. from 1973 (187Re/185Re = 1.6739).46 However, a 187Re/185Re = 1.6755 was proposed by Suzuki et al. in 2004.47 Using this value, Re-based mass bias corrected data are lowered by about 5ε, which is indistinguishable from the Yb-based mass bias corrected value within its standard deviation of the mean. The typical mass bias for heavier masses around 1% per u (ref. 36) is reduced through the high sensitivity interface as more lighter ions are transmitted relative to heavier ones.48 The observed mass bias in this study ranges from 0.5–0.7% u−1 (in case of Re-based correction) to 0.7–1% u−1 for Yb (after Albalat et al.34). The somewhat lower mass discrimination of Re compared to Yb may relate to the higher average mass of Re. On the contrary, mass discrimination calculated relative to Yb ratios of Wang et al.40 scatters more and often yields unusual low values (0.3–0.8% u−1), calling the applicability of their Yb composition for mass bias correction on our instrument into question.
A strong indication that our mass discrimination correction works sufficiently accurate is the consistency between Re- and Yb-normalised Ta isotope compositions (Yb after Albalat et al.,34Table 4). The difference in mass discrimination correction due to different reference Yb and Re isotope ratios amounts to 0.3% shift in 180Ta/181Ta, while tailing effects reduce the Ta isotope ratio by 2.5%. Therefore, in this study, mass discrimination effects are regarded as minor with respect to the uncertainty of the proposed absolute Ta isotope ratio. The use of two different elements to correct for instrumental mass discrimination is an advantage over earlier studies. The use of two different instruments and methods also corroborates the consistency of our results by inter-laboratory comparison. Therefore, potential systematic contributions arising from the use of only one instrument, one method of mass bias correction and inaccuracies in the tailing correction should be, at least in part, reflected by the random measurement uncertainty of the large amount of data obtained with different instruments and methods.
Potential additional sources of uncertainty are evaluated separately and are included in the combined uncertainty. Individual components of uncertainty that contribute to the final measurement uncertainty of the Ta isotope ratio are listed in Table 5. The combined Type A random uncertainty associated with our measurement are calculated as the mean of the individual measurement uncertainties propagated with the standard deviation of the mean of all independent sessions (Tables 3 and 5). We further evaluated the influence of Type B uncertainties on the estimate of the Ta isotope ratio. The tailing correction typically lowers the measured 180Ta/181Ta ratio by 0.00000250. This value scatters with a standard deviation of 0.00000040, depending on the particular vacuum quality encountered in the respective session. This approach would be an overestimation of tailing-induced uncertainty on the Ta isotope ratio, because the tailing correction reduces the overall variability in the data set present prior to application of the correction. Thus, uncertainty caused by the correction is to a large extent already covered in the standard deviation from the individual sessions. Because the empirical fit describes the tailing correctly (Fig. 1), we assume an additional source of uncertainty deriving from inaccuracies of our empirical tailing estimation to be less than 5% of the correction value. This additional uncertainty component added to the mean value is of comparable magnitude as the combined random measurement uncertainty (Table 5). With this additional uncertainty contribution, all individual session means (combined uncertainty, k = 2) are in agreement with the arithmetic mean of the sessions. The mass discrimination correction is always less than the tailing correction. The accuracy of the correction and the extent to which differences in instrumental mass discrimination are already covered in the random uncertainty of the session is not known. We estimate a 10% uncertainty on the typical correction of 0.00000100, which roughly corresponds to the experimental standard deviation of this correction observed in independent sessions. Systematic offsets due to the use of the exponential mass discrimination law (also known as Russell's law) might exist but are considered as being negligible, as our applied correction is of the expected magnitude.36 The uncertainty from isobaric corrections is already propagated in the measured ratio, as illustrated in Fig. 3, and the accuracy of this correction is ensured by the doping tests. The gain correction of the amplifiers, especially of the 1013 Ω resistor equipped amplifiers, exhibits an intermediate precision of the calibration of 0.01% (1ε), which is negligible with respect to other sources of uncertainty. The expanded measurement uncertainty on 180Ta/181Ta of 0.00000041 is given as the propagated Type A and B combined standard measurement uncertainty and a coverage factor of k = 2 (Table 5).
| 180Ta/181Ta | 181Ta/180Ta | |
|---|---|---|
| Type A random uncertainty components | ||
| Mean of individual uncertainties of independent sessions | 0.00000012 | 9.0 |
| Standard deviation of independent sessions | 0.00000013 | 9.7 |
| Number of independent sessions | 12 | 12 |
| Standard deviation of the mean of independent sessions | 0.00000004 | 2.8 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Type B uncertainty components | ||
| Mass discrimination correction | 0.00000010 | 7.3 |
| Tailing correction | 0.00000013 | 9.1 |
| Combined measurement uncertainty | 180Ta/181Ta | 181Ta/180Ta | ||
|---|---|---|---|---|
| Type A | Type A and B | Type A | Type A and B | |
| Combined measurement uncertainty | 0.00000013 | 0.00000021 | 9.4 | 15.0 |
| Expanded measurement uncertainty (k = 2) | 0.00000026 | 0.00000041 | 18.8 | 30.0 |
| % relative expanded measurement uncertainty (k = 2) | 0.22 | 0.35 | 0.22 | 0.35 |
Our best estimate of the 180Ta/181Ta isotope ratio of 0.00011705(41) equals a recalculated 181Ta/180Ta ratio of 8543(30). This translates to absolute isotope abundances of 0.011704(41) % for 180Ta and 99.988296(41) % for 181Ta (Table 6). Using the Ta isotope masses with their reported uncertainties of 179.9474648(48) u and 180.9479958(38) u,49 the absolute atomic weight of Ta is 180.9478787(38) u (propagated uncertainty with k = 2 and Monte Carlo approach50). This atomic weight is in good agreement with the value proposed by de Laeter and Bukilic3 of 180.9478780(20) u. The reason for the somewhat better precision stated in the previous work is not reconciled, as the total uncertainty mainly depends on the uncertainty on the mass of 181Ta.
| Unit | Value | Uncertainty | |
|---|---|---|---|
| Abundance of 180Ta | % | 0.011708 | 0.000041 |
| Abundance of 181Ta | % | 99.988292 | 0.000041 |
| Atomic mass | u | 180.9478787 | 0.0000038 |
4. Conclusions
We developed a high-precision method to measure 180Ta/181Ta isotope ratios, targeted for measurements of extraterrestrial samples with low concentrations of Ta. Our analytical method yields an intermediate precision (geochemistry: external reproducibility) of ca. ±4ε for measurements relative to a standard, which appears to be sufficient to resolve isotope anomalies in early solar system materials.51 The very low abundance of 180Ta and the substantial isobaric interference by 180Hf have previously hampered high-precision measurements. Newly developed 1013 Ω resistor Faraday cup amplifiers were tested for the first time in solution MC-ICP-MS and demonstrated to be of paramount importance for applications of Ta isotopes systematics in small sample sizes, as is the case for extraterrestrial materials. This claim is underlined by comparable intermediate precision for measurements of ∼100 ng with 1012 Ω resistors in relation to 25 ng with 1013 Ω resistors. To obtain precise Ta stable isotope data from bulk meteorites (typically having Ta contents of approximately 20 ppb (ref. 52)), only ∼1.2 g compared to ∼4 g (with 1012 Ω amplifiers) are now required. Three terrestrial standard materials were measured and their stable isotope composition proved to be indistinguishable.Abundance sensitivity is shown to be a very important issue for accurate Ta isotope ratio measurements. Changes in vacuum conditions of the mass-spectrometer can exert a strong influence on the measured 180Ta/181Ta ratios. Therefore, a tail measurement routine was performed at the beginning and end of each sequence 0.5 u away from the peak masses. An empirical fit plotted through these half mass data allowed the accurate correction of tail contributions from 181Ta onto 180Ta. Data acquisition in medium and high resolution is less prone to these tailing effects than data acquisition in low resolution and results in more robust data for a trade-off in sensitivity. Furthermore, it is shown that the tailing contribution is correlated with the IGP pressure but, in part, also derives from the front part of the instrument.
Considering the importance of tailing effects, the IUPAC recommended Ta isotope ratio was re-evaluated and abundance sensitivity issues appear to have been underestimated in the past, leading to an overestimation of the previously proposed 180Ta isotope abundance by ca. 2.5%. Errors imparted from possibly inaccurate Yb and Re isotope ratios reported in the literature or inaccurate mass discrimination correction are less significant than the effects of other uncertainties such as tail correction or counting statistics. For the first time, we present Ta isotope data that include a robust tail correction. Employing this tail correction, consistent Ta isotope data were obtained with different methods and instruments. The newly proposed 180Ta/181Ta ratio of 0.00011705(41) translates to isotope abundances of 0.011704(41) % for 180Ta and 99.988296(41) % for 181Ta, and an absolute atomic weight of 180.9478787(38) u for tantalum (combined uncertainties with coverage factor of k = 2).
Acknowledgements
We gratefully acknowledge funding by the Special Priority Program 1385 – “The first 10 Million Years of the Solar System – A Planetary Materials Approach” of the Deutsche Forschungsgemeinschaft (grant MU 1406/10-2/3). We thank Maxwell Thiemens for editing of the paper and Peter Sprung for help with calculation of propagated uncertainties. We thank two anonymous reviewers for their constructive comments, which greatly improved the quality of the paper.References
- J. Meija, T. B. Coplen, M. Berglund, W. A. Brand, P. De Bièvre, M. Gröning, N. E. Holden, J. Irrgeher, R. D. Loss, T. Walczyk and T. Prohaska, Pure Appl. Chem., 2016, 88, 293 CAS.
- F. A. White, T. L. Collins, J. R. Rourke and F. M. Rourke, Phys. Rev., 1955, 97, 566 CrossRef CAS.
- J. R. de Laeter and N. Bukilic, Phys. Rev. C: Nucl. Phys., 2005, 72, 25801 CrossRef.
- M. Hult, J. Gasparro, G. Marissens, P. Lindahl, U. Wätjen, P. Johnston, C. Wagemannns and M. Köhler, Phys. Rev. C: Nucl. Phys., 2006, 74, 54311 CrossRef.
- M. E. Wieser and J. B. Schwieters, Int. J. Mass Spectrom., 2005, 242, 97 CrossRef CAS.
- M. Schönbächler, D.-C. Lee, M. Rehkämper, A. N. Halliday, M. A. Fehr, B. Hattendorf and D. Günther, Earth Planet. Sci. Lett., 2003, 216, 467 CrossRef.
- N. Dauphas, B. Marty and L. Reisberg, Astrophys. J., 2002, 565, 640 CrossRef CAS.
- Q. Yin, S. B. Jacobsen and K. Yamashita, Nature, 2002, 415, 881 CrossRef CAS PubMed.
- N. Dauphas, A. M. Davis, B. Marty and L. Reisberg, Earth Planet. Sci. Lett., 2004, 226, 465 CrossRef CAS.
- H. Hidaka, Y. Ohta and S. Yoneda, Earth Planet. Sci. Lett., 2003, 214, 455 CrossRef CAS.
- M. Boyet and R. W. Carlson, Science, 2005, 309, 576 CrossRef CAS PubMed.
- R. Andreasen and M. Sharma, Science, 2006, 314, 806 CrossRef CAS PubMed.
- G. R. Huss, A. P. Meshik, J. B. Smith and C. Hohenberg, Geochim. Cosmochim. Acta, 2003, 67, 4823 CrossRef CAS.
- A. Trinquier, T. Elliott, D. Ulfbeck, C. Coath, A. N. Krot and M. Bizzarro, Science, 2009, 324, 374 CrossRef CAS PubMed.
- A. Cameron and J. Truran, Icarus, 1977, 30, 447 CrossRef CAS.
- A. Makishima and E. Nakamura, J. Anal. At. Spectrom., 2010, 25, 1712 RSC.
- J. M. Koornneef, C. Bouman, J. B. Schwieters and G. R. Davies, J. Anal. At. Spectrom., 2013, 28, 749 RSC.
- J. Liu and D. G. Pearson, Chem. Geol., 2014, 363, 301 CrossRef CAS.
- C. Sarkar, D. Pearson, L. M. Heaman and S. Woodland, Chem. Geol., 2015, 395, 27 CrossRef CAS.
- M. Schiller, C. Paton and M. Bizzarro, J. Anal. At. Spectrom., 2012, 27, 38 RSC.
- T. Schulz, C. Münker and S. T. M. Peters, Earth Planet. Sci. Lett., 2013, 362, 246 CrossRef CAS.
- S. T. M. Peters, C. Münker, H. Becker and T. Schulz, Earth Planet. Sci. Lett., 2014, 391, 69 CrossRef CAS.
- S. T. M. Peters, C. Münker, F. Wombacher and B.-M. Elfers, Chem. Geol., 2015, 413, 132 CrossRef CAS.
- D. Wielandt and M. Bizzarro, J. Anal. At. Spectrom., 2011, 26, 366 RSC.
- M. O. Naumenko, K. Mezger, T. F. Nägler and I. M. Villa, Geochim. Cosmochim. Acta, 2013, 122, 353 CrossRef CAS.
- J. Koornneef, C. Bouman, J. Schwieters and G. Davies, Anal. Chim. Acta, 2014, 819, 49 CrossRef CAS PubMed.
- J. M. Koornneef, I. Nikogosian, M. J. van Bergen, R. Smeets, C. Bouman and G. R. Davies, Chem. Geol., 2015, 397, 14 CrossRef CAS.
- M. Klaver, R. J. Smeets, J. M. Koornneef, G. R. Davies and P. Z. Vroon, J. Anal. At. Spectrom., 2016, 31, 171 RSC.
- J.-I. Kimura, Q. Chang, N. Kanazawa, S. Sasaki and B. S. Vaglarov, J. Anal. At. Spectrom., 2016, 31, 790 RSC.
- S. Weyer, C. Münker, M. Rehkämper and K. Mezger, Chem. Geol., 2002, 187, 295 CrossRef CAS.
- M. Thirlwall, J. Anal. At. Spectrom., 2001, 16, 1121 RSC.
- M. Thirlwall and R. Anczkiewicz, Int. J. Mass Spectrom., 2004, 235, 59 CrossRef CAS.
- W. Russell, D. Papanastassiou and T. Tombrello, Geochim. Cosmochim. Acta, 1978, 42, 1075 CrossRef CAS.
- E. Albalat, P. Telouk and F. Albarède, Earth Planet. Sci. Lett., 2012, 355–356, 39 CrossRef CAS.
- J. R. de Laeter and N. Bukilic, Int. J. Mass Spectrom., 2006, 252, 222 CrossRef CAS.
- C. N. Maréchal, P. Telouk and F. Albarède, Chem. Geol., 1999, 156, 251 CrossRef.
- H. P. Longerich, B. J. Fryer and D. F. Strong, Spectrochim. Acta, Part B, 1987, 42, 39 CrossRef.
- F. Albarède, P. Telouk, J. Blichert-Toft, M. Boyet, A. Agranier and B. Nelson, Geochim. Cosmochim. Acta, 2004, 68, 2725 CrossRef.
- T. Breton and G. Quitté, J. Anal. At. Spectrom., 2014, 29, 2284 RSC.
- J. Wang, T. Ren, H. Lu, T. Zhou and Y. Zhou, J. Anal. At. Spectrom., 2015, 30, 1377 RSC.
- Thermo Fisher Scientific, Neptune Plus Hardware Manual Revision C – 1250710, Thermo Fisher Scientific, Bremen, 2010 Search PubMed.
- M. Willbold, J. Anal. At. Spectrom., 2007, 22, 1364 RSC.
- Joint Committee for Guides in Metrology (JCGM), International vocabulary of metrology – basic and general concepts and associated terms (VIM), BIPM, 2012 Search PubMed.
- Joint Committee for Guides in Metrology (JCGM), Evaluation of measurement data — guide to the expression of uncertainty in measurement, ISO/BIPM, 2008 Search PubMed.
- W. Pritzkow, S. Wunderli, J. Vogl and G. Fortunato, Int. J. Mass Spectrom., 2007, 261, 74 CrossRef CAS.
- J. W. Gramlich, T. J. Murphy, E. L. Garner and W. R. Shields, J. Res. Natl. Bur. Stand., Sect. A, 1973, 77, 691 CrossRef CAS.
- K. Suzuki, Y. Miyata and N. Kanazawa, Int. J. Mass Spectrom., 2004, 235, 97 CrossRef CAS.
- K. Newman, J. Anal. At. Spectrom., 2012, 27, 63 RSC.
- M. Wang, G. Audi, A. Wapstra, F. Kondev, M. MacCormick, X. Xu and B. Pfeiffer, Chin. Phys. C, 2012, 36, 1603 CrossRef.
- P. Sprung, T. Kleine and E. E. Scherer, Earth Planet. Sci. Lett., 2013, 380, 77 CrossRef CAS.
- M. Pfeifer, C. Münker and N. S. Lloyd, Presented in part at Goldschmidt 2015, Prague, 2015 Search PubMed.
- C. Münker, J. A. Pfänder, S. Weyer, A. Buchl, T. Kleine and K. Mezger, Science, 2003, 301, 84 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |