Analysis of rocks by CSigma laser-induced breakdown spectroscopy with fused glass sample preparation
J. A.
Aguilera
 *ab and
C.
Aragón
*ab and
C.
Aragón
 ab
ab
aDepartamento de Física, Universidad Pública de Navarra, Campus de Arrosadía, E-31006 Pamplona, Spain. E-mail: j.a.aguilera@unavarra.es
bInstitute for Advanced Materials (INAMAT), Public University of Navarre, Campus de Arrosadía, E-31006 Pamplona, Spain
First published on 17th November 2016
Abstract
We report a validation experiment of the Cσ-LIBS method, proposed recently by our group for quantitative laser-induced breakdown spectroscopy. This method is applied to determine eight elements (Si, Al, Ca, Mg, Fe, Ti, Mn, and V) in rocks prepared as fused glass samples, having a wide range of certified concentrations. The characterization stage of the method is performed using only two standard fused glass samples prepared from mixtures of pure compounds (SiO2, Al2O3, Fe2O3 and CaCO3). The average precision obtained is 3.4% for concentrations higher than 0.1 wt%. This validation suggests that the accuracy and precision of this technique, if combined with fused glass sample preparation under favourable conditions, may become as good as those produced by certification laboratories.
1 Introduction
Among the efforts to improve the performance of laser-induced breakdown spectroscopy (LIBS) for quantitative analysis, an increasing interest exists in methods in which the conventional calibration procedure with a wide set of standard samples is avoided or at least simplified. These methods take advantage of the broad information about atomic data available in databases, compilations and research articles to switch from univariate calibration to procedures that use several spectral lines of each element of interest. The starting point of all these analytical procedures is the physical equations governing the spectral emission of plasmas in local thermodynamic equilibrium. The first approach proposed within such methods was the calibration-free procedure (CF-LIBS), introduced in 1999 by Ciucci et al.1 This approach is based on the determination of the temperature of the plasma from Boltzmann plots constructed including spectral lines of all the elements of the sample. Concentrations are obtained from the intercept of the Boltzmann plots, after applying a closure relation. Since its publication, CF-LIBS has been applied to analyse many types of samples, as described in a review2 and in a recent article3 published by the group that proposed the method. Also, improvements of CF-LIBS to account for self-absorption4 and plasma inhomogeneity5 have been introduced. A different group of methods for calibration-free LIBS were proposed by Gornushkin et al.,6 Yaroshchyk et al.,7 D'Angelo et al.,8 and Beldjilali et al.,9 based on the comparison of measured spectra to theoretical spectral radiance computed for a plasma in local thermodynamic equilibrium. These methods differed in the model of the plasma, and the algorithms used to determine the parameters such as temperature and elemental concentrations, which were based on fitting procedures7–9 or Monte Carlo optimization.6 Besides calibration-free, other efforts for calibration in LIBS are based on different chemometric methods, as discussed in the review article by Hahn and Omenetto.10In recent years, some approaches for quantitative LIBS have relaxed the complete absence of calibration by including a previous measurement with a reduced number of reference standard samples, with the aim of increasing the trueness in the analysis.3 Gaudiuso et al.11 proposed the so-called calibration-free inverse method (CF-IM), in which the plasma temperature, a key parameter of all these methods, is determined as the one providing the best agreement between the composition determined from the original calibration-free algorithm and the known composition of the certified standard. Cavalcanti et al.12 presented a variation of the original CF-LIBS approach, called the one-point calibration (OPC) method, based on the empirical determination of the product of an experimental and spectroscopic factor, whose knowledge is often imprecise or lacking, from the spectrum measured for one standard of known composition.
Our group has also recently proposed an approach for quantitative analysis by LIBS that may be applied using a few standard samples.13,14 This method takes its name (Cσ-LIBS) from the so-called Cσ graphs, generalized curves of growth that allow including several lines of different elements in the same plot.15 In Cσ-LIBS, conventional calibration for each element using a wide set of standards is replaced with a characterization procedure based on Cσ graphs, performed using usually one or two samples of known composition. Once the characteristic plasma parameters have been determined, the elemental concentrations of unknown samples are obtained by an iterative procedure supported also in a Cσ-graph representation. The first validation of the Cσ-LIBS method was carried out using fused glass samples prepared from certified slags.13 A satisfactory accuracy was obtained, especially for relative concentrations, for which the average relative error was 3.2%, whereas the error for absolute concentrations was 9.2%. In recent work, Grifoni et al.3 have compared three methods for quantitative LIBS using spectra acquired on bronze samples, obtaining an average percent error for Cσ-LIBS results of 19%. This accuracy may be considered reasonable taking into account the high difficulty of the direct analysis of samples, as opposed to their dilution in fused glass, due to the possible failure of the homogeneous model of the plasma and the higher complexity of the spectra. In fact, fused glass sample preparation, introduced in LIBS by Pease,16 has important advantages to check calibration models using samples from many different sources. These advantages are mainly due to the improved line-to-background of the spectra obtained with those samples, whose borate matrix contributes with only a few spectral lines to plasma emission.17 Moreover, the reduced concentrations of the elements of interest in fused glass samples result in low self-absorption. Although this method for developing standards eliminates the readiness of direct analysis, it is valuable for the initial validation of new approaches for quantitative analysis.
In this work, we apply the Cσ-LIBS method to analyse certified rocks prepared as fused glass disks. Quantitative analysis of rocks by LIBS has attracted great attention in recent years, due to its relevant applications in environmental science and geology. Also, the interest in rock analysis has been enhanced by the contribution of the LIBS ChemCam instrument on board the Curiosity rover on its Mars mission.18 Different approaches for quantitative LIBS have been applied to rock analysis, including conventional calibration,16,19,20 chemometric methods16,20,21 and CF-LIBS.19 Our aim in the present work is to improve and evaluate the analytical performance of the Cσ-LIBS method, including fused glass sample preparation, in the analysis of rocks, where the range of concentrations of the elements determined is much wider than in our first validation performed with certified slags.13
2 Experimental
The LIBS system is the same as that used previously,17 so it is only described briefly. For plasma generation, a Nd:YAG laser (1064 nm, 4.5 ns, 60 mJ per pulse, 20 Hz) is focused by a lens of 126 mm focal length at right angles to the sample, placed in air at atmospheric pressure. A system consisting of a pair of flat and concave mirrors collects the emission from the plasma at a small angle from the laser beam, and forms a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 image on the entrance slit of a spectrometer (Czerny-Turner, 0.5 m focal length, 3600 lines per mm grating), equipped with an intensified charge-coupled device (1200 × 256 effective pixels). We have measured the spectral efficiency of the system using deuterium and tungsten calibration standards of spectral irradiance. The sample rotates at 100 rpm during the measurements, in which the emission from 100 laser shots is accumulated.
1 image on the entrance slit of a spectrometer (Czerny-Turner, 0.5 m focal length, 3600 lines per mm grating), equipped with an intensified charge-coupled device (1200 × 256 effective pixels). We have measured the spectral efficiency of the system using deuterium and tungsten calibration standards of spectral irradiance. The sample rotates at 100 rpm during the measurements, in which the emission from 100 laser shots is accumulated.
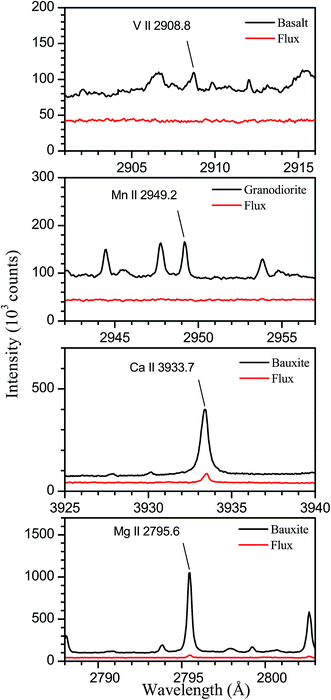
The samples analysed are four certified rocks; two of them (basalt and granodiorite) have been supplied by the United States Geological Survey (USGS) and the other two (dolomite and bauxite) by the Bureau of Analysed Samples (BAS). Table 1 shows the certified concentrations (wt%) of the eight elements analysed in this work. As can be seen, the four rocks selected for this study present a wide range of concentrations for these elements, which include the main constituents of the rocks with the exceptions of K and Na, whose emission lines are out of the spectral range of our system. In addition, we have prepared for characterization two fused glass samples from mixtures of compounds (SiO2, Al2O3, Fe2O3, and CaCO3 from Alfa Aesar) in powder form, having purities of at least 99.99%. Both the certified reference materials and the pure compounds were dried at 120 °C for 24 hours prior to their preparation as fused glass disks by borate fusion. The flux used consisted of a mixture of lithium tetraborate and lithium borate of 50/50 composition and a total mass of 6 g. The mass fraction of the dissolved material was 5 wt% in all cases. To assess that the purity of the flux is enough to avoid contamination in the analysis of minor elements, we have compared spectra obtained from the fused glass samples prepared from rocks to those measured for a sample prepared by fusion of the flux itself. The compared spectra are shown in Fig. 1, where we have indicated the analytical lines for elements present in rocks at concentrations lower than 0.05 wt%. As can be seen, for V in basalt and Mn in granodiorite, the analytical lines are not observed in the flux spectra, which allows us to deduce that contamination of these elements is negligible in our experiment. In the case of Ca and Mg in bauxite, the analytical lines are observed with low intensity in the flux spectra, indicating the presence of traces of these elements. From the line intensity ratios between both spectra, we have estimated threshold values for the contents in the flux of 1.9 ppm for Ca and 0.17 ppm for Mg that, taking into account the dilution in the fused samples, correspond to concentrations of 38 and 3.4 ppm, respectively, in the bauxite sample. Comparing these values to the certified contents of 360 ppm for Ca and 120 ppm for Mg, we deduce that contamination has a reduced effect on the analytical results obtained for these elements. The fluxer (Claisse Fluxy) allows simultaneous fusion of three samples in Pt–Au crucibles and molds. The general fusion program has been used, comprising six heating stages with increasing values of gas flow and rotation speed of the crucible, and a total operation time of nearly 2 minutes.
| Basalta | Granodioriteb | Dolomitec | Bauxited | |
|---|---|---|---|---|
| a Original reference: USGS BHVO-2. b Original reference: USGS GSP-2. c Original reference: BAS 782-1. d Original reference: BAS 395. | ||||
| Si | 23.3 | 31.1 | 0.124 | 0.580 |
| Al | 7.16 | 7.88 | 0.055 | 27.7 |
| Ca | 8.17 | 1.50 | 21.68 | 0.036 |
| Mg | 4.36 | 0.58 | 12.84 | 0.012 |
| Fe | 8.63 | 3.43 | 0.314 | 11.4 |
| Ti | 1.63 | 0.40 | 0.0025 | 1.16 |
| Mn | 0.1290 | 0.0320 | 0.063 | — |
| V | 0.0317 | 0.0052 | — | — |
3 Results and discussion
The Cσ-LIBS procedure comprises two separate stages, described in the next subsections: a characterization procedure using standard samples and the analysis of samples with unknown composition.3.1 Characterization
The Cσ-LIBS method relies on characterization of the plasma and the LIBS system by a set of parameters, namely βA (instrumental factor β times transverse area of the plasma A), ηNl (concentration unit factor η times columnar density Nl), T (temperature), and Ne (electron density).To accomplish characterization, we determined first the electron density of the plasma from the Stark broadening of the Hα line.17 The electron density was the same within the error for the two standard samples. The resulting Ne values were (0.82 ± 0.01) × 1017 cm−3 and (1.78 ± 0.02) × 1017 cm−3 for neutral atoms and ions, respectively. Then, experimental Cσ graphs, defined as plots with ordinate I/(LPΔλL) and abscissa Cσl, are constructed, using experimental and atomic data for selected lines of the elements of interest. In the ordinate of Cσ graphs, I is the measured line intensity, LP is the Planck radiance of a blackbody calculated at the plasma temperature and at the central wavelength of the transition, and ΔλL is the Lorentzian width, obtained by multiplying the Stark width by the electron density. In the abscissa, C is the concentration in the sample expressed in mol g−1 and σl(T,Ne) is the line cross-section, a key parameter defined as13,15
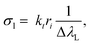 | (1) |
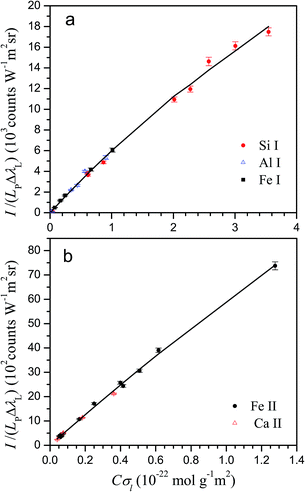
The lines used in the present work for characterization and analysis, together with their atomic data are listed in Table 2. The line cross-sections of the lines are also provided in the last column for typical values of T and Ne. Next, we describe the criteria used to select neutral atom or ion lines for a given element. (1) For some elements, at the typical temperature of the plasma, ion lines in the near ultraviolet to visible region are too weak, having small kt values. For example, at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, kt values for Si II and Al II lines in the spectral range 200–700 nm are lower than 0.1 × 10−20 m2 Å. Consequently, these lines are not observed or they show a very low line-to-background ratio, so neutral lines are used for these elements. (2) As described in our former work,13 too intense lines exceed the model limit of the method. As the plasma is strongly ionized, ion lines most commonly exceed the model limit than neutral ones for the same concentration. Therefore, for elements with high concentrations, neutral lines are generally preferred, unless weak ion lines are available. In the case of Mg, for example, the intense ion lines are avoided and Mg I lines are used except for the bauxite sample, which has a small Mg content. (3) For some elements, especially transition metals, both neutral and ion lines are available that do not exceed the model limit; in this case, ion lines are usually preferred, due to their higher overall line-to-background ratio. Fig. 2 shows the experimental Cσ graphs obtained for characterization of neutral atom and ion emissions using the selected spectral lines.
000 K, kt values for Si II and Al II lines in the spectral range 200–700 nm are lower than 0.1 × 10−20 m2 Å. Consequently, these lines are not observed or they show a very low line-to-background ratio, so neutral lines are used for these elements. (2) As described in our former work,13 too intense lines exceed the model limit of the method. As the plasma is strongly ionized, ion lines most commonly exceed the model limit than neutral ones for the same concentration. Therefore, for elements with high concentrations, neutral lines are generally preferred, unless weak ion lines are available. In the case of Mg, for example, the intense ion lines are avoided and Mg I lines are used except for the bauxite sample, which has a small Mg content. (3) For some elements, especially transition metals, both neutral and ion lines are available that do not exceed the model limit; in this case, ion lines are usually preferred, due to their higher overall line-to-background ratio. Fig. 2 shows the experimental Cσ graphs obtained for characterization of neutral atom and ion emissions using the selected spectral lines.
| λ (Å) | E i (eV) | E k (eV) | g i | g k | A ki (108 s−1) | f | Acc. | w (Å) | Acc. | σ l (10−20 m2) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
a References: Fe I, Fe II;22 Si I;23 Al I;24 Ca I, Mg I, Mg II, Ti II, V II;25 Ca II;25,26 Mn II.27
b Stark widths at electron density Ne = 1017 cm−3. References: Fe I;28 Si I;29 Al I;30 Ca I;31 Fe II;17,32,33 Ca II;34 Mn II;35 Mg II;36,37 Ti II.38 When the uncertainty is not displayed in the table, the experimental Stark width is not available, and the average of known Stark widths for lines of the same multiplet has been used. An uncertainty M means that the data provided come from a rough measurement performed in our laboratory. When the Stark width is not provided in the table, a value of 0.1 Å has been used.
c Calculated for T = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K and Ne = 1017 cm−3.
d The Mg II lines at 2797.930 Å and 2797.998 Å have been grouped, and the resulting data are indicated. 000 K and Ne = 1017 cm−3.
d The Mg II lines at 2797.930 Å and 2797.998 Å have been grouped, and the resulting data are indicated.
|
|||||||||||
| Fe I | 3631.463 | 0.96 | 4.37 | 7 | 9 | 0.517 | 0.131 | A | — | — | 8.73 |
| 3647.843 | 0.91 | 4.31 | 9 | 11 | 0.291 | 0.0711 | A | — | — | 6.46 | |
| 3734.864 | 0.86 | 4.18 | 11 | 11 | 0.901 | 0.189 | A | 0.08 | — | 23.4 | |
| 3749.485 | 0.91 | 4.22 | 9 | 9 | 0.763 | 0.161 | A | 0.08 | — | 15.4 | |
| 3763.789 | 0.99 | 4.28 | 5 | 5 | 0.544 | 0.116 | A | 0.08 | 20 | 5.70 | |
| 3765.539 | 3.24 | 6.53 | 13 | 15 | 0.951 | 0.233 | B+ | 0.07 | 20 | 2.20 | |
| 3767.192 | 1.01 | 4.30 | 3 | 3 | 0.639 | 0.136 | A | 0.08 | 20 | 3.92 | |
| Si I | 2207.978 | 0.00 | 5.61 | 1 | 3 | 0.262 | 0.0575 | B | 0.065 | 34 | 11.4 |
| 2210.892 | 0.01 | 5.62 | 3 | 5 | 0.346 | 0.0423 | B | 0.061 | 38 | 26.6 | |
| 2211.745 | 0.01 | 5.61 | 3 | 3 | 0.181 | 0.0133 | B | 0.063 | — | 8.11 | |
| 2216.669 | 0.03 | 5.62 | 5 | 7 | 0.454 | 0.0469 | B | 0.063 | — | 46.9 | |
| 2218.057 | 0.03 | 5.62 | 5 | 5 | 0.109 | 0.00805 | B | 0.063 | — | 8.06 | |
| 2506.897 | 0.01 | 4.95 | 3 | 5 | 0.547 | 0.0859 | B | 0.141 | 29 | 30.0 | |
| 2516.112 | 0.03 | 4.95 | 5 | 5 | 1.68 | 0.159 | B | 0.117 | 31 | 110 | |
| 2524.108 | 0.01 | 4.92 | 3 | 1 | 2.22 | 0.0708 | B | 0.104 | 33 | 34.0 | |
| 2528.508 | 0.03 | 4.93 | 5 | 3 | 0.904 | 0.052 | B | 0.107 | 35 | 39.7 | |
| Al I | 2652.475 | 0.00 | 4.67 | 2 | 2 | 0.142 | 0.015 | 12 | 0.78 | M | 0.337 |
| 2660.386 | 0.01 | 4.67 | 4 | 2 | 0.284 | 0.0151 | 11 | 0.78 | M | 0.671 | |
| 3082.153 | 0.00 | 4.02 | 2 | 4 | 0.59 | 0.168 | 12 | 0.45 | B | 11.3 | |
| 3092.710 | 0.01 | 4.02 | 4 | 6 | 0.71 | 0.153 | 2 | 0.49 | B | 18.6 | |
| 3944.006 | 0.00 | 3.14 | 2 | 2 | 0.47 | 0.11 | 10 | 0.37 | B | 14.4 | |
| 3961.520 | 0.01 | 3.14 | 4 | 2 | 0.99 | 0.117 | 6 | 0.38 | B | 29.7 | |
| Ca I | 4283.011 | 1.89 | 4.78 | 3 | 5 | 0.434 | 0.199 | C+ | 0.15 | M | 7.07 |
| 4289.367 | 1.88 | 4.77 | 1 | 3 | 0.600 | 0.500 | C+ | 0.15 | M | 5.99 | |
| 4298.988 | 1.89 | 4.77 | 3 | 3 | 0.466 | 0.129 | C+ | 0.15 | M | 4.62 | |
| 4302.528 | 1.90 | 4.78 | 5 | 5 | 1.360 | 0.378 | C+ | 0.15 | M | 22.3 | |
| 4318.652 | 1.90 | 4.77 | 5 | 3 | 0.740 | 0.120 | C+ | 0.155 | D | 4.59 | |
| Mg I | 2776.690 | 2.71 | 7.18 | 3 | 5 | 1.320 | 0.254 | B+ | — | — | 14.4 |
| 2778.271 | 2.71 | 7.17 | 1 | 3 | 1.820 | 0.632 | C+ | — | — | 12.0 | |
| 2779.834 | 2.72 | 7.18 | 8 | 8 | 3.010 | 0.356 | B | — | — | 53.5 | |
| 2781.416 | 2.71 | 7.17 | 3 | 1 | 5.430 | 0.210 | C+ | — | — | 11.9 | |
| 2782.971 | 2.72 | 7.17 | 5 | 3 | 2.140 | 0.149 | B+ | — | — | 14.1 | |
| Fe II | 2582.584 | 1.08 | 5.88 | 4 | 4 | 0.88 | 0.088 | B | 0.051 | 15 | 14.8 |
| 2585.876 | 0.00 | 4.79 | 10 | 8 | 0.894 | 0.0717 | B+ | 0.0411 | 15 | 131 | |
| 2591.543 | 1.04 | 5.82 | 6 | 6 | 0.572 | 0.0576 | B | 0.0523 | — | 14.9 | |
| 2592.785 | 4.08 | 8.86 | 14 | 16 | 2.74 | 0.316 | C | 0.045 | 15 | 6.53 | |
| 2598.370 | 0.05 | 4.82 | 8 | 6 | 1.43 | 0.108 | B+ | 0.0391 | — | 158 | |
| 2599.396 | 0.00 | 4.77 | 10 | 10 | 2.35 | 0.239 | B+ | 0.045 | 15 | 402 | |
| 2607.088 | 0.08 | 4.84 | 6 | 4 | 1.73 | 0.117 | B | 0.0394 | 14 | 123 | |
| 2611.874 | 0.05 | 4.79 | 8 | 8 | 1.2 | 0.122 | B+ | 0.0368 | 14 | 192 | |
| 2613.825 | 0.11 | 4.85 | 4 | 2 | 2.12 | 0.109 | B+ | 0.0384 | 14 | 76.7 | |
| 2617.618 | 0.08 | 4.82 | 6 | 6 | 0.488 | 0.0501 | B | 0.038 | 15 | 55.1 | |
| 2621.670 | 0.12 | 4.85 | 2 | 2 | 0.56 | 0.0577 | B+ | 0.0391 | — | 19.7 | |
| 2711.842 | 3.15 | 7.72 | 12 | 14 | 0.436 | 0.056 | C | 0.045 | — | 3.17 | |
| 2714.413 | 0.99 | 5.55 | 8 | 6 | 0.57 | 0.0473 | B | 0.0541 | — | 18.4 | |
| 2716.218 | 3.42 | 7.99 | 6 | 6 | 1.15 | 0.127 | C | 0.045 | — | 2.63 | |
| 2724.884 | 1.04 | 5.59 | 6 | 6 | 0.0958 | 0.0107 | C+ | 0.0524 | — | 3.04 | |
| 2730.734 | 1.08 | 5.62 | 4 | 4 | 0.279 | 0.0313 | B | 0.05 | 14 | 5.99 | |
| 2743.197 | 1.10 | 5.62 | 2 | 4 | 1.97 | 0.445 | B+ | 0.0515 | 14 | 40.7 | |
| 2753.288 | 3.27 | 7.77 | 10 | 12 | 1.89 | 0.258 | C | 0.0532 | 14 | 9.28 | |
| Ca II | 3158.869 | 3.12 | 7.05 | 2 | 4 | 2.83 | 0.847 | 10 | 0.53 | 15 | 20.1 |
| 3179.331 | 3.15 | 7.05 | 4 | 6 | 3.44 | 0.782 | 10 | 0.49 | 15 | 39.4 | |
| 3706.024 | 3.12 | 6.47 | 2 | 2 | 0.837 | 0.172 | 10 | 0.66 | 15 | 4.47 | |
| 3736.902 | 3.15 | 6.47 | 4 | 2 | 1.57 | 0.164 | 10 | 0.67 | 15 | 8.27 | |
| 3933.663 | 0.00 | 3.15 | 2 | 4 | 1.47 | 0.682 | C | 0.17 | 15 | 2890 | |
| 3968.469 | 0.00 | 3.12 | 2 | 2 | 1.40 | 0.033 | C | 0.16 | 15 | 1510 | |
| Mn II | 2593.724 | 0.00 | 4.78 | 7 | 7 | 2.77 | 0.2795 | 4.7 | 0.14 | 16 | 509 |
| 2605.684 | 0.00 | 4.76 | 7 | 5 | 2.72 | 0.1979 | 4.8 | 0.148 | 16 | 344 | |
| 2933.055 | 1.17 | 5.40 | 5 | 3 | 2.01 | 0.1556 | 5 | 0.163 | 16 | 56.7 | |
| 2939.308 | 1.17 | 5.39 | 5 | 5 | 1.95 | 0.2527 | 4.6 | 0.122 | 16 | 124 | |
| 2949.205 | 1.17 | 5.38 | 5 | 7 | 1.94 | 0.3544 | 4.6 | 0.16 | 16 | 133 | |
| Mg II | 2790.777 | 4.42 | 8.86 | 2 | 4 | 4.01 | 0.937 | A | 0.162 | B+ | 20.5 |
| 2795.528 | 0.00 | 4.43 | 2 | 4 | 2.60 | 0.608 | A+ | 0.087 | B+ | 4210 | |
| 2797.998d | 4.43 | 8.86 | 8 | 10 | 3.19 | 0.469 | A | 0.144 | B+ | 45.8 | |
| 2802.705 | 0.00 | 4.42 | 2 | 2 | 2.57 | 0.303 | A+ | 0.0945 | B+ | 1940 | |
| Ti II | 3341.875 | 0.57 | 4.28 | 6 | 8 | 1.68 | 0.375 | B+ | 0.0887 | 15 | 126 |
| 3361.212 | 0.03 | 3.72 | 8 | 10 | 1.58 | 0.335 | C | 0.0702 | 15 | 287 | |
| 3372.793 | 0.01 | 3.69 | 6 | 8 | 1.41 | 0.321 | B+ | 0.0724 | 15 | 212 | |
| 3380.277 | 0.05 | 3.72 | 10 | 10 | 0.137 | 0.0235 | C+ | 0.075 | — | 24.8 | |
| 3383.758 | 0.00 | 3.66 | 4 | 6 | 1.39 | 0.358 | B+ | 0.0688 | 15 | 160 | |
| V II | 2893.311 | 0.37 | 4.65 | 9 | 7 | 1.20 | 0.120 | B | — | — | 59.8 |
| 2908.808 | 0.39 | 4.65 | 11 | 9 | 1.60 | 0.170 | B | — | — | 102 | |
| 2924.636 | 0.37 | 4.61 | 9 | 9 | 1.20 | 0.150 | B | — | — | 76.4 | |
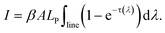 | (2) |
The optical depth is factorized as
| τ(λ) = ηNlCktriV(λ), | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 ± 200 K.
500 ± 200 K.
3.2 Analysis results
The knowledge of the characteristic parameters of the plasma and the LIBS system allows the analysis of unknown samples. The procedure13 starts from the measurement of spectra and construction of initial experimental Cσ graphs for neutral atoms and ions including selected spectral lines and using an arbitrary value of concentration for all elements. To perform the analysis, an iterative process is carried out by varying the concentrations and obtaining the value of χ2 of the experimental data with respect to the curve of the LIBS system, calculated from the plasma parameters. The convergence of this process leads to the absolute concentrations of the elements and to the final Cσ graphs, as shown in Fig. 3 for neutral atoms and in Fig. 4 for ions. From the comparison of the plots of the four rocks in each figure, we notice the high difference of the concentrations among the samples, particularly between dolomite and bauxite in respect of the similar composition of basalt and granodiorite.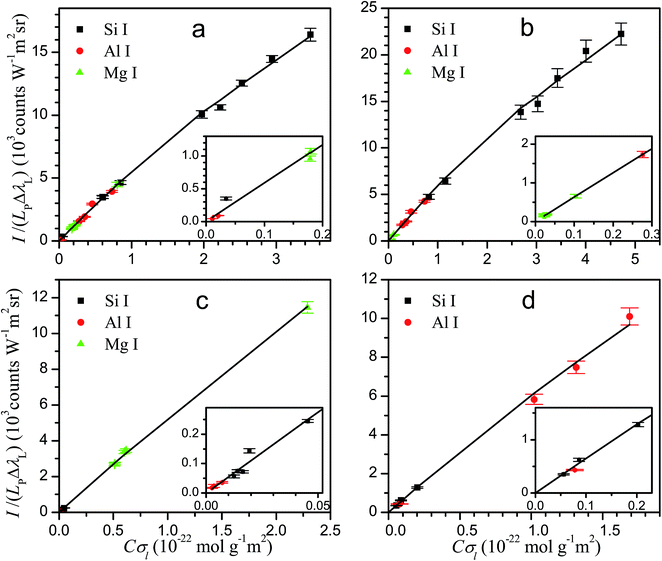 | ||
| Fig. 3 Cσ graphs of neutral atom emission lines, providing the elemental concentrations for basalt (a), granodiorite (b), dolomite (c) and bauxite (d) samples. | ||
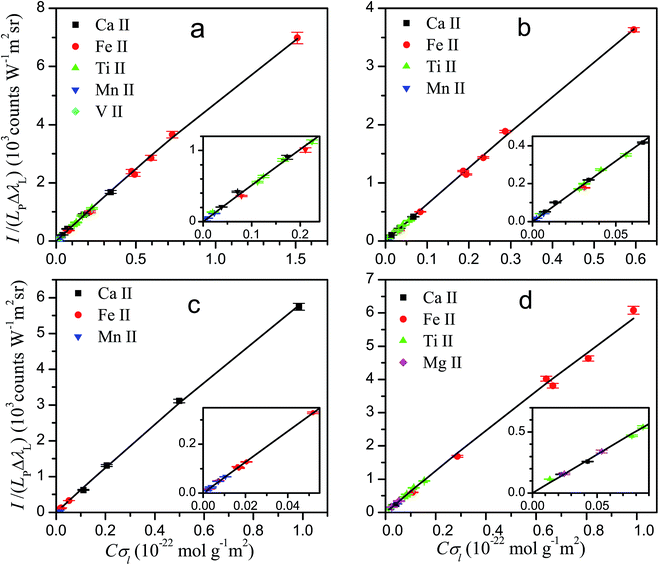 | ||
| Fig. 4 Cσ graphs for ion emission lines, providing the elemental concentrations for basalt (a), granodiorite (b), dolomite (c) and bauxite (d) samples. | ||
The analytical results obtained are presented in Table 3. For the four rocks prepared as fused glass samples, the elemental concentrations resulting from Cσ-LIBS analysis are compared to certified values. The last column of the table shows the relative difference between Cσ-LIBS and certified values. To summarize, the difference is 13% on average for concentrations lower than 0.1 wt%, and 3.4% for higher concentrations. It is worth noting that, taking into account the dilution at 5 wt% of the rock powder in the borate solvent, the real concentration in the fused glass samples is in the range 6.0–31 μg g−1 for the elements with concentrations in the rock lower than 0.1 wt%. For these low concentrations in the fused glass sample, the signal-to-noise ratio of the analytical lines becomes poor, which explains the higher error of the determined concentrations. Overall, the precision is improved with respect to that obtained in our previous validation with slag fused glass samples.13
| Sample | Element | Certified (wt%) | σ lab (%) | Cσ-LIBS (wt%) | Diff.b (%) |
|---|---|---|---|---|---|
| a Standard deviation of concentrations provided by different laboratories. b Relative difference between Cσ-LIBS and certified concentration. | |||||
| Basalt | Si | 23.3 | 1.3 | 22.7 | 2.4 |
| Al | 7.16 | 1.1 | 7.04 | 1.7 | |
| Ca | 8.17 | 1.5 | 7.73 | 5.4 | |
| Mg | 4.36 | 1.5 | 4.37 | 0.2 | |
| Fe | 8.63 | 1.6 | 8.59 | 0.5 | |
| Ti | 1.63 | 1.2 | 1.59 | 2.5 | |
| Mn | 0.1290 | 3.1 | 0.1295 | 0.4 | |
| V | 0.0317 | 3.4 | 0.0308 | 2.8 | |
| Granodiorite | Si | 31.1 | 1.3 | 30.4 | 2.3 |
| Al | 7.88 | 1.4 | 6.96 | 12 | |
| Ca | 1.50 | 2.7 | 1.52 | 1.2 | |
| Mg | 0.58 | 3.4 | 0.558 | 3.8 | |
| Fe | 3.43 | 3.2 | 3.41 | 0.5 | |
| Ti | 0.40 | 2.5 | 0.401 | 0.3 | |
| Mn | 0.0320 | 6.2 | 0.0381 | 19 | |
| Dolomite | Si | 0.124 | 5.0 | 0.131 | 5.6 |
| Al | 0.055 | 8.2 | 0.067 | 21 | |
| Ca | 21.68 | 0.4 | 22.30 | 2.8 | |
| Mg | 12.84 | 1.3 | 12.09 | 5.9 | |
| Fe | 0.314 | 3.0 | 0.295 | 6.1 | |
| Mn | 0.063 | 5.5 | 0.060 | 5.4 | |
| Bauxite | Si | 0.580 | 3.2 | 0.565 | 2.6 |
| Al | 27.73 | 3.8 | 25.98 | 6.2 | |
| Ca | 0.036 | 20 | 0.028 | 23 | |
| Mg | 0.012 | 50 | 0.011 | 7.2 | |
| Fe | 11.40 | 0.6 | 11.62 | 1.9 | |
| Ti | 1.157 | 3.6 | 1.085 | 6.5 | |
To estimate the limit of detection in Cσ-LIBS, we first obtain the quantity (Cσl)L = 3s/b, where s is the standard deviation of the ordinate of the graph for low Cσl values corresponding to data of low concentration C, and b is the slope of the linear limit, given by the product of parameters b = βA × Nl. Then, (Cσl)L is divided by the line cross-section σl to obtain the detection limit CL. We have determined in this way the detection limit for the element with lower concentration in each rock, with the following results: 4.0 μg g−1 for V in the basalt fused sample, 1.5 μg g−1 for Mn in that prepared from granodiorite, 1.4 μg g−1 for Mn in that prepared from dolomite, and 0.6 μg g−1 for Mg in the sample prepared from bauxite. It is worth mentioning that these limits of detection correspond to the analysis of the fused glass samples, where the rocks are diluted at 5 wt%, and therefore they are higher, in the 10–100 ppm range, in the rock samples.
It is interesting to compare the differences of Cσ-LIBS results relative to certified values with the data provided by the laboratories participating in the certification of the reference samples. To this aim, Table 3 includes the column with heading σlab, meaning the relative standard deviation of concentrations provided by different laboratories, taken from the certification sheet. As can be seen, the difference between Cσ-LIBS and certified values is not far from σlab, which means that the accuracy of the technique obtained under the conditions of the present work is comparable to that of the methods used by the laboratories, such as XRF, ICP-MS, etc. However, it should be noted that the results of the present validation have been obtained under favourable conditions using fused glass samples that, as mentioned before, are particularly suitable for initial validation of calibration methods, specifically for the CSigma-LIBS approach. The four main factors that contribute to improved analytical performance when using fused glass sample preparation are (1) the accurate measurement of line intensities, resulting from the high line-to-background of spectra obtained with these samples (2) the high sample homogeneity, (3) the absence or limited influence of matrix effects due to the common borate matrix, and (4) the low elemental concentration range resulting from dilution in the borate solvent. All these factors contribute to the accurate results collected in Table 3, which therefore may not be extrapolated to possible applications of the method involving other types of samples. The latter factor has particular relevance in Cσ-LIBS, as low elemental concentrations help to overcome its limitations to describe plasma inhomogeneity. Indeed, as described in detail in our previous work,13 the method is based on a so-called double homogeneous plasma model. This simple model is only an approximation of the true complex distribution of physical parameters in the plasma. Therefore, the model is expected to fail in describing the emission of elements with high ionization energies, such as H, C, N and O. Also, we have checked that it fails to describe Cσ data for intense lines or high concentrations. Therefore, a further development of the method including a more realistic model of the plasma will be necessary to apply it to samples with higher elemental contents or in cases where the mentioned elements have to be determined.
4 Conclusions
The Cσ-LIBS method for quantitative laser-induced breakdown spectroscopy has been applied to analyse certified rocks prepared as fused glass samples. The characterization stage prior to analysis is performed using only two standard samples prepared from mixtures of pure compounds. The four rocks selected for this experiment have a wide range of concentrations for the eight elements analysed. The average precision obtained for absolute concentrations is 3.4% for concentrations in the rock higher than 0.1 wt%. The comparison of the precision obtained with the standard deviation of values provided by certification laboratories shows that the accuracy of Cσ-LIBS, when combined with fused glass sample preparation under favourable conditions, is comparable to that of the methods used in the certification analysis. It is clear that this type of sample preparation removes the versatility and speed of LIBS analysis. Moreover, the dilution of the sample of interest prevents the determination of trace (ppm level) elements. However, as a counterpart, various problems that limit the accuracy of the analysis of non-prepared samples are mitigated by fused glass preparation, which turns out to be very convenient to perform the initial validations of the method. In particular, the main limitation of Cσ-LIBS in its present stage, related to the failure of the simple plasma model used, is overcome due to the low elemental concentrations present in the diluted samples. Further work is necessary to extend the applicability of the method to other types of samples, in particular to direct analysis by LIBS, without sample preparation. However, we consider that this new validation of the Cσ-LIBS method is a step forward towards the acceptance of laser-induced breakdown spectroscopy as one of the established techniques for reliable quantitative analysis. Our next goal is to extend the applicability of the method to direct analysis of alloy samples.Acknowledgements
This work has been supported by the project FIS2014-54285-P of the Spanish Ministerio de Economía y Competitividad.References
- A. Ciucci, M. Corsi, V. Palleschi, S. Rastelli, A. Salvetti and E. Tognoni, Appl. Spectrosc., 1999, 53, 960 CrossRef CAS.
- E. Tognoni, G. Cristoforetti, S. Legnaioli and V. Palleschi, Spectrochim. Acta, Part B, 2010, 65, 1 CrossRef.
- E. Grifoni, S. Legnaioli, G. Lorenzetti, S. Pagnotta, F. Poggialini and V. Palleschi, Spectrochim. Acta, Part B, 2016, 124, 40 CrossRef CAS.
- D. Bulajic, M. Corsi, G. Cristoforetti, S. Legnaioli, V. Palleschi, A. Salvetti and E. Tognoni, Spectrochim. Acta, Part B, 2002, 57, 339 CrossRef.
- J. A. Aguilera, C. Aragón, G. Cristoforetti and E. Tognoni, Spectrochim. Acta, Part B, 2009, 64, 685 CrossRef.
- I. B. Gornushkin, A. Y. Kazakov, N. Omenetto, B. W. Smith and J. D. Winefordner, Spectrochim. Acta, Part B, 2005, 60, 215 CrossRef.
- P. Yaroshchyk, D. Body, R. J. S. Morrison and B. L. Chadwick, Spectrochim. Acta, Part B, 2006, 61, 200 CrossRef.
- C. A. D'Angelo, D. M. D. Pace, G. Bertuccelli and D. Bertuccelli, Spectrochim. Acta, Part B, 2008, 63, 367 CrossRef.
- S. Beldjilali, D. Borivent, L. Mercadier, E. Mothe, G. Clair and J. Hermann, Spectrochim. Acta, Part B, 2010, 65, 727 CrossRef.
- D. W. Hahn and N. Omenetto, Appl. Spectrosc., 2012, 66, 347 CrossRef CAS PubMed.
- R. Gaudiuso, M. Dell'Aglio, O. De Pascale, A. Santagata and A. De Giacomo, Spectrochim. Acta, Part B, 2012, 74–75, 38 CrossRef CAS.
- G. H. Cavalcanti, D. V. Teixeira, S. Legnaioli, G. Lorenzetti and V. Palleschi, Spectrochim. Acta, Part B, 2013, 87, 51 CrossRef CAS.
- C. Aragón and J. A. Aguilera, Spectrochim. Acta, Part B, 2015, 110, 124 CrossRef.
- J. A. Aguilera and C. Aragón, WO2015–104049, US Pat., 15110476, European Pat. 14700162.2, Public University of Navarre, 2016.
- C. Aragón and J. A. Aguilera, J. Quant. Spectrosc. Radiat. Transfer, 2014, 149, 90 CrossRef.
- P. Pease, Spectrochim. Acta, Part B, 2013, 83–84, 37 CrossRef CAS.
- C. Aragón, J. A. Aguilera and J. Manrique, J. Quant. Spectrosc. Radiat. Transfer, 2014, 134, 39 CrossRef.
- S. Maurice, S. M. Clegg, R. C. Wiens, O. Gasnault, W. Rapin, O. Forni, A. Cousin, V. Sautter, N. Mangold, L. Le Deit, M. Nachon, R. B. Anderson, N. L. Lanza, C. Fabre, V. Payré, J. Lasue, P.-Y. Meslin, R. J. Léveillé, B. L. Barraclough, P. Beck, S. C. Bender, G. Berger, J. C. Bridges, N. T. Bridges, G. Dromart, M. D. Dyar, R. Francis, J. Frydenvang, B. Gondet, B. L. Ehlmann, K. E. Herkenhoff, J. R. Johnson, Y. Langevin, M. B. Madsen, N. Melikechi, J.-L. Lacour, S. Le Mouélic, E. Lewin, H. E. Newsom, A. M. Ollila, P. Pinet, S. Schröder, J.-B. Sirven, R. L. Tokar, M. J. Toplis, C. d'Uston, D. T. Vanimanj and A. R. Vasavada, J. Anal. At. Spectrom., 2016, 31, 863 RSC.
- B. Sallé, J.-L. Lacour, P. Mauchien, P. Fichet, S. Maurice and G. Manhès, Spectrochim. Acta, Part B, 2006, 61, 301 CrossRef.
- H. K. Shangapi, J. Jain, A. Bol'shakov, C. Lopano, D. McIntyre and R. Russo, Spectrochim. Acta, Part B, 2016, 122, 9 CrossRef.
- Q. Shi, G. Niu, Q. Lin, T. Xu, F. Li and Y. Duan, J. Anal. At. Spectrom., 2015, 30, 2384 RSC.
- J. R. Fuhr and W. L. Wiese, J. Phys. Chem. Ref. Data, 2006, 35, 1669 CrossRef CAS.
- D. E. Kelleher and L. I. Podobedova, J. Phys. Chem. Ref. Data, 2008, 37, 1285 CrossRef CAS.
- V. Vujnović, K. Blagoev, C. Fürböck, T. Neger and H. Jäger, Astron. Astrophys., 2002, 338, 704 CrossRef.
- A. Kramida, Y. Ralchenko, J. Reader and NIST ASD Team, NIST Atomic Spectra Database (Version 5.3), http://physics.nist.gov/asd, Wed Sep 28 2016, National Institute of Standards and Technology, Gaithersburg, MD, 2015 Search PubMed.
- J. A. Aguilera, C. Aragón and J. Manrique, J. Quant. Spectrosc. Radiat. Transfer, 2015, 160, 10 CrossRef CAS.
- R. Kling and U. Griesmann, Astrophys. J., 2000, 531, 1173 CrossRef CAS.
- J. A. Aguilera and C. Aragón, Spectrochim. Acta Part B, 2008, 63, 784 CrossRef.
- S. Bukvić, S. Djeniže and A. Srećković, Astron. Astrophys., 2009, 508, 491 CrossRef.
- N. Konjević, M. S. Dimitrijević and W. L. Wiese, J. Phys. Chem. Ref. Data, 1984, 13, 649 CrossRef.
- N. Konjević and J. R. Roberts, J. Phys. Chem. Ref. Data, 1976, 5, 209 CrossRef.
- C. Aragón, P. Vega and J. A. Aguilera, J. Phys. B: At., Mol. Opt. Phys., 2011, 44, 055002 CrossRef.
- J. A. Aguilera, J. Manrique and C. Aragón, J. Phys. B: At., Mol. Opt. Phys., 2011, 44, 245701 CrossRef.
- J. A. Aguilera, C. Aragón and J. Manrique, Mon. Not. R. Astron. Soc., 2014, 444, 1854 CrossRef CAS.
- S. Djeniže, S. Bukvić, A. Srećković and Z. Nikolić, New Astron., 2006, 11, 256 CrossRef.
- S. Bukvić, A. Srećković and S. Djeniže, New Astron., 2004, 9, 629 CrossRef.
- S. Djeniže, S. Bukvić, A. Srećković and M. Platiša, Astron. Astrophys., 2004, 424, 561 CrossRef.
- J. Manrique, J. A. Aguilera and C. Aragón, Mon. Not. R. Astron. Soc., 2016, 462, 1501 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |