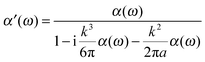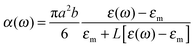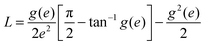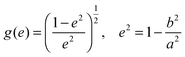Far-field plasmonic coupling in 2-dimensional polycrystalline plasmonic arrays enables wide tunability with low-cost nanofabrication

Abstract

We report the experimental observation and numerical modeling study of far-field plasmonic coupling (FFPC) in 2-dimensional polycrystalline plasmonic arrays consisting of “single crystalline” domains of a random size and orientation. Even though polycrystalline plasmonic arrays are routine products of low-cost nanosphere lithography (NSL), their FFPC behavior has not been well understood. Herein, FFPC observed from gold nanodisk (AuND) arrays fabricated using NSL appears, qualitatively, to be in keeping with that of highly regular nanoparticle arrays, where they induced cyclic modulations on the peak position and linewidth of the localized surface plasmon resonance (LSPR). Remarkable blue shifts as large as 1000 nm with nearly doubled linewidth were observed experimentally. Numerical modeling was systematically carried out and showed quantitative agreement with the experimental results. Using the modeling approach, the influences of array randomness and particle size on FFPC have been studied independently for the first time. Finally, two potential applications have been developed for FFPC-based LSPR tuning. Firstly, when AuND arrays are fabricated on flexible substrates, a novel transduction mechanism can be established between the LSPR peak position and the substrate strain. Owing to the far-field propagating nature, FFPC-based transduction can effectively extend the strain-tuning displacement range by an order of magnitude compared with those based on near-field coupling. Secondly, we show that FFPC leads to an LSPR peak within 1 μm for nanoporous gold disk arrays, which otherwise have a single particle LSPR peak beyond 1.5 μm. Such a significant FFPC-induced blue shift is critically important for compatibility with the use of silicon-based detectors.

---

Conceptual insights

We report the first experimental observation and numerical modeling study of far-field plasmonic coupling (FFPC) in 2-dimensional polycrystalline plasmonic arrays consisting of “single crystalline” domains of a random size and orientation. Even though polycrystalline plasmonic arrays are routine products of low-cost nanosphere lithography (NSL), their FFPC behavior has not been well understood. Previous studies concluded that FFPC doesn't exist in disordered array due to the lack of phase coherence. However, we have proven otherwise. Herein, FFPC observed from gold nanodisk (AuND) arrays fabricated using NSL appears qualitatively in keeping with that of highly regular nanoparticle arrays, where they induced cyclic modulations on the peak position and linewidth of the localized surface plasmon resonance (LSPR). Remarkable blue shifts as much as 1000 nm with nearly doubled linewidth were observed experimentally. This mechanism has been employed to demonstrate two potential applications: LSPR tuning based on substrate strain and a tailored LSPR peak position in nanoporous gold arrays. In the former, FFPC-based transduction can effectively extend the strain-tuning displacement range by an order of magnitude compared with those based on near-field couplings. In the latter, FFPC leads to an LSPR peak within 1 μm for nanoporous gold disk arrays, which otherwise have a single particle LSPR peak beyond 1.5 μm. Such a significant FFPC-induced blue shift is critically important for compatibility with the use of silicon-based detectors.

Introduction

Metallic nanoparticles and nanostructures possess intriguing optical properties mainly due to the resonant interaction of incident light with free electrons, known as localized surface plasmon resonance (LSPR).^1–3 LSPR and its consequential local electric field (E-field) enhancement have been extensively studied and employed for sensing,⁴ photovoltaics,⁵ imaging,⁶ catalysis,⁷ nanolaser,⁸ light manipulation,⁹ and biomedicine.¹⁰ Significant efforts have been placed on the understanding and fine-tuning the properties of plasmonic nanostructures. For single particles, these aspects have been carefully studied by altering the dimension, shape, or material of the nanostructures.^11–13 However, the LSPR of plasmonic “ensembles” consisting of multiple nanoparticles warrants the consideration of their interactions.^14–17 Plasmon hybridization is one of the preeminent models for studying coupling effects, where the plasmonic properties of complex nanostructures are derived from those of simpler geometries akin to molecular orbital theory.¹⁸ Plasmon hybridization has been successfully applied to model nanostars,¹⁹ nanoshells,¹⁸ and nanoparticle dimers,²⁰etc.

Plasmonic coupling can also be understood as E-field/free electron interactions, where the electron oscillation in one nanoparticle not only depends on its own light excitation but also on the E-fields generated by other nanoparticles. For a single nanoparticle, LSPR results in two types of E-field: an evanescent near-field and a propagating far-field induced by dipolar or higher mode radiation. The strong but exponentially decaying nature makes the near-field coupling dominant in nanoparticle ensembles with narrow inter-particle gaps typically smaller than a few dozen nanometers, whereas the propagating nature of the far-field makes the resulting far-field plasmonic coupling (FFPC) dominant at relatively longer inter-particle distances.

Inter-particle coupling effects for a variety of nanoparticle systems have been investigated.^14,21 In the two-particle scenario, with a particle center-to-center distance (CD) ≪ LSPR wavelength (λ_LSPR), near-field coupling induces red-shifts and far-field coupling induces blue-shifts in λ_LSPR.²² The distance dependence of near-field coupling can be described by an exponential decay function.²³ When the CD is comparable to λ_LSPR, FFPC is cyclically modulated by CD and consequently influences the λ_LSPR and linewidth,²⁴ which is attributed to the retardation effects of the dipolar emission. In the multiple-particle or particle oligomer scenario, the combined effects of near- and far- field coupling can induce various plasmonic phenomena such as Fano resonance,^25–27 optical transparency,²⁸etc.

Beyond the multi-particle scenario, various plasmonic arrays have also been studied. Analogous to crystal structures, three types of planar arrangements can be defined based on the regularity of constituents: “single crystalline”, where the arrangement is strictly lattice-like; “amorphous”, where the arrangement is completely random; and in between, “polycrystalline”, featuring small regular domains.

For single crystalline plasmonic arrays, when the CD (i.e. the grating constant in a 2D array) is comparable to λ_LSPR, it modulates the λ_LSPR and line width in a cyclic fashion,¹⁵ whereas when the CD is smaller than half of the λ_LSPR, the plasmon resonance blue shifts and broadens as the CD decreases.¹⁶ In existing single crystalline array studies, FFPC played the dominant role. In contrast to single crystalline plasmonic arrays, P. Hanarp et al. failed to find any significant coupling among amorphous plasmonic arrays prepared by colloidal lithography.²⁹ The amorphous nanoparticle arrays had an average center-to-center/diameter ratio (CDR) larger than 2 and the nanodisks being studied for a coupling effect were relatively small with 70 nm diameter and 20 nm thickness.

To date, FFPC has only been studied among single crystalline plasmonic arrays with high array regularity or periodicity. The preparation of such arrays typically requires time-consuming, costly techniques such as electron-beam lithography. In contrast, “nanosphere lithography” (NSL) and the like have gained significant attention and become a low-cost alternative for fabricating nanoparticle arrays. Wafer-scale monolayer polystyrene beads can be fabricated on nearly any substrate with merely a syringe, a pump, and a petri dish.³⁰ However, plasmonic crystals fabricated by these methods typically have polycrystalline features, hence warranting the consideration of coupling effects among them. The study detailed herein is a systematic study on the FFPC effect in such arrays based on polycrystalline gold nanodisk (AuND) arrays with CDRs ranging from ∼1.15 to 2.5.

Moreover, limited by the experimental methods, array randomness and particle size had limited tunability with existing studies; therefore, their effects on the coupling effect have not been studied systematically so far. To tackle such a challenge, a finite-difference-time-domain (FDTD) simulation model was developed to quantitatively reproduce the experimental results in this study. Using such a simulation model, the range of the study was extended and the effects of array randomness and particle size on FFPC are studied independently.

Results and discussion

Characterization of AuND array

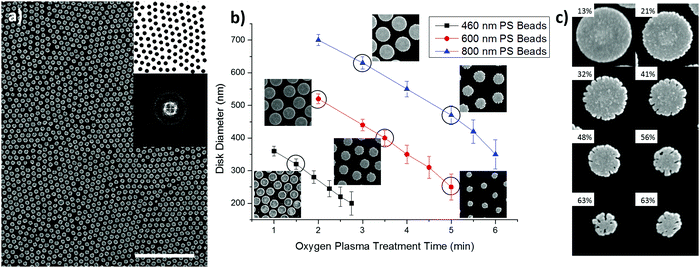
As shown in Fig. 1, polycrystalline AuND arrays were fabricated on glass substrates using nanosphere lithography. The Fig. 1 insets show a binarized SEM image containing 115 AuNDs and its Fourier transform (FT) image. The centroids of the binarized SEM images are used as array arrangement in later FDTD simulation as explained in the Materials and methods, and the ring pattern in the FT image demonstrates the polycrystalline nature of the array. Depending on the initial PS bead diameter and oxygen plasma treatment time, the diameters of the fabricated disks ranged from 200 nm to 700 nm. Fig. 1b depicts the diameter of the resulting AuNDs plotted as a function of the oxygen plasma treatment time. SEM images of disks corresponding to certain data points are also included in Fig. 1b. It is noted that extended oxygen plasma treatments roughened the PS bead surfaces, which subsequently roughened the AuND edges. SEM images of AuNDs fabricated from the PS beads with different diameter shrinkages are shown in Fig. 1c. Note that diameter shrinkage beyond the 60% mark resulted in excessive edge roughening, and non-circular AuNDs were thus excluded from later analysis. Defects existed for less shrunk AuNDs; in the interest of extending the range of the study, they were included in the data set. The defect-induced uncertainties can be alleviated by the simulation model described later. Extinction spectra of the fabricated samples are provided in Fig. S4 (ESI†). From these spectra, the LSPR peak position and the linewidth (full width at half maximum, FWHM) were obtained for further analysis and discussion.

Fig. 1 (a) A typical SEM image of the fabricated polycrystalline AuND array. Scale bar: 5 μm. Inset: A binarized SEM image containing 115 AuNDs and its FT image. The binarized image is used for FDTD simulation and the ring-shaped pattern in its FT image demonstrates the polycrystalline nature. (b) Disk diameter vs. O₂ plasma treatment time. The initial PS bead diameters are 460, 600 and 800 nm. SEM images correspond to the circled data points. Each image is 2 × 2 μm². (c) SEM images of the AuNDs fabricated from PS beads with different diameter shrinkages, as labeled on the images.

Coupling induced LSPR peak shift

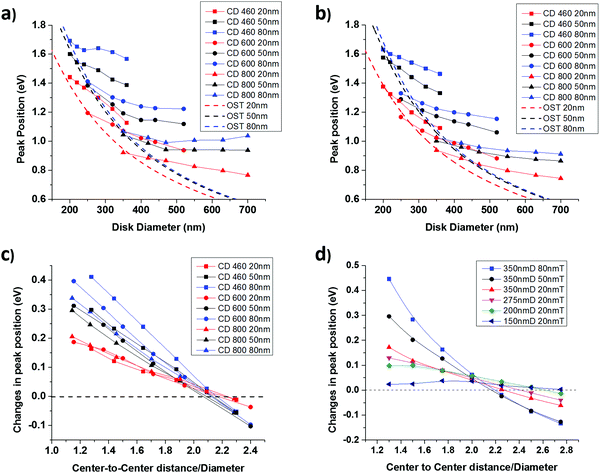
The peak positions of each sample and the FDTD simulation results under the same conditions, which are plotted as a function of the disk diameters in Fig. 2a and b along with the oblate spheroid theory (OST) predicted the LSPR peak position for single disks. Excellent agreement has been observed between the experimental and simulation results. The CDs were represented using different symbols: square: 460 nm, circle: 600 nm, and triangle: 800 nm. The thicknesses of the disks were represented using different colors (red: 20 nm, black: 50 nm, and blue: 80 nm). The designation of symbols and colors is consistent throughout the paper.

Fig. 2 (a) Experimentally obtained LSPR peak position vs. disk diameter. CDs are determined by the initial PS bead diameter. (b) FDTD simulation results with parameters matching the experimental conditions. In (a) and (b), the calculated OST model (dotted lines) represents the single disk response. The lines that connect the dots are visual guides. (c) LSPR peak shift (mismatch to single disk) vs. CDR. (d) LSPR peak shift of disk arrays with fixed dimensions and varying CDRs.

A salient feature in Fig. 2a and b is the branching out from the OST model by following a particular sample series. Taking the CD 460 thickness 20 nm sample series (red squares) as an example, the smallest diameter (∼200 nm) shows a peak close to the OST single disk position. However, increasing blue shifts, i.e., deviations from the OST dashed curve, are observed as the disk becomes larger, suggesting stronger FFPC. To further accentuate on FFPC-induced LSPR peak shifts, the differences in the peak position of polycrystalline AuND arrays with respect to that of a single disk of the same diameter are plotted versus their corresponding CDR in Fig. 2c. For better clarity, subsets of the data are also reproduced with various CDs and disk thicknesses in Fig. S5 (ESI†). Simulations were also carried out at a fixed AuND dimension and varying CDRs and the results are shown in Fig. 2d. Based on these plots, a few observations are worthy of attention.

Compared to single AuND, array samples with a CDR of less than 2 have an LSPR peak position at a higher energy level (blue shift). Such a blue shift has the same characteristic to that observed in single crystalline nanoparticle arrays.^16,31 In these studies, the blue shift was attributed to the radiative dipole coupling between nanodisks. The characteristically similar observations here strongly advocate the presence of FFPC in polycrystalline AuND arrays.

FFPC is known to generate interparticle-distance dependent cyclic modulation (i.e. alternating blue and red shift) in the LSPR peak position in single crystalline nanoparticle arrays owing to the retardation effect.^15,32 Our results indicate that such properties still hold true with polycrystalline arrays. The exact dividing points of the peak shift are particle dependent, where smaller thickness and diameter lead to a dividing point at larger CDRs, as clearly indicated in Fig. 2d. The coupling effect here can be understood from a dipole–dipole coupling model. A detailed discussion of the mechanism can be found in the studies of W. Rechberger et al.²² and such a model has been applied to nanoparticle oligomers³³ and single crystalline plasmonic arrays.³⁴ It is noticed that the dipole approximation for a nanoparticle is not accurate at a short inter-particle distance; therefore, such a model can only provide a qualitative description of the coupling effect with high-density nanoparticle arrays.

It seems unsurprising that higher packing density (i.e. smaller CDR) and thicker disks lead to a stronger coupling strength, as shown in Fig. 2c, d and Fig. S5a–c (ESI†) without further considering the particle diameter. At a fixed AuND thickness and CDR, if the diameter is scaled by a factor of r (i.e. D becomes rD), the volume scales with r², whereas the CD scales with r. Since the far-field scales with 1/CD, if the radiation strength increases linearly with the volume, one would expect that the coupling strength becomes stronger with larger AuND diameter. This argument holds true for smaller AuNDs. As shown in Fig. 2d, for AuNDs with a diameter of less than 350 nm, the reduction in disk diameter significantly reduces the coupling strength. Using disks smaller than 150 nm diameter and 20 nm thickness, the coupling in a polycrystalline array is weakened to a point that it is negligible. Therefore, in these cases, the polycrystalline array can be considered to be coupling-free. On the other hand, with AuND diameters comparable with the LSPR wavelength, due to the dynamic depolarization process, the radiation strength no longer increases linearly with the volume.³⁵ Under such a situation, at a fixed CDR and thickness, an increase in the AuND diameter results in an unchanged or even reduced coupling strength in FFPC, as shown in Fig. 2c and Fig. S5d–f (ESI†).

It is also worth mentioning here that the coupling strength can be substantial. In terms of the wavelength, the largest peak shift was experimentally obtained from the polycrystalline AuND array with 800 nm CD, 700 nm diameter, and 80 nm thickness. Compared to the LSPR located at ∼2180 nm for a single disk, the array peaks at 1192 nm, which is a remarkable 1000 nm of absolute blue shift or a fractional shift Δλ/λ₀ over 45%.²³

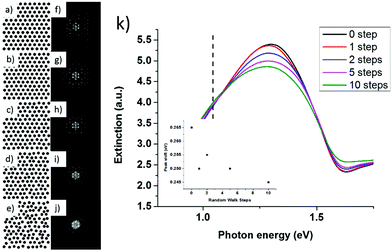
Unlike previous results, which attributed the lack of FFPC among amorphous plasmonic arrays entirely to its randomness,²⁹ our results suggest otherwise. Indeed, the transition from single crystalline to amorphous requires further investigation. Herein, we present a numerical study of how the randomness in nanoparticle arrangement can influence FFPC. The detailed simulation setups are described in the Materials and methods section and the results are shown in Fig. 3. Starting with a hexagonal array, randomness was produced by various random walk steps of 0, 1, 2, 5, and 10, as shown in Fig. 3a–e and the corresponding FT images are shown in Fig. 3f–j. By examining the FT images, increasing randomness can be identified as the disappearing of the discrete spots, and the more salient ring-shaped patterns. At the highest randomness allowed without AuND overlapping, the discrete spots completely transitioned into ring-shaped patterns.

Fig. 3 (a–e) Images of a hexagonally packed array consisting of 120 AuNDs with random walk steps of 0, 1, 2, 5, and 10. (f–j) The corresponding FT images show the disappearing discrete spots and more salient ring-shaped pattern with increasing randomness. (k) FDTD simulation results of the arrays from (a–e). The inset shows the peak shifts plotted against the number of random walk steps. Increased randomness caused an intensity drop and less coupling in the LSPR. The dotted line is the peak position of a single AuND with the same dimension.

The simulated extinction spectra from the AuND arrays of various randomness are plotted in Fig. 3k and the amount of the peak shift is plotted against the randomness in the inset. The randomness essentially plays the role of perturbation, which causes reductions in the LSPR intensity and coupling strength (i.e. the peak position of arrays with higher randomness is moving toward single nanoparticle response). Judging from the inset, the AuND array after 10 step random walk still retains 90% of the peak shift of a single crystalline array. The above results indicate that the FFPCs not only exist with single- or poly-crystalline arrays, but also with high-density amorphous plasmonic arrays.

Another point worth noting here is that the high packing density and “complete” randomness are inherently mutually exclusive. In the highly packed scenario, the allowable randomness is presumably less than that of a lower packing density array. The level of randomness discussed here is thus limited within a certain packing density array, where the CD between AuNDs is relatively uniform and the AuNDs have a limited range of random walk. This provides a partial explanation for why FFPC has not been observed with an amorphous plasmonic array with low packing density. Nevertheless, our results unambiguously demonstrate remarkable FFPC in polycrystalline AuND arrays that can be fabricated using low-cost nanosphere lithography.

Coupling induced LSPR line-width variation

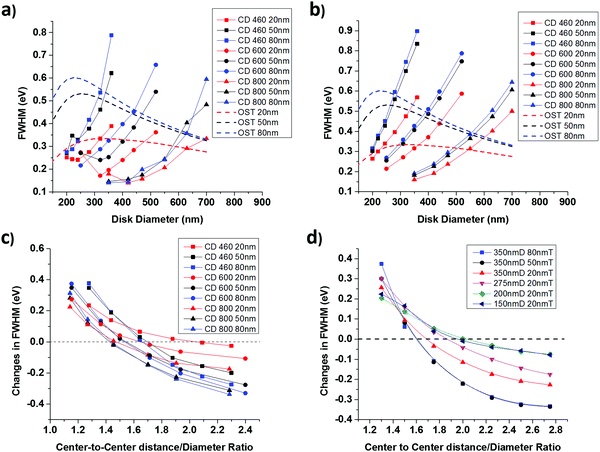
The LSPR spectral linewidth is known to be indicative of damping, which was extracted from the experimental data and the numerical simulations as shown in Fig. 4a and b. Without losing generality, the total damping can be modeled as the summation of three underlying damping mechanisms: intraband, interband and radiative damping. In this study, the intraband damping can be considered to be a constant because the particle sizes are significantly larger than the electron mean free path, which is around 40 nm,³⁶ and the interband damping is negligible because the LSPR energy levels are lower than the interband threshold (2.3 eV for gold). Therefore, the observed LSPR linewidth variation (i.e. FWHM) is dominated by radiative damping.

Fig. 4 (a) Experimentally obtained FWHM vs. disk diameter. CDs are determined by the initial PS bead diameters. (b) FDTD simulation results with parameters matching the experimental conditions. In (a) and (b), the calculated OST model (dotted lines) represents a single disk response. The lines that connect the dots are visual guides. (c) Changes in FWHM (compared with single disk) vs. CDR. (d) Changes in FWHM of the disk arrays with fixed disk diameters and varying CDRs.

Fig. 4a and b depict different trends in FWHM for single AuNDs and polycrystalline AuND arrays by following a specific sample series. Taking the CD 460 thickness 80 nm sample series (blue squares) as an example, the smallest diameter (∼200 nm) shows an FWHM narrower than that of the OST single disk. However, broadened FWHM can be observed as the disk becomes larger, and eventually surpasses the FWHM of the OST single disk, suggesting enhanced radiative damping. Using the same data processing method and simulation setup as described in the peak shift discussion, the FWHM variations are obtained and plotted in Fig. 4c, d and Fig. S6 (ESI†). Similar to the observations made in the LSPR peak shift discussion, FFPC also induced CD dependent cyclic modulations in the FWHM. The results here further support the dependence of coupling strength on CDR, diameter, and thickness, as described previously. The trend in the FWHM observed here agrees with the observation made with low-density single crystalline plasmonic arrays but with much stronger effect.¹⁵ In the current study, the FWHM can be tuned to be nearly twice or below half of the single disk response. Such tunability has potential applications in many fields, such as photo-energy conversion where a broad peak is desired or LSPR sensing where a narrow peak can improve the quality factor.

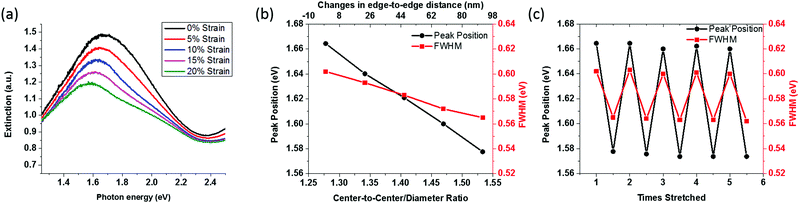
Strain-tuning by CDR-modulated FFPC

Herein, we demonstrate a novel transduction mechanism between the LSPR peak position and substrate strain enabled by CDR-modulated FFPC. Polycrystalline AuND arrays were fabricated on a flexible polydimethylsiloxane (PDMS) substrate following the same fabrication process. The process conditions were chosen such that the resulting AuNDs were 360 nm in diameter, 80 nm in thickness and 460 nm in CDR. The PDMS substrate was then stretched along a single direction while the extinction spectra were measured. As shown in Fig. 5a, increased strain leads to increased CDR and reduced extinction intensity, reduced peak energy, and reduced FWHM, consistent with all the previous discussions. The peak position and FWHM are plotted against the CDR in Fig. 5b, showing a linear trend across 0–92 nm in edge-to-edge displacement or equivalently 1.28–1.54 in CDR change. The linear trend and no sign of plateauing suggest a much larger effective sensing range with constant sensitivity, likely a few hundred nanometers of edge-to-edge displacement as the FFPC was observed with CDRs up to 2.5. Here the range is limited by the stretchability of the PDMS substrate used, which tears at over 20% strain. In contrast, near-field plasmonic coupling based modulation has exponentially diminishing sensitivity with respect to the CDR and the demonstrated maximal tuning displacement is approximately 50 nm.²³ Therefore, FFPC can effectively extend the displacement range by more than an order of magnitude.

Fig. 5 (a) Extinction spectra of a polycrystalline AuND array on the PDMS substrate with different strains. The AuNDs have 360 nm diameter, 80 nm thickness, and 460 nm CD without strain. (b) Extinction peak position and FWHM plotted against CDR. (c) Peak position and FWHM without strain or with 20% strain repeated 5 times.

The stretching experiments were repeated 5 times, and the peak position and FWHM at 0 and 20% strain are plotted in Fig. 5c. The highly reproducible results suggest good reusability of the substrate, which benefits from large interparticle separation. The mechanically tunable plasmonic substrate has potential applications in displacement and strain sensing³⁷ and mechanically tunable plasmonic substrates.³⁸

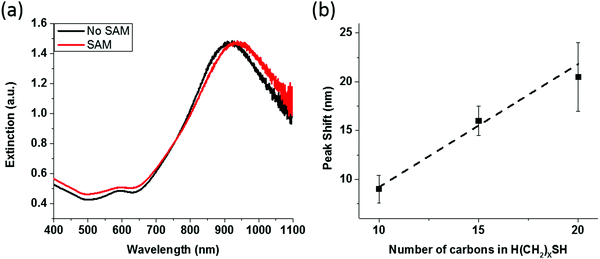
Tuning plasmonic properties of nanoporous gold disk

FFPC can also be an effective means for tailoring the plasmonic peak of nanoparticles into the desired wavelength range. Recently, our group developed nanoporous gold disks (NPGDs) as a new type of plasmonic nanoparticles with advantages such as increased surface area, tunable plasmonics and high-density hot spots,³⁰ resulting in several applications.^39–41 The E-field hot-spots that are exposed to the sensing medium are known to be a key factor for refractive index sensing^42,43 and NPGDs have demonstrated a superior refractive index sensitivity, which makes them attractive candidates for LSPR sensing applications. Due to the less metallic nature, NPGDs possess much redder peaks compared with AuND with similar outer dimensions. For instance, a single NPGD with a diameter of 360 nm and a thickness of 80 nm peaks at ∼1500 nm, which prevents the characterization and LSPR sensing using silicon detectors, hence requiring more specialized equipment. However, high-density (CDR ∼ 1.3) polycrystalline NPGD arrays with the same disk dimensions peak at ∼950 nm, which can be readily measured by a silicon detector, as shown in Fig. 6a (black line).

Fig. 6 (a) Extinction spectra of a high-density (CDR ∼ 1.3) polycrystalline array of NPGD with 360 nm diameter and 80 nm thickness before (black) and after (red) SAM modification of the H(CH₂)₂₀SH molecule. The single particle extinction peak of such NPGD is expected to be ∼1500 nm. (b) Peak shift vs. carbon chain length of the SAM molecule. A linear relationship is observed.

To demonstrate the ability of utilizing NPGD arrays for refractive index sensing, the surface was coated with H(CH₂)_nSH self-assembled monolayer (SAM) with varying carbon chain lengths (n) of 10, 15 and 20. Extinction spectra were measured before and after surface modifications. The extinction spectrum of NPGD modified with H(CH₂)₂₀SH SAM is plotted in Fig. 6a (red line) and the amount of peak shift is plotted against the carbon chain length, as shown in Fig. 6b. Since the molecule layer is much thinner than the decay length of the field associated with the surface plasmon,^44,45 a linear fitting can be applied to the peak shift⁴⁶ and the slope indicates a sensitivity of 1 nm per CH₂. There have been other molecular sensing techniques based on coupled nanoparticles, such as the plasmon Fano resonance with nanoparticle oligomers that can offer a better sensitivity and a higher figure of merit.²⁶ However, FFPC has the unique capability of tuning the resonance peak positions of nanoparticles without changing its physical properties or the fundamental plasmon behavior.

Conclusions

In conclusion, we report a systematic study of FFPC in polycrystalline AuND arrays fabricated using nanosphere lithography. In such arrays, FFPC is qualitatively in keeping with that of single crystalline nanoparticle arrays, which induced CD dependent cyclic modulation in the LSPR peak position and FWHM. With a low CDR, blue shift and broadening of the LSPR have been observed for arrays compared with single AuND, whereas with a high CDR, a red shift and narrowing effect are observed. The maximum coupling induced blue shift observed experimentally was a remarkable 1000 nm, which corresponds to a fractional peak shift of 45% with regard to the single AuND peak position. The experimental results were compared with systematic modeling and numerical simulations to gain additional insight. The results show a negligible FFPC effect with polycrystalline arrays consisting of AuNDs smaller than 150 nm in diameter and 20 nm in thickness, providing an explanation for the lack of FFPC in amorphous arrays in past reports. Finally, the CDR-modulated FFPC has been applied to monitor the displacement of AuNDs on flexible substrates, as well as tailoring the LSPR peak position of NPGD arrays for the ultrasensitive detection and characterization of self-assembled monolayers. Our results can have a profound impact in plasmonic nanoparticle array engineering from the following perspectives. By FFPC, the LSPR peak position within 1 μm is now accessible using AuND arrays with a disk diameter as large as 500 nm, which enables the use of silicon-based detectors for measurements. In addition, the cost of making these arrays is much lower than high-resolution patterning techniques such as electron-beam lithography. This work also demonstrates that FFPC can effectively extend the distance modulation by an order of magnitude compared with near-field coupling.

Materials and methods

Materials

Chloroform (anhydrous, ≥99.0%) and latex beads (polystyrene (PS) beads 10% aqueous suspension) with mean particle sizes of 460, 600 and 800 nm were purchased from Sigma-Aldrich. The size distributions of the purchased PS beads were analyzed using SEM images, and their histograms are provided in Fig. S1 (ESI†). Ethanol (200 proof) was purchased from Decon Laboratories, Inc. without modification. Coverglass (22 × 40 mm, No. 1) was purchased from VWR. Gold pellets (>99.99%) for evaporation were purchased from ACI Alloys, Inc. Oxygen gas (99.99%) and Argon gas (99.999%) were used for reactive ion etching and ion milling, respectively.

Fabrication process

The fabrication process is described in detail in ref. 30. Briefly, a gold film of prescribed thickness was deposited onto coverglass pre-cleaned in ethanol using electron-beam evaporation. A monolayer of PS beads exhibiting a polycrystalline structure was then assembled on the gold layer. The PS beads were then shrunk to the desired diameter in O₂ plasma, followed by Ar⁺ ion milling to transfer the bead pattern into the gold film. The remaining PS beads were then removed by sonication in chloroform.

Spectrum measurement and analysis

The extinction spectra were measured using a Cary 5000 spectrophotometer (Agilent) in the transmission configuration. The spectral peak position was determined by fitting the resonance peak using the Lorentz function. The spectral line width was determined by multiplying the fitted peak half-width (measured from the resonance peak toward the low energy side) by a factor of two.

Finite difference time domain (FDTD) simulations

FDTD simulations were first carried out with closely packed (CDR = 1.3) periodic arrays containing 1 × 1 to 15 × 15 AuNDs in both hexagonal and rectangular packing, and the results are provided in the ESI,† Fig. S2. The simulations show an increasing peak shift (coupling strength) with a larger number of AuNDs being simulated, and the coupling strength reaches the maximum for arrays with more than 100 AuNDs. Such results indicate that a 10 × 10 array is sufficient to represent the coupling effect in an infinite array. The centroids of the AuNDs from a typical SEM image containing 115 particles were read out, and their relative locations were used as the array arrangement in the FDTD simulations. The AuND arrays used in the FDTD simulation were generated first by scaling the centroid position to the desired CD, then 3D AuND structures with predetermined thicknesses and diameters were added to all the centroid positions. In the simulation, AuNDs were located on a glass substrate with a refractive index of 1.52.

For the randomness study, we started with a hexagonally packed array consisting of 120 AuNDs with 350 nm diameter, 80 nm thickness and 1.75 CDR. Randomness was gradually added into the array using a random walk method.⁴⁷ To ensure no overlapping in the AuNDs, each random walk was set to be 1/20 of the gap between the AuNDs, and the maximum number of random walk steps allowed was 10. The resulting structures were simulated under the same conditions as described previously.

Oblate spheroid theory calculations

The LSPR spectra of single disks were calculated using electrostatic oblate spheroid theory (OST) in the modified long wavelength approximation. OST has been proven to provide excellent quantitative agreement with experimental results, as shown in Fig. S3 (ESI†) as well as in ref. 35. The calculations were carried out using the following equations following the work of Langhammer et al.^35,48

Here, α′(ω) is the modified polarizability with long wavelength approximation, k is the wave vector of the incident light, k² is the dynamic depolarization, k³ is the radiative damping, α(ω) is the dipolar polarizability of the oblate spheroid, L is the geometric factor, ε(ω) is the dielectric function of gold,⁴⁹ε_m is the dielectric constant of the surrounding media, and a and b are the major axis and minor axis of the spheroid, i.e., the disk diameter and thickness, respectively. The effective refractive index used in the calculations is the average of the substrate (glass, 1.52) and ambient (air, 1).

The extinction cross-section can be obtained by

σ_ext(ω) = k Im[α′(ω)]

Author contributions

The manuscript was written through contributions from all authors. All authors have given approval to the final version of the manuscript.

Funding sources

National Science Foundation (NSF) CAREER Award CBET-1151154, NSF CBET-1605683, NSF CBET-1643391.

Abbreviations

CD	Center-to-center distance
CDR	Center-to-center/diameter ratio
FFPC	Far-field plasmonic coupling
AuND	Gold nanodisk
LSPR	Localized surface plasmon resonance
FT	Fourier transform
FWHM	Full width at half maximum
FDTD	Finite-difference-time-domain

Acknowledgements

W. C. S. acknowledges the National Science Foundation (NSF) CAREER Award CBET-1151154, NSF CBET-1605683, and NSF CBET-1643391.

References

1. E. Hutter and J. H. Fendler, Exploitation of localized surface plasmon resonance, Adv. Mater., 2004, 16(19), 1685–1706.
2. K. A. Willets and R. P. Van Duyne, Localized surface plasmon resonance spectroscopy and sensing, Annu. Rev. Phys. Chem., 2007, 58, 267–297.
3. H. J. Huang, C. P. Yu, H. C. Chang, K. P. Chiu, H. Ming Chen, R. S. Liu and D. P. Tsai, Plasmonic optical properties of a single gold nano-rod, Opt. Express, 2007, 15(12), 7132–7139.
4. J. N. Anker, W. P. Hall, O. Lyandres, N. C. Shah, J. Zhao and R. P. Van Duyne, Biosensing with plasmonic nanosensors, Nat. Mater., 2008, 7(6), 442–453.
5. H. A. Atwater and A. Polman, Plasmonics for improved photovoltaic devices, Nat. Mater., 2010, 9(3), 205–213.
6. E. Ringe, B. Sharma, A. I. Henry, L. D. Marks and R. P. Van Duyne, Single nanoparticle plasmonics, Phys. Chem. Chem. Phys., 2013, 15(12), 4110–4129.
7. X. Huang, S. Tang, X. Mu, Y. Dai, G. Chen, Z. Zhou, F. Ruan, Z. Yang and N. Zheng, Freestanding palladium nanosheets with plasmonic and catalytic properties, Nat. Nanotechnol., 2011, 6(1), 28–32.
8. A. Yang, D. Wang, W. Wang and T. W. Odom, Coherent Light Sources at the Nanoscale, Annu. Rev. Phys. Chem., 2017, 68, 83–99.
9. P. C. Wu, W. Zhu, Z. X. Shen, P. H. J. Chong, W. Ser, D. P. Tsai and A.-Q. Liu, Broadband Wide-Angle Multifunctional Polarization Converter via Liquid–Metal-Based Metasurface, Adv. Opt. Mater., 2017, 5(7), 1600938.
10. G. A. Sotiriou, Biomedical applications of multifunctional plasmonic nanoparticles, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2013, 5(1), 19–30.
11. I. Doron-Mor, Z. Barkay, N. Filip-Granit, A. Vaskevich and I. Rubinstein, Ultrathin gold island films on silanized glass. Morphology and optical properties, Chem. Mater., 2004, 16(18), 3476–3483.
12. R. G. Freeman, K. C. Grabar, K. J. Allison, R. M. Bright, J. A. Davis, A. P. Guthrie, M. B. Hommer, M. A. Jackson, P. C. Smith, D. G. Walter and M. J. Natan, Self-Assembled Metal Colloid Monolayers: An Approach to SERS Substrates, Science, 1995, 267(5204), 1629–1632.
13. H. Wang, J. Kundu and N. J. Halas, Plasmonic nanoshell arrays combine surface-enhanced vibrational spectroscopies on a single substrate, Angew. Chem., 2007, 46(47), 9040–9044.
14. P. K. Jain and M. A. El-Sayed, Plasmonic coupling in noble metal nanostructures, Chem. Phys. Lett., 2010, 487(4–6), 153–164.
15. B. Lamprecht, G. Schider, R. T. Lechner, H. Ditlbacher, J. R. Krenn, A. Leitner and F. R. Aussenegg, Metal nanoparticle gratings: influence of dipolar particle interaction on the plasmon resonance, Phys. Rev. Lett., 2000, 84(20), 4721–4724.
16. C. L. Haynes, A. D. McFarland, L. L. Zhao, R. P. Van Duyne, G. C. Schatz, L. Gunnarsson, J. Prikulis, B. Kasemo and M. Kall, Nanoparticle optics: The importance of radiative dipole coupling in two-dimensional nanoparticle arrays, J. Phys. Chem. B, 2003, 107(30), 7337–7342.
17. J. Henzie, M. H. Lee and T. W. Odom, Multiscale patterning of plasmonic metamaterials, Nat. Nanotechnol., 2007, 2(9), 549–554.
18. E. Prodan, C. Radloff, N. J. Halas and P. Nordlander, A hybridization model for the plasmon response of complex nanostructures, Science, 2003, 302(5644), 419–422.
19. F. Hao, C. L. Nehl, J. H. Hafner and P. Nordlander, Plasmon resonances of a gold nanostar, Nano Lett., 2007, 7(3), 729–732.
20. P. Nordlander, C. Oubre, E. Prodan, K. Li and M. I. Stockman, Plasmon Hybridization in Nanoparticle Dimers, Nano Lett., 2004, 4(5), 899–903.
21. M. W. Chen, Y.-F. Chau and D. P. Tsai, Three-Dimensional Analysis of Scattering Field Interactions and Surface Plasmon Resonance in Coupled Silver Nanospheres, Plasmonics, 2008, 3(4), 157–164.
22. W. Rechberger, A. Hohenau, A. Leitner, J. R. Krenn, B. Lamprecht and F. R. Aussenegg, Optical properties of two interacting gold nanoparticles, Opt. Commun., 2003, 220(1–3), 137–141.
23. P. K. Jain, W. Y. Huang and M. A. El-Sayed, On the universal scaling behavior of the distance decay of plasmon coupling in metal nanoparticle pairs: A plasmon ruler equation, Nano Lett., 2007, 7(7), 2080–2088.
24. P. Olk, J. Renger, M. T. Wenzel and L. M. Eng, Distance dependent spectral tuning of two coupled metal nanoparticles, Nano Lett., 2008, 8(4), 1174–1178.
25. M. Hentschel, M. Saliba, R. Vogelgesang, H. Giessen, A. P. Alivisatos and N. Liu, Transition from isolated to collective modes in plasmonic oligomers, Nano Lett., 2010, 10(7), 2721–2726.
26. M. Konig, M. Rahmani, L. Zhang, D. Y. Lei, T. R. Roschuk, V. Giannini, C. W. Qiu, M. H. Hong, S. Schlucker and S. A. Maier, Unveiling the Correlation between Nanometer-Thick Molecular Monolayer Sensitivity and Near-Field Enhancement and Localization in Coupled Plasmonic Oligomers, ACS Nano, 2014, 8(9), 9188–9198.
27. J. A. Fan, C. Wu, K. Bao, J. Bao, R. Bardhan, N. J. Halas, V. N. Manoharan, P. Nordlander, G. Shvets and F. Capasso, Self-assembled plasmonic nanoparticle clusters, Science, 2010, 328(5982), 1135–1138.
28. P. C. Wu, W. T. Chen, K.-Y. Yang, C. T. Hsiao, G. Sun, A. Q. Liu, N. I. Zheludev and D. P. Tsai, Magnetic plasmon induced transparency in three-dimensional metamolecules, Nanophotonics, 2012, 1(2), 131–138.
29. P. Hanarp, M. Kall and D. S. Sutherland, Optical properties of short range ordered arrays of nanometer gold disks prepared by colloidal lithography, J. Phys. Chem. B, 2003, 107(24), 5768–5772.
30. F. Zhao, J. Zeng, M. M. Parvez Arnob, P. Sun, J. Qi, P. Motwani, M. Gheewala, C. H. Li, A. Paterson, U. Strych, B. Raja, R. C. Willson, J. C. Wolfe, T. R. Lee and W. C. Shih, Monolithic NPG nanoparticles with large surface area, tunable plasmonics, and high-density internal hot-spots, Nanoscale, 2014, 6(14), 8199–8207.
31. L. Zhao, K. L. Kelly and G. C. Schatz, The Extinction Spectra of Silver Nanoparticle Arrays: Influence of Array Structure on Plasmon Resonance Wavelength and Width, J. Phys. Chem. B, 2003, 107(30), 7343–7350.
32. H. Fischer and O. J. Martin, Retardation-induced plasmonic blinking in coupled nanoparticles, Opt. Lett., 2009, 34(3), 368–370.
33. M. Rahmani, A. E. Miroshnichenko, D. Y. Lei, B. Luk'yanchuk, M. I. Tribelsky, A. I. Kuznetsov, Y. S. Kivshar, Y. Francescato, V. Giannini, M. Hong and S. A. Maier, Beyond the hybridization effects in plasmonic nanoclusters: diffraction-induced enhanced absorption and scattering, Small, 2014, 10(3), 576–583.
34. L. L. Zhao, K. L. Kelly and G. C. Schatz, The extinction spectra of silver nanoparticle arrays: Influence of array structure on plasmon resonance wavelength and width, J. Phys. Chem. B, 2003, 107(30), 7343–7350.
35. I. Zoric, M. Zach, B. Kasemo and C. Langhammer, Gold, Platinum, and Aluminum Nanodisk Plasmons: Material Independence, Subradiance, and Damping Mechanisms, ACS Nano, 2011, 5(4), 2535–2546.
36. D. Gall, Electron mean free path in elemental metals, J. Appl. Phys., 2016, 119(8), 085101.
37. L. Minati, A. Chiappini, F. Benetti, G. Speranza, D. Zonta, A. Piotrowska, M. Marciniak, A. Vaccari and M. Ferrari, Fabrication and optical properties of assembled gold nanoparticles film on elastomeric substrate, Colloids Surf., A, 2015, 482, 431–437.
38. H. Kang, C. J. Heo, H. C. Jeon, S. Y. Lee and S. M. Yang, Durable plasmonic cap arrays on flexible substrate with real-time optical tunability for high-fidelity SERS devices, ACS Appl. Mater. Interfaces, 2013, 5(11), 4569–4574.
39. J. Qi, J. Zeng, F. Zhao, S. H. Lin, B. Raja, U. Strych, R. C. Willson and W. C. Shih, Label-free, in situ SERS monitoring of individual DNA hybridization in microfluidics, Nanoscale, 2014, 6(15), 8521–8526.
40. G. M. Santos, F. Zhao, J. Zeng, M. Li and W. C. Shih, Label-free, zeptomole cancer biomarker detection by surface-enhanced fluorescence on nanoporous gold disk plasmonic nanoparticles, J. Biophotonics, 2015, 8(10), 855–863.
41. W. C. Shih, G. M. Santos, F. Zhao, O. Zenasni and M. M. Arnob, Simultaneous Chemical and Refractive Index Sensing in the 1–2.5 mum Near-Infrared Wavelength Range on Nanoporous Gold Disks, Nano Lett., 2016, 16(7), 4641–4647.
42. P. C. Wu, G. Sun, W. T. Chen, K.-Y. Yang, Y.-W. Huang, Y.-H. Chen, H. L. Huang, W.-L. Hsu, H. P. Chiang and D. P. Tsai, Vertical split-ring resonator based nanoplasmonic sensor, Appl. Phys. Lett., 2014, 105(3), 033105.
43. P. C. Wu, W. L. Hsu, W. T. Chen, Y. W. Huang, C. Y. Liao, A. Q. Liu, N. I. Zheludev, G. Sun and D. P. Tsai, Plasmon coupling in vertical split-ring resonator metamolecules, Sci. Rep., 2015, 5, 9726.
44. C. D. Bain, E. B. Troughton, Y. T. Tao, J. Evall, G. M. Whitesides and R. G. Nuzzo, Formation of Monolayer Films by the Spontaneous Assembly of Organic Thiols from Solution onto Gold, J. Am. Chem. Soc., 1989, 111(1), 321–335.
45. M. D. Malinsky, K. L. Kelly, G. C. Schatz and R. P. Van Duyne, Chain length dependence and sensing capabilities of the localized surface plasmon resonance of silver nanoparticles chemically modified with alkanethiol self-assembled monolayers, J. Am. Chem. Soc., 2001, 123(7), 1471–1482.
46. S. Chen, M. Svedendahl, M. Kall, L. Gunnarsson and A. Dmitriev, Ultrahigh sensitivity made simple: nanoplasmonic label-free biosensing with an extremely low limit-of-detection for bacterial and cancer diagnostics, Nanotechnology, 2009, 20(43), 434015.
47. Y. Nishijima, L. Rosa and S. Juodkazis, Surface plasmon resonances in periodic and random patterns of gold nano-disks for broadband light harvesting, Opt. Express, 2012, 20(10), 11466–11477.
48. C. Langhammer, Z. Yuan, I. Zoric and B. Kasemo, Plasmonic properties of supported Pt and Pd nanostructures, Nano Lett., 2006, 6(4), 833–838.
49. P. B. Johnson and R. W. Christy, Optical Constants of the Noble Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 6(12), 4370–4379.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary data and raw extinction spectra. See DOI: 10.1039/c7nh00067g

---