The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) N⋯C–X σ-hole interaction acts as a conformational lock†
N⋯C–X σ-hole interaction acts as a conformational lock†
Zhenfeng
Zhang‡
*a,
Li
Wang‡
b and
Xiaopeng
Xuan
a
aSchool of Chemistry and Chemical Engineering, Henan Normal University, Xinxiang 453007, P. R. China. E-mail: zzf@htu.cn; Fax: +86 373-3326336; Tel: +86 373-3326335
bThe First Affiliated Hospital of Xi'an Medical University, Xi'an, 710000, China
First published on 26th October 2016
Abstract
An interesting C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–X conformation lock, which determines the linear alignment of the C
N⋯C–X conformation lock, which determines the linear alignment of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and C–X fragments, has been found for the first time and is rationalized by density functional theory calculations. Second-order perturbation theory analysis based on the NBO method further reveals that the nature of the C
N and C–X fragments, has been found for the first time and is rationalized by density functional theory calculations. Second-order perturbation theory analysis based on the NBO method further reveals that the nature of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–X interaction is mainly the lp(C
N⋯C–X interaction is mainly the lp(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) → σ*(C–X) interaction.
N) → σ*(C–X) interaction.
Conformations of single molecules are primarily dominated by noncovalent interactions.1–4 The interaction dictating molecular conformation is frequently referred to as a conformation lock. The usual type of conformation lock is hydrogen bonding.1,2 There are also other types of noncovalent interactions3,4 which can serve as a conformation lock, where the bridging atom is not a H but a member of group IV, V, VI or VII. These interactions usually share certain structural features: there is a positive region on the extension of the σ-bonds in the acceptor segment, which is frequently called a σ-hole,5–8 or (and) a positive region above groups, such as C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C
O, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N etc., which is sometimes denoted as a π-hole. Whether a σ-hole or π-hole, one of the positive regions is drawn toward either a lone pair or a π-bond, thus leading to two intramolecular segments lying close to one another. Given that molecular conformation influences supramolecular assembly of any crystal, the physical properties of materials,9 and the reactivity and selectivity of the reactions,10 it is of vital importance to explore the molecular conformation and the conformation lock.
N etc., which is sometimes denoted as a π-hole. Whether a σ-hole or π-hole, one of the positive regions is drawn toward either a lone pair or a π-bond, thus leading to two intramolecular segments lying close to one another. Given that molecular conformation influences supramolecular assembly of any crystal, the physical properties of materials,9 and the reactivity and selectivity of the reactions,10 it is of vital importance to explore the molecular conformation and the conformation lock.
(E)-N′-Benzylidene-2-cyanoacetohydrazides are interesting model molecules with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and CH2C
N and CH2C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N groups separated by rotatable chemical bonds. The former, C
N groups separated by rotatable chemical bonds. The former, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, can serve as an electron-donor (N lone pair), and the latter, C
N, can serve as an electron-donor (N lone pair), and the latter, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N, can generate two positive regions, one on the neighboring atom C2 (σ-hole), and one above itself (π-hole). Would the CH2C
N, can generate two positive regions, one on the neighboring atom C2 (σ-hole), and one above itself (π-hole). Would the CH2C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N group generate a σ-hole interaction or a competitive π-hole interaction with the C
N group generate a σ-hole interaction or a competitive π-hole interaction with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N group? Once one of the two interactions occurs, it would lock up the molecular conformation. Therefore, here the σ-hole (or the π-hole) interaction is expected to be an effective and reliable instrument for conformation control. As far as our knowledge extends, the C
N group? Once one of the two interactions occurs, it would lock up the molecular conformation. Therefore, here the σ-hole (or the π-hole) interaction is expected to be an effective and reliable instrument for conformation control. As far as our knowledge extends, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN conformation lock has not been studied in the literature. Thus, we have designed and synthesized a series of such model compounds, and examined their X-ray crystal structures. Due to the strong electron-withdrawing ability of the C
N⋯C–CN conformation lock has not been studied in the literature. Thus, we have designed and synthesized a series of such model compounds, and examined their X-ray crystal structures. Due to the strong electron-withdrawing ability of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N group, the σ-hole on C2 becomes more positive. Thus, it is probable that the imino (C
N group, the σ-hole on C2 becomes more positive. Thus, it is probable that the imino (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) lone pair will approach the σ-hole of the intramolecular CH2C
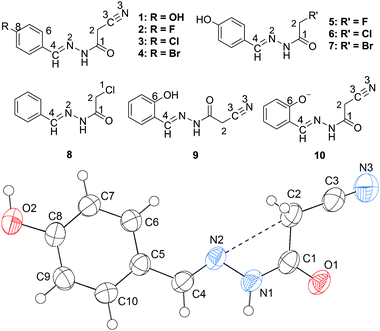
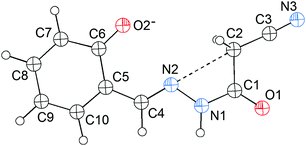
N) lone pair will approach the σ-hole of the intramolecular CH2C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N fragment. Interestingly, this expectation is confirmed first by the X-ray crystal structure of 1 (Fig. 1). As shown in Fig. 1, the cyanomethyl group adopts a linear alignment to the imino fragment, the conformation allows the N2 lone pair to approach the σ-hole of the CH2C
N fragment. Interestingly, this expectation is confirmed first by the X-ray crystal structure of 1 (Fig. 1). As shown in Fig. 1, the cyanomethyl group adopts a linear alignment to the imino fragment, the conformation allows the N2 lone pair to approach the σ-hole of the CH2C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N group. The distance of 2.761(2) Å between C2 and N2 is significantly shorter than the sum of the van der Waals radii, 3.25 Å. The characteristic geometry suggests a C
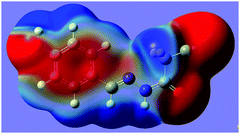
N group. The distance of 2.761(2) Å between C2 and N2 is significantly shorter than the sum of the van der Waals radii, 3.25 Å. The characteristic geometry suggests a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN σ-hole interaction. Molecular electrostatic potentials (Fig. 2) of 1 have further confirmed its existence. As illustrated in Fig. 2, there is a red negative region above the imino atom N2 corresponding to the N lone pair, and a blue positive region (the σ-hole) on the extension of the N
N⋯C–CN σ-hole interaction. Molecular electrostatic potentials (Fig. 2) of 1 have further confirmed its existence. As illustrated in Fig. 2, there is a red negative region above the imino atom N2 corresponding to the N lone pair, and a blue positive region (the σ-hole) on the extension of the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C bond.
C–C bond.
Recent studies have shown the existence of N⋯C interactions.11–13 However, the studies on this subject still remain theoretical, and the reported N⋯C interactions occur only intermolecularly. Computational study shows that the N⋯C interactions can occur between electron-donors, such as NH3 or C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N, and electron-acceptors CH3X (X = CN, OH, F), and that the amino (or cyano) atom N was found to lie on the extension of X–C bond. Here the C
N, and electron-acceptors CH3X (X = CN, OH, F), and that the amino (or cyano) atom N was found to lie on the extension of X–C bond. Here the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN interaction in 1, though different in the electron-donor, is very similar to the C
N⋯C–CN interaction in 1, though different in the electron-donor, is very similar to the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N⋯CH3CN and H3N⋯CH3OH interactions.
N⋯CH3CN and H3N⋯CH3OH interactions.
Considering that the natural bond orbital (NBO) theory14,15 is quite useful for quantitatively analyzing intramolecular interactions,16 in order to characterize the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN conformation lock via orbital interactions, the density functional theory (DFT) calculations were conducted on molecule 1 at the WB97XD17/6-311+G(d,p) levels using the crystal coordinates. The optimized geometries were further used for the NBO analysis with NBO version 3.118 incorporated in the GAUSSIAN 0919 package. The result shows that the optimized conformation is in good agreement with crystallographically determined structure 1 (Fig. 1), suggesting that the linear orientation of the C
N⋯C–CN conformation lock via orbital interactions, the density functional theory (DFT) calculations were conducted on molecule 1 at the WB97XD17/6-311+G(d,p) levels using the crystal coordinates. The optimized geometries were further used for the NBO analysis with NBO version 3.118 incorporated in the GAUSSIAN 0919 package. The result shows that the optimized conformation is in good agreement with crystallographically determined structure 1 (Fig. 1), suggesting that the linear orientation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N to C–CN unit is caused not by crystal packing but by a certain intramolecular noncovalent interaction between imino and cyanomethyl fragments. The NBO analysis further shows that there are three intramolecular orbital interactions, A, B, C (Table 1) involved in the C
N to C–CN unit is caused not by crystal packing but by a certain intramolecular noncovalent interaction between imino and cyanomethyl fragments. The NBO analysis further shows that there are three intramolecular orbital interactions, A, B, C (Table 1) involved in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN interaction, out of which only the strongest interaction, A is shown in Fig. 3. As shown in Fig. 3 and the Table 1, the lone pair on the imino atom N2 interacts with the σ*-antibonding orbital of the C2–CN bond, with a concomitant second-order stabilization energy of E(2) = 1.03 kcal mol−1. The total orbital interaction energy that attributed to the C
N⋯C–CN interaction, out of which only the strongest interaction, A is shown in Fig. 3. As shown in Fig. 3 and the Table 1, the lone pair on the imino atom N2 interacts with the σ*-antibonding orbital of the C2–CN bond, with a concomitant second-order stabilization energy of E(2) = 1.03 kcal mol−1. The total orbital interaction energy that attributed to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN interaction is 2.49 kcal mol−1. The result has theoretically confirmed that the orbital interactions, though not strong, are the decisive factors for the linear alignment of the cyanomethyl and imino fragments.
N⋯C–CN interaction is 2.49 kcal mol−1. The result has theoretically confirmed that the orbital interactions, though not strong, are the decisive factors for the linear alignment of the cyanomethyl and imino fragments.
| Compounds | Pair name | Donor NBO | Acceptor NBO | E(2) energy (kcal mol−1) |
|---|---|---|---|---|
| 1 | A | lp(N2) | σ*(C2–CN) | 1.03 |
| B | lp(N2) | σ*(C2–C1) | 0.76 | |
| C | σ(C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N2) N2) |
RY*(C2) | 0.70 | |
| 2 | A | lp(N2) | σ*(C2–CN) | 1.00 |
| B | lp(N2) | σ*(C2–C1) | 0.75 | |
| C | σ(C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N2) N2) |
RY*(C2) | 0.69 | |
| 3 | A | lp(N2) | σ*(C2–CN) | 1.00 |
| B | lp(N2) | σ*(C2–C1) | 0.75 | |
| C | σ(C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N2) N2) |
RY*(C2) | 0.69 | |
| 4 | A | lp(N2) | σ*(C2–CN) | 1.00 |
| B | lp(N2) | σ*(C2–C1) | 0.75 | |
| C | σ(C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N2) N2) |
RY*(C2) | 0.70 | |
| 5 | A | lp(N2) | σ*(C2–F1) | 1.54 |
| B | lp(N2) | σ*(C2–C1) | 0.54 | |
| 6 | A | lp(N2) | σ*(C2–Cl1) | 1.52 |
| B | lp(N2) | σ*(C2–C1) | 0.65 | |
| 7 | A | lp(N2) | σ*(C2–Cl1) | 1.66 |
| B | lp(N2) | σ*(C2–C1) | 0.67 | |
| 8 | A | lp(N2) | σ*(C2–Cl1) | 1.50 |
| B | lp(N2) | σ*(C2–C1) | 0.65 | |
| 10 | A | lp(N2) | σ*(C2–CN) | 1.47 |
| B | lp(N2) | σ*(C2–C1) | 1.00 | |
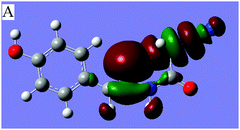 | ||
Fig. 3 Dominant orbital interaction A, lp(N2)→σ*(C2–C3![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N3), corresponding to the C N3), corresponding to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN interaction in 1. N⋯C–CN interaction in 1. | ||
Given that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN conformation lock occurs in 1, it is very probable that this kind of interaction will be found in analogues, 2–8. In order to verify our expectation, we have conducted the geometry optimization on molecules 2–8 using the same method as 1. Interestingly, the optimized molecular conformations and the main geometry parameters are in perfect accordance with those in 1 (Fig. 1); each of the cyanomethyl or halogenmethyl groups in 2–8 adopts a linear alignment to the imino fragment; the distance between C2 and N2 ranges from 2.722 to 2.741 Å. Molecular electrostatic potentials show that the conformations are fixed by the C
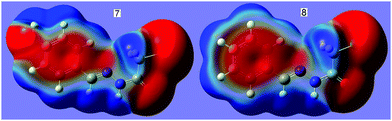
N⋯C–CN conformation lock occurs in 1, it is very probable that this kind of interaction will be found in analogues, 2–8. In order to verify our expectation, we have conducted the geometry optimization on molecules 2–8 using the same method as 1. Interestingly, the optimized molecular conformations and the main geometry parameters are in perfect accordance with those in 1 (Fig. 1); each of the cyanomethyl or halogenmethyl groups in 2–8 adopts a linear alignment to the imino fragment; the distance between C2 and N2 ranges from 2.722 to 2.741 Å. Molecular electrostatic potentials show that the conformations are fixed by the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–X (X = CN, Cl, Br) σ-hole interaction. As typical representatives, the molecular electrostatic potentials of 7 and 8 are shown in Fig. 4. From this figure, it can be easily found that there exists a stronger C
N⋯C–X (X = CN, Cl, Br) σ-hole interaction. As typical representatives, the molecular electrostatic potentials of 7 and 8 are shown in Fig. 4. From this figure, it can be easily found that there exists a stronger C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯CH2X σ-hole interaction where the red negative region above N2 (N lone pair) interacts with the blue positive region (the σ-hole) on the atom C2. The results are in good agreement with data from the second-order perturbation theory analysis in the NBO basis. NBO analysis shows that there are three orbital interactions in 2–4 and two in 5–8 involved in the C
N⋯CH2X σ-hole interaction where the red negative region above N2 (N lone pair) interacts with the blue positive region (the σ-hole) on the atom C2. The results are in good agreement with data from the second-order perturbation theory analysis in the NBO basis. NBO analysis shows that there are three orbital interactions in 2–4 and two in 5–8 involved in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–X interaction (Table 1). The total orbital interaction energy that attributed to the C
N⋯C–X interaction (Table 1). The total orbital interaction energy that attributed to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–X interaction is in the range of 2.15–2.49 kcal mol−1, which is enough strong to stabilize the molecular conformation. The results reveal that the C
N⋯C–X interaction is in the range of 2.15–2.49 kcal mol−1, which is enough strong to stabilize the molecular conformation. The results reveal that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–X (X = CN, F, Cl, or Br) conformation lock does work universally in N′-[(1E)-phenylmethylidene]acetohydrazides.
N⋯C–X (X = CN, F, Cl, or Br) conformation lock does work universally in N′-[(1E)-phenylmethylidene]acetohydrazides.
In the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–X (X = CN, F, Cl, or Br) interaction, the imino unit acts as an electron-donor (lone pair), and the cyanomethyl (or halogenmethyl) as an electron-acceptor. If a strong and competitive electron-acceptor, such as the C6–OH in 9, is imported, a strong O–H⋯N
N⋯C–X (X = CN, F, Cl, or Br) interaction, the imino unit acts as an electron-donor (lone pair), and the cyanomethyl (or halogenmethyl) as an electron-acceptor. If a strong and competitive electron-acceptor, such as the C6–OH in 9, is imported, a strong O–H⋯N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond would be expected to be formed, thus probably preventing the formation of the C
C hydrogen bond would be expected to be formed, thus probably preventing the formation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN interaction. Consequently, the molecular conformation should undergo a great change. Keeping our motivation in mind, we also crystallized compound 9. The crystal structure of 9 is illustrated in Fig. 5. As shown in this figure, the C6–OH group does form a strong O–H⋯N
N⋯C–CN interaction. Consequently, the molecular conformation should undergo a great change. Keeping our motivation in mind, we also crystallized compound 9. The crystal structure of 9 is illustrated in Fig. 5. As shown in this figure, the C6–OH group does form a strong O–H⋯N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond, the O2–H2⋯N2 distance being only 1.76 Å, and the associated angle, 152°. According to NBO calculations, the total orbital interaction energy involved in the O–H⋯N
C hydrogen bond, the O2–H2⋯N2 distance being only 1.76 Å, and the associated angle, 152°. According to NBO calculations, the total orbital interaction energy involved in the O–H⋯N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interaction is up to 25.81 kcal mol−1. Due to the formation of the strong H-bond, the relatively weak C
C interaction is up to 25.81 kcal mol−1. Due to the formation of the strong H-bond, the relatively weak C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN interaction has been prevented. As a result, the plane O1\C1\C2\C3\N3 rotates about 180° around the N1–C1 axis with respect to that in 1–4. From this point of view, the O2–H2⋯N2 hydrogen bond can be considered as an “obstacle” to the C
N⋯C–CN interaction has been prevented. As a result, the plane O1\C1\C2\C3\N3 rotates about 180° around the N1–C1 axis with respect to that in 1–4. From this point of view, the O2–H2⋯N2 hydrogen bond can be considered as an “obstacle” to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN conformation lock.
N⋯C–CN conformation lock.
If the above “obstacle” doctrine is true, once the “obstacle” in 9 is destroyed by basification, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN conformation lock should come into action, and are expected to be stronger than those in 1–4. In view of this, we also conducted a geometry optimization on the phenolic oxygen anion 10. Interestingly, the C
N⋯C–CN conformation lock should come into action, and are expected to be stronger than those in 1–4. In view of this, we also conducted a geometry optimization on the phenolic oxygen anion 10. Interestingly, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN conformation lock does come back! As shown in Fig. 6, the linear alignment of the cyanomethyl and the imino is locked by the C
N⋯C–CN conformation lock does come back! As shown in Fig. 6, the linear alignment of the cyanomethyl and the imino is locked by the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN interaction, the distance between N2 and C2 being 2.670 Å, which is markedly shorter than the ones in 1–4. This reveals that once the O2–H2⋯N2 hydrogen bond is no longer in existence, the C
N⋯C–CN interaction, the distance between N2 and C2 being 2.670 Å, which is markedly shorter than the ones in 1–4. This reveals that once the O2–H2⋯N2 hydrogen bond is no longer in existence, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN conformation lock is then in operation in the phenolic oxygen anion 10. NBO analysis shows that the stabilizing energies of the orbital interactions, A and B, involved in the C
N⋯C–CN conformation lock is then in operation in the phenolic oxygen anion 10. NBO analysis shows that the stabilizing energies of the orbital interactions, A and B, involved in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN conformation lock in 10 are 1.47 and 1.00 kcal mol−1, respectively. So far, these examples from both sides have proved that the C
N⋯C–CN conformation lock in 10 are 1.47 and 1.00 kcal mol−1, respectively. So far, these examples from both sides have proved that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–X conformation lock exists universally in N′-[(1E)-phenylmethylidene]acetohydrazides, and the lock can be opened by a strong intramolecular H-bond, such as O2–H2⋯N2 in 9. This suggests that the conformation of these compounds can be modified by pH adjustment.
N⋯C–X conformation lock exists universally in N′-[(1E)-phenylmethylidene]acetohydrazides, and the lock can be opened by a strong intramolecular H-bond, such as O2–H2⋯N2 in 9. This suggests that the conformation of these compounds can be modified by pH adjustment.
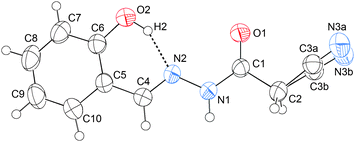
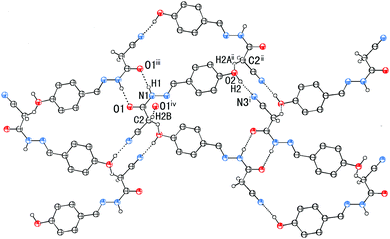
In addition to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–CN conformation lock, there are four intermolecular hydrogen bonds involved in the crystal packing of 1, one of N–H⋯O, one of O–H⋯N, and two of C–H⋯O type (Fig. 7). The distances N1–H1⋯O1, O2–H2⋯N3, C2–H2B⋯O1 and C2–H2A⋯O2 are 1.96, 1.86, 2.33 and 2.58 Å, respectively, and the corresponding angles 171, 171, 168 and 127°, respectively. These hydrogen bonds synergistically constitute a complicated 3D structure, the formation of which can be easily understood in the following way (Fig. 7). The molecules related by an n-glide plane form a zig–zag [101] chain via a strong O–H⋯N hydrogen bond; antiparallel chains of this type are laterally linked into a (−301) sheet by N–H⋯O and C2–H2A⋯O2 hydrogen bonds; these parallel sheets are finally interconnected into a 3D structure via a C2–H2B⋯O1 hydrogen bond.
N⋯C–CN conformation lock, there are four intermolecular hydrogen bonds involved in the crystal packing of 1, one of N–H⋯O, one of O–H⋯N, and two of C–H⋯O type (Fig. 7). The distances N1–H1⋯O1, O2–H2⋯N3, C2–H2B⋯O1 and C2–H2A⋯O2 are 1.96, 1.86, 2.33 and 2.58 Å, respectively, and the corresponding angles 171, 171, 168 and 127°, respectively. These hydrogen bonds synergistically constitute a complicated 3D structure, the formation of which can be easily understood in the following way (Fig. 7). The molecules related by an n-glide plane form a zig–zag [101] chain via a strong O–H⋯N hydrogen bond; antiparallel chains of this type are laterally linked into a (−301) sheet by N–H⋯O and C2–H2A⋯O2 hydrogen bonds; these parallel sheets are finally interconnected into a 3D structure via a C2–H2B⋯O1 hydrogen bond.
In conclusion, the work has revealed an interesting σ-hole C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–X conformation lock existing universally in N′-[(1E)-phenylmethylidene]acetohydrazides. Ab initio calculations provided effective support for the interaction; second-order perturbation theory analysis of the Fock matrix on the NBO basis has confirmed that the conformation lock is in nature intramolecular charge transfer from the C
N⋯C–X conformation lock existing universally in N′-[(1E)-phenylmethylidene]acetohydrazides. Ab initio calculations provided effective support for the interaction; second-order perturbation theory analysis of the Fock matrix on the NBO basis has confirmed that the conformation lock is in nature intramolecular charge transfer from the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N lone pair into the σ*(C–X) antibonding orbital. We believe that the present work may be the first study on the conformation effect of the C
N lone pair into the σ*(C–X) antibonding orbital. We believe that the present work may be the first study on the conformation effect of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N⋯C–X σ-hole interaction.
N⋯C–X σ-hole interaction.
Experimental
Synthesis of 1 and 9
To a solution of ethyl cyanoacetate (0.2 mol) in anhydrous ethanol (50 mL), was added hydrazine (80%, 0.25 mol), the reaction mixture was stirred at room temperature. The precipitate was filtered off, washed with anhydrous ethanol and dried to give pure cyanoacetohydrazide (12 g). As an intermediate, cyanoacetohydrazide (0.1 mol) was dissolved in anhydrous ethanol (50 mL), and then 4-hydroxy or 2-hydroxybenzaldehyde (0.1 mol) was added. The reaction mixture was refluxed for 20 min, and then cooled to room temperature. The solid was collected by filtration, washed with ethanol, and dried to yield compound 1 or 9 (15 g) as a crystalline solid. Crystals 1 and 9 suitable for an X-ray analysis were obtained by slow cooling of a hot acetonitrile solution of the corresponding product.Crystal data of compounds 1 and 9
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 reflections collected, 2971 unique (Rint = 0.035), 1796 observed with I > 2σ(I); final R = 0.0496, wR2 = 0.1400, goodness-of-fit S = 1.01.
740 reflections collected, 2971 unique (Rint = 0.035), 1796 observed with I > 2σ(I); final R = 0.0496, wR2 = 0.1400, goodness-of-fit S = 1.01.
Acknowledgements
We gratefully acknowledge the support from the High Performance Computing Center of Henan Normal University.Notes and references
- C. Cabezas, M. Varela, I. Peña, S. Mata, J. C. López and J. L. Alonso, Chem. Commun., 2012, 48, 5934–5936 RSC.
- A. M. Vibhute and K. M. Sureshan, J. Org. Chem., 2014, 79, 4892–4908 CrossRef CAS PubMed.
- D. Dey, S. Bhandary, A. Sirohiwal, V. R. Hathwar and D. Chopra, Chem. Commun., 2016, 52, 7225–7228 RSC.
- J. Brioche, S. J. Pike, S. Tshepelevitsh, I. Leito, G. A. Morris, S. J. Webb and J. Clayden, J. Am. Chem. Soc., 2015, 137, 6680–6691 CrossRef CAS PubMed.
- (a) M. D. Esrafili, N. Mohammadirad and M. Solimannejad, Chem. Phys. Lett., 2015, 628, 16–20 CrossRef CAS; (b) S. P. Thomas, D. Jayatilaka and T. N. G. Row, Phys. Chem. Chem. Phys., 2015, 17, 25411–25420 RSC; (c) R. Shukla and D. Chopra, Phys. Chem. Chem. Phys., 2016, 18, 29946–29954 RSC.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296 CrossRef CAS PubMed.
- P. Politzer, P. Lane, M. C. Concha, Y. G. Ma and J. S. Murray, J. Mol. Model., 2007, 13, 305–311 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and M. C. Concha, J. Mol. Model., 2007, 13, 643 CrossRef CAS PubMed.
- (a) S. Suzuki, T. Yukiyama, A. Ishikawa, Y. Yuguchi, K. Funane and S. Kitamura, Carbohydr. Polym., 2014, 99, 432–437 CrossRef CAS PubMed; (b) I. A. Ronova and M. Bruma, Struct. Chem., 2013, 24, 993–1000 CrossRef CAS; (c) J. Pitawala, J. Scheers, P. Jacobsson and A. Matic, J. Phys. Chem. B, 2013, 117, 8172–8179 CrossRef CAS PubMed.
- (a) H. Satoh and S. Manabe, Chem. Soc. Rev., 2013, 42, 4297–4309 RSC; (b) A. E. Christina, J. A. Muns, J. Q. A. Olivier, L. Visser, B. Hagen, L. J. van den Bos, H. S. Overkleeft, J. D. C. Codée and G. A. van der Marel, Eur. J. Org. Chem., 2012, 5729–5737 CrossRef CAS; (c) M. Karimiahmadabadi, S. Erfan, A. Földesi and J. Chattopadhyaya, J. Org. Chem., 2012, 77, 6855–6872 CrossRef CAS PubMed; (d) D. Crich, J. Org. Chem., 2011, 76, 9193–9209 CrossRef CAS PubMed.
- M. D. Esrafili, N. Mohammadirad and M. Solimannejad, Chem. Phys. Lett., 2015, 628, 16–20 CrossRef CAS.
- D. Mani and E. Arunan, Phys. Chem. Chem. Phys., 2013, 15, 14377–14383 RSC.
- S. Yourdkhani, T. Korona and N. L. Hadipour, J. Comput. Chem., 2015, 36, 2412–2428 CrossRef CAS PubMed.
- E. A. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef.
- E. A. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073 CrossRef.
- L. Song, Y. Lin, W. Wu, Q. Zhang and Y. Mo, J. Phys. Chem. A, 2005, 109, 2310–2316 CrossRef CAS PubMed.
- (a) S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed; (b) J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, Theoretical Chemistry Institute, University of Wisconsin, Madison, USA, 1995 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1447696 and 1447697. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6nj02622b |
| ‡ L. Wang and Z. Zhang contributed equally to this work. |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2017 |