Emulation of synaptic metaplasticity in memristors

Abstract

Recent studies have shown that nanoionic-based memristors can offer rich internal dynamics during ion movement that enables these solid-state devices to emulate various synaptic functions in biological systems naturally. The experimental observations can be explained within the 2nd-order memristor theoretical framework, which states that the device conductance (weight) can be determined by multiple internal state variables that can be modulated at different time scales and lead to different activity-dependent synaptic behaviors. Here, we show experimentally that not only the synaptic weight, but also synaptic plasticity (i.e. polarity and the rate of weight change) depends on the history of the input activities. This “plasticity of plasticity” resembles metaplasticity effects observed in biological systems, which have been found to facilitate neuron competition and stability. Specifically, we show that the memristor device may exhibit the same apparent weight (conductance) after experiencing different history of activities, but when subjected to additional, identical stimulation conditions, the device will however exhibit very different responses including the polarity and rate of weight (conductance) change. These findings serve to further our knowledge of fundamental physical mechanisms in memristors, and help advance adaptive artificial neuromorphic systems based on these emerging devices.

---

Introduction

Memristors refer to a class of resistive devices whose conductance depends on the history of the external applied voltage and/or current, and have attracted great attention over the last decade due to their great potential for memory, logical and computing applications.^1,2 Recently, memristors have been successfully used in the emulation of various synaptic behaviors observed in biological systems, and demonstrated great potential for neuromorphic systems that can perform learning, memory and complex information processing tasks efficiently.^3–12

In biological systems, synaptic plasticity, the ability to change the connectivity and strength between neuron cells based on the input activity, forms the physical basis of learning and memory. In nanoionic-based memristors, the synaptic weight is represented by the conductance of the device and synaptic plasticity is demonstrated by the device's ability to change its conductance when stimulated with different input signals. Physically, the conductance change is realized by electrically controlled ion migration and related formation/annihilation of conductive filaments.^2,13,14 Mathematically, these effects can be explained in the memristor theoretical framework by the following equations:¹⁵

I = G(w, V)V (1)

where eqn (1) is the I–V equation of the device and w represents the state variable that determines the device's conductance. Eqn (2) is the dynamic equation of w, and the change of w enables the implementation of synaptic plasticity in memristors.^{1,3,6,10–12} Specifically, eqn (2) implies that the synaptic weight (controlled by w) cannot be fully determined by the present input but instead is determined by the history of activities (e.g. 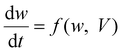through time integral of eqn (2)).

In this study, we highlight the fact that eqn (2) also implies that not only the weight, but also the polarity and rate of the weight change depend on the history of activities (through the w term on the right side of eqn (2)) and cannot be determined by the present inputs alone. This “plasticity of plasticity”,¹⁶ termed metaplasticity in neuroscience studies, highlights the importance of previous history of activities on subsequent synaptic plasticity.^16–18 For example, in the CA1 region of the hippocampus, it has been observed that the long-term potentiation (LTP) of the synapse can be successfully induced by high frequency spike stimulation. However, this process can be inhibited if an additional low frequency spike stimulation was applied earlier that did not change the synaptic efficacy directly.¹⁹ From a macroscopic point of view, metaplasticity is important to learning and memory, since it functions as an internal modulator that dynamically regulates the synaptic plasticity according to its previous activities and maintains the synaptic efficacy within a dynamic range.

We show that memristors can exhibit general features of metaplasticity, by utilizing the different configurations of the filament geometry to record the history of activities and control subsequent filament evolution dynamics. Different pre-programming conditions (history of activities) including pulse trains with different pulse numbers, frequencies and amplitudes can lead to the same memristor conductance (synaptic weight), but result in very different weight changes including differences in the polarity (i.e. potentiation or depression) and the rate of the weight change when subjected to additional, identical stimulation conditions.

These observations are consistent with earlier studies on 2nd-order memristor effects.^10–12 Here w can be described by a set of (more than one) state variables such as the filament length, width and location, all of which are history dependent through their own specific dynamic eqn (2). As a result, the synaptic plasticity cannot be predicted simply through the knowledge of only one parameter (i.e. the present conductance). This work further supports the notion that memristors may not only emulate synaptic function emphatically, but also offer interesting internal dynamics that allow them to implement complex synaptic functions faithfully.

Experimental

Device fabrication

The Pt/Ta₂O_5−x/TaO_y/Pt memristor devices studied here were fabricated in a crossbar structure. The Pt bottom electrodes with 50 nm thickness and 200 nm width were first fabricated on an SiO₂/Si substrate by e-beam lithography and e-beam evaporation of Pt metal, followed by a lift-off process. A 35 nm TaO_y layer was deposited by DC reactive sputtering of a Ta metal target in an Ar/O₂ environment at room temperature, followed by the deposition of a 5 nm-thick Ta₂O_5−x switching layer through sputtering of a Ta₂O₅ ceramic target in the same chamber but without O₂. Subsequently, a 30 nm thick Pt electrode with a width of 200 nm was fabricated through lithography and lift-off processes. Afterwards, a reactive ion etching process using SF₆/Ar was performed to expose the contact area of the bottom electrodes.

Electrical characterization

Electrical characterization was performed using a Keithley 4200S semiconductor parameter analyzer system.

Results and discussion

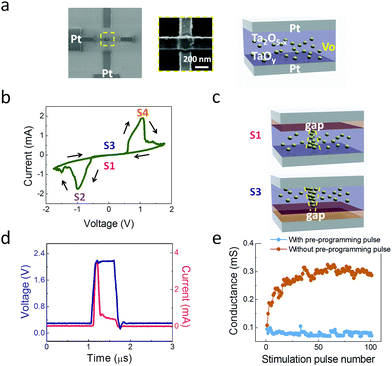
The memristor studied here is based on the Pt/Ta₂O_5−x/TaO_y/Pt structure, in which the oxygen-rich Ta₂O_5−x and oxygen-deficient TaO_y films act as the resistive switching (RS) layer and the oxygen vacancy (V_O) reservoir layer, respectively. The device has a typical crossbar configuration and the width of both the top electrode (TE) and the bottom electrode (BE) is 200 nm. Device SEM images and a schematic are shown in Fig. 1a. After a forming and subsequent RESET process (Fig. S1†), the device shows typical hysteretic current–voltage (I–V) characteristics, as shown in Fig. 1b. During the negative voltage sweep (with the bias voltage applied on the TE and the BE grounded), the device was switched from a high-resistance state (S1) to a low-resistance state (S2) when the voltage was increased to around −1.0 V. Interestingly, further increasing the bias to −1.8 V led the device switching back to another high-resistance state (S3). Similar resistance changes were also observed during the positive voltage sweep process (0 V → 1.8 V → 0 V) where the device was switched from S3 to a low-resistance state S4 and back to the original high-resistance state S1. These effects are consistent with the complementary resistive switching (CRS) behavior found in oxide-based devices.^20–22 The underlying mechanism of the observed CRS behavior can be understood based on the movement and redistribution of a limited amount of V_Os between the Ta₂O_5−x and the TaO_y layers (Fig. 1c).²¹ For example, switching the device from S1 to S3 (marked in Fig. 1b) corresponds to (1) the closing of the depletion gap near the TE/Ta₂O_5−x interface through the growth of the V_O filament, leading to the low-resistance state S2, followed by (2) the exhaustion of V_Os in the TaO_y layer and the opening of a depletion gap near the opposite TaO_y/BE interface, leading to the switching to the high-resistance state S3. However, the contribution of Ta⁵⁺ ion redistribution to the CRS effect cannot be excluded according to a recent study.²² Note that although both S1 and S3 show very similar (high) resistance, they correspond to different internal states and have different filament geometries (with the depletion gap near the TE interface in S1 and an opposite structure with the depletion gap near the BE in S3).

Fig. 1 Synaptic plasticity affected by a single pulse in the Pt/Ta₂O_5−x/TaO_y/Pt memristive device. (a) Device SEM images and device schematic of the Pt/Ta₂O_5−x/TaO_y/Pt structure. The device size is 200 nm × 200 nm. (b) DC I–V characteristics of the device. (c) Schematics of V_O distributions in the device at the two different high-resistance states (S1 and S3) as shown in (b). (d) Evolution of voltage and current with time during the application of the pre-programming pulse (2.2 V, 0.5 μs) initiated at time t = 1 μs. A constant read bias (0.3 V) was applied throughout the measurement to monitor the device current. (e) Dependence of the device conductance (measured with a read pulse (0.3 V, 5 μs)) on the number of applied stimulation pulses (0.9 V, 0.5 μs) for cases with/without the pre-programming pulse shown in (d).

In the following, we show that the different configurations of the internal filament geometry in these devices can be used to emulate metaplasticity, i.e. synaptic plasticity that depends on the previous activity, instead of just the present synaptic weight and the simulation pattern.

We first demonstrate different plasticity behaviors at the same weight (conductance), depending on whether the device has been pre-programmed with a simple, single voltage pulse. As shown in Fig. 1d, the device was initially programmed to S3. The device conductance was then monitored by a constant read bias voltage (0.3 V). When subjected to a single pre-programming pulse (2.2 V, 0.5 μs) at time t = 1 μs, the device conductance was found to first increase then decrease. Afterwards, the device conductance returned to the initial value (∼0.1 mS). As a result, the pre-programming pulse stimulation becomes untraceable by simply measuring the device conductance. The device was then subjected to a series of stimulation pulses (0.9 V, 0.5 μs). The dependence of the device conductance (measured with a read pulse (0.3 V, 5 μs) after each stimulation pulse) on the number of applied stimulation pulses is shown in Fig. 1e. Here the device showed a weak response to the pulse stimulation. On the other hand in a control experiment, the device, initially switched to S3 with the same initial conductance value but did not experience the pre-programming pulse, showed a continuous increase of the conductance with the number of stimulation pulses (Fig. 1e). This behavior is similar to the potentiation of synapse in biological systems. After 100 stimulation pulses, the device conductance in the control experiment was found to reach a saturation level of ∼0.3 mS, corresponding to a 200% increase in the conductance.

The observed difference in the two cases can be attributed to the differences of the filament geometry configuration. In the control experiment without the pre-programming pulse, the device retained the filament geometry at S3 (with a depletion gap near the BE). Subsequent positive pulses lead to the drift of V_Os accumulated near the TE towards the BE and filling of the depletion gap, resulting in an increase of the device conductance. In contrast, the pre-programming pulse in Fig. 1d switched the device from S3 to S1, creating an opposite filament geometry with a depletion gap near the TE. The subsequent pulses cannot induce further significant conductance changes since the V_Os near the TE were fully depleted already. This experiment clearly demonstrates that the filament geometry can record the memristor's history of activity and affect its plasticity, while such a capability will be missed by simply measuring the synaptic weight (memristor conductance).

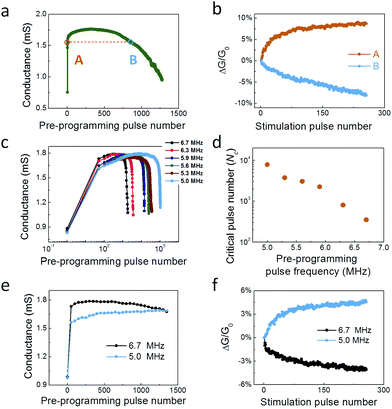
One typical feature of metaplasticity is the activity-dependent polarity of synaptic plasticity, that is, the device can exhibit either potentiation or depression depending on the history of activity. We first demonstrate the modulation of the polarity of plasticity by subjecting the device to different numbers of pre-programming pulses (before plasticity measurements). Fig. 2a shows the evolution of conductance of a device at S3 with the number of programming pulses (1.2 V, 0.5 μs). It can be seen that the conductance first increased quickly and then the increase slowed down with the increased pulse number, corresponding to the growth of the initial length of the V_O filament followed by expansion of the filament diameter near the TaO_y/BE interface.^23,24 When the pulse number reached a critical value (N_c, ∼300), the device conductance began to decrease instead, suggesting the depletion of V_Os near the TE and creation of a depletion gap near the TE/Ta₂O_5−x interface. Note that the overall transition of conductance change is more gradual during the conductance decreasing region than that in the increasing region, and such behavior was also observed during the opposite transition from S1 to S3 (Fig. S2†). This can be explained by the fact that during the filament growth, the V_O drift and diffusion flow in the same direction and accelerate the V_O movement, whereas during the filament rupture the V_O drift and diffusion flow in opposite directions and thus decrease the net V_O migration.²⁵ The non-monotonic change of the device conductance with the pulse number suggests that the device can either exhibit potentiation or depression, depending on whether the previously applied (pre-programming) pulse number is larger or smaller than N_c. This hypothesis is verified by the results shown in Fig. 2b. After switching from S3 to state A by 5 pulses (1.2 V, 0.5 μs) and state B by 921 pulses, the device conductance in both states is nearly identical, ∼1.5 mS. However, the device exhibits opposite plasticity behaviors, i.e., potentiation in case A and depression in case B when subjected to the same stimulation pulses (1.1 V, 0.5 μs) (Fig. 2b). Equivalently, pre-programming the device using a single short (wide) pulse can also result in either potentiation or depression behavior of the device later on (Fig. S3†). These results suggest the pulse number (or width)-dependent metaplasticity in our memristive device.

Fig. 2 Effects of the pre-programming pulse number and pulse frequency on the polarity of plasticity. (a) Dependence of the device conductance on the number of applied pre-programming pulses (1.2 V, 0.5 μs). (b) Evolution of the device conductance (pre-programmed to states A and B shown in (a), respectively) as a function of the number of applied stimulation pulses (1.1 V, 0.5 μs). The conductance is measured with a read pulse (0.3 V, 5 μs). (c) Dependence of the device conductance on the number of pre-programming pulses using different frequencies (6.7 MHz, 6.3 MHz, 5.9 MHz, 5.6 MHz, 5.3 MHz and 5.0 MHz). (d) Evolution of the critical pulse number N_c as a function of pre-programming pulse frequency. N_c corresponds to the value beyond which the device conductance starts to decrease with the increased pulse number. (e) Evolution of the device conductance with pre-programming pulse frequencies of 6.7 MHz and 5.0 MHz, respectively. (f) Evolution of the conductance change when the device is subjected to subsequent stimulation pulses (1.1 V, 0.5 μs). The conductance is measured with a read pulse (0.3 V, 5 μs).

The dependence of plasticity polarity was further demonstrated by using different pre-programming pulse frequencies in the memristive device. First we note that the device shows a frequency-dependent response to the pre-programming pulses. As shown in Fig. S4,† the device, starting from the initial S3 state, when subjected to 100 programming pulses (1.2 V, 100 ns) at different frequencies (6.7 MHz, 6.3 MHz, 5.9 MHz, 5.6 MHz, 5.3 MHz and 5.0 MHz) shows a higher final conductance at a higher pulse frequency. This frequency dependence can be attributed to the dynamic effects of Joule heating during filament growth, as first discussed in ref. 10. If the pulse frequency is high, the local temperature elevated by the previous pulse does not fully decay and will accelerate the migration of V_Os during the subsequent pulses.¹⁰ The effect of pulse frequency becomes more pronounced when more pulses are applied, as shown in Fig. 2c. As expected, with a higher frequency, fewer pulses were needed to switch the device to the same conductance value. The critical pulse number N_c, at which the conductance starts to decrease with the applied pulses, also shows a strong frequency dependence, as shown in Fig. 2d. When the device is brought to the same conductance with different (pre-programming) pulse frequencies, different plasticity behaviors are also observed. Fig. 2e shows that pre-programming the device using 1350 pulses with a frequency of 6.7 MHz and 5.0 MHz can both lead to almost the same device conductance value (∼1.65 mS), whereas the subsequent stimulation pulses (1.1 V, 0.5 μs) induced depression in the former but potentiation in the latter (Fig. 2f) since 1300 is >N_c in the 6.7 MHz case (∼350) but <N_c in the 5.0 MHz case (∼7850), thus highlighting the strong effect of the previous pulse frequency on the subsequent polarity of plasticity.

The modulation of the polarity of plasticity demonstrated here is intrinsically based on the CRS effect, such that two different internal filament geometry configurations can offer the same conductance value but with depletion gaps at opposite electrode interfaces. This allows the device conductance to either increase or decrease under the same pulse stimulation conditions, depending on which state the device has been previously set to.

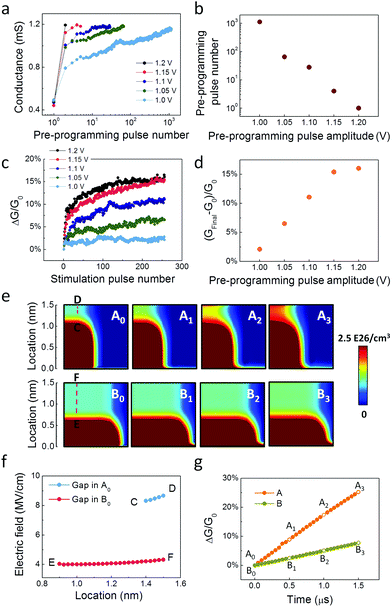
Another important feature of metaplasticity is that the degree of plasticity can be significantly different, depending on the previous activities. In ionic memristors, the velocity of the ion migration exponentially depends on the local electric field,^14,26,27 which is in turn affected by the existing filament and the electrode structure²⁸ and suggests the possibility to modulate plasticity by controlling the internal filament geometry. To demonstrate this effect, we pre-programmed the device conductance to the same value (∼1.2 mS) during the filament formation process, using pulses with different amplitudes, as shown in Fig. 3a. As expected, fewer pulses are needed for pulses with higher amplitudes, as shown in Fig. 3b. Afterwards, the device is subjected to the same stimulation pulses (1.0 V, 0.5 μs), and its conductance is monitored, as shown in Fig. 3c. It can be seen that a larger conductance change occurs if the device was pre-programmed by higher amplitude pulses. This effect is more clearly shown in Fig. 3d, highlighting the effect of the pre-programming pulse amplitude on the device's response to subsequent, identical stimulation conditions.

Fig. 3 The effect of the pulse amplitude during the pre-programming process on the degree of plasticity (filament formation process). (a) Dependence of the device conductance on the number of applied pre-programming pulses with different amplitudes (1.0 V, 1.05 V, 1.1 V, 1.15 V and 1.2 V). (b) Relationship between the required pre-programming pulse number to reach the same conductance value (∼1.2 mS) and the amplitude of the pre-programming pulses shown in (a). (c) Evolution of the conductance change when the device is then subjected to identical stimulation pulses. (d) Dependence of the final conduction change ratio on the pre-programmed pulse amplitude, extracted from (c). (e) Evolution of simulated 2D maps of V_O concentration distributions in device A (with a narrow and long filament shape) and B (with a wide and short filament shape) under 0.93 V. A₀/B₀, A₁/B₁, A₂/B₂ and A₃/B₃ correspond to the stage at t = 0 μs, 0.5 μs, 1 μs and 1.5 μs respectively. (f) Distribution of the electric field in the depletion gap of device A₀ (plotted along the dotted line C–D) and B₀ (plotted along the dotted line E–F) shown in (e) under 0.93 V. (g) Time dependent conductance change in device A and B under 0.93 V. The open circles correspond to t = 0 μs, 0.5 μs, 1 μs and 1.5 μs, respectively.

Generally speaking, the filament shape is determined by both the drift (along the electric field direction and exponentially depends on the electric field) and diffusion (along the V_O concentration gradient direction and independent of the electric field) of V_Os. As a result, different filament geometries can be obtained, depending on the amplitude of the applied electric bias, as have been verified by previous simulation and experimental studies.^29,30 Under a small bias voltage, ion drift is suppressed and the effect of (isotropic) ion diffusion is enhanced, leading to the expansion of the filament in the lateral direction and the formation of a wide filament. On the other hand, under a high bias voltage the fast drift of ions along the electric field direction will dominate, leading to the formation of a narrower filament. As a result, to reach the same conductance value, filaments in devices programmed by high amplitude pulses tend to be narrower but longer than those in devices switched by low amplitude pulses, resulting in the formation of a thinner but narrower gap between the filament tip and the electrode. Therefore, when being subjected to additional stimulation pulses, the thinner depletion gap creates a higher local electric field and will induce a faster and more pronounced ion migration and filament growth, as observed in Fig. 3c and d.

To verify this hypothesis, we performed numerical simulations based on a coupled ionic drift/diffusion model.²⁵Fig. 3e A₀ and B₀ show the 2D maps of V_O concentration distribution for two cases A and B, having a thin and narrow gap (A) and a thick and wide gap (B), respectively. The V_O concentrations in the two devices were such that they lead to the same conductance value. Under a bias voltage of 0.93 V, the electric field in the narrow gap case (plotted along the line C–D in A₀) is found to be much higher than that in B (plotted along the line E–F in B₀), as shown in Fig. 3f. Evolution of the 2D maps of the V_O distribution in the two devices after applying 0.93 V for 0.5 μs (A₁/B₁), 1.0 μs (A₂/B₂) and 1.5 μs (A₃/B₃) is shown in Fig. 3e. Significantly higher V_O concentrations were found in the depletion gap of device A, in contrast to that of device B. The conductance changes were also measured from the simulation for the two cases, shown in Fig. 3g, showing the higher degree of plasticity in device A and consistent with the experimental results.

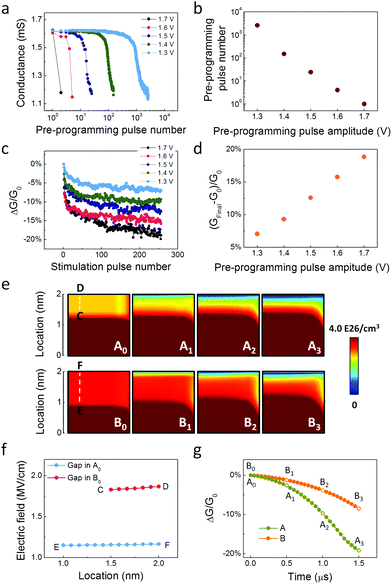
Control of the degree of plasticity was also achieved by using different pulse amplitudes in the pre-programming stage during the filament rupture process. Fig. 4a–d show that different pre-programming pulses can reduce the device conductance to the same conductance value but lead to different degrees of plasticity when the device is subjected to subsequent identical stimulation pulses. It is known that the filament rupture process in memristors usually involves the thermal dissipation of the filament along the lateral direction that decreases the filament diameter, followed by the migration of ions along the electric field direction that creates the depletion gap.²³ High amplitude pulses could induce a pronounced Joule heating effect and thus higher temperature elevation to facilitate ion migration. In this situation, significant dissipation of V_Os during the filament rupture process can lead to the formation of a highly insulating gap filled with a low concentration of residual V_Os.³¹ On the other hand, low amplitude pulses are likely to result in the formation of a less insulating gap filled with a higher concentration of residual V_Os.³² To reach the same conductance, the width of the gap with a lower V_O concentration must be narrower. As a result, under the same stimulation pulse the relatively higher electric field in the narrower gap case will lead to a higher degree of plasticity. This hypothesis is further demonstrated by the simulation results shown in Fig. 4e–g. The evolution of the 2D maps of the V_O distribution in the two devices after applying 1.0 V for 0.5 μs (A₁/B₁), 1.0 μs (A₂/B₂) and 1.5 μs (A₃/B₃) is shown in Fig. 4e. The V_Os were found to gradually migrate downward in both the gaps, leading to the continued formation of a V_O depletion gap near the TE. Nevertheless, time dependent quantitative evolution of the conductance change ratio in the two devices shown in Fig. 4f confirms the higher degree of plasticity in device A, consistent with our experimental results. We note that the possible migration behaviours of Ta⁵⁺ ions,²² along with those of V_Os, are worthy of further studies since the involvement of different kinds of ions that offer dynamics at different time scales will allow the memristors to better emulate synaptic functions naturally.^10–12

Fig. 4 The effect of the pulse amplitude during the pre-programming process on the degree of plasticity (filament rupture process). (a) Dependence of the device conductance on the number of applied pre-programming pulses with different amplitudes (1.3 V, 1.4 V, 1.5 V, 1.6 V and 1.7 V). (b) Relationship between the required pre-programming pulse number to reach the same conductance value (∼1.2 mS) and the amplitude of the pre-programming pulses shown in (a). (c) Stimulated pulse number dependent conductance changes in the device, after pre-programmed using pluses with different amplitudes. (d) Dependence of the final conduction change on the pre-programmed pulse amplitude, extracted from (c). (e) Evolution of simulated 2D maps of V_O concentration distributions in device A (with a low V_O residue concentration in the gap) and B (with a high V_O residue concentration in the gap) under 1 V. A₀/B₀, A₁/B₁, A₂/B₂ and A₃/B₃ correspond to t = 0 μs, 0.5 μs, 1 μs and 1.5 μs respectively. (f) Distribution of the electric field in the depletion gap in device A₀ (plotted along the dotted line C–D) and B₀ (plotted along the dotted line E–F) shown in (e) under 1 V. (g) Time dependent conductance change in device A and B under 1 V. The open circles correspond to t = 0 μs, 0.5 μs, 1 μs and 1.5 μs, respectively.

Conclusions

In summary, we show that by controlling the internal filament geometry configuration, the history of activities can significantly affect the memristor's response to future stimulations. This effect was successfully used to emulate metaplasticity in biological systems, where the polarity, rate and degree of synaptic plasticity can be modulated. These findings further support the notion of using internal dynamics of memristors to naturally emulate synaptic functions. Continued studies on these effects will not only deepen our understanding on the underlying mechanisms of nanoionic devices at the atomic scale but also provide guidance towards bio-realistic advanced adaptive neuromorphic systems.

Acknowledgements

The authors thank W. Ma and J. Zhou for helpful discussions. This work was supported in part by the National Science Foundation (NSF) through grant CCF-1617315 and by the Defense Advanced Research Projects Agency (DARPA) through award HR0011-13-2-0015. The views expressed in this paper are those of the authors and do not reflect the official policy or position of the Department of Defense or the U. S. Government. Approved for Public Release. Distribution unlimited.

Notes and references

1. D. B. Strukov, G. S. Snider, D. R. Stewart and R. S. Williams, Nature, 2008, 453, 80–83.
2. J. J. Yang, D. B. Strukov and D. R. Stewart, Nat. Nanotechnol., 2013, 8, 13–24.
3. S. H. Jo, T. Chang, I. Ebong, B. B. Bhadviya, P. Mazumder and W. Lu, Nano Lett., 2010, 10, 1297–1301.
4. M. Prezioso, F. Merrikh-Bayat, B. D. Hoskins, G. C. Adam, L. K. K. Ikharev and D. B. Strukov, Nature, 2015, 521, 61–64.
5. T. Ohno, T. Hasegawa, T. Tsuruoka, K. Terabe, J. K. Gimzewski and M. Aono, Nat. Mater., 2011, 10, 591–595.
6. T. Chang, S. H. Jo and W. Lu, ACS Nano, 2011, 5, 7669–7676.
7. Y. Yang, B. Chen and W. D. Lu, Adv. Mater., 2015, 27, 7720–7727.
8. Y. Li, Y. Zhong, L. Xu, J. Zhang, X. Xu, H. Sun and X. Miao, Sci. Rep., 2013, 3, 1619.
9. Z.-H. Tan, R. Yang, K. Terabe, X.-B. Yin, X.-D. Zhang and X. Guo, Adv. Mater., 2016, 28, 377–384.
10. S. Kim, C. Du, P. Sheridan, W. Ma, S. Choi and W. D. Lu, Nano Lett., 2015, 15, 2203–2211.
11. C. Du, W. Ma, T. Chang, P. Sheridan and W. D. Lu, Adv. Funct. Mater., 2015, 25, 4290–4299.
12. Z. Wang, S. Joshi, S. E. Savel'ev, H. Jiang, R. Midya, P. Lin, M. Hu, N. Ge, J. P. Strachan, Z. Li, Q. Wu, M. Barnell, G.-L. Li, H. L. Xin, R. S. Williams, Q. Xia and J. J. Yang, Nat. Mater., 2016 DOI:10.1038/nmat4756.
13. Y. Yang and W. Lu, Nanoscale, 2013, 5, 10076–10092.
14. R. Waser, R. Dittmann, G. Staikov and K. Szot, Adv. Mater., 2009, 21, 2632–2663.
15. L. O. Chua and S. M. Kang, Proc. IEEE, 1976, 64, 209–223.
16. W. C. Abraham and M. F. Bear, Trends Neurosci., 1996, 19, 126–130.
17. W. C. Abraham and W. P. Tate, Prog. Neurobiol., 1997, 52, 303–323.
18. W. C. Abraham, Nat. Rev. Neurosci., 2008, 9, 387–387.
19. Y.-Y. Huang, A. Colino, D. K. Selig and R. C. Malenka, Science, 1992, 255, 730–733.
20. E. Linn, R. Rosezin, C. Kugeler and R. Waser, Nat. Mater., 2010, 9, 403–406.
21. Y. Yang, P. Sheridan and W. Lu, Appl. Phys. Lett., 2012, 100, 203112.
22. A. Wedig, M. Luebben, D.-Y. Cho, M. Moors, K. Skaja, V. Rana, T. Hasegawa, K. K. Adepalli, B. Yildiz, R. Waser and I. Valov, Nat. Nanotechnol., 2016, 11, 67–74.
23. D. Ielmini, IEEE Trans. Electron Devices, 2011, 58, 4309–4317.
24. Y. Jeong, S. Kim and W. D. Lu, Appl. Phys. Lett., 2015, 107, 173105.
25. S. Kim, S. Choi and W. Lu, ACS Nano, 2014, 8, 2369–2376.
26. S. H. Jo, K.-H. Kim and W. Lu, Nano Lett., 2009, 9, 870–874.
27. D. B. Strukov and R. S. Williams, Appl. Phys. A, 2009, 94, 515–519.
28. Z. Q. Wang, H. Y. Xu, L. Zhang, X. H. Li, J. G. Ma, X. T. Zhang and Y. C. Liu, Nanoscale, 2013, 5, 4490–4494.
29. S. Menzel, P. Kaupmann and R. Waser, Nanoscale, 2015, 7, 12673–12681.
30. F. Pan, S. Yin and V. A. Subramanian, IEEE Electron Device Lett., 2011, 32, 949–951.
31. A. Marchewka, B. Roesgen, K. Skaja, H. Du, C.-L. Jia, J. Mayer, V. Rana, R. Waser and S. Menzel, Adv. Electron. Mater., 2016, 2, 1500233.
32. Y. Nishi, K. Fleck, U. Bottger, R. Waser and S. Menzel, IEEE Trans. Electron Devices, 2015, 62, 1561–1567.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6nr08024c

‡ These authors contributed equally to this work.

---