Effect of alkoxy-spacer length and solvent on diluted solutions of cationic isothiouronium polythiophenes

Abstract

This contribution presents a study on two cationic isothiouronium polythiophenes (poly-3-(N,N-diethyl-S-iso-thiouronium)alkoxy-4-methyl thiophene), with alkoxy chains of different length in the 3-position of the thiophene ring, results of steady-state absorption and fluorescence spectroscopies in four solvents of different polarities: protic water, protic–protic water–isopropanol, protic–aprotic water–tetrahydrofuran and protic–non polar water–1,4-dioxane (all mixtures 0.5 v/v) are presented. Molar absorption coefficient (ε), quantum yield (ϕ_f), spectral maxima (λ_max, λ_em) and Stokes shift (Δν) are presented, and the effect of solvents on these parameters is discussed. Empirical optical and electrochemical energy levels were estimated using drop cast films on glass and on glassy carbon electrode, respectively. Density functional theory was used to gain supporting structural, energy and electronic information of different oligomers, simulating solvents of different polarity.

---

1 Introduction

Conjugated polymers (CPs) are organic molecules with a base structure of alternating single and double/triple bonds which generates a delocalized electronic structure which gives these materials particular semiconducting and optical properties (absorption–fluorescence).¹ Polythiophene is a well known CP which modifies its fluorescence emission profile in response of different stimuli, such as temperature (thermochromism), solvent (solvatochromism), surfactants (surfactochromism), irradiation (photochromism) and other chemical species (affinitychromism, i.e. iono-chromism).²

Besides that, their optical and semiconducting properties depend to a great extent on the functional groups attached to the conjugated backbone and on their conformation in organic solutions.³ Because of these reasons CP are widely used in optoelectronic and fluorescence-based sensing applications.⁴

When CPs are functionalized by ionic groups a conjugated polyelectrolyte (CPE) is obtained, which is soluble in polar solvents, and therefore their driving forces for interaction are not only those related to CPs (pi–pi stacking and hydrophobic interactions),^5–7 but also those interactions characteristic of polyelectrolytes, such as electrostatic forces¹ and hydrogen bonding.⁸ The first set of CPEs were thiophene-based,⁹ and since their introduction thiophene-CPEs have been used for several applications: (i) as fluorescence-based sensors for temperature, solvent polarity, pH, and also chemical and bio-chemical species.^1,4,10–12

Despite this, the molecular mechanisms that drive their optical properties remain not totally understood. One reason is the difficulty of distinguishing conformational changes of individual molecules (intrachain association) from intermolecular interactions (multimolecular aggregation).⁴

In this regard, cationic thiourea-functionalized thiophenes could be useful model molecules for different studies, since their amino group in the thiourea functionality protonates in water at pH = 7, bearing then a positive charge which allows electrostatic interactions with anions and increasing solubility in water, besides of acting as H-bond donors.^13,14 Besides that, the Y-shaped structure of thioureas also allows two-point complementary hydrogen bonding with Y-shaped anions, such as the carboxylate group, or allowing chelating of spherical anions (e.g. halides) and phosphates.¹⁵ For example, previously a Y-shaped anionic carboxylate thiophene CPE was used to study the H-bond stabilization during self-assembly.³ Thiourea molecules are also convenient since the pK_a value of the isothiouronium moiety gives a good stability (avoidance of protonation or deprotonation) in a good range of pH values.

In particular, the isothiouronium functional group possesses Lewis acidity, due to its cationic state, which allows their use as anion-binding units, cationic detergents and nonlinear optical materials.¹⁶ Besides that, in the solid state, the cationic nitrogens with Lewis acidic properties possess a surrounding electron density which participates in hydrogen bonds with certain substrates (e.g. ITO).¹⁷

It is known that solvent polarity provides additional control over the nanostructure conformation of hydrophilic copolymers¹⁸ and CPEs allow the use of a large range of solvent polarities, which could be useful for gaining understanding on their intra- and inter-molecular interactions, since: (i) higher solvent polarities modify the relation between polarity and rigidity of their constituent blocks¹⁹ and (ii) conformational changes in both backbone and side chains of CPEs can be induced by changing the solvent. These allow more expanded conformations in ideal solvents, which also change the optical properties in diluted conditions. Furthermore, solvents modify the Stokes shift, which opens up the possibility to obtain information on possible specific solvent–fluorophore interactions.^20–23

In this regard, 1,4-dioxane is an interesting cosolvent because besides being miscible with water in all proportions, it is a non-polar aprotic solvent with a boiling point and density similar to water, but possessing a dielectric constant significantly lower to water. Also, when used as cosolvent, 1,4-dioxane disrupt the normal structure of water, because it has relatively bulky ether groups and is capable to accept two hydrogen bonds without donating any. Density functional theory (DFT) studies have shown that complexation of molecules can be modulated by changing the presence of 1,4-dioxane in water.²⁴

DFT has been also used to gain understanding on the molecular geometry and electronic properties of frontier molecular orbitals (FMOs) of polythiophenes,^25–27 together with the impact of alkoxy side chains on conjugation and frontier energy levels of thiophene-based copolymers.²⁸

To the best of our knowledge the only reported study using a thiourea-polythiophene was focused on the use of these molecules as selective fluorophore sensors of phytate in solution.¹⁶

This contribution presents a study on the photophysical properties of two cationic isothiouronium polythiophenes, namely poly-3-(N,N-diethyl-S-iso-thiouronium)alkoxy-4-methylthiophene, containing ethyloxy and hexyloxy spacer chains at position 3 of the thiophene ring, termed PT1 and PT2, respectively (Scheme 1). We used steady-state absorption and fluorescence spectrophotometric techniques in four solvents with different polarities: protic water, protic–protic water–isopropanol, protic–aprotic water–tetrahydrofuran and protic–non polar water–1,4-dioxane (all mixtures 0.5 v/v). The values of molar absorption coefficient (ε), quantum yield (ϕ_f), spectral maxima (λ_max, λ_em) and Stokes shift (Δν) are discussed, as well as the effect solvent polarity on these parameters. Empirical optical and electrochemical energy levels were estimated using drop cast films on glass and on glassy carbon electrode, respectively and DFT calculations were performed to gain understanding of the influence of the side chains on molecular conformation, MOs and frontier energy levels of different oligomers with variable alkoxy spacer chain length, in the ground (S0) state, in water and 1,4-dioxane.

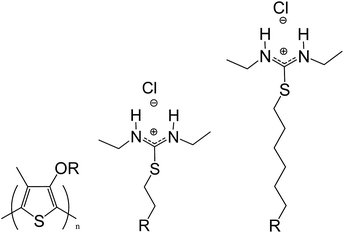Scheme 1 Poly-3-(N,N-diethyl-S-iso-thiouronium)ethyloxy-4-methylthiophene (PT1) and poly-3-(N,N-diethyl-S-iso-thiouronium)hexyloxy-4-methyl thiophene (PT2).

2 Experimental

2.1 Materials

Unless otherwise stated, it was used deionized water, and all reagents and solvents used are commercially available, analytical grade and used as supplied (Sigma Aldrich). Table S1 in ESI† shows reported values of different physical–chemical parameters of all solvents used in this study.

Scheme 1 shows the structure of the two cationic isothiouronium polythiophenes, as previously described.^29–31 The degree of polymerization (DP) of analogous cationic CPEs synthesized by our group was estimated to be around 20–30 repeating units,^29,30 which is in agreement with the DP estimation of a cationic polythiophene synthesized under the same conditions by a different group¹⁰ (both estimations made using the polymer precursor), and is also in agreement with the DP values estimated for anionic poly(3-alkoxy-4-methylthiophene)s.^32,33

In regard to the dispersity (Ð = M_w/M_n) of those molecules, a value of around 1–3 was estimated consistently.^29,32,33

About tacticity, it is known that oxidative polymerization of alkyl-thiophenes using FeCl₃ minimizes 2,4-linkages, therefore generating mainly head-to-tail (HT) couplings between adjacent thiophene rings, through 2,5-linkages.^16,34

Since precursors with the same purity were used under identical polymerization conditions, PT1 and PT2 are assumed to have the same tacticity and Ð.

The estimation of molecular weights of cationic polythiophenes using size-exclusion chromatography (SEC) is not possible since the material inside the SEC columns contain anionic groups, which lead to a strong adsorption of the polymers. Polythiophenes are also challenging because of the structural differences with polystyrene standards.^29,33,35,36

In fact, inconsistent data is reported in literature, with some references reporting M_n values of 6000–13 100 g Mol⁻¹,^29,35 while other report values of 200 000–800 000 g Mol⁻¹.^4,16

On top of that, some of these references use gel permeation chromatography (GPC), while others use matrix-assisted laser-desorption ionization time-of flight (MALDI-TOF), and it is known that M_n values obtained by GPC are approximately 1.5–2 times higher than those obtained by MALDI-TOF, because GPC overestimates the molecular weight of semi-rigid poly(3-alkylthiophene)s due to comparison with more coil-like polystyrene standards.³⁵

2.2 Methods

Each polymer was dissolved in water at a concentration of 0.5 mg mL⁻¹ and stirred during 30 minutes, generating aqueous stock solutions of PT1 and PT2 at 2.1 and 1.7 mM, respectively (monomer base). Then, stock solutions in each solvent were obtained by duplicating the volume of solvent, using either water or isopropanol (IPA), tetrahydrofuran (THF) or 1,4-dioxane (DI). These stock solutions have the highest polymer concentrations used in this work, and the different concentrations reported here were obtained by serial dilution of the stock solutions using either water or 50 : 50 v/v mixtures of water–IPA, water–THF or water–DI. Aqueous solutions of both polymers showed to be stable during months (results not shown), however, fresh aqueous stock solutions and dilutions in all the solvents were used in all experiments.

Averages and standard deviations of position and absorbance (intensity) of the absorption (emission) maxima, were obtained from duplicates (at least) of measurements made to samples obtained from different aqueous stock solutions. For the estimation of averages and standard deviations of Stokes shifts, only paired data (i.e. obtained from the same experimental unit) were considered. The estimations of molar absorption coefficients (ε) and fluorescence quantum yields (ϕ_f) in the four solvents, were obtained using samples from the same aqueous stock solution.

Both polymers generate a pH value of 5 at the highest concentration in water. Preliminary results (not shown) adding diluted HCl and NaOH solutions, showed that the absorption and fluorescence of the polymers remain constant for acidic pH values, while an increase up to a pH = 8 causes the disappearance of absorption and fluorescence. As Table S1 in ESI† shows, all solvents used in this work generate a pH ≤ 7, which allows avoiding the use of buffer in order to keep the optical properties constant.

2.3 Steady state spectrophotometric techniques

Absorption measurements were performed using a Hewlett-Packard 8453 spectrophotometer, using a slit width of 5 nm. These measurements were performed either on solutions in the four solvents, or on drop cast films deposited on plasma-cleaned glass slides, which were used to estimate optical bandgaps (EgOPT) by means of the wavelength onset of absorption.³⁷

Fluorescence spectra in solution were recorded using a Cary Eclipse steady-state fluorescence spectrophotometer (Varian), using a slit width of 15 nm, using three excitation wavelengths (λ_exc), in order to find the highest possible fluorescence intensity. To avoid fluorescence quenching by atmospheric O₂, the samples were de-aired with a N₂ flow before each measurement. Since both spectrophotometers have thermostated cell holders, all measurements in solution were performed at 25 °C, using a Suprasil cuvette of 10 mm path length.

Molar absorption coefficient (ε) and self-quenching concentration were estimated from curves of concentration vs. absorption- or fluorescence-maxima, respectively, in the four solvents, in a 0.01 to 1 mg mL⁻¹ concentration range.

The estimation of the fluorescence quantum yield (ϕ_f) was performed using the standard method³⁸ (detailed in ESI†). Solvatochromic shifts were studied according to the Lippert–Mataga equation, using the dielectric continuum model²³ (detailed in ESI†). It must be mentioned that in this work the Lippert–Mataga model was used only as a qualitative tool of analysis, since previous studies were unsuccessful in trying to correlate the dielectric constant with spectral shifts of anionic CPEs, either directly or by using the Lippert–Mataga or Onsager functions.³⁹

2.4 Cyclic voltammetry (CV)

CV was used to study the electrochemical features of polymer films and also to estimate the frontier energy orbitals, because this technique allows estimating the ionization potential (I_p) and electron affinity (E_a)⁴⁰ (details in ESI†). The films were produced by drop cast of 10 μL of a solution at 0.5 mg mL⁻¹ on top of a clean polished glassy carbon mini working electrode (diameter 1 mm), and allowed to dry in a vacuum desiccator overnight. The measurements were performed in a glass three electrode electrochemical cell with an approximate volume of 10 mL, using a platinum coil as counter electrode, and a AgCl-coated Ag wire as pseudo reference (calibrated vs. ferrocene),^41,42 in dry acetonitrile (MeCN) with tetrabutylammonium tetrafluoroborate (TBATFB) as conductive electrolyte.

Previous to measurements, both TBATFB and the pseudoreference electrode were dried in oven at 150 °C overnight, while the electrolyte solution was degassed with a flow of N₂ during 2 minutes previous to experiments, and during the experiments the headspace of the electrochemical cell was kept saturated with nitrogen. The peak potentials were evaluated from the first potential sweep,⁴³ starting at a potential of 0 V, and then using an anodic scan followed by a cathodic scan.

2.5 Density functional theory (DFT)

DFT calculations were carried out in order to analyze the effect of DP and solvent on (i) energy levels, (ii) shape of FMOs and (iii) degree of twisting, of molecules in the ground state. DFT calculations were performed at the B3LYP/6-31G** level of theoretical model chemistry, with implicit solvation in water and 1,4-dioxane via the polarizable continuum model (PCM). For details about the selection of this level of theory please see ESI.†

There were simulated di-, tetra- and hexamers of both PT1 and PT2, possessing head-to-tail tacticity. Hexamers were chosen as the largest molecule to keep reasonable computational costs and because in preliminary simulations hexamers showed a stabilization of the theoretical energy levels.

In order to evaluate the effect of degree of polymerization, dimer, trimer and hexamer oligomers with hexyloxy side-chains were built by removing the outermost monomers at both ends of a frozen dodecamer. Thereafter, in order to evaluate the effect of the alkoxy side chain, the hexyloxy side chain from the oligomers with hexyloxy spacers was reduced until ethyloxy, keeping the relative angles between atoms in the isothiouronium group and conjugated backbone in equal values to the oligomers with hexyloxy spacers.

All the calculations were carried out with the Gaussian 09 (G09) package,⁴⁴ and the frontier energy orbitals and degree of twisting of the conjugated backbone of the molecules were visualized using the software Avogadro, Open Babel Version 2.3.2.⁴⁵

3 Results and discussion

3.1 Steady-state absorption and fluorescence spectrophotometry

Fig. 1 shows the normalized absorption and fluorescence emission spectra of 0.08 mM solutions (monomer base), of both polymers in all solvents, at 25 °C.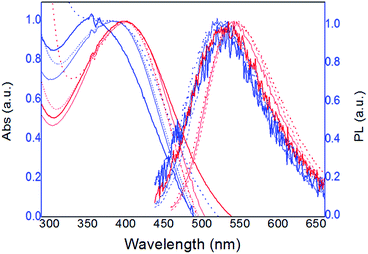

Fig. 1 Normalized absorption and fluorescence spectra of 0.08 mM solutions of PT1 (blue lines) and PT2 (red lines), at 8 × 10⁻⁵ M, in all solvents (thicker lines for water) at 25 °C.

As Fig. 1 shows, in all solvents both polymers display a single emission fluorescence band, which corresponds to the thiophene backbone, and is associated with the efficiency in energy migration along the chain.¹² The maxima of absorbance and fluorescence intensity (λ_max and λ_em, respectively) observed in this figure were used to characterize both polymers, the data of each curve is in Table 2 ahead.

Fig. 2 shows the change in λ_max and λ_em as a function of concentration. In Fig. 2a is observed that in all solvents, both polymers have a linear relationship between absorbance and concentration, in the monomer-base 0.02 to 1 Mm concentration range, fulfilling the Beer–Lambert law, which allows to estimate their molar absorption coefficient (ε).

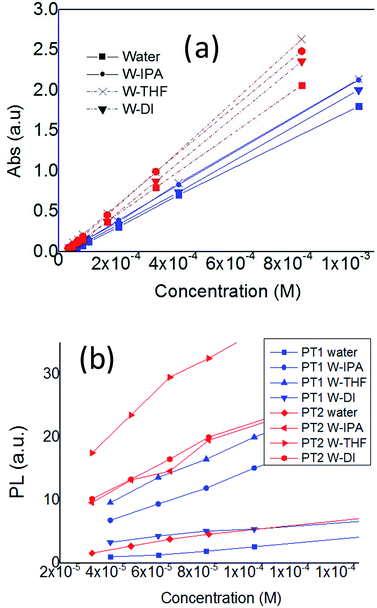Fig. 2 Plots of (a) λ_max and (b) λ_em of PT1 and PT2, as a function of polymer concentration, in all the solvents, at 25 °C.

On the other hand, Fig. 2b shows that for concentrations below 0.1 mM (monomer base), both polymers present an almost linear relationship between λ_em and concentration. At higher concentrations these plots decrease (Fig. S1 in ESI†), which indicates self-quenching due to aggregation. Therefore, in this work it was used a concentration of 0.08 mM in order to have diluted solutions. The data from aggregated solutions is currently under study in our group.

Table 1 shows the estimated values of molar absorption coefficient (ε) and fluorescence quantum yield (ϕ_f) of both polymers in all the solvents, and the increment of these two parameters due to the cosolvents. The ϕ_f values of both polymers were estimated from the linear zone of the plot of λ_max vs. the integral of the fluorescence spectra of quinine sulfate in H₂SO₄ 0.1 M of both polymers in the four solvents (Fig. S2 in ESI†).

Table 1 ε and ϕ_f of PT1 and PT2 in the different solvents, and the increments caused by cosolvents (Δε) and (Δϕ_f)

POL	Solvent	ε^a (M cm^−1)	Δε^b	ϕf (%)	Δϕf^c
a ε estimated in monomer base.b Δε = ε in mixed solvent/ε in water.c Δϕf = ϕf in mixed solvent/ϕf in water.
PT1	Water	1692	—	0.35	—
	W–IPA	2010	1.19	1.28	3.65
	W–THF	2022	1.19	1.69	4.8
	W–DI	1871	1.11	1.04	2.97
PT2	Water	2397	—	0.55	—
	W–IPA	2907	1.21	1.9	3.45
	W–THF	2714	1.13	3.55	6.45
	W–DI	3053	1.27	2.38	4.32

---

In Table 1 is observed that the values of ε_PT2 are larger than ε_PT1 in each solvent, with W–DI causing the largest difference (63%), while in the other three solvents this difference is around 35–45% (for a graphical representation see Fig. S3 in ESI†). These indicate that PT2 has better absorption properties, especially in presence of 1,4-dioxane.

In regard to the effect cosolvents on ε, the values of Δε in Table 1 (plotted in Fig. S4 in ESI†), show that isopropanol causes around a 20% increase in the absorbance of both polymers, while 1,4-dioxane increases ε_PT2 around 30%, and ε_PT1 only 10%. These data indicate that the length of the alkoxy spacer only has an impact on the absorption of these CPEs when 1,4-dioxane disrupts the normal structure of water.

In regard to ϕ_f, Minami and Kubo reported a value of ϕ_f = 1.2% for a molecule similar to PT1.¹⁶ As Table 2 shows, in water we obtain a smaller ϕ_f value (0.35%), and a very similar value in W–IPA (1.28%). Table 1 and Fig. S5 in ESI† show that in water ϕ_fPT2 is around 57% larger than ϕ_fPT1, and that cosolvents increase such difference, particularly THF.

Table 2 Wavelengths of λ_max, λ_em (λ_ex = 400 nm) and Stokes shift (Δν), of 0.08 mM solutions of both polymers in all solvents, at 25 °C

	Solvent	λmax (nm)	λem (nm)	Δν^a
a Δν = λem − λmax.
PT1	Water	363.7(±2.08)	530.3(±0.58)	168(±0)
	W–IPA	389.5(±2.12)	519.5(±3.53)	130(±1.41)
	W–THF	396(±2.83)	527(±1.41)	131(±4.24)
	W–DI	389(±1.14)	519.5(±0.7)	130.5(±0.7)
PT2	Water	406.5(±0.7)	533(±2.83)	126.5(±2.12)
	W–IPA	406(±1)	535(±2.83)	128.5(±2.12)
	W–THF	402(±2.83)	530(±3.54)	128.5(±0.7)
	W–DI	402(±1.14)	529(±1.41)	127(±0)

---

In this regard, for polymers with the same DP, changes in ϕ_f have been associated with changes in the pi-conjugation of conjugated ring molecules,⁴⁷ or with significant triplet formation, in thiophene-fluorene copolymers.¹²

Since both ε and ϕ_f are parameters estimated using a range of concentrations, instead of a punctual concentration, it is reasonable to focus specifically on the diluted 0.08 mM solutions, in regard to both λ_max and λ_em, together with their absorbance and fluorescence intensities, respectively. Table 2 shows the positions of λ_max, λ_em (λ_ex = 400 nm) and Stokes shifts (Δν) of 0.08 mM solutions of both polymers in all solvents. A graphical representation of λ_max and λ_em is presented in Fig. S6 and S7 in ESI.†

The wavelengths of λ_max and λ_em, of PT1 in water, shown in Table 2, are around 47 and 16 nm smaller, respectively, to those reported by Minami and Kubo for a similar molecule dissolved in water.¹⁶ Of course these discrepancies are related with differences in molecular structure and molecular weight.

In regard to the effect of solvents on the λ_max of each polymer, in Table 2 and Fig. S6 in ESI,† is observed that cosolvents generate a positive solvatochromism on PT1, because the λ_max wavelength of PT1 (λ_maxPT1) gets bathochromically (red) shifted around 25–30 nm when cosolvents are used, while λ_maxPT2 shows a slight 5 nm negative solvatochromism in W–THF and W–DI, while W–IPA does not shift λ_maxPT2 at all.

In this regard, it is known that for thiophenes, solvatochromism can be understood as an order-disorder phenomenon,⁴⁶ in which a well-extended backbone conformation results in a red shift in absorption spectra, whereas a disordered backbone conformation results in a blue shift.⁴⁸ Red shifts can also be understood in terms of a lower separation between adjacent energy levels, or HOMO–LUMO energy gap, while blue shifts indicate a deviation from coplanarity, due to a twist in the backbone, which reduces the conjugation length, generating blue shifts because of a larger separation between energy levels, or a tighter conformation of the chain coil via twisting of the conjugated backbone, resulting in segments with a shorter effective conjugation length.⁴

Also, for small conjugated molecules (fluorenones), positive solvatochromism is also related with a decrease in the HOMO–LUMO energy gap, and has been explained in terms of changes in the orientation of solvent around the solute molecules, which makes it to fit with the ground state charge distribution of the solute.⁴⁹

Therefore, the positive solvatochromism of λ_maxPT1, together with the negative or null solvatochromism of λ_maxPT2 due to cosolvents, indicate that PT2 has improved solubilization, with a more planar conformation.

Table 2 and Fig. S6 in ESI† also show that in each solvent, λ_maxPT2 is red shifted in comparison with λ_maxPT1, particularly in water. In this regard, previous studies with unsubstituted oligothiophenes³⁸ and also with polyphenylene vinylene oligoelectrolytes,⁵⁰ showed that an increase in the degree of polymerization (DP) causes red shifts in both, λ_max and λ_em, generating also larger ε values, due to a more extended conjugation length.

In this regard, Table 2 and Fig. S6 and S7,† show that in water and W–THF, λ_maxPT2 is red shifted in comparison with λ_maxPT1, but their λ_em values are almost the same.

Therefore, even when our λ_max and ε results seem to indicate that apparently PT2 has a larger DP than PT1, the fact that (i) in water and W–THF, both polymers have different λ_max, but similar λ_em, together with (ii) the solvatochromic behavior each polymer show, seem to indicate that the red shift of λ_maxPT2 in comparison with λ_maxPT1 in each solvent, could be mainly related with a worse solubilization and planarity of PT1, particularly in water, instead of a difference in their DP.

Table 3 shows the average of the absorbance at λ_max, and fluorescence intensity at λ_em, of both polymers in all solvents (Fig. S8 and S10 in ESI† show a graphical representation of these data).

Table 3 Absorbances at λ_max and fluorescence intensities at λ_em of diluted solutions of both polymers in all solvents, at 25 °C, together with the increases in the absorbance and intensity caused by cosolvent (Δλ_maxS, Δλ_emS)

POL	Solvent	λmax (a.u.)	ΔλmaxS^a	λem (a.u.)	ΔλemS^b
a ΔλmaxS = λmax in mixed solvent/λmax in water (ratio of averages).b ΔλemS = Δλem in mixed solvent/Δλem in water (ratio of averages).
PT1	Water	0.08(±0.01)	—	1.99(±0.34)	—
	W–IPA	0.125(±0.02)	1.56	12.46(±0.34)	5.72
	W–THF	0.14(±0.014)	1.75	16.65(±0.21)	7.64
	W–DIOX	0.115(±0.02)	1.44	5.5(±0.28)	2.52
PT2	Water	0.125(±0.02)	—	4.04(±0.11)	—
	W–IPA	0.13(±0.014)	1.04	14.76(±0.15)	3.65
	W–THF	0.165(±0.02)	1.32	30.05(±0.07)	7.44
	W–DIOX	0.13(±0.014)	1.04	16.8(±0.14)	4.16

---

In regard to absorbance, Table 3 and Fig. S8† show that in water, the absorbance at λ_maxPT2 is larger than that of PT1, while in the solvent mixtures the absorbance of both polymers is statistically equal. It is also observed that for both polymers, cosolvents generate an increase in absorbance, particularly in THF. Therefore, same as happens with the wavelength of λ_max, water is the only solvent in which the length of the alkoxy spacer generates a significant difference in the behavior of the polymers.

In regard to the effect of cosolvents on the absorbance of each polymer, the ratios Δλ_maxS in Table 3 (plotted in Fig. S9 in ESI†), show that THF causes the largest increase in the absorbance of both polymers, increasing 75% and 32% the absorbance of PT1 an PT2, respectively, while isopropanol and 1,4-dioxane increases the absorbance of PT1 around 50%, but does not increase the absorbance of PT2.

Analyzing the position and intensity λ_em allows gaining understanding on the conformations in the relaxed excited state (S1) of the polymers in diluted solutions. Thus, Table 2 and Fig. S7 in ESI† show that the three cosolvents generate blue shifts of λ_emPT1, while λ_emPT2 is blue shifted in W–THF and W–DI, and blue shifted in W–IPA.

In this regard, it is known that shifts in λ_em are related with conformational changes in the polythiophene backbone of copolymers.¹² Therefore, it seems that in the S1 state, W–IPA generates opposite conformational changes between the polymers.

Comparing Fig. S6 and S7,† it is clear that in W–IPA, W–THF and W–DI the positions of λ_max and λ_em of both polymers show the same trend, with W–THF generating statistically similar positions between the polymers in both plots, and W–IPA and W–DI generating largest differences. Interestingly, water generates a clearly different behavior, because it maximizes the difference between the wavelengths of λ_maxPT1 and λ_maxPT2, but minimizes the difference between their λ_em wavelengths. This means that in this solvent is visible a clear effect of the length of the alkoxy spacer on the conformation in the S0 state, which could indicate a specific solute–solvent interaction in the ground state, that afterwards becomes minimized in the S1 state. This is discussed ahead using the Lippert–Mataga equation, which allows evaluating possible specific solute–solvent interactions, by analyzing simultaneously the positions of λ_max and λ_em, by using the Stokes shift (Δν).

In regard to fluorescence intensity, Table 3 and Fig. S10 in ESI† show that the presence of cosolvents increase the intensity of λ_em of both polymers, and that water and W–IPA generate similar emission intensities between the polymers. The values of the ratios Δλ_emS in Table 3 (plotted in Fig. S11 in ESI†), show that THF generates the same increase in the fluorescence intensity of the polymers, while isopropanol generates a larger increase in the intensity of PT1, and 1,4-dioxane generates a larger increase in the intensity of PT2.

The data of Δλ_maxS and Δλ_emS (Fig. S9 and S11 in ESI†) give evidence of the structural similarity of PT1 and PT2, because the absorption and emission intensity of both polymers are increased in the same way due to cosolvents.

It is worth to mention, that the plots of ϕ_f and fluorescence intensity (Fig. S5 and S10† respectively), are similar between each other, while the plots of ε and absorbance (Fig. S3 and S8,† respectively) are not. This is related with the fact that the values of ε are estimated using a concentration range larger than the range used to estimate ϕ_f, and indicates that even when the plots used to estimate ε are linear, they reflect in some way the effect of molecular aggregation.

Fig. 3 shows the Lippert–Mataga plots of diluted solutions of both polymers in all solvents, generated using paired data from Table 1.

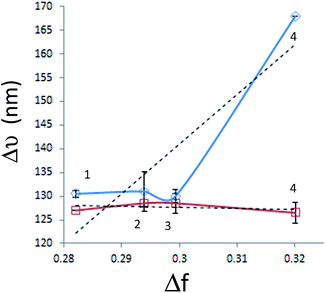Fig. 3 Lippert–Mataga plots of PT1 (blue diamonds) and PT2 (red squares) in (1) W–DI, (2) W–THF, (3) W–IPA and (4) water. Dashed lines show the linear regressions for each polymer.

This figure shows that in all the solvents, the average Δν values of PT1 are larger than those of PT2, with isopropanol and THF generating statistically equal values. It is also observed that the plot of PT2 has a slight negative slope, while the plot of PT1 has a positive slope, mainly due to the big difference in Δν observed in water. These results give more evidence about the improved solubilization of PT2.

On the other hand, it seems that W–IPA generates a valley in the plot of PT1 and also a slight maximum in the plot of PT2.

In this regard, large Δν values indicate a large structural difference between S0 and S1 states.⁵¹ Also, increases of Δν in protic hydrogen bonding solvents indicate specific solvent–fluorophore interactions,^23,52 and negative deviations in alcohols are related with the presence of non-specific interactions in the S0 state, such as hydrogen bonding, which become weaker in the excited state²³ and/or molecular aggregation, both phenomena are not accounted by the Lippert–Mataga correlation.⁵³ Therefore, these results indicate that apparently PT1 is the only polymer capable of forming hydrogen bonds. It is worth to mention that this conclusion is valid regardless a possible difference in DP between the polymers, since they behave similarly in three solvents, and show a dramatic difference in water.

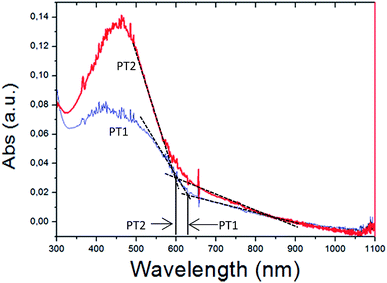
In regard to the estimation of optical band gap (EgOPT), thin films did not generate an absorption spectrum, reason why thick films (visible with the naked eye) were used. It is known that thick films generate scattering which may degrade the accuracy of the EgOPT estimation, however, Fig. S12 in ESI† shows that thinner and thicker regions of the films (i.e. darker and lighter zones, watched by the naked eye) generate the same absorption onset.

Fig. 4a shows the absorption spectra of thick films of both polymers and the onset of absorption used to estimate EgOPT. It is observed that the absorption spectra of the films of PT1 and PT2 have cut off absorption wavelength values of 630 and 600 nm respectively, which imply EgOPT values of 1.968 and 2.066 eV, respectively (E (eV) = 1240/λ).

Fig. 4 Absorption spectra of drop cast films on glass of PT1 (thin blue line) and PT2 (thick red line). Black continuous lines show the interception of the black-dashed tangential lines used to estimate EgOPT.

These EgOPT values are smaller than those obtained by Page in a thiophene based zwitterionic copolymers,³⁷ and are relatively small in comparison with those obtained from films of several neutral polythiophenes,⁴³ which are in the range of 2.3–4 eV. In Fig. 5 is also observed that the spectra of the PT1 films generate shorter λ_max wavelengths, which also occurs in every solvent at all concentrations (Table 2).

Fig. 5 Cyclic voltammograms of drop cast films of PT1 (thin blue line) and PT2 (thick red line) on glassy carbon mini-electrodes, in MeCN with TBATFB 0.1 M, scanned at 10 mV s⁻¹ during (a) the first cycle, and (b) subsequent cycles. Vertical arrows indicate the oxidation onset at 0 current. The black dashed cyclic voltammogram shows the blank measurement.

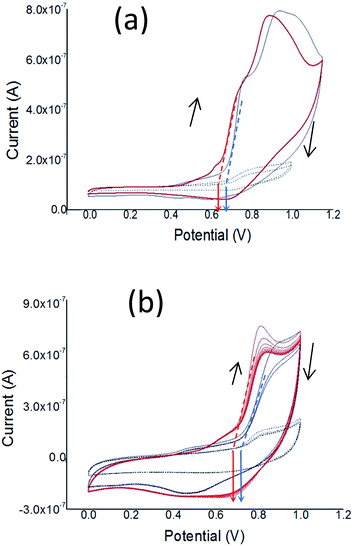
In regard to the electrochemical properties in solid state, the electrochemical reduction (n-doping) of the films was not possible, because negative potentials cause irreversible destruction of the films (results not shown). Therefore, cyclic voltammetry was used only for p-doping and de-doping of the films of both polymers, in order to estimate the ionization potential (I_p).

Fig. 5 shows the cyclic voltammograms (CVs) for p-doping of drop-cast films of both polymers during the first and subsequent cycles. In Fig. 5a is observed that during the first oxidation cycle both polymers present two oxidation p-doping peaks, with the peaks of PT1 anodically shifted (i.e. at higher potential values) in comparison to those of PT2. The first peak is located at 0.78 and 0.74 V for PT1 and PT2 respectively, while the second is located at 0.93 and 0.89 for PT1 and PT2, respectively. The oxidation onset of PT1 is also anodically shifted, with onsets of 0.68 and 0.62 V for PT1 and PT2 respectively, which indicates that the ionization potentials of PT1 and PT2 are:

I_pPT1 = −(0.68 + 4.8) = −5.08 eV and I_pPT2 = −(0.62 + 4.8) = −5.02 eV.

More negative values of I_p indicate that it is more difficult to remove an electron from the highest occupied molecular orbital (HOMO) of a molecule, PT1 in this case.

Fig. 5a also shows that during the first cycle, both polymers show a single and subtle de-doping peak, located at 0.7 and 0.6 V for PT2 and PT1 respectively.

Fig. 5b shows that during subsequent cycles the two oxidation peaks observed during the first cycle disappear and fuse into a single p-doping peak, with oxidation onsets and p-doping peaks being anodically shifted in comparison with those at the first cycle, however keeping constant the difference between polymers observed during the first cycle (around 0.03 V). For subsequent cycles, the onsets are located at 0.71 and 0.68 V for PT1 and PT2, respectively, while the p-doping peaks are 0.84 and 0.81 V for PT1 and PT2, and the de-doping peaks are observed at 0.48 and 0.69 for PT1 and PT2.

In this regard, changes between first and subsequent doping cycles of polythiophenes films have been explained in terms of non-faradaic and faradaic currents, generated during the first and subsequent oxidations, respectively.

Fig. 5b also shows that the peak potential difference (ΔE) between p-doping and de-doping peaks is different between polymers, with ΔE values of 0.41 V (0.89–0.48 V) for PT1 and 0.12 V (0.81–0.69 V) for PT2. The fact that PT2 shows a smaller ΔE indicates a more reversible charge–discharge process.

Finally, during the first and subsequent cycles both polymers generate similar currents, which indicate qualitatively that both films have similar charging capabilities.

The electrochemical response of the films indicate that both polymers have essentially the same features, however with PT2 being more easily dopable and de-dopable, which indicates a difference in the packing between polymers.

3.2 Density functional theory

In regard to theoretical ionization potentials, Fig. 7 and in Table S2 in ESI† show the energy levels of the HOMO and LUMO of dimers, tetramers and hexamers, of oligomers possessing either ethyloxy or hexyloxy spacers (OT1 and OT2 respectively), in water and 1,4-dioxane.

In Fig. 6a is observed that for hexamers in water, the energy level of the HOMO frontier energy level of OT1 (HOMO-OT1) is more negative than that HOMO-OT2, with values of −4728 and −4413 eV for PT1 and PT2 respectively. This is in agreement with the empirical EgCV values, which also show that it is more difficult to remove an electron from the HOMO level of PT1 in comparison with PT2.

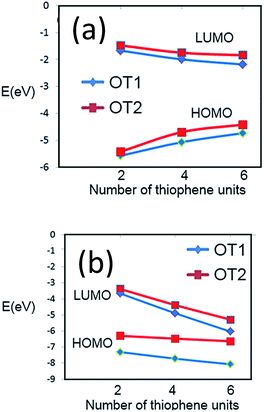Fig. 6 Values of frontier energy orbitals for dimer, tetramer and hexamer of PT1 (blue diamonds) and PT2 (red squares) in (a) water and (b) 1,4-dioxane.

In regard to band gaps, Table S2 in ESI† shows that the band gaps of the hexamers of OT1 and OT2 are 2.55 and 2.57 eV, respectively, which means that the molecule with the longest alkoxy spacer has the largest band gap.

This is in agreement with the experimental estimation of EgOPT, which indicated a larger band gap for PT2. It is worth to mention that our empirical and theoretical results also in agreement with a previous study using films of poly(3-alkyl) thiophene, which showed that longer spacer chains generate larger band gaps.⁵⁴

Fig. 6b shows that the simulation in 1,4-dioxane does not generate an stabilization of the FMOs as it occurs in water, because the energy levels of the theoretical FMOs of both molecules decrease with the increase of monomer units, generating HOMO–LUMO energy gaps of −2032 and −1346 eV for the hexamers of OT1 and OT2 respectively.

To further analyze these differences, it is useful to plot directly the HOMO–LUMO energy gap values as a function of oligomer size. Fig. 7 shows the HOMO–LUMO gap (eV) of OT1 and OT2 in water and 1,4-dioxane.

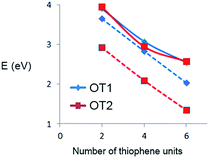Fig. 7 HOMO–LUMO gap values (eV) of oligomers of OT1 (blue diamonds) and OT2 (red squares) in water (solid lines) and 1,4-dioxane (dashed lines).

Fig. 7 shows that in water, the value of the HOMO–LUMO gaps of OT1 and OT2 are quite similar, for all the oligomer sizes, while in 1,4-dioxane, the oligomers of OT2 have smaller gaps than the oligomers of OT1, which in turn has gap values similar to those calculated in water. These indicate that in the framework of the level of theoretical model chemistry used, the length of the alkoxy spacer has a clear effect on the HOMO–LUMO bandgap only in 1,4-dioxane.

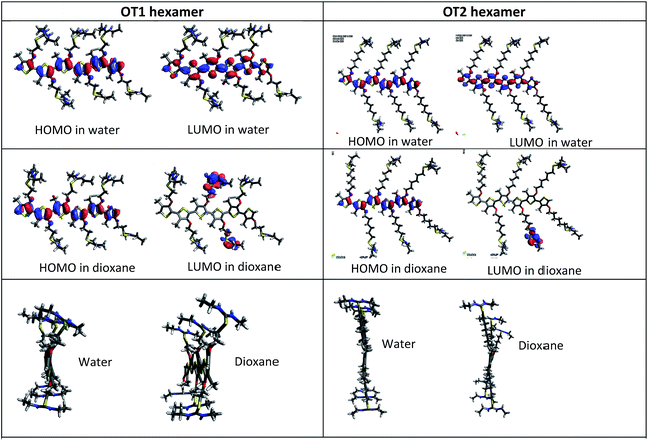
Also, Fig. 8 shows the shape and spatial positions of the HOMOs and LUMOs in the hexamers of OT1 and OT2, in water and 1,4-dioxane.

Fig. 8 Frontier orbitals and lateral views of hexamers of OT1 (left column) and OT2.

It is observed that in water, the HOMOs and LUMOs of both molecules are located on the thiophene backbone. In regard to the LUMOs, in 1,4-dioxane these are located at the isothiouronium groups of OT1 and OT2, and the same behavior is observed in the tetramers of both molecules (Fig. S9 in ESI†). These results indicate that theoretically, 1,4-dioxane reduces the efficiency of electron transitions between HOMO and LUMO after photoexcitation (han 2015 homo lumo separados). This is not in agreement with the results from fluorescence, however a more detailed study with time-dependent DFT should be necessary to gain insight on these results.

Besides the values of the HOMO–LUMO gaps, the theoretical degree of twisting in the conjugated backbone provides more information about the conformation of the molecules. In this regard, Fig. 8 shows that in both solvents, the hexamers of OT2 are less twisted than OT1, in which the isothiouronium groups are clearly more bent. It is also observed that the hexamers of OT2 are almost flat in water. Fig. S13† shows that the same trends are observed in tetramers.

These results are in agreement with the empirical λ_max values of the polymers, which suggest a smaller conjugation length in PT1, which causes smaller λ_max wavelengths than PT2. This should be related with the flexibility of the hexyloxy spacer in PT2.

4 Conclusions

In every solvent, the polymers show a difference in the value of λ_max, λ_em, ε, ϕ_f and Δν. The data suggest that such difference seems to be mainly related with a difference in solubilization instead of a difference in the degree of polymerization, with water generating the biggest difference between polymers.

The theoretical oligomers OT1 indicate that shorter and more rigid spacers twist the conjugated backbone, while both, empirical and theoretical results, indicate that shorter spacers also increase the ionization potential and decrease the band gap.

A more twisted conformation of PT1 explains its larger sensitivity to cosolvents and could be the result of specific solute–solvent interactions that only this polymer has in water.

Acknowledgements

Sergio E. Domínguez deeply acknowledges the Mexican National Council for Science and Technology (CONACyT) for the international doctoral scholarship No. 310828, and also for the partial support from the Finnish National Doctoral Programme in Nanoscience (NGS-NANO) and the Doctoral Programme in Physical and Chemical Sciences (PCS) from University of Turku. The authors wish to acknowledge CSC – IT Center for Science, Finland, for computational resources.

References

1. H. Li, R. Yang and G. C. Bazan, Macromolecules, 2008, 41, 1531–1536.
2. A. C. Carreon, W. L. Santos, J. B. Matson and R. C. So, Polym. Chem., 2014, 5, 314–317.
3. R. McCullough, P. Ewbank and R. Loewe, J. Am. Chem. Soc., 1997, 119, 633–634.
4. M. Wang, S. Zou, G. Guerin, L. Shen, K. Deng, M. Jones, G. C. Walker, G. D. Scholes and M. A. Winnik, Macromolecules, 2008, 41, 6993–7002.
5. R. Prince, J. Saven, P. Wolynes and J. Moore, J. Am. Chem. Soc., 1999, 121, 3114–3121.
6. D. A. M. Egbe, S. Tuerk, S. Rathgeber, F. Kuehnlenz, R. Jadhav, A. Wild, E. Birckner, G. Adam, A. Pivrikas, V. Cimrova, G. Knoer, N. S. Sariciftci and H. Hoppe, Macromolecules, 2010, 43, 1261–1269.
7. T. Yamamoto, NPG Asia Mater., 2010, 2, 54–60.
8. A. F. Thünemann, M. Müller, H. Dautzenberg, J. Joanny and H. Löwen, in Polyelectrolytes with Defined Molecular Architecture II, ed. M. Schmidt, Springer, Germany, 2004, p. 113.
9. A. Patil, Y. Ikenoue, F. Wudl and A. Heeger, J. Am. Chem. Soc., 1987, 109, 1858–1859.
10. M. Knaapila, R. C. Evans, V. M. Garamus, L. Almasy, N. K. Szekely, A. Gutacker, U. Scherf and H. D. Burrows, Langmuir, 2010, 26, 15634–15643.
11. A. Alvarez, A. Salinas-Castillo, J. M. Costa-Fernandez, R. Pereiro and A. Sanz-Medel, TrAC, Trends Anal. Chem., 2011, 30, 1513–1525.
12. A. Gutacker, N. Koenen, U. Scherf, S. Adamczyk, J. Pina, S. M. Fonseca, A. J. M. Valente, R. C. Evans, J. S. de Melo, H. D. Burrows and M. Knaapila, Polymer, 2010, 51, 1898–1903.
13. A. Li, J. Wang, F. Wang and Y. Jiang, Chem. Soc. Rev., 2010, 39, 3729–3745.
14. C. Bazzicalupi, A. Bencini and V. Lippolis, Chem. Soc. Rev., 2010, 39, 3709–3728.
15. D. Gomez, L. Fabbrizzi, M. Licchelli and E. Monzani, Org. Biomol. Chem., 2005, 3, 1495–1500.
16. T. Minami and Y. Kubo, Chem.–Asian J., 2010, 5, 605–611.
17. K. Tsai, C. Chueh, S. T. Williams, T. Wen and A. K. Y. Jen, J. Mater. Chem. A, 2015, 3, 9128–9132.
18. G. Tu, H. Li, M. Forster, R. Heiderhoff, L. J. Balk, R. Sigel and U. Scherf, Small, 2007, 3, 1001–1006.
19. M. J. Tapia, M. Montserin, A. J. M. Valente, H. D. Burrows and R. Mallavia, Adv. Colloid Interface Sci., 2010, 158, 94–107.
20. H. M. Rosenber and E. Eimutis, Spectrochim. Acta, 1966, 22, 1751.
21. T. Werner and D. Hercules, J. Phys. Chem., 1969, 73, 2005.
22. T. Werner and R. Hoffman, J. Phys. Chem., 1973, 77, 1611–1615.
23. B. F. Hermenegildo, G. Pereira, A. S. Abreu, E. M. S. Castanheira, P. M. T. Ferreira and M. R. P. Queiroz, J. Photochem. Photobiol., A, 2011, 221, 47–57.
24. A. Chaudhari, Int. J. Quantum Chem., 2010, 110, 1092–1099.
25. A. Kukhta, I. Kukhta and S. Salazkin, Mater. Sci., 2011, 17, 266–270.
26. A. Irfan, H. Aftab and A. G. Al-Sehemi, J. Saudi Chem. Soc., 2014, 18, 914–919.
27. A. Irfan and A. G. Al-Sehemi, J. Saudi Chem. Soc., 2014, 18, 574–580.
28. P. Leveque, L. Biniek, S. Fall, C. L. Chocos, N. Leclerc and T. Heiser, Alkoxy side chains in low band-gap co-polymers: impact on conjugation and frontier energy levels, Elsevier Science Bv, Sara Burgerhartstraat 25, Po Box 211, 1000 Ae Amsterdam, Netherlands, 2012.
29. J. Lukkari, M. Salomaki, A. Viinikanoja, T. Aaritalo, J. Paukkunen, N. Kocharova and J. Kankare, J. Am. Chem. Soc., 2001, 123, 6083–6091.
30. A. Viinikanoja, S. Areva, N. Kocharova, T. Aaritalo, M. Vuorinen, A. Savunen, J. Kankare and J. Lukkari, Langmuir, 2006, 22, 6078–6086.
31. P. Damlin, M. Hatonen, S. E. Dominguez, T. A. Aaritalo, H. Kivela and C. Kvarnstrom, RSC Adv., 2014, 4, 8391–8401.
32. M. Chayer, K. Faid and M. Leclerc, Chem. Mater., 1997, 9, 2902–2905.
33. H. Ho, M. Boissinot, M. Bergeron, G. Corbeil, K. Dore, D. Boudreau and M. Leclerc, Angew. Chem., Int. Ed., 2002, 41, 1548–1551.
34. M. Jeffries-El and R. D. McCullough, in conjugated polymers. Theory, synthesis, properties, and characterization, ed. T. A. Skotheim and J. R. Reynolds, CRC Press, Boca Raton, FL 33487-2742, 2007, pp. 9–3.
35. J. Liu, R. Loewe and R. McCullough, Macromolecules, 1999, 32, 5777–5785.
36. F. Goldoni, Thiophene-based pi-conjugated polymers. Synthetic design towards the control of their supramolecular architecture, Technische Universiteit Eindhoven, 2000.
37. Z. A. Page, V. V. Duzhko and T. Emrick, Macromolecules, 2013, 46, 344–351.
38. H. Chosrovian, S. Rentsch, D. Grebner, D. Dahm, E. Birckner and H. Naarmann, Synth. Met., 1993, 60, 23–26.
39. H. D. Burrows, M. Knaapila, S. M. Fonseca and T. Costa, in Conjugated Polyelectrolytes Fundamentals and Applications, ed. B. Liu and G. C. Bazan, Wiley-VCH, Boschstr. 12, 69469 Weinheim, Germany, 2013, p. 127.
40. J. Bredas, R. SILBEY, D. Boudreaux and R. Chance, J. Am. Chem. Soc., 1983, 105, 6555–6559.
41. P. Wu, F. S. Kim, R. D. Champion and S. A. Jenekhe, Macromolecules, 2008, 41, 7021–7028.
42. S. Hwang and Y. Chen, Macromolecules, 2002, 35, 5438–5443.
43. T. Johansson, W. Mammo, M. Svensson, M. Andersson and O. Inganas, J. Mater. Chem., 2003, 13, 1316–1323.
44. M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford, Conn, USA, 2009.
45. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
46. S. Ko, E. T. Hoke, L. Pandey, S. Hong, R. Mondal, C. Risko, Y. Yi, R. Noriega, M. D. McGehee, J. Bredas, A. Salleo and Z. Bao, J. Am. Chem. Soc., 2012, 134, 5222–5232.
47. K. Higashiguchi, K. Matsuda, Y. Asano, A. Murakami, S. Nakamura and M. Irie, Eur. J. Org. Chem., 2005, 91–97.
48. F. Goldoni, Thiophene-based pi-conjugated polymers. Synthetic design towards the control of their supramolecular architecture, Technische Universiteit Eindhoven, 2000.
49. A. I. Adeogun, N. W. Odozi, N. O. Obiegbedi and O. S. Bello, Afr. J. Biotechnol., 2008, 7, 2736.
50. L. E. Garner, J. Park, S. M. Dyar, A. Chworos, J. J. Sumner and G. C. Bazan, J. Am. Chem. Soc., 2010, 132, 10042–10052.
51. S. Li, K. Jiang, C. Yu, J. Huang, L. Yang and Y. Song, New J. Chem., 2014, 38, 4404–4408.
52. J. R. Lakowicz, in Principles of Fluorescence Spectroscopy, ed. J. R. Lakowicz, Springer, 2006, p. 63.
53. D. Kumar and K. R. J. Thomas, J. Photochem. Photobiol., A, 2011, 218, 162–173.
54. W. Y. Huang, C. C. Lee, S. G. Wang, Y. K. Han and M. Y. Chang, J. Electrochem. Soc., 2010, 157, B1336–B1342.

---

Footnote

† Electronic supplementary information (ESI) available: Table with physical chemical properties of solvents, detailed methods, plots used to estimate all the ϕ_f values, graphical resumes of λ_max and λ_em maxima values, table with theoretical HOMO and LUMO energy level values. See DOI: 10.1039/c6ra21451g

---