Theoretical investigation of interactions between palladium and fullerene in polymer

Abstract

Applying density functional theory (DFT) calculations, we predict the structural and electronic properties of different types of palladium–fullerene polymers. We examine the structures of one- (1-D), two- (2-D), and three-dimensional (3-D) polymers. We find that the most stable polymer is that represented by bonding via the [6,6] position of the fullerene molecules with Pd in a distorted tetrahedral coordination. Special attention is paid to the electronic structure. We demonstrate clearly that changes in the Pd coordination geometry strongly affect the projected density-of-states picture of the 4d orbitals. The energy band gaps in the 1-D and 2-D systems obviously differ from that in the 3-D one; thus, we can directly modify the electronic properties of polymers. The results at the AM1* level of theory for the reduced 1-D polymer show that isolated polarons are the preferred electronic states.

---

1 Introduction

Many studies of fullerene-containing polymers have been reported recently, because of their potential application in many areas such as solar energy conversion, bio- and chemisensors, catalysis, adsorption and separation, energy accumulation, electroactive batteries, hydrogen storage, and electronics.^1–4 Fullerene cages can bond in many different ways to form a polymeric network.² Like alkenes, fullerenes can form homopolymers through [2 + 2] cycloadditions.^5–9 They can also be incorporated into a polymeric backbone^10–12 or attached to the main chain as pendant substituents.^13–16

An attractive approach to forming polymeric structures in which fullerene moieties are incorporated into the main polymeric backbone is to bond fullerene cages with transition metal atoms or their complexes.^17–22 To date, coordination polymers with fullerene cages covalently bonded to palladium and platinum atoms have been synthesised.^17,18,20,22 Structures with fullerenes coordinated through –Ir(CO)₂– and –Rh(CF₃CO₂)₂Rh– units have also been reported.^20,21 Saito and co-workers recently reported the formation of one-dimensional (1-D) fullerene polymeric chains in which C₆₀ moieties are bonded to Ni[P(CH₃)₃]₂ units in η²-fashion.¹⁹ Coordination polymers of fullerene and palladium, C₆₀Pd_x (x = 1–3), have been investigated most intensively. They can be formed under chemical^17,18 and electrochemical conditions.^20,22 The chemical synthesis is carried out in benzene solution containing fullerene and a zero-valent palladium complex as precursors of the polymerisation process. Electrochemical polymerisation occurs during the reduction of Pd(II) ions in solution, in the presence of C₆₀. The composition and properties of C₆₀Pd_x polymers depend on the concentration of the precursors in solution. By changing the polymerisation conditions, it is possible to produce materials that range from long 1-D chains to a highly cross-linked three-dimensional (3-D) networks.

Very few studies have investigated the structure of C₆₀Pd_x and other fullerene-based coordination polymers. Electron diffraction and high-resolution electron microscopy demonstrated that C₆₀Pd₃ exhibits an ordered body-centred cubic (bcc) structure of fullerene units with a slight rhombohedral distortion.²³ The fullerene cage is octahedrally coordinated to six palladium atoms. Each palladium atom is bonded to two C₆₀ units. X-ray photoelectron spectra of poly-Pd₃C₆₀ indicated that charge is transferred from the metal atoms to the C₆₀ moieties during bond formation.²⁴ The structure of the polymer is closely related to its electronic properties.

The electrical properties of the C₆₀Pd₃ polymer are particularly important in terms of potential application of this material in charge storage devices^25–28 and solar energy conversion systems.²⁹ The C₆₀Pd₃ polymer shows low electrical conductivity in its neutral state. Reduction of the polymer results in a significant increased conductivity³⁰ and creates mixed valence states along the polymeric chain. Electron exchange between the redox centres is responsible for the increase in the conductivity of the polymeric material.

Experimental investigations of the electronic properties of conducting polymers can be significantly supported by theoretical studies. For a number of oligomeric and polymeric materials, such theoretical studies have contributed greatly to the rationalisation of their properties.^31–34 They also enable prediction of the electronic behaviour of yet unknown polymers.³⁵ Theoretical prediction of the electronic structure of macromolecular systems is an extremely important step towards the rational design of high-performance materials.

Up to now, there have been only a few theoretical studies on the interaction of fullerene with palladium.^36–38 Gal'pern and Stankevich^36,37 considered the structure and electronic configuration of such complexes with different ratios of both components within the DFT approximation. They showed the formation of the quasi-one-dimensional polymer structure C₆₀Pd₃ in which the adjacent fullerenes are bound via Pd₃ clusters. More recently, El Mahdy³⁸ studied hydrogen adsorption and dissociation on Pd-doped C₆₀. Different types of fullerene–metal complexes with PH₃ ligands were analysed, showing that the bond dissociation energies increase in the order Pd < Pt < Ni.³⁹ Accurate theoretical calculations of metal-containing fullerene complexes concerning the electronic structures and optical spectra properties have been reported by Zhou and Zhao.⁴⁰

In this paper, we analyse the geometrical and electronic structure of different types of C₆₀Pd polymers using first-principles periodic density functional theory (DFT) with some contribution from the semiempirical AM1* method. It is well accepted that expanding the dimensionality of polymers may significantly change their physical and chemical properties. In our studies, we consider 1-D, two-dimensional (2-D), and 3-D polymer structures. For the 1-D polymer, we analyse two types of Pd binding motif on the fullerene molecules and its coordination environment. Following these results, we study the 2-D and 3-D polymers. Here, we also report the electronic structure of all the polymers, which is of significant importance for the fundamental understanding of their transport, optical, and electrochemical properties. Finally, we present the results of calculations obtained at the AM1* level of theory for the relative stability of a polaron pair vs. a bipolaron for the reduced 1-D polymer.

2 Computational methods

First-principles calculations were computed using the DFT periodic approach with a plane-wave basis set. The calculations were performed using the PWSCF⁴¹ program to solve the Kohn–Sham equations and obtain the electronic ground state. The interaction between the ions and the valence electrons is described by Vanderbilt ultrasoft pseudopotentials.⁴² For Pd and C, the 4d electrons on the one hand and the 2s and 2p electrons on the other hand were treated as valence electrons. The remaining electrons were kept frozen. Additional test calculations for a Pd pseudopotential that also included semicore states (4s, 4p) resulted in a 0.9 kcal mol⁻¹ smaller binding energy than that including only 4d electrons; therefore, we used the latter type of pseudopotential. A plane-wave cutoff of 30 Ry was chosen for these calculations. Increasing the cutoff energy from 30 to 35 Ry caused an increase in the binding energy of less than 0.1 kcal mol⁻¹. The generalised gradient approximation (GGA)-type Perdew–Burke–Ernzerhof (PBE)⁴³ exchange-correlation functional with Grimme's correction (D2)⁴⁴ was used to describe the van der Waals interactions throughout this work. This approach (DFT-D2) consists of adding a semiempirical dispersion potential (a pairwise force field) to the Kohn–Sham DFT energy. The total energy was minimised using the Hellman–Feynman forces. The examined systems were fully relaxed until the residual forces on the ions were below 5 × 10⁻³ eV Å⁻¹.

Periodic boundary conditions and a supercell approximation were applied for all the polymers studied. The 1-D polymer was described as an infinite chain oriented along the z axis. Two supercells containing 61 atoms (one C₆₀Pd unit) and 122 atoms (two C₆₀Pd units) were used. The vacuum space in the lateral direction was set to 13 Å. For the supercell with one C₆₀Pd unit, the geometry was fully optimised using a 1 × 1 × 1, 1 × 1 × 2, 1 × 1 × 4, or 1 × 1 × 6 Monkhorst–Pack k-point mesh⁴⁵ for the integration in the first Brillouin zone. The relative total energy differences between two subsequent k-point grids were −5.5, −0.1, and 0.0 kcal mol⁻¹, respectively. Therefore, a 1 × 1 × 4 grid for the supercell with one C₆₀Pd unit and a 1 × 1 × 2 grid for the supercell with two C₆₀Pd units were used. For the 2-D and 3-D polymers, we used tetragonal and bcc supercells, respectively; there were two types of supercell, small and large, with corresponding k-point meshes of 4 × 4 × 4 and 2 × 2 × 2. To calculate the density of states (DOS), linear tetrahedron smearing was used. For better visualisation of the DOS, the peak width for broadening was set to 0.05 eV.

Semiempirical calculations were performed with the AM1* Hamiltonian^46,47 using EMPIRE13 ^48,49 on the DFT-optimised geometries.

All the figures were produced using the visualisation programs VESTA⁵⁰ and XcrySDen.⁵¹

3 Results and discussion

3.1 1-D polymers

3.1.1 Geometry. The fullerene molecule with icosahedral symmetry has two types of bonds, namely, 6–6 bonds (1.39 Å) and 6–5 bonds (1.45 Å).⁵² Many different organometallic complexes of fullerene have been prepared to date, the vast majority of which show η²-coordination at the [6,6] position.⁵³ The stability of this structure is confirmed by theoretical studies of the interaction between C₆₀ and transition metal atoms (Co, Rh, Ir, Ni, Pd, and Pt).⁵⁴ The second most stable coordination type involves η²-coordination at the [6,5] position.⁵⁴ Therefore, we considered only these two energetically most favourable positions.

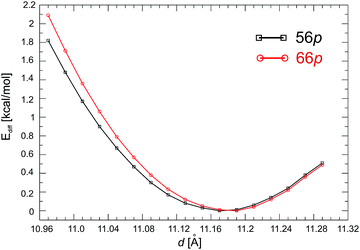
First, we examined the structure of the 1-D C₆₀Pd polymer represented by two configurations with different Pd binding motifs on the fullerene molecules, namely, [5,6] and [6,6] binding, which are denoted as 56p and 66p, respectively. The initial (1 × 1 × 1) supercell contains one C₆₀Pd unit in which the Pd atom is bound to two fullerene molecules by two η²-type Pd–C bonds. Next, we estimated the equilibrium Pd–C₆₀–Pd distance (d). By varying the distance from 10.97 to 11.29 Å in 0.02 Å steps during the geometry optimisation, we obtained 17 structures for both polymers. The stability of these structures was compared using their total energy differences, where the most stable structure was used as a reference (E_diff) and set to 0 kcal mol⁻¹. The obtained equilibrium distances for the 56p and 66p polymers are 11.17 and 11.19 Å, respectively (Fig. 1). The total energy difference between the most stable configurations of the 66p and 56p polymers is −6.7 kcal mol⁻¹, confirming that binding via the [6,6] position is energetically favourable. For both polymers, the Pd atoms exhibit a distorted square-planar geometry involving coordination to two C₆₀ molecules (four Pd–C bonds). It is noteworthy that varying the distance (d) from about 10.05 to 10.29 Å changes the relative total energy by less than 1 kcal mol⁻¹, which shows that the Pd–C bonds are very flexible. The equilibrium Pd–C bond lengths and the C–Pd–C angles are 2.184 Å and 39.8° and 2.174 Å and 38.8° for 56p and 66p, respectively. The corresponding 5–6 and 6–6 bonds adjacent to the Pd are elongated by 0.033 and 0.044 Å, respectively, compared to those in the isolated molecule.

Fig. 1 Relative total energy differences (E_diff in kcal mol⁻¹) of the 56p and 66p C₆₀Pd polymers calculated for various Pd–C₆₀–Pd distances (d, Å) in GGA(PBE) + D2 calculations. The lowest value of the total energy is set to 0 kcal mol⁻¹.

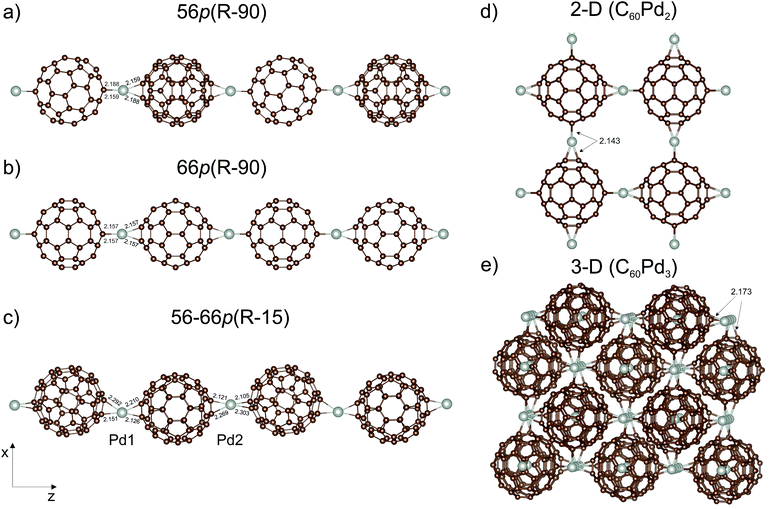
It is very likely that a more stable structure can be obtained by changing the orientation of the C₆₀ moieties with respect to the palladium. Therefore, in the second step, we analysed the gradual change in the Pd coordination geometry from distorted square-planar to distorted tetrahedral. This was done by sequential rotation of one C₆₀ molecule around the Pd⋯Pd axis in a (1 × 1 × 2) supercell containing two C₆₀Pd units, in order to determine the energetic stability. The rotation angle (R) was defined as the dihedral angle between four carbon atoms directly bound to Pd. The procedure involved changing the value of the rotation angle in 15° steps in combination with geometrical optimisation. Here, we also included a mixed polymer type, denoted as 56–66p, with an alternating two [5,6] and two [6,6] palladium–carbon bond motif. Taking into account the symmetry of the individual polymer chains, rotation between 0° and 90° for 66p and 56–66p and between 0° and 180° for 56p were considered. Altogether, 27 nonequivalent configurations were created; their energies are summarised in Table 1. Application of the above procedure to the mixed 56–66p polymer led to nonlinear polymer with two different values of the rotation angle for each C₆₀. Rotation of the C₆₀ molecule in the supercell representing the 66p polymer gives a much lower energy minimum than that of the 56p and mixed 56–66p polymers (Table 1). The calculations yield an optimal dihedral angle (R_opt) of 88.5° and 17.0°/39.6° for the two latter polymers, respectively, where the total energies are only 3.4 and 2.7 kcal mol⁻¹ lower than the initial ones, respectively. Furthermore, we note here that the relative total energies in the whole range of the rotation angle are very close to each other that should lead to an easy rotation of the fullerene molecules around the longitudinal axis. In contrast, the 66p polymer is characterised by the existence of a stable global minimum (R_opt = 88.2°) that is 9.4 kcal mol⁻¹ more favourable than that for R_opt = 0°. Based on Table 1, it can be seen that the system easily reaches the global minimum starting from different initial dihedral angles, while the R_opt of 59.9° and 74.0° correspond to local minima (7.9 and 9.0 kcal mol⁻¹, respectively) which are energetically close to the global minimum. The most stable configurations of the C₆₀Pd polymer, namely, 56p(R − 90), 66p(R − 90), and 56–66p(R − 15), are shown in Fig. 2 with the relevant Pd–C bond lengths. For clarity, we refer to them using the initial value of the rotation angle (R). The 66p(R − 90) polymer is 7.4 and 19.4 kcal mol⁻¹ more stable than the 56–66p(R − 15) and 56p(R − 90) ones (Table 2), respectively. For both the linear 56p(R − 90) and 66p(R − 90) polymers, the preferred coordination of Pd is distorted tetrahedral, whereas for the nonlinear 56–66p(R − 15), it is distorted square-planar. The corresponding Pd–C distances (2.105–2.303 Å) predicted by the DFT calculations for all the systems are presented in Fig. 2.

Table 1 Relative total energies [kcal mol⁻¹] with rotation of one fullerene molecule along the Pd⋯Pd axis for the 1-D C₆₀Pd polymers: 56p, 66p, and 56–66p, calculated within the GGA(PBE) + D2 approach. R and R_opt [in degrees] denote the initial and final value(s) of the rotation angle, respectively

R [°]	56p		66p		56–66p
	Ropt [°]	ΔE [kcal mol^−1]	Ropt [°]	ΔE [kcal mol^−1]	Ropt [°]	ΔE [kcal mol^−1]
0	0	0	0	0	0.3/0.1	0
15	16.0	−3.0	15.8	−0.9	17.0/39.6	−2.7
30	31.7	−3.2	88.2	−9.4	29.4/29.8	−0.2
45	46.6	−3.2	88.2	−9.4	44.2/44.2	−0.2
60	59.9	−2.9	59.9	−7.9	59.2/59.1	0.0
75	74.2	−3.3	74.0	−9.0	74.2/74.3	−0.5
90	88.5	−3.4	88.2	−9.4	88.2/88.4	−0.7
105	103.0	−3.3
120	117.6	−2.8
135	132.4	−2.9
150	148.1	−2.9
165	164.0	−2.9
180	180.0	−1.2

---

Fig. 2 GGA(PBE) + D2-optimised structures of the most stable configurations of the palladium–fullerene polymer: (a) 56p(R − 90), (b) 66p(R − 90), (c) 56–66p(R − 15), (d) 2-D (C₆₀Pd₂), and (e) 3-D (C₆₀Pd₃). The bonds of interest are displayed (in Å).

Table 2 Binding (E_b) and relative total (ΔE) energy [in kcal mol⁻¹] and band gap energy [eV] for the most stable 1-D polymers calculated within the GGA(PBE) + D2 approach (Fig. 2)

	56p(R − 90)	66p(R − 90)	56–66p(R − 15)
ΔE [kcal mol^−1]	19.4	0	7.4
Eb [kcal mol^−1]	−161.2	−180.6	−173.2
Egap [eV]	1.11	1.39	1.13

---

To date, there are no experimental data for the 1-D C₆₀Pd polymer; however, slightly shorter bond lengths (2.087(8)–2.149(8) Å) were reported for a 1-D Ni-bridged fullerene polymer,¹⁹ where Ni is coordinated to the 6–6 position of the fullerene molecule (η²-type bond) as well as to two trimethylphosphine ligands, which form a four-fold coordination environment around the metal centre. However, the Ni⋯Ni distance within the polymer chains was found to be slightly longer (11.230(6) Å at 280 K) than the Pd⋯Pd distances. Recently, 1-D C₆₀Ru polymeric chains were theoretically studied by Leng et al.⁵⁵ using periodic DFT calculations. According to their calculations, the most stable polymer is that with Ru atoms in a η²⁽⁶⁾–η⁶ coordination geometry. However, they did not apply a systematic procedure to find the most stable polymer structure.

3.1.2 Electronic structures. The band structure and DOS for three types of the 1-D polymers are shown in Fig. 3a–c. The left side of each graph shows the band structure, whereas the right side shows the DOS. The partial contributions from Pd states, obtained by projecting the self-consistent DOS onto the corresponding atomic orbitals (projected density of states, PDOS) are also presented. The Fermi energy is set to 0 eV. The calculated highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) gaps for the 56p(R − 90), 56–66p(R − 15), and 66p(R − 90) polymers are 1.11, 1.13, and 1.39 eV, respectively. For comparison, the calculated HOMO–LUMO gap of the isolated C₆₀ molecule is 1.64 eV, in very good agreement with other GGA calculations.^56,57

Fig. 3 Electronic band structure and total (black line) and projected (red/green/blue) DOS for the (a) 56p(R − 90), (b) 66p(R − 90), and (c) 56–66p(R − 15) C₆₀Pd polymers from GGA(PBE) + D2 calculations. The dashed line in (b) corresponds to the DOS for the gas phase fullerene molecule. The Fermi energy is set to 0 eV. Calculated energy band of the optimised (d) 2-D (C₆₀Pd₂) and (e) 3-D (C₆₀Pd₃) polymeric structure.

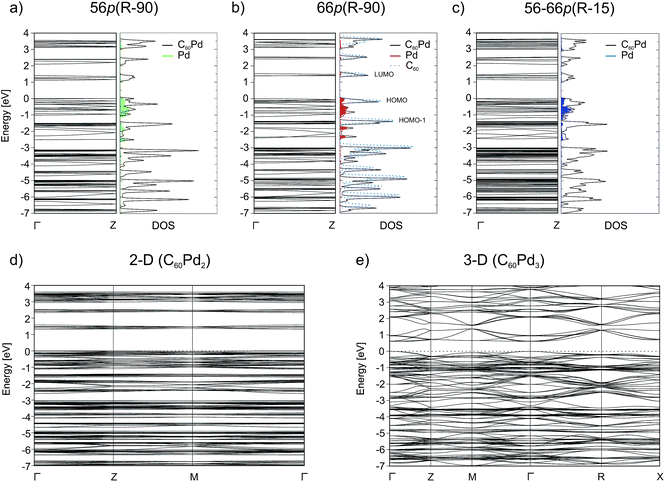
Binding via the [6,6] position increases the band gap by 0.28 eV with respect to that for binding via the [5,6] position. The influence of the Pd coordination environment on the electronic structure is rather small and does not seem to play an important role. All the band structures show many dispersionless bands, which suggest strong localisation of these electronic states. The band dispersion appears mainly between −2.75 and −1.8 eV and originates from the overlap between the Pd 4d and C 2p/2s orbitals (Fig. 3). The conduction band (CB) consists of three separate groups of bands located in the 1–4 eV range. The electronic density isosurface [ρ(r) = 0.001 e Å⁻³] of the LUMO for the most stable 66p(R − 90) polymer is presented in Fig. 4. The charge density distribution is delocalized over the whole fullerene molecules, whereas the contribution from the palladium states is small. Consequently, conduction occurs predominantly by electron hopping through the fullerene networks. The band structure for the mixed 56–66p(R − 15) polymer, which contains Pd in a distorted square-planar coordination, differs somewhat from that of others containing Pd in a distorted tetrahedral coordination. Although the DOSs of all the 1-D polymers show some differences, the general appearance of the individual peaks is very similar. A comparison of the carbon PDOSs of isolated and in-polymer fullerene (Fig. 3b) shows that the interaction with Pd modifies its HOMO and HOMO−1 levels. They become more dispersed owing to hybridisation with the Pd 4d states, which lie in the between −2.75 eV and the Fermi level. The remaining part of the valence band (VB) is rather weakly perturbed and slightly downshifted from fullerene gas phase positions. A closer inspection reveals that for the 66p(R − 90) polymer the top of the VB and the bottom of the CB are much narrower as compared to the others. This could be validated by spectroscopy (e.g. valence photoemission spectroscopy).

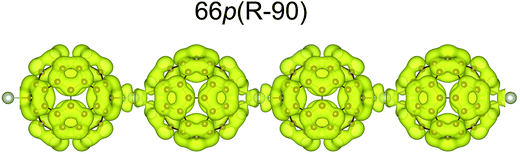Fig. 4 Electronic density isosurfaces [ρ(r) = 0.001 e Å⁻³] of the LUMO state (electron density integrated between 1.3 and 1.6 eV; see Fig. 3b) for the most stable 1-D polymer.

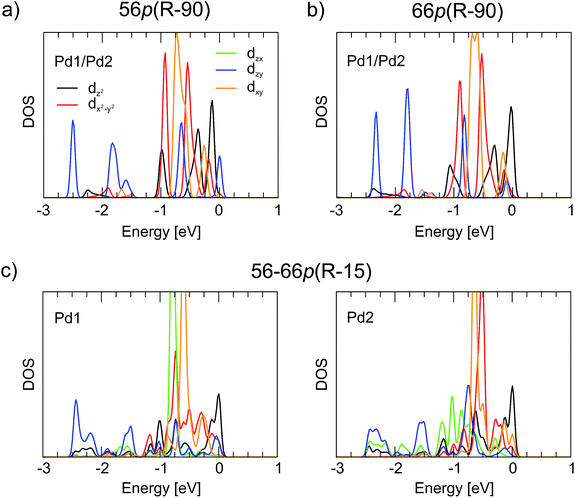
Upon interaction with fullerene, the 4d states of Pd split into individual components. As seen in Fig. 5, the splitting is very similar for the 56p(R − 90) and 66p(R − 90) polymers with Pd in a distorted tetrahedral coordination. In both cases, the lowest-lying d_zx and d_zy states (−2.75 to −1.8 eV, where the d_zx states are covered by the d_zy ones) make a similar contribution to the hybridisation with the C states. The other two low-lying 4d states, namely, d_x²−y² and d_xy, are located predominantly in the −1.0 to −0.5 eV range, whereas d_z² is more densely populated between −0.5 eV and the Fermi level. For the 56–66p(R − 15) polymer with Pd in a distorted square-planar coordination, the splitting of the 4d states is different. The highest intensity of the 4d states falls between −1.0 and −0.5 eV and consists of d_zx and d_xy for Pd1 and of d_x²−y² and d_xy for Pd2 (Fig. 5c). The lowest-energy states are found to be d_zy, whereas the d_z² orbitals are localised close to or at the top of the VBs. Although the changes in the Pd coordination obviously have a strong effect on the PDOS picture of the 4d orbitals, both the CB and the VB of the 1-D polymer are less sensitive towards it.

Fig. 5 Pd 4d electronic densities of states (PDOS) for the 1-D C₆₀Pd polymers (a) 56p(R − 90), (b) 66p(R − 90), and (c) 56–66p(R − 15) from GGA(PBE) + D2 calculations. The Fermi energy is set to 0 eV.

The formation of Pd–C bonds is the results of charge transfer from Pd atoms to the interstitial C atoms of C₆₀. For all three polymers, the obtained Löwdin charges⁵⁸ are almost the same, with an increase of +0.05e in the charge on the C atoms bound to the Pd atoms with respect to a fullerene gas phase. The variation in the Löwdin charges on all the other carbon atoms was negligible (<0.01e). We also estimated a charge transfer of +0.21e to each C₆₀ molecule as the difference in the charge of carbon atoms in the gas phase relative to that in the polymer. This result shows that the charge transfer basically involves only two C atoms directly bound to each Pd atom. Taking into account the limitations of population analysis, this finding may be interpreted as a slight polarization of the Pd atoms, meaning that they provide a small amount of electron density to the fullerenes but remain in the neutral oxidation state.

3.2 2-D and 3-D polymers

3.2.1 Geometry. As we found that linking by the [6,6] position in the 1-D C₆₀Pd polymer is energetically the most favourable, we then investigated the 2-D and 3-D structures. There are no experimental data for the 2-D palladium–fullerene polymer; however, the 3-D C₆₀Pd₃ polymeric structure was reportedly produced under a large excess of the palladium complex.¹⁷ Experimental techniques showed that the 3-D polymer exhibits an ordered bcc structure of fullerene units with a slight rhombohedral distortion.²³ Each palladium atom is bonded to two C₆₀ units, and each fullerene cage is octahedrally coordinated by six palladium atoms. Extended X-ray absorption fine structure studies of the C₆₀Pd_n (n = 1.0–3.2) polymer series indicated that the Pd atoms are located at the centre of the C=C bond between two hexagons of the fullerene cage.⁵⁹

Two structures were chosen to represent the 2-D polymer; the first contains one C₆₀Pd₂ unit formula (62 atoms), and the second contains four C₆₀Pd₂ unit formulas (248 atoms). The second structure, which has a distorted tetrahedral coordination of Pd (Fig. 2d), is energetically more stable by 4.5 kcal mol⁻¹ (per C₆₀Pd₂ unit) than the first one, which has a distorted square-planar coordination. Both supercells are tetragonal with an optimised distance (d) of 11.13 Å (22.26 Å for the large supercell). The introduction of the second dimension clearly reduces the Pd–C₆₀–Pd distance relative to that of the most stable 1-D polymer (11.19 Å).

To create the 3-D polymer, we took two bcc supercells including 2 C₆₀Pd₃ units (126 atoms) and 16 C₆₀Pd₃ units (1008 atoms). The second structure, with a distorted tetrahedral coordination of Pd (Fig. 2e), is 5.6 kcal mol⁻¹ (per C₆₀Pd₃ unit) more stable than the first one. We obtained a lattice constant of 11.21 Å in both cases (22.42 Å for the large supercell), which is slightly smaller (0.8%) than the experimental value of 11.3 Å.²³ The carbon atoms in neighbouring C₆₀ molecules interact via van der Waals forces with calculated minimum distances of about 3.24 Å. For comparison, the shortest experimental C–C distance between two neighbouring C₆₀ molecules in the face-centred cubic (fcc) C₆₀ crystalline structure is about 3.4 Å.⁶⁰ This shows no significant shrinkage of the fullerene sublattice bounded by Pd atoms compared to the fcc fullerene crystal. Note that different van der Waals-corrected DFT methods give slightly different van der Waals distances.⁶¹

3.2.2 Electronic structures. The calculated energy bands of the 2-D and 3-D polymers are shown in Fig. 3d and e. The DOSs for both polymers are not presented, as a picture similar to that for the 1-D 66p(R − 90) polymer emerges. For the 2-D polymer, the band structure (Γ–Z) is very close to that of the 1-D one, with an energy band gap of 1.33 eV (compared to 1.39 eV for the 1-D polymer). Dispersed bands, appearing mainly between −2.75 and −1.75 eV, originate from the overlap between Pd 4d (d_zx and d_zy) and C 2p/2s, and the CB also consists of three separate groups of bands.

For the 3-D polymer, we observe strong reduction of the electronic band gap relative to that of the 2-D structure (from 1.33 to 0.61 eV). The band structure of the 3-D system, which exhibits a larger band dispersion in this case, is also different from that of the 2-D system. Because the 3-D polymer structure is represented by bcc structure, and hence is twice as dense as the simple cubic structure, which has a relatively loose network, one may expect different band structures. The results clearly indicate that the electronic properties change with the dimensionality of the polymer, and this finding should be considered during the construction of electronic devices.

3.3 Polarons and bipolarons

The n-doped C₆₀Pd polymer exhibits electrochemical activity at negative potentials, which is related to reduction of the fullerene molecules.³⁰ This process, which is responsible for the observed conductivity, produces bipolarons that move along the polymer chain in an electrolyte solution.³⁰ For p-doped oligomers, theoretical DFT studies have shown that such bipolaronic states (dications) are usually delocalised over several monomer units (e.g., for polythiophene⁶² and polypyrrole⁶³). Theoretical studies unambiguously showed that the description of polaron–bipolaron equilibrium depends on the polymer length.⁶³ Therefore, to comprehensively study the relative stability of the polaron pair and bipolaron (dianion) for the n-doped C₆₀Pd polymer, we took a long chain of the 1-D 66p(R − 90) polymer including 16 C₆₀Pd units, but at the expense of lower accuracy using the fast semiempirical AM1* technique.^46,47 The calculations were performed with the frozen geometry taken from the DFT(PBE + D2) calculations. For the singlet state, we used spin-restricted and spin-unrestricted wave functions, where the first corresponds to a bipolaron state, and the second corresponds to a polaron pair (with some contribution from the bipolaron state). In addition, a triplet state was also calculated. The singlet case is significantly more stable than the triplet for separate charges. The bipolaron state did not converge, but it appears to be even more unstable than the triplet. Fig. 6 shows the singly occupied molecular orbitals (SOMOs) for the spin-unrestricted (singlet and triplet) wave function. For the singlet state, the SOMOs have coefficients at the third and fourth opposite terminal fullerene molecules, whereas for the triplet, the coefficients include the seven fullerene molecules on both ends of the polymer and are separated by two C₆₀Pd units.

Fig. 6 Spin-unrestricted AM1* wave function for the SOMOs [singlet (S) and triplet (T)] of the 1-D 66p(R − 90) polymer (dianion).

To conclude, it is clear that in the reduced 1-D polymer, isolated polarons are the most stable, and, according to the experimental results, we can only speculate that bipolarons form if the charge carrier density is high.³⁰ However, further studies using introduced counterions and more sophisticated methods are needed to verify the current results.

4 Conclusions

We analysed the structural and electronic properties of different types of palladium–fullerene polymers using a periodic DFT approach. We studied 1-D, 2-D, and 3-D polymer structures. For each system, the optimal lattice constant was found.

Detailed calculations were performed for the 1-D polymer with two types of Pd–C connections via the [5,6] and [6,6] positions, including also a mixed type with an alternating two [5,6] and two [6,6] palladium–carbon bond motif. We found that the most stable polymer type is represented by bonding via the [6,6] position, whereas the least stable is that with bonding via the [5,6] position. For both polymers, the most stable coordination of Pd is distorted tetrahedral, whereas for the mixed polymer, it is distorted square-planar. The tendency of the geometry to change from distorted square-planar to distorted tetrahedral is especially evident for the most stable 1-D polymer. For all three types of 1-D polymer, a comparison of the carbon PDOS of isolated and in-polymer fullerene shows that the interaction with Pd modifies its HOMO and HOMO−1 states. The changes in the Pd coordination strongly affect the PDOS picture of the 4d orbitals, however, both the valence and the conduction band are less sensitive towards it.

The 2-D and 3-D structures were created from the most stable 1-D polymer, where the 3-D system is described by a bcc supercell that shows good agreement with the experimental lattice constant. We found that the band structure depends on the spatial dimensionality of the polymer structure. Those of the 1-D and 2-D systems are very similar, in contrast to that of the 3-D system, where a strong reduction in the band gap is observed. Therefore, we should expect the electronic properties of the 3-D polymer to differ from those of the 1-D and 2-D polymers. Going further in this area, we showed, using the semiempirical AM1* method, that isolated polarons are the preferred electronic states for the reduced polymer. We believe our combined periodic DFT and semiempirical study will further motivate future studies on different metal–fullerene polymers or similar systems.

Acknowledgements

We thank Regionalen Rechenzentrums Erlangen (RRZE) for computational resources.

References

1. C. Wang, Z.-X. Guo, S. Fu, W. Wu and D. Zhu, Prog. Polym. Sci., 2004, 29, 1079–1141.
2. F. Giacalone and N. Martin, Chem. Rev., 2006, 106, 5136–5190.
3. F. Giacalone and N. Martin, Adv. Mater., 2010, 22, 4220–4248.
4. A. L. Balch and K. Winkler, Chem. Rev., 2016, 116, 3812–3882.
5. C. Yeretzian, K. Hansen, F. N. Diedrich and R. Whetten, Nature, 1992, 359, 44–47.
6. Y. B. Zhao, D. M. Poirier, R. J. Pechman and J. H. Weaver, Appl. Phys. Lett., 1994, 64, 577–579.
7. H. Yamawaki, M. Yoshida, Y. Kakudate, S. Usuwa, H. Yokoi, S. Fujiwara, K. Aoki, R. Ruoff, R. Malhorta and D. C. Lorents, J. Phys. Chem., 1993, 97, 11161–11163.
8. P. W. Stephens, G. Bortel, G. Faigel, M. Terze, A. Janossy, S. Pekker, G. Oszlanyi and L. Forro, Nature, 1994, 370, 636–639.
9. A. Hug, P. W. Stephens, G. M. Bedele and R. M. Ibberson, Chem. Phys. Lett., 2001, 347, 13–22.
10. P. L. Nayak, K. Yang, P. K. Dhal, S. Alva, J. Kumar and S. K. Tripathy, Chem. Mater., 1998, 10, 2058–2066.
11. Y. Huang, H. Peng, J. W. Y. Lam, Z. Xu, F. S. M. Leung, Y. W. Mays and B. Z. Tang, Polymer, 2004, 45, 4811–4817.
12. R. Nuffer, Y. Ederle and C. Mathis, Synth. Met., 1999, 103, 2376–2377.
13. Z. Y. Wang, L. Kuang, X. S. Meng and J. P. Cao, Macromolecules, 1998, 31, 5556–5558.
14. F. Audouin, R. Nuffer and C. Mathias, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 3456–3463.
15. X. Zhang, A. B. Sieval, J. C. Hummelen and B. Hessen, Chem. Commun., 2005, 1616–1618.
16. H. L. Anderson, C. Boudon, F. Diederich, J. P. Gisselbrecht, M. Gross and P. Seiler, Angew. Chem., Int. Ed. Engl., 1994, 33, 1628–1632.
17. H. Nagashima, A. Nakaoka, Y. Saito, M. Kato, T. Kawanishi and K. Itoh, J. Chem. Soc., Chem. Commun., 1992, 377–379.
18. H. Nagashima, Y. Kato, H. Yamaguchi, E. Kiura, T. Kawanishi, M. Kato, Y. Saito, M. Haga and K. Itoh, Chem. Lett., 1994, 1207–1210.
19. D. V. Konarev, S. S. Khasanov, Y. Nakano, A. Otsuka, H. Yamochi, G. Saito and R. N. Lyubovskaya, Inorg. Chem., 2014, 53, 11960–11965.
20. A. L. Balch, D. A. Costa and K. Winkler, J. Am. Chem. Soc., 1998, 120, 9614–9620.
21. E. Gradzka, J. Grabowska, M. Wysocka-Zolopa and K. Winkler, J. Solid State Electrochem., 2008, 12, 1267–1278.
22. A. Hayashi, A. de Bettencourt-Dias, A. L. Balch and K. Winkler, J. Mater. Chem., 2002, 12, 2116–2122.
23. J. M. Cowley, M.-Q. Liu, B. L. Ramakrishna, T. S. Peace, A. K. Wertsching and M. R. Pena, Carbon, 1994, 32, 746–748.
24. Y. M. Shulga, A. S. Lobach, I. N. Ivleva and W. N. Spektor, Dokl. Akad. Nauk, 1996, 348, 783.
25. K. Winkler, E. Gradzka, F. D'Souza and A. L. Balch, J. Electrochem. Soc., 2007, 154, K1–K10.
26. E. Gradzka, P. Pieta, P. Dluzewski, W. Kutner and K. Winkler, Electrochim. Acta, 2009, 54, 5621–5628.
27. P. Pieta, E. Gradzka, K. Winkler, M. Warczak, A. Sadowski, G. Z. Żukowska, G. M. Venukadasula, F. D'Souza and W. Kutner, J. Phys. Chem. B, 2009, 113, 6682–6691.
28. E. Gradzka, K. Winkler, M. Borowska, M. E. Plonska-Brzezinska and L. Echegoyen, Electrochim. Acta, 2013, 54, 274–284.
29. E. Brancewicz, E. Gradzka, A. Z. Wilczewska and K. Winkler, ChemElectroChem, 2015, 2, 253–262.
30. E. Grądzka, M. Wysocka-Żołopa and K. Winkler, J. Phys. Chem. A, 2014, 118, 14061–14072.
31. J. Ma, S. H. Li and Y. S. Jiang, Macromolecules, 2002, 35, 1109–1115.
32. P. M. Lahti, J. Obrzut and F. E. Karasz, Macromolecules, 1987, 20, 2023–2026.
33. L. Yang, A. M. Ren, J. K. Feng and J. Wang, J. Org. Chem., 2005, 70, 3009–3020.
34. A. Rehaman, M. Shahi, C. J. Cramer and L. Gagliardi, Phys. Chem. Chem. Phys., 2009, 11, 10964–10972.
35. M. A. D. Oliveira, H. A. Duarte, J. M. Pernaut and W. B. D. Almeida, J. Phys. Chem. A, 2000, 104, 8256–8262.
36. E. G. Gal'pern and I. V. Stankevich, Phys. Solid State, 2010, 52, 439–443.
37. E. G. Gal’pern and I. V. Stankevich, Fullerenes, Nanotubes, Carbon Nanostruct., 2010, 18, 450–454.
38. A. M. E. Mahdy, Mol. Phys., 2015, 113, 3531–3544.
39. F. Nunzi, A. Sgamellotti, N. Re and C. Floriani, Organometallics, 2000, 19, 1628–1634.
40. C.-H. Zhou and X. Zhao, J. Comput. Chem., 2012, 33, 861–867.
41. The PWscf code, http://www.pwscf.org.
42. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
44. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
45. H. Monkhorst and J. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
46. H. Kayi and T. Clark, J. Mol. Model., 2011, 17, 2585–2600.
47. M. J. S. Dewar and D. M. Storch, J. Am. Chem. Soc., 1985, 107, 3902–3909.
48. M. Hennemann and T. Clark, J. Mol. Model., 2014, 20, 2331–2411.
49. J. T. Margraf, M. Hennemann, B. Meyer and T. Clark, J. Mol. Model., 2015, 21, 144–147.
50. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1222–1276.
51. A. Kokalj, Comput. Mater. Sci., 2003, 28, 155–168.
52. H. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
53. M. R. Axet, O. Dechy-Cabaret, J. Durand, M. Gouygou and P. Serp, Coord. Chem. Rev., 2016, 308, 236–345.
54. O. Loboda, Fullerenes, Nanotubes, Carbon Nanostruct., 2009, 17, 457–475.
55. F. Leng, I. C. Gerber, P. Lecante, W. Bacsa, J. Miller, J. R. Gallagher, S. Moldovan, M. Girleanu, M. R. Axet and P. Serp, RSC Adv., 2016, 6, 69135–69148.
56. T. A. Beu, J. Onoe and A. Hida, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 155416–155421.
57. R. E. Estrada-Salas and A. A. Valladares, J. Phys. Chem. A, 2009, 113, 10299–10305.
58. P.-O. Löwdin, J. Chem. Phys., 1953, 21, 374–375.
59. V. A. Chernov, V. N. Ivanova, A. N. Kozhevnikova, G. A. Mardezhova, S. G. Nikitenko and A. A. Nikiforov, Nucl. Instrum. Methods Phys. Res., Sect. A, 1995, 359, 250–253.
60. S. Saito and A. Oshiyama, Phys. Rev. Lett., 1991, 66, 2637–2640.
61. K. Berland, V. R. Cooper, K. Lee, E. Schröder, T. Thonhauser, P. Hyldgaard and B. I. Lundqvist, Rep. Prog. Phys., 2015, 79, 066501.
62. N. Zamoshchik, U. Salzner and M. Bendikov, J. Phys. Chem. C, 2008, 112, 8408–8418.
63. Y. Daia, C. Weia and E. Blaisten-Barojas, Comput. Theor. Chem., 2012, 993, 7–12.

---