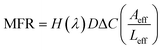Open Access Article
Open Access ArticleReversible gating of ion transport through DNA-functionalized carbon nanotube membranes†
Samaneh Shadmehr,
Michael Coleman,
Biwu Liu ,
Juewen Liu and
Xiaowu (Shirley) Tang*
,
Juewen Liu and
Xiaowu (Shirley) Tang*
Department of Chemistry & Waterloo Institute for Nanotechnology, University of Waterloo, 200 University Ave West, Waterloo, N2L 3G1, Ontario, Canada. E-mail: tangxw@uwaterloo.ca; Fax: +1-519-746-0435; Tel: +1-519-888-4567 ext. 38037
First published on 3rd January 2017
Abstract
Carbon nanotubes (CNTs) can be used to create unique fluidic systems for studying ion transport in nanochannels due to their well-defined geometry, atomically smooth and chemically inert surface, and similarity to transmembrane protein pores. Here, we report the reversible molecular gating of ion transport across DNA-functionalized CNT membranes. The diffusive transport rates of ferricyanide ions through membranes, each with an array of aligned transmembrane CNT channels, were monitored. Single-stranded DNA (T15) gate molecules were covalently linked to CNT channel entrances, and reversible opening and closing of CNT channels were achieved by the addition and removal of complementary DNAs (A15) with a remarkable open/close flux ratio of >1000, which is substantially higher than the protein-gated CNT systems reported previously. Furthermore, at least two-orders of magnitude difference in ion fluxes was observed when single base-pair mismatched DNAs were used in place of the complementary DNAs. Comprehensive theoretical analysis is also presented. The experimental results can be explained by steric hindrance, ion partitioning, and electrostatic repulsion at the CNT entrances, as well as the thermodynamics of DNA binding.
Protein channels are fascinating structures, which can selectively and efficiently transport essential chemicals through cell membranes. The fabrication of synthetic membranes with nanopores that mimic biological transmembrane protein channels have numerous applications, ranging from drug delivery, water purification, and molecular sieving, to DNA sensing.1–4 These membranes possess selective gate chemistry at the pore entrance, a mechanism for fast hydrodynamic flow, and a mechanism to stimulate the channel.5 Several different approaches were developed to create biomimetic membranes. Previous studies have investigated the use of porous alumina or track-etched polycarbonate substrates with well-ordered nanoporous structures and selective chemistry.3,4,6–8 However, these works did not show the capability to create an efficient chemical layer to act as a gatekeeper over the pores and no enhancement to hydrodynamic flow was observed either. Recently, carbon nanotubes (CNTs) have been investigated as biomimetic fluidic channels due to their fast hydrodynamic velocity profiles, highly uniform and tunable pore diameters, and potential gating capabilities.9–14 Early molecular dynamics (MD) simulations predicted strong hydrogen bonding of water in hydrophobic CNTs, resulting in a faster hydrodynamic flow rate than that expected for conventional porous platforms9 and on the same order as water through Aquaporin-1. MD simulations and experiments have shown that the increased hydrodynamic flow velocities through CNTs can be attributed to the atomic smoothness of the graphitic surface displaying near-perfect slip properties.9,11 In other studies, a fast flow rate of molecules was also predicted based on the near frictionless nature of the CNT walls.11,15,16
A key challenge in implementing biomimetic membranes is to achieve highly selective and reversible control of transmembrane ion/molecular transport. Gating membranes have been made using stimuli-responsive hydrogels, which exhibit reversible phase changes in response to temperature, pH, or electric charge.1,17–19 Some disadvantages are associated with applying hydrogels though. For example, hydrogel membranes have low mechanical stability and low molecular diffusivity. In contrast, CNT membranes, which are studied in the present report, are remarkable candidates that can be mechanically strong and allow ion diffusion at near bulk diffusivity. Researchers have fabricated membranes using vertically-aligned CNTs in polymer12,14 or ceramic matrices.20 Furthermore, ionic diffusion, gas and liquid flow through CNT channels have been studied.10,21 However, only a few reports can be found so far, using protein and peptide binding for the gating of ion flux through CNT channels. Nednoor et al. demonstrated that the binding and releasing of streptavidin from the desthiobiotin-functionalized tips of CNTs introduced a 24-fold difference in the flux of methyl viologen ion (MV2+).22 In another study by the same group of researchers, antibody binding to the phosphorylated peptide tethered at the CNT tips enhanced cation flux while reduced anion flux by 4–5 folds. Both electrostatic interaction and steric hindrance played a role in regulating ion flux.23 Compared to proteins, DNA has excellent structural programmability, allowing systematic mechanistic studies. Here, we present a robust CNT membrane using DNA as the gatekeeper molecule to reversibly open and close CNT inner pores for ion transport. The membrane consists of a high density of vertically aligned multiwalled carbon nanotubes (MWNTs) embedded in polydimethylsiloxane (PDMS). The inner pores of the MWNTs serve as transmembrane cylindrical nanochannels. DNA hybridization on the MWNT tips led to a remarkable three-orders of magnitude difference in the open and closed-state ion fluxes. Furthermore, the CNT membranes can be potentially used for DNA sensing capable of detecting single-base mismatch.
The MWNT synthesis and membrane fabrication procedures are shown in Fig. 1. Vertically-aligned MWNTs were grown on a silicon substrate with a 4 nm thick Fe film as the catalyst, as previously reported.24 The growth was done using chemical vapor deposition (CVD) with high purity ethylene as the carbon source, mixed with hydrogen and argon (70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 sccm), in a 25 mm tube furnace (Lindberg) at a growth temperature of 725 °C. Ultra-long and aligned MWNTs were grown in 1 hour, as determined by scanning electron microscopy (SEM) (Fig. 1a). Growth time can be varied to obtain the desired tube length. In this study, the CNTs were ∼500 μm long (ESI, Fig. S1†). In order to fabricate the membranes, MWNTs were embedded in PDMS (Sylgard 184, 1
70 sccm), in a 25 mm tube furnace (Lindberg) at a growth temperature of 725 °C. Ultra-long and aligned MWNTs were grown in 1 hour, as determined by scanning electron microscopy (SEM) (Fig. 1a). Growth time can be varied to obtain the desired tube length. In this study, the CNTs were ∼500 μm long (ESI, Fig. S1†). In order to fabricate the membranes, MWNTs were embedded in PDMS (Sylgard 184, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 catalyst
10 catalyst![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) resin ratio) and cured in a vacuum oven for 1 hour at 70 °C (CNT–PDMS) (Fig. 1b). CNT–PDMS membranes were then submerged in HF for 10 minutes to detach them from the silicon substrate. Following this, the CNT–PDMS membranes were wet etched in a 3
resin ratio) and cured in a vacuum oven for 1 hour at 70 °C (CNT–PDMS) (Fig. 1b). CNT–PDMS membranes were then submerged in HF for 10 minutes to detach them from the silicon substrate. Following this, the CNT–PDMS membranes were wet etched in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution of N-methyl pyrrolidinone (NMP) and tetra-butyl ammonium fluoride (TBAF) in water for 1.5 hours to chemically etch away excess PDMS. Subsequently, membranes were exposed to plasma oxidation for 20 minutes to further remove excess polymer from the surface, open CNT tips (Fig. 1c), and create carboxylic acid groups at the CNT ends.
1 solution of N-methyl pyrrolidinone (NMP) and tetra-butyl ammonium fluoride (TBAF) in water for 1.5 hours to chemically etch away excess PDMS. Subsequently, membranes were exposed to plasma oxidation for 20 minutes to further remove excess polymer from the surface, open CNT tips (Fig. 1c), and create carboxylic acid groups at the CNT ends.
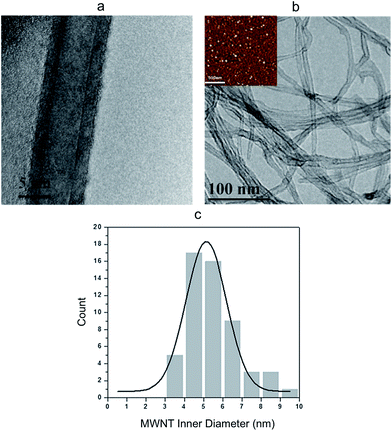
High-resolution transmission electron microscopy (HR-TEM) images show that the MWNTs are geometrically smooth cylindrical tubes with 10–15 wall layers and an inner diameter of about 5 nm (Fig. 2a), which is closely correlated to the size of the iron catalyst particles (Fig. 2b inset). Using TEM images of hundreds of tubes, a histogram of the tube inner diameter size was generated. As shown in Fig. 2c, majority of the CNT channels had a diameter around 5 nm and a narrow size distribution was achieved.
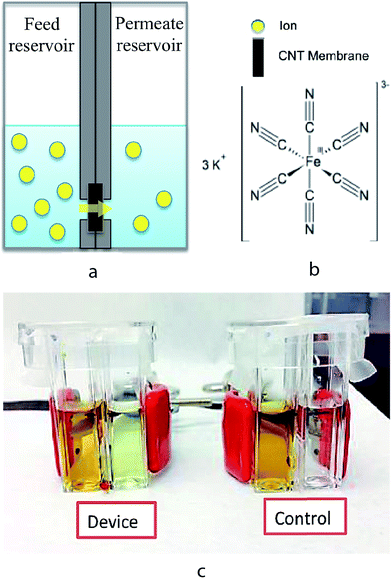
The experimental setup for measuring ion transport through the CNT membranes is shown in Fig. 3. The setup consists of a CNT–PDMS membrane inserted between two additional PDMS O-rings and then sandwiched between two polystyrene (PS) cuvettes, which function as the feed and permeate reservoirs. The PDMS O-rings have a 4 mm inner diameter, which defines the effective membrane area to be 12.56 mm2. Prior to each experiment, both feed and permeate reservoirs were filled with 1 mL of 0.1 M KCl solution to ensure thorough wetting of the membrane. At the start of each transport experiment, the KCl solution in the feed reservoir was replaced by an aqueous solution of 1 M K3[Fe(CN)6] (Sigma-Aldrich) in 0.1 M KCl. In order to prevent any pressure-driven effect, the solution levels were ensured to be the same height on both the feed and permeate sides. At various time points over 48 hours, the [Fe(CN)6]3− concentration in the permeate solution was measured by differential pulse voltammetry (DPV) using a CHI650A potentiostat (CH Instruments). Calibration plots of the [Fe(CN)6]3− concentrations in the range of 1 to 10−7 M were obtained and the detection limit of this technique was determined to be 10−7 M (Fig. S2, ESI†).
The functionalization of CNT membranes was done in the same setup so that ion transport can be measured before and after membrane functionalization sequentially without taking the membrane out. Amino-modified single stand DNA (ssDNA) was used to graft ssDNA onto the CNT tips using carbodiimide chemistry, similar to that used in previous studies to graft small and large molecules onto CNTs.25 The conjugation reaction was carried out by mixing 10 μM amino-modified and Cy3-labelled ssDNA (Cy3-T15-NH2), 10 mM EDC·HCl (freshly prepared), 25 mM NaCl, and 25 mM MES (pH 6.0) in the feed reservoir and left overnight at room temperature. For DNA hybridization, 2 μL of 200 nM complimentary DNA (cDNA, A15) or single-base mismatched DNA (mDNA, AAAAAAACAAAAAAA) was diluted in 1 mL of buffer solution (50 mM NaCl and 50 mM PBS, pH 7.5) in the feed reservoir. After each chemical modification (i.e. ssDNA grafting, DNA hybridization), the feed reservoir, along with the CNT membrane surface, was washed with copious of deionized water to remove free DNA and salt, and replenished with 0.1 M KCl to get ready for the next set of ion transport experiments. Fluorescence images were taken to confirm the grafting of ssDNA (Cy3-labelled) onto the CNT membranes using an inverted epi-fluorescence microscope (Eclipse Ti–S, Nikon) with a CCD camera (Qimaging Retiga 2000R Fast 1394) (Fig. S3, ESI†). Fluorescence spectrum of the permeate solution after the conjugation reaction showed that there was no DNA transport through the CNT membranes (Fig. S4, ESI†).
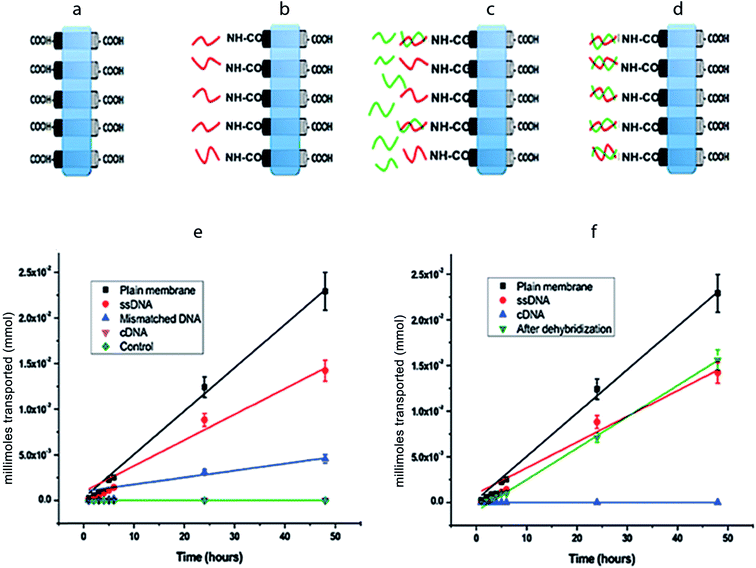
Fig. 4a–d is the schematic representations of CNT membranes, which are plain (as-fabricated), ssDNA grafted, after mDNA hybridization, and after cDNA hybridization. Through measurement of [Fe(CN)6]3− ion concentrations in the permeate reservoir (1 mL), the moles of [Fe(CN)6]3− ions permeated through each CNT membrane over a 48 hour period was calculated and plotted in Fig. 4e and f. The net flow of ions from the feed to the permeate reservoir was driven exclusively by the concentration difference across the membrane, which was 1 M initially and assumed to be constant during all transport experiments. No detectable amount of [Fe(CN)6]3− was found in the permeate reservoir across a control PDMS membrane (without CNT), confirming that our setup had no leakage. The moles of [Fe(CN)6]3− permeated through each CNT membrane showed a linear increase over time, i.e. constant ion flux, indicating that the CNT membranes were stable over the tested period with negligible blockage or deterioration. By applying linear regression to the data points in Fig. 4e and f, molar flux (J) values were obtained for each CNT membrane for quantitative comparison (Table 1).
| CNT membrane type | Molar flux (mmol h−1 m−2) |
|---|---|
| Plain | 37.7 ± 2.1 |
| ssDNA | 22.2 ± 3.0 |
| Dehybridized | 27.3 ± 6.1 |
| Mismatched | 6.01 ± 1.2 |
| cDNA | <3.15 × 10−2 |
For plain CNT membranes (Fig. 4a), an average molar flow rate of 4.74 × 10−4 mmol h−1 was observed over a membrane area of 12.56 mm2, equivalent to a molar flux of 37.7 mmol h−1 m−2. We also calculated the theoretical molar flow rate (MFR) through a plain CNT membrane using the following equation,
After immobilizing ssDNA on CNT tips (Fig. 4b), the experimentally measured molar flux decreased to 22.2 mmol h−1 m−2. Assuming that the ssDNA molecules are flexible brushes with a diameter of 1 nm, the attachment of ssDNAs around the circumference at the CNT tips can reduce the effective diameter of each pore by 1 nm, resulting in a reduced Aeff ∼ 1.1 × 10−3 cm2 and H(λ) = 0.31, and therefore a reduced theoretical molar flux of 17.3 mmol h−1 m2 is obtained. Consistently, the experimentally measured ion flux is in good agreement with, but higher than, the theoretically predicted. Following the same analysis as presented for the plain and ssDNA membranes; the theoretically calculated ion flux is 5.65 mmol h−1 m−2 after cDNA hybridization onto the CNT–ssDNA membranes to form CNT–dsDNA (Fig. 4d). Strikingly though, no detectable amount of [Fe(CN6)]3− permeated through the CNT–dsDNA membrane even after 48 hours, indicating that the formation of dsDNA on CNT tips effectively blocked the CNT channels leading to a molar flux lower than our detection limit of 3.15 × 10−2 mmol h−1 m−2, which is 3 orders lower than that with ssDNA alone. This phenomenon can't be explained by steric hindrance alone. We suspect that the more rigid structure of dsDNA and the bonding angle on the CNT entrance might have facilitated more effective pore blockage. Furthermore, compared to ssDNA, formation of dsDNA doubles the amount of negative charge at the CNT entrances. Considering each dsDNA as a rod with a 2 nm diameter, the dsDNAs formed around the circumference of each CNT tip would reduce the CNT entrance diameter to <3 nm. We suspect that the additional negative charge and reduced entrance diameter introduced by dsDNA formation make electrostatic repulsion more effective compared to CNTs with carboxylic acids or ssDNA on the tips, resulting in complete rejection of [Fe(CN6)]3−.
To rule out the possibility of channel blocking by DNA trapped inside the CNT inner pores, we further tested single-base mismatched DNA (mDNA) as well as dehybridization of dsDNA. Hybridization of mDNA (AAAAAAACAAAAAAA) onto the CNT–ssDNA membrane only partially blocked the membrane with a 3.7 fold reduction in ion flux to 6.01 mmol h−1 m−2. The mDNA contains a single-base mismatch at the 8th base position of the 15 mer DNA. The binding energies for ssDNA–cDNA and ssDNA–mDNA are 39.2 kJ mol−1 and 27.4 kJ mol−1 respectively. Consequently, the binding equilibrium constants Keq at room temperature are 7.4 × 106 M−1 for ssDNA–cDNA and 6.3 × 104 M−1 for ssDNA–mDNA. Thus, according to Langmuir isotherm, the percentage hybridization on the ssDNA–cDNA membrane is more than 100 times of that on the ssDNA–mDNA surface. In another word, with mDNA, the percentage of blocked CNT channels due to DNA hybridization is very small, and well explains the more than 2 orders of magnitude difference in ion fluxes through cDNA vs. mDNA hybridized membranes. Finally, it is worth noting that after treating the CNT–dsDNA membrane (with no detectable ion flux) for 2 hours in 60 °C deionized water, the molar flux across the membrane fully recovered to that of CNT–ssDNA (Fig. 4f), indicating no loss to ion permeation upon cDNA removal. Therefore, we conclude that the closure of CNT channels is due to DNA hybridization at the entrances, instead of randomly trapped DNAs inside the channels. Furthermore, we demonstrated reversible gating of ion transport through CNT channels with a remarkable 3 orders of magnitude difference between the open- and closed-state ion fluxes, significantly higher than those protein-gated systems reported previously.22,23
In summary, the transport of [Fe(CN)6]3− across ssDNA-functionalized carbon nanotube membranes was studied. DNA hybridization and de-hybridization at the entrances of CNTs are shown to fully close and open the CNT channels reversibly for ion permeation. The experimentally measured ion fluxes through plain CNT (as fabricated) and ssDNA grafted membranes are in excellent agreement with those predicted theoretically, taking into account the effects of steric hindrance and partitioning at the CNT entrances. But electrostatic repulsion might have played an important role in fully blocking the CNT channels after cDNA hybridization. The 2 orders of magnitude difference in ion fluxes after cDNA and mDNA hybridization on the CNT–ssDNA membranes can be explained by the Langmuir isotherm, taking into account the lower binding energy of ssDNA–mDNA compared to that of ssDNA–cDNA. This study has demonstrated the ability to gate ion transport through CNT channels, which can potentially lead to novel biomimetic systems for controlled drug release and DNA sensing capable of detecting single-base mismatch in the future.
Acknowledgements
This research is financially supported by a Discovery grant from the Natural Sciences and Engineering Research Council of Canada (NSERC).References
- M. Sugawara, K. Kojima, H. Sazawa and Y. Umezawa, Anal. Chem., 1987, 59(24), 2842–2846 CrossRef CAS PubMed.
- S. P. Adiga, C. Jin, L. A. Curtiss, N. A. Monteiro-Riviere and R. J. Narayan, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2009, 1(5), 568–581 CrossRef CAS PubMed.
- E. D. Steinle, D. T. Mitchell, M. Wirtz, S. B. Lee, V. Y. Young and C. R. Martin, Anal. Chem., 2002, 74(10), 2416–2422 CrossRef CAS PubMed.
- S. B. Lee, D. T. Mitchell, L. Trofin, T. K. Nevanen, H. Söderlund and C. R. Martin, Science, 2002, 296(5576), 2198–2200 CrossRef CAS PubMed.
- K. Murata, K. Mitsuoka, T. Hirai, T. Walz, P. Agre, J. B. Heymann, a. Engel and Y. Fujiyoshi, Nature, 2000, 407(6804), 599–605 CrossRef CAS PubMed.
- K. B. Jirage, J. C. Hulteen and C. R. Martin, Science, 1997, 278(5338), 655–658 CrossRef CAS.
- S. W. Kowalcyzk, T. R. Blosser and C. Dekker, Trends Biotechnol., 2011, 29(12), 607–614 CrossRef PubMed.
- Q. Liu, L. Wen, K. Xiao, H. Lu, Z. Zhang, G. Xie, X. Y. Kong, Z. Bo and L. Jiang, Adv. Mater., 2016, 28(16), 3181–3186 CrossRef CAS PubMed.
- G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414(6860), 188–190 CrossRef CAS PubMed.
- W. Choi, Z. W. Ulissi, S. F. E. Shimizu, M. D. E. Bellisario and M. S. Strano, Nat. Commun., 2013, 4, 2397 Search PubMed.
- W. P. Sokhan, D. Nicholson and N. Quirke, J. Chem. Phys., 2002, 117(18), 8531–8539 CrossRef.
- B. J. Hinds, N. Chopra, T. Rantell, R. Andrews, V. Gavalas and L. G. Bachas, Science, 2004, 303(5654), 62–65 CrossRef CAS PubMed.
- J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Science, 2006, 312(5776), 1034–1037 CrossRef CAS PubMed.
- P. Krishnakumar, P. B. Tiwari, S. Staples, T. Luo, Y. Darici, J. He and S. M. Lindsay, Nanotechnology, 2012, 23(45), 455101 CrossRef CAS PubMed.
- M. Majumder, N. Chopra and B. J. Hinds, J. Am. Chem. Soc., 2005, 127(25), 9062–9070 CrossRef CAS PubMed.
- T. Ohba, H. Kanoh and K. Kaneko, Nano Lett., 2005, 5(2), 227–230 CrossRef CAS PubMed.
- A. S. Hoffman, P. S. Stayton, V. Bulmus, G. Chen, J. Chen, C. Cheung, A. Chilkoti, Z. Ding, L. Dong and R. Fong, et al., J. Biomed. Mater. Res., 2000, 52(4), 577–586 CrossRef CAS PubMed.
- Y. Ito, M. Inaba, D. Chung and Y. Imanishi, Macromolecules, 1992, 25(26), 7313–7316 CrossRef CAS.
- X. Lin, R. Huang and M. Ulbricht, J. Mater. Chem. B, 2016, 4(5), 867–879 RSC.
- D. T. Tran, G. Thieffry, M. Jacob, C. Batiot-Dupeyrat and B. Teychene, Water Sci. Technol., 2015, 72(8), 1404–1410 CrossRef CAS PubMed.
- M. Majumder, N. Chopra and B. J. Hinds, ACS Nano, 2011, 5(5), 3867–3877 CrossRef CAS PubMed.
- P. Nednoor, N. Chopra, V. Gavalas, L. G. Bachas and B. J. Hinds, Chem. Mater., 2005, 17(14), 3595–3599 CrossRef CAS.
- P. Nednoor, V. G. Gavalas, N. Chopra, B. J. Hinds and L. G. Bachas, J. Mater. Chem., 2007, 17(18), 1755–1757 RSC.
- M. Mazloumi, S. Shadmehr, Y. Rangom, L. F. Nazar and X. S. Tang, ACS Nano, 2013, 7(5), 4281–4288 CrossRef CAS PubMed.
- C. V. Nguyen, L. Delzeit, A. M. Cassell, J. Li, J. Han and M. Meyyappan, Nano Lett., 2002, 2(10), 1079–1081 CrossRef CAS.
- F. Fornasiero, H. G. Park, J. K. Holt, M. Stadermann, C. P. Grigoropoulos, A. Noy and O. Bakajin, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(45), 17250–17255 CrossRef CAS PubMed.
- P. Dechadilok and W. M. Deen, Ind. Eng. Chem. Res., 2006, 45(21), 6953–6959 CrossRef CAS.
- V. Silva, P. Prádanos, L. Palacio and A. Hernández, Desalination, 2009, 245(1–3), 606–613 CrossRef CAS.
- P. M. Bungay and H. Brenner, Int. J. Multiphase Flow, 1973, 1(1), 25–26 CrossRef.
- M. Coleman and X. S. Tang, Nano Res., 2015, 8(4), 1128–1138 CrossRef CAS.
- K. Sears, L. Dumée, J. Schütz, M. She, C. Huynh, S. Hawkins, M. Duke and S. Gray, Materials, 2010, 3(1), 127–149 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra24827f |
| This journal is © The Royal Society of Chemistry 2017 |