Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Propulsion of copper microswimmers in folded fluid channels by bipolar electrochemistry†
Jin-Zhi Jiang,
Mei-Hong Guo,
Fen-Zeng Yao,
Ju Li and
Jian-Jun Sun *
*
Ministry of Education Key Laboratory of Analysis and Determination for Food Safety, Fujian Provincial Key Laboratory of Analysis and Detection for Food Safety, College of Chemistry and Chemical Engineering, Fuzhou University, Fuzhou, 350108, China. E-mail: jjsun@fzu.edu.cn; Fax: +86 591 22866135
First published on 19th January 2017
Abstract
We report for the first time that conducting objects could be propelled in folded liquid filled channels by bipolar electrochemistry. This approach was based on controlling the formation of hydrogen bubbles at one extremity of a bipolar electrode. In this work, copper wires used as microswimmers could move in folded channels with angles from 30° to 180° by bubble propulsion and the velocity fluctuated over time. A proportional relation between polarization voltage and average velocity in linear channel was verified. The motion of microswimmers could be controlled within these types of channels in space and time, which might broaden the applications of micromachines in bipolar electrochemistry.
Introduction
The fabrication and characterization of artificial autonomous micro/nanomachines that can move in a controlled direction and perform various tasks at a small scale have attracted a great deal of attention in the last two decades.1–9 Various applications about these self-propelled micro/nanodevices have been reported, such as objects transporting,10–13 isolation,14–18 detection,19–22 environmental remediation23–27 or immunoassay.28,29 Various driving mechanisms including bubble propulsion,30 self-electrophoresis,31,32 interfacial tension induced motion,33 and diffusiophoresis34 have been explored. Due to the efficient propulsion in the fluids and high ionic strength-media, bubble propulsion mechanism was particular the most attractive. However hydrogen peroxide is primary fuel for bubble formation, which block the application of these micro/nanomachines in somewhere.4,35 Thus fuel-free propulsion manners such as light,36,37 temperature,38,39 magnetic field,40–43 ultrasound44–46 and electric filed47–51 also attracted great interest.One of the present application challenges of self-propelled micro/nanomotors is the way to control the motion of motors in time and space. In this context, Schmidt and co-workers have reported that Ti/Fe/Pt rolled up microtubes could move in the microchannels and transport of multiple spherical microparticles into desired locations by an external magnetic field.5 Also Schmidt and the other workers trapped self-propelled micromotors in microfluidic chips containing chevron and hearted-shaped structures. Kuhn et al. have proposed bipolar electrochemistry (BPEC) as a novel mechanism to control the motion of swimmers by dynamic bipolar self-regeneration52 or bubble propulsion47 in fluid chips. In the first case, a Zn BPE filament produced in a capillary was propelled by Zn filament electrochemically dissolved at the anodic and redeposited at the cathodic pole. In the second case, a glassy carbon bead moved due to the formation of H2 and O2 bubbles arising from water oxidation and hydrogen evolution. Using bipolar electrochemistry, all of conducting objects placed in a fluid channel with a strong enough electric field, redox reaction could take place in the two sides of conductors. One can take advantage of the intrinsic asymmetric reactivity to drive conductors in a controlled way. Kuhn and co-workers have designed a lot of devices to get this approach. Such as, microfluidic chips, horizontal and vertical rotors,47 U-tubes.53 The conducting objects can walk along or turn around the channels by switching external electric field, thus an interesting Yo–Yo motion53 and a wireless electrochemical valve54 were proposed.
Previous studies have shown that some conducting objects could move straight in linear channels by BPEC.47,52 Here we demonstrate a new design for triggering copper wires motion in different folded channels with angles of 30°, 60°, 90°, 120°, 150° and 180°. Due to the lower oxidation voltage than water, copper wire was used as micromachine, which was allowed to reduce the external electric field. In the recent publications, Kuhn and co-workers also accomplished this by adding a lower oxidation voltage sacrificial chemical compound (for instance hydroquinone).47,53 In comparison, self-oxidation copper wire can eliminate the interference of added reagent in the electrochemical analysis. After recording the movement of copper wires in different channels, a proportional relation between polarization voltage and average velocity in linear channel was verified, also a meaningful velocity fluctuation related to bubble formation was found. The dramatic motion of copper wires in the multiple channels with different angles illustrated that the motion of the micromotors can be controlled in space and time by changing the angles of channels or the external electric field optionally.
Materials and methods
All the solutions were prepared using ultrapure water (over 18.2 MΩ cm), platinum wires (Ø = 0.5 mm) used as electrodes were purchased from Sinopharm Chemical Reagent Co., ltd. Copper wires (Ø = 50 μm) pre-processed by concentrated sulfuric acid were used as micromotors. The cells of folded channels were made by splicing of general glass slides (see Fig. S1†). A mirror polished glass slide (dimension: 10 cm × 8 cm × 0.5 cm) was used as basement. Microscope slides (dimension: 25.4 mm × 76 mm × 1 mm) were cut and polished in regular styles with different angles (from 30° to 180°) and then attached to basement to form different folded and opened channels. The width of fluid channels were designed as 1 mm. The electric field was applied using a DC high-voltage power (Dongwen High-voltage Power Company, DW-SA502-50ACF1). The movies were recorded using a stereo microscope equipped with a digital camera (COIC, ZSA302). TSview 7.1.0.0 software and Avidemux 2.5 software were used for calculating the speed of copper wires.A few drops of water were carefully added to the folded and opened channels to prevent air bubble formation, and then copper microwires was put into the channel. Due to the water's surface tension, copper wires could float on the water. Pt electrodes were inserted into the both side of the channels. If the external electric field was strong enough, copper wires could be propelled by bubbles formed in the extremity of bipolar electrode. To observe the movement of copper wires in different folded channels, the motion videos were often recorded around the corner.
Results and discussion
As the recent reports indicated, when an electronic conductor was placed in a fluid filled channel with an appropriate external electric field, faradaic reactions could take place at both ends of the conductor, which was called a bipolar electrode (BPE).52 The main difference between conventional electrode and BPE is that there is no direct electrical connection between the external electric field and the BPE. The maximum polarization voltage (ΔE) between BPE is related to the length of conductor (d) and the external electric field (E). The relation of them can be summarized as following equation:| ΔE = Ed | (1) |
On the basis of this concept, bipolar electrochemistry has been used for materials preparation and fabrication,55 sensing,56 screening,57 microswimmers.58 Based upon the splitting of water, Kuhn and co-workers have designed and fabricated a lot of bipolar micromotors and channels.47
| 4H+ + 4e− → 2H2 (g), E1 = 0 V versus NHE | (2) |
| 2H2O → O2 (g) + 4H+ + 4e−, E2 = 1.23 V versus NHE | (3) |
A minimum value of ΔE = E2 − E1 = 1.23 V we calculated across the conductor is necessary to drive the splitting of water. To keep the electroneutrality condition of bipolar electrode, the production of electron in cathode and the consumption of electron in anode must be equal, so the volume of hydrogen is twice of the oxygen. As a result, asymmetric bubble propulsion could drive the conductor in a directional motion. The formation of O2 at anodic side offset the driving force derived from the formation of H2 at cathode side. Kuhn and co-workers have approved that bubble-induced motion could be thermodynamically facilitated by adding a sacrificial chemical compound (such as hydroquinone).48,53,54 The oxidation potential of hydroquinone (0.70 V versus NHE) is lower than water, which could eliminate the effect of O2 produced at the anode side and reduced the external applied voltage.
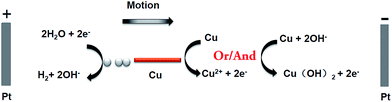
In this work, copper wires were used as swimmers, they were easier to be oxidized into Cu2+ ions than water to oxygen, and they had the advantage that no bubble evolution was associated with the oxidation reaction. The principle of this bubble-induced motion was illustrated in Fig. 1. The reactions happening at the anode and cathode of copper wires were as follows:
| Cu2+ + 2OH− → Cu(OH)2 (s), E3 = −0.22 V versus NHE | (4) |
| 2H2O + 2e− → H2 (g) + 2OH−, E4 = −0.82 V versus NHE | (5) |
Using this redox couple, a value of ΔE = E3 − E4 = 0.60 V across the distance d was enough to drive the redox reaction between copper wires. In order to find the minimum external voltage needed in experiments, a longer and thicker copper wire (d = 2.3 mm, Ø = 0.2 mm) was chosen as example, for the reason that it can sink in the bottom and easy to be observed. After applying 1.2 kV m−1 external electric field on the opened 180° channel (with a length of 12.07 cm between the two electrode positions) for 2 minutes, the bubble formation took place in the cathodic side. The potential difference ΔE across the distance d was 2.65 V, which was higher than the standard voltage 0.60 V. It was mainly due to the polarization of bipolar electrode and resistance of solution.
Bipolar electrochemistry relied on the polarization of conducting particles, a maximum polarization voltage between the two extremities of conducting particle was proportional to the applied electric field and the size of particles, just as shown in eqn (1). In this experiment, polarization voltage across the copper wire directly affected the formation of hydrogen bubbles. According to Faraday's law of electrolysis, stating that the number of moles of substance produced at an electrode during electrolysis is directly proportional to the number moles electrons transferred at that electrode. Since two electrons were involved in the cathode reaction, eqn (5), where one hydrogen molecule reacts, the molar amount of hydrogen (n) can be calculated as
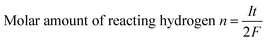 | (6) |
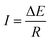 | (7) |
| n = ks | (8) |
| s = vt | (9) |
According to eqn (6)–(9), we can write the following relation:
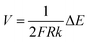 | (10) |
As a result, the velocity of conducting was in proportion to its polarization voltage. In order to find effect of applied voltage on the motion of copper microwires in experiments, series of external electric field were applied on a channel with angle of 180°. As seen in Fig. 2 and Table S1,† the relation between average velocity (v) and polarization voltage (ΔE) or the applied electric field (E) can be fit by v = 0.26ΔE − 1.00 = 1.55 × 10−3E − 1.00 (R2 = 0.9978). The proportionality relation between displacement (s) of microswimmer and amount of reacting hydrogen (n) was conformed to the eqn (10) we mentioned above. The offset factor of plot (−1.00) was mainly due to that a threshold polarization voltage was necessary to drive the redox reaction between the copper bipolar electrode and to overcome the resistance of fluid. By using this linear equation, one can calculate that the value of constant (k) between displacement (s) of microswimmer and amount of reacting hydrogen (n) was 3.16 × 10−3 mol C−1 Ω−1. This constant can be used for establishing a bond of electrochemistry and kinematics in this experiment.
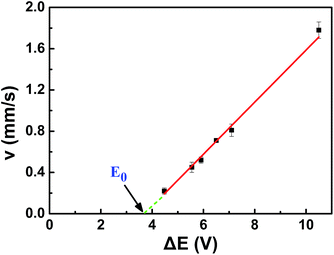 | ||
| Fig. 2 Curvilinear illustration of proportional relation between average speed (v) and polarization voltage (ΔE) of 720 μm copper wire in 180° fluid channel (l = 12.07 cm). | ||
As shown in Fig. 2, the point “E0” in the graph was the intersection between reversed extended line of v–ΔE plot and ΔE-axis. One can calculate that the minimum propelled polarization voltage (v = 0 mm s−1) was 3.84 V, and the corresponding minimum applied external voltage was 644 V. Unlike the minimum polarization voltage of redox reaction 2.65 V, the drag force of fluid to motion must be involved in propelled polarization voltage. Compared with other bipolar micromotors, copper bipolar microswimmers was a consumptive bubble induced motors. The electro-dissolution of copper reduced the polarization voltage pass through the bipolar electrode, leading the lower produced rate of hydrogen. As a result, copper microswimmer would stop eventually. According to eqn (1) and the minimum propelled polarization, one can calculate the minimum length corresponded to the external electric field, which meant that the speed of motor was zero. For example, if the external applied voltage was 1090 V, the length of copper wire must be larger than the minimum length of 425 μm. The allowed length difference of copper wire was 295 μm. The lifetime of micromotors related to the initial length of copper wire and the intensity of external applied voltage. For the purpose of estimating the life time of motors, a consistent external voltage 1090 V was applied on the linear channel, after five repeated tests, the length difference of copper wire was 144 μm, total time was about 90 s. As a result, with an applied voltage 1090 V, an initial length 720 μm, the lifetime of copper microswimmer was about 184 s, the average electro-dissolution rate of copper was almost 4.5 × 10−9 mol s−1.
Fig. 3 and Video S5† showed the motion of 800 μm copper wire in a 150° folded channel. The asymmetric bubble propulsion can be clearly observed at the cathode side of copper wire. The applied voltage was 10.58 kV m−1. By using eqn (1) one can calculate that this corresponded to a polarization voltage ΔE of 8.46 V between the two sides of the copper microswimmer. Calculating from Video S5,† the average velocity of copper microswimmer was 0.56 mm s−1, or 1 body length every 1.4 s. Videos S1–S4, S6 and Fig. S1–S5† showed the motion of copper wire in the other folded channel.
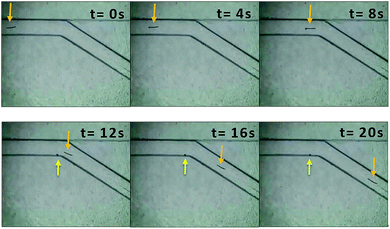 | ||
| Fig. 3 Images of the copper wire (l = 800 μm, Ø = 50 μm) propelled by releasing of bubbles in the folded channel with angle of 150°. The arrows represent the location of copper microswimmer and bubble. See also the Video S5† in the ESI. | ||
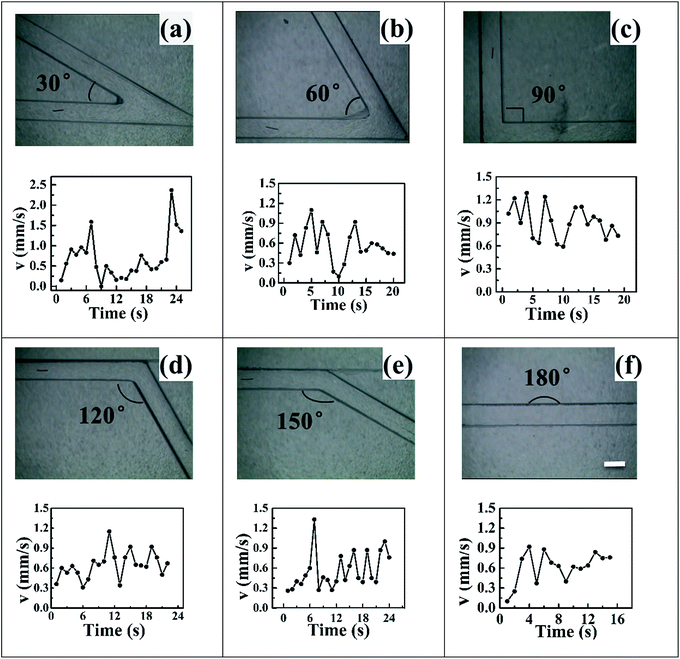
Table 1 illustrated the relevant parameters of folded channels and the velocities corresponded to applied voltages. The length of channels and copper wires, the polarization voltage were all not consistent in different channels, which meant that there were nothing comparable within these channels. However, it's worth mentioning that for angle of 60° folded channel, the polarization voltage 2.41 V was far more smaller than the other channels and also the nearest to standard potential 0.60 V, which indicated that 60° folded channel could be much more efficient than the others. Traditional bipolar micromotors were propelled in the linear or U-tube liquid filled channels in a linear way. Comparing to the previous studies, Videos S1–S6† showed that conducting objects could also be propelled in folded channels with different angles. All of the copper wires can easily turn around the corner. Suggesting that one could use this technique to control motion of micromotors by changing the angles of channels or applied voltages. One might also use these channels to deliver some useful objects in some complicated and non-linear channels.
| l/cm | d/mm | E/kV m−1 | ΔE/V | v/mm s−1 | |
|---|---|---|---|---|---|
| a Plus: l was the length of channel, d was length of copper wire, E was the external applied voltage, ΔE was the polarization voltage, v was the average velocity of copper microswimmers. | |||||
| 30° | 11.26 | 0.73 | 9.95 | 7.26 | 0.69 |
| 60° | 12.15 | 0.77 | 3.13 | 2.41 | 0.56 |
| 90° | 12.42 | 0.69 | 7.81 | 5.39 | 0.77 |
| 120° | 8.20 | 0.82 | 9.39 | 7.70 | 0.64 |
| 150° | 7.37 | 0.80 | 10.58 | 8.46 | 0.56 |
| 180° | 12.07 | 0.72 | 7.87 | 5.66 | 0.45 |
Fig. 4 illustrates the velocity–time curves of copper microswimmers in different channels, the speed of copper micromotors varied over time and fluctuated obviously. This fluctuated phenomenon can be regarded as a spraying water sepia or a launching rocket, all of them can get a big driver and acceleration instantly. In our case hydrogen formation took place constantly in the cathode side of copper wire, while bubble formation required the accumulation of hydrogen and the bubble gradually got bigger until releasing in the water. During this period, copper wire sit still until the moment bubble releasing. Blocking by the surface tension of water, the unreleased bubbles could hinder motion and a negative acceleration reduced the speed of motors. Repeatedly, a fluctuation of velocity was formed. Even if the motion was in principle regular and reproducible, some irregularities can also be observed, this was related to the size and releasing time of bubbles. The fluid viscosity had an influence on the radius of bubbles. One might use this phenomenon to learn the bubble behaviour of micromotors and the effect of solvent fluid on bubble formation.
Conclusions
In this work, we demonstrated the possibility of propelling copper microswimmers in different channels with angles from 30° to 180° by bipolar electrochemistry. This approach was based on the formation of hydrogen bubble in the cathode side of copper bipolar electrode. In the linear channel with angle of 180°, average velocity of copper wire was proportion to its polarization voltage, the constant as an experience points between molar amounts of hydrogen reacting and displacement was calculated. Due to the polarization of electrode and resistance of solution, the minimum polarization voltage was larger than the standard potential. Due to the drag force of fluid, the minimum propelled polarization voltage was larger than the minimum polarization voltage.We finally illustrated the velocity perturbation phenomenon of bubble-induced motors. One might imagine using this to learn the size and releasing time of bubbles, and study the effect of solvents on bubble behaviours. Except for controlling the motion time and position of motors by turning on/off the external electric field, the other advantages of our devices was that one can use our folded channels to control the motion direction of motors by transforming the angle of channels or making a group of them, and transport goods which can be loaded on or fastened to conducting objects in complicated non-linear routes.
Acknowledgements
This work is financially supported from the National Science Foundation of China (No. 21275030 and 21475023), and Program for Changjiang Scholars and Innovative Research Team in University (No. IRT_15R11).Notes and references
- W. Gao, S. Sattayasamitsathit, J. Orozco and J. Wang, J. Am. Chem. Soc., 2011, 133, 11862–11864 CrossRef CAS PubMed.
- S. Fournier-Bidoz, A. C. Arsenault, I. Manners and G. A. Ozin, Chem. Commun., 2005, 441–443 RSC.
- J. M. Catchmark, S. Subramanian and A. Sen, Small, 2005, 1, 202–206 CrossRef CAS PubMed.
- W. Gao, A. Uygun and J. Wang, J. Am. Chem. Soc., 2012, 134, 897–900 CrossRef CAS PubMed.
- S. Sanchez, A. A. Solovev, S. M. Harazim and O. G. Schmidt, J. Am. Chem. Soc., 2011, 133, 701–703 CrossRef CAS PubMed.
- K. M. Manesh, M. Cardona, R. Yuan, M. Clark, D. Kagan, S. Balasubramanian and J. Wang, ACS Nano, 2010, 4, 1799–1804 CrossRef CAS PubMed.
- Y. P. He, J. S. Wu and Y. P. Zhao, Nano Lett., 2007, 7, 1369–1375 CrossRef CAS PubMed.
- B. Dong, T. Zhou, H. Zhang and C. Y. Li, ACS Nano, 2013, 7, 5192–5198 CrossRef CAS PubMed.
- N. Mano and A. Heller, J. Am. Chem. Soc., 2005, 127, 11574–11575 CrossRef CAS PubMed.
- D. Kagan, R. Laocharoensuk, M. Zimmerman, C. Clawson, S. Balasubramanian, D. Kang, D. Bishop, S. Sattayasamitsathit, L. Zhang and J. Wang, Small, 2010, 6, 2741–2747 CrossRef CAS PubMed.
- S. Sundararajan, P. E. Lammert, A. W. Zudans, V. H. Crespi and A. Sen, Nano Lett., 2008, 8, 1271–1276 CrossRef CAS PubMed.
- J. Orozco, A. Cortes, G. Cheng, S. Sattayasamitsathit, W. Gao, X. Feng, Y. Shen and J. Wang, J. Am. Chem. Soc., 2013, 135, 5336–5339 CrossRef CAS PubMed.
- Z. Wu, Y. Wu, W. He, X. Lin, J. Sun and Q. He, Angew. Chem., Int. Ed., 2013, 52, 1–5 CrossRef.
- S. Campuzano, J. Orozco, D. Kagan, M. Guix, W. Gao, S. Sattayasamitsathit, J. C. Claussen, A. Merkoci and J. Wang, Nano Lett., 2012, 12, 396–401 CrossRef CAS PubMed.
- J. Orozco, S. Campuzano, D. Kagan, M. Zhou, W. Gao and J. Wang, Anal. Chem., 2011, 83, 7962–7969 CrossRef CAS PubMed.
- D. Kagan, S. Campuzano, S. Balasubramanian, F. Kuralay, G. U. Flechsig and J. Wang, Nano Lett., 2011, 11, 2083–2087 CrossRef CAS PubMed.
- S. Balasubramanian, D. Kagan, C. J. Hu, S. Campuzano, M. J. Lobo-Castanon, N. Lim, D. Y. Kang, M. Zimmerman, L. F. Zhang and J. Wang, Angew. Chem., Int. Ed., 2011, 50, 4161–4164 CrossRef CAS PubMed.
- F. Kuralay, S. Sattayasamitsathit, W. Gao, A. Uygun, A. Katzenberg and J. Wang, J. Am. Chem. Soc., 2012, 134, 15217–15220 CrossRef CAS PubMed.
- C. C. Mayorga-Martinez, M. Guix, R. E. Madrid and A. Merkoci, Chem. Commun., 2012, 48, 1686–1688 RSC.
- D. Kagan, P. Calvo-Marzal, S. Balasubramanian, S. Sattayasamitsathit, K. M. Manesh, G. Flechsig and J. Wang, J. Am. Chem. Soc., 2009, 131, 12082–12083 CrossRef CAS PubMed.
- J. Orozco, V. García-Gradilla, M. D'Agostino, W. Gao, A. Cortés and J. Wang, ACS Nano, 2013, 7, 818–824 CrossRef CAS PubMed.
- J. G. S. Moo, H. Wang, G. J. Zhao and M. Pumera, Chem.–Eur. J., 2014, 20, 4292–4296 CrossRef CAS PubMed.
- M. Guix, J. Orozco, M. García, W. Gao, S. Sattayasamitsathit, A. Merkoc, A. Escarpa and J. Wang, ACS Nano, 2012, 6, 4445–4451 CrossRef CAS PubMed.
- L. Soler, V. Magdanz, V. M. Fomin, S. Sanchez and O. G. Schmidt, ACS Nano, 2013, 7, 9611–9620 CrossRef CAS PubMed.
- J. Orozco, G. Cheng, D. Vilela, S. Sattayasamitsathit, R. Vazquez-Duhalt, G. Valdes-Ramirez, O. S. Pak, A. Escarpa, C. Kan and J. Wang, Angew. Chem., Int. Ed., 2013, 52, 13276–13279 CrossRef CAS PubMed.
- V. V. Singh, A. Martin, K. Kaufmann, S. D. S. de Oliveira and J. Wang, Chem. Mater., 2015, 27, 8162–8169 CrossRef CAS.
- S. K. Srivastava, M. Guix and O. G. Schmidt, Nano Lett., 2016, 16, 817–821 CrossRef CAS PubMed.
- X. Yu, Y. Li, J. Wu and H. Ju, Anal. Chem., 2014, 86, 4501–4507 CrossRef CAS PubMed.
- D. Vilela, J. Orozco, G. Cheng, S. Sattayasamitsathit, M. Galarnyk, C. Kan, J. Wang and A. Escarpa, Lab Chip, 2014, 14, 3505–3509 RSC.
- R. F. Ismagilov, A. Schwartz, N. Bowden and G. M. Whitesides, Angew. Chem., Int. Ed., 2002, 41, 652–654 CrossRef CAS.
- R. Liu and A. Sen, J. Am. Chem. Soc., 2011, 133, 20064–20067 CrossRef CAS PubMed.
- W. F. Paxton, P. T. Baker, T. R. Kline, Y. Wang, T. E. Mallouk and A. Sen, J. Am. Chem. Soc., 2006, 128, 14881–14888 CrossRef CAS PubMed.
- W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. S. Angelo, Y. Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Cres, J. Am. Chem. Soc., 2004, 126, 13424–13431 CrossRef CAS PubMed.
- L. K. E. A. Abdelmohsen, F. Peng, Y. Tu and D. A. Wilson, J. Mater. Chem. B, 2014, 2, 2395–2408 RSC.
- W. Gao, X. Feng, A. Pei, Y. Gu, J. Li and J. Wang, Nanoscale, 2013, 5, 4696–4700 RSC.
- Z. G. Wu, X. K. Lin, Y. J. Wu, T. Y. Si, J. M. Sun and Q. He, ACS Nano, 2014, 8, 6097–6105 CrossRef CAS PubMed.
- R. Dong, Q. Zhang, W. Gao, A. Pei and B. Ren, ACS Nano, 2016, 10, 839–844 CrossRef CAS PubMed.
- S. Balasubramanian, D. Kagan, K. M. Manesh, P. Calvo-Marzal, G. U. Flechsig and J. Wang, Small, 2009, 5, 1569–1574 CrossRef CAS PubMed.
- V. Magdanz, G. Stoychev, L. Ionov, S. Sanchez and O. G. Schmidt, Angew. Chem., Int. Ed., 2014, 53, 2673–2677 CrossRef CAS PubMed.
- W. Gao, S. Sattayasamitsathit, K. M. Manesh, D. Weihs and J. Wang, J. Am. Chem. Soc., 2010, 132, 14403–14405 CrossRef CAS PubMed.
- G. Zhao and M. Pumera, Langmuir, 2013, 29, 7411–7415 CrossRef CAS PubMed.
- S. Ahmed, W. Wang, L. O. Mair, R. D. Fraleigh, S. Li, L. A. Castro, M. Hoyos, T. J. Huang and T. E. Mallouk, Langmuir, 2013, 29, 16113–16118 CrossRef CAS PubMed.
- R. Cheng, W. J. Huang, L. J. Huang, B. Yang, L. J. Mao, K. L. Jin, Q. C. ZhuGe and Y. P. Zhao, ACS Nano, 2014, 8, 7746–7754 CrossRef CAS PubMed.
- W. Wang, L. A. Castro, M. Hoyos and T. E. Mallouk, ACS Nano, 2013, 6, 6122–6132 CrossRef PubMed.
- V. Garcia-Gradilla, S. Sattayasamitsathit, F. Soto, F. Kuralay, C. Yardimci, D. Wiitala, M. Galarnyk and J. Wang, Small, 2014, 10, 4154–4159 CAS.
- J. Li, T. Li, T. Xu, M. Kiristi, W. Liu, Z. Wu and J. Wang, Nano Lett., 2015, 15, 4814–4821 CrossRef CAS PubMed.
- G. Loget and A. Kuhn, Nat. Commun., 2011, 2, 535 CrossRef PubMed.
- M. Sentic, G. Loget, D. Manojlovic, A. Kuhn and N. Sojic, Angew. Chem., Int. Ed., 2012, 51, 11284–11288 CrossRef CAS PubMed.
- G. Loget, D. Zigah, L. Bouffier, N. Sojic and A. Kuhn, Acc. Chem. Res., 2013, 46, 2513–2523 CrossRef CAS PubMed.
- G. Loget, G. Larcade, V. Lapeyre, P. Garrigue, C. Warakulwit, J. Limtrakul, M. H. Delville, V. Ravaine and A. Kuhn, Electrochim. Acta, 2010, 55, 8116–8120 CrossRef CAS.
- Z. Fattah, G. Loget, V. Lapeyre, P. Garrigue, C. Warakulwit, J. Limtrakul, L. Bouffier and A. Kuhn, Electrochim. Acta, 2011, 56, 10562–10566 CrossRef CAS.
- G. Loget and A. Kuhn, J. Am. Chem. Soc., 2010, 132, 15918–15919 CrossRef CAS PubMed.
- G. Loget and A. Kuhn, Lab Chip, 2012, 12, 1967–1971 RSC.
- L. Bouffier and A. Kuhn, Nanoscale, 2013, 5, 1305–1309 RSC.
- S. W. Kong, O. Fontaine, J. Roche, L. Bouffier and A. Kuhn, Langmuir, 2014, 30, 2973–2976 CrossRef CAS PubMed.
- M. S. Wu, D. J. Yuan, J. J. Xu and H. Y. Chen, Anal. Chem., 2013, 85, 11960–11965 CrossRef CAS PubMed.
- S. E. Fosdick and R. M. Crooks, J. Am. Chem. Soc., 2012, 134, 863–866 CrossRef CAS PubMed.
- J. Wang and K. M. Manesh, Small, 2010, 6, 338–345 CrossRef CAS PubMed.
- G. Loget and A. Kuhn, Electrochemistry, 2013, 11, 71–103 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting videos (S1–S6). See DOI: 10.1039/c6ra25162e |
| This journal is © The Royal Society of Chemistry 2017 |