Influence of electronic structure on visible light photocatalytic activity of nitrogen-doped TiO₂

Abstract

Nitrogen (N)-doped TiO₂ thin films were synthesized by sol–gel methods from precursor solutions with or without urea and post calcination in NH₃ gas. Their structural and electronic properties were characterized by X-ray diffraction and X-ray photoelectron spectroscopy utilizing synchrotron radiation. N-doped TiO₂ powders were synthesized for the estimation of visible light photocatalytic activities. N-doped TiO₂ thin films revealed polycrystalline anatase phases. N was chiefly doped into substitutional sites. The densities of N and defects (oxygen vacancies and reduced Ti species) increased with elevating calcination temperature. Localized states associated with doped N were successfully found from shoulder structures of valence band spectra, which were located at 0.24 eV to 0.34 eV above the valence band maximum in the band gap. Incorporated N enhanced the photocatalytic activity, whereas defects reduced it. The highest photocatalytic activity was obtained by synthesizing N-doped TiO₂ powders from a precursor solution with urea and subsequent calcination at 550 °C due to high-density N and low-density defects. Consequently, the optimum N/O atomic ratio was shown to be approximately 0.06. It became possible to achieve heavier N doping and better photocatalytic activity under vis light irradiation using urea than any other study only using NH₃ gas for nitridation.

---

1. Introduction

Semiconductor photocatalysis is one of the most effective methods for chemical utilization of solar energies. Of all photocatalytic materials, TiO₂ is the most promising because of its photoactivity, nontoxicity to environments and low cost of fabrication.^1–3 However, the optical response of TiO₂ is limited to ultraviolet (UV) light because of its wide band gap (3.0 eV for rutile and 3.2 eV for anatase). For more efficient use of solar energies in photocatalytic reactions, it is necessary to extend the optical response of TiO₂ to the visible (vis) light region.⁴ Thus, the fabrication of nitrogen (N)-doped TiO₂ with vis light activity has been considered as a promising approach because the N2p derived states are generated just above the valence band (VB) in the band gap.^5,6

N atoms are known to be incorporated into interstitial and/or substitutional sites (replacement of O) in TiO₂ lattices. The interstitial nitrogen (N_i) and substitutional nitrogen (N_s) are supposed to have different influences on the electronic states as well as vis light activities. Some authors have reported that N_s contributes the generation of N-derived states and facilitates vis light photocatalysis,^3,5,7–9 whereas others have claimed that photoactive nitrogen is not N_s but just N_i.^10–13 Very recently, DFT (density functional theory) calculation has shown that N prefers to replace Ti (Ti-vacancy-site: N_Ti) rather than O to form NO_x.¹⁴ Furthermore, oxygen vacancies (V_O) near surface regions act as recombination centers and depress photocatalytic activities. In general, photocatalytic activities under vis light have been discussed using UV-vis optical absorption experiments. However, defect states originated from oxygen vacancies and reduced Ti species (Ti³⁺, Ti²⁺) in the band gap as well as N-derived states were shown to contribute to light absorption characteristics of N–TiO₂ in vis light region, which makes the situations more complicated. In reality, defect states due to V_O located at 2.02 to 2.45 eV above VBM were chiefly responsible for absorption of vis light with wavelength shorter than 614 nm.¹⁵ Therefore, in spite of intensive theoretical and experimental studies on N–TiO₂, primary issues such as the origin of vis light photocatalytic activities and the effect of chemical and electronic states of constituent elements (Ti, O, N) and defects on photocatalytic activities are still under debate. One of the most suitable techniques for direct observation of occupied N-derived states is X-ray photoelectron spectroscopy (XPS) since N-derived states are easily distinguished from defect states in terms of binding energy (E_bin) of photoelectrons. Nevertheless, few works have been carried out so far to observe N-derived states in the band gap using XPS with excellent S/N (signal to noise) ratio.

In the present study, N–TiO₂ thin films were synthesized on Si(100) using the combination of sol–gel method and nitridation in NH₃ gas. This combination is one of the most widely-used and reproducible methods to synthesize N–TiO₂ photocatalysts.^10,12,13 The crystalline structures were investigated by X-ray diffraction (XRD) and electronic structures were examined by XPS utilizing synchrotron radiation. Synchrotron radiation is best suited as a X-ray source for XPS measurements on N–TiO₂ with high S/N ratios owing to its high intensity. Photocatalytic activities of N–TiO₂ powders prepared by sol–gel methods using urea ((NH₂)₂CO) as a N source were shown to be higher than those using NH₃ solution.¹⁶ Therefore, N–TiO₂ powders were synthesized by nitridation in NH₃ gas with or without urea for estimation of photocatalytic activities under vis light irradiation. Then, N species active for vis light, energy levels of N-derived states in the band gap, the optimum density of N and the influence of defects on photocatalytic activities are discussed based on XRD and XPS results.

2. Experimental

N–TiO₂ thin films were synthesized on Si(100) substrates by two kinds of sol–gel methods for characterization of N–TiO₂.

In method A, precursor solutions were prepared from a mixture of titanium tetra-n-butoxide monomer and 2-methoxyethanol. The solution was deposited on Si(100) surfaces using a syringe and the samples were rotated at 3000 rpm for 50 seconds using a spin-coater, followed by post gelation at 150 °C for 60 seconds. The samples were subsequently calcined in NH₃ gas for 3 hours at 450 °C, 500 °C, 550 °C or 600 °C for N doping or in the air to produce pure TiO₂ films for a comparison. The N–TiO₂ thin films were called A-450, A-500, A-550 and A-600, respectively.

In method B, urea powders were added to sol–gel precursor solutions with controlling nitrogen dosage at 3, 6, 20 or 40 at% by changing the amount of urea powders and calcination temperature in NH₃ flow at 450 °C, 500 °C or 550 °C. Urea is known as a reductant of NO_x from combustors such as diesel engines and boilers. It has an ability to produce V_O in TiO₂ lattices and simultaneously act as a N source. The subsequent processes were similar to method A. The synthesized films with dosage of x at% N followed by calcination in NH₃ flow at 450 °C, 500 °C and 550 °C are called Bx-450, Bx-500 and Bx-550, respectively.

XRD patterns of the films were analyzed by X-ray diffraction with Cu Kα radiation (NEW D8 ADVANCE, Bruker AXS). The XPS measurements were performed utilizing synchrotron radiation at Beam Line (BL)-3B and -13A of Photon Factory (PF) in high energy accelerator research organization (KEK). The measurements were carried out at room temperature in ultrahigh vacuum chamber with base pressure of 2.0 × 10⁻⁸ Pa at both BLs. The samples were fixed on a Ta holder. Prior to XPS measurements, in situ treatment to remove surface contaminations included mild Ar⁺ sputtering (2 kV, 1.0 μA) and annealing at 900 °C in vacuum. At BL-3B, a hemispherical electron energy analyzer (HA45, VSW) was used to acquire the spectra with the typical overall energy resolution of 200 meV at the photon energy of 60 eV. For the core-level XPS measurements at BL-13A, a Gamma Date/Scienta SES200 electron-energy analyser was used. The typical overall energy resolution of the spectra was 170 meV at the photon energy of 600 eV. The binding energy of XPS spectra was referenced to Fermi level, which was determined from Fermi cutoff in the spectra of Ta sample holder. N/O atomic ratios of films were deduced from XPS N1s and O1s peaks.³²

Photocatalytic activities of N–TiO₂ were evaluated by degradation of methylene blue (MB) under vis light (1.5 × 10⁴ lx) from a 180 W metal halide lamp. Although the change in the total organic carbon concentration (TOC), the chemical oxygen demand (COD), or the biochemical oxygen demand (BOD) in the dye solution by light irradiation should be measured for overall evaluation of photocatalytic activities,¹⁸ this simple method using MB has also been recognized as a standard one in case of TiO₂ photocatalysts.¹⁹ In the experiments of photocatalytic degradation of MB, N–TiO₂ powders were utilized in place of N–TiO₂ thin films because N–TiO₂ thin films had too small surface areas to degrade MB substantially during irradiation time. Hence, N–TiO₂ powders were synthesized by two kinds of procedures for estimation of photocatalytic activities under vis light irradiation. In the first procedure, pure anatase TiO₂ powders were nitrided in NH₃ gas flow for 3 hours at 450 °C, 500 °C, 550 °C or 600 °C, respectively, analogous to method A. In an alternative procedure analogous to method B, urea powders with different ratios of 3, 6, 10, 20, or 40 at% N were added prior to nitridation in NH₃ gas at the temperatures similar to the first procedure. A fixed amount of N–TiO₂ powders (0.06 g) were added into 100 ml of MB aqueous solution (10 μmol l⁻¹). However, since there is a possibility of direct photolytic degradation of MB by irradiation of vis light with wavelength λ around 665 nm (peak maximum in absorption spectra), a low-pass optical filter with cutoff wavelength of 500 nm was inserted between lamp and solution. In addition, another high-pass optical filter with cutoff wavelength of 420 nm was used for elimination of UV light. Accordingly, direct photolytic degradation of MB under vis light irradiation was found to be negligible in comparison with photocatalytic degradation.

3. Results and discussion

3.1 X-ray diffraction patterns

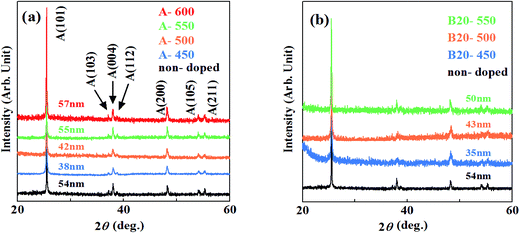
XRD patterns of the samples grown by method A are shown in Fig. 1(a). Several Bragg reflections of anatase phase are identified, demonstrating that the polycrystalline anatase was obtained by method A. The crystallinity of the films deduced from full width at the half maximum (FWHM) of anatase (101) peak improved with the increase in the calcination temperature. The crystal size D of each film is also indicated in Fig. 1. It was calculated from Scherrer's equation

D = 0.94λ/β cos θ

where D is the crystal size, λ is the wavelength of X-ray radiation, β is FWHM of anatase (101) peak, and θ is the diffraction angle.²⁰

Fig. 1 XRD patterns of the samples grown by (a) method A and (b) B.

As shown in Fig. 1(b), XRD patterns of the films synthesized by method B also revealed the polycrystalline anatase phase. The crystal sizes were almost similar, indicating that incorporation of N hardly degrades the crystallinity of the films grown at these temperatures.

3.2 Core-level XPS spectra

Fig. 2 shows the N1s, Ti2p core-level XPS spectra for the samples synthesized by method A. In Fig. 2(a), there appear no peaks in N1s spectra for the samples grown below 500 °C, while peaks appear at around E_bin = 397 eV with a small peak at around E_bin = 400 eV (A-600) for the samples grown above 550 °C. For more quantitative understanding of chemical states of N, each N1s spectrum was decomposed into components by least-square fitting using Gaussian functions.²¹ In the fitting procedures, linear functions were assumed for background of spectra. Though two Gaussian functions were used for first fitting, it resulted in failure to reproduce the background-subtracted spectra. Hence, another Gaussian function was added to them. Consequently, all N1s spectra were successfully decomposed into three Gaussian components (α₁, α₂ and α₃) with E_bin ≈ 397 eV, 398 eV and 400 eV, respectively. One example of them is shown in Fig. 2(b) for A-600. Thus, N species in different chemical environments coexist. N1s spectra for N–TiO₂ have been reported by many authors. Asahi et al. has reported that two peaks at E_bin = 402 and 400 eV are due to molecularly chemisorbed N₂ (γ-N₂), while a peak observed at E_bin = 396 eV is originated from substitutional N (N_s).⁵ 403 eV peak was ascribed to Ti–N–O bonds by Wang et al.²² Okato et al. rather assigned the peak at E_bin = 400 eV to Ti–O–N linkage.³ O–Ti–N linkage was responsible for the signal at E_bin = 399.2 eV,²³ 398.2 eV ²⁴ and 401.3 eV.²⁵ N1s peaks at around E_bin = 400–401.5 eV were supposed to be contribution of nitrogen compounds such as NO_x.²⁶ Zhang et al. insisted that photoactive centers observed at E_bin = 399.8 eV are complex [O²⁻–Ti⁴⁺–N³⁻–Ti⁴⁺–V_O⁻] clusters.¹² On the other hand, Feng et al. revealed that the photoactive 400 eV peaks are due to interstitial NO molecules bound to V_O (V_O–NO).²⁷ It was demonstrated that the peaks of N_i appear at E_bin > 399 eV ²⁸ and the peak at E_bin = 396–397 eV is attributed to N_s,²⁹ respectively. Thus, according to the literature, N atoms are chiefly doped into N_s sites at temperatures higher than 550 °C by method A. The peak position of α₁ is near the binding energy of N1s in TiN (E_bin = 397.2 eV).²⁹ Therefore, α₁ is assigned to ‘nitride peak’, where N ions are in substitutional sites (N_s).^5,28,29 α₃ may be ascribed to NO_x (or Ti–O–N, Ti–N–O), where positively charged N is located at interstitial site (N_i) or Ti-vacancy site (N_Ti).¹⁴ On the other hand, α₂ peak with the binding energy higher than α₁ can be assigned to N ions with less negative charge than −2. Thus, it is likely that O–Ti–N bonds are responsible for α₂ because negative charge density on N is expected to be reduced from −2 due to higher electronegativity of O than N. The possibility of NH_x adsorbed on the surface should be ruled out because N species still remain after surface treatments (Ar⁺ sputtering and annealing). N/O atomic ratios deduced from N1s and O1s peaks were estimated to be 0.008 and 0.086 for A-550 and A-600, respectively. Table 1 lists the binding energies and ratios of α₁, α₂, α₃ peaks and N/O atomic ratios.

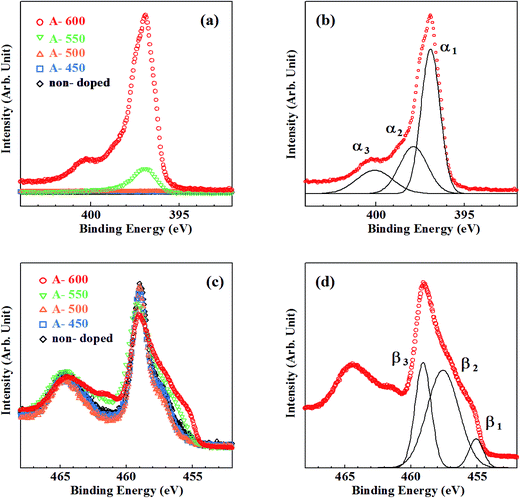Fig. 2 Core-level XPS spectra for the samples synthesized by method A. (a) N1s spectra, (b) decomposition of N1s spectrum for A-600, (c) Ti2p spectra, (d) decomposition of Ti2p spectrum for A-600.

Table 1 The binding energies and ratios of α₁, α₂, α₃, β₁, β₂ and β₃ peaks and N/O atomic ratios for N–TiO₂ and non-doped samples. “N.D.” means “no detection”

	Non-doped	A-450	A-500	A-550	A-600	B3-450	B3-500	B3-550	B6-550	B20-550	B40-550
α1 energy	N.D.	N.D.	N.D.	396.7	396.9	397.1	397.0	396.8	396.9	396.9	396.9
Ratio	N.D.	N.D.	N.D.	0.817	0.630	1.00	0.755	0.575	0.570	0.552	0.594
α2 energy	N.D.	N.D.	N.D.	397.9	397.9	N.D.	398.0	397.7	397.8	397.9	397.9
Ratio	N.D.	N.D.	N.D.	0.183	0.239	N.D.	0.245	0.297	0.313	0.321	0.305
α3 energy	N.D.	N.D.	N.D.	N.D.	400.1	N.D.	N.D.	399.9	400.0	400.3	400
Ratio	N.D.	N.D.	N.D.	N.D.	0.131	N.D.	N.D.	0.133	0.117	0.127	0.101
N/O atomic ratio	N.D.	N.D.	N.D.	0.008	0.086	0.002	0.008	0.054	0.057	0.064	0.065
β1 energy	455.6	N.D.	N.D.	455.2	455.5	N.D.	455.3	455.1	455.3	455.8	455.4
Ratio	0.023	N.D.	N.D.	0.069	0.080	N.D.	0.063	0.044	0.046	0.092	0.101
β2 energy	457.4	457.4	457.5	457.5	457.6	457.4	457.2	457.4	457.2	457.7	457.5
Ratio	0.296	0.310	0.300	0.376	0.596	0.284	0.341	0.348	0.369	0.380	0.394
β3 energy	459.0	459.0	459.0	459.0	459.1	458.9	458.9	458.8	458.9	459.4	459.0
Ratio	0.681	0.690	0.700	0.555	0.324	0.716	0.596	0.608	0.585	0.528	0.505

---

The density of N_s (in proportion to α₁ and α₂ peaks) is by far larger than that of N_i (in proportion to α₃ peak) at 550 °C and 600 °C. This feature is in sharp contrast with the results of previous studies using N sources other than NH₃ in sol–gel methods, where N_i peaks are dominant.^22,28,30 Incorporation of N into N_i sites induces compressive stress in TiO₂ lattices. Heavy N_i doping leads to the structural phase transformations into rutile phase. Hence, maximum density of N_i remains small (<1.5 at%).³ In contrast, N_s doping with the density higher than 1.5 at% is possible due to smaller lattice distortion.²⁹ However, because the binding energy of Ti–N is smaller than that of Ti–O, substitution of O by N hardly occurs spontaneously in TiO₂. Reduction of TiO₂ (i.e., production of V_O) is needed for incorporation of N into N_s sites. NH₃ is known to be decomposed at temperatures higher than 550 °C.³¹ Atomic H produced by decomposition of NH₃ removes O from TiO₂ lattice (i.e., produce V_O) and promotes incorporation of N into V_O sites. However, because decomposition occurs at temperatures higher than 550 °C, the onset temperature of reduction of TiO₂ and subsequent N incorporation using NH₃ is 550 °C.

Fig. 2(c) shows Ti2p XPS spectra for the samples synthesized by method A. Three contributions (β₁, β₂ and β₃) were obtained by decomposition of Ti2p_3/2 peaks. One example for A-600 is shown in Fig. 2(d). A lot of researchers observed Ti2p XPS spectra in TiO₂, TiN and TiON, and four kinds of peaks with different Ti chemical states were found.^12,17,27,32 Peaks associated with Ti⁴⁺ (in TiO₂), Ti³⁺ (in reduced TiO₂ or N–TiO₂) and Ti²⁺ (in TiN) were shown to appear at E_bin = 458.6–459.5 eV, 456.7–457.8 eV and 454.8–456.0 eV, respectively.^33–35 An ‘additional peak’ with positive charge between +3 and +4 originated from Ti in distorted lattices of TiO₂ and TiN was shown to be observed at E_bin = 457.7–458.7 eV. Consequently, β₁, β₂ and β₃ can be assigned to Ti²⁺, Ti³⁺ and Ti⁴⁺ respectively.

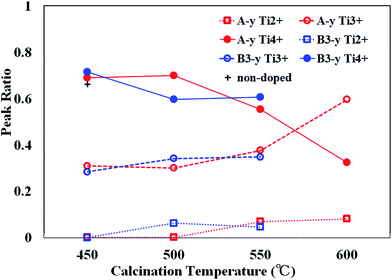
In Fig. 3, the ratios of β₁, β₂ and β₃ peaks as a function of calcination temperature are plotted by open circles. Small traces of β₂ peaks were recognized for the samples calcined below 500 °C (∼0.3). The ratios of β₃ (∼0.7) are almost equivalent to that for non-doped samples (indicated by a cross) and thus, the existence of β₂ peaks was not caused by N doping, but rather due to surface treatment of samples (i.e., Ar⁺ sputtering and sequential annealing). However, β₃ peak steeply decreases and β₁, β₂ peaks grow at elevated calcination temperatures. This is in line with the rapid evolution of N1s peaks above 550 °C.

Fig. 3 The peak ratios of Ti²⁺(β₁), Ti³⁺(β₂) and Ti⁴⁺(β₃) for the samples synthesized by method A (A-y, red) and B (B3-y: blue) as a function of calcination temperature (y). The ratio of Ti⁴⁺(β₃) for non-doped sample is indicated by a cross.

As already mentioned, TiO₂ must be reduced (i.e., V_O is needed to be produced) prior to incorporation of N into N_s. Reduction of TiO₂ is evidenced by the appearances of reduced Ti species (Ti³⁺ and Ti²⁺). Therefore, the reduction of TiO₂ takes place at 550 °C. This onset temperature is consistent with the decomposition temperature of NH₃ and therefore, the reduction and subsequent N incorporation are indeed caused by atomic H generated by decomposition of NH₃.³⁶ The present results are supported by theoretical prediction showing that the introduction of V_O stabilizes the formation of N_s.^37–39

Fig. 4 shows the XPS spectra of the samples prepared by method B, where the amount of urea dopant was fixed at 3 at%. N1s XPS spectra are shown in Fig. 4(a). Peaks at E_bin ∼ 397 eV were seen in Fig. 4(a) for all samples, while a very small peak was observed at E_bin ∼ 400 eV only for the sample calcined at 550 °C. Decomposition of observed N1s spectra in a manner similar to Fig. 2(b) gives rise to α₁, α₂ and α₃ peaks, again (Fig. 4(b)). In Table 1, detailed data on N1s states are listed. Only a small amount of N was incorporated in B3-450. Substantial N doping took place at 500 °C. The N peak grew further at 550 °C. Therefore, the onset temperature of N doping is at least 50 °C lower by using urea. N/O ratio for B3-550 is by far larger than that for A-550, whereas smaller than that for A-600. N/O ratios are evaluated to be 0.002, 0.008 and 0.054 for B3-450, B3-500 and B3-550, respectively.

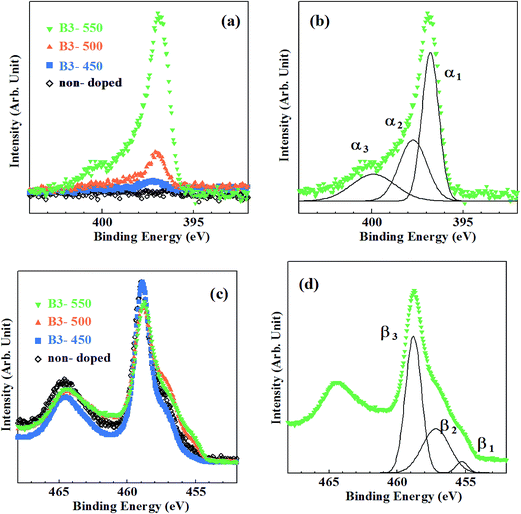Fig. 4 Core-level XPS spectra for the samples synthesized by method B. (a) N1s spectra, (b) decomposition of N1s spectrum for B3-550, (c) Ti2p spectra, (d) decomposition of Ti2p spectrum for B3-550.

Ti2p XPS spectra are shown in Fig. 4(c). They were also composed of three fundamental peaks (β₁, β₂ and β₃) associated with Ti²⁺, Ti³⁺ and Ti⁴⁺ (Fig. 4(d)). The changes in the ratio of β₁, β₂ and β₃ with the rise in calcination temperature are revealed by blue symbols and lines in Fig. 3.

N density is closely related to the development of β₁, β₂ peaks and the declination of β₃ peak. As shown in Fig. 3, β₃ peak ratio of B3-450 is almost equivalent to those of A-450, A-500 and non-doped sample, indicating that reduction of TiO₂ hardly occurred in B3-450. However, β₃ peak ratio distinctly decreased and β₁, β₂ peak ratios increased at 500 °C. These phenomena correspond to the onset of substantial N doping at 500 °C for the samples synthesized by method B. It can be ascribed to urea. Urea was shown to be decomposed into NH₃ and biuret.⁴⁰ The reductant source of urea is isolated NH₃. However, the role of urea in the present study is apparently different from that of NH₃ in that the former act as a N reagent even at 500 °C. Urea may be dissociated not into NH₃ but directly into N and H at 500 °C although the evidence is absent.

We have also changed the amount of urea to investigate the influence on the electronic properties. All films were synthesized at 550 °C. As can be seen in Fig. S1(a),† the intensity of N1s peak slightly increased with increasing the amount of urea. N/O atomic ratios were estimated to be 0.054, 0.057, 0.064 and 0.065 for B3-550, B6-550, B20-550 and B40-550, respectively. Fig. S1(b)† shows Ti2p XPS spectra for these samples. Ratios of β₁, β₂ and β₃ peaks are given in Table 1. Although the reduction of TiO₂ was slightly enhanced with the increase in urea dosage, the extent of reduction did not strongly depend on the amount of urea. Therefore, the reduction activity of urea at 550 °C is almost saturated at 3%.

3.3 Extended structures of VB edge

The VB XPS spectra measured using synchrotron radiation are shown in Fig. 5(a) and (b) for samples synthesized by method A and B together with non-doped samples, respectively. There have been carried out several studies on VB spectra of N–TiO₂ measured using XPS.^{10,32,41–43} However, most of them used X-ray tubes as a X-ray source and spectra with low quality made it difficult to discuss minutely the features of band gap states and the changes in VB structures induced by N doping. Synchrotron radiation is suitable as a X-ray source for measurement of VB spectra with high S/N ratios owing to its high intensity.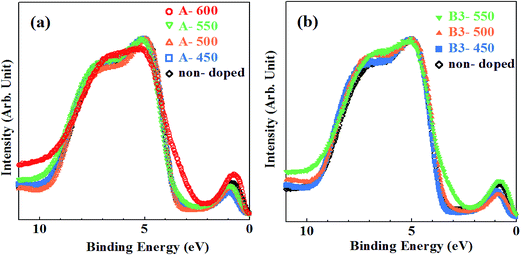

Fig. 5 The VB XPS spectra for samples synthesized by (a) method A with non-doped sample and (b) method B (urea: 3%) with non-doped sample.

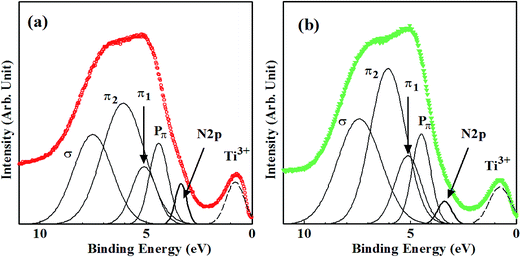
The VB edges for A-450, A-500 and B3-450 coincide with that for non-doped sample, while those for A-550, A-600, B3-500 and Bx-550 (where x = 3, 6, 20, 40) are extended into band gap with smaller binding energies. In particular, remarkable shoulder structures were recognized for A-600 and B3-550. Separate peaks at E_bin ≈ 0.8 eV are associated with Ti³⁺ species.^39,43

The VB structures of non-doped anatase TiO₂ have been investigated by angle-resolved photoelectron spectroscopy (ARPES) in detail.²¹ The VB of anatase is mainly composed of O2p states with a minor contribution of Ti3d states, lying between 4 and 10 eV below Fermi level. The VB XPS spectra are characterized by two intense peaks at smaller and larger binding energy regions and weak emission structures in between them. These features have already been identified by photoemission studies.⁴⁴ One of the intense peaks at E_bin = 4–5 eV is associated with O2p-derived P_π nonbonding band, while the other at E_bin = 7–9 eV is ascribed to σ bonding band formed by Ti e_g and O2p_σ states. Weak emissions correspond to π-bonding band formed by Ti t_2g and O2p_π states. Another ARPES measurement using linearly-polarized synchrotron radiation demonstrated that π-bonding band is resolved into two peaks with different polarization dependence, i.e., the shallower peak (π₁) at E_bin ≈ 5 eV and the deeper peak (π₂) at E_bin ≈ 6 eV.⁴⁵ An “angle-integrated” XPS spectrum of VB for non-doped sample in this study was also successfully decomposed into four bands (P_π, π₁, π₂, σ), similar to previous ARPES study.^21,45 The balance band maximum (VBM) of non-doped sample was estimated to be 3.7 eV below Fermi level by linearly extrapolating slope of VB edge. The position of conduction band minimum (CBM) and band gap are also crucial for photocatalytic activity.^46,47 The band gap was successfully determined to be 3.2 eV in the recent study of time-resolved photoelectron spectroscopy (TRPES).^48,49 According to the results of TRPES, TiO₂ bands were shown to bend downwardly from the bulk to the surface. The magnitude of downward band bending ranged from 0 to 0.8 eV, depending on the surface conditions such as surface-specific structures and the density and/or the type of surface defects. It was estimated to be 0.5 eV in the present study. Therefore, the position of VBM is likely to be reliable. Then, CBM was indirectly estimated to be 0.5 eV below Fermi level.

Decomposition of all VB XPS spectra for samples synthesized by method A and B reproduced four bands (P_π, π₁, π₂, σ). However, the fifth new peaks apparently appeared for A-600 and Bx-550 (where x = 3, 6, 20, 40) on the smaller binding energy side of P_π band. They are originated from shoulder structures of VB edges and are clearly induced by N doping. They disappeared (under detection limit) for A-450, A-500, A-550, B3-450 and B3-500. The results of decomposition of VB spectra for A-600 and B3-550 are shown in Fig. 6(a) and (b), respectively. The peak energies, widths (FWHM) and the ratios of areas of all VB bands, N-derived states and Ti³⁺ defect states for non-doped sample and N–TiO₂ samples are summarized in Table 2, where the ratio of area is defined to be the division of area of each peak by total VB area.

Fig. 6 Decomposition of the VB XPS spectra for (a) A-600 and (b) B3-550.

Table 2 The peak energies (E_bin), widths (FWHM) and the ratios of areas of VB bands, N-derived states and Ti³⁺ defect states for non-doped and N–TiO₂ samples

	Non-doped	A-600	B3-550	B6-550	B20-550	B40-550
Pπ band
Energy	4.35	4.41	4.49	4.44	4.42	4.42
FWHM	0.900	1.042	1.039	1.183	0.976	1.095
Ratio of area	0.100	0.169	0.164	0.138	0.106	0.111
π1 band
Energy	4.98	5.10	5.22	5.05	4.92	5.05
FWHM	1.230	1.390	1.450	1.611	1.486	1.367
Ratio of area	0.204	0.118	0.139	0.200	0.188	0.181
π2 band
Energy	5.89	6.08	6.06	6.07	5.98	6.17
FWHM	1.723	2.344	1.950	1.878	2.094	2.192
Ratio of area	0.235	0.387	0.336	0.253	0.333	0.402
σ band
Energy	7.40	7.52	7.41	7.35	7.61	7.81
FWHM	2.427	2.165	2.424	2.642	2.301	2.061
Ratio of area	0.462	0.326	0.361	0.409	0.373	0.306
N-Derived state
Energy	N.D.	3.36	3.39	3.42	3.46	3.38
Energy (above VBM)	N.D.	0.34	0.31	0.28	0.24	0.30
FWHM	N.D.	0.631	0.796	0.702	0.662	0.694
Ratio of area	0.000	0.053	0.033	0.030	0.024	0.026
Ti^3+ defect state
Energy	0.87	0.80	0.78	0.87	0.83	0.83
FWHM	1.135	1.006	1.188	1.036	1.361	1.298
Ratio of area	0.057	0.083	0.060	0.070	0.062	0.060

---

In particular, peak energies of N-derived states range between 0.24 eV and 0.34 eV above VBM in the band gap, which are larger than ∼0 eV by UPS⁴³ and 0.04–0.13 eV by UV-vis optical absorption experiments,^24,50 while smaller than 0.52 eV by deep-level optical spectroscopy⁶ and 0.75 eV by photocurrent measurement.⁵¹

It was insisted that N-derived states in N–TiO₂ form ‘hybridized’ VB with O2p states.⁵ However, other studies have shown that N atoms incorporated in TiO₂ generate N-derived ‘localized’ states in the band gap.^43,52–54 As shown in Table 2, the findings that both FWHM and areas of new peaks induced by N doping are very small compared with VB and that four bands (in particular, P_π band) are hardly affected by N doping imply that they are ‘localized’ from VB rather than ‘hybridized’ with VB of TiO₂⁴³ although the larger binding energy sides of them are slightly overlapped with VB of TiO₂. N doping into N_s inevitably accompanies the production of V_O and reduced Ti species (Ti³⁺, Ti²⁺). They form ‘defect states’ in upper half of the band gap.¹⁵ Therefore, such defect states are also likely to have small effect on VB structures of TiO₂.

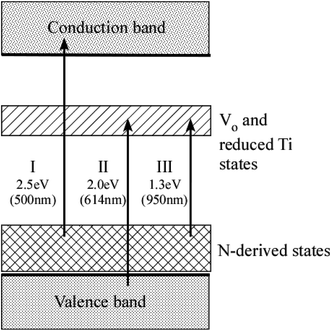
The energy diagram of N–TiO₂ is illustrated in Fig. 7. The wavelength of vis light absorbed by N–TiO₂ must be shorter than approximately 500 nm (i.e., the energy of light ≥ 2.5 eV, transition I in Fig. 7) according to the peak energies and FWHM of N-derived states listed in Table 2. It is in excellent agreement with typical UV-vis optical absorption spectra for N–TiO₂ showing the onset wavelength of absorption at ∼500 nm.^5,11,38,55 However, the absorption spectra for N–TiO₂ with heavy N doping or those subjected to high-temperature annealing were extended into the wavelength longer than 500 nm, which was attributable to the absorption associated with V_O and reduced Ti defect states.^52,56,57 In reality, it was demonstrated that V_O states produced in plasma-treated TiO₂ are responsible for the absorption at wavelength between 506 nm and 614 nm (related to the transition II from VB to V_O and reduced Ti defect states).¹⁵ Then, the transition from N-derived states to V_O and reduced Ti defect states (transition III) accounts for the absorption at wavelength from 614 nm to 950 nm.

Fig. 7 The energy diagram of N–TiO₂. Arrows denote three kinds of transition of electrons induced by absorption of vis light. The energy level of V_O and reduced Ti states was quoted from the literature.¹⁵ Numerical values given below each transition represent the smallest energy and longest wavelength capable of inducing transition, respectively.

According to DFT calculations, N_s produces half-occupied N-derived states slightly (0.14 eV) above VBM, while N_i also generates anti-bonding localized states due to N–O π bonds (but higher, 0.73 eV) above VBM.²⁸ Therefore, it is likely that peak energies of N-derived states of N_s listed in Table 2 are a little larger than theoretically predicted value (0.14 eV above VBM). Another DFT calculation demonstrated that the formation energy of oxygen vacancy (V_O) is drastically reduced by substitution of O by N.⁴² This explains why N_s is promoted in the presence of V_O. When one N atom simply replaces one O²⁻ ion in TiO₂ lattices, one N-derived state is singly occupied because the number of 2p electrons is smaller in N (3) than that in O (4). If V_O coexists with N_s, there are two possibilities in spin configuration. One is the high-spin configuration where one electron is trapped by V_O site (i.e., Ti³⁺ site), whereas the other is trapped by a N-derived state and spins of them are parallel. The other possibility is the low-spin configuration where two electrons originated from one V_O are trapped by a N-derived state and thus, a N-derived state is fully occupied and spins of electrons are anti-parallel. The latter configuration is always more stable than the former one because V_O states are higher in energy than N-derived states (see Fig. 7). Thus, the low-spin configuration is more favorable than the high-spin configuration, which was supported by the results of EPR measurement.²⁸ In the low-spin configuration, the energy levels of N-derived states are almost equivalent, i.e., 0.59 eV and 0.75 eV above VBM for N_s and N_i, respectively. The increase in energy from high-spin to low-spin configuration is larger for N_s due to the difference in orbital nature. Photovoltage and impedance measurements have shown that V_O sites are much more numerous than doped N atoms, which suggests that low-spin configuration is realized.⁵⁸ Another EPR measurement demonstrated that only electrons in low-spin configuration contribute to vis light activities.³¹ However, the energy levels of N-derived states listed in Table 2 are smaller than those for N_s in the low-spin configuration (0.59 eV above VBM), whereas larger than those for N_s in the high-spin configuration (0.14 eV above VBM). Therefore, it cannot be determined which spin configuration is achieved from the present results. Recent DFT calculation has shown that the formation energy of N_Ti (substitution of Ti by N) is always lower than those of N_s and N_i.¹⁴ In this case, N is located at Ti-vacancy site to form NO³⁻ (nitrate) or NO²⁻ (nitrite) with neighboring O²⁻. These O²⁻ ions experience local electronic potential different from those of ordinary O²⁻ ions, which leads to the formation of localized states above VB in the band gap. The energy level of them was estimated to be only 0.1 eV above VBM. These states had large DOS (density of state) with P_π character and accompanied urbach tail into the band gap region, resulting in the absorption of vis light. However, this is not the case with the present study because the ratio of α₃ peak due to NO_x was very small, as shown in Table 1. Hence, the origin of N-derived states in Table 2 is N_s rather than N_i or N_Ti.

3.4 Photocatalytic activities

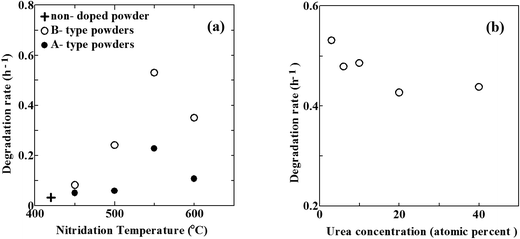
Photocatalytic activities of N–TiO₂ powders were evaluated by degradation of MB under vis light irradiation. The concentration of MB in aqueous solution exponentially decreased with exposure time. Degradation rate is represented by time constant of degradation per hour (h⁻¹).

Fig. 8(a) reveals the degradation rates of MB using N–TiO₂ powders without urea (referred to as A-type powders, filled circles) and N–TiO₂ powders with urea (referred to as B-type powders, open circles) as a function of temperature in NH₃ gas, respectively. The degradation rate increased with elevating temperature and reached a maximum at 550 °C, followed by a rapid decrease with the further elevation of nitridation temperature for both types. This trend with nitridation temperature coincides with the previous studies for N–TiO₂ powders obtained by sol–gel method and post nitridation in NH₃ gas.^12,27,56 The optimum nitridation temperature giving highest degradation rate was 550 °C, regardless of whether urea was used or not. However, the degradation rate was always larger for B-type powders than A-type powders, compared at the same temperature. Hence, urea was shown to improve photocatalytic activity under vis light. Moreover, there are considerable differences between the degradation of two types.

Fig. 8 (a) The degradation rates of MB as a function of nitridation temperature for A-type powders (closed circles), B-type powders (open circles) and non-doped TiO₂ powder (cross). (b) The change in the degradation rate of MB with the concentration of urea for B-type powders nitrided at 550 °C.

In case of A-type powders, the degradation rates of MB under vis light irradiation were very low below 500 °C. They were almost similar to that of non-doped powder indicated by a cross in Fig. 8(a). It reflects small densities of N (under detection limit), as shown in Table 1. At the elevated temperature of 550 °C, the degradation rate abruptly increased. This increase corresponds to substantial N doping due to the onset of decomposition of NH₃, as already mentioned. However, the degradation rate decreased with further elevation of temperature to 600 °C. The generation of defects is needed for incorporation of N into N_s. Taking the N/O atomic ratios and β₁, β₂ ratios into account, defect densities are likely to be always larger than N densities. It indicates that a number of defects (V_O) remain unfilled with N. Since reduction power of NH₃ was relatively low, the number of such unfilled defects was still small at 550 °C. However, the reduction power greatly increased at 600 °C. Consequently, the density of defects unfilled with N became extremely large, giving rise to the steep decrease of degradation rate at 600 °C in spite of the increase in N/O atomic ratio from 0.008 at 550 °C to 0.086 at 600 °C. Highest vis light activity is obtained at N/O ratio of ∼0.01 at 550 °C for A-type powders. This is mostly in line with optimum N density of 1–2%,³ N/Ti ratio of 1.73% (ref. 59) and N/O ratio of 0.017,⁵ 0.003.⁵² On the other hand, aqueous NH₃ solution has also been utilized for production of N–TiO₂.^22,24,59 A notable feature of NH₃ solution is that N–TiO₂ can be synthesized at temperatures as low as 260 °C, which enables the formation of N–TiO₂ films on thermally-weak organic materials. However, unlike NH₃ gas, NH₃ solution has no reduction power since atomic H is never generated from the solution. This was supported by the finding that only N_i was formed in N–TiO₂ fabricated from NH₃ solution.

In case of B-type powders, the degradation rate was also very low at 450 °C due to small N density. It steeply increased at 500 °C. This increase obviously arises from the increase in N/O atomic ratio. Therefore, urea substantially begins to act as a reductant and a N source at 500 °C. Further increase in the degradation rate at 550 °C is also caused by the increase in N density. Since the effect of NH₃ is still low at 550 °C, this increase from 500 °C to 550 °C is greatly indebted to the enhanced ability of urea as a reductant and a N source. Therefore, the onset temperature of N doping for B-type powders is at least 50 degrees lower than that for A-type powders. In this respect, the nitriding ability of urea at 550 °C compares to that of NH₃ at 600 °C. However, the reduction power of urea at 550 °C is not so large as that of NH₃ at 600 °C because the densities of β₁ and β₂ in B3-550 are considerably smaller than those in A-600. Then, the density of defects unfilled with N in B-type powders nitrided at 550 °C is much smaller than that in A-type powders nitrided at 600 °C. This leads to by far higher degradation rate of B-type powders nitrided at 550 °C than that of A-type powders nitrided at 600 °C. However, the degradation rate of B-type powders steeply decreased at 600 °C. The reason for it is possibly the same as the case of A-type powders at 600 °C, namely, high-density defects were produced due to the enhanced reduction power of NH₃ at 600 °C. Consequently, the optimum N/O ratio giving highest degradation rate is ∼0.06 (corresponding to N density of 4 at%) at 550 °C for B-type powders. This optimum N density (4 at%) of the present study is far larger than any other optimum N density reported in the literature (∼2 at% at most). In other words, it became possible to achieve heavier N doping using urea without degrading the photocatalytic activity.

Fig. 8(b) shows the change in the degradation rate with the concentration of urea at the nitridation temperature of 550 °C. The degradation rate has a maximum value with urea at 3 at% N although the effect of the concentration of urea upon the degradation rate is by far smaller than that of the nitridation temperature. In N–TiO₂ films, N/O atomic ratio increases from 0.054 for B3-550 to 0.062 for B40-550. In contrast, the ratio of β₃ (Ti⁴⁺) tends to decrease with the increase in urea concentration. However, the degrees of these changes are small, which results in a rather small effect of urea concentration on the degradation rate.

As indicated above, the optimum N/O ratio of ∼0.06 for B-type powders is far higher than that of ∼0.01 for A-type powders. Therefore, urea is shown to be superior to NH₃ as a N source in photocatalytic activity under vis light irradiation. Table S1† shows the comparison of vis light photocatalytic activities in terms of degradation rate (h⁻¹) and quantum yield (%) among various studies using NH₃ gas for nitridation.^5,11,56 The present study gave the highest activity, demonstrating that urea is superior to mere NH₃ gas. The optimum N density greatly depends on the density of defects. Taking the values revealed in Table 1 into account, the upper limit of the defect density for high activities is likely to be ∼0.5 in terms of ratio of reduced Ti species (Ti³⁺, Ti²⁺). When the defect density exceeds this limit, these defects greatly degrade the activities even though much N is incorporated in TiO₂.

In the pioneering study performed by Asahi et al., it was suggested that N_s is the origin of vis light activity of N–TiO₂.⁵ On the other hand, the general agreement has been likely to be obtained among recent studies that N_i is responsible for vis light activity rather than N_s.^10,12,13 However, the present study implied that N_s is still effective for vis light activities. Possibly, a lot of V_O coexisted with N_s in the N_s-dominant specimens of recent studies, which degrades photocatalytic activities. Although the production of a certain amount of V_O is necessary for N doping into substitutional sites, the strict control of V_O density is required for the achievement of high activity. In this respect, NH₃ gas is hard to be controlled because of the abrupt increase in the reduction power above the onset temperature (i.e., 550 °C). In contrast, urea can be more easily controlled since the reduction power gradually increases with the elevation of temperature.

It has been well known that the photocatalytic activity of N–TiO₂ under vis light irradiation is still lower than that of TiO₂ under UV light irradiation.^2,55 A major reason for it is shorter lifetimes of photoexcited carriers in N–TiO₂. N-derived states were not ‘hybridized’ with VB of TiO₂ but possibly ‘localized’ from it, as indicated in Section 3.3. A photoexcited hole has to move by hopping from one dopant N site to another many times to reach the photocatalyst surface. However, the average distance among neighboring dopant N sites is large due to small N density (as large as several %). Accordingly, the probability of photoexcited holes to be recombined with electrons becomes fairly large, which results in short lifetimes of holes. Nevertheless, the reliable lifetimes of photoexcited carriers (in particular, holes) in N–TiO₂ have hardly been provided by any techniques so far. Our next attempt to measure carrier lifetimes in N–TiO₂ using TRPES is about to get underway.

4. Conclusions

The structural and electronic properties of N–TiO₂ thin films synthesized by sol–gel methods with or without urea and post calcination in NH₃ gas were characterized by XRD and XPS utilizing synchrotron radiation. N–TiO₂ powders were also prepared for the estimation of visible light photocatalytic activities. N-doped TiO₂ thin films revealed polycrystalline anatase phases. N was shown to be chiefly doped into substitutional site. The VB structures of N–TiO₂ samples were composed of four bands similar to that of non-doped anatase TiO₂. However, remarkable shoulder structures were recognized in VB XPS spectra for samples with high N densities. From these shoulder structures, localized states associated with doped N were successfully found at 0.24 eV to 0.34 eV above VBM in the band gap. This finding is roughly consistent with a lot of previous studies. Decomposition of NH₃ took place at 550 °C. Above this temperature, N incorporation and the reduction of TiO₂ (i.e., the generation of oxygen vacancies and reduced Ti species) simultaneously occur by NH₃. The former enhances photocatalytic activity, whereas the latter reduces it. In particular, the ratio of defect (Ti²⁺ and Ti³⁺) density higher than ∼0.5 greatly degrades vis light photocatalytic activity. It is difficult to achieve both high-density N and low-density defects using NH₃ because of the abrupt increase in reduction power at 550 °C. However, urea reduced the onset temperature of N incorporation to 500 °C. Moreover, the increase in reduction power of urea was gradual at around 550 °C. This enabled the synthesis of N–TiO₂ with high-density N and low-density defects by using urea at 550 °C, giving the highest vis light photocatalytic activity. Consequently, the optimum N/O atomic ratio was shown to be approximately 0.06 (corresponding to N density of 4 at%). Namely, it became possible to achieve heavier N doping and better photocatalytic activity under vis light irradiation using urea than any other study only using NH₃ gas for nitridation.

Acknowledgements

The XPS measurements were performed under the approval of the Photon Factory Advisory Committee (Proposal No. 2011G599). The authors thank Mr Taku Higuchi for his help in the XPS measurements.

References

1. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
2. (a) T. L. Thompson and T. Yates Jr, Chem. Rev., 2006, 106, 4428–4453; (b) S.-K. Lee, P. K. J. Robertson, A. Mills, D. McStay, N. Elliott and D. McPhail, Appl. Catal., B, 2003, 44, 173–184.
3. T. Okato, T. Sakano and M. Obara, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 115124.
4. S. S. Soni, M. J. Henderson, J.-F. Bardeau and A. Gibaud, Adv. Mater., 2008, 20, 1493–1498.
5. R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269–271.
6. Y. Nakano, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Appl. Phys. Lett., 2005, 86, 132104.
7. X. Chen, Y.-B. Lou, A. C. S. Samia, C. Burda and J. L. Gole, Adv. Funct. Mater., 2005, 15, 41–49.
8. R. G. Palgrave, D. J. Payne and R. G. Egdell, J. Mater. Chem., 2009, 19, 8418–8425.
9. T. Yoshida, S. Niimi, M. Yamamoto, T. Nomoto and S. Yagi, J. Colloid Interface Sci., 2015, 447, 278–281.
10. A. Kafizas, C. Crick and I. P. Parkin, J. Photochem. Photobiol., A, 2010, 216, 156–166.
11. O. Diwald, T. L. Thompson, T. Zubkov, E. G. Goralski, S. D. Walck and J. T. Yates Jr, J. Phys. Chem. B, 2004, 108, 6004–6008.
12. Z. Zhang, X. Wang, J. Long, Q. Gu, Z. Ding and X. Fu, J. Catal., 2010, 276, 201–214.
13. S. Sato, Chem. Phys. Lett., 1986, 123, 126–128.
14. H. Chen and J. A. Dawson, J. Phys. Chem. C, 2015, 119, 15890–15895.
15. I. Nakamura, N. Negishi, S. Kutsuna, T. Ihara, S. Sugihara and K. Takeuchi, J. Mol. Catal. A: Chem., 2000, 161, 205–212.
16. F. Dong, W. Zhao, Z. Wu and S. Guo, J. Hazard. Mater., 2009, 162, 763–770.
17. J. Zhao, E. G. Garza, K. Lam and C. M. Jones, Appl. Surf. Sci., 2000, 158, 246–251.
18. L. Mohapatra, K. Parida and M. Satpathy, J. Phys. Chem. C, 2012, 116, 13063–13070.
19. L. G. Devi and R. Kavitha, Appl. Catal., B, 2013, 140, 559–587.
20. A. L. Patterson, Phys. Rev., 1939, 56, 978–982.
21. M. Emori, M. Sugita, K. Ozawa and H. Sakama, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035129.
22. J. Wang, W. Zhu, Y. Zhang and S. Liu, J. Phys. Chem. B, 2007, 111, 1010–1014.
23. Y. Cong, J. Zhang, F. Chen and M. Anpo, J. Phys. Chem. C, 2007, 111, 6976–6982.
24. M. Sathish, B. Viswanathan, R. P. Viswanath and S. Gopinath, Chem. Mater., 2005, 17, 6349–6353.
25. X. Chen and C. Burda, J. Phys. Chem. B, 2004, 108, 15446–15449.
26. (a) L. A. DeLouise and N. Winograd, Surf. Sci., 1985, 159, 199–213; (b) T. Jirsak, J. Dvorak and J. A. Rodgiguez, Surf. Sci., 1999, 436, L683–L690.
27. C. Feng, Y. Wang, Z. Jin, J. Zhang, S. Zhang, Z. Wu and Z. Zhang, New J. Chem., 2008, 32, 1038–1047.
28. C. D. Valentin, E. Finazzi, G. Pacchioni, A. Selloni, S. Livraghi, M. C. Paganini and E. Giamello, Chem. Phys., 2007, 339, 44–56.
29. A. V. Emeline, V. N. Kuznetsov, V. K. Rybchuk and N. Serpone, Int. J. Photoenergy, 2008, 2008, 258394.
30. J. L. Gole, J. D. Stout, C. Burda, Y. Lou and X. Chen, J. Phys. Chem. B, 2004, 108, 1230–1240.
31. F. E. Oropeza, J. Harmer, R. G. Egdell and R. G. Palgrave, Phys. Chem. Chem. Phys., 2010, 12, 960–969.
32. S. H. Cheung, P. Nachimuthu, M. H. Engelhard, M. K. Bowman and S. A. Chambers, Surf. Sci., 2007, 601, 1754–1762.
33. N. Saha and G. Tompkins, J. Appl. Phys., 1992, 72, 3072–3079.
34. Y. Zang, P. Xiao, X. Zhou, D. Liu, B. B. Garciaa and G. Cao, J. Mater. Chem., 2009, 19, 948–953.
35. E. Gyoegy, A. P. Pino, P. Serra and J. L. Morenza, Surf. Coat. Technol., 2003, 173, 265–270.
36. C. H. Shin, G. Bugli and G. D. Mariadassou, J. Solid State Chem., 1991, 95, 145–155.
37. M. Ceotto, L. L. Presti, G. Cappelletti, D. Meroni, F. Spadavecchia, R. Zecca, M. Leoni, P. Scardi, C. Bianchi and S. Ardizzone, J. Phys. Chem. C, 2012, 116, 1764–1771.
38. S. Livraghi, M. C. Paganini, E. Giamello, A. Selloni, C. D. Valentin and G. Pacchioni, J. Am. Chem. Soc., 2006, 128, 15666–15671.
39. C. D. Valentin and G. Pacchioni, Phys. Rev. Lett., 2006, 97, 166803.
40. S. Yin, K. Ihara, M. Komatsu, Q. Zhang, F. Saito, T. Kyotani and T. Sato, Solid State Commun., 2006, 137, 132–137.
41. Z. Wu, F. Dong, W. Zhao and S. Guo, J. Hazard. Mater., 2008, 157, 57–63.
42. A. K. Rumaiz, J. C. Woicik, E. Cockayne, H. Y. Lin, G. H. Jaffari and S. I. Shah, Appl. Phys. Lett., 2009, 95, 262111.
43. M. Batzill, E. H. Morales and U. Diebold, Phys. Rev. Lett., 2006, 96, 026103.
44. (a) Z. Zhang, S.-P. Jeng and V. E. Henrich, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 12004–12011; (b) R. Asahi, Y. Taga, W. Mannstadt and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 7459–7465; (c) A. G. Thomas, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 035105.
45. M. Emori, A. Sakino, K. Ozawa and H. Sakama, Solid State Commun., 2014, 188, 15–18.
46. L. Mohapatra and K. M. Parida, Phys. Chem. Chem. Phys., 2014, 16, 16985–16996.
47. S. Nayak, L. Mohapatra and K. Parida, J. Mater. Chem. A, 2015, 3, 18622–18635.
48. K. Ozawa, M. Emori, S. Yamamoto, R. Yukawa, S. Yamamoto, R. Hobara, K. Fujikawa, H. Sakama and I. Matsuda, J. Phys. Chem. Lett., 2014, 5, 1953–1957.
49. K. Ozawa, S. Yamamoto, R. Yukawa, K. Akikubo, M. Emori, H. Sakama and I. Matsuda, Org. Electron., 2016, 31, 98–103.
50. S. Sakthivel, M. Janczarek and H. Kisch, J. Phys. Chem. B, 2004, 108, 19384–19387.
51. R. Nakamura, T. Tanaka and Y. Nakato, J. Phys. Chem. B, 2004, 108, 10617–10620.
52. H. Irie, Y. Watanabe and K. Hashimoto, J. Phys. Chem. B, 2003, 107, 5483–5486.
53. X. Cheng, X. Yu, Z. Xing and J. Wan, Energy Procedia, 2012, 16, 598–605.
54. T. Lindgren, J. M. Mwabora, E. Avendaño, J. Jonsson, A. Hoel, C.-G. Granqvist and S.-E. Lindquist, J. Phys. Chem. B, 2003, 107, 5709–5716.
55. R. Q. Carbrera, C. S. Vazquez, J. A. Darr and I. P. Parkin, Appl. Catal., B, 2014, 160–161, 582–588.
56. X. Fang, Z. Zhang, Q. Chen, H. Ji and X. Gao, J. Solid State Chem., 2007, 180, 1325–1332.
57. E. A. Reyes-Garcia, Y. Sun, K. Reyes-Gil and D. Raftery, J. Phys. Chem. C, 2007, 111, 2738–2748.
58. F. Spadavecchia, G. Cappelletti, S. Ardizzone, M. Ceotto and L. Falciola, J. Phys. Chem. C, 2011, 115, 6381–6391.
59. H. Li, X. Li and Y. Huo, J. Phys. Chem. B, 2006, 110, 1559–1565.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra25238a

---