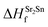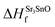Open Access Article
Open Access ArticleThe role of intrinsic vacancy defects in the electronic and magnetic properties of Sr3SnO: a first-principles study
Javaria Batool,
Syed Muhammad Alay-e-Abbas,
Adnan Ali,
Khalid Mahmood,
Shaheen Akhtar and
Nasir Amin *
*
Department of Physics, Government College University Faisalabad, 38040 Faisalabad, Pakistan. E-mail: nasir786a@yahoo.com
First published on 20th January 2017
Abstract
In this study, we use first-principles electronic structure calculations to investigate the structural, electronic and magnetic properties of pristine and intrinsic vacancy containing Sr3SnO inverse perovskite. The thermodynamic stability diagram of Sr3SnO is computed which provides useful information regarding stable synthesis of this material. The limits of atomic chemical potentials of Sr, Sn and O are obtained to determine the relative stability of the formation of metal-atom and oxygen vacancies in Sr3SnO. The DFT calculations reveal Sr vacancy to be the most stable form of vacancy defect under O-rich conditions, while O and Sn vacancies are found to have low formation energies under O-poor and Sn-poor conditions, respectively. It is concluded that Sr and O vacancy containing Sr3SnO is non-magnetic, while Sn vacancy containing Sr3SnO gives rise to stable ferromagnetism. The electronic properties of pristine and Sn, O, and Sr deficient Sr3SnO are discussed. The Sn vacancy containing Sr3SnO, displays stable ferromagnetism which originates from spin-polarization of partially filled Sr dangling bonds with a predominant Sr-4d character. Our results explain the origins of experimentally observed room temperature ferromagnetism in non-stoichiometric Sr3SnO.
1. Introduction
Technological advances in the field of electronics have always been stimulated by the discovery of multifunctional characteristics and enhanced performance in traditional semiconductor metal oxides. Among the wide range of semiconductor materials, inverse perovskites have recently gained the extensive fascination of the materials research community owing to their promising role in devices requiring thermoelectricity,1 superconductivity,2 spin glass behavior (negative thermal expansion),3 giant magnetoresistance (GMR),4 giant magneto-striction effect5 and magneto-caloric effect6 capabilities. The most striking feature of some inverse perovskites is the existence of a 3D topological insulator (TI) phase where the bulk of the material behaves as a narrow band gap semiconductor while a conducting nature is achieved at the surface.7 In addition, inverse perovskites also exhibit dilute magnetic semiconductor (DMS) behavior that combines ferromagnetism (FM) with semiconducting properties.8 The DMS are an exciting new class of materials which provide magnetic functionalities in electronic devices that can be controlled by means of an electric field.9The presence of above-mentioned functionalities in inverse perovskites make them potential candidates for the realization of quantum computing and high speed spintronic devices. Strontium tin oxide, Sr3SnO (SSO), is one such inverse perovskite material that crystallizes stably in the ideal cubic structure (space group # 221, Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with a lattice parameter of 5.12 Å.10 Although a report on the stable crystallization of SSO in inverse perovskite structure has been present in literature since the 80's,10 the recent upsurge in research activities related to SSO are due to its promise for combining TI and DMS properties in a single material.8,11–13 Klintenberg et al. performed density functional theory (DFT) based comprehensive computational data-mining of several materials to reveal the topological behavior of narrow band gap SSO.11 They concluded that the topological behavior of SSO originates from the spin-orbital coupling (SOC) of Sn and the metallic surface states which are comparable to Dirac cones in graphene. On the other hand, experimental investigations carried out by Lee et al.8 unveiled stable DMS in non-stoichiometric SSO where the origins of room temperature FM originates was assigned to the presence of intrinsic vacancy defects. Owing to topological nature of the SSO, experimental investigations have revealed both semiconducting8 and metallic12 nature for this material.
m) with a lattice parameter of 5.12 Å.10 Although a report on the stable crystallization of SSO in inverse perovskite structure has been present in literature since the 80's,10 the recent upsurge in research activities related to SSO are due to its promise for combining TI and DMS properties in a single material.8,11–13 Klintenberg et al. performed density functional theory (DFT) based comprehensive computational data-mining of several materials to reveal the topological behavior of narrow band gap SSO.11 They concluded that the topological behavior of SSO originates from the spin-orbital coupling (SOC) of Sn and the metallic surface states which are comparable to Dirac cones in graphene. On the other hand, experimental investigations carried out by Lee et al.8 unveiled stable DMS in non-stoichiometric SSO where the origins of room temperature FM originates was assigned to the presence of intrinsic vacancy defects. Owing to topological nature of the SSO, experimental investigations have revealed both semiconducting8 and metallic12 nature for this material.
Since the assumptive nature of experimental models for the origins of FM in DMS can lead to controversies in assigning the type of point defects responsible for magnetic behavior,14,15 it is instructive to explore the origins of FM by means of first-principles calculations. For example, some recent studies conducted for SSO have considered cation8 as well as oxygen vacancies16,17 to be responsible for the experimentally observed room temperature FM. Keeping this in mind, in the present work we have explored the thermodynamic stability, formation energies of intrinsic vacancy defects and the electronic structures of pristine and defective SSO by means of density functional theory calculations. Our results may prove useful in explaining the origins of the electronic and magnetic behavior of SSO.
2. Computational details
For exploring the physical properties of pristine and intrinsic vacancy containing SSO we employ the WIEN2k code which utilizes full-potential linear-augmented plane-wave (FP-LAPW) method of DFT for computing the electronic structure of solids.18 The Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) parametrization scheme has been used as the exchange-correlation functional.19 By partitioning the crystal space into non-overlapping sphere and interstitial region, the wave functions, potentials and charge density are expanded spherical harmonically within the non-overlapping muffin-tin spheres of radii RSr = 1.80 a.u., RSn = 2.00 a.u. and RO = 1.75 a.u. On the other hand, plane-wave basis set is used in the interstitial region. The electronic structure of pristine and defective SSO are computed with the inclusion of SOC interactions which plays a significant role in the gapless surface states of SSO.11The convergence tests for the DFT calculations are performed by systematically increasing the calculations parameters of FP-LAPW method for achieving a precision of ±1 meV per atom in the calculated enthalpies of formation for SSO, SrO and Sr2Sn. Based on these tests, we have set the plane-wave cut off (ROKmax), charge density expansion (Gmax) and the angular momentum (lmax) to 8, 18 and 10, respectively, for calculations involving all sizes of supercells. Due to deep lying 4p states of Sn, the energy cut-off between valence and core states is set to −7.0 Ry. For the case of bulk SSO the calculations were performed self-consistently with 12 × 12 × 12 k-mesh and an energy convergence criteria of 10−4 Ry, while a k-mesh of 6 × 6 × 6 is used for the 2 × 2 × 2 supercell. Table 1 displays the calculated lattice parameters of SSO, SrO and Sr2Sn which have been optimized using above-mentioned calculations parameters. A comparison with experimental data (also presented in Table 1) shows good agreement and justifies the reliability of calculations reported in this work.
For simulating intrinsic vacancy defects in SSO, a 40-atom 2 × 2 × 2 supercell with composition Sr24Sn8O8 has been constructed from the structurally optimized bulk unit cell with lattice parameter 5.181 Å. The isolated neutral vacancies have been introduced by removing one Sr, Sn or O atom from the 2 × 2 × 2 supercell22 which leads to non-stoichiometric SSO with compositions Sr23Sn8O8, Sr24Sn7O8 and Sr24Sn8O7, respectively. All vacancy containing supercells are allowed to relax until forces on each atom are below 1 mRy a.u.−1. In order to test the stability of FM magnetic order in non-stoichiometric SSO, the structural relaxation were performed with and without spin-polarization. This allowed us to evaluate the possibility of achieving stable FM in intrinsic vacancy defect containing supercell of SSO.23
3. Results and discussion
3.1. Thermodynamic stability diagram of Sr3SnO
The valid ranges of atomic chemical potentials can be had from Thermodynamic Stability Diagram (TDS).24 For computing the TSD of SSO, we proceed by assuming that the atomic chemical potentials of the atomic species in their stable reference states are an upper bound to the valid ranges of atomic chemical potentials25| μx = μgas/solidx + Δμ. | (1) |
With this assumption the values of the atomic chemical potentials of Sn, O and Sr must satisfy
| ΔμSr + ΔμO ≤ ΔHSrOf | (2) |
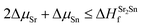 | (3) |
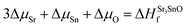 | (4) |
In eqn (2) to (4), the enthalpies of formation of SrO, Sr2Sn, Sr3SnO have been computed using
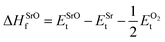 | (5) |
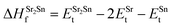 | (6) |
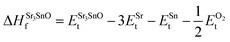 | (7) |
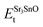 ,
, 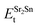 , ESrOt, ESnt and ESrt are the minimum total energies of PBE-GGA optimized bulk unit cells of SSO, Sr2Sn, SrO, Sn and Sr, respectively.
, ESrOt, ESnt and ESrt are the minimum total energies of PBE-GGA optimized bulk unit cells of SSO, Sr2Sn, SrO, Sn and Sr, respectively. 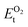 , on the other hand represents the energy of O2 molecule.
, on the other hand represents the energy of O2 molecule. 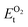 is computed by adding the PBE-GGA cohesive energy of oxygen molecule
is computed by adding the PBE-GGA cohesive energy of oxygen molecule 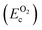 26 in twice the total energy of a single oxygen atom (EOt) which is computed using Γ-point k sampling in a large supercell:
26 in twice the total energy of a single oxygen atom (EOt) which is computed using Γ-point k sampling in a large supercell:
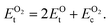 | (8) |
It is evident from Table 2 that the calculated enthalpies of formation agree well with available experimental data. Since the sum of enthalpies of formation of SrO and Sr2Sn is greater than the enthalpy of formation of SSO, the process of creation of SSO is exothermic and supports the stable formation of this material in an inverse perovskite structure.27
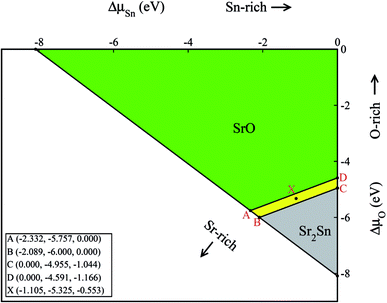
With the help of the calculated enthalpies of formation listed in Table 2, we have computed the TSD of SSO which is shown in Fig. 1. In the TSD, the region enclosed by points A–B–C–D represent thermodynamically stable SSO without the formation of secondary phases Sr2Sn and SrO. Both points A and B give us the Sr-rich condition, while points C and D satisfy the Sn-rich condition. The Sr-poor and Sn-poor conditions are satisfied at point D and point A, respectively. On the other hand, the oxidation (O-rich) and reduction (O-poor) conditions are satisfied at point D and B, respectively. The stability points shown in the TSD provide us the valid ranges of atomic chemical potentials (ΔμSn, ΔμO, ΔμSr) which dictate defect formation energies of intrinsic vacancy defects in SSO.
3.2. Isolated intrinsic vacancy defects in Sr3SnO
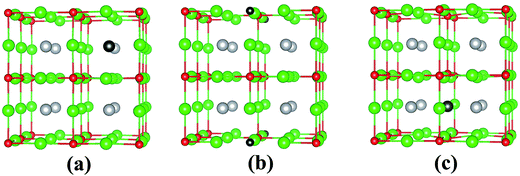
In its pristine form, the Sr–Sn, Sr–O and Sn–O bond lengths of PBE-GGA optimized cubic unit cell of SSO are found to be 3.664 Å, 2.591 Å and 4.487 Å, respectively. When an atomic site is vacated in the 2 × 2 × 2 supercell of SSO, the minimization of internal forces causes changes in the atomic positions of the atoms surrounding the vacant site (Fig. 2). In the present work we have performed force minimization of intrinsic vacancy defect containing supercells of SSO with and without spin-polarization. Comparison of the non-magnetic (NM) and FM calculations only show significant differences in the calculated total energies, charge densities and structural properties for the case of Sn vacancy containing 2 × 2 × 2 supercell of SSO. On the other hand, the relaxation of internal parameters for NM and FM cases of O and Sr vacancy containing 2 × 2 × 2 supercell of SSO reveal insignificant differences in the relaxed atomic positions. Since our results predict only the Sn vacancy containing supercell of SSO to be energetically stable in the FM phase (as discussed in next section), Fig. 2(b) and (c) display the relaxed supercell of O and Sr vacancy containing SSO obtained with NM calculations.
The movements of 1st and 2nd nearest neighbor (NN) atoms away (positive values) and towards (negative values) the vacancy site in non-stoichiometric SSO for both NM and FM cases are presented in Table 3. For the case of Sn vacancy, the 1st NN Sr atom and 2nd NN O atom move outward and inward, respectively. Similarly, the 1st NN Sr atom to the vacant O site experiences an outward relaxation, while the 2nd NN Sn atoms move towards the vacant O site. In case of V0Sr, the 1st and 2nd NN anions move away from the vacant Sr site, while the 2nd NN Sr atoms are attracted towards the Sr vacancy. These results are consistent with the above-mentioned 2+, 4− and 2− charge states of Sr, Sn and O, respectively, which give rise to attractive and repulsive electrostatic interactions in Sr–O and Sn–O bonds, respectively.25,32 It is worth pointing out here that a comparison of the atomic movements in supercells relaxed with and without spin-polarization reveal that the outward and inward relaxation of Sr and O atoms around the vacant Sn site is reduced in case of FM ordering. This difference provides a clear indication of the birth of ferromagnetism in Sn deficient SSO.
| Vacancy type | NN | Calculation mode | Bond lengths in pristine SSO (Å) | Inward/outward movements |
|---|---|---|---|---|
| Sn | 1st (Sr × 12) | NM | 3.664 | +0.068 |
| FM | 3.664 | +0.058 | ||
| 2nd (O × 8) | NM | 4.487 | −0.013 | |
| FM | 4.487 | −0.009 | ||
| O | 1st (Sr × 6) | NM | 2.591 | +0.077 |
| FM | 2.591 | +0.077 | ||
| 2nd (Sn × 8) | NM | 4.487 | −0.002 | |
| FM | 4.487 | −0.002 | ||
| Sr | 1st (O × 2) | NM | 2.591 | +0.155 |
| FM | 2.591 | +0.155 | ||
| 2nd (Sn × 4) | NM | 3.664 | +0.105 | |
| FM | 3.664 | +0.105 | ||
| 2nd (Sr × 8) | NM | 3.664 | −0.188 | |
| FM | 3.664 | −0.188 |
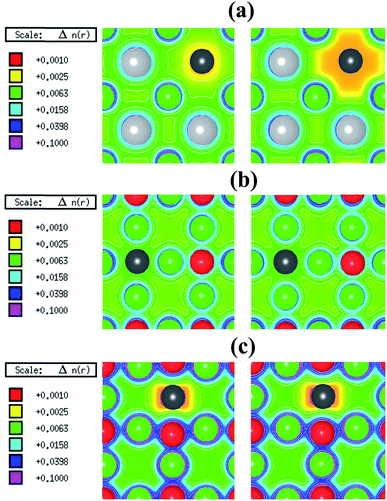
The spin-polarized electronic charge densities of Sn, O and Sr deficient SSO are displayed in Fig. 3. It is evident from these plots that only the electronic charge density of V0Sn containing supercell of SSO (Fig. 3(a)) shows dependence on spin-polarization. Although both O and Sn atoms are in negative charge state, the charge density at the vacant O site does not show any sensitivity to the application of spin-polarization. Similar behaviour is evident for Sr deficient SSO (Fig. 3(c)) where equal charge localization is seen for both majority spin and minority spin channels. The effective Bader charges of 1st NN O atom (−1.498 e) and 2nd NN Sn atom (−2.196 e) clearly support the charge localized for Sr deficient SSO. Since the effective Bader charge of 2nd NN Sn atom shows large reduction in case of Sr vacancy as compared to the Bader charge of 1st NN O atom, an anion-orbital like defect level with Sn-5p character would appear in the band structure of Sr deficient SSO.
In case of V0O, the calculated effective Bader charges of the 1st NN Sr (1.180 e) and 2nd NN Sn (−2.316 e) atoms reveal that breaking the Sr–O bond results in large reduction of e for the Sr atom. On the other hand, the calculated effective Bader charges of the 1st NN Sr atom (1.266 e) and 2nd NN O atom (−1.513 e) to the vacant Sn site show that tin vacancy does not lead to a significant charge reduction of Sr atom when the Sr–Sn bond is broken. The difference in the redistribution of Sr charge indicates that the bonding nature and coordination environments of the two anions (Sn4− and O2−) dictates the charge localization/delocalization in case of Sn/O vacancy. For a further analysis, we have also computed the effective Bader charges of the 3rd NN anions for both O and Sn vacancy cases. For the case of O vacancy, the 3rd NN O atom attains an effective Bader charge of −1.508 e, which is slightly less than the Bader charge of O in pristine SSO and confirms the completely charge delocalization of the six 1st NN Sr atom around the vacant oxygen site. This allows us to predict that the electronic structure of O deficient SSO results in a defect level populated by equal number of majority and minority spin charge carriers between the valence band maxima (VBM) and the conduction band minima (CBM) of bulk SSO. On the other hand, the effective Bader charge of 3rd NN Sn atom in case of a Sn vacancy containing supercell of SSO increases to −2.560 e. This shows that creation of V0Sn results in charge localization at the 1st NN Sr atom surrounding the vacant Sn site. Since the CBM of pristine SSO is made up of a hybridized Sr-4d and Sn-5p orbitals,12 the above analysis allows us to predict that partially filled Sr dangling bond with a Sr-4d character are responsible for stable ferromagnetism in SSO.
The evaluation of defect formation energies, Ω(X), by DFT in a supercell geometry has developed into useful tool to predict the equilibrium concentrations of extrinsic and intrinsic point defects and defect complexes in semiconductors.33 The defect formation energies for Sr, Sn and O vacancy defects in SSO have been computed using the following equation34
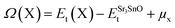 | (9) |
The first and second term in eqn (9) are the minimum total energies of structurally optimized SSO supercell containing a vacancy defect of type X (where X = Sn, O and Sr) and pristine SSO, respectively. The last term, μx, represents the atomic chemical potential limits of atom X that vary according to the chemical coordinates shown in Fig. 1.
The calculated defect formation energies for V0Sn, V0O and V0Sr under various growth conditions are shown in Fig. 4. Since both points A and B are the Sr-rich conditions, the formation energy of V0Sr is higher than V0O at these points. On the other hand, Sn vacancy assumes a formation energy less than the Sr vacancy at point A, which is the Sn-poor condition. This shows that under the Sr-rich condition, anion vacancies can be achieved relatively easily as compared to Sr vacancy. At points X, C and D Ω(Sr) is found to be less than both Ω(Sn) and Ω(O), which suggests easy incorporation of Sr vacancy in SSO at these stability points. The defect formation energies of Sn vacancy is found to be lowest at both points A.
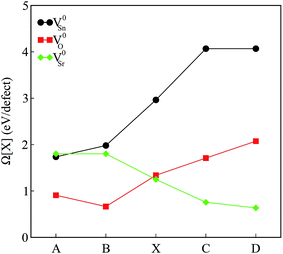 | ||
| Fig. 4 The calculated formation energies of charge neutral intrinsic vacancies in Sr3SnO at the stability points defined in Fig. 1. | ||
As mentioned earlier, our calculations reveal that only the incorporation of Sn vacancy in SSO leads the system into a FM phase. At a first sight, this finding may seem contradictory to the experimental observations16 which suggested oxygen vacancies to be responsible for enhancement of room temperature FM in SSO. Although Lee et al.16 show that vacuum annealing of SSO film enhances its FM, the oxygen vacancies are not solely responsible for magnetism in this material. According to bound magnetic polaron (BMP) model adopted in ref. 16 the magnetism in SSO requires oxygen vacancies to generate other vacancy defects (Sr and Sn vacancies) which interact with the host lattice to cause charge redistribution and increase the strength of FM. Comparison of the magnetic properties presented in next section and the formation energies shown in Fig. 4 also support this argument. Since the reduction (O-poor) conditions in Fig. 4 are also highly favorable for tin vacancies, it is likely for SSO to have Sn vacancies according to the BMP model.35 We have also tested the reliability of the formation energies presented in Fig. 4 by analyzing the effect of the size of the supercell on the calculated formation energies. To do this, we have computed Ω(Sn) for a single Sn vacancy containing 60-atom 2 × 2 × 3 supercell of SSO. A small difference in the calculated formation energies (25 meV) shows that the 2 × 2 × 2 supercell of SSO gives reliable account of the relative stability of the intrinsic vacancy defects studied in this work.
| Vacancy type | MMtot (μB) | MMI (μB) | MMSr (μB) | MMO (μB) | MMSn (μB) | ΔE = ENM − EFM (meV) |
|---|---|---|---|---|---|---|
| Sr24Sn7O8 | 1.282 | 1.076 | 0.015 | 0.003 | −0.002 | +32.856 |
| Sr24Sn8O7 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.461 |
| Sr23Sn8O8 | 0.011 | 0.011 | 0.000 | 0.000 | 0.000 | −0.155 |
Contrary to the predictions for the origins of FM in SSO in some earlier experimental studies,8,17 our results suggest that both cation (Sr) and oxygen vacancies are not responsible for FM in SSO. A close inspection of the magnetic moments at 1st and 2nd NN atoms of the vacancy site show that the total magnetic moment does not reside at the atoms surrounding the vacancy site. Since the anionic nature of Sn in SSO results in different charge localization for majority and minority spin channels, the large total magnetic moment in case of Sn vacancy containing supercell is caused by the spin-polarization of Sr dangling bond with partially filled Sr-4d states.
From the calculated ΔE listed in Table 4 we can estimate the TC of intrinsic vacancy containing SSO by using the Heisenberg model38
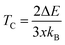 | (10) |
In above relation, kB is the Boltzmann constant, while x represents the Sn vacancy concentration in the 2 × 2 × 2 supercell of SSO. Using the values of ΔE listed in Table 4, we find that only the Sn vacancy containing supercell can lead to stable room temperature FM in SSO with a TC = 290 K. This agrees well with experimentally observed room temperature FM ordering in SSO.8
The left panel of Fig. 5 displays the energy band structure of pristine SSO computed using bare PBE-GGA functional, while the effect of the inclusion of SOC on the PBE-GGA electronic band structure is shown in the right panel of Fig. 5. When SOC is not taken into account for PBE-GGA calculations, the electronic band structure of SSO shows an energy gap between the VBM and CBM at Γ-point which is also confirmed by the DOS plots shown in Fig. 6. However, the most striking feature of the band structure obtained with bare PBE-GGA is the energy bands crossing the EF between Γ–X and Γ–X directions. This crossing is a well known shortcoming of bare GGA/LDA band structures for TI materials which can be corrected by the inclusion of SOC.11,42 The inset in the right panel of Fig. 5 displays the typical avoided-crossing feature43 in the band structure of SSO which appears when SOC is included in the PBE-GGA electronic structure calculations. In a recent work, it was reported that the band structure obtained using WIEN2k12 appears to be substantially different as compared to the one computed using Heyd–Scuseria–Ernzerhof (HSE) functionals.42 However, it is clear from Fig. 5 that our calculated electronic band structure qualitatively resembles the screened Coulomb hybrid density functional band structure reported in ref. 44. In addition we also note that the electronic band structure of SSO obtained using WIEN2k PBE-GGA + SOC calculation along M–Γ–R k-path agrees well with the band structure obtained from full-potential linear muffin-tin orbital method as reported in ref. 11. It is clear from Fig. 5 that the electronic band structure of SSO computed using PBE-GGA + SOC has an energy band gap of 0.316 eV at the Γ point. On the other hand, the valence bands crossing the EF around Γ point and the avoided-crossing supports the idea that SSO lies at the border line between topological insulator and a trivial insulator.40 Since electronic band structure of inverse perovskites are very sensitive to lattice parameters, we suspect that the choice of lattice parameter and/or the energy cut-off for the FP-LAPW may be responsible for the electronic band structure of SSO presented in ref. 12. For a further confirmation of bulk TI phase of SSO, we have computed the inversion energy, Δi = ε4d − ε5p,40 which is found to be −0.435 eV. Moreover, an analysis of the irreducible representation of eigenvalue for the electronic bands at the Γ point reveals even (+) and odd (−) parities of the orbitals at the edges of VBM and CBM, respectively. These results confirm the inverted parities of SSO, suggesting the possibility of achieving TI behaviour in this material.42
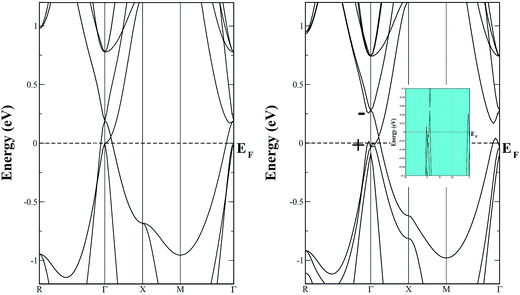 | ||
| Fig. 5 The energy band structure diagrams of pristine Sr3SnO calculated using PBE-GGA (left panel), and PBE-GGA + SOC (right panel). | ||
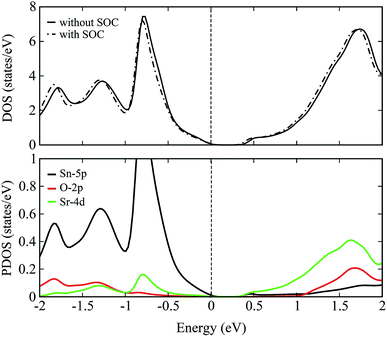
The total density of states (DOS) plots corresponding to band structures shown in Fig. 5 are displayed in Fig. 6(a). Comparison of the total DOSs indicate that the inclusion of SOC causes the Sn-5p orbitals in the upper valence band to slightly shift away from the EF. The partial DOS plots shown in Fig. 6(b), reveal that the VBM of SSO is predominantly made up of the Sn-5p states, while Sr-4d states contribute below the VBM. The contributions of Sr-4d states in the valence band reduces around −1 eV where O-2p states become dominant. The lowest edge of CBM, on the other hand, appears to be dominated by a hybridization of Sn-5p orbitals and Sr-4d orbitals. This trend changes to a dominant Sr-4d character in the conduction band as one moves farther away from the EF. Fig. 6(b) clearly shows a hybridized p–d DOS in the lowest edge of conduction band of pristine SSO which resemble the characteristics of DOS in Sr2Sn44 and confirms the highly covalent bonding nature of Sr–Sn bond in SSO. Compared to the case of bare PBE-GGA, the absence of Fermi level crossing, negative inversion energy and a narrow band gap encourages us to explore the electronic structure of intrinsic vacancy containing SSO using only the PBE-GGA + SOC.
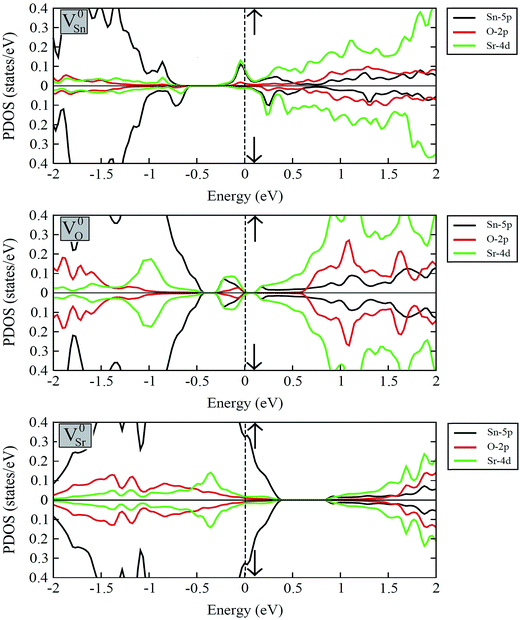
Fig. 7 displays the calculated spin-polarized partial DOS plots of intrinsic vacancy defect containing supercells of SSO with the inclusion of SOC. Comparison of Fig. 6 and 7 shows that in case of V0Sr upper valence band crosses the Fermi level, giving rise to a p-type nature to SSO. As discussed earlier, the incorporation of Sr vacancy results in removal of electrons from the occupied anion orbitals of the valance band. Consequently, the charge densities of neighboring O and Sn atoms become localized, which causes the unoccupied states in the upper valence band to move towards positive energy values. Contrary to this, the removal of an O atom from SSO results in breaking of the Sr–O bond. Since the effective Bader charges of neighboring Sn and O atoms do not show large changes upon creation of V0O, the charge density of Sr atoms surrounding the oxygen vacancies become highly delocalized. As evident from Fig. 7, the delocalization of Sr charge density upon introduction of an oxygen vacancy results in the creation of an occupied defect level between the CBM and VBM which is predominantly made up of Sn-5p and Sr-4d orbitals. The delocalized nature of charge in case of oxygen vacancy defect is, therefore, responsible for equal majority and minority spin carriers, no spin-polarization.
The strong covalent nature of the Sr–Sn bond (as evident from the calculated effective Bader charges) emerges from the p–d hybridization.45 On the introduction of Sn vacancy in SSO the charge in the defective supercell is redistributed in such a way that it does not undergo delocalization which is commonly observed in anion deficient perovskite oxides. This leads to unequal majority and minority spin carriers localized at the dangling bonds of the 1st NN Sr atoms resulting in a spin-polarized band structure of V0Sn containing SSO. This is clearly visible in the partial DOS plots of Sn deficient SSO where an occupied defect level predominantly made up of Sr-4d orbitals appears in the majority spin channel, while the same orbital contributions are unoccupied and positioned above the EF for minority spin channel. The spin-polarization of Sn vacancy containing SSO leads to a metallic nature for the majority spin channel, while an insulating character is achieved for the minority spin channel. The spin-polarized electronic DOS of V0Sn containing supercell of SSO, therefore, confirms the experimentally observed ferromagnetism in SSO.
4. Conclusions
First-principles DFT calculations have been performed to evaluate electronic, thermodynamic and magnetic properties of pristine and intrinsic vacancy defect containing SSO. Our calculated thermodynamic stability diagram of SSO shows good agreement with experimental data and provides appropriate limits of atomic chemical potentials of Sr, Sn and O. The calculated formation energies show that O and Sn vacancies have low formation energies under O-poor and Sn-poor conditions, respectively, while Sr vacancy is found to be the most stable form of neutral intrinsic vacancy defect under O-rich condition. We found that Sr and O vacancy containing SSO is non-magnetic, while Sn vacancy containing SSO give rise to stable ferromagnetism. Our results indicate that electronic and magnetic properties of Sr3SnO are strongly dependent upon chemical environment which allows tuning these properties during experimental synthesis. The calculated band structure and density of states confirm the topological behavior of pristine SSO, while the calculated values of effective Bader charges reveal ionic and covalent nature of bonding in Sr–O and Sr–Sn bonds, respectively. The Sr and O vacancy containing SSO is found to be non-magnetic, while Sn vacancy containing SSO gives rise to stable ferromagnetism. We shows that the ferromagnetism in Sn deficient SSO originates from spin-polarization of partially occupied Sr dangling bond which have a predominant Sr-4d character.References
- S. V. Ovsyannikov and V. V. Schchenniikov, Chem. Mater., 2009, 22, 635–647 CrossRef.
- B. He, C. Dong, L. Yang, X. Chen, L. Ge, L. Mn and Y. Shi, Supercond. Sci. Technol., 2013, 26, 1–6 CrossRef.
- R. Huang, L. Li, Z. Wu, X. Chu, X. Xu and L. Qian, Solid State Commun., 2010, 150, 1617–1620 CrossRef CAS.
- K. Kamishima, T. Goto, H. Nakagawa, N. Miura, M. Ohashi and N. Mori, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 24426–24429 CrossRef.
- K. Asano, K. Koyama and K. Takenaka, Appl. Phys. Lett., 2008, 92, 161909 CrossRef.
- B. S. Wang, P. Tong, Y. P. Sun, W. Tang, L. J. Li, X. B. Zhu, Z. R. Yang and W. H. Song, Phys. B, 2010, 405, 2427–2430 CrossRef CAS.
- M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045–3066 CrossRef CAS.
- Y. F. Lee, R. Kumar, F. Hunte, J. Schwartz and J. Narayan, Appl. Phys. Lett., 2013, 103, 112011 Search PubMed.
- T. Ditl, Nat. Mater., 2010, 9, 965–974 CrossRef PubMed.
- A. Widera and H. Schafer, Mater. Res., 1980, 15, 1805–1809 CAS.
- M. Klintenberg, J. T. Haraldsen and A. V. Balastsky, Appl. Phys. Res., 2014, 6, 31–41 CAS.
- M. Oudah, A. Ikeda, S. Yonezawa, T. Fukumoto, S. Kobayashi, M. Sato and Y. Maeno, 2016, arXiv: 1604.06238 Cond-Mat. Supr-Con, 1–24.
- D. Cherrad, M. Maouche, M. Maamache and L. Krache, Phys. B, 2011, 406, 2714–2722 CrossRef CAS.
- H. L. Tuller and S. R. Bishop, Annu. Rev. Mater. Res., 2011, 41, 369 CrossRef CAS.
- S. Ghosh, G. G. Khan and K. Mandal, ACS Appl. Mater. Interfaces, 2012, 4, 2048 CAS.
- Y. F. Lee, J. Narayan and J. Schwatz, MRS Commun., 2014, 4, 7–13 CrossRef CAS.
- Y. F. Lee, J. Narayan and J. Schwatz, J. Appl. Phys., 2014, 116, 164901–164907 CrossRef.
- P. Blaha, K. Schwarz, G. Madsew, D. Kvasnicka and J. Luitz, WIEN 2k: An Augmented Plane Wave Plus Local Orbital Program, Vienna University of Technology, Austeria, 2014 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396–1399 CrossRef CAS.
- M. C. Verbraeken, E. Suard and J. T. S. Irvine, J. Mater. Chem., 2009, 19, 2766–2770 RSC.
- A. Wadera and H. Schafer, J. Less-Common Met., 1981, 77, 29–36 CrossRef.
- S. M. Alay-e-Abbas and A. Shaukat, J. Phys.: Condens. Matter, 2014, 26, 44501–44510 CrossRef PubMed.
- K. Sato, P. H. Dederichs, H. Katayama-Yoshida and J. Kudrnovsky, J. Phys.: Condens. Matter, 2004, 16, S5491–S5497 CrossRef CAS.
- S. B. Zhang and J. E. Northup, Phys. Rev. Lett., 1991, 67, 2339–2342 CrossRef CAS PubMed.
- P. Erthart and K. Albe, J. Appl. Phys., 2007, 102, 084111 CrossRef.
- F. Tran, R. Laskowski, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 115131 CrossRef.
- K. H. Xue, P. Blaise, L. R. C. Fonseca and Y. Nishi, Phys. Rev. Lett., 2013, 110, 065502 CrossRef PubMed.
- M. W. Chase Jr, NIST-JANAF Thermodynamics Tables, NIST, 4th edition. J. Phys. Chem. Ref. data, Monograh, No 9, 1998 Search PubMed.
- J. Zhao, Y. Du, L. Zhang, A. Wang, L. Zhou, D. Zhao and J. Liang, Thermochim. Acta, 2012, 529, 74–79 CrossRef CAS.
- J. Nuss, C. Muhle, K. Hayama, V. Abdolazimi and H. Takagi, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 300–312 CAS.
- R. F. W. Bader, Acc. Chem. Res., 1859, 18, 9 CrossRef.
- T. Tanaka, K. Matsunaga, Y. Ikuhara and T. Yamamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 2052131 Search PubMed.
- C. Freysoldt, B. Lange and J. Neugebauer, Phys. Rev. B, 2016, 93, 165206 CrossRef.
- N. D. M. Hine, K. Frensch, W. M. C. Foulkes and M. W. Finnis, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 024112 CrossRef.
- J. M. D. Coey, K. Wongsaprom, J. Alaria and M. Venkatesan, J. Phys. D: Appl. Phys., 2008, 41, 134012 CrossRef.
- G. Z. Xing, Y. H. Lu, Y. F. Tian, J. B. Yi, C. C. Lim, Y. F. Li, G. P. Li, D. D. Wang, B. Yao, J. Ding, Y. P. Feng and T. Wu, AIP Adv., 2011, 1, 221521 Search PubMed.
- S. Ning, P. Zhan, Q. Xie, W. Wang and Z. Zhang, J. Mater. Sci. Technol., 2015, 31, 969–978 Search PubMed.
- V. A. Dinh and H. K. Yoshida, J. Electron Microsc., 2005, 54, 161–164 CrossRef PubMed.
- V. Stevanović, S. Lany, X. Zhang and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115104 CrossRef.
- J. Vidal, X. Zhang, L. Yu, J. W. Luo and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 041109(R) CrossRef.
- X. L. Qi and S. Zhang, Phys. Today, 2010, 63, 33–38 CrossRef CAS.
- T. H. Hsieh, J. Liu and L. Fu, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 081112(R) CrossRef.
- T. Kariyado and M. Ogata, J. Phys. Soc. Jpn., 2011, 80, 083704 CrossRef.
- X. M. Du, R. Q. Chen and L. L. Liu, Dig. J. Nanomater. Biostruct., 2016, 11, 719–729 Search PubMed.
- K. Schwarz, CRC Crit. Rev. Solid State Mater. Sci., 1987, 13, 211 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |