Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural, electronic and optical properties of 2,5-dichloro-p-xylene: experimental and theoretical calculations using DFT method†
G. Venkatesh*a,
M. Govindarajub,
C. Kamalc,
P. Vennilad and
S. Kayae
aR&D Centre, Bharathiar University, Coimbatore-641 046, India. E-mail: venkateshindhuja@gmail.com; Tel: +91 9965285541
bDepartment of Chemistry, Arignar Anna Government Arts College, Namakkal-638 052, India
cDepartment of Chemistry, VSA Group of Institutions, Salem, Tamil Nadu-636010, India
dDepartment of Chemistry, Thiruvalluvar Government Arts College, Rasipuram-638 052, India
eDepartment of Chemistry, Cumhuriyet University, Sivas-58140, Turkey
First published on 5th January 2017
Abstract
The vibrational spectra including FT-IR and FT-Raman for 2,5-dichloro-p-xylene (DCPX) have been recorded. All the energies, the geometry of the compound and vibrational frequencies of (DCPX) have been calculated using density functional theory (DFT/B3LYP) method coupled with 6-31G* and 6-311+G** functionals. The occurrence of charge transfer was known from the HOMO–LUMO energy gap of DCPX. In order to find out the electronic excitation energies, oscillator strength and nature of the respective excited states, the closed-shell singlet calculation method has been utilized for DCPX. The values of the total dipole moment (µ) and the first order hyperpolarizability (β) of DCPX have been investigated. The non-linear optical (NLO) behavior of DCPX has been identified from the results of hyperpolarizability values.
1 Introduction
Xylene is an aromatic hydrocarbon which has two methyl groups substituted in benzene at various positions. Xylene is a major petrochemical produced by the carbonisation of coal in the manufacturing of coke fuel, which represents about 0.5–1% of crude oil and is established in a small amount in gasoline and aircraft fuels. p-Xylene is a benzene based aromatic hydrocarbon having two substituted methyl groups with the molecular formula C8H10 or C6H4(CH3)2. The position of the two methyl groups in the aromatic ring has been identified from the symbol “p” which revealed it as para position. Xylene is used on a large scale for the manufacture of terephthalic acid for polyester.1–4Xylene is the principal precursor to terephthalic acid and dimethyl terephthalate, both are used in the production of polyethylene terephthalate (PET) plastic bottles and polyester clothing. It is widely used as a solvent in the leather, rubber and printing industries. Xylene is used as a sealer/carrier solvent in acrylic concrete which is a widely used concrete protector.5–9 Arjunan et al., examined the vibrational properties of 4-nitro and 5-nitro-m-xylene.10 Govindarajan and his co-workers have reported vibrational, spectral and NLO properties of 2-chloro-xylene.11 Chemical properties and anticancer activity of α,α,α′,α′ tetra bromo-p-xylene were reported by M. Manzoor ali and his co-workers.12 Arivazhagan et al., reported the vibrational spectroscopic studies of 4-bromo-o-xylene.13
True to the best of our knowledge, the structural features and vibrational analysis of 2,5-dichloro xylene by DFT methods have not been reported, so far. Thus, considering the industrial importance of xylene derivatives, the experimental and theoretical calculation of DCPX using DFT method with the B3LYP (Becke's three-parameter (B3) Lee–Yang–Parr's (LYP) correlation exchange in functional) functional has been reported in the present study with a view to explore the structural characteristics.14,15 Quantum chemical computational methods have been proved to be very significant in interpreting and assuming the vibrational spectra, recent past. For instance, a complete vibrational and molecular structure analysis of 2-methoxy-5-nitrophenol and 2-methoxy-4-methylphenol isomers has been evaluated using quantum mechanical approach by HF and DFT calculations by Meenakshi.16 Spectroscopic, single crystal XRD structure, DFT and molecular dynamics investigation of Sheena mary et al., examined 1-(3-chloro-4-fluorophenyl)-3-[3-(trifluoromethyl)phenyl]thiourea using DFT for it molecular dynamics.17 DFT has also been applied to examine the structural features, NLO properties of heterocyclic 5-nitro-1,3-benzodioxole and its applications on solar cells.18
A significant development has been achieved by combining the empirical method with DFT information in the scaled quantum mechanical (SQM) force field method. In SQM approach, the deviations of the computed harmonic force field are rectified using some scale factors which are found to be well transferable between chemically related molecules and they were preferred to use. The calculated IR and Raman vibrational spectral assessment of DCPX were also simulated using the computed dipole moments for IR intensities and polarizabilities for Raman intensities.
2 Experimental details
DCPX as finely powdered solid was obtained from Lancaster Chemical Company of UK. The FT-IR spectra of DCPX have been recorded using KBr pellet technique in the region 4000–400 cm−1 with a resolution of 1 cm−1 using BRUKER IFS 66 V spectrophotometer coupled with He–Ne laser source at room temperature. The FT-Raman spectra has also been recorded on a same instrument equipped with FRA-106 FT-Raman accessory in 4000–100 cm−1 stoke region with 1064 nm line of a Nd:YAG Laser for excitation which is operating at 200 mW power. The minimal accuracy of wave numbers was assumed to be ±1 cm−1.3 Computational details
To provide the complete information regarding the molecular structural characteristics and the fundamental vibrational modes of DCPX, the restricted DFT-B3LYP correlation functional calculations have been carried out.14,15 The calculations of geometrical parameters in the ground state were performed using the GAUSSIAN 09W programs. The geometry optimization was carried out using the initial geometry generated from standard geometrical parameters and B3LYP methods adopting 6-31G*/6-311+G** functional to characterize all stationary points as minima. The optimized structural parameters of the compound were used for harmonic vibrational frequency calculations resulting in IR and Raman frequencies together with intensities and Raman depolarization ratios. In DFT methods, Becke's three parameter exchange-functional (B3) jointed with gradient-corrected correlation functional of Lee, Yang and Parr (LYP) by employ the split-valence polarized 6-311+G** functional have been developed for the computation of molecular structure optimization, vibrational frequencies and energies of the molecular optimized structures.The vibrational modes were assigned by means of visual inspection using the GAUSSVIEW program. The symmetry of the vibrational modes was determined by standard procedure of decomposition of the traces of the symmetry operations into the irreducible representations. The derivation (given below) obtained from the theory of Raman scattering has been utilized to convert the Raman activities (Si) calculated by GAUSSIAN 09W program into relative Raman intensities (Ii)
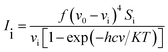 | (1) |
4 Results and discussion
4.1. Geometrical parameters
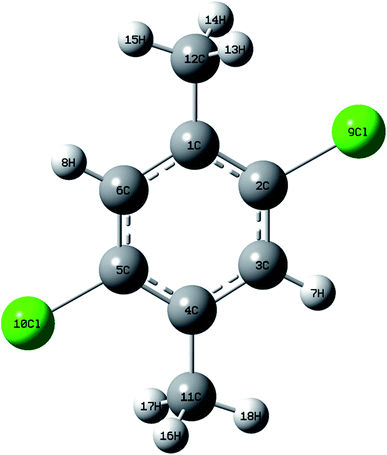
DCPX contains two methyl groups at para position and two chlorine atoms in aromatic benzene ring. The optimized molecular structure has been obtained from Gaussion09W program.19 The non linear molecular structure of DCPX illustrates Cs symmetry (Fig. 1). The global minimum energy has been obtained by the DFT molecular optimization structure and is given in Table S1 ESI.† The obtained energies are as follows −1229.95 (Hartee) B3LYP/6-31G*, −1230.07 (Hartee) by B3LYP/6-311G** for gaseous phase and −1229.54 (Hartee) by B3LYP/6-311G** −1230.09 (Hartee) aqueous phase. Table 1 compares the theoretically calculated bond lengths, bond angles and dihedral angles with X-ray data values. The optimized bond lengths are in the order as follows C2–C3 < C5–C6 < C1–C2 < C4–C5 < C1–C6 < C3–C4. It is clear from Table 1 that, the carbons substituted by methyl groups have larger bond lengths and the carbons substituted by halogens possess lower bond lengths when compared to all other ring atoms.10,12,20 This could be due to the inductive effect of methyl group and chlorine atoms as well as resonance effect of phenyl ring (substitution effect). +I effect of methyl group pushed out the electrons towards the phenyl ring. But, the −I effect of chlorine atoms and resonance effect of phenyl ring competed with each other to pull the electrons towards themselves. These effects resulted in larger bond lengths of carbons substituted by methyl group meanwhile shorter bond lengths of carbons substituted by halogen atoms.21,22 From the bond lengths, it is clearly known that, the aromatic ring is slightly distorted from perfect hexagonal structure. It could be due to the substitutions of halogens and methyl groups in para position. The calculated bond lengths for C1–C12 & C4–C12 of about 1.51 Å, the methyl C–H in the range 1.09–1.10 Å and ring C–H as 1.08 Å are correlated well with the standard values. But, the bond length of C–Cl observed as 1.83 Å is higher than the standard values.21,22| Gaseous phase | Aqueous phase | X-ray data values (Å) | ||||
|---|---|---|---|---|---|---|
| B3LYP/6-31G* | B3LYP/6-311G** | B3LYP/6-311G** | ||||
| Bond length | Value (Å) | Bond length | Value (Å) | Bond length | Value (Å) | |
| C1–C2 | 1.389 | C1–C2 | 1.396 | C1–C2 | 1.396 | 1.399 |
| C1–C6 | 1.398 | C1–C6 | 1.403 | C1–C6 | 1.402 | 1.399 |
| C1–C11 | 1.508 | C1–C11 | 1.507 | C1–C11 | 1.507 | 1.511 |
| C2–C3 | 1.381 | C2–C3 | 1.387 | C2–C3 | 1.386 | 1.399 |
| C2–Cl9 | 1.831 | C2–Cl9 | 1.835 | C2–Cl9 | 1.836 | 1.771 |
| C3–C4 | 1.406 | C3–C4 | 1.405 | C3–C4 | 1.405 | 1.399 |
| C3–H7 | 1.083 | C3–H7 | 1.080 | C3–H7 | 1.080 | 1.098 |
| C4–C5 | 1.391 | C4–C5 | 1.398 | C4–C5 | 1.397 | 1.399 |
| C4–C12 | 1.508 | C4–C12 | 1.507 | C4–C12 | 1.507 | 1.511 |
| C5–C6 | 1.383 | C5–C6 | 1.389 | C5–C6 | 1.388 | 1.399 |
| C5–Cl10 | 1.831 | C5–Cl10 | 1.835 | C5–Cl10 | 1.836 | 1.771 |
| C6–H8 | 1.083 | C6–H8 | 1.080 | C6–H8 | 1.080 | 1.098 |
| C11–H13 | 1.096 | C11–H13 | 1.092 | C11–H13 | 1.092 | 1.120 |
| C11–H14 | 1.096 | C11–H14 | 1.092 | C11–H14 | 1.092 | 1.120 |
| C11–H15 | 1.093 | C11–H15 | 1.090 | C11–H15 | 1.088 | 1.120 |
| C12–H16 | 1.096 | C12–H16 | 1.092 | C12–H16 | 1.092 | 1.120 |
| C12–H17 | 1.093 | C12–H17 | 1.090 | C12–H17 | 1.088 | 1.120 |
| C12–H18 | 1.096 | C12–H18 | 1.092 | C12–H18 | 1.092 | 1.120 |
| Bond angle | Value (°) | Bond angle | Value (°) | Bond angle | Value (°) | X-ray data values (Å) |
|---|---|---|---|---|---|---|
| C2–C1–C6 | 117.130 | C2–C1–C6 | 117.059 | C2–C1–C6 | 117.124 | 118.6 |
| C2–C1–C11 | 120.945 | C2–C1–C11 | 120.008 | C2–C1–C11 | 120.346 | — |
| C6–C1–C11 | 120.925 | C6–C1–C11 | 120.983 | C6–C1–C11 | 120.930 | — |
| C1–C2–C3 | 121.574 | C1–C2–C3 | 121.691 | C1–C2–C3 | 121.683 | 120.0 |
| C1–C2–Cl9 | 119.333 | C1–C2–Cl9 | 119.281 | C1–C2–Cl9 | 119.063 | — |
| C3–C2–Cl9 | 118.623 | C3–C2–Cl9 | 117.528 | C3–C2–Cl9 | 117.255 | — |
| C2–C3–C4 | 119.326 | C2–C3–C4 | 119.320 | C2–C3–C4 | 119.393 | 120.0 |
| C2–C3–H7 | 119.740 | C2–C3–H7 | 119.746 | C2–C3–H7 | 120.123 | — |
| C4–C3–H7 | 119.433 | C4–C3–H7 | 119.455 | C4–C3–H7 | 119.283 | — |
| C3–C4–C5 | 117.130 | C3–C4–C5 | 117.069 | C3–C4–C5 | 111.124 | 120.0 |
| C3–C4–C12 | 120.925 | C3–C4–C12 | 120.983 | C3–C4–C12 | 120.930 | — |
| C5–C4–C12 | 120.945 | C5–C4–C12 | 120.008 | C5–C4–C12 | 120.346 | — |
| C4–C5–C6 | 119.044 | C4–C5–C6 | 119.191 | C4–C5–C6 | 119.683 | 120.0 |
| C4–C5–Cl10 | 119.333 | C4–C5–Cl10 | 119.281 | C4–C5–Cl10 | 119.063 | — |
| C6–C5–Cl10 | 118.623 | C6–C5–Cl10 | 118.528 | C6–C5–Cl10 | 118.255 | — |
| C1–C6–C5 | 119.326 | C1–C6–C5 | 119.390 | C1–C6–C5 | 119.393 | 120.0 |
| C1–C6–H8 | 119.433 | C1–C6–H8 | 119.455 | C1–C6–H8 | 119.283 | — |
| C5–C6–H8 | 119.740 | C5–C6–H8 | 119.746 | C5–C6–H8 | 120.123 | — |
| C1–C11–H13 | 110.273 | C1–C11–H13 | 111.307 | C1–C11–H13 | 111.271 | — |
| C1–C11–H14 | 111.271 | C1–C11–H14 | 111.304 | C1–C11–H14 | 111.270 | — |
| C1–C11–H15 | 110.763 | C1–C11–H15 | 110.744 | C1–C11–H15 | 110.706 | — |
| H13–C11–H14 | 109.851 | H13–C11–H14 | 109.906 | H13–C11–H14 | 109.101 | — |
| H13–C11–H15 | 108.258 | H13–C11–H15 | 108.206 | H13–C11–H15 | 108.165 | — |
| H14–C11–H15 | 108.268 | H14–C11–H15 | 108.215 | H14–C11–H15 | 108.175 | — |
| C4–C12–H16 | 111.271 | C4–C12–H16 | 111.304 | C4–C12–H16 | 111.270 | — |
| C4–C12–H17 | 110.763 | C4–C12–H17 | 110.744 | C4–C12–H17 | 110.706 | — |
| C4–C12–H18 | 111.273 | C4–C12–H18 | 111.307 | C4–C12–H18 | 111.271 | — |
| H16–C12–H17 | 108.268 | H16–C12–H17 | 108.215 | H16–C12–H17 | 108.175 | — |
| H16–C12–H18 | 107.851 | H16–C12–H18 | 107.906 | H16–C12–H18 | 107.101 | — |
| H17–C12–H18 | 108.258 | H17–C12–H18 | 108.206 | H17–C12–H18 | 108.165 | — |
| Dihedral angle | Value (°) | Dihedral angle | Value (°) | Dihedral angle | Value (°) | — |
|---|---|---|---|---|---|---|
| C6–C1–C2–C3 | 0.013 | C6–C1–C2–C3 | 0.025 | C6–C1–C2–C3 | 0.016 | — |
| C6–C1–C2–Cl9 | −179.981 | C6–C1–C2–Cl9 | −179.990 | C6–C1–C2–Cl9 | −179.980 | — |
| C11–C1–C2–C3 | 179.992 | C11–C1–C2–C3 | 180.009 | C11–C1–C2–C3 | 179.999 | — |
| C11–C1–C2–Cl9 | −0.003 | C11–C1–C2–Cl9 | −0.008 | C11–C1–C2–Cl9 | −0.001 | — |
| C2–C1–C6–C5 | −0.014 | C2–C1–C6–C5 | −0.014 | C2–C1–C6–C5 | −0.013 | — |
| C2–C1–C6–H8 | −179.992 | C2–C1–C6–H8 | −180.000 | C2–C1–C6–H8 | −180.000 | — |
| C11–C1–C6–C5 | −179.993 | C11–C1–C6–C5 | −180.000 | C11–C1–C6–C5 | −180.000 | — |
| C11–C1–C6–H8 | 0.013 | C11–C1–C6–H8 | 0.011 | C11–C1–C6–H8 | 0.014 | — |
| C2–C1–C11–H13 | −59.519 | C2–C1–C11–H13 | −59.577 | C2–C1–C11–H13 | −59.687 | — |
| C2–C1–C11–H14 | 59.520 | C2–C1–C11–H14 | 59.575 | C2–C1–C11–H14 | 59.665 | — |
| C2–C1–C11–H15 | −179.993 | C2–C1–C11–H15 | −180.000 | C2–C1–C11–H15 | −180.010 | — |
| C6–C1–C11–H13 | 120.459 | C6–C1–C11–H13 | 120.405 | C6–C1–C11–H13 | 120.295 | — |
| C6–C1–C11–H14 | −120.502 | C6–C1–C11–H14 | −120.440 | C6–C1–C11–H14 | −120.350 | — |
| C6–C1–C11–H15 | −0.016 | C6–C1–C11–H15 | −0.014 | C6–C1–C11–H15 | −0.023 | — |
| C1–C2–C3–C4 | 0.001 | C1–C2–C3–C4 | −0.012 | C1–C2–C3–C4 | −0.004 | — |
| C1–C2–C3–H7 | −180.005 | C1–C2–C3–H7 | −180.020 | C1–C2–C3–H7 | −180.010 | — |
| Cl9–C2–C3–C4 | 179.995 | Cl9–C2–C3–C4 | 180.005 | Cl9–C2–C3–C4 | 179.997 | — |
| Cl9–C2–C3–H7 | −0.011 | Cl9–C2–C3–H7 | −0.004 | Cl9–C2–C3–H7 | −0.013 | — |
| C2–C3–C4–C5 | −0.014 | C2–C3–C4–C5 | −0.014 | C2–C3–C4–C5 | −0.013 | — |
| C2–C3–C4–C12 | −179.993 | C2–C3–C4–C12 | −180.000 | C2–C3–C4–C12 | −180.000 | — |
| H7–C3–C4–C5 | 179.992 | H7–C3–C4–C5 | −180.000 | H7–C3–C4–C5 | −180.000 | — |
| H7–C3–C4–C12 | 0.013 | H7–C3–C4–C12 | 0.011 | H7–C3–C4–C12 | 0.014 | — |
| C3–C4–C5–C6 | 0.013 | C3–C4–C5–C6 | 0.025 | C3–C4–C5–C6 | 0.016 | — |
| C3–C4–C5–Cl10 | −179.981 | C3–C4–C5–Cl10 | −179.990 | C3–C4–C5–Cl10 | −179.980 | — |
| C12–C4–C5–C6 | 179.992 | C12–C4–C5–C6 | 180.009 | C12–C4–C5–C6 | 179.999 | — |
| C12–C4–C5–Cl10 | −0.003 | C12–C4–C5–Cl10 | −0.008 | C12–C4–C5–Cl10 | −0.001 | — |
| C12–C4–C5–H16 | −120.502 | C12–C4–C5–H16 | −120.440 | C12–C4–C5–H16 | −120.350 | — |
| C3–C4–C12–H17 | −0.016 | C3–C4–C12–H17 | −0.014 | C3–C4–C12–H17 | −0.023 | — |
| C3–C4–C12–H18 | 120.459 | C3–C4–C12–H18 | 120.405 | C3–C4–C12–H18 | 120.295 | — |
| C5–C4–C12–H16 | 59.520 | C5–C4–C12–H16 | 59.575 | C5–C4–C12–H16 | 59.665 | — |
| C5–C4–C12–H17 | −179.993 | C5–C4–C12–H17 | −180.000 | C5–C4–C12–H17 | −180.010 | — |
| C5–C4–C12–H18 | −59.519 | C5–C4–C12–H18 | −59.577 | C5–C4–C12–H18 | −59.687 | — |
| C4–C5–C6–C1 | 0.001 | C4–C5–C6–C1 | −0.012 | C4–C5–C6–C1 | −0.004 | — |
| C4–C5–C6–H8 | −180.005 | C4–C5–C6–H8 | −180.020 | C4–C5–C6–H8 | −180.010 | — |
| Cl10–C5–C6–C1 | 179.995 | Cl10–C5–C6–C1 | 180.005 | Cl10–C5–C6–C1 | 179.997 | — |
| Cl10–C5–C6–H8 | −0.011 | Cl10–C5–C6–H8 | −0.004 | Cl10–C5–C6–H8 | −0.013 | — |
In addition, C2–C3–C4, C1–C6–C5 (119.3°), C2–C1–C6 & C3–C4–C5 (117.1°) bond angles are reduced than that of a benzene ring, but the C1–C2–C3 (121.6°) bond angle is enlarged. The dihedral angles obtained are represented in Table 1. From the Table, it can be seen that, the dihedral angels C6–C1–C2–C3, C2–C1–C6–C5 and C1–C2–C3–C4 are supported the planer nature of aromatic ring. The optimization geometry of DCPX showed that, two substituted methyl groups are out-of-plane of the ring.20–22 This has been evidenced from the dihedral angels of C2–C1–C11–H14 ≈ 60°, C6–C1–C11–H13 ≈ 120° and C5–C4–C12–H16 ≈ 60°, C3–C4–C12–H18 ≈ 120°. Similarly other two C11–H15 and C12–H17 are in-plane-bending of ring which has been known from the following dihedral angles C6–C1–C11–H15 ≈ 0° and C3–C4–C12–H17 ≈ 0°.
4.2. Assignments of spectra
Normal coordinate analysis provides a detailed description of vibrational modes. For this purpose, the full set of 62 standard internal coordinates containing 14 redundancies have been calculated and listed in Table S2 of ESI.† From these, a non-redundant set of local symmetry coordinates was constructed by appropriate linear combinations of internal coordinates according to Pulay et al.23 and they are presented in Table S3 of ESI.† DFT force fields calculated theoretically have been transformed as a set of vibrational coordinates and then used for all subsequent calculations. The fundamental modes of DCPX in terms of vibrational assignments associated with theoretical IR, Raman intensities and normal mode descriptions (characterized by PED) are listed in Table 2.| S. no. | Symmetry of species Cs | Observed frequency (cm−1) | Calculated frequency (cm−1) with B3LYP/6-311G** force field | PED (%) among type of internal coordinatesd | ||||
|---|---|---|---|---|---|---|---|---|
| Infrared | Raman | Unscaled | Scaled | IRb Ai | Ramanc Ii | |||
| a Abbreviations: ν – stretching, b – bending, γ – in-plane bending, β – out-of-plane bending, t – torsion, r – rocking, g – waging, ips – in-plane stretching, ops – out-of-plane stretching.b Relative absorption intensities normalized with highest peak absorption.c Relative Raman intensities calculated by eqn (1) and normalized to 100.d For the notations used see Table S3. | ||||||||
| 1 | A′ | 3249 | 3247 | 3245 | 14.762 | 63.175 | νCH (99) | |
| 2 | A′ | 3239 | 3237 | 3235 | 14.611 | 64.334 | νCH (99) | |
| 3 | A′ | 3160 | 3159 | 3157 | 0.004 | 152.4 | CH3 ips (98) | |
| 4 | A′ | 3158 | 3159 | 3155 | 4.946 | 0.094 | CH3 ips (98) | |
| 5 | A′ | 3115 | 3111 | 16.428 | 185.539 | CH3 ops (96) | ||
| 6 | A′ | 3114 | 3113 | 3110 | 20.01 | 152.897 | CH3 ops (96) | |
| 7 | A′ | 3061 | 3060 | 3056 | 12.537 | 73.311 | CH3 ops (96) | |
| 8 | A′ | 3057 | 3058 | 3055 | 9.822 | 93.552 | νCH3 (96) | |
| 9 | A′ | 1656 | 1653 | 0 | 42.075 | νCC (67), bCH (12), bring (11) | ||
| 10 | A′ | 1605 | 1602 | 1601 | 0.008 | 23.423 | νCC (53), γCH3 (15), bring (8), βCH3 (11) | |
| 11 | A′ | 1535 | 1532 | 1530 | 46.449 | 1.068 | γCH3 (49), βCH3 (45) | |
| 12 | A′ | 1526 | 1524 | 1521 | 44.231 | 0.632 | νCC (33), bCH (22), βCH3 (17), γCH3 (19) | |
| 13 | A′ | 1521 | 1518 | 2.961 | 20.565 | βCH3 (37), γCH3 (49), βCH3 (18) | ||
| 14 | A′ | 1515 | 1517 | 1514 | 8.508 | 14.364 | βCH3 (91), (CH3)r (5) | |
| 15 | A′ | 1510 | 1509 | 1506 | 3.936 | 17.38 | γCH3 (72), βCH3 (22) | |
| 16 | A′ | 1451 | 1448 | 0.41 | 22.795 | γCH3 (79), νCC (7), βCH3 (5) | ||
| 17 | A′ | 1447 | 1449 | 1446 | 0.271 | 30.536 | γCH3 (79), νCC (7), βCH3 (5) | |
| 18 | A′ | 1401 | 1399 | 1397 | 22.045 | 0.011 | νCC (38), γCH3 (12), βCH3 (15) | |
| 19 | A′ | 1334 | 1332 | 1329 | 2.69 | 0.004 | νCC (84) | |
| 20 | A′ | 1295 | 1294 | 0.015 | 0.098 | bCH (72), νCC (9) | ||
| 21 | A′ | 1262 | 1261 | 1257 | 0 | 26.44 | γCH (49), νCC (42), CCl (7) | |
| 22 | A′ | 1225 | 1223 | 1221 | 1.6 | 0 | γCH (37), νCC (42), bring (15) | |
| 23 | A′ | 1092 | 1089 | 123.645 | 0 | bring (46), νCCl (20), νCC (17), bCH (10) | ||
| 24 | A″ | 1081 | 1080 | 1078 | 5.982 | 0.113 | gCC (60), CH3r (23), gCH (5), βCH3 (5) | |
| 25 | A″ | 1078 | 1075 | 1070 | 0.706 | 1.022 | gCC (57), CH3r (24), tring (8) | |
| 26 | A′ | 1067 | 1065 | 1062 | 1059 | 1.492 | 2.605 | CH3r (56), γCH3 (13), βCH3 (9), νCC (7) |
| 27 | A′ | 1024 | 1020 | 26.262 | 0.204 | CH3r (45), γCC (17), γCH3 (11), βCH3 (8) | ||
| 28 | A″ | 954 | 952 | 949 | 0.001 | 5.648 | gCCl (34), νCC (24), bring (23), νCC (16) | |
| 29 | A″ | 895 | 893 | 890 | 19.957 | 0.001 | βCH (84), tring (8) | |
| 30 | A″ | 881 | 887 | 885 | 0.008 | 3.534 | βCH (80), tring (14) | |
| 31 | A′ | 775 | 776 | 774 | 26.255 | 0 | γCC (57), bring (21), νCCl (13) | |
| 32 | A′ | 726 | 725 | 721 | 0 | 16.305 | bring (58), γCC (19), νCCl (15) | |
| 33 | A″ | 704 | 702 | 0 | 0.525 | tring (62), gCCl (20), gCC (15) | ||
| 34 | A″ | 605 | 603 | 600 | 0.161 | 0 | tring (35), gCCl (34), gCC (27) | |
| 35 | A″ | 536 | 534 | 24.613 | 0 | gCCl (67), bring (14) | ||
| 36 | A′ | 530 | 528 | 525 | 0 | 5.872 | βCC (46), bCC (23), βCCl (38) | |
| 37 | A′ | 479 | 478 | 474 | 0 | 9.65 | bring (52), βCCl (7) | |
| 38 | A″ | 461 | 458 | 3.958 | 0 | tring (61), gCCl (19), gCC (16) | ||
| 39 | A″ | 352 | 350 | 348 | 0 | 1.355 | βCC (47), βCCl (47) | |
| 40 | A′ | 331 | 328 | 0 | 9.239 | bring (45), νCCl (43) | ||
| 41 | A′ | 295 | 294 | 290 | 3.36 | 0 | βCCl (41), bCCl (10) | |
| 42 | A″ | 246 | 244 | 0 | 2.35 | tring (31), gCCl (26), gCC (20), gCH (12) | ||
| 43 | A′ | 243 | 241 | 240 | 0 | 1.604 | bCCl (28), βCC1 (32), bring (9) | |
| 44 | A′ | 225 | 220 | 1.339 | 0 | bCCl1 (45) | ||
| 45 | A″ | 165 | 167 | 164 | 0.132 | 0 | βCH3 (40), gCCl (20), tring (16), gCH (11), gCC (10) | |
| 46 | A″ | 153 | 151 | 147 | 0.001 | 0.568 | tCH3 (56), gCC (7) | |
| 47 | A″ | 139 | 137 | 1.009 | 0 | tCH3 (6), gCC (20), tring (17), tCH3 (16), gCCl (9), gCH (8) | ||
| 48 | A″ | 90 | 88 | 1.352 | 0 | tring (90) | ||
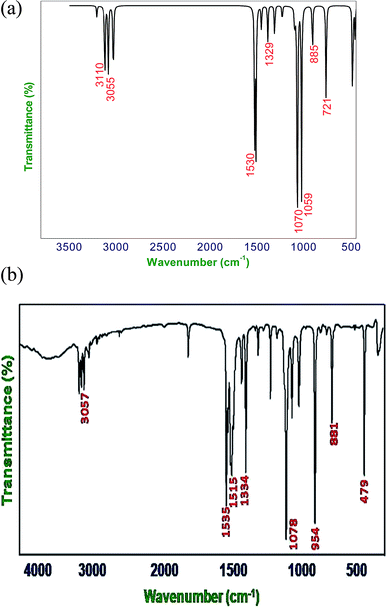
When using computational methods to predict theoretical normal vibrations for relatively complex polyatomic molecules, scaling strategies are used to bring computed wave numbers. The observed FT-IR and FT-Raman spectra of the DCPX were presented in Fig. 2 and 3. The 48 normal modes of DCPX are distributed among the symmetry species as Γ3N–6 = 33 A′ (in-plane) + 15 A″ (out-of-plane). The detailed vibrational assignments of fundamental modes of DCPX have been reported in Table S3.† Root mean square (RMS) values of frequencies were obtained in the study using the following expression,
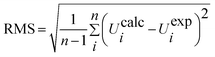 | (2) |
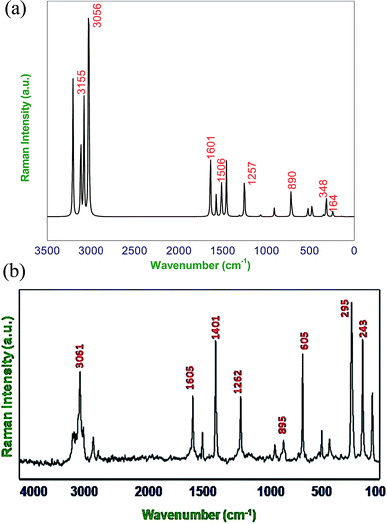 | ||
| Fig. 3 (a) Calculated (B3LYP/6-311G**) FT-Raman spectra of DCPX, (b) observed FT-Raman spectra of DCPX. | ||
The RMS frequency error is being 101 cm−1. Earlier report revealed that other methods than B3LYP such as HF showed more deviation in experimental and calculated values for substituted xylene derivative. Hence, B3LYP method has been adopted in the present study to calculate vibrational frequencies for DCPX according to Govindarajan et al.11 Systematic assignment is produced using the unscaled computed frequencies. Then for comparing the theoretical values, with the calculated frequencies, they were multiplied by a common scale factor of less than one to reduce the overall deviation. Pulay24 recommended a set of transferable coordinates to refine the scale factors. The least square refinement of the scale factors led to a mean deviation of 7.09 cm−1 for DCPX. The least square refinement of results relies on the frequencies observed and on the initial band assignments. The uniform scaling force field does not change the nature of calculated intensity patterns of simulated spectra, because it does not changes the vibrational modes. The selective scaling changes the frequencies in addition to changing the normal modes of vibrations. The changes in relative band intensities were caused by the changes in PED values which are corresponding to vibrational vectors.
The C–H out-of-plane bending vibrations which are strongly coupled vibrations usually occurred in the region 1000–750 cm−1.28,29 For DCPX, the strong bands in experimental FT-IR spectrum at 881 cm−1 (80%) suggested the existence of aromatic C–H out-of-plane bending vibrations and very strong band in experimental FT-Raman spectrum at 895 cm−1 (84%) confirmed the presence of aromatic C–H out-of-plane bending vibrations which are well correlated (885 cm−1 and 890 cm−1) with calculated vibrational spectra using B3LYP/6-311G** methods. The observation of smaller deviation of calculated vibrational frequencies with experimental vibrational frequencies validated the adoption of the above said functional in the present study. The theoretically computed frequencies are presented in Table 2.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrations (semicircle stretching region) are generally appears in the region 1625–1400 cm−1 and 1380–1280 cm−1,28–31 respectively. The ring stretching vibrations are expected within the region 1620–1390 cm−1. In the present study, the absorption at 1605, 1526, 1401, 1262 cm−1 (FT-Raman), 1447, 1334, 1225 cm−1 (FT-IR) are assigned to C–C stretching vibrations. The FT-IR bands observed at 725 and 530 cm−1 and FT-Raman at 776 and 352 cm−1 are assigned to C–C in-plane and out-of-plane bending vibrations, respectively. These assignments are in quite agreement with the literature and in addition the nature and position of the substitution affected the band in this region.30,31 Aromatic ring vibrational modes are pretentious by the substitution in the aromatic ring.
C stretching vibrations (semicircle stretching region) are generally appears in the region 1625–1400 cm−1 and 1380–1280 cm−1,28–31 respectively. The ring stretching vibrations are expected within the region 1620–1390 cm−1. In the present study, the absorption at 1605, 1526, 1401, 1262 cm−1 (FT-Raman), 1447, 1334, 1225 cm−1 (FT-IR) are assigned to C–C stretching vibrations. The FT-IR bands observed at 725 and 530 cm−1 and FT-Raman at 776 and 352 cm−1 are assigned to C–C in-plane and out-of-plane bending vibrations, respectively. These assignments are in quite agreement with the literature and in addition the nature and position of the substitution affected the band in this region.30,31 Aromatic ring vibrational modes are pretentious by the substitution in the aromatic ring.4.3. NMR
The isotropic chemical shifts are normally used to identify the organic reactive sites. It is important to predict exact molecular geometries in order to calculate the magnetic properties of molecules.12,34 Hence, complete optimized geometry of DCPX was performed using TMS B3LYP/6-311+G (2d, p) and TMS HF/6-31G (d) GIAO methods in order to get better understanding in the structural features of the title compound.16 The 1H and 13C NMR chemical shift values of the DCPX have been calculated by Gauge Invariant Atomic Orbital (GIAO) method.12,35,36 The experimental and theoretical chemical shift values for 1H and 13C NMR of DCPX are given in Table 3. The theoretical and experimental NMR spectra include 1H & 13C for DCPX is given in Fig. S1 (ESI),† where TMS has been used as a reference. The theoretically calculated and experimentally observed chemical shifts values of DCPX in both 1H & 13C NMR are reliably in good agreement with each other. Ring carbons had greater chemical shift values than the aliphatic carbons, due to the influence of the resonance effect of the aromatic ring.33 Further, the poor electron donating nature (+I effect) of methyl group increased the chemical shift of the ring carbon (C1 and C4). The chlorine substituted carbon atoms have greater chemical shift than all other carbons of DCPX. This could be attributed to the electro negativity of chlorine atoms. The signals of the aromatic proton (H7 & H8) were observed at 5.8 ppm. The H atom is the smallest of all atoms and mostly localized on the periphery of molecules. The methyl group protons showed less chemical shift values than the aromatic ring protons. The ring protons involved in the delocalization of π electrons in the benzene ring. Among the methyl protons, of H16 and H14 have higher chemical shift values as they might be involved in the intra molecular hydrogen bonding (H14–Cl and H16–Cl).37–41| Atoms | Experimental chemical shift (ppm) | TMS B3LYP/6-311G* (2d, p) | TMS HF/6-31G (d) GIAO |
|---|---|---|---|
| C1 | 138.56 | 137.526 | 155.05 |
| C2 | 135.12 | 145.241 | 162.72 |
| C3 | 132.24 | 128.239 | 146.42 |
| C4 | 131.15 | 137.526 | 155.05 |
| C5 | 128.24 | 145.241 | 162.72 |
| C6 | 119.21 | 128.239 | 146.42 |
| C11 | 20.9 | 12.92 | 30.46 |
| C12 | 20.9 | 12.92 | 30.46 |
| H7 | 7.04 | 6.069 | 6.784 |
| H8 | 7.02 | 6.069 | 6.784 |
| H13 | 2.29 | 1.209 | 1.925 |
| H14 | 2.24 | 0.839 | 1.554 |
| H15 | 2.12 | 0.449 | 1.164 |
| H16 | 2.22 | 0.839 | 1.554 |
| H17 | 2.03 | 0.449 | 1.164 |
| H18 | 2.25 | 1.209 | 1.925 |
4.4. Natural bond orbital (NBO) analysis
Natural bond orbital (NBO) analysis gives the information about nature of hydrogen bonding and interaction among bonds, and also gives information about transfer or conjugative interactions of molecular systems.25,35,36 In addition, it gives essential information on the interactions of donor and accepter orbitals of molecules which enable the assessment of intra and intermolecular interactions. This is carried out by considering all possible interactions between filled and empty NBOs and calculating their energy importance by second order perturbation theory. For each electron donor (i) and electron acceptor (j), the stabilization energy (E2) associates with electron delocalization between Lewis (filled) and non Lewis (unfilled) is estimated as:
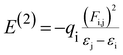 | (3) |
NBO analysis has been calculated at the DFT/B3LYP/6-311G** functional in order to clarify the charge transfer or conjugative interaction, the intra compound rehybridization and delocalization of electron density within the molecule. The second-order perturbation theory of Fock matrix in the NBO of the DCPX showed the presence of strong intramolecular hyperconjugative interactions which are listed in Table 4. In NBO analysis of DCPX, we had observed two types of halogen (Cl9 & Cl10) antibonding with their respective stabilization energies. They were observed as follows Cl9 (LP1) undergoes π*C2–C3, σ*C1–C2 interaction with E(2) of 12.45, 11.68 kJ mol−1 where as Cl10 (LP1) σ*C5–C6, π*C4–C5 resulted the stabilization energy E(2) of 11.24, 12.19 kJ mol−1, respectively. This stronger interaction around the ring could enhance the bioactivity of DCPX. The p-character of chlorine lone pair contributes the electron donating ability of DCPX.
| Occupancy | Acceptor (J) | Occupancy | E(2) kcal mol−1 | E(i) − E(j) a.u. | F(i,j) | |
|---|---|---|---|---|---|---|
| σC1–C2 | 1.97581 | π*C2–C3 | 0.0248 | 4.4 | 1.3 | 0.068 |
| σ*C3–H7 | 0.0141 | 2.34 | 1.14 | 0.046 | ||
| σC1–C12 | 1.97895 | π*C2–C3 | 0.0248 | 2.88 | 1.18 | 0.052 |
| πC1–C6 | 1.96137 | π*C2–C3 | 0.03546 | 4.42 | 1.29 | 0.067 |
| σ*C2–Cl9 | 0.03141 | 4.62 | 0.85 | 0.056 | ||
| σ*C5–Cl10 | 0.03126 | 4.84 | 0.85 | 0.057 | ||
| σC2–Cl9 | 1.98917 | σ*C3–C4 | 0.02238 | 2.27 | 1.3 | 0.049 |
| π*C1–C6 | 0.02278 | 2.7 | 1.3 | 0.053 | ||
| πC2–C3 | 1.97839 | σ*C3–C4 | 0.02238 | 3.1 | 1.32 | 0.057 |
| σC3–H7 | 1.97816 | π*C2–C3 | 0.0248 | 0.84 | 1.09 | 0.027 |
| σC3–C4 | 1.96134 | π*C2–C3 | 0.0248 | 3.47 | 1.28 | 0.06 |
| σ*C2–Cl9 | 0.03141 | 4.84 | 0.85 | 0.057 | ||
| σ*C5–Cl10 | 0.03126 | 4.62 | 0.85 | 0.056 | ||
| πC4–C5 | 1.97535 | σ*C3–C4 | 0.02238 | 3.7 | 1.32 | 0.062 |
| σ*C3–H7 | 0.0141 | 2.02 | 1.14 | 0.043 | ||
| σC4–C11 | 1.9791 | π*C2–C3 | 0.0248 | 2.77 | 1.18 | 0.051 |
| σC5–C6 | 1.97841 | π*C1–C6 | 0.02278 | 3.14 | 1.32 | 0.057 |
| σ*C1–C12 | 0.01562 | 3.11 | 1.11 | 0.053 | ||
| σC5–Cl10 | 1.98913 | σ*C3–C4 | 0.02238 | 2.72 | 1.3 | 0.053 |
| π*C1–C6 | 0.02278 | 2.26 | 1.3 | 0.049 | ||
| σC6–H8 | 1.97804 | σ*C1–C2 | 0.03546 | 4.56 | 1.09 | 0.063 |
| σC12–H14 | 1.98275 | σ*C1–C2 | 0.03546 | 1.65 | 1.07 | 0.038 |
| σC12–H15 | 1.99086 | π*C1–C6 | 0.02278 | 3.6 | 1.08 | 0.056 |
| σC11–H16 | 1.98226 | σ*C3–C4 | 0.02238 | 1.63 | 1.09 | 0.038 |
| σC11–H17 | 1.99186 | π*C4–C5 | 0.035 | 3.62 | 1.07 | 0.056 |
| Cl9 (LP1) | 1.96427 | π*C2–C3 | 0.0248 | 12.45 | 0.32 | 0.062 |
| σ*C12–H14 | 0.01205 | 0.31 | 1.74 | 0.044 | ||
| σ*C1–C2 | 0.39909 | 11.68 | 0.34 | 0.062 | ||
| Cl10 (LP1) | 1.99351 | σ*C5–C6 | 0.02482 | 11.24 | 1.49 | 0.039 |
| π*C4–C5 | 0.035 | 12.19 | 0.32 | 0.062 | ||
| σ*C12–H16 | 0.01526 | 0.74 | 1.73 | 0.041 |
4.5. Mulliken population analysis
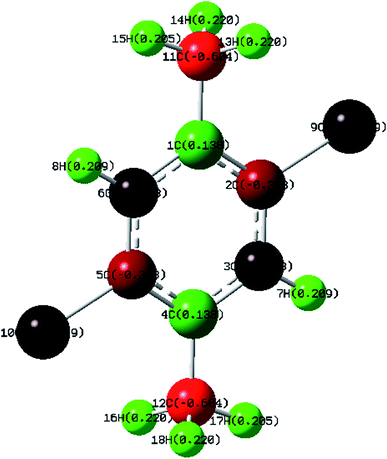
Mulliken Population Analysis (MPA) of Mulliken atomic charge (MAC) is a significant tool which analyzes the electronic properties of a particular molecule.43 Further, it helps in the determination of atomic charges, dipole moment, molecular polarizability and electronic structure of a molecule. The total atomic charges of DCPX were obtained by Mulliken population analysis with B3LYP/6-311G** functional (Fig. 4). The negative values of C2, C3, C5, C6, C11, C12, Cl9 and Cl10 in the aromatic ring indicated the redistribution of electron density (Table S4 in ESI†). Due to these strong negative charges C2 and C5 accommodated higher positive charge and become more acidic. The substitution of halogen implied negative values on ring carbons where as the methyl group's substitution kept C4 of aromatic ring as positive.4.6. Molecular electrostatic potential (MEP)
MEP is an extensive analytical tool for the description of non-covalent interactions particularly hydrogen bonds. MEP analysis enables the identification of high susceptible interactive centre with a proton in the surrounding space of a molecule.12,40,44 This can be used to predict potential interactions between the molecule and a particular host. To predict the reactive sites of electrophilic and nucleophilic attack for the investigated molecule, MEP at the B3LYP/6-311G** optimized geometry was drawn (Fig. S2 in ESI†). From Fig. S2 (ESI†) negative (red and orange) area of the MEP are relative to the electrophilic reactivity and the positive blue area are related to nucleophilic reactivity. From the MEP map of the DCPX molecule, it is clear that negative potential are on the electronegative halogen atoms (Cl9 & Cl10), where as the regions having the positive potential are over the hydrogen atoms. Blue color (Fig. S2 of ESI†) indicates the strongest attraction and a red color indicated the strongest repulsion of DCPX towards electrophiles.4.7. Global molecule reactivity descriptors
The structure–activity relationship (SAR) of a particular molecule can well be explained by calculating the global reactivity descriptors using conceptual DFT. Regarding the reactivity of a molecule, the most serious concern is the assumption the direction of reaction and the product formation in various environments. At the time of development of quantum chemical methods, there are several calculation methods have been designed for the calculation of the electronic properties of molecular systems. Among the several concepts derived the one which used to correlate the frontier molecular orbitals with reactivity of molecules designed by Fukui & his co-workers has been utilized extensively to assume the nature of photo-chemical reaction.45 Meanwhile, Pearson has derived the HSAB concept to explore the reactivity of acids and bases through their hardness and softness. Pearson stated that, there will be an enhanced stabilization when the soft acid and hard acid combine with soft base and hard base, respectively.46,47 HSAB principle is one of the most prominent concepts as it covers almost all the acid–base reactions and it has been become very popular due to the applicability and simplicity.DFT methods stay better than conventional ab initio method because of economy ratio. The most quantum chemical methods are hybrid DFT based B3LYP functional level which predicts the global and local reactivity descriptors. The value of this innovative molecular reactivity quantity has newly been demonstrated in considerate the toxicity of a range of pollutants in terms of their molecular reactivity and site selectivity.48,49 The quantum chemical parameters calculated using DFT with B3LYP/6-311G** functional viz., molecular orbital energies (HOMO and LUMO), energy gap (ΔE), electron affinity (EA), ionization potential (IP), global hardness (η), dipole moment (µ), global softness (σ), absolute electronegativity (χ) and electrophilicity index (ω) are listed in Table 5.
| Methods | EHOMO (eV) | ELUMO (eV) | I | A | ΔE | η | σ | χ | ω | ε |
|---|---|---|---|---|---|---|---|---|---|---|
| HF/SDD | −9.35154 | 2.71436 | 9.35154 | −2.71436 | 12.06590 | 6.03295 | 0.16576 | 3.31859 | 0.91274 | 1.09560 |
| HF/6-311G | −9.40895 | 2.82837 | 9.40895 | −2.82837 | 12.23733 | 6.11866 | 0.16343 | 3.29029 | 0.88467 | 1.13036 |
| HF/6-31++G | −9.37385 | 1.11704 | 9.37385 | −1.11704 | 10.49089 | 5.24544 | 0.19064 | 4.12841 | 1.62462 | 0.61553 |
| B3LYP/SDD | −6.77569 | −0.84628 | 6.77569 | 0.84628 | 5.92941 | 2.96470 | 0.33730 | 3.81098 | 2.44942 | 0.40826 |
| B3LYP/6-311G++ | −7.00209 | −0.92792 | 7.00209 | 0.92792 | 6.07417 | 3.03709 | 0.32926 | 3.96500 | 2.58821 | 0.38637 |
| B3LYP/6-31++G | −6.94440 | −0.97690 | 6.94440 | 0.97690 | 5.96750 | 2.98375 | 0.33515 | 3.96065 | 2.62869 | 0.38042 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| DCPX/aqueous phase | ||||||||||
| HF/SDD | −9.36705 | 2.73939 | 9.36705 | −2.73939 | 12.10644 | 6.05322 | 0.16520 | 3.31383 | 0.90708 | 1.10244 |
| HF/6-311G | −9.41004 | 2.85014 | 9.41004 | −2.85014 | 12.26019 | 6.13009 | 0.16313 | 3.27995 | 0.87748 | 1.13963 |
| HF/6-31++G | −9.37304 | 1.23405 | 9.37304 | −1.23405 | 10.60708 | 5.30354 | 0.18855 | 4.06949 | 1.56130 | 0.64049 |
| B3LYP/SDD | −6.84834 | −0.86669 | 6.84834 | 0.86669 | 5.98165 | 2.99083 | 0.33436 | 3.85752 | 2.48768 | 0.40198 |
| B3LYP/6-311G++ | −7.04263 | −0.91404 | 7.04263 | 0.91404 | 6.12860 | 3.06430 | 0.32634 | 3.97834 | 2.58251 | 0.38722 |
| B3LYP/6-31++G | −6.96780 | −0.93445 | 6.96780 | 0.93445 | 6.03336 | 3.01668 | 0.33149 | 3.95112 | 2.58751 | 0.38647 |
The molecular energies of HOMO and LUMO are related to the IP and EA, respectively in the framework of Koopmans' theorem.48
| IP = −EHOMO | (4) |
| EA = −ELUMO | (5) |
Using Koopman's theorem for closed shell molecules η, µ and χ can be redefined as
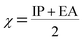 | (6) |
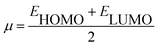 | (7) |
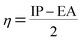 | (8) |
The σ is defined as the inverse of the η eqn (8).
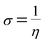 | (9) |
The electrophilicity index (ω) formula is
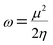 | (10) |
In addition, he described the nucleophilicity (ε) as the multiplicative inverse of electrophilicity (ε = 1/ω).
The chemical hardness and softness of DCPX is clue of the stability of the molecule. Molecules having low energy gap are called as soft molecules which are polarisable, whereas molecules having high energy gap are called as hard molecules which are less polarisable (non-polar). From the Table 5, it is clear that, DCPX having larger energy gap. The values denoted DCPX as hard and less polarisable (non-polar) molecule.
4.8. HOMO and LUMO analysis
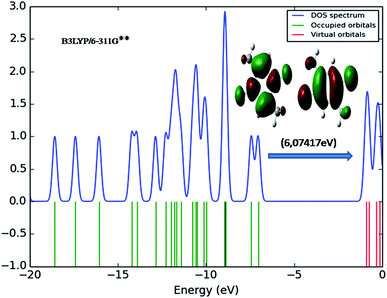
Molecules having conjugated electrons are recognized as hyper-polarisabilities and are analyzed in terms of vibrational spectroscopy. In several cases, even in the absence of an inversion center, the intense bands in the Raman spectrum are broad in the IR spectrum and vice versa. But the intra-molecular charge transfer from the donor to accepter group through a single- double-bond conjugated path can induce large variations of both the molecular dipole moment and the molecular polarisability, making IR and Raman activity strong at the same time. The above said experimental spectroscopic behavior can well be correlated using DFT calculations in conjugated systems which assume large Raman and infrared intensities for the similar normal modes. It is also observed in the present study that the bands in FT-IR spectrum have their counterparts in the Raman which reveals that the relative intensities in both the spectra are reliable and also explains the result from the movement of electron cloud via π conjugated electron donor to acceptor species.The transition of electrons from ground state to first excited state due to the absorption by means of one electron excitation from the HOMO to LUMO has been known from the wave function analysis. The Gauss Sum program is used to obtain DOS diagram which was drawn by plotting molecular orbital data. The DOS diagram50 of DCPX is shown in Fig. 5. It is well known that chemical stability of a molecule is largely affected by the frontier orbitals. The electron donating capability of a molecule can be explained by HOMO–LUMO energy. Thus, it is assumed that the energy gap between the HOMO and LUMO reveals the molecules reactivity.
Fig. 6 shows the energy of HOMO–LUMO energy gap (ΔE) of DCPX. The calculated HOMO–LUMO energy gap of the DCPX is 12.06, 12.23, 10.49, 5.92, 6.07, 5.96 and 12.10, 12.26, 10.60, 5.98, 6.12, 6.03 eV at the HF/SDD, HF/6-311G, HF/6-31G++, B3LYP/SDD, B3LYP/6-311G++, B3LYP/6-31++G (Gaseous phase) and HF/SDD, HF/6-311G, HF/6-31G++, B3LYP/SDD, B3LYP/6-311G++, B3LYP/6-31++G levels (aqueous phase), respectively. Hence, this value revealed that DCPX has relatively less kinetic stability than other derivatives. Orbitals involved in the electronic transition of (a) HOMO−0 (b) LUMO+0 (c) HOMO−1 (d) LUMO+1 (e) LUMO+2 are represented in Fig. S3 in ESI.† The NLO responses can be understood by examining the energies of frontier molecular orbitals. There is an inverse relationship between hyperpolarizability and HOMO–LUMO.
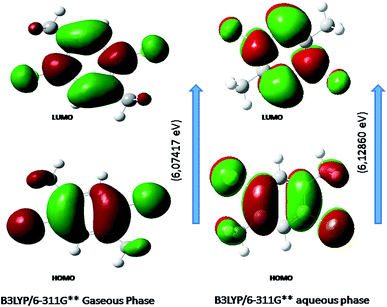 | ||
| Fig. 6 Representation of the orbitals involved in the electronic transition of DCPX for HOMO and LUMO. | ||
4.9. First-order hyperpolarizability calculations
Under the applied electric field, first-order hyperpolarizability (a third rank tensor) can be described by a 3 × 3 × 3 matrix. The Kleinman symmetry reduces the components of the 3D matrix to 10 components.51 The lower tetrahedral format can be used to explain the matrix. It is very clear that, the tetrahedral's lower part is 3 × 3 × 3 matrix. The calculation of NLO properties with high accuracy is challenging and requires consideration of many different issues. Computational techniques are becoming valuable in designing, modeling and screening novel NLO materials. The hyperpolarizability of DCPX is 11.583 × 10−30 esu (calculated) which is sixty times greater than that of urea (0.1947 × 10−30 esu). From the observation, it is clear that DCPX having NLO properties. The dipole moment and hyperpolarizability values are listed in Table S5 in ESI.† Oscillator strength, electronic excitation energies and nature of the respective excited states were calculated by the closed-shell singlet calculation method and are summarized in Table S6 of ESI.† Table S6† clearly indicated the higher first static polarizability of DCPX.5 Conclusions
The symmetry of DCPX has been identified as Cs point group from the optimized structure. In addition, the bond lengths and bond angels of all atoms of DCPX have also been calculated. The difference in bond lengths of various substituents has been due to the inductive and resonance effects in DCPX. The 48 normal modes of DCPX were calculated using DFT coupled with B3LYP/6-311+G** functional. Computed vibrational modes include FT-IR and FT-Raman was compared with experimentally observed values and which is in quite agreement with each other. The very least mean deviation of about 7.09 cm−1 for DCPX has been observed after the least square refinement of the scale factors validated the adoption of B3LYP method. The structural features of DCPX have been confirmed from the results of NMR spectral analysis. The occurrence of intra-molecular hydrogen bonding in DCPX has been confirmed from NBO analysis in addition to biological activity. The charge distribution of DCPX is known from Mulliken population analysis. The positive and negative regions followed by nucleophilic and electrophilic reactive centres have been identified from MEP analysis. The SAR of DCPX based on global reactivity descriptors suggested DCPX as hard and non-polar species. The HOMO–LUMO analysis of DCPX revealed the donor–acceptor nature, reactivity and NLO property of DCPX. Further, the NLO property of DCPX has been supported by the observation of larger hyperpolarizability value.References
- R. Vedula, S. Kaza and S. B. Desu, in Chemical Vapor Deposition, ed. J. H. Park and T. S. Sudarshan, ASM International, Ohio2, vol. 43, 2001 Search PubMed.
- M. E. Vaschetto, B. A. Retamal and A. P. Monkman, J. Mol. Struct.: THEOCHEM, 1999, 468, 209–221 CrossRef CAS.
- V. Arjunan, I. Saravanan, C. V. Mythili, K. Balakrishnan and S. Mohan, Spectrochim. Acta, Part A, 2012, 91, 166–177 CrossRef CAS PubMed.
- K. Kimura, J. Electron Spectrosc. Relat. Phenom., 1999, 100, 273 CrossRef CAS.
- P. J. Breen, J. A. Warren and E. R. Bernstein, J. Chem. Phys., 1987, 87, 1917–1935 CrossRef CAS.
- K. Walter, K. Scherm and U. Boesl, Chem. Phys. Lett., 1989, 161, 473–478 CrossRef CAS.
- A. P. Singh, S. Sharma and S. M. Kale, J. Mol. Catal. A: Chem., 1997, 127, 101–111 CrossRef CAS.
- C. E. H. Dessent and K. Muller-Dethlefs, Chem. Rev., 2000, 100, 3999–4021 CrossRef CAS PubMed.
- M. Govindarajan, K. Ganasan, S. Periandy, M. Karabacak and S. Mohan, Spectrochim. Acta, Part A, 2010, 77, 1005–1013 CrossRef CAS PubMed.
- V. Arjunan, P. S. Balamourougane, I. Saravanan and S. Mohan, Spectrochim. Acta, Part A, 2009, 74, 798–807 CrossRef CAS PubMed.
- M. Govindarajan and M. Karabacak, Spectrochim. Acta, Part A, 2012, 94, 36–47 CrossRef CAS PubMed.
- M. Manzoor ali, G. George, S. Ramalingam, S. Periandy and V. Gokulakrishnan, J. Mol. Struct., 2016, 1106, 36–52 CrossRef.
- M. Arivazhagan and R. Meenakshi, Spectrochim. Acta, Part A, 2012, 91, 419–430 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev., 1988, 1337, 785 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- R. Meenakshi, RSC Adv., 2016, 6, 21821–21832 Search PubMed.
- S. Mary, V. V. Aswathy, P. C. Yohannan, A. Bielenica, P. Brzózka, O. Savczenko, S. Armaković, S. J. Armaković and C. V. Alsenoy, RSC Adv., 2016, 6, 111997–112015 RSC.
- R. Meenakshi, RSC Adv., 2016, 6, 63690–63703 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Asegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Ioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. AlLaham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision E.01, Gaussian Inc., Pittsburgh. B.A, 2000 Search PubMed.
- S. Ramalingam, S. Periandy, B. Elanchezhian and S. Mohand, Spectrochim. Acta, Part A, 2011, 78, 429–436 CrossRef CAS PubMed.
- E. B. Wilson Jr, J. C. Decius and P. C. Cross, Molecular Vibrations, MecGraw Hill, New York, 1955 Search PubMed.
- C. J. Pouchert, The Aldric Library of FT-IR spectra, Aldrich Chemicals Co., Milwaukee, WI, 1985 Search PubMed.
- P. Pulay, G. Fogarasi, G. Pongar, J. E. Boggs and A. Vargha, J. Am. Chem. Soc., 1983, 105, 7073 CrossRef.
- G. Fogarasi, X. Zhou, P. W. Jaylor and P. Pulay, J. Am. Chem. Soc., 1992, 114, 819 CrossRef.
- P. Vennila, M. Govidaraju, G. Venkatesh and C. Kamal, J. Mol. Struct., 2016, 1111, 151–156 CrossRef CAS.
- S. Ramalingam, S. Periandy, B. Narayanan and S. Mohan, Spectrochim. Acta, Part A, 2010, 76, 84–92 CrossRef CAS PubMed.
- V. Krishnakumar and R. John Xavier, Indian J. Pure Appl. Phys., 2003, 41, 95–98 Search PubMed.
- N. Sundaraganesan, B. Anand, C. Meganathan and B. D. Joshua, Spectrochim. Acta, Part A, 2007, 68, 561–566 CrossRef CAS PubMed.
- M. Arivazhagan and R. Meenakshi, Spectrochim. Acta, Part A, 2012, 91, 419–430 CrossRef CAS PubMed.
- G. Varsanyi and S. Szoke, Vibrational Spectra of Benzene Derivatives, Academic Press, New York, 1969 Search PubMed.
- G. Socrates, Infrared and Raman Characteristic Group Frequencies—Tables and Charts, Wiley, New York, 3rd edn, 2001 Search PubMed.
- V. Krishnakumar, N. Prabavathi and S. Muthunatesan, Spectrochim. Acta, Part A, 2008, 70, 991–996 CrossRef CAS PubMed.
- K. Haruna, A. A. Alenaizan and A. A. Al-Saadi, RSC Adv., 2016, 6, 67794–67804 RSC.
- P. B. Nagabalasubramanian, S. Periandy and S. Mohan, Spectrochim. Acta, Part A, 2010, 77, 150 CrossRef CAS PubMed.
- S. Sebastian, N. Sundaraganesan, B. Karthikeiyan and V. Srinivasan, Spectrochim. Acta, Part A, 2011, 78, 590–600 CrossRef CAS PubMed.
- S. P. Saravanan, A. Sankar and K. Parimala, J. Mol. Struct., 2017, 1127, 784–795 CrossRef CAS.
- S. Higuchi, Spectrochim. Acta, Part A, 1974, 30, 463–467 CrossRef.
- J. Murto, Spectrochim. Acta, Part A, 1973, 29, 1125 CrossRef.
- N. F. Chamberlain, The Practice of NMR Spectroscopy with Spectra Structure Correlations for Hydrogen-1, Plenum Press, 1974 Search PubMed.
- H. E. Gottlieb, V. Kotlyar and A. Nudelman, J. Org. Chem., 1997, 62, 7512–7515 CrossRef CAS PubMed.
- G. Venkatesh, M. Govindaraju and P. Vennila, Indian J. Chem., 2016, 55, 413–422 Search PubMed.
- C. James, A. Amal Raj, R. Reghunathan, I. H. Joe and V. S. Jayakumar, J. Raman Spectrosc., 2006, 37, 1381–1392 CrossRef CAS.
- K. Parimala and V. Balachandran, Spectrochim. Acta, Part A, 2013, 110, 269–284 CrossRef CAS PubMed.
- S. Miertus, E. Scrocco and J. Tomasi, Theor. Chem. Acc., 2000, 103, 343–345 CrossRef.
- W. Yang and R. G. Parr, Hardness, softness and the Fukui function in the electronic theory of metals and catalysis, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 6723–6726 CrossRef CAS.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533 CrossRef CAS.
- R. G. Pearson, Inorg. Chem., 1988, 27, 734 CrossRef CAS.
- T. Koopmans, Physica, 1933, 1, 104 CrossRef CAS.
- S. Kaya and C. Kaya, Mol. Phys., 2015, 113, 1311 CrossRef CAS.
- N. M. O'Boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- D. A. Kleinman, Phys. Rev., 1962, 126, 1977 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra25535c |
| This journal is © The Royal Society of Chemistry 2017 |