Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigation of the post-annealing electromagnetic response of Cu–Co oxide coatings via optical measurement and computational modelling†
M. Mahbubur Rahmanab,
Hussein A. Miranac,
Zhong-Tao Jiang *a,
Mohmmednoor Altarawneh
*a,
Mohmmednoor Altarawneh d,
Lee Siang Chuahe,
Hooi-Ling Leef,
Amun Amrig,
Nicholas Mondinosa and
Bogdan Z. Dlugogorskid
d,
Lee Siang Chuahe,
Hooi-Ling Leef,
Amun Amrig,
Nicholas Mondinosa and
Bogdan Z. Dlugogorskid
aSurface Analysis and Materials Engineering Research Group, School of Engineering & Information Technology, Murdoch University, Murdoch, Western Australia 6150, Australia. E-mail: Z.Jiang@murdoch.edu.au; Tel: +61 8 9360 2867
bDepartment of Physics, Jahangirnagar University, Savar, Dhaka 1342, Bangladesh
cDepartment of Physics, College of Education for Pure Sciences, Ibn Al-Haitham, University of Bagdad, 10071, Baghdad, Iraq
dSchool of Engineering & Information Technology, Murdoch University, Murdoch, Western Australia 6150, Australia
eDepartment of Physics, School of Distance Education, Universiti Sains Malaysia, 11800 Minden, Penang, Malaysia
fSchool of Chemical Sciences, Universiti Sains Malaysia, 11800 Minden, Penang, Malaysia
gDepartment of Chemical Engineering, Universitas Riau, Pekanbaru, Indonesia
First published on 16th March 2017
Abstract
The optical frequency response and changes to the dielectric and optical parameters due to annealing temperature variation (200–500 °C) of sol–gel derived CuCoOx thin film coatings were investigated. The optical constants such as absorption coefficient, band-gaps, Urbach energy, complex refractive index, complex dielectric constants, optical dispersion parameters, and energy loss functions were determined from reflectance data analysis recorded in the ultraviolet to near-infrared (190–2200 nm) range. The absorption coefficient and the broadening of absorption edge (steepness parameter), energy band-gaps, Urbach energy, loss tangent and energy loss functions decreased with the increase in annealing temperatures. The refractive index displayed normal dispersion behaviors at higher frequency with the maximum value at a temperature of 500 °C. First-principles simulations, density functional theory (DFT+U) as implemented in the Cambridge Serial Total Energy Package (CASTEP), based on a cluster structure of Cu0.5Co2.5O4 system, optimized the crystalline structure and calculated the electronic structure of the framework. The calculated density of states (DOS) and associated absorption coefficient and dielectric constant results reasonably support the experimental findings.
1. Introduction
Mixed metal oxide based coatings with general composition AB2O4, where A is a divalent metal ion occupying the tetrahedral A-sites, and B is a trivalent ion occupying at octahedral B-sites, e.g., CuFe2O4, CuCo2O4, and CuMn2O4, have been extensively studied by different groups.1–4 These materials possess widespread applications as catalysts for volatile organic compounds,5 gas sensors,6 electrocatalysts for the oxygen electrode,7 photovoltaics and photocatalysis,8 selective solar absorbers,9,10 batteries and memory devices,11,12 and for absorption optimizations and industrial applications.13 High-tech applications of cobalt based metal oxide coatings are demonstrated in the literature.11,12,14,15 Pure copper oxide,16 cobalt–copper oxide, manganese–cobalt oxide, nickel–cobalt oxide,13 copper–aluminum oxide17,18 have been reported in studies of spectrally selective solar absorbers, high absorption optical coatings and industrial applications. Manganese-cobalt oxides have been studied with a focus on the influence of synthesis conditions on the oxidation states and cationic distribution in the tetragonal and cubic phases.19 Optical characterization of industrial roll-coating sputtered nickel–nickel oxide solar selective surface has been reported by Adsten et al.20 Structural and optical properties of pulsed sputter deposited CrxOy/Cr/Cr2O3 solar selective coatings on Cu substrates were found to demonstrate high selectivity after being annealed at 300 °C for 2 hours in air.21 In another study, Shaklee et al.22 examined the spectral selectivity of composite enamel coatings consisting of spinel-type transition-metal-oxide pigments embedded in a borosilicate-glass matrix deposited on stainless steel substrate.The cobalt oxide (Co3O4) films containing 1-D interlinked nanowires synthesized via spray pyrolysis technique showed better values of absorptance (0.94), emittance (0.17) compared to the data reported studies. The selectivity of coatings was reported to be 5.529. These coatings have the potential of being good selective absorbers. Their optical properties indicate the red shift of absorption peaks, thereby showing a quantum-confined effect and semiconducting nature.23 In Amun's study,24 the combined CuCoO thin films showed a selectivity of just over 14. There have been numerous investigations available in studies on metal oxide thin films for the improvement and optimization of physiochemical, optical, thermal, electro-chemical, photo-chemical, magnetic, dielectric and electro-magnetic properties focusing on their practical applications such as clean energy devices, solar cells, photovoltaics, thermal collectors, selective solar surfaces and smart windows.
In view of these facts, generally, the optical analyses of materials are mainly involved with the absorption, reflection, emission and transmission measurements in the ultraviolet through visible to infrared and far-infrared regions of the solar spectra to realize their solar absorptance mechanisms and solar selectivity topographies. It is also seen, there has been very limited effort toward elucidating the post annealing effects on the other properties of these coatings. Optical characterizations of these materials play remarkable roles to comprehend their fundamental behaviors and make them preferable in several applications. However, using the optical data, we can conduct further studies e.g., optical dispersion analyses, dielectric features and energy loss phenomena that afford them with the identification of their potentiality in the new promising extents to be used more competently. Thus, in this study, we have carried out detailed studies to understand the post-annealing electromagnetic responses of energy band-gaps, single oscillator model optical dispersion analysis, dielectric characterizations, and energy loss mechanisms of sol–gel derived copper–cobalt oxide coatings.
2. Experimental and modeling
2.1 Specimen synthesis
Cobalt(II) chloride (CoCl2·6H2O, APS Chemical, >99%), copper(II) acetate monohydrate ((Cu(OOCCH3))2·H2O, Alfa Aesar, >98%), propionic acid (C2H5COOH, Chem Supply, >99%), and absolute ethanol (E. Mark of Germany, >99%.) were used to synthesize CuCo-oxide coating onto highly-reflective commercial aluminium substrates. The aluminium substrates (Anofol, size 2 cm × 4 cm) were cleaned with a hot mixture of chromium(VI) oxide and phosphoric acid followed by final rinse using Milli-Q water. The cleaned substrates were dried with high purity N2 gas. The sol–gel solutions consisted of 1.502 gm cobalt(II) chloride (CoCl2·6H2O, 0.25 mol L−1) and 1.273 gm of copper(II) acetate monohydrate (Cu(OOCCH3))2·H2O mixed with absolute ethanol. Propionic acid (C2H5COOH) was used to make a complex solution with the metal ions and to stabilize the solution from unwanted precipitation. After stirring the mixed solution for 2 h, the sol was coated onto aluminium substrates using a dip-coating technique. A dipping and withdrawal rate of 180 mm min−1 and 60 mm min−1, respectively was maintained throughout the synthesis process which was repeated four times to increase the thickness of film with better uniformity. Finally, the coatings were annealed at 200, 300, 400 and 500 °C in air. A constant heating rate of 10 °C min−1 was maintained throughout and the samples were left in the furnace for 15 min after power was turned off. More details about the sol–gel dip-coating method are described elsewhere.18,24–262.2 Characterization techniques
A UV-Vis (UV-670 UV-Vis spectrophotometer, JASCO, USA) double beam spectrophotometer with 60 mm integrating sphere was used to record the UV-Vis reflectance spectra in the range of 190 to 2200 nm. The UV-Vis reflectance spectrum was utilized to investigate the various characteristics of the copper–cobalt oxide thin films.2.3 Density functional theory
First-principles calculation is one of the most promising approaches to predict the ground state properties of a material. The XRD results from Miran et al.27 revealed that the adopted phase for this coating material, as annealing temperature progress within the same range of temperatures is, Cu0.56Co2.44O4. The Cu0.5Co2.5O4 system was dealt with the level of density functional theory (DFT+U) proposed by Dudarev et al.28 as implemented in the Cambridge Serial Total Energy Package (CASTEP)29,30 of Material Studio. For the interactions of the electrons with the ion cores, a plane wave and non-local ultra-soft pseudopotentials presented by Vanderbilt31 have been applied together with the generalized-gradient approximation (GGA).32 The electronic wave functions are expanded in a plane wave basis set with an energy cutoff of 351 eV. For the Brillouin-zone k-point sampling, we adopted the Monkhorst–Pack mesh with 4 × 4 × 4 k-points. Finally, the electron-correlated systems (i.e., d-orbital) were modeled considering Hubbard U value of 9.5 eV that leads to a well agreed band gap with experiment measurements.3. Results and discussion
3.1 Structural and morphological features of Cu–Co oxide coatings before and after annealing
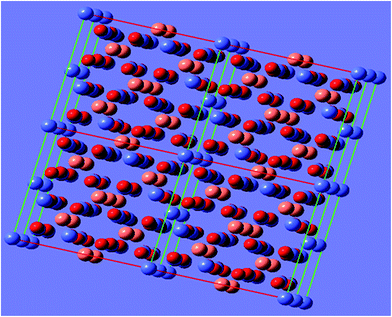
Structural and morphological analyses of these coatings carried out via XRD, XPS, FESEM and AFM spectroscopic methods, before annealing and after annealing, were reported in our most recent studies.27 Before annealing the CuCo-oxide coatings, FESEM showed mould-like structures. However after thermal treatment homogeneously distributed particles with compact and smooth morphologies were observed. The mean and rms surface roughness of the coatings improved ∼120% and ∼140%, respectively, with an average surface area of ∼115 μm2. Annealing results in the occurrence of major grain growth around the coating surface.27XRD studies attributed that the Cu–Co oxide coatings possesses the cubic symmetry consisting of Cu0.95Co2.05O4 (ICSD 78-2177), Cu0.75Co2.25O4 (ICSD 78-2176), Cu0.56Co2.44O4 (ICSD 78-2175), and Cu0.37Co2.63O4 (ICSD 78-2174) phases. In the Cu0.75Co2.25O4 system (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (227), Z = 8, lattice parameter 0.809 nm) the unit cell consists of 6 copper atoms, 18 cobalt atoms and 32 oxygen atoms. Copper and cobalt atoms are shared in tetrahedral and octahedral sites. Fig. 1 shows the spinel structure of Cu–Co oxide system drawn using GaussView 5.0.8 software.
m (227), Z = 8, lattice parameter 0.809 nm) the unit cell consists of 6 copper atoms, 18 cobalt atoms and 32 oxygen atoms. Copper and cobalt atoms are shared in tetrahedral and octahedral sites. Fig. 1 shows the spinel structure of Cu–Co oxide system drawn using GaussView 5.0.8 software.
3.2 Electronic structure and Urbach energy studies
The dependence of optical absorption coefficient on the photon energy is useful for studying the band structure and the types of electron transition involved in absorption process. The linear absorption coefficient can be determined by using the reflectance spectra of the films via following relation,
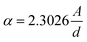 | (1) |
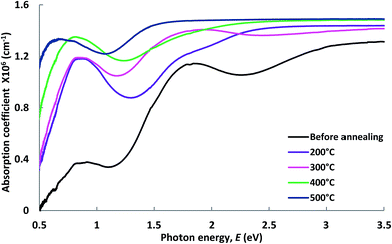 | ||
| Fig. 2 Absorption coefficient of Cu–Co oxide coatings before and after annealing at different temperatures. | ||
In crystalline and amorphous materials the photon absorption obeys the Tauc relation,33–36
| αhν = B(hν − Eg)y | (2) |
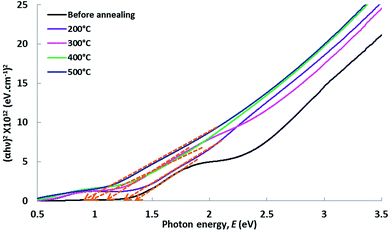
Tauc plots of (αhν)2 vs. hν for Cu–Co oxide coatings before and after annealing are shown in Fig. 3. The energy band-gaps estimated from the intercepts of the linear portion of the curves extrapolated to zero in the photon energy axis are presented Table 1. The values of direct and indirect transition energy gaps lie between 0.80 and 1.40 eV. It is found that the energy band-gap values are monotonically reduced with the rise in annealing temperature of the Cu–Co oxide systems. This drop of energy band-gap values is very important in enhancing the photon absorption capability of these coatings.
| Annealing temperature | Energy band-gap, Eg (eV) |
|---|---|
| Prior-annealing | 1.40 |
| 200 °C | 1.35 |
| 300 °C | 1.20 |
| 400 °C | 0.90 |
| 500 °C | 0.80 |
The spectral absorption in materials strongly depends on the presence of localized states around the forbidden band gap. The absorption profiles offer valuable information on these localized states and indicate the presence of disorderness in the films. Since, Urbach's absorption edges are, normally, formed in the region of photon energies below the forbidden band gaps i.e., in regions of the so-called Urbach tails, where the absorption coefficient follows an exponential decay for decreasing the incident photon energy, and is expressed as,
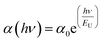 | (3) |
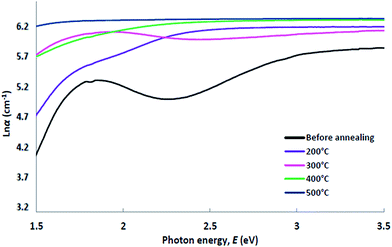 | ||
Fig. 4 Variation of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α with photon energy of Cu–Co oxide coatings before and after annealing at different temperatures. α with photon energy of Cu–Co oxide coatings before and after annealing at different temperatures. | ||
| Annealing temperature | Urbach energy, EU (meV) | Steepness parameter, γ |
|---|---|---|
| Prior-annealing | 500 | 0.0514 |
| 200 °C | 400 | 0.0643 |
| 300 °C | 318 | 0.0801 |
| 400 °C | 267 | 0.0963 |
| 500 °C | 188 | 0.1367 |
The spectral dependence of the absorption coefficient with the incident photon energy might arise originate from trapping levels around the film boundaries. According to Tauc's theory the density of these states fall off exponentially with the photon energy by the following relation,
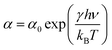 | (4) |
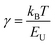 | (5) |
Estimated values of the steepness parameters are shown in Table 2. From Table 2, it is seen that the steepness of the Urbach band tails linearly increase with the increase in annealing temperatures. An increase in the steepness parameter originates from the diminution of the localized density of states, relaxation of the distorted bonds and thereby the degree of crystallinity of the films is enhanced. These features also support the consistency of our energy band-gap and Urbach energy studies. It is well known that the optical band structure and optical transitions are sturdily influenced by the width of the localized states around the band gaps of the films. The absorption coefficient near the fundamental absorption edge is exponentially dependent on the photon energy and obeys the Urbach rule. Interactions between lattice vibrations and localized states in tail of the band-gap of the films have a substantial consequence on the optical properties of these films.
3.3 Optical properties – parameters and dispersions
Using the UV-Vis reflectance spectra, the optical constants such as the refractive index (n) and the extinction coefficient (k) of the films were computed in the wavelength range of 190–2200 nm. The complex refractive index, an important optical parameter that is used to elucidate other materials' properties, is defined as,| n* = n + ik | (6) |
The imaginary part of the complex refractive index, the extinction coefficient (k) can be directly calculated from the absorption coefficient via following relation,
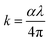 | (7) |
The refractive index n is calculated from the UV-Vis reflectance data, R and k values using the following equation,
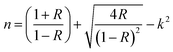 | (8) |
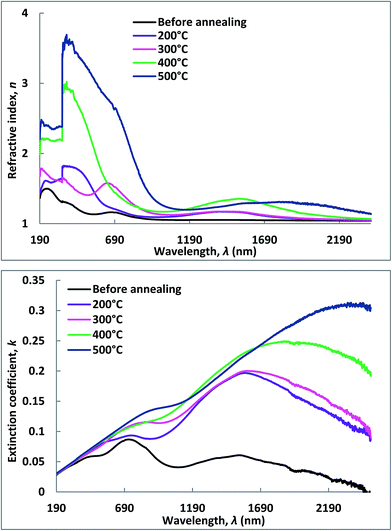 | ||
| Fig. 5 Real and imaginary parts of the complex refractive index of Cu–Co oxide coatings before and after annealing at different temperatures. | ||
Analysis of Fig. 5 indicates that both the values of n and k significantly increased with the increase in annealing temperatures. This confirms the enhancement of films qualities and lower porosities. Further investigations also reveal that in the lower wavelength region up to 390 nm, the refractive index is linearly increased and reached to a peak value and then sharply dropped with the increase in wavelength. Similarly, the k values increase with the increasing of wavelength and reached to the maximum and then fell gradually. These features indicate that n shows normal dispersion in the higher wavelength regions and anomalous dispersions in the lower wavelength sides whereas the inverse phenomena were detected for the k. The dispersion of refractive index exhibits a peak at 3.22 eV (386 nm) corresponding to π–π* transitions of the UV oscillator. On the other hand, the anomalous nature arises due to the resonance effects between incoming solar radiation and electronic polarizability. This leads to the coupling of electrons and oscillating electric fields of the incident electromagnetic radiation. Our observations are consistent with an earlier report.38 The refractive index is closely related to the electronic polarizability of ions and local filed of inside the films. Estimation of refractive indices of these films are very important for their applications in integrated optical devices such as filters, switches, laser diodes, couplers, lens, detectors and amplifiers. Refractive index is a key parameter for the design of such devices.
Using the single oscillator model suggested by Wemple and DiDomenico et al.,38,39 we present the functional relation for the dispersion of refractive index below the optical band-gap of the films. The dispersion relation of the refractive can be represented by the following terms,38,39
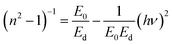 | (9) |
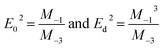 | (10) |
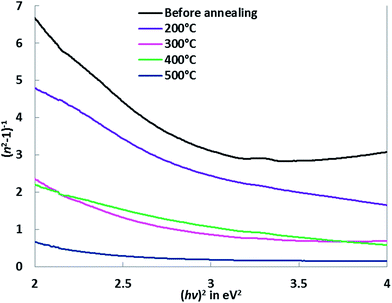 | ||
| Fig. 6 Plots of (n2 − 1)−1 vs. (hν)2 of Cu–Co oxide coatings before and after annealing at different temperatures. | ||
| Annealing temperature | Oscillator energy, E0 (eV) | Dispersion energy, Ed (eV) | Transition moment, M−1 | Transition moment, M−3 (eV2) | Oscillator strength, f = E0Ed (eV2) | Static dielectric constant, ε∞ |
|---|---|---|---|---|---|---|
| Before annealing | 3.96 | 7.05 | 2.084 | 0.175 | 24.39 | 3.08 |
| 200 °C | 3.35 | 8.75 | 2.865 | 0.345 | 25.20 | 3.86 |
| 300 °C | 3.18 | 9.44 | 2.433 | 0.454 | 25.96 | 4.43 |
| 400 °C | 2.87 | 10.20 | 3.923 | 0.580 | 26.52 | 4.92 |
| 500 °C | 2.49 | 12.15 | 5.283 | 0.998 | 27.95 | 6.28 |
The calculated values of the transition moments M−1 and M−3 are listed in the following Table 3.
Fig. 6 shows that plots of (n2 − 1)−1 vs. (hν)2, for the Cu–Co oxides films before and after annealing, shows that the refractive index values decline towards the longer wavelength regions due to the lattice absorption. From Table 3, it is seen that oscillator energy E0, transition moments, M−1 and M−3 decrease with the increase in annealing temperatures while the dispersion energy, Ed, is monotonically enhanced. Dispersion energy measures the intensity of the inter-band optical transition but does not have much effect on the energy band-gap, Eg. The oscillator energy and dispersion energy values are associated with the crystalline structure and ionicity of ionic or covalent materials.41 This essentially indicates that in addition to the optical characterizations, the single oscillator model can be successfully applied to determine the structural properties of these films.
Furthermore the oscillator strength, f is defined by Wemple and di Domenico for a single oscillator model such as39
| f = E0Ed | (11) |
The results using the eqn (11) are included in Table 3. The optical dielectric constant at high frequency, ε∞ also known as the static dielectric constant can be found from the intersection point of the line at (hν)2 = 0 while the refractive index at zero photon energy, n0 (static refractive index) is also related to ε∞ as, ε∞ = n02. The static dielectric constant is expressed by the following relation,40
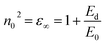 | (12) |
The estimated values of the oscillator strength and static dielectric constants of the Cu–Co oxide coatings before and after being annealed at 200–500 °C are shown in Table 3. Table 3 shows that the oscillator strength and static dielectric constant of the coatings are linearly increased with the gradual increase in annealing temperature of the films. The variation in these optical dispersion parameters and other constants strongly correlated to the thermally driven defects that yield localized states around the energy band-gaps and thereby influence the other optical properties of the films.
3.4 Dielectric characterizations
The frequency dependence of electron excitation spectra of a solid material is defined in terms of complex dielectric function| ε(ω) = ε1(ω) + iε2(ω) = (n(ω) + ik(ω))2 | (13) |
| ε1 = n2 − k2 and ε2 = 2nk | (14) |
Plots of the real and imaginary parts of the dielectric functions as a function of the incident photon energies are given in the following Fig. 7.
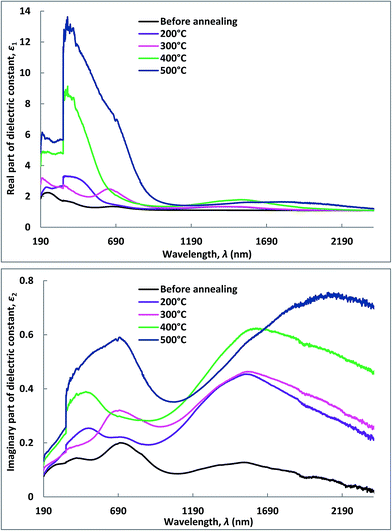 | ||
| Fig. 7 Real and imaginary part of the dielectric constant vs. photon energy of Cu–Co oxide coatings before and after annealing at different temperatures. | ||
In general, the ε1 and ε2 values increase with the annealing temperature in the visible and UV-region. A greater ratio between ε1 and ε2 demonstrate the thin film coatings having very good low-loss dielectric nature in this frequency range of interest. This is due to the increase in the electron density of the films. In general, the improvement in crystallinity of the film can decrease the degree of electron scattering and increase the free-electron density.43,44 The fundamental electron excitation spectrum of the thin film was inferred from the frequency dependence of the complex electronic dielectric constant. The frequency response of the dielectric constant signposts the interactions of the photons and electrons in the film is originated in this wavelength range.
In thin film materials, power loss in the form of heat termed as loss factor generally originated from the inelastic scattering process during the charge transfer and charge conduction mechanisms. The ε1 and ε2 represent the amount of energy stored in dielectrics as polarization and loss energy, respectively. The power loss factor is associated with electric behaviors of the films and device operations of materials as well. The loss factor is described by,
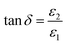 | (15) |
The loss tangent measures the loss-rate of power in a oscillatory dissipative system. Fig. 8 exhibits the variation of the loss factor with the incident photon energy of copper–cobalt oxide thin films before and after being annealed at different temperatures within the range of 200–500 °C. It is clearly seen that the variation loss tangent executes the same trend as ε2. Since ε2 is lower than ε1, then the energy loss of the films is relatively low. This suggests that the films possess good optical qualities due to lower energy losses and lower scattering of the incident radiation. From Fig. 8, it can be seen that in the small photo energy (or low frequency) region (up to 2.0 eV) the loss tangent value of the films increases gradually with the increase of annealing temperatures. However, for photo energy greater than 2.0 eV (or high frequency range), the loss tangent is strongly affected by the annealing temperature.
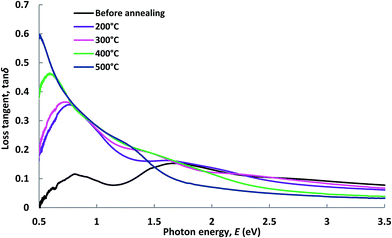 | ||
| Fig. 8 Loss tangent vs. photon energy of Cu–Co oxide coatings before and after being annealed at different temperatures. | ||
This feature is associated with the fact that the dipole orientations become minimal at lower temperatures. But as the temperature increases, the orientations of dipoles are facilitated by thermal agitations, consequently the loss tangent increases. It is also assumed that at lower temperatures the conduction loss is minimum and as the temperature increases conduction loss increases as well due to the higher rate of dipole movements.45 Also from Fig. 8, the energy loss shows a subtle change in magnitude over the whole spectral range. At lower energy sides it shows a maximum value of 0.6 at 0.5 eV, and decreases gradually with the rise in photon energy.
In the dielectric theory, inelastic scattering of electrons in solid films is associated with the energy loss functions. The energy loss functions are known as volume energy loss function, Vel and surface energy loss function, Sel.42
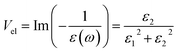 | (16) |
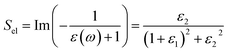 | (17) |
The energy loss functions are related to the optical properties of a material through the real and imaginary parts of dielectric constant. The volume and surface energy loss functions of these coatings before and after annealing at different temperatures are shown in Fig. 9. Both Vel and Sel follow the same trend as the loss tangent data shown in Fig. 8. It is clear that in the lower frequency regions both functions increase with increasing annealing temperatures. However, in the higher frequency sides (above 1.4 eV), the annealed films exhibit lower loss then the unannealed one and at energies above 2.5 eV both functions become almost constant with further increase in frequency on the solar spectrum. It is observed that surface energy loss of the films is much lower compared to the value of the volume energy loss functions (Vel > Sel) for any incident photon energies at all annealing conditions. This may indicates that the loss of energy of a free charge carrier when passing through the volume of the film is larger than that when traveling through to the surface of the film. These features are also found to be consistent with previous reports.46,47 According to Pines and Bohm,48 due to the excitation of plasma oscillations of conduction electrons, while passing through a medium, specific energy losses are experienced by the fast moving electrons.
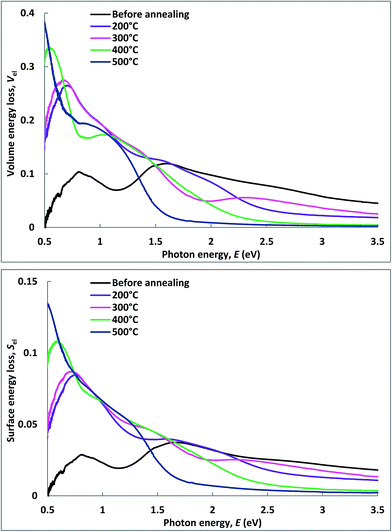 | ||
| Fig. 9 Variation of volume energy loss and surface energy loss functions of Cu–Co oxide coatings before and after annealing. | ||
3.5 Theoretical predictions
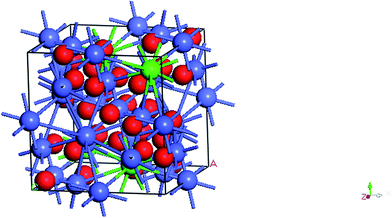
Structural optimization of Cu–Co-oxide (Cu0.5Co2.5O4) system was carried out via theoretical modeling. The Cu0.5Co2.5O4 structure exhibits an cubic symmetry in a space group of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (#225) having eight formula units in a unit cell. The lattice constants, in equilibrium condition, of CuCo-oxide systems are 8.29 Å as estimated via numerical predictions. These parameters are consistent with that obtained from our previous X-ray diffraction study: a = 8.09 Å.27 In the current cluster model of Cu0.5Co2.5O4, there are 4 Cu, 20 Co and 32 O atoms. The crystal structure was optimized and is shown in Fig. 10.
m (#225) having eight formula units in a unit cell. The lattice constants, in equilibrium condition, of CuCo-oxide systems are 8.29 Å as estimated via numerical predictions. These parameters are consistent with that obtained from our previous X-ray diffraction study: a = 8.09 Å.27 In the current cluster model of Cu0.5Co2.5O4, there are 4 Cu, 20 Co and 32 O atoms. The crystal structure was optimized and is shown in Fig. 10.
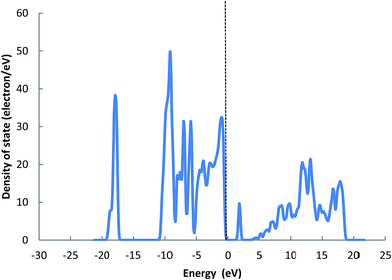
Fig. 11 shows the density of states (DOS) for this Cu0.5Co2.5O4 cluster. The electronic properties of the structure were determined via computing the total density of states at the Fermi level. The analysis shows that the Cu0.5Co2.5O4 system presents a non-metallic character due to d-orbital of Co and Cu which results in semiconducting nature. The range of the top most valance band is from −11 to 0 eV (Fermi level) and the conduction band above the Fermi level is located at 1.10 eV.
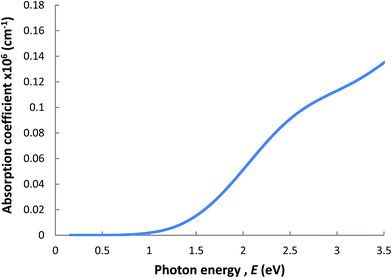
The simulated absorption spectrum of Cu0.5Co2.5O4 system as a function of photon energies in the range of 0.5 to 3.5 eV is shown in Fig. 12. The spectra clearly indicate that the absorption coefficient of this cluster are strongly dependent on the incident energies. Moreover, the absorption coefficient curve confirms that this material exhibits non-metallic nature.49 Our modeled compound exhibits a good absorption coefficient that can be used to investigate a wider E-M frequency range for promising optical applications.
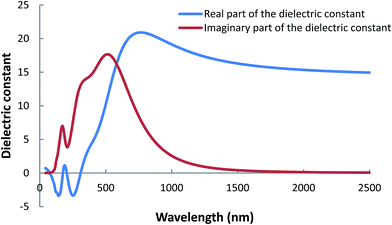
The dielectric response of a material indicates the interaction between photons and electrons. The energy dependent complex dielectric functions of Cu0.5Co2.5O4 system in the wavelength range of 0 to 2500 nm are displayed in Fig. 13. The calculated dielectric function includes the intra-band effects from free electrons (conduction electrons contribution) and inter-band effects (from bound-electron contribution). Fig. 13 shows an increasing trend of the dielectric constants at shorter wavelengths which become constant in longer wavelength regions. This can be attributed to the band gap absorption in these coatings. The main peak of imaginary part ε2 of the dielectric constant is located at 510 nm and reasonably agrees with the experimental results discussed in (Section 3.3). The ε2 magnitudes reduces to zero in the wavelength range greater than 1600 nm suggesting that this material becomes transparent for longer wavelengths while absorption will occur for nonzero ε2.50
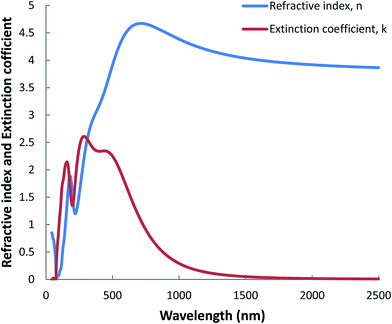
The refractive index (n) and extinction coefficient (k) spectra of such cluster calculated via DFT+U modelling, in the wavelength range of 0–2500 nm, are presented in Fig. 14. Similar to the dielectric functions, the refractive index and extinction coefficient plots exhibit maxima in the shorter wavelength regions. The computational and measured refractive index have similar value in the wavelength range from 0 to 2500 nm. Furthermore, the extinction coefficient from the experimental and computational modeling has similar trends but slightly different values. The differences may be due to (i) an ideal situation (T = 0 K, P = 0 atm), (ii) the mixed phase nature of real films, and (iii) the effect of highly polished Al substrate in the real film materials.
For comparison, we calculate optical properties of a CoCu2O3 system which can be considered as a metal to oxygen ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, while the actual system discussed above is a 3
3, while the actual system discussed above is a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 metal to oxygen ratio. The CoCu2O3 system modeling shows similar trends as the Cu0.5Co2.5O4 system. The details for this CoCu2O3 system are included in the ESI† document.
4 metal to oxygen ratio. The CoCu2O3 system modeling shows similar trends as the Cu0.5Co2.5O4 system. The details for this CoCu2O3 system are included in the ESI† document.
4. Conclusions
The post-annealing electromagnetic response of optical and dielectric properties of Cu–Co oxide coatings were investigated within the temperature range of 200–500 °C. The optical coefficients such as absorption coefficient, band-gaps, Urbach energy, complex refractive index, optical dispersion parameters; and the dielectric coefficient (such as real and imaginary parts of the complex dielectric constants), loss tangent, and energy loss functions of these coatings were significantly modified by the annealing temperatures up to 500 °C. The refractive index exhibited normal and anomalous dispersions at higher and lower frequencies, respectively. The results based on theoretical modeling of (DFT+U) by the CASTEP Package on Cu0.5Co2.5O4 cluster suggests that the electronic density of states of Cu–Co oxide systems have a semiconducting nature with a band gap ∼1.10 eV. The predicted numerical values of the refractive index, extinction coefficient, and complex dielectric functions are in good agreement with the experimental data.Acknowledgements
M. Mahbubur Rahman gratefully acknowledges the financial support provided by the Murdoch University. Hussein A. Miran thanks the Iraqi government for the award of PhD scholarship.References
- L. Yuezin and J. N. Armor, Appl. Catal., B, 1993, 3, L1–L11 CrossRef.
- N. A. Youssef, M. M. Selim and E. S. Kamel, Bull. Soc. Chim. Fr., 1991, 128, 648–653 Search PubMed.
- W. M. Shaheen and M. M. Selim, Thermochim. Acta, 1998, 322, 117–128 CrossRef CAS.
- R. Sundararajan and V. Srinivason, Recent Developments in Catalysis Technip, Paris, 1992 Search PubMed.
- Z. Y. Tian, N. Bahlawane, V. Vannier and K. Kohse-Höinghaus, Proc. Combust. Inst., 2013, 34, 2261–2268 CrossRef CAS.
- F. Iacomi, G. Calin, C. Scarlat, M. Irimia, C. Doroftei, M. Dobromir, G. G. Rusu, N. Iftimie and A. V. Sandu, Thin Solid Films, 2011, 520, 651–655 CrossRef CAS.
- E. Ríos, S. Abarca, P. Daccarett, H. Nguyen Cong, D. Martel, J. F. Marco, J. R. Gancedo and J. L. Gautier, Int. J. Hydrogen Energy, 2008, 33, 4945–4954 CrossRef.
- M. A. Alpuche-Aviles and Y. Wu, J. Am. Chem. Soc., 2009, 131, 3216–3224 CrossRef CAS PubMed.
- L. Kaluža, B. Orel, G. Dražič and M. Kohl, Sol. Energy Mater. Sol. Cells, 2001, 70, 187–201 CrossRef.
- L. Kaluža, A. Šurca-Vuk, B. Orel, G. Dražič and P. Pelicon, J. Sol-Gel Sci. Technol., 2001, 20, 61–83 CrossRef.
- A. V. Chadwick, S. L. P. Savin, S. Fiddy, R. Alcántara, D. F. Lisbona, P. Lavela, G. F. Ortiz and J. L. Tirado, J. Phys. Chem. C, 2007, 111, 4636–4642 CAS.
- R. Alcántara, M. Jaraba, P. Lavela and J. L. Tirado, Chem. Mater., 2002, 14, 2847–2848 CrossRef.
- A. Amri, Z. T. Jiang, T. Pryor, C. Y. Yin, Z. Xie and N. Mondinos, Surf. Coat. Technol., 2012, 207, 367–374 CrossRef CAS.
- A. Balland, P. Gannon, M. Deibert, S. Chevalier, G. Caboche and S. Fontana, Surf. Coat. Technol., 2009, 203, 3291–3296 CrossRef CAS.
- T. Y. Wei, C. H. Chen, H. C. Chien, S. Y. Lu and C. C. Hu, Adv. Mater., 2010, 22, 347–351 CrossRef CAS PubMed.
- X. Xiao, L. Miao, G. Xu, L. Lu, Z. Su, N. Wang and S. Tanemura, Appl. Surf. Sci., 2011, 257, 10729–10736 CrossRef CAS.
- A. Amri, X. Duan, C. Y. Yin, Z. T. Jiang, M. M. Rahman and T. Pryor, Appl. Surf. Sci., 2013, 275, 127–135 CrossRef CAS.
- D. Ding, W. Cai, M. Long, H. Wu and Y. Wu, Sol. Energy Mater. Sol. Cells, 2010, 94, 1578–1581 CrossRef CAS.
- E. Vila, R. M. Rojas, J. L. Martín De Vidales and O. García-Martínez, Chem. Mater., 1996, 8, 1078–1083 CrossRef CAS.
- M. Adsten, R. Joerger, K. Järrendahl and E. Wäckelgård, Sol. Energy, 2000, 68, 325–328 CrossRef CAS.
- H. C. Barshilia, N. Selvakumar, K. S. Rajam and A. Biswas, J. Appl. Phys., 2008, 103, 023507 CrossRef.
- H. J. Brown-Shaklee, W. Carty and D. D. Edwards, Sol. Energy Mater. Sol. Cells, 2009, 93, 1404–1410 CrossRef CAS.
- P. N. Shelke, Y. B. Khollam, R. R. Hawaldar, S. D. Gunjal, R. R. Udawant, M. T. Sarode, M. G. Takwale and K. C. Mohite, Fuel, 2013, 112, 542–549 CrossRef CAS.
- A. Amri, Z. T. Jiang, N. Wyatt, C. Y. Yin, N. Mondinos, T. Pryor and M. M. Rahman, Ceram. Int., 2014, 40, 16569–16575 CrossRef CAS.
- A. Amri, Z. T. Jiang, P. A. Bahri, C. Y. Yin, X. Zhao, Z. Xie, X. Duan, H. Widjaja, M. M. Rahman and T. Pryor, J. Phys. Chem. C, 2013, 117, 16457–16467 CAS.
- A. Amri, Z. T. Jiang, X. Zhao, Z. Xie, C. Y. Yin, N. Ali, N. Mondinos, M. M. Rahman and D. Habibi, Surf. Coat. Technol., 2014, 239, 212–221 CrossRef CAS.
- H. Miran, M. Mahbubur Rahman, Z.-T. Jiang, M. Altarawneh, L. Siang Chuah, H.-L. Lee, E. Mohammedpur, A. Amri, N. Mondinos and B. Z. Dlugogorski, J. Alloys Compd., 2017, 701, 222–235 CrossRef CAS.
- S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CAS.
- M. Segall, P. J. Lindan, M. a. Probert, C. Pickard, P. Hasnip, S. Clark and M. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef.
- J. F. Nye, Physical properties of crystals: their representation by tensors and matrices, Oxford university press, 1985 Search PubMed.
- Z.-T. Jiang, K. Ohshimo, M. Aoyama and T. Yamaguchi, Jpn. J. Appl. Phys., 1998, 37, 4008–4013 CrossRef CAS.
- M. M. Rahman, Z. T. Jiang, P. Munroe, L. S. Chuah, Z. F. Zhou, Z. Xie, C. Y. Yin, K. Ibrahim, A. Amri, H. Kabir, M. M. Haque, N. Mondinos, M. Altarawneh and B. Z. Dlugogorski, RSC Adv., 2016, 6, 36373–36383 RSC.
- A. Millar, M. M. Rahman and Z.-T. Jiang, J. Adv. Phys., 2014, 3, 179–193 CrossRef.
- H. Kabir, M. M. Rahman, T. S. Roy and A. Bhuiyan, Int. J. Mech. Mechatron. Eng., 2012, 12, 30–34 Search PubMed.
- S. W. Xue, X. T. Zu, W. L. Zhou, H. X. Deng, X. Xiang, L. Zhang and H. Deng, J. Alloys Compd., 2008, 448, 21–26 CrossRef CAS.
- A. A. M. Farag and M. Fadel, Opt. Laser Technol., 2013, 45, 356–363 CrossRef CAS.
- S. H. Wemple and M. Didomenico Jr, Phys. Rev. B, 1970, 1, 193–202 CrossRef CAS.
- M. Yıldırım, F. Özel, N. Tuğluoğlu, Ö. F. Yüksel and M. Kuş, J. Alloys Compd., 2016, 666, 144–152 CrossRef.
- F. Yakuphanoglu, A. Cukurovali and I. Yilmaz, Phys. B, 2004, 353, 210–216 CrossRef CAS.
- B. Barış, H. G. Özdemir, N. Tuğluoğlu, S. Karadeniz, Ö. F. Yüksel and Z. Kişnişci, J. Mater. Sci.: Mater. Electron., 2014, 25, 3586–3593 CrossRef.
- C. Fournier, O. Bamiduro, H. Mustafa, R. Mundle, R. B. Konda, F. Williams and A. K. Pradhan, Semicond. Sci. Technol., 2008, 23, 085019 CrossRef.
- Y. Kim and J. Y. Leem, Phys. B, 2015, 476, 71–76 CrossRef CAS.
- A. A. Atta, J. Alloys Compd., 2009, 480, 564–567 CrossRef CAS.
- H. E. Atyia and N. A. Hegab, Phys. B, 2014, 454, 189–196 CrossRef CAS.
- S. Sarkar, N. S. Das and K. K. Chattopadhyay, Solid State Sci., 2014, 33, 58–66 CrossRef CAS.
- D. Pines and D. Bohm, Phys. Rev., 1952, 85, 338–353 CrossRef CAS.
- J. Sun, X.-F. Zhou, Y.-X. Fan, J. Chen, H.-T. Wang, X. Guo, J. He and Y. Tian, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045108 CrossRef.
- A. Rahman, et al., J. Adv. Phys., 2016, 5(4), 354 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra25626k |
| This journal is © The Royal Society of Chemistry 2017 |