Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of temperature on the growth and surface morphology of Fe3+ poisoned KDP crystals
Weidong Li ab,
Guangwei Yua,
Shenglai Wang*ab,
Jianxu Dingc,
Xinguang Xuab,
Qingtian Guab,
Duanliang Wangab and
Pingping Huangab
ab,
Guangwei Yua,
Shenglai Wang*ab,
Jianxu Dingc,
Xinguang Xuab,
Qingtian Guab,
Duanliang Wangab and
Pingping Huangab
aState Key Laboratory of Crystal Materials, Shandong University, Jinan 250100, China. E-mail: slwang67@sdu.edu.cn; Tel: +86 15662650891
bKey Laboratory of Functional Crystal Materials and Device (Shandong University), Ministry of Education, Jinan 250100, China
cCollege of Materials Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China
First published on 20th March 2017
Abstract
A series of potassium dihydrogen phosphate (KDP) crystals and Fe3+ doped KDP crystals were grown at different temperatures and at the same supersaturation value of 0.02. The prismatic face growth rates of the KDP crystals were measured using a laser polarization interference system. The surface morphologies of the growth steps on the {100} face were comparatively studied using an atomic force microscope systematically. The results showed that the bunching of steps was related to the supersaturation interval in which it was located, and approached the supersaturation dead zone of σd in which the bunching and the slope of the steps were high. The supersaturation dead zone σd and linear zone σ* decreased with rising temperature. Varying the temperature caused considerable changes in the growth speed, step morphology and step motion speed. For the crystal grown in a doped solution, the bunching and slope of the steps reached a maximum value at around 45 °C. It was interesting that the crystal growth rate in the doped solution was higher than that in the undoped solution at around 65 °C and 75 °C, the bunching of the steps was reduced and the width of the steps widened significantly. At the same supersaturation, the growth rate increased with rising temperature and the steps became straight.
1. Introduction
Crystals of potassium dihydrogen phosphate (KDP) are widely used in laser frequency materials, electro-optic modulators, and other applications due to their excellent electro-optical and nonlinear optical properties. They are also currently the preferred laser frequency and switching materials in high-power laser systems of inertial confinement fusion (ICF).1,2 In order to obtain high-quality KDP crystals, researchers have paid close attention to various factors affecting the crystal growth rate and performance, such as impurities,3–5 supersaturation,6–8 acidity9–11 and hydrodynamics.12,13 Research into the influence of temperature on the growth and surface morphology of KDP crystals is scarce, even though temperature is one of the most important parameters controlling crystal growth.14,15There are unavoidable impurity ions in raw materials. Studies on the effects of impurities on crystal growth have been reviewed several times. Trivalent ion impurities affect the prismatic faces of KDP crystals much more than the pyramidal faces.16 The adsorption of Fe3+ impurities could increase the value of the surface energy, which could lead to a decrease in the nucleation rate in the 2D nucleation models and increase the radius of the critical 2D nucleus and hence the spacing between the spiral steps.3 The growth of prismatic layers was retarded by Fe3+ impurity adsorption, and bunched growth layers were generated which would result in tapering of the crystals.17 In general, the growth rate of crystals decreases with rising Fe3+ concentration adsorbed on the surface or kink positions. On the other hand, the impurity ions could extend the metastable zone width18 and could be used as an inhibitor in the traditional growth method. Due to the development of atomic force microscopy technology, researchers can now study the influence of impurities on the growth of crystals at the atomic scale. K. Sangwal et al.19 found that the association of elementary steps to form bunched steps on the growth surface was a statistical process, and that the Schwoebel effect was responsible for the step bunching and face tapering. Terry A. Land et al.4 observed the process of impurity poisoning of the steps at constant and different supersaturation by in situ AFM. The crystal exhibits a dead zone in which no growth occurs below supersaturation σd. Above a sufficiently high supersaturation σ*, the step velocity rises rapidly, and approaches a linear value. The values of σd and σ* increase with rising Fe3+ concentration. L. N. Rashkovich20 studied the influence of supersaturation on the step velocity moving in the [001] direction on the prism face at different concentrations of Fe3+ and Al3+. The dependence of σd and σ* on impurity concentration was most probably a square-root-type relationship. The influence of temperature on the mechanism of the impurity effect is not yet resolved, therefore it is necessary to carry out related research.
In this paper, we studied the influence of temperature on the surface morphology of Fe3+ doped and undoped KDP crystals. A series of the same concentration of Fe3+ doped KDP crystals were grown at different temperatures, and the morphologies of the growth steps on the (100) faces were observed using an atomic force microscope. Finally the relationship between the temperature and step growth rate, step bunching, step width and step slope was obtained.
2. Experimental
2.1. Crystal growth
The aqueous solutions used to grow the KDP crystals were prepared using high purity KH2PO4 (Merck Co., Germany, the amounts of Fe3+, Cr3+ and Al3+ were less than 1 ppm) and de-ionized water according to the solubility curve21 in a standard 1000 ml glass crystallizer.| S = 6.02 × 10−3 × T2 + 0.208 × T + 15.9 (g KDP per 100 g H2O) | (1) |
| σ = ln(C/C0) | (2) |
| C0 = 10.68 + 0.3616 T ± 0.04 (g KDP per 100 g solution) | (3) |
After the crystals were grown to the required size, they were removed from the solution and transferred into CHCl3. The organic solvent CHCl3 eliminates the mother solutions from the crystal surface and protects the growth steps. Finally, the crystals were naturally cooled to room temperature. The crystals grown from the undoped solution were grown under the same conditions.
2.2. Real-time measurement of growth rate
The growth rates for the (100) face of the KDP crystals were measured using a laser polarization interference system. The preparation of the solution is described in section 2.1. A laser beam with a wavelength of 473 nm was used. The crystals prepared beforehand which possessed good optical quality and no obvious macroscopic defects were put into the solution at a temperature that was 1 °C above the saturation point and rotated to ensure that the laser entered vertically through the (100) face. The temperature was controlled via the circulating water. The solution cooling rate was 3 °C h−1. The intensity of the laser and the temperature were measured by a computer in real time. The growth rate R was calculated in terms of the relationship between the laser intensity I and the crystal thickness:22
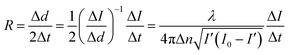 | (4) |
2.3. AFM characterization
Commercial Nanoscope IIIa MultiMode and Dimension Icon instruments were used. Before AFM observation, the crystals were removed from CHCl3 and the residue on the crystal surface was allowed to evaporate. The crystal was adjusted in order to keep the observed surface horizontal. The surface structures on the (100) faces of the crystals were studied in an ambient atmosphere at room temperature in the Contact or ScanAsyst modes. The influence of scanning itself on the original morphology could be ignored.3. Results
3.1. The growth rate of the crystals
The growth rate of the crystals varied according to the temperature and supersaturation. Charts showing the step growth rate (R) on the (100) faces of the KDP crystals versus supersaturation at different saturation temperatures in the doped Fe3+ and undoped solutions are presented in Fig. 1(a) and (b). It can be seen that in both the doped and undoped solutions, the growth rates of the crystals in different saturation temperature solutions started to increase gradually after a “dead zone” in which no growth occurred with rising supersaturation. At low supersaturation, the step growth rate increased slowly. After crossing another supersaturation zone, with rising supersaturation the growth rate increased rapidly, and approached linearity. At the same supersaturation, the higher the saturation temperature, the faster the growth rate of the crystal in different saturation temperature solutions.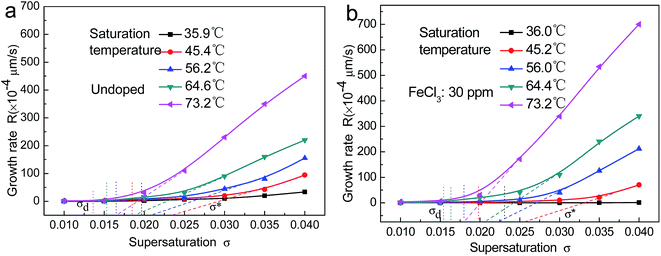 | ||
| Fig. 1 The growth rate on the (100) face of the KDP crystal at different saturation temperatures and supersaturation: (a) undoped; (b) Fe3+: 30 ppm. | ||
There were also obvious differences between the crystal growth rates in the doped and undoped solutions. The increase in the growth rate in the undoped solution was much larger than that in the doped solution, while the supersaturation was increased for the low saturation temperature solution. The opposite trend was observed for the high saturation temperature solution.
Terry A. Land et al.4 proposed the existence of a supersaturation dead zone, denoted by σd, in the process of step movement. When the supersaturation was below σd, the step did not move and no growth of the prismatic faces of the crystal was observed. As the supersaturation increased beyond σd, the crystal growth rate increased slightly. When the supersaturation exceeded σ*, the step velocity increased and approached linearity. There was a corresponding relationship between the step normal growth rate R and the tangential growth speed V of the steps, and the ratio was the slope of the steps. Therefore, it could be considered that the supersaturation dead zone σd and linear zone σ*′ similarly exist in the process of normal crystal growth rate R with changing supersaturation. Referring to the method used by Terry A. Land et al.,4 two critical supersaturation values, σd and σ*′, were obtained in the process of normal crystal step growth at different temperatures, and the values are shown in Tables 1 and 2. It can be seen that both σd and σ*′ decreased with increasing temperature for the doped and undoped solutions, and σ*′ reduced faster than σd. At similar temperatures, the values of σd and σ*′ for the doped solution were larger than those for the undoped solution, and the difference between the values of σd and σ*′ in the doped solutions and in the undoped solutions decreased with increasing temperature. It is suggested that the effect of impurities weakened with increasing temperature. Furthermore, the difference between σd and σ*′ decreased with increasing temperature, and the deviation in the doped solutions decreased quicker than in the undoped solution.
| Saturation temperature | 35.9 °C | 45.4 °C | 56.2 °C | 64.6 °C | 73.2 °C |
|---|---|---|---|---|---|
| σd (10−2) | 1.97 | 1.83 | 1.64 | 1.52 | 1.36 |
| σ*′ (10−2) | 3.3 | 2.35 | 2.12 | 1.89 | 1.66 |
| Saturation temperature | 36.0 °C | 45.2 °C | 56.0 °C | 64.4 °C | 73.2 °C |
|---|---|---|---|---|---|
| σd (10−2) | 2.31 | 1.98 | 1.78 | 1.63 | 1.54 |
| σ*′ (10−2) | 4.7 | 2.59 | 2.26 | 2.07 | 1.82 |
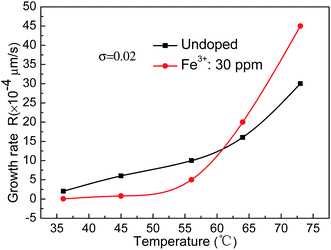
In order to display the effect of temperature on the growth rate, curves showing the growth rate on the (100) face of the KDP crystals at the same supersaturation of 0.02 for different saturation temperature solutions are displayed in Fig. 2. It can be observed that the influence of temperature on the growth rate was very obvious. When the temperature was increased from around 35 °C to around 75 °C, the growth rate of the undoped crystal increased by more than one order of magnitude from 2 × 10−4 μm s−1 to 30 × 10−4 μm s−1. In the doped solution, the crystal growth rate increased by about three orders of magnitude from 0.054 × 10−4 μm s−1 to 45 × 10−4 μm s−1. When the saturation temperature was below 55 °C, the crystal growth rate in the undoped solution was higher than that in the Fe3+ doped solution. A transition occurred in the temperature range of 55–65 °C. The growth rate in the undoped solution was lower than that in the Fe3+ doped solution at temperatures above 65 °C.
3.2. Morphology of the growth step on the (100) face
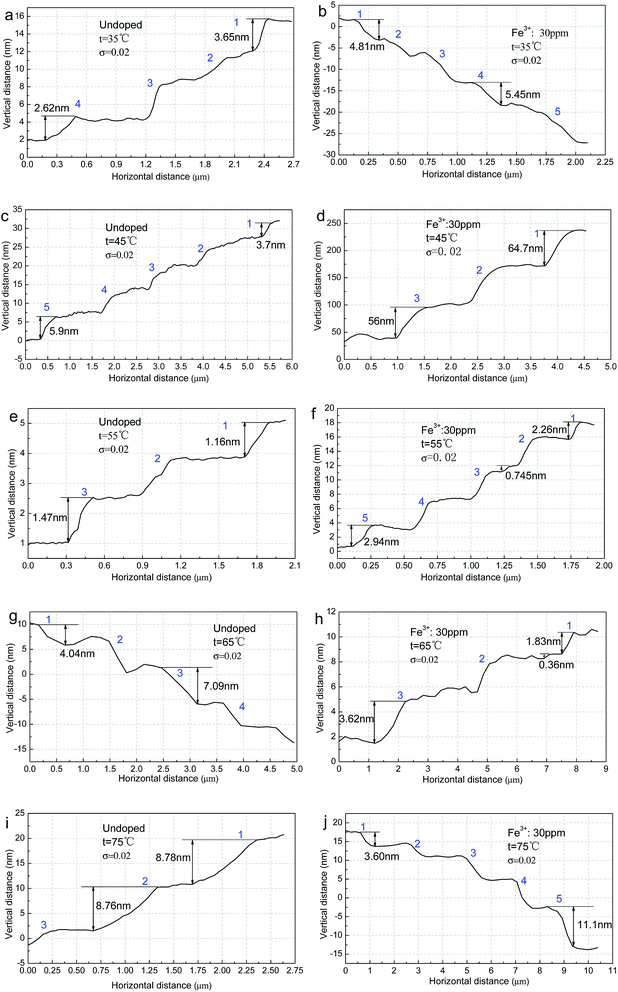
The morphologies of the (100) faces of undoped KDP and the same concentration of Fe3+ doped KDP crystals, grown at different saturation temperatures of about 35 °C, 45 °C, 55 °C, 65 °C and 75 °C at the same supersaturation of 0.02, are illustrated in Fig. 3(a)–(j). The inset images show the corresponding 3-D graphics. The blue arrow represents the step motion direction. The step structures of the areas marked with white dotted boxes in the AFM images are shown in Fig. 4(a)–(j).Combined with the results shown in Fig. 3 and 4, it is obvious that the bending of the steps reduced, and the steps became more straight with increasing temperature. The bending of the steps on the surfaces of the Fe3+ doped KDP crystals was greater than that on the undoped KDP crystal surfaces.
For KDP crystals grown in undoped solutions, most of the growth steps on the surface were straight or nearly straight, except for the crystals grown at around 45 °C and 55 °C where element steps and more macrosteps existed on the crystal surface. Some macrosteps with their ledges tilted with respect to the adjacent step ledge existed at around 35 °C. At the temperatures of 45 °C and 55 °C, the steps intertwined with each other and many protrusions appeared on the steps, which were more pronounced at around 55 °C. When the temperature was 65 °C and 75 °C, the steps became straight, and formed a stable step array which was composed of several element steps. The step edge presented “gentle slopes”.
For the KDP crystals grown in the Fe3+ doped solutions, most of the steps were distorted except for the steps grown at around 75 °C. There were mainly macrosteps on the surfaces of the crystals. The growth steps exhibited a “sawtooth” shape at around 35 °C. The twisting points and protrusions became greater in number on the steps which had “wave-like” shapes at around 55 °C. When the temperature was about 65 °C, individual large step protrusions appeared on the crystal surface. The steps became straight when the temperature was about 75 °C.
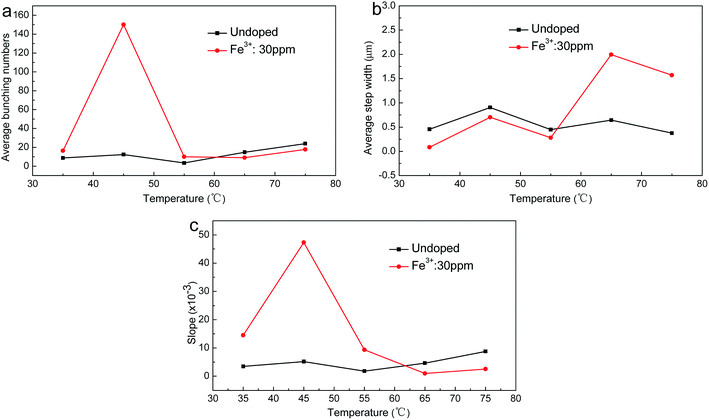
At a consistent supersaturation of 0.02, the relationships between temperature and the step bunching number, average width and slope are shown in Fig. 5. It can be seen that these three relationships showed little change for the undoped crystals. The number of macrostep contained element steps reached a minimum value of about 4 at around 55 °C, and increased to a maximum of about 24 at around 75 °C. The slopes were about 1.82 × 10−3 and 8.78 × 10−3, respectively. The average width of the steps reached a minimum at around 75 °C and a maximum at around 45 °C, and the values were about 0.376 μm and 0.906 μm, respectively. For the crystals grown in doped solutions, the step morphology changed significantly. The bunching and slope of the steps were larger than those of the crystals grown in undoped solutions at around 35 °C. The average number of macrostep contained element steps was 16, and the slope was about 14.5 × 10−3. When the temperature was 45 °C and 55 °C, the bunching and slope of the steps both drastically changed, and presented a trend of first increasing then decreasing with rising temperature. The two both reached maximum values at around 45 °C; the number was about 153 and the slope of the step was approximated as 47.3 × 10−3. When the temperature was 55 °C, the number was 6–10 and the slope was about 9.33 × 10−3, thus demonstrating that the number and slope of the steps both reduced significantly. It was interesting that the width of the steps had not changed much in this process, and was just slightly lower than for the undoped case. When the temperature was 65 °C and 75 °C, the bunching of the steps changed little, and although the slope of the steps decreased obviously, the decrease was lower than for the undoped case. The average width of the steps increased obviously with rising temperature, and was a much larger increase than for the undoped case.
4. Discussion
Supersaturation was one of the most important factors that influenced the crystal growth; the larger the supersaturation, the faster the crystal growth rate. Temperature was also one of the most important parameters that affected the crystal growth; the higher the temperature, the faster the growth rate. At the same supersaturation of 0.02, the growth rates were about 2 × 10−4 μm s−1 and 30 × 10−4 μm s−1 at around 35 °C and 75 °C, respectively. The growth rate increased by more than one order of magnitude. When the temperature increased, the solute molecules or ions sped up. The diffusion rate was fast, and more ions diffused to the growth surface per unit time. The speed of the diffusion of the growth units and attachment to the growth sites on the surface was also fast. This led to an increased step motion speed with rising temperature, and the normal growth rate increased. As a result, the supersaturation dead zone σd and linear region σ*′ were both significantly reduced with rising temperature.The rule that high temperature leads to a fast growth rate was also applicable to the Fe3+ doped solution. The studies carried out by Terry A. Land et al.4 and L. N. Rashkovich et al.20 showed that both the supersaturation dead zone σd and linear region σ* values increase with increasing Fe3+ concentration in the process of KDP crystal growth. In this experiment, the Fe3+ concentration was kept constant and the temperature was changed. The supersaturation dead zone σd and linear region σ*′ values both reduced with rising temperature. In the doped solution the values of σd and σ*′ were larger than those in the undoped solution, and the difference between the values of σd and σ*′ in the doped solutions and in the undoped solutions decreased with rising temperature.
The morphology and evolution pathway of the steps were changed with rising temperature when a constant supersaturation of 0.02 was maintained in this experiment. In the undoped solution, the supersaturation value of 0.02 just exceeded the supersaturation dead zone σd value at around 35 °C; the movement of element steps was the primary evolution pathway, and the step speed was very low and close to no movement. The difference of speed among the element steps formed the macrosteps. When the temperature was around 45 °C and 55 °C, the supersaturation value of 0.02 was located between the supersaturation dead zone σd and the linear region σ*′, i.e., σd < σ < σ*′. The speed of the macrosteps was low, and the element steps moved faster than the macrosteps. The speed difference between the element steps caused the coalescence of the steps. When the temperature was around 65 °C and 75 °C, the supersaturation value of 0.02 was beyond the linear region σ*′, i.e., σ > σ*′. Both the element steps and macrosteps moved, and the step speed gradually improved. The difference of speed among the element steps was so large that a stable step array was formed. The macrosteps exhibited a larger contribution than the element steps towards the improvement of the normal crystal growth rate which increased by more than one order of magnitude.
In the doped solution, the supersaturation value of 0.02 was located in the growth dead zone at around 35 °C, i.e. σ < σd. The element steps and the macrosteps were both immobile. There was no normal growth rate. When the temperature was about 45 °C, the supersaturation value of 0.02 just exceeded the supersaturation dead zone σd, i.e., σd < σ ≪ σ*′. According to the research carried out by N. Cabrera et al.,23 the element steps were motionless when the average impurity spacing became less than approximately twice the Gibbs–Thomson critical radius. The other element steps that had not been fixed by impurities would move forward continuously until they caught up with the motionless macrostep; the element steps would arrive at the top of the macrosteps and merge into the macrosteps. The bunching and slope of the steps increased rapidly. The supersaturation value of 0.02 was located between the supersaturation dead zone σd and the linear region σ*′ at around 55 °C, i.e., σd < σ < σ*′. According to the model of step evolution in impurity doped solutions presented by Terry A. Land et al.,4 the elementary steps from the top of the macrosteps became pinned in place due to the attached impurities; the other parts of the macrosteps moved with low velocity until they encountered an immobile elementary step, at which point the element step became the bottom step of the macrostep and began to advance. In this fashion, the bunching and slope of the steps decreased. The supersaturation value of 0.02 neared the linear region σ*′ at around 65 °C, i.e., σd ≪ σ < σ*′. The step evolution pathway was similar to that at around 55 °C, the difference being that the macrostep had sped up, the element steps began to move and gradually increased up to the macrostep rate. The supersaturation value of 0.02 was beyond the linear region σ*′ at around 75 °C, i.e., σ > σ*′. The element steps and macrosteps moved together, and the macrosteps exhibited a much larger contribution than the element steps towards the normal crystal growth rate.
The traditional theory and model presented by Terry A. Land et al.4 could explain why the crystal growth rate in the doped solution was lower than that in the undoped solution at low temperature. However, in contrast with the above theory and model, the growth rate of the crystals in the doped solution was higher than that in the undoped solution when the temperature was around 65 °C and 75 °C. In addition, the average width of the steps grown in the doped solution was larger than that in the undoped solution, and the bunching and slope of the steps grown in the doped solution were both lower than those in the undoped solution. By comparison of the changes in the surface morphology between the crystals grown in doped and undoped solutions, as shown in Fig. 3, it was found that the step bending was large, and the number of protrusions on the steps increased obviously after doping with impurities at around 65 °C and 75 °C. This possibly led to the increase of the growth positions on the steps, thus making the growth rate of the crystals in the doped solution higher than that in the undoped solution at high temperature.
5. Conclusion
The prismatic face growth rates of the KDP crystals were measured using a laser polarization interference system. The effect of temperature on the surface morphology of Fe3+ doped and undoped KDP crystals was studied systematically using atomic force microscopy. The growth rate of the crystals and the motion pathway of the element steps and macrosteps were all measured at different temperatures. The studies showed that the higher the temperature, the faster the growth rate. The bunching of steps was related to the supersaturation interval in which it was located, and when the supersaturation dead zone of σd was approached, the bunching and slope of the steps were both high. The supersaturation dead zone σd and linear region σ*′ reduced with rising temperature, which caused variation in the growth rate, morphology and motion pathway of the steps. It was interesting that the growth rate of the KDP crystals in the Fe3+ doped solution was faster than that in the undoped solution at around 65 °C and 75 °C, the bunching of the steps was reduced and the width of the steps increased significantly.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (No. 51321062) and the National Science Foundation for Young Scientists of China (No. 51202131).References
- N. Zaitseva and L. Carman, Prog. Cryst. Growth Charact. Mater., 2001, 43(1), 1–118 CrossRef CAS.
- J. J. De Yoreo, A. K. Burnham and P. K. Whitman, Int. Mater. Rev., 2002, 47(3), 113–152 CrossRef CAS.
- K. Sangwal, Prog. Cryst. Growth Charact. Mater., 1996, 32, 3–43 CrossRef CAS.
- T. A. Land, T. L. Martin, P. Sergey, G. Tayhas Palmore and J. J. De Yoreo, Nature, 1999, 399, 442–445 CrossRef CAS.
- S.-J. Zhu, S.-L. Wang, J.-X. Ding, G.-X. Liu, W.-J. Liu, L. Liu, D.-L. Wang, W.-D. Li, Q.-T. Gu and X.-G. Xu, J. Cryst. Growth, 2014, 388, 98–102 CrossRef CAS.
- G.-Y. Yang, K. Noriaki, Z.-L. Sha, L. K. Marjatta and J.-F. Wang, Cryst. Growth Des., 2006, 6(12), 2799–2803 CAS.
- N. Zaitseva, L. Carman, I. Smolsky, R. Torres and M. Yan, J. Cryst. Growth, 1999, 204, 512–524 CrossRef CAS.
- L. Julien, Z. Julien, I. Manuel, V. Stephane, B. Jose and I. Alain, Cryst. Growth Des., 2011, 11, 2592–2598 Search PubMed.
- M. Cheng, M.-W. Li, Y.-C. Cao, X.-D. Wang and J.-L. Guo, Cryst. Res. Technol., 2009, 44(11), 1215–1222 CrossRef CAS.
- D. Kaminski, N. Radenovic, M. A. Deij, W. J. P. Van Enckevort and E. Vlieg, Cryst. Growth Des., 2006, 6(2), 588–591 CAS.
- F.-F. Liu, L.-S. Zhang, G.-W. Yu and X. Sun, Cryst. Res. Technol., 2015, 50(2), 164–170 CrossRef CAS.
- H. F. Robey and D. Maynes, J. Cryst. Growth, 2001, 222, 263–278 CrossRef CAS.
- G.-X. Liu, S.-L. Wang, Q.-T. Gu, J.-X. Ding, Y. Sun, W.-J. Liu, S.-J. Zhu and L. Liu, J. Synth. Cryst., 2013, 42(7), 1261–1266 CAS +1271.
- H. Eisenschmidt, A. Voigt and K. Sundmacher, Cryst. Growth Des., 2015, 15, 219–227 CAS.
- S. Selemani, J.-M. Chang, B. Kamala, P. Benjamin and R. B. Lal, Cryst. Growth Des., 2001, 1(5), 359–362 Search PubMed.
- L. N. K. D. P. Rashkovich, Family of Crystals, Hilger-Bristol, 1991 Search PubMed.
- C. Belouet, E. Dunia and J. F. Petroff, J. Cryst. Growth, 1974, 23(4), 243–252 CrossRef CAS.
- O. Shimomura and M. Suzuki, J. Cryst. Growth, 1989, 98(4), 850–852 CrossRef CAS.
- K. Sangwal, J. T. Burgues, P. Gorostiza and F. Sanz, Cryst. Res. Technol., 1999, 34, 667–675 CrossRef CAS.
- L. N. Rashkovich and N. V. Kronsky, J. Cryst. Growth, 1997, 182, 434–441 CrossRef CAS.
- W. K. Burton, N. Cabrera and F. C. Frank, Philos. Trans. R. Soc., A, 1951, 243(866), 299–358 CrossRef.
- B. Liu, S.-L. Wang, C.-S. Fang, Q.-T. Gu, X. Sun and Y.-P. Li, J. Inorg. Mater., 2006, 21, 22–28 CAS.
- N. Cabrera and D. A. Vermilyea, Growth and perfection of crystals, Chapman and Hall, London, 1958 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |