Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the mechanism, thermodynamic and kinetic features of the Kukhtin–Ramirez reaction in carbamate synthesis from carbon dioxide†
Hossein Sabet-Sarvestani,
Hossein Eshghi* and
Mohammad Izadyar
Department of Chemistry, Faculty of Sciences, Ferdowsi University of Mashhad, Mashhad, Iran. E-mail: heshghi@um.ac.ir; Fax: +98 5118795457; Tel: +98 5118795457
First published on 5th January 2017
Abstract
In this article, thermodynamic and kinetic aspects of the Kukhtin–Ramirez reaction of the carbamate formation from carbon dioxide have been investigated in the presence of various phosphorous reagents (PRs), in the gas and solvent phases, theoretically. The obtained carbamate is a precursor for the synthesis of oxazolidine-2,4-dione as a biologically important compound. Two kinds of phosphorous reagents have been considered: type 1 is the PRs which have variable numbers of nitrogen atoms while, type 2 is composed of PRs without nitrogen atoms. By investigation of the local nucleophilicity indices (Nk) and steric exchange energy (dE), the reaction kinetics was studied in the presence of these kinds of PRs. It was illustrated that the steric repulsion between the lone pair electrons of the phosphorus atom and its bonded groups and the nucleophilicity character of this atom are impressive factors in the reaction kinetics. On the other hand, the analysis of stabilization energies associated with the donor–acceptor orbitals of the oxide forms of PRs (PORs) shows that the number of nitrogen atoms of the studied PRs have remarkable effects on the thermodynamics of the overall reaction. Finally, it has been shown that the obtained ΔEReaction by MPWB95 and B3LYP functionals, are in an acceptable correlation with the Mulliken atomic spin density (Pk−) of the phosphorous atom.
Introduction
A significant increase in global fuel consumption and emission of enormous quantities of CO2 are vital issues in energy and environmental fields. CO2 is one of the main components of greenhouse gases and after pre-industrial times, its amount has been increased.1 These gases are primarily responsible for the rise in atmospheric temperature and probably abnormal changes in the global climate. Human industrialization has led to a substantial increase in CO2 in our atmosphere and its emission to be continuously increasing; an event that is now implicated in increased ocean acidification and extreme weather phenomena.2 Therefore, utilization of CO2 as the C1 building block for fuels and chemicals is one of the most interesting strategies to solve the CO2 production matter.3The vast majority of carbon resources are based on crude oil, natural gas and coal.4 One of the most interesting issues in many fields of chemistry is the application of CO2 as a reactant in the production of valuable materials.5,6 Organometallic reagents, three-membered heterocyclic compounds, hydrogen and other reductive reagents and materials which contain oxygen or nitrogen atoms are able to react with CO2 and produce valuable materials such as urea derivatives, cyclic carbonates, polycarbonates, acetylsalicylic acid and salicylic acid.7 For example, catalytic coupling of CO2 with high energy substrates, such as epoxides and aziridines, to generate polycarbonates, polycarbamates, cyclic carbonates and carbamates has considerable attention over the past decades.3
One of the valuable compounds in organic synthesis is heterocyclic rings which their production by carbon dioxide is currently receiving considerable and increasing attention by the scientific community.8 Oxazolidine-2,4-diones are heterocyclic rings that their traditional synthesis strategies suffer from harsh reaction conditions, multi-step procedures and the use of very toxic compounds like phosgene and isocyanates.9 The frequently used methods for their synthesis are the cyclizations of α-hydroxy ester with urea or isocyanates and α-hydroxy amide with chloroformates or carbonates.
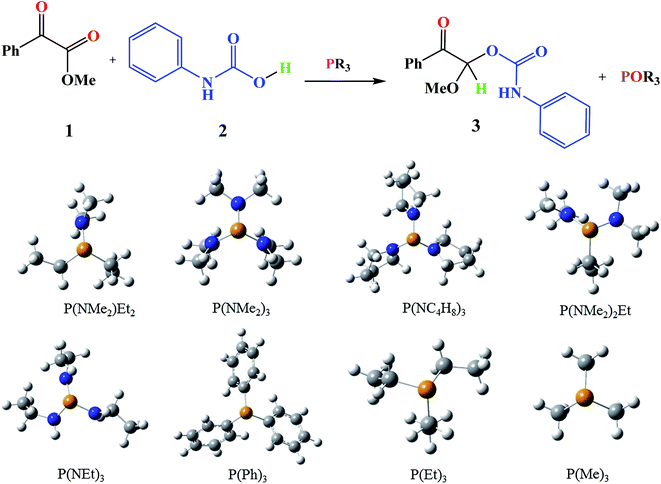
Moreover, the conversions of heterocyclic intermediates to oxazolidine-2,4-diones are another strategies for oxazolidine-2,4-diones production.10–12 However, Zhang and coworkers reported a mild, convenient and environmentally friendly method by using CO2 for synthesis of oxazolidine-2,4-diones.13 Oxazolidine-2,4-diones are important class of the chemical compounds that are widely used in medicine and pharmaceutical industry.14 P(NMe2)3 was used by Zhang and coworkers as a valuable phosphorous reagent for oxazolidine-2,4-diones synthesis.13
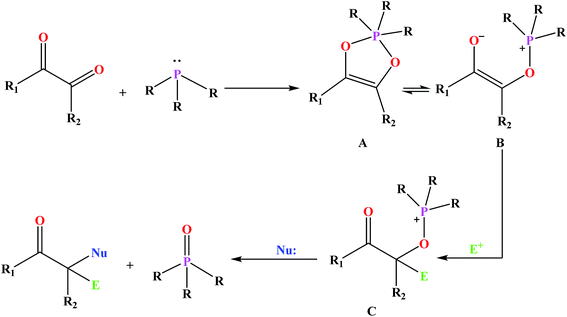
Among the numerous organophosphorus with different valence states, trivalent phosphorus derivatives are known15 which undergo an addition reaction with 1,2-dicarbonyl compounds to give 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adducts formulated as either dioxaphospholene (A) or oxyphosphonium enolate (B) (Fig. 1). This reaction is known as Kukhtin–Ramirez addition which have been the issues of numerous investigations.16 The reaction of B with electrophilic reagents yields alkoxyphosphonium species C which acts as an electrophile for nucleophilic displacement.17
1 adducts formulated as either dioxaphospholene (A) or oxyphosphonium enolate (B) (Fig. 1). This reaction is known as Kukhtin–Ramirez addition which have been the issues of numerous investigations.16 The reaction of B with electrophilic reagents yields alkoxyphosphonium species C which acts as an electrophile for nucleophilic displacement.17
Based on the importance of the PRs in new organic synthesis, and because of their vital effect as efficient catalysts in Kukhtin–Ramirez addition, a comprehensive kinetic and thermodynamic study has been carried out on the effects of PRs in the reaction which reported by Zhang and coworkers. For this purpose, besides of P(NMe2)3 that has been used by Zhang and coworkers, different PRs has been considered in which two kinds of PRs are distinguishable. Type 1 has nitrogen atom while type 2 is N atom free. It is notable that the considered PRs were synthesized already and the synthetic strategies of all considered PRs are available.18–22 Fig. 2 shows the overall reaction and considered PRs. In order to have an insight into the kinetic and thermodynamic aspects, a knowledge of the reaction mechanism at the molecular level is necessary which is provided here by using quantum chemistry calculations with different analyses.
Computational details
All structures corresponding to the reactants, transition states (TSs), intermediates and the products of the reaction were optimized, using the Gaussian09 computational package23 with the density functional theory (DFT) method as implemented in the computational package.24 Optimized geometries of the stationary points on the potential energy diagrams were obtained using the B3LYP functional and 6-31+G(d,p) basis set. Single point energy calculations on the optimized structures were performed using the meta-GGA functional of MPWB95.25–29 The synchronous transit-guided quasi-Newton (STQN) method as implemented by Schlegel et al.30 was applied to locate the TSs. Intrinsic reaction coordinate (IRC) method31 was also used in order to check and obtain the profiles connecting the TSs to the reactants and products.Vibrational frequencies of these points along the reaction paths were specified to provide an estimation of the zero point vibrational energies (ZPVEs) and TSs validation. Natural bond orbital (NBO) analysis were applied to determine the donor–acceptor interaction energies, steric exchange energy (dE) and orbital overlap integrals, Sij.32,33 Base on this analysis, some important quantum molecular descriptor have been evaluated and analyzed. Because, the solvent–solute interactions are more considerable in the solution, conductor like polarizable continuum model (CPCM) was applied for the calculation of the solvent effects on the kinetic and thermodynamic aspects of the reaction.34 In order to describe the intermolecular interaction during the reaction, 3D-NCI (non-covalent interactions) plots35,36 were calculated using the MultiWFN 3.1 software.37
Results and discussion
Mechanism investigation
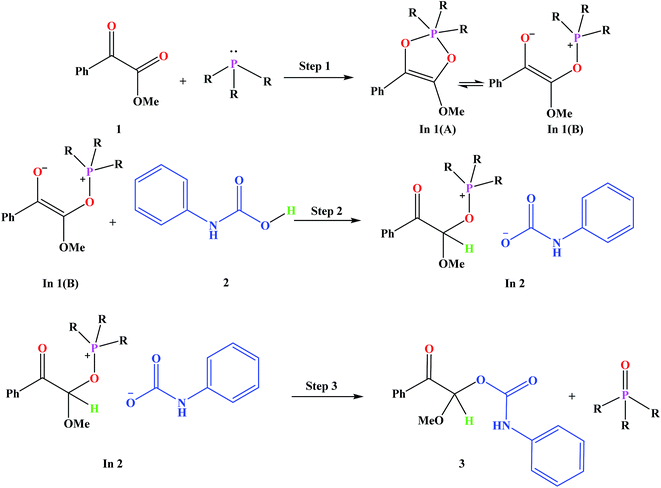
Fig. 3 shows the proposed reaction mechanism and the corresponding potential energy diagram (PED) for the reaction in the gas and solvent phases has been depicted in Fig. 4. The reaction proceeding through the intermediates leads to different energy levels in the reaction pathway on the PED which has been depicted by numbers in Fig. 4. Total Gibbs free energy of phenyl carbamic acid (2), P(NMe2)3 and α-keto ester (1) has been considered as the reference in the PED. In order to decrease the cost of the calculations, ethyl group of applied α-keto ester (1), in experimental report, has been replaced by methyl group. Absolute values of the Gibbs free energy, entropy and enthalpy of the intermediates, during the reaction, have been provided in Table 1(s).† In addition to the relative Gibbs free energy of the studied levels, relative activation Gibbs free energy of the TSs and imaginary vibrational frequencies were also included in this table.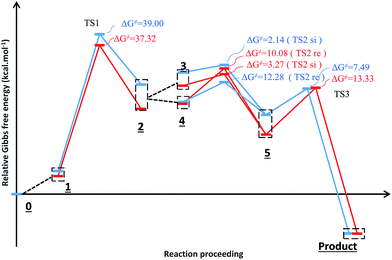 | ||
| Fig. 4 Potential energy diagram for the reaction in the gas phase (blue diagram) and solvent (red diagram). | ||
Phenyl carbamic acid (2) is produced by nucleophilic attack of aniline to carbon dioxide. Since, there are numerous methods for the synthesis of 2,38 it is possible to be prepared separately, and added to the desire reaction. In 1 is produced due to the nucleophilic attack of P(NMe2)3 to the ketone carbonyl group of α-keto ester (1) which has two isomeric forms of In 1(A) and In 1(B). Calculated absolute Gibbs free energies of In 1(B) and In 1(A) are −1318.211 and −1318.207 (a.u) in the gas phase, respectively. Our tries for optimization of In 1(A) to take the global minimum energy was not successful in CH2Cl2 as the solvent and during the optimization process, its five membered ring was opened and In 1(A) was converted to In 1(B). It can be concluded that, In 1(B) is the most stable isomer of In 1. In step 2, the proton of phenyl carbamic acid (2) is adsorbed by nucleophilic attack of carbon atom of In 1, yielding In 2.
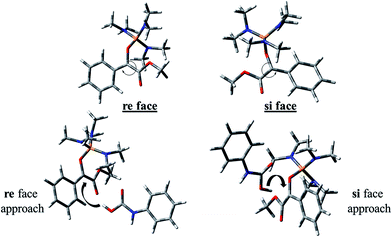
The carbon atom bonded to OMe group in In 1(B) is a prochiral center and the configurations of the prochiral centers are determined by the Cahn–Ingold–Prelog sequence rules.39 Therefore, In 1(B) has two faces which bears a mirror-image and diastereotopic relationship to each other. These two faces are classified as re or si. Therefore, two directions can be considered for phenyl carbamic acid approaching to In 1(B). Fig. 5 depicts si and re faces and two approaching paths for In 1(B) reaction with phenyl carbamic acid.
Levels 3 and 4 on the PED correspond to the relative Gibbs free energies of si and re faces approaching, respectively in which, the energy of si face approaching is higher than re. None-covalent interaction (NCI) concept is a useful tool for justification of this energy difference which enables the identification of the interactions in 3D space using the electron density. In a 3D NCI plot, each type of chemical interactions is represented by a color-filled isosurface. van der Waals interactions, in a 3D NCI plot are described by the region marked by green or light brown isosurfaces.
For this purpose NCI analysis, In 1(B) was optimized using the DFT-D3 method which includes atom–atom dispersion corrections according to the scheme proposed by Grimme.40 Our investigation shows a remarkable van der Waals interaction between the oxygen atom of phenyl carbamic acid and linked methyl groups to nitrogen atoms in In 1(B) for re face approaching which has been illustrated in Fig. 6. Therefore, it can be concluded that due to van der Waals interaction, that re face approaching (level 4 on the PED) has lower relative energy than si face. However, relative Gibbs free energy of activation (ΔG≠) for the corresponding si face approaching transition state (TS si) is lower than the corresponding re face approaching transition state (TS re). The steric repulsion of transferring hydrogen atom at the TS re with methyl groups linked to nitrogen atom is a reason for the higher value of ΔG≠. Finally, phenyl carbamate acts as another nucleophile in step 3 and because of its nucleophilic attack to carbon atom of In 2, final product (3) is formed. The reaction of 3 and sodium methoxide as a base yields oxazolidine-2,4-diones. Table 1 shows the activation and thermodynamic parameters of all involved steps in the reaction mechanism in the gas phase and CH2Cl2.
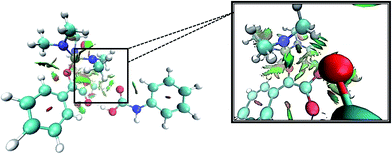 | ||
| Fig. 6 3D-NCI plot corresponding to re face approaching and green isosurfaces between oxygen atom of carbamic acid and methyl groups linked to nitrogen atoms in In 1(B). | ||
| Steps | Gas phase | Solvent phase | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ΔG (kcal mol−1) | ΔH (kcal mol−1) | ΔS (cal mol−1 K−1) | ΔG≠ (kcal mol−1) | ΔG (kcal mol−1) | ΔH (kcal mol−1) | ΔS (cal mol−1 K−1) | ΔG≠ (kcal mol−1) | ||
| 1 | 24.66 | 16.13 | −28.61 | 39.00 | 19.18 | 8.49 | −35.84 | 37.32 | |
| 2 | re face approaching | −3.63 | −3.12 | 1.69 | 12.28 | −8.77 | −7.15 | 5.45 | 10.08 |
| si face approaching | 12.08 | 11.27 | −2.72 | 2.14 | 13.94 | 12.77 | −3.90 | 3.27 | |
| 3 | −33.83 | −22.91 | 36.62 | 7.49 | −28.25 | −18.47 | 32.80 | 13.33 | |
Kinetic studies
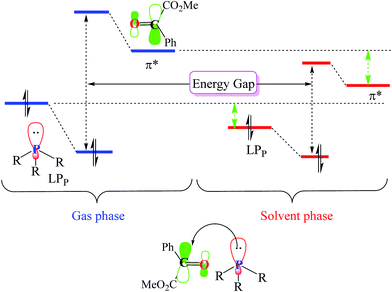
As illustrated in Fig. 4, in the case of P(NMe2)3, step 1 is the rate determining step (RDS) of the reaction in which activation Gibbs free energy, ΔG≠, decreases by CH2Cl2. This behavior can be described by investigation of the energies of involved orbitals in step 1. In this step, the nucleophilic attack of the phosphorous atom to carbonyl group of α-keto ester occurs. Therefore, lone pair electrons of the phosphorus atom (LPP) and anti-bonding π orbital of the carbonyl group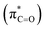 are the involved orbitals in the reaction. Table 2 illustrates the energies of these orbitals and energy gap between them in two phases. Fig. 7 depicts a schematic presentation of the orbital interaction in the solvent and gas phases. A low difference in the orbital energies of the interacting group makes their interaction more probable. In the solvent phase the energy gap is lower than gas phase which leads to a more facility orbital interactions and reduces ΔG≠ values.
are the involved orbitals in the reaction. Table 2 illustrates the energies of these orbitals and energy gap between them in two phases. Fig. 7 depicts a schematic presentation of the orbital interaction in the solvent and gas phases. A low difference in the orbital energies of the interacting group makes their interaction more probable. In the solvent phase the energy gap is lower than gas phase which leads to a more facility orbital interactions and reduces ΔG≠ values.
| PRs | dE (kcal mol−1) | Gas phase | CH2Cl2 | ||||
|---|---|---|---|---|---|---|---|
| ΔG≠ (kcal mol−1) | ELPP (a.u) | EπC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O − ELPPa (a.u) O − ELPPa (a.u) |
ΔG≠ (kcal mol−1) | ELPP (a.u) | EπC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O − ELPPb (a.u) O − ELPPb (a.u) |
||
a EπC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(gas) = 0.139829 (a.u).b EπC O(gas) = 0.139829 (a.u).b EπC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(CH2Cl2) = −0.00966 (a.u). O(CH2Cl2) = −0.00966 (a.u). |
|||||||
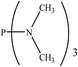 |
24.59 | 39.00 | −0.39801 | 0.53783 | 37.32 | −0.40049 | 0.39083 |
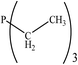 |
15.00 | 33.48 | −0.37247 | 0.51229 | 31.07 | −0.37376 | 0.3641 |
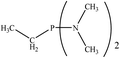 |
22.54 | 35.09 | −0.287 | 0.42682 | 33.55 | −0.39651 | 0.38685 |
 |
22.06 | 34.87 | −0.37527 | 0.51509 | 33.01 | −0.37804 | 0.36838 |
 |
20.64 | 32.28 | −0.39664 | 0.53646 | 31.73 | −0.40201 | 0.39235 |
 |
20.77 | 37.33 | −0.3792 | 0.51902 | 36.31 | −0.38393 | 0.37427 |
 |
25.46 | 36.10 | −0.37884 | 0.51866 | 32.42 | −0.38219 | 0.37253 |
 |
11.83 | 37.70 | −0.3887 | 0.52852 | 33.70 | −0.38862 | 0.37896 |
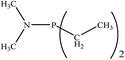
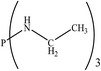
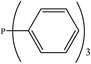
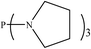
There are interesting results in the case of other PRs effects on the RDS and ΔG≠ which reported in Table 2. Based on this table, P(NEt)3 and P(Et)3 have the lowest ΔG≠ values in two phases among the studied PRs. In order to have a better description of ΔG≠ values in the RDS, two important factors have been considered. One of them is the reactivity descriptor as a powerful criterion to predict the chemical reactivity of PRs, and the other factor is the steric repulsion between lone pair electrons of the phosphorus atom and the linked groups. Table 2 shows total steric exchange energy (dE) between lone pair electrons of phosphorous atom and closest linked groups of the PRs. dE values (kcal mol−1) of P(NM2)3, P(NC4H8)3, P(NMe2)2Et and P(NMe2)Et2 are higher than P(Et)3, P(Me)3, P(Ph)3 and P(NEt)3. It is reasonable to be noted that, larger values of dE make nucleophilic attack of PRs harder and ΔG≠ larger. However, steric effect is not the only factor for investigation of ΔG≠. For example, dE values of P(Et)3 and P(Me)3 are lower than P(NEt)3, while ΔG≠ values are larger than P(NEt)3. Therefore, the reactivity descriptors of PRs can be considered as a helpful scale for justification of the difference in ΔG≠ value of P(Et)3, P(Me)3, P(Ph)3 and P(NEt)3.
Global nucleophilicity can be expressed in terms of the equation: N = εHomo(Nu) − εHomo(TCE) which reported by Domingo. The nucleophilicity is defined relative to tetracyanoethylene (TCE) because it has the lowest HOMO energy in a large series of molecules. Also, Parr function P(r) as a new local reactivity index was proposed by Domingo which provides new parameters of the electrophilicity, Pk+, and nucleophilicity, Pk−, based on the Mulliken atomic spin density distribution on the radical anion and radical cation of a neutral molecule.41 Based on the electrophilic and nucleophilic Parr functions, it is possible to define the local electrophilicity as: ωk = ωPk+ and local nucleophilicity indices as: Nk = NPk−.41 These concepts of local reactivity index are more modern than the Fukui function, f(r), which was suggested by Parr and Yang. These new local reactivity indices have been applied for numerous kinds of reactions such as polar cycloadditions, Michael-type addition and radical additions.41,42
The polarity character of transition state is requisite for application of the proposed local indices which for step 1 was evaluated by computing the global electron density transfer (GEDT) at the TS1.43 Natural atomic charges at the TS, obtained through the NBO analysis, are shared between the PRs and α-keto ester frameworks. Based on the GEDT values of the TS1, step 1 is a polar reaction and PRs play as the nucleophiles during this step. On the other hand, a knowledge of μ is necessary, in order to specify the electrophilic or nucleophilic behaviors of the reactants in a reaction. Because, in a polar reaction the electronic charge always transfers from the species with a higher μ, the nucleophiles, to the species with a lower μ, the electrophiles.40 Based on this analysis in step 1, obtained values of μ for the PRs (a.u) are higher than α-keto ester. Therefore, PRs show a nucleophilic behavior in this step. Table 3 shows HOMO, LUMO energies (a.u), global nucleophilicity index, electronic chemical potential, global electron density transfer, Parr functions and local nucleophilicity index for phosphorous atom of the studied PRs and α-keto ester in the gas phase.
| PRs | HOMO | LUMO | μ | GEDT | N | Pk− | Nk |
|---|---|---|---|---|---|---|---|
| P(Ph)3 | −0.2206 | −0.0334 | −0.1270 | 0.804 | 0.1252 | 0.5097 | 0.0638 |
| P(Me)3 | −0.2270 | −0.0034 | −0.1152 | 0.858 | 0.1187 | 0.7923 | 0.0941 |
| P(Et)3 | −0.2168 | −0.005 | −0.1110 | 0.890 | 0.1290 | 0.8148 | 0.1051 |
| P(NMe2)3 | −0.2024 | 0.0008 | −0.1008 | 0.886 | 0.1434 | 1.2751 | 0.1828 |
| P(NEt)3 | −0.2076 | 0.0018 | −0.1029 | 0.843 | 0.1382 | 1.2364 | 0.1709 |
| P(NC4H8)3 | −0.1798 | −0.0005 | −0.0902 | 0.959 | 0.1660 | 1.7654 | 0.2931 |
| P(NMe2)2Et | −0.1964 | 0.0005 | −0.0979 | 0.870 | 0.1494 | 1.1718 | 0.1751 |
| P(NMe2)Et2 | −0.2144 | −0.0031 | −0.1088 | 0.870 | 0.1314 | 0.7917 | 0.1040 |
| α-Keto ester | −0.2658 | −0.0895 | −0.1777 | — | — | — | — |
Local nucleophilicity indices (Nk) of phosphorous atom in P(Et)3, P(Me)3, P(Ph)3 and P(NEt)3 are 0.1051, 0.0941, 0.0638 and 0.1828 (a.u), respectively. Therefore, the nucleophilicity character for P(NEt)3 is higher than P(Et)3, P(Me)3 and P(Ph)3. This factor lowers ΔG≠ value of step 1 in the presence of P(NEt)3. Although, other PRs such as P(NC4H8)3 and P(NM2)3 have the largest Nk, but their high steric exchange energies elevate ΔG≠. Therefore, the compilation of local nucleophilicity indices and steric exchange energy help us to justify the kinetic behavior of the PRs. Based on these criteria, P(NEt)3 is the best reagent in Kukhtin–Ramirez reaction from the kinetic view point.
Thermodynamic studies
There are some discrepancies for the studied PRs from the thermodynamic view point. This means that the overall reaction is favorable or unfavorable in the presence of some PRs, thermodynamically. Fig. 2 shows the overall reaction in which PRs and PORs are variable components. The stability or instability of the product can be explained by using second-order perturbation energy, (E2), based on donor–acceptor interaction.33 It is reasonable to investigate the thermodynamic stability by studying the electronic interactions between the orbitals of PORs. Table 4 shows energy differences between the products and reactants (ΔEReaction) for the overall reaction. Geometry optimization by hybrid GGA functionals such as B3LYP, followed by a single-point calculation using a hybrid meta-GGA functional such as MPWB95, gives reasonably good results in comparison to the optimized structures obtained by the more expensive hybrid meta-GGA functionals. On the other hand, the hybrid meta-GGA functionals are improved by dispersion effects.44 In order to increase the accuracy of the energies, in addition to B3LYP, MPWB95 functional was applied in the gas phase and CH2Cl2.| PRs | Gas | CH2Cl2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B3LYP | MPWB95 | Error bara | B3LYP | MPWB95 | Error bara | |||||
| ΔEReaction | Pk− | ΔEReaction | Pk− | ΔEReaction | Pk− | ΔEReaction | Pk− | |||
| a Error bar = ΔEMPWB95 − ΔEB3LYP. | ||||||||||
| P(NC4H8)3 | −29.99 | 1.7654 | −42.10 | 1.6899 | −12.11 | −32.13 | 1.8065 | −44.38 | 1.7397 | −12.25 |
| P(NMe2)2Et | −28.17 | 1.1718 | −39.26 | 1.1287 | −11.09 | −29.76 | 1.2052 | −41.08 | 1.1502 | −11.32 |
| P(NEt)3 | −27.89 | 1.2364 | −40.44 | 1.2539 | −12.55 | −29.61 | 1.2965 | −42.39 | 1.2763 | −17.22 |
| P(NMe2)3 | −26.86 | 1.2751 | −39.20 | 1.2621 | −12.34 | −27.85 | 1.3001 | −40.40 | 1.2795 | −12.55 |
| P(NMe2)Et2 | −22.55 | 0.7917 | −32.73 | 0.7671 | −10.18 | −24.67 | 0.7563 | −34.90 | 0.8151 | −10.23 |
| P(Et)3 | −19.69 | 0.8148 | −28.23 | 0.7082 | −8.54 | −22.45 | 0.8616 | −31.32 | 0.7563 | −8.87 |
| P(Me)3 | −18.14 | 0.7923 | −26.87 | 0.7255 | −8.73 | −21.39 | 0.8410 | −30.30 | 0.7757 | −8.91 |
| P(Ph)3 | −15.66 | 0.5097 | −24.43 | 0.3416 | −8.77 | −16.40 | 0.5381 | −25.11 | 0.3901 | −8.71 |
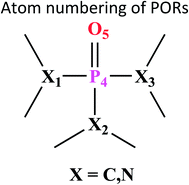
Atom numbering for the PORs and main orbital interaction energies, E2 (kcal mol−1), were reported in Table 5. Three main interactions are distinguishable, the first, is the interaction between the lone pairs electron of nitrogen atom (LPN) and anti-bonding orbital of the phosphorous–oxygen bond (σ*P–O), the second interaction is corresponding to LPO → σ*P–N and the last one is LPO → σ*P–C. The first interaction is possible for PORs possessing N atom, however, because of an unsuitable spatial orientation of LPN, this interaction is very weak in PO(NMe2)Et2. The stabilization energies associated with the donor (i) → acceptor (j) interactions are directly proportional to the magnitudes of the orbital overlap integrals Sij.45,46 More orbital overlap integrals Sij, means higher stabilization energies. Fig. 8 shows spatial orientation of LPN2 and σ*P–O and Sij values in N-containing PORs. Sij value for PO(NMe2)Et2 is lower than other PORs which lowers the stabilization energies for the LPN2 → σ*P–O interaction in this POR.
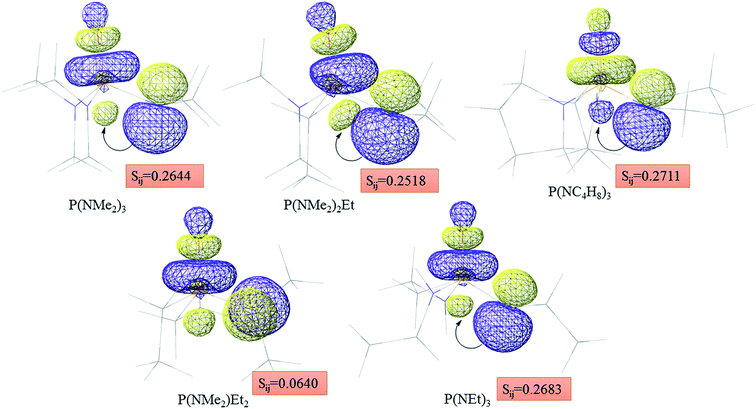 | ||
| Fig. 8 Spatial orientation of LPN2 and σ*P–O and values of Sij for the corresponding interactions in the N-containing PORs. | ||
According to Table 5, there are also important stabilizing interactions of LPO → σ*P–N and LPO → σ*P–C which the first one is more important from the energy viewpoint. Since, σ*P–N is a better acceptor than σ*P–O for the electrons of LPO, the stability of N-containing PORs is higher than the other PORs. As the stabilizing interactions of POPh3 are negligible in comparison to other PORs, ΔEReaction for PPh3 is larger than the others and this PR is the worst candidate for the overall reaction. Therefore, it can be concluded that, the presence and the number of N atoms in PRs structure have a considerable effect on the stabilizing interactions in PORs and carrying out the overall reaction. Nitrogen-free PRs are not reasonable candidate for the overall reaction thermodynamically.
Apart from the stabilization effects due to the number of N atoms of PORs, there is a correlation between ΔEReaction and Mulliken atomic spin density (Pk−) of phosphorous atom in PRs. Table 4 shows their calculated values by two functionals in both phases. P(NC4H8)3 and PPh3 as the PRs with minimum and maximum ΔEReaction which have the highest and the lowest Pk− of phosphorous atom, respectively. Fig. 9 shows the plots of ΔEReaction against Pk− calculated by two functionals with blue and yellow lines related to MPWB95 and B3LYP respectively. Both plots in the gas phase and solvent phases show a better correlation by MPWB95 functional. The obtained result is according to orbital interaction analyses of PORs which show that N-containing PRs with larger Pk− are more efficient for the reaction.
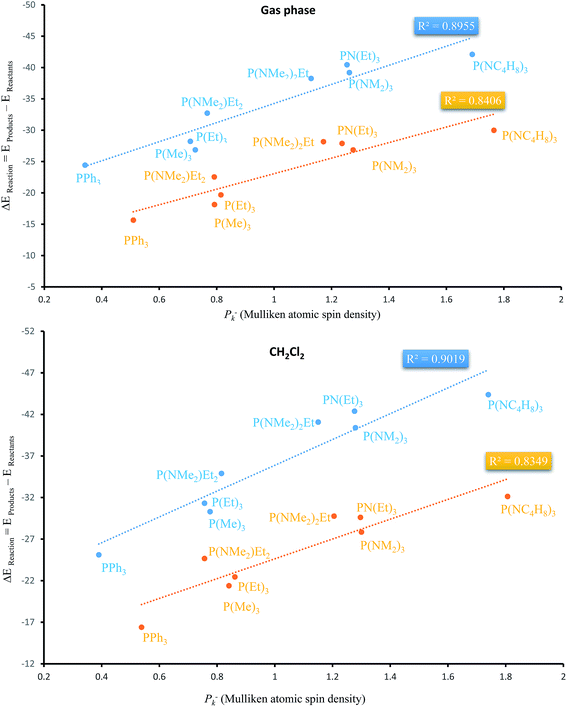 | ||
| Fig. 9 Liner correlation of ΔEReaction against Pk− of phosphorous atom in the gas and solvent phases calculated by MPWB95 (blue line) and B3LYP (yellow line) functionals. | ||
In addition to stabilizing orbital interactions of PORs, Pk− values of phosphorous atom in PRs play an important role in the reaction thermodynamic, so that P(NC4H8)3 and P(NEt)3 are considered as the efficient reagents for the reaction, thermodynamically. However, based on the reaction kinetics of the studied PRs and high steric repulsion of P(NC4H8)3, P(NEt)3 is considered the best phosphorus reagent for the overall reaction from the kinetic and thermodynamic viewpoints.
Conclusion
In this research a phosphorus-mediated carboxylative condensation of aniline amines and α-keto ester, using carbon dioxide as a carboxylative reagent was investigated, theoretically. This addition reaction is known as Kukhtin–Ramirez addition in which oxazolidine-2,4-dione as a biologically important compound is obtained. Reaction mechanism and the effects of various PRs were investigated from thermodynamic and kinetic viewpoints.MPWB95 and B3LYP functionals in CH2Cl2 and gas phases were applied for this study. Two criteria of the steric repulsion between lone pair electrons of the phosphorus atom and its nucleophilic character were used for justification of the kinetic parameters of PRs reaction. Total steric exchange energy (dE) and local nucleophilicity indices (Nk) of phosphorous atom were demonstrated that P(NEt)3 is the best PRs for the reaction.
Furthermore, stabilizing interactions between the lone pair electron of oxygen and nitrogen atoms with anti-bonding orbitals of the oxide form of PRs (PORs) were applied for thermodynamic analysis. On the other hand, quantum chemistry descriptor analyses showed a reasonable correlation between ΔEReaction and Mulliken atomic spin density (Pk−) of phosphorous atom of the PRs. Obtained ΔEReaction values by MPWB95 functional are in better correlation with Pk− than B3LYP. Therefore, N-containing PRs such as P(NC4H8)3 and P(NEt)3 with larger Pk− are more efficient in the reaction, thermodynamically. Finally, it was demonstrated that P(NEt)3 is the best phosphorus reagent for the overall reaction from the kinetic and thermodynamic viewpoints.
Acknowledgements
Research Council of Ferdowsi University of Mashhad is gratefully acknowledged for the financial support of this project (Grant No. 3/33572). Also, we hereby acknowledge that some parts of this computation were performed in the HPC center of Ferdowsi University of Mashhad.References
- Y.-N. Li, R. Ma, L.-N. He and Z.-F. Diao, Catal. Sci. Technol., 2014, 4, 1498 CAS.
- K. A. Grice, M. C. Groenenboom, J. D. A. Manuel, M. A. Sovereign and J. A. Keith, Fuel, 2015, 150, 139 CrossRef CAS.
- J. Lin, Z. Ding, Y. Hou and X. Wang, Sci. Rep., 2013, 3, 1056 Search PubMed.
- Q. Liu, L. Wu, R. Jackstell and M. Beller, Nat. Commun., 2015, 6, 5933 CrossRef PubMed.
- Y. Zhu, S. Zhang, Y. Ye, X. Zhang, L. Wang, W. Zhu, F. Cheng and F. Tao, ACS Catal., 2012, 2, 2403 CrossRef CAS.
- J. Kothandaraman, A. Goeppert, M. Czaun, G. A. Olah and G. S. Prakash, J. Am. Chem. Soc., 2016, 138, 778 CrossRef CAS PubMed.
- T. Sakakura, J.-C. Choi and H. Yasuda, Chem. Rev., 2007, 107, 2365 CrossRef CAS PubMed.
- Z.-Z. Yang, L.-N. He, J. Gao, A.-H. Liu and B. Yu, Energy Environ. Sci., 2012, 5, 6602 CAS.
- J. Clark-Lewis, Chem. Rev., 1958, 58, 63 CrossRef CAS.
- T. L. Patton, J. Org. Chem., 1967, 32, 383 CrossRef CAS.
- A. Benavides, R. Martinez and H. A. Jiménez-Vázquez, Heterocycles, 2001, 55, 469 CrossRef CAS.
- A. Zask, J. Org. Chem., 1992, 57, 4558 CrossRef CAS.
- W.-Z. Zhang, T. Xia, X.-T. Yang and X.-B. Lu, Chem. Commun., 2015, 51, 6175 RSC.
- G. Chen, C. Fu and S. Ma, Org. Biomol. Chem., 2011, 9, 105 CAS.
- F. H. Osman and F. A. El-Samahy, Chem. Rev., 2002, 102, 629 CrossRef CAS PubMed.
- S. R. Wang and A. T. Radosevich, Org. Lett., 2013, 15, 1926 CrossRef CAS PubMed.
- W. Zhao, D. M. Fink, C. A. Labutta and A. T. Radosevich, Org. Lett., 2013, 15, 3090 CrossRef CAS PubMed.
- A. V. Alexandrova, T. Mašek, S. M. Polyakova, I. Císařová, J. Saame, I. Leito and I. M. Lyapkalo, Eur. J. Org. Chem., 2013, 1811 CrossRef CAS.
- L. Maier, Helv. Chim. Acta, 1964, 47, 2129 CrossRef CAS.
- Y. Xu, N. W. Alcock, G. J. Clarkson, G. Docherty, G. Woodward and M. Wills, Org. Lett., 2004, 6, 4105 CrossRef CAS PubMed.
- C. A. Busacca, R. Raju, N. Grinberg, N. Haddad, P. James-Jones, H. Lee, J. C. Lorenz, A. Saha and C. H. Senanayake, J. Org. Chem., 2008, 73, 1524 CrossRef CAS PubMed.
- O. I. Kolodiazhnyi and N. Prynada, Tetrahedron Lett., 2000, 41, 7997 CrossRef CAS.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Wallingford, CT, 2009 Search PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS.
- A. McLean and G. Chandler, J. Chem. Phys., 1980, 72, 5639 CrossRef CAS.
- E. Salter, G. W. Trucks and R. J. Bartlett, J. Chem. Phys., 1989, 90, 1752 CrossRef.
- C. Tratz, P. L. Fast and D. G. Truhlar, Commun. - Czech-Pol. Colloq. Chem. Thermodyn. Phys. Org. Chem., 2nd, 1999, 2, 9 Search PubMed.
- C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, J. Comput. Chem., 1996, 17, 49 CrossRef CAS.
- K. Fukui, J. Phys. Chem., 1970, 74, 4161 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899 CrossRef CAS.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066 CrossRef CAS.
- M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed.
- R. Chaudret, B. De Courcy, J. Contreras-García, E. Gloaguen, A. Zehnacker-Rentien, M. Mons and J.-P. Piquemal, PCCP Phys. Chem. Chem. Phys., 2014, 16, 9876 RSC.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
- S. L. Peterson, S. M. Stucka and C. J. Dinsmore, Org. Lett., 2010, 12, 1340 CrossRef CAS PubMed.
- F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry: Part A: Structure and Mechanisms, Springer Science & Business Media, 2007 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486 RSC.
- L. R. Domingo and P. Pérez, Org. Biomol. Chem., 2013, 11, 4350 CAS.
- L. R. Domingo, RSC Adv., 2014, 4, 32415 RSC.
- L. Simón and J. M. Goodman, Org. Biomol. Chem., 2011, 9, 689 Search PubMed.
- N. D. Epiotis, R. L. Yates, J. Larson, C. R. Kirmaier and F. Bernardi, J. Am. Chem. Soc., 1977, 99, 8379 CrossRef CAS.
- I. V. Alabugin, M. Manoharan and T. A. Zeidan, J. Am. Chem. Soc., 2003, 125, 14014 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary tables and Cartesian coordinate of the molecules. See DOI: 10.1039/c6ra25769k |
| This journal is © The Royal Society of Chemistry 2017 |