DOI:
10.1039/C6RA25804B
(Paper)
RSC Adv., 2017,
7, 27881-27894
Absolute ion hydration enthalpies and the role of volume within hydration thermodynamics†
Received
25th October 2016
, Accepted 24th April 2017
First published on 25th May 2017
Abstract
This paper reports that various thermodynamic properties in aqueous media for certain individual ions and for compounds are linear functions of the inverse cube root of the solid respective ionic and compound solid state volumes, Vm−1/3. This is similar to the situation which has been fully exploited in solid state thermodynamics and out of which volume-based thermodynamics, VBT, evolved. A short resume of these various VBT applications is provided for the general reader and an improved lattice potential energy equation emerges using the state of the art data presented in this paper.
Introduction
Volume-based thermodynamics
The primary aim of this paper is to investigate whether the inverse cube root of the formula unit volume, Vm−1/3 of solid state species (as either single ions or as compounds) correlates with any of the thermodynamic functions associated with hydration (e.g. ΔhydHo or ΔhydGo or any of the more complex functions). There are several advantages if this were to be the case. Firstly it would bring the thermodynamic functions associated with hydration (and possibly also solvation functions in non-aqueous media) under the remit of Volume Based Thermodynamics (VBT). The availability of standard thermodynamic functions for non-aqueous media is rather sparse and such a link would enable expansion of the data in this area then possible. Secondly it would link hydration parameters with volume, Vm, which is, in turn, intimately linked to and can be determined from crystal structure data which is routinely acquired for all new materials.
In 1999 Jenkins1–7 and co-workers first introduced what they later termed VBT. The early ideas were based on work by Mallouk and Bartlett8 and were later extended by Jenkins and co-workers to a range of applications.9–28 The recognition of a link between the areas of crystallography (which supplies volume data) and hydration thermodynamics would provide considerable scope for the extension of hydration/solvation studies to more complex materials and applications. This would offer a number of advantages. The first is simplicity; VBT can be used easily by non-specialists in thermodynamics since all that is needed is an EXCEL spreadsheet; the equations involved have a simple format. Secondly, linking thermodynamics and crystallography gives access to volume data for modern solid state materials. If crystal structure data fail to provide volume information then it is possible to estimate formula unit volume, Vm, using individual average volumes for each element in the formula unit, as derived from an analysis of the Cambridge Structural Database (CSD) by Hofmann.29 Examples are shown later. Using the cube root of the formula unit volume, Vm1/3, means that the effect of any errors in the volume estimation are minimised by the need to extract the cube root.
Apart from one or two applications, the object of VBT so far has not been to obtain pristinely accurate thermodynamic values but rather to obtain reasonable approximations of such values which are good enough to show trends and which are accurate enough to guide synthetic work. Up until now no applications of VBT have been made for aqueous media but it is preparation for such an extension that is sought in this current work.
Specific applications of VBT to solving solid state chemistry problems include access to thermochemical studies in advance of synthesis. Examples have included a study9 of homopolyatomic cation species of S and Se (e.g., S82+ and Se82+). Prior to chemical synthesis, VBT predicted the lattice stabilisation for the compound S8(AsF6)2. Estimation of the formula unit volume, Vm permitted a rudimentary understanding of the energetics of this new area of chemistry. When used in tandem with the Thermodynamic Difference Rule (TDR),30–35 VBT has made possible the provision of thermodynamic data for solvated materials. For example, it was possible to establish13 that the solvated salt, S4(AsF6)2·AsF3 was more stable than its unsolvated counterpart, S4(AsF6)2, as well being more stable than the likely decomposition products formed from S4(AsF6)2·AsF3. Similar questions concerning stability investigated using VBT can be found in our most sophisticated study to date,20 which used VBT coupled with TDR and enabled the study of species in liquid sulfur dioxide as solvent. VBT has been used quantitatively to arbitrate10–12 between two experimental measurements of ΔfHo(AsF6−,g). A trend among some experimentalists, who believed that in order to synthesise new and more effective fluoride ion donors one needed to increase the size of the cation involved, was curbed by a VBT study.14,15 This was able to show that there was very little to be gained energetically in going beyond a critical cation size since the thermodynamics showed a plateau. In a more hypothetical vein, salts such as N5+N3− and N5+N5− were initially thought of as potential, environmentally clean, rocket propellants in advance of synthesis. VBT and ab initio calculations17,18 showed that once synthesised they would be likely to decompose into N3 radicals and N2 gas and later bench experiments confirmed this fact. VBT, because of its versatility has made contributions to evolving technology, as for example in the case of electrochromic reactions which, inter alia, often depend on cation exchanges taking place in prussian blue. At the time of carrying this work “best formulations” were still being sought. VBT enabled us to unravel19 some of the ill-understood ion exchange reactions accompanying the early electrochromic cycles. Such applications involve production of light sensitive glass windows for example. In addition, VBT has been used also to investigate the energetics of defence materials36 of current interest. We have found it possible to make thermodynamic predictions regarding the formation of such new materials. VBT37,38 has been used to predict the likely stability of certain alkali sulfoxalates and selenoxylates in the solid state. Since this publication37 appeared we were contacted by Makarov to report that he had already detected the SO22− moiety not in the solid state however but in aqueous solution.39–41
Coupled with TDR, VBT is able to examine reactions in non-aqueous media13,20 Most recently TDR itself has been used to estimate thermodynamic data in the area of actinoid thermochemistry. Uranium salts are radioactive and therefore need thermochemical measurements to be made in specially equipped laboratories. Their hydrolysis reactions can often create the need to make challenging thermochemical adjustments35 which means that TDR has a useful function in avoiding such requirements. Questions of academic interest have also been explored using VBT. While [P(C6H5)4]+N3− and [As(C6H5)4]+N3− are known to exist as ionic salts while later members of the group: [Sb(C6H5)4]+N3− and [Bi(C6H5)4]+N3− are covalent solids. VBT was used to explain26 why this should be.
The above applications are but a few to capture the interest of the general reader. Many other applications possess novel features4,23,45 and have shown themselves capable of unravelling quite complex thermochemistry.21,23,43–45 Further applications continue to emerge,42 and a recent review of the main features of VBT has appeared.7
More recently, ionic strength, I and formula unit volume, Vm – essential components of VBT – have found application as measures of the enhanced stability brought about to Zintl structures as part of a recently emerging interpretation and new realm of crystallography in which the Zintl–Klemm46–49 concept has been revived and extended and which now, once correctly applied, enables the prediction and rationalisation of crystal structures.48,49 This area of crystallography is destined to yield new and exciting ideas in the future.50
The above examples illustrate some of the problems it has been possible to tackle once the connection between crystallography and thermodynamics via volume had been established. If a link can similarly be established between Vm−1/3 and hydration thermodynamics then, by analogy with these solid state developments, this should promote new developments in a number of areas of hydration and solvation chemistry. This paper represents the very beginnings of this process.
Volume estimation
In order to estimate ion volumes, Vm, there are four immediate sources one can use which separate into two categories. Three relate to data evolving from crystal structure determinations and the other (which is often much less appropriate for correlation with hydration thermodynamics) derives volume from radii, r, (4πr3) and therefore the assumption that the ion is spherical. Since the majority of ions are patently non-spherical it is better to use volume data from crystal structure sources (Vcell/Z). Such volume data is to be found in our seminal publication1 providing estimates by dividing up space and apportioning it without invoking assumptions about sphericity. Another source of volume data can come directly from density, ρ, measurements:3| | |
Vcell/nm3 = 1.66 × 10−3Z(Mm/g)/(ρ/g cm−3)
| (1) |
where Mm is the chemical formula mass of the material and Z is the number of formula units per cell . Finally Hofmann,29 persuing an analysis of the Cambridge Structure Database (CSD) has produced average atomic volumes which can then be used in conjunction with chemical formulae to estimate volumes of materials or of ions. This latter approach is, however, not entirely satisfactory.
Revisions of hydration thermodynamics
In 2006 Kelly, Cramer and Truhlar51 were able to confirm the absolute aqueous solvation free energy of the proton, ΔhydGo(H+,g) as −1112.5 kJ mol−1 in close agreement to the value −1104.5 kJ mol−1 obtained by Tissendier et al.52 in 1998 using the cluster-pair-based approximation and thermodynamic properties of ion–water clusters. Tawa et al. also made a similar theoretical determination.68 They showed that historical data were mostly inconsistent with the cluster data. As further confirmation, their value is also consistent with the absolute free energy of the OH− ion as obtained via Monte Carlo calculations.69,70 The corresponding absolute aqueous solvation enthalpy of the proton, ΔhydHo(H+,g), as determined by these latter workers was −1150.1 kJ mol−1 which in turn agreed with the value −1152.6 kJ mol−1 recorded by Coe.53 In the case of ΔhydHo(H+,g) traditional values had previously spanned a much higher range (−1085 > ΔhydHo(H+,g)/kJ mol−1 > −1125) and their derivation had almost always needed to rely on the use of an extra-thermodynamic assumption. The cluster-derived data does not, however, need to rely on such an assumption and Tissendier's data are currently the most commonly accepted values (see also Camaioni and Schwerdtfeger62). The determinations of single ion hydration values made before 1998 can differ by, on average 50 kJ mol−1, from the more recent values. This has naturally led to the necessity for quantitative reassessment of traditional thermodynamic values in hydration thermochemistry.
Results and discussion
The Born equation and correlation of hydration data with V−1/3
The first question is: why might one expect hydration thermodynamic functions to follow the pattern of VBT for solids and be functions of V−1/3? The first clue comes from the fact that the Born55 equation (now almost a century old) for the Gibbs free energy of transfer of a gaseous ion of charge z and radius, r into a medium whose relative permittivity (or dielectric constant) is εr (=78.7 for water) is given by:| | |
ΔGohyd(ion,g)/J mol−1 = −10−3Lz2e2[1 − (1/εr)]/8πεor
| (2) |
where L is the Avogadro number (6.022 × 1023 mol−1), e is the charge on the electron (1.602 × 10−19 C); z for monatomic cations is +1 and for anions −1; ε0 is the relative permittivity of a vacuum (8.854 × 10−3 F nm−1) and r is the radius of the ion (in m). In practice this expression gives unsatisfactory results since the relative permittivity of bulk water of 78.7 is not appropriate to use close to an ion so we can therefore anticipate that this expression can, at best, only be relied on to show the functional dependence of ΔGohyd(ion,g) whilst failing to give the precise values of the coefficients of the dependence (see later however). We proceed by relating the radius of the ion, r to volume, Vm, of the ion as follows:where r is in nm, so that we are restricting the equation generated to apply only to spherical ions:and| | |
r/nm = (3)1/3Vm1/3/(4π)1/3 = 0.6203Vm1/3
| (5) |
where Vm1/3 is in nm−1. Substituting for r/nm in eqn (2) leads to the expression:| | |
ΔGohyd(ion,g)/kJ mol−1 = −10−3Lz2e2[1 − (1/εr)]/{8πεo[0.6203]Vm1/3}
| (6) |
Inserting the constants in eqn (6) for a cation having charge z = 1 gives:
| |
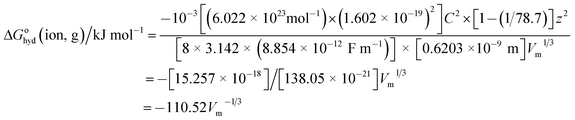 | (7) |
We should note also that since z2 = 1 for both cation and anion, eqn (7) represents the approximate form of the relationship hoped for to apply to thermodynamic properties in solution and one which is directly in keeping with VBT namely that:
| | |
ΔGohyd(ion,g)/kJ mol−1 is proportional to f(Vm−1/3)
| (8) |
Assembling of state-of-the-art thermodynamic data
In the ESI to this paper Table S1† lists ΔfHo(ion,g)/kJ mol−1 and ΔfGo(ion,g)/kJ mol−1 data54 for the proton, alkali metal and halide ions according to the electron convention using Boltzmann statistics. Further state-of-the-art thermodynamic values (in kJ mol−1) are to be found in Table S2† ΔfHo(M+,aq) and ΔfHo(X−,aq); in Table S3† ΔfHo(MX,s); in Table S4† ΔfGo(MX,s); in Table S5† ΔlattHo(MX,s); and in Table S6† UPOT(MX) and in Table S7† ΔsolnHo(MX,s). Table S8† lists values of Vm(MX)−1/3 in nm−1 for the alkali halides.
VBT as applied to hydration studies
Alkali metal ion plots versus Vm−1/3. Table 1 gives the values of ΔhydHo(M+,g) and ΔhydGo(M+,g) for proton and the alkali metal ions and the appropriate values of Vm−1/3 for the spherical ions in question and Fig. 1 and 2 give the plots of ΔhydHo(M+,g)/kJ mol−1 versus Vm−1/3/nm−1 and ΔhydGo(M+,g)/k mol−1 versus Vm−1/3/nm−1 respectively from which we see rectilinear relationships emerging with correlation coefficients of R2 = 0.9999 and R2 = 0.9996 – almost perfect straight lines – the analytical forms of which are:| | |
ΔhydHo(M+,g) = −48.2Vm−1/3 − 154.6 (N = 6; R2 = 0.9999)
| (9) |
| | |
ΔhydGo(M+,g) = −47.1Vm−1/3 − 128.5 (N = 6; R2 = 0.9996)
| (10) |
Table 1 Values of absolute single-ion hydration enthalpies and free energies: ΔhydHo(M+,g) and ΔhydGo(M+,g) in kJ mol−1 for alkali metal ions and proton together with associated radii, r (in nm) volume, Vm (=4πr3/3) (in nm3) and Vm−1/3 in nm
| Cation |
Radius, r/nm |
Volume, Vm/nm3 |
Vm−1/3/nm−1 |
ΔhydHo(M+,g)/kJ mol−1 |
ΔhydGo(M+,g)/kJ mol−1 |
| Proton radius taken from Marcus Table 3 ref. 56. Li+ radius taken from Vieillard57 as cited by Marcus.56 Taken from Table 4, ref. 1. Goldschmidt radius.58 Calculated from radius (column 1) from Marcus56 Table 3, charge ignored. Ions are spherical so calculation for radius, r, as 4πr3/3 is acceptable here. |
| H+ |
0.030a |
0.000115e |
20.67558 |
−1150.1 |
−1104.5 |
| Li+ |
0.071b |
0.0015e |
8.736159 |
−578.1 |
−529.3 |
| Na+ |
0.098c,d |
0.00394e |
6.331422 |
−463.3 |
−423.7 |
| K+ |
0.133c,d |
0.00986c |
4.663454 |
−380.3 |
−351.8 |
| Rb+ |
0.149c,d |
0.01386c |
4.163056 |
−355.2 |
−329.3 |
| Cs+ |
0.165c,d |
0.01882c |
3.759471 |
−330.6 |
−306.4 |
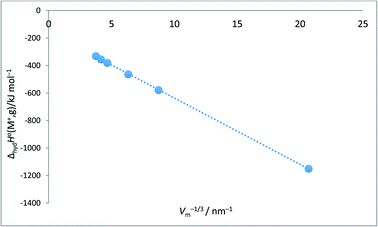 |
| | Fig. 1 Plot of ΔhydHo(M+,g)/kJ mol−1 as ordinate versus Vm−1/3/nm−1 for proton and alkali metal ions as listed in Table 2. ΔhydHo(M+,g)/kJ mol−1 = −48.2Vm−1/3 − 154.6 (N = 6, R2 = 0.9999). | |
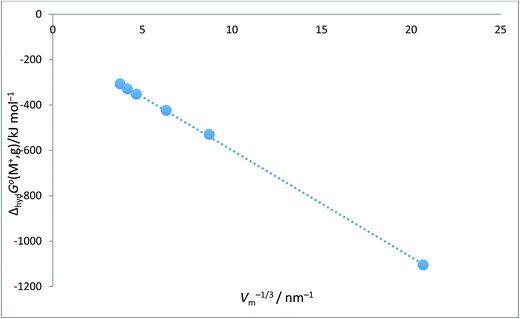 |
| | Fig. 2 Plot of ΔhydGo(M+,g)/kJ mol−1 as ordinate versus Vm−1/3/nm−1 for proton and alkali metal ions as listed in Table 2. ΔhydGo(M+,g)/kJ mol−1 = −47.1Vm−1/3 − 128.5 (N = 6, R2 = 0.9996). | |
These relationships, in respect of their linear dependence on Vm−1/3 are similar to those found for thermodynamic functions in VBT in the solid state.
The hydration data given in Table 1 is currently the most up to data (2017) and is obtained by using the thermochemical cycle shown in Fig. 3, from which we see that:
| | |
ΔhydHo(M+,g) + ΔhydHo(X−,g) = ΔfHo(M+,aq) + ΔfHo(X−,aq) − ΔfHo(M+,g) − ΔfHo(X−,g)
| (11) |
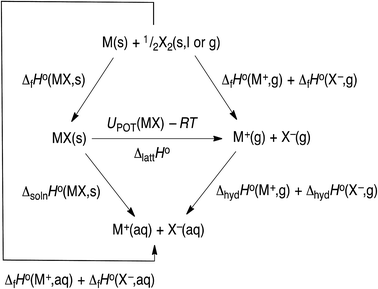 |
| | Fig. 3 Thermochemical cycle. | |
The NIST-JANAF tables54 give the gaseous ion formation data (Table S1†) and using conventional solvated ion thermodynamics we have the ΔfHo(M+,aq) and ΔfHo(X−,aq) values (Table S2†) since:
| | |
[ΔfHo(M+,aq) + ΔfHo(X−,aq)] = ΔfHo(MX,s) + ΔsolnHo(MX,s)
| (12) |
Lattice potential energy equation for MX (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1) salts using latest data
1) salts using latest data
Using data54,63–65 from Tables S1 and S3† and the cycle in Fig. 3 we can obtain the lattice potential energy, UPOT(MX) (Table S6†) using the equation:| | |
UPOT(MX) = ΔfHo(M+,g) + ΔfHo(X−,g) − ΔfHo(MX,s) + RT
| (13) |
which when plotted versus V(MX)−1/3 (Table S8†) as shown in Fig. 4, leads to the equations:| | |
UPOT(MX)/kJ mol−1 = |z+||z−|ν(α/V−1/3 + β) = ∑nkzk2(α/V−1/3 + β) = 2I(117.8V−1/3 + 64.5) (R2 = 0.996)
| (14) |
where ν is the number of ions in the formula unit (=2), I is the ionic strength of the lattice (=1) defined for (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) salts by:
1) salts by:| | |
I = 1/2∑nizi2 = ½[(1)(+1)2 + (1)(−1)2] = 1
| (15) |
where ni is the number of ions in the lattice with charge zi and the summation is over the whole lattice.
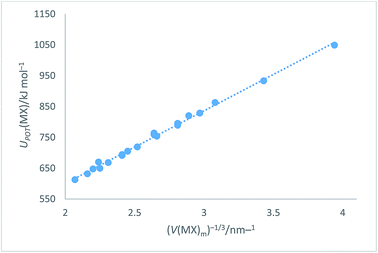 |
| | Fig. 4 Plot of UPOT(MX)/kJ mol−1 as ordinate versus V(MX)m−1/3 as abscissa. The plot takes the analytical form: UPOT(MX)/kJ mol−1 = 2I[117.8(V(MX)m)−1/3 + 64.5] with correlation coefficient R2 = 0.996, N = 20. | |
In the cycle the lattice enthalpy, ΔlattHo(MX,s) (Table S5†) can replace UPOT(MX) − RT.
Eqn (14) represents an improved rectilinear fit, (Fig. 4), in the sense that R2 = 0.996 when compared to R2 = 0.94 previously1 used for the alkali halides in VBT. This update refers, of course, to the solid state but, being a significant improvement on the main VBT equation, it is important to record this update in this paper. Section S3 of the ESI† lists other enthalpy and free energy relationships which can be inferred from the cycle (Fig. 3).
Prediction of hydration data. Eqn (9) and (10) can be used to regenerate the data used to create them. The results (shown in Table 2) are, in both cases, highly satisfactory.
Table 2 Test of the extent to which eqn (9) and (10) are capable of reproducing the absolute hydration data used to determine them
| Cation |
Vm−1/3/nm−1 |
ΔhydHo(M+,g)/kJ mol−1 |
ΔhydHo(M+,g)/kJ mol−1 as generated from eqn (9) |
% age difference |
ΔhydGo(M+,g)/kJ mol−1 |
ΔhydGo(M+,g)/kJ mol−1 as generated from eqn (10) |
% age difference |
| H+ |
20.67558 |
−1150.1 |
−1151.4 |
−0.1 |
−1104.5 |
−1101.4 |
0.3 |
| Li+ |
8.736159 |
−578.1 |
−575.8 |
0.4 |
−529.3 |
−539.5 |
−1.9 |
| Na+ |
6.331422 |
−463.3 |
−459.9 |
0.7 |
−423.7 |
−426.4 |
−0.6 |
| K+ |
4.663454 |
−380.3 |
−379.4 |
0.2 |
−351.8 |
−347.9 |
1.1 |
| Rb+ |
4.163056 |
−355.2 |
−355.3 |
0.0 |
−329.3 |
−324.4 |
1.5 |
| Cs+ |
3.759471 |
−330.6 |
−335.9 |
−1.6 |
−306.4 |
−305.4 |
0.3 |
Table 2 (columns 3 and 6) shows the original datasets (taken from Table 1, in columns 5 and 6) and alongside them the regenerated data (in columns 4 and 7) and the percentage differences (in columns 5 and 8) from which can be seen that eqn (9) predicts ΔhydHo(M+,g) values at least to within 5.3 kJ mol−1 (or to within 1.6%) whilst eqn (10) predicts ΔhydGo(M+,g) values to at least to within 4.9 kJ mol−1 (or to within 1.5%). This level of certainty gives confidence that values predicted for other M+ ions, using data for the inverse cube root of their volumes, Vm−1/3 should be reasonably close to their true values.
Some of the ions in Table 3 are clearly spherical (Cu+, Ag+, Au+, Ga+, In+, Tl+) whereas the remainder are not. For the ions that are spherical we can calculate the volume using their radius (column 2) as a basis. For those that are non-spherical the volumes used are best sourced from crystallography1 (and not from radii). In Table 3 we compare the volumes of two of the ions (Me4N+ and Et4N+) sourced from radii and also from crystallography. Comparing ΔhydHo(R4N+,g) and ΔhydGo(R4N+,g), the values predicted for ΔhydHo(Me4N+,g) for Me4N+ differ by only 7.1 kJ mol−1 and in the case of Et4N+, ΔhydHo(Et4N+,g) differs by 6.2 kJ mol−1. For ΔhydGo(R4N+,g) the situation is similar, Table 3 shows a difference in ΔhydGo(Me4N+,g) of some 6.9 kJ mol−1 whilst for Et4N+ it reduces to 6.0 kJ mol−1. Although these two cases are reassuring they do not necessarily reflect the situation for other ions.
Table 3 Prediction of values of absolute single-ion hydration enthalpies and free energies: ΔhydHo(M+,g) and ΔhydGo(M+,g) (in kJ mol−1) for a series of spherical and non-spherical singly charged cations
| Cation |
Radius, r/nm |
Vm/nm3 |
Vm−1/3/nm−1 |
Estimated ΔhydHo(M+,g)/kJ mol−1 from eqn (9) |
Values of ΔhydHo(M+,g)/kJ mol−1 from other work |
Estimated ΔhydGo(M+,g) kJ mol−1 from eqn (10) |
Values of ΔhydGo(M+,g)/kJ mol−1 from other work |
| Goldschmidt radius.58 Pauling radius.59 Taken from Table 6 ref. 1 from crystal structure data. Taken from ref. 60 and also selected value of radius given in Table 3 ref. 56. In the case of Me4N+ and Et4N+ two estimates of volume are provided, the entry labelled d using radius and calculating V as 4πr3/3 and the entry labelled c taken from crystallographically-based volume in Table 6 of ref. 1. This is to enable us to compare the results. Value appearing in ref. 67. Value appearing in ref. 51. Value appearing in ref. 66. Value appearing in ref. 71. |
| Cu+ |
0.096a |
0.0037 |
6.461 |
−466.1 |
— |
−432.5 |
−591.2g |
| Ag+ |
0.113a |
0.0060 |
5.489 |
−419.2 |
— |
−386.8 |
−496.6g |
| Au+ |
0.137a |
0.0108 |
4.527 |
−372.9 |
— |
−341.5 |
— |
| Ga+ |
0.113b |
0.0060 |
5.489 |
−419.2 |
— |
−386.8 |
— |
| In+ |
0.132b |
0.0096 |
4.699 |
−381.2 |
— |
−349.6 |
— |
| Tl+ |
0.149a |
0.0139 |
4.163 |
−355.3 |
— |
−324.4 |
−366.5g |
| NH4+ |
|
|
|
|
|
|
−349.8h |
| |
|
|
|
|
|
−356.5i |
| |
0.021c |
3.625 |
−329.4 |
— |
−299.0 |
−355.2f |
| CH3NH3+ |
|
|
|
|
|
|
−313.0h |
| |
|
|
|
|
|
−320.1i |
| |
0.051c |
2.697 |
−284.6 |
— |
−255.4 |
−319.7g |
| Me4N+e |
|
0.113c |
2.068 |
−254.3 |
— |
−225.8 |
— |
| Me4N+e |
0.280d |
0.0919 |
2.215 |
−261.4 |
— |
−232.7 |
— |
| Et4N+e |
|
0.199c |
1.713 |
−237.2 |
— |
−232.7 |
— |
| Et4N+e |
0.337d |
0.2281 |
1.841 |
−243.4 |
— |
−215.1 |
— |
| Pr4N+ |
0.379d |
0.2952 |
1.636 |
−233.5 |
— |
−205.4 |
— |
| Bu4N+ |
0.413d |
0.0736 |
1.502 |
−227.0 |
— |
−199.1 |
— |
Halide ion plots versus Vm−1/3. Fig. 5 and 6 give the plots of ΔhydHo(X−,g)/kJ mol−1 versus Vm−1/3/nm−1 and ΔhydGo(X−,g)/kJ mol−1 versus Vm−1/3/nm−1 respectively using the data displayed in Table 4. Here we see rectilinear relationships emerging with correlation coefficients indicative of them being very close to perfect straight lines:| | |
ΔhydHo(X−,g) = −214.71Vm−1/3 + 271.96 (N = 4; R2 = 0.9992)
| (16) |
| | |
ΔhydGo(X−,g) = −185.22Vm−1/3 + 205.72 (N = 4; R2 = 0.9985)
| (17) |
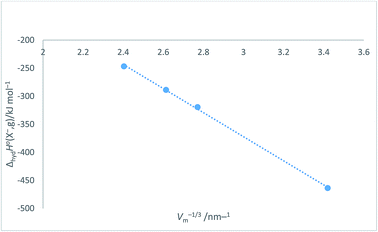 |
| | Fig. 5 Plot of ΔhydHo(X−,g)/kJ mol−1 as ordinate versus Vm−1/3/nm−1 as abscissa for halide ions listed in Table 4. ΔhydHo(X−,g) = −214.7Vm−1/3 + 272.0, N = 4, R2 = 0.9992. | |
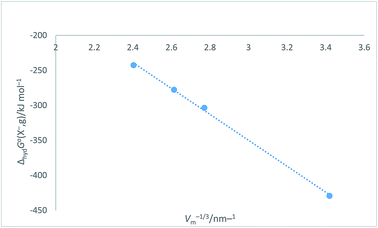 |
| | Fig. 6 Plot of ΔhydGo(X−,g)/kJ mol−1 as ordinate versus Vm−1/3/nm−1 as abscissa for halide ions listed in Table 4. ΔhydGo(X−,g) = −185.2Vm−1/3 + 205.7, N = 4, R2 = 0.9985. | |
Table 4 Values of absolute single-ion hydration enthalpies and free energies: ΔhydHo(X−,g) and ΔhydGo(X−,g) in kJ mol−1 for spherical halide ions together with associated radii, r (in nm) volume, Vm (=4πr3/3) (in nm3) and Vm−1/3 in nm
| Cation |
Radius, r/nm |
Volume, Vm/nm3 |
Vm−1/3/nm−1 |
ΔhydHo(X−,g)/kJ mol−1 |
ΔhydGo(X−,g)/kJ mol−1 |
| Goldschmidt radius.58 |
| F− |
0.133a |
0.025 |
3.420 |
−463.7 |
−429.3 |
| Cl− |
0.181a |
0.047 |
2.771 |
−319.5 |
−303.5 |
| Br− |
0.196a |
0.056 |
2.614 |
−288.7 |
−277.7 |
| I− |
0.220a |
0.072 |
2.404 |
−246.8 |
−242.6 |
Eqn (7), (10) and (17), when compared, differ considerably in respect of the magnitude of their gradients, eqn (17) being considerably lower (more negative at −185 kJ mol−1 nm) than that of eqn (10) (at −47 kJ mol−1 nm). However both are negative and have correlation coefficients which are virtually unity. If one averages the gradients of eqn (10) for the alkali metal cations and eqn (17) for the halide anions their average (=(−47 − 185)/2 = −116 kJ mol−1) nm is then quite close to that given in the Born equation in the form of (7) (at −110 kJ mol−1 nm).
If we now use eqn (16) and (17) to regenerate the data used to form them, this gives us an idea of the accuracy which these rectilinear equations can be expected to give. Table 5 gives the figures from which we see that ΔhydHo(X−,g) is reproduced with an error of usually less than 9.7 kJ mol−1 (3.9% error) whilst ΔhydGo(X−,g) is more accurately reproduced with errors less than 4.0 kJ mol−1 (or 1.3%). Now we direct eqn (16) and (17) towards prediction of values of ΔhydHo(X−,g) and ΔhydGo(X−,g) for the series of anions as listed in Table 6.
Table 5 Test of the extent to which eqn (16) and (17) are capable of reproducing the absolute hydration data used to determine thema
| Anion |
Vm−1/3/nm−1 |
ΔhydHo(X−,g)/kJ mol−1 |
ΔhydHo(X−,g)/kJ mol−1 predicted by eqn (11) |
% age difference |
ΔhydGo(X−,g)/kJ mol−1 |
ΔhydGo(X−g)/kJ mol−1 predicted by eqn (12) |
% age difference |
| Volume data taken from Table 6 of ref. 1 (column 3 of Table 4). |
| F− |
3.419952 |
−463.7 |
−455.3 |
1.8 |
−429.3 |
−427.7 |
0.4 |
| Cl− |
2.770984 |
−319.5 |
−316.0 |
1.1 |
−303.5 |
−307.5 |
−1.3 |
| Br− |
2.61379 |
−288.7 |
−282.2 |
2.2 |
−277.7 |
−278.4 |
−0.3 |
| I− |
2.403749 |
−246.8 |
−237.1 |
3.9 |
−24 |
−239.5 |
+1.3 |
Table 6 Prediction of values of absolute single-ion hydration enthalpies and free energies of anions: ΔhydHo(X−,g) and ΔhydGo(X−,g) (in kJ mol−1) for singly-charged cations
| Anion |
Vm/nm3a |
Vm−1/3/nm−1 |
Estimated ΔhydHo(X−,g)/kJ mol−1 from eqn (16) |
Values of ΔhydHo(X−,g)/kJ mol−1 from other work |
Estimated ΔhydGo(X−,g)/kJ mol−1 from eqn (17) |
Values of ΔhydGo(X−,g)/kJ mol−1 from other work |
| Anions are non-spherical so all Vm data are taken from Table 6 of ref. 1. Value appearing in ref. 66. Value appearing in ref. 68. Value appearing in ref. 51. Value appearing in ref. 67. |
| OH− |
|
|
|
|
|
−444.8b |
| 0.032 |
|
−404.3 |
|
−377.7 |
−439.3c |
| |
|
|
|
|
−438.1d |
| |
3.1498 |
|
— |
|
−439.3e |
| SH− |
|
|
|
|
|
−308.4b |
| |
|
|
|
|
−299.6c |
| |
|
|
|
|
−301.7d |
| 0.057 |
2.5984 |
−285.9 |
— |
−275.6 |
−295.8e |
| SeH− |
0.070 |
2.4264 |
−249.0 |
— |
−243.7 |
— |
| NH2− |
|
|
|
|
|
−384.1c,e |
| 0.043 |
2.8544 |
−340.9 |
— |
−323.0 |
−397.5e |
| O2− |
|
|
|
|
|
−355.2b |
| 0.046 |
2.7909 |
−327.3 |
— |
−311.2 |
−348.5b |
| CN− |
|
|
|
|
|
−300.4b |
| |
|
|
|
|
−282.8c |
| |
|
|
|
|
−293.7d |
| 0.050 |
2.7144 |
−310.8 |
— |
−297.0 |
−301.4e |
| NCO− |
0.054 |
2.6457 |
−296.1 |
— |
−284.3 |
— |
| N3− |
0.058 |
2.5834 |
−282.7 |
— |
−272.8 |
— |
| I3− |
0.171 |
1.8016 |
−114.9 |
— |
−128.0 |
— |
| HF2− |
0.047 |
2.7710 |
−323.0 |
— |
−307.5 |
— |
| ClO2− |
0.056 |
2.6138 |
−289.2 |
— |
−278.4 |
— |
| ClO3− |
0.073 |
2.3927 |
−241.8 |
— |
−237.5 |
— |
| ClO4− |
0.082 |
2.3018 |
−222.2 |
— |
−220.6 |
— |
| NO2− |
0.055 |
4.3991 |
−672.6 |
— |
−609.1 |
— |
| NO3− |
0.064 |
3.1809 |
−411.0 |
— |
−383.4 |
— |
Test of functional forms of volume. Hydration thermodynamic data sums in the form [ΔhydHo(M+,g) + ΔhydHo(X−,g)] or of [ΔhydGo(M+,g) + ΔhydGo(X−,g)] may also be functions of volume which, in turn, could take various alternative forms: [Vm(M+)−1/3 + Vm(X−,g)−1/3], [Vm(M+) + Vm(X−,g)]−1/3, Vm(MX)−1/3 or [Vm(M+) + Vm(X−,g)], in order to produce rectilinear correlations. This is tested in the ESI Section S4 of this paper in which [ΔhydGo(M+,g) + ΔhydGo(Cl−,g)] is plotted as ordinate versus [Vm(M+) + Vm(Cl−,g)]−1/3 in Fig. S1, versus [Vm(M+)−1/3 + Vm(Cl−,g)−1/3] in Fig. S2 and versus Vm(MCl)−1/3 in Fig. S3 and versus [Vm(M+) + Vm(X−,g)] in Fig. S4.†Fig. S2 is the only plot to show actual rectilinear characteristics and thus [Vm(M+)−1/3 + Vm(X−,g)−1/3] is identified as the abscissa needed to plot versus hydration sums whilst the alternatives (Fig. S1, S3 and S4) are curves and are distinctly non-linear with Fig. S3† being the curve closest to linearity.
Plot of [ΔhydHo(M+,g) + ΔhydHo(X−,g)] versus [Vm(M+)−1/3 + Vm(X−,g)−1/3]. Eqn (18) and (20) summarise the good rectilinear correlations – of which eqn (19) is a specific example – resulting from plots of the sum of hydration enthalpies [ΔhydHo(M+,g) + ΔhydHo(X−,g)] versus, the sum of the inverse cube roots of the ions volumes [Vm(M+)−1/3 + Vm(X−,g)−1/3] (see Section S5 and Tables S9–S11† for the data used) In these equations δM+ and δX− represent Kronecker deltas. If the ions being considered are, for example, M+ = Na+ and X− = Cl− then: δNa+ = δCl− = 1 whilst δH+ = δLi+ = δK+ = δRb+ = δCs+ = δF− = δBr− = δI− = 0. All the parallel rectilinear correlations represented by eqn (18) and (20) have at least an R2 value of 0.9992.| | |
[ΔhydHo(M+,g) + δF−ΔhydHo(F−,g) + δCl−ΔhydHo(Cl−,g) + δBr−ΔhydHo(Br−,g) + δI−ΔhydHo(I−,g)] = −48.208[Vm(M+)−1/3 + δF−Vm(F−,g)−1/3 + δCl−Vm(Cl−,g)−1/3 + δBr−Vm(Br−,g)−1/3 + δI−Vm(I−,g)−1/3] − 453.45δF− − 343.3δCl− − 317.32δBr− − 285.55δI− (R2 = 0.9999)
| (18) |
thus for NaBr: δNa+ = δBr− = 1 whilst δH+ = δLi+ = δK+ = δRb+ = δCs+ = δF− = δCl− = δI− = 0 and so, for example:| | |
[ΔhydHo(Na+,g) + ΔhydHo(Br−,g)]/kJ mol−1 = −48.208[Vm(Na+)−1/3 + Vm(Br−)−1/3]/nm − 317.32 (R2 = 0.9999)
| (19) |
using [Vm(Na+)−1/3 + Vm(Br−)−1/3] = 8.9452 nm−1 yields a value for [ΔhydHo(Na+,g) + ΔhydHo(Br−,g)]/kJ mol−1 = −749 kJ mol−1 or only a 0.4% error and also:| | |
[δH+ΔhydHo(H+,g) + δLi+ΔhydHo(Li+,g) + δNa+ΔhydHo(Na+,g) + δK+ΔhydHo(K+,g) + δRb+ΔhydHo(Rb+,g) + δCs+ΔhydHo(Cs+,g) + −ΔhydHo(X−,g)] = −214.69[δH+Vm(H+)−1/3 + δLi+Vm(Li+)−1/3 + δNa+Vm(Na+)−1/3 + δK+Vm(K+)−1/3 + δRb+Vm(Rb+)−1/3 + δCs+Vm(Cs+)−1/3 + −Vm(X−,g)−1/3] + 3560.6δH+ + 1569.4δLi+ + 1167.9δNa+ + 892.8δK+ + 810.5δRb+ + 748.4δCs+ (R2 = 0.9992)
| (20) |
which gives an alternative, equally valid, equation to that of eqn (19) in the form:| | |
[ΔhydHo(Na+,g) + ΔhydHo(Br−,g)]/kJ mol−1 = −214.69[Vm(Na+)−1/3 + Vm(Br−)−1/3]/nm + 1167.9 (R2 = 0.9992)
| (21) |
using a test input of [Vm(Na+)−1/3 + Vm(Br−)−1/3] = 8.9452 nm−1 yields a value for [ΔhydHo(Na+,g) + ΔhydHo(Br−,g)] = −752 kJ mol−1 with no error. The two test calculations confirm the satisfactory nature of the correlations. The full set of equations, of which (18) and (20) are summaries are to be found in the ESI Section S6, eqn (S8)–(S17).†Plots of [ΔhydGo(M+,g) + ΔhydGo(X−,g)] versus [Vm(M+)−1/3 + Vm(X−,g)−1/3].
Eqn (22) and (23) summarize the good rectilinear correlations resulting from plots of the sum of hydration free energies [ΔhydGo(M+,g) + ΔhydGo(X−,g)] versus, the sum of the inverse cube roots of the ions volumes [Vm(M+)−1/3 + Vm(X−,g)−1/3]. All the parallel rectilinear correlations represented by eqn (22) and (23) have at least an R2 value of 0.9993.
| | |
[ΔhydGo(M+,g) + δF−ΔhydGo(F−,g) + δCl−ΔhydGo(Cl−,g) + δBr−ΔhydGo(Br−,g) + δI−ΔhydGo(I−,g)] = −47.057[Vm(M+)−1/3 + δF−Vm(F−,g)−1/3 + δCl−Vm(Cl−,g)−1/3 + δBr−Vm(Br−,g)−1/3 + δI−Vm(I−,g)−1/3] − 396.82δF− − 301.56δCl− − 283.16δBr− − 254.85δI− (R2 = 0.9996)
| (22) |
and also:
| | |
[δH+ΔhydGo(H+,g) + δLi+ΔhydGo(Li+,g) + δNa+ΔhydGo(Na+,g) + δK+ΔhydGo(K+,g) + δRb+ΔhydGo(Rb+,g) + δCs+ΔhydGo(Cs+,g) + −ΔhydGo(X−,g)] = −187.34[δH+Vm(H+)−1/3 + δLi+Vm(Li+)−1/3 + δNa+Vm(Na+)−1/3 + δK+Vm(K+)−1/3 + δRb+Vm(Rb+)−1/3 + δCs+Vm(Cs+)−1/3 + −Vm(X−,g)−1/3] + 2981.4δH+ + 1319.8δ|Li+ + 974.9δNa+ + 734.3δK+ + 663.1δRb+ + 610.4δCs+ (R2 = 0.9993)
| (23) |
The full set of individual equations are given in Section S7 of the ESI which lists eqn (S18)–(S27).† Note also that the gradients of the lines (18)–(22) are identical and in the case of eqn (23) very close to those of eqn (9), (10), (16) and (17).
A sample of the graphical plot is to be found for MCl salts (M = Li–Cs) in Fig. S2† in Section S4 and other alkali halide salts have very similar plots.
From the above analyses the uniqueness of the Vm−1/3 functions has been demonstrated and we reach our main conclusion that VBT clearly applies to the hydration thermodynamic data tested thus far.
Examination of thermodynamic data from literature sources and the use of V−1/3 as a correlation parameter
In what follows we retain the notation used in the publications highlighted for consideration and note when this corresponds to an (alternative) notation used earlier in the paper. Listed in Tables 7 and 8 are the conventional aqueous solvation free energies of gaseous cations and anions, determined using the eqn (13) and (16) of ref. 51 by use of pKa values. Because this represents a large database of thermochemical solvation values we examine how this data behaves when plotted versus V−1/3. Statistics applied to the end results tells us that there is virtually no probability of being wrong in assuming that a linear correlation exists between the solvation free energies and V−1/3. Hofmann's volumes61 have been employed in the absence of direct volume data.
Table 7 Assembly of cation values for ΔGo,conS(BH+)/kJ mol−1 from ref. 51 and Hofmann volumes Vm to make plot in Fig. 7. The rectilinear regression equation of best fit is used to predict single-ion free energy values for cations, ΔGo,conS(BH+)/kJ mol−1 using eqn (24) of best fit. ΔGoS(BH+)/kJ mol−1 = −98.0[Vm(BH+)/nm3] + 1027.1 (N = 50, R2 = 0.6747) (24)
| Cation BH+ |
B |
Hofmann Vm/nm3 |
Vm−1/3/nm−1 |
ΔGo,conS(BH+)/kJ mol−1 |
Predicted ΔGo,conS(BH+)/kJ mol−1 using eqn (24) |
% age error |
| H3O+ |
Water |
0.02663 |
3.3487 |
651.0 |
698.9 |
−7.4 |
| CH3OH2+ |
Methanol |
0.05003 |
2.713875 |
723.4 |
761.1 |
−5.2 |
| CH3CH2OH2+ |
Ethanol |
0.07343 |
2.388043 |
742.7 |
793.1 |
−6.8 |
| (CH3)2OH+ |
Dimethyl ether |
0.07343 |
2.388043 |
779.1 |
793.1 |
−1.8 |
| (C2H5)2OH+ |
Diethyl ether |
0.12023 |
2.026107 |
813.4 |
828.5 |
−1.9 |
| CH3C(OH)CH3+ |
Acetone |
0.08667 |
2.259663 |
789.9 |
805.7 |
−2.0 |
| CH3C(OH)C6H5+ |
Acetophenone |
0.16303 |
1.830533 |
842.7 |
847.7 |
−0.6 |
| NH4+ |
Ammonia |
0.03212 |
3.145875 |
756.0 |
718.8 |
4.9 |
| CH3NH3+ |
Methylamine |
0.05552 |
2.621301 |
792.9 |
770.2 |
2.9 |
| CH3(CH2)2NH3+ |
n-Propylamine |
0.10232 |
2.138027 |
813.4 |
817.6 |
−0.5 |
| (CH3)2CHNH3+ |
Isopropylamine |
0.10232 |
2.138027 |
821.3 |
817.6 |
0.5 |
| C(CH3)3NH3+ |
t-Butylamine |
0.12572 |
1.996175 |
830.9 |
831.5 |
−0.1 |
| o-C6H11NH3+ |
Cyclohexanamine |
0.16236 |
1.833047 |
825.1 |
847.5 |
−2.7 |
H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2NH3+ CHCH2NH3+ |
Allylamine |
0.09216 |
2.213872 |
811.3 |
810.1 |
0.1 |
| (CH3)2NH2+ |
Dimethylamine |
0.07892 |
2.331333 |
825.5 |
798.6 |
3.3 |
| (C2H5)2NH2+ |
Diethylamine |
0.12572 |
1.996175 |
847.3 |
831.5 |
1.9 |
| (n-C3H7)2NH2+ |
Di-n-propylamine |
0.17252 |
1.796333 |
859.4 |
851.1 |
1.0 |
(H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2)2NH2+ CHCH2)2NH2+ |
Diallylamine |
0.1522 |
1.87296 |
854.8 |
843.5 |
1.3 |
| (CH3)3NH+ |
Trimethylamine |
0.10232 |
2.138027 |
856.0 |
817.6 |
4.5 |
| (C2H5)3NH+ |
Triethylamine |
0.17252 |
1.796333 |
884.1 |
851.1 |
3.7 |
| (n-C3H7)3NH2+ |
Tri-n-propylamine |
0.24272 |
1.603115 |
900.0 |
870.0 |
3.3 |
| C6H5NH3+ |
Aniline |
0.13188 |
1.964598 |
809.6 |
834.6 |
−3.1 |
| o-CH3C6H4NH3+ |
2-Methylaniline |
0.15528 |
1.860494 |
818.4 |
844.8 |
−3.2 |
| m-CH3C6H4NH3+ |
3-Methylaniline |
0.15528 |
1.860494 |
821.3 |
844.8 |
−2.9 |
| p-CH3C6H4NH3+ |
4-Methylaniline |
0.14876 |
1.887287 |
820.4 |
842.1 |
−2.6 |
| m-NH2C6H4NH3+ |
3-Aminoaniline |
0.15528 |
1.860494 |
837.2 |
844.8 |
−0.9 |
| C6H5NH2CH3+ |
N-Methylaniline |
0.15528 |
1.860494 |
850.6 |
844.8 |
0.7 |
| C6H5NH2CH2CH3+ |
N-Ethylaniline |
0.17868 |
1.775448 |
852.3 |
853.1 |
−0.1 |
| C6H5NH(CH3)2+ |
N,N-Dimethylaniline |
0.17868 |
1.775448 |
873.2 |
853.1 |
2.3 |
| p-CH3C6H4NH(CH3)2+ |
4-Methyl-N,N-dimethylaniline |
0.20208 |
1.704089 |
878.6 |
860.1 |
2.1 |
| C6H5NH(CH2CH3)2+ |
N,N-Diethylaniline |
0.22548 |
1.642974 |
886.6 |
866.1 |
2.3 |
| C10H7NH3+ |
1-Aminonaphthalene |
0.195 |
1.724468 |
830.5 |
858.1 |
−3.3 |
| C2H4NH2+ |
Aziridine |
0.06876 |
2.440927 |
815.9 |
787.9 |
3.4 |
| C3H6NH2+ |
Azetidine |
0.09216 |
2.213872 |
829.3 |
810.1 |
2.3 |
| C4H8NH2+ |
Pyrrolidine |
0.11556 |
2.05304 |
836.4 |
825.9 |
1.3 |
| C5H10NH2+ |
Piperidine |
0.13896 |
1.930649 |
843.9 |
837.9 |
0.7 |
| C6H12NH2+ |
Azacycloheptane |
0.16236 |
1.833047 |
847.7 |
847.5 |
0.0 |
| C4H5NH+ |
Pyrrole |
0.09524 |
2.189745 |
855.6 |
812.5 |
5.0 |
| C9H7NH+ |
Quinolone |
0.1716 |
1.799538 |
878.2 |
850.7 |
3.1 |
| C4H8NHNH2+ |
Piperazine |
0.13244 |
1.961825 |
836.4 |
834.8 |
0.2 |
| CH3CNH+ |
Acetonitrile |
0.0586 |
2.574547 |
797.5 |
774.8 |
2.8 |
| H2NNH3+ |
Hydrazine |
0.049 |
2.732759 |
758.6 |
759.3 |
−0.1 |
| p-CH3OC6H4NH3+ |
4-Methoxyaniline |
0.16667 |
1.817108 |
814.6 |
849.0 |
−4.2 |
| p-NO2C6H4NH3+ |
4-Nitroaniline |
0.16138 |
1.83675 |
795.0 |
847.1 |
−6.6 |
| C4H8ONH2+ |
Morpholine |
0.12695 |
1.989707 |
821.3 |
832.1 |
−1.3 |
| CH3COHNH2+ |
Acetamide |
0.08015 |
2.319346 |
803.3 |
799.8 |
0.4 |
| C6H5COHNH2+ |
Benzamide |
0.15651 |
1.855607 |
831.4 |
845.3 |
−1.7 |
| (CH3)2SH+ |
Dimethyl sulfide |
0.08724 |
2.254731 |
842.7 |
806.1 |
4.3 |
| (CH3)2SOH+ |
Dimethyl sulfoxide |
0.09863 |
2.164364 |
820.9 |
815.0 |
0.7 |
| m-ClC6H4NH3+ |
3-Chloraniline |
0.1526 |
1.871322 |
800.0 |
843.7 |
−5.5 |
| p-ClC6H4NH3+ |
4-Chloraniline |
0.1526 |
1.871322 |
802.5 |
843.7 |
−5.1 |
Table 8 Assembly of anion values for ΔGo,conS(A−)/kJ mol−1 from ref. 51 and Hofmann volumes Vm to make plot in Fig. 8. The rectilinear regression equation of best fit is used to predict single-ion free energy values for anions, ΔGo,conS(A−)/kJ mol−1 using eqn (25) of best fit. ΔGoS(A−)/kJ mol−1 = −54.36[Vm(A−)/nm3] − 1298.1 (N = 57, R2 = 0.2725) (25)
| Anion A− |
AH |
Hofmann Vm/nm3 |
Vm−1/3/nm−1 |
ΔGo,conS (A−)/kJ mol−1 |
Predicted ΔGo,conS(A−)/kJ mol−1 using eqn (25) |
% age error |
| OH− |
Water |
0.032 |
3.930388 |
−1550.6 |
−1511.8 |
2.5 |
| HO2− |
Hydrogen peroxide |
0.02786 |
3.298676 |
−1519.6 |
−1477.4 |
2.8 |
| O2− |
Hydroperoxyl radical |
0.046 |
2.79092 |
−1461.1 |
−1449.8 |
0.8 |
| HS− |
Hydrogen sulfide |
0.057 |
2.598414 |
−1414.2 |
−1439.4 |
−1.8 |
| HC2− |
Acetylene |
0.03156 |
3.164373 |
−1432.6 |
−1470.1 |
−2.6 |
| CN− |
Hydrogen cyanide |
0.05 |
2.714418 |
−1406.2 |
−1445.7 |
−2.8 |
| CH3O− |
Methanol |
0.03987 |
2.927192 |
−1510 |
−1457.2 |
3.5 |
| C2H5O− |
Ethanol |
0.06327 |
2.509578 |
−1492 |
−1434.5 |
3.9 |
| C3H7O− |
1-Propanol |
0.08667 |
2.259663 |
−1482 |
−1420.9 |
4.1 |
| C3H7O− |
2-Propanol |
0.08667 |
2.259663 |
−1473.6 |
−1420.9 |
3.6 |
| C4H9O− |
2-Butanol |
0.11007 |
2.086621 |
−1464.8 |
−1411.5 |
3.6 |
| C4H9O− |
t-Butanol |
0.11007 |
2.086621 |
−1456.9 |
−1411.5 |
3.1 |
| C3H5O− |
Allyl alcohol |
0.07651 |
2.355559 |
−1474.9 |
−1426.2 |
3.3 |
| C3H7O2− |
2-Methoxyethanol |
0.09806 |
2.16855 |
−1486.6 |
−1416 |
4.7 |
| C2H5O2− |
1,2-Ethanediol |
0.07466 |
2.374856 |
−1469.4 |
−1427.2 |
2.9 |
| C7H7O− |
Benzyl alcohol |
0.13963 |
1.927556 |
−1468.6 |
−1402.9 |
4.5 |
| C2F3H2O− |
2,2,2-Trifluoroethanol |
0.08154 |
2.306091 |
−1436.8 |
−1423.5 |
0.9 |
| C3HF6O− |
1,1,1,3,3,3-Hexafluoropropan-2-ol |
0.12321 |
2.009639 |
−1386.6 |
−1407.4 |
−1.5 |
| CH3O2− |
Methyl hydroperoxide |
0.05126 |
2.691992 |
−1502.5 |
−1444.4 |
3.9 |
| C2H5O2− |
Ethyl hydroperoxide |
0.07466 |
2.374856 |
−1485.7 |
−1427.2 |
3.9 |
| CHO2− |
Formic acid |
0.0411 |
2.897695 |
−1431.3 |
−1455.6 |
−1.7 |
| C2H3O2− |
Acetic acid |
0.0645 |
2.493523 |
−1437.2 |
−1433.7 |
0.2 |
| C2H3O2− |
Propanoic acid |
0.0645 |
2.493523 |
−1431.3 |
−1433.7 |
−0.2 |
| C6H11O2− |
Hexanoic acid |
0.1581 |
1.849365 |
−1424.7 |
−1398.6 |
1.8 |
| C3H3O2− |
Acrylic acid |
0.07774 |
2.343069 |
−1422.1 |
−1425.5 |
−0.2 |
| C2H2ClO2− |
Pyruvic acid |
0.08522 |
2.272407 |
−1399.1 |
−1421.6 |
−1.6 |
| C2HCl2O2− |
Chloroacetic acid |
0.10594 |
2.113392 |
−1404.2 |
−1413 |
−0.6 |
| C2HCl2O2− |
Dichloroacetic acid |
0.08277 |
2.294611 |
−1373.2 |
−1422.8 |
−3.6 |
| C2F2O2− |
Trifluoroacetic acid |
0.04926 |
2.727942 |
−1360.6 |
−1446.4 |
−6.3 |
| C7H5O2− |
Benzoic acid |
0.14086 |
1.921929 |
−1410.4 |
−1402.6 |
0.6 |
| C6H5O− |
Phenol |
0.11623 |
2.049088 |
−1413.4 |
−1409.5 |
0.3 |
| C7H7O− |
2-Methylphenol |
0.13963 |
1.927556 |
−1406.2 |
−1402.9 |
0.2 |
| C7H7O− |
3-Methylphenol |
0.13963 |
1.927556 |
−1410 |
−1402.9 |
0.5 |
| C7H7O− |
4-Methylphenol |
0.13963 |
1.927556 |
−1413.8 |
−1402.9 |
0.8 |
| C6H5O2− |
3-Hydroxyphenol |
0.12762 |
1.986219 |
−1421.3 |
−1406.1 |
1.1 |
| C6H5O2− |
4-Hydroxyphenol |
0.12762 |
1.986219 |
−1437.2 |
−1406.1 |
2.2 |
| C6H4NO3− |
2-Nitrophenol |
0.14573 |
1.900277 |
−1364 |
−1401.4 |
−2.7 |
| C6H4NO3− |
3-Nitrophenol |
0.14573 |
1.900277 |
−1371.5 |
−1401.4 |
−2.2 |
| C6H4NO3− |
4-Nitrophenol |
0.14573 |
1.900277 |
−1354.4 |
−1401.4 |
−3.5 |
| C6H4ClO− |
2-Chlorophenol |
0.13695 |
1.940049 |
−1389.1 |
−1403.6 |
−1 |
| C6H4ClO− |
4-Chlorophenol |
0.13695 |
1.940049 |
−1388.7 |
−1403.6 |
−1.1 |
| C2H3O2− |
Acetaldehyde |
0.0645 |
2.493523 |
−1432.6 |
−1433.7 |
−0.1 |
| C3H5O− |
Acetone |
0.07651 |
2.355559 |
−1431.3 |
−1426.2 |
0.4 |
| C5H9O− |
3-Pentanone |
0.12331 |
2.009095 |
−1420.9 |
−1407.3 |
1 |
| CHN2− |
Cyanamide |
0.04192 |
2.878677 |
−1414.6 |
−1454.6 |
−2.8 |
| C2H2N− |
Acetonitrile |
0.04844 |
2.743249 |
−1391.2 |
−1447.2 |
−4 |
| C6H6N− |
Aniline |
0.12172 |
2.017806 |
−1375.7 |
−1407.8 |
−2.3 |
| C6H6N2O2− |
4-Nitroaniline |
0.1563 |
1.856438 |
−1352.7 |
−1399 |
−3.4 |
| C12H10N− |
Diphenylamine |
0.23287 |
1.625407 |
−1341 |
−1386.5 |
−3.4 |
| C2H4NO− |
Acetamide |
0.06999 |
2.426543 |
−1448.1 |
−1430 |
1.2 |
| CH2NO2− |
Nitromethane |
0.05798 |
2.583691 |
−1432.6 |
−1438.6 |
−0.4 |
| CH3S− |
Methanethiol |
0.05368 |
2.650915 |
−1421.3 |
−1442.2 |
−1.5 |
| C2H5S− |
Ethanethiol |
0.02712 |
3.328406 |
−1412.9 |
−1479 |
−4.7 |
| C3H7S− |
1-Propanethiol |
0.10048 |
2.150999 |
−1407.5 |
−1415 |
−0.5 |
| C6H5S− |
Thiophenol |
0.13004 |
1.973821 |
−1377.8 |
−1405.4 |
−2 |
| C2H5OS− |
Dimethyl sulfoxide |
0.08847 |
2.244233 |
−1395.8 |
−1420.1 |
−1.7 |
| CCl3− |
Chloroform |
0.09064 |
2.226179 |
−1338.9 |
−1419.1 |
−6 |
The plot in Fig. 7 for organic cations can be examined73 to determine the probability, P, of being wrong in assuming a linear correlation exists between ΔGoS(BH+)/kJ mol−1 and Vm(BH+)/nm3. The Student's t(2-sided) is first calculated72 and found to be 9.98, N = 50 data
| | |
t(2-sided) = [R2(N − 2)/(1 − R2)]1/2
| (24) |
points and
P = 0.00001 showing that it is correct to assume that correlation exists between the thermodynamic parameter and the inverse cube root of the volume. There is considerable scatter which, to some extent, is probably due to the use of the Hofmann volumes. The nature of the organic cations considered (see
Table 7) is such that many have strong internal interactions between functional groups which cannot be reflected in just considering elementary atom volumes making up the formula unit. The analytical form of the rectilinear fit takes the form:
| | |
ΔGoS(BH+)/kJ mol−1 = −98.0[Vm(BH+)/nm3] + 1027.1 (N = 50, R2 = 0.6747)
| (25) |
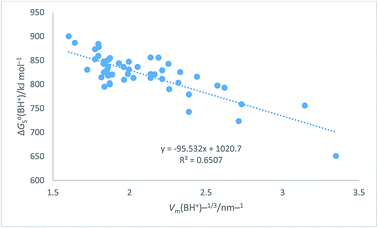 |
| | Fig. 7 Plot of conventional aqueous solvation free energies of cations for a standard state concentration of 1 mol dm−3 in both the gas and aqueous phases, ΔGoS(BH+)/kJ mol−1 taken from Table 2 of ref. 51 as ordinate versus Vm(BH+)−1/3/nm−1 (calculated from Hofmann volumes29) as abscissa. | |
The plot in Fig. 8 for organic anions can be used to investigate the nature of any correlation that might exist between ΔGoS(A−)/kJ mol−1 and Vm(A−)−1/3/nm−1 Even though the regression coefficient, R2, is quite low and there is considerable scatter we can infer that the correlation is valid. The Student's t(2-sided) is first calculated72,73 (eqn (24)) and found to be 92.741 with N = 57 data points, R2 = 0.2725 (eqn (26)) and P, the probability that it is wrong to assume the correlation is found to be equal to 0.0082. This can be interpreted to mean that in only 8 instances in 1000 would one be wrong to infer a correlation existed between the thermodynamic parameter and the inverse cube root of the volume. There is even more scatter in the case of these anions as compared to Fig. 7 which, to some extent, is probably made worse due to the use of the Hofmann volumes. Hofmann mentions that additional terms can be added to improve his procedure and take account of the local environment of individual atoms. These terms depend on the nature of the functional groups present and is more complicated to take account of and is, of course, based on significantly more parameters than the simple approach we have adopted. Nor has the effect of the charge been considered. The analytical form of the rectilinear fit takes the form (Fig. 8):
| | |
ΔGoS(A−)/kJ mol−1 = −54.36[Vm(A−)/nm3]−1/3 − 1298.1 (N = 57, R2 = 0.2725)
| (26) |
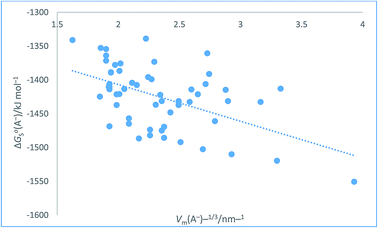 |
| | Fig. 8 Plot of conventional aqueous solvation free energies of anions for a standard state concentration of 1 mol dm−3 in both the gas and aqueous phases, ΔGoS(A−)/kJ mol−1 taken from Table 2 of ref. 51 as ordinate versus Vm(A−)−1/3/nm−1 (calculated from Hofmann volumes29) as abscissa. | |
The above two correlations, although found to be satisfactory, represent extremes and could possibly be improved and scatter reduced if density data (see eqn (1)) were employed to estimate volume of each of the materials. The reason they were selected for study was that they offered a large dataset which also conformed to being an example of the newer generation of hydration data.
Turning now to a further application, in the ESI Section Table S12† presents data for [ΔGoaq(M+,g) + ΔGoaq(X−,g)]/kJ mol−1 (which is equivalent to [ΔGohyd(M+,g) + ΔGohyd(X−,g)] adopting our earlier notation) as found in Table 1 of ref. 52 for the alkali halides. The data in Table S12 can be compared to that obtained in Table S9 obtained using eqn (S6) or (S7) in Section S3 and will be seen to vary slightly from data derived as state of the art in Table S9.† [ΔGoaq(M+,g) + ΔGoaq(X−,g)] represents the free energy change brought about by placing a pair of separate and oppositely charged gaseous ions into water at 298 K. Results in Table S12† are the results of Tissendier et al. computations. Fig. 9 displays a plot of the whole of this alkali halide solvation free energy data = [ΔGoaq(M+,g) + ΔGoaq(X−,g)] as ordinate versus V(MX)−1/3 as abscissa.
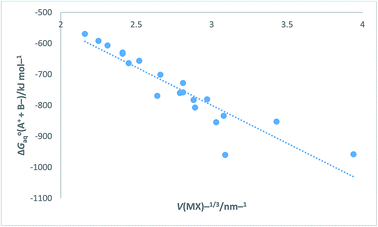 |
| | Fig. 9 Plot of Tissendier et al.'s data in Table 1 of ref. 52 for alkali halides (excluding OH− and H+ data) of ΔGoaq(A+ + B−) = [ΔGoaq(M+,g) + ΔGoaq(X−,g)] = [ΔGohyd(M+,g) + ΔGohyd(X−,g)]/kJ mol−1 versus V(MX)−1/3/nm−1. ΔGoaq(A+ + B−)/kJ mol−1 = −245.38V(MX)−1/3 − 63.607 (N = 20, R2 = 0.8420). | |
The rectilinear fit is represented by eqn (27) which takes the analytical form
| | |
ΔGoaq(A+ + B−) = [ΔGoaq(M+,g) + ΔGoaq(X−,g)] = −245.38V(MX)−1/3 − 63.607 (N = 20, R2 = 0.8420)
| (27) |
Additional to this we can take sections of the data and plot it versus V(MX)−1/3. The following rectilinear equations result:
For the individual alkali metal (except Cs) salts:
| | |
[ΔGoaq(Li+,g) + ΔGoaq(X−,g)]/kJ mol−1 = −144.73V(LiX)−1/3 − 388.01 (N = 4, R2 = 1)
| (28) |
| | |
[ΔGoaq(Na+,g) + ΔGoaq(X−,g)]/kJ mol−1 = −193.86V(NaX)−1/3 − 186.34 (N = 4, R2 = 0.999)
| (29) |
| | |
[ΔGoaq(K+,g) + ΔGoaq(X−,g)]/kJ mol−1 = −263.35V(KX)−1/3 + 3.81 (N = 4, R2 = 0.999)
| (30) |
| | |
[ΔGoaq(Rb+,g) + ΔGoaq(X−,g)]/kJ mol−1 = −293.91V(RbX)−1/3 + 69.99 (N = 4, R2 = 0.997)
| (31) |
Here we see high correlation coefficients this time indicating an almost perfect linear fit and how the inverse cube root of the volume, V−1/3 serves to correlate well with hydration derived data which was the aim of this paper.
If the hydrogen data in the free energy Table 1 in ref. 52 is plotted versus V(HX)−1/3 we have the following correlations. Where X = F, Cl, Br, I:
| | |
[ΔGoaq(H+,g) + ΔGoaq(X−,g)]/kJ mol−1 = −187.29V(HX)−1/3 − 892.85 (N = 4, R2 = 0.999)
| (32) |
and where hydroxides are also included:
| | |
[ΔGoaq(H+,g) + ΔGoaq(X−,g)]/kJ mol−1 = −198.8V(HX)−1/3 − 863.84 (N = 5, R2 = 0.991)
| (33) |
again an extension of VBT procedures to hydration and other solution data is indicated.
The above correlations are made traversing across Tissandier's table (retaining a constant M+ and H+). Tables S13 and S14† give the results of making correlations down the table (retaining a constant X−) and are used to make a prediction of the results for the cesium salts.
Tissandier's included no data for cesium salts in his table and the various correlations give us a chance to compare the predictions for this data since we have results derived from state of the art data (in Table S9†). The results are:
Overall rectilinear fit (Fig. 9, plotted versus V(MX)−1/3) has the following errors of prediction: CsF (3.3%), CsCl (0.6%), CsBr (3.3%), CsI (4.7%);
Rectilinear fits made down the table (Table S13,† plotted versus V(MX)−1/3) give errors of prediction: CsF (1.6%), CsCl (5.7%), CsBr (4.1%), CsI (4.4%);
Polynomial is fitted (Table S14,† plotted versus V(MX)−1/3) to data from down the table errors are significantly reduced; CsF (0.4%), CsCl (1.1%), CsBr (1.7%), CsI (2.0%);
This leaves us to conclude that, as was found in Fig. S3,† plots made against V(MX)−1/3 usually exhibit some curvature and thus a polynomial fit provides the preferred results.
Truhlar's thermodynamic data for clusters
Finally Table 4 in ref. 52 reproduced here as Table 9 provides data for cluster-ion solvation free energy (and enthalpy) and again in column 4 and 5 is seen that functions of V[M(H2O)n+] provide satisfactory representations in the form of smooth fits of the data and would support an extrapolation to give solvation free energies for M(H2O)10+ although probably not beyond. The fitted regression lines and polynomial (shown in Fig. S7 and S8† respectively) take the analytical forms:| | |
ΔGocis/kJ mol−1 = 137.28[V(Li(H2O)n+)]−1/3 − 571.38 (N = 6; R2 = 0.9959)
| (34) |
and| | |
ΔGocis/kJ mol−1 = −6.451[V(Li(H2O)n+)]−2/3 + 171.15[V(Li(H2O)n+)]−1/3 − 613.95 (N = 6; R2 = 0.9963)
| (35) |
Table 9 Truhlar et al.51 Li+ ion cluster solvation free energy data taken from Table 4 of ref. 52
| n value for ion Li(H2O)n+ |
Hydrated ion volume−1/3 V[M(H2O)n+] = [V(Li+) + nV(H2O)]−1/3 = [0.0015 + 0.0245n]−1/3 nm−1 |
Experimental cluster-ion solvation free energy, ΔGocis/kJ mol−1 |
Least squares fitted linear prediction ΔGocis/kJ mol−1 eqn (34) |
Least squares polynomial degree = 2 prediction ΔGocis/kJ mol−1 eqn (35) |
| 1 |
3.376 |
−113.8 |
−110.6 |
−112.4 |
| 2 |
2.705 |
−192.9 |
−201.5 |
−199.3 |
| 3 |
2.371 |
−248.5 |
−246.8 |
−245.1 |
| 4 |
2.158 |
−279.9 |
−275.6 |
−275.1 |
| 5 |
2.005 |
−298.7 |
−296.3 |
−297.1 |
| 6 |
1.888 |
−309.2 |
−312.2 |
−314.1 |
| 10 |
3.355 |
|
−352.3 |
−357.6 |
The hydrated ion volumes are calculated as:
| | |
[V(Li(H2O)n+)]−1/3 = [V(Li+) + nV(H2O)]−1/3
| (36) |
where
V(H
2O) is taken to be 0.0245 nm
3.
Table 9 gives the example of the hydrated Li
+ ion data. The fit to
V−1/3 gives a useful way to extrapolate the data from which is predicted for M(H
2O)
10+ Δ
Gocis = −352 kJ mol
−1 from
eqn (34) and −358 kJ mol
−1 from the polynomial fit of
eqn (35) (see graph in Fig. S8
†). Extrapolation by this means is preferable to using Δ
Gocis plotted
versus n because the latter is in the form shown in Fig. S9,
† the analytical form being:
| |
ΔGocis/kJ mol−1 = −112.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(n) − 117.05 (N = 6; R2 = 0.9924) ln(n) − 117.05 (N = 6; R2 = 0.9924)
| (37) |
For n = 10, ΔGocis = −376 kJ mol−1 from eqn (37) assuming the fit to a logarithmic form is appropriate.
Conclusion
The conclusion is straightforward and short. It seems clear that the inverse cube root of the solid state volume, V−1/3 usually correlates well with hydration thermodynamic parameters and can be used in a variety of ways, including extrapolations, interpolations as well as providing comparative data. As an extension of VBT the requirement to be very accurate is not usually necessary.
Acknowledgements
The University of Warwick and of Basle are thanked by the authors for providing facilities. We thank our reviewers (especially #2!) for his/her kind assistance in making sure our database was up to date. HDBJ is grateful for support from the Jenkins–Albright–Wilson fund for a trip to lecture at the University of Oviedo.
References
- H. D. B. Jenkins, H. K. Roobottom, J. P. Passmore and L. Glasser, Inorg. Chem., 1999, 38, 3609 CrossRef CAS PubMed.
- H. D. B. Jenkins and L. Glasser, J. Am. Chem. Soc., 2000, 122, 632 CrossRef.
- H. D. B. Jenkins, D. Tudela and L. Glasser, Inorg. Chem., 2002, 41, 2364 CrossRef CAS PubMed.
- H. D. B. Jenkins and D. Tudela, J. Chem. Educ., 2003, 80, 1482 CrossRef CAS.
- L. Glasser and H. D. B. Jenkins, Chem. Soc. Rev., 2005, 34, 866 RSC.
- H. D. B. Jenkins, Sci. Prog., 2009, 92, 91 CrossRef.
- L. Glasser and H. D. B. Jenkins, Phys. Chem. Chem. Phys., 2016, 18, 21226 RSC.
- T. E. Mallouk, G. L. Rosenthal, G. Muller, R. Busasco and N. Bartlett, Inorg. Chem., 1984, 23, 3167 CrossRef CAS.
- T. S. Cameron, R. J. Deeth, I. Dionne, H. B. Du, H. D. B. Jenkins, I. Krossing, J. Passmore and H. K. Roobottom, Inorg. Chem., 2000, 39, 5614 CrossRef CAS PubMed.
- S. Brownridge, I. Krossing, J. Passmore, H. D. B. Jenkins and H. K. Roobottom, Coord. Chem. Rev., 2000, 197, 397 CrossRef CAS.
- H. D. B. Jenkins, H. K. Roobottom and J. Passmore, Inorg. Chem., 2003, 42, 2886 CrossRef CAS PubMed.
- H. D. B. Jenkins, I. Krossing, J. Passmore and I. Raabe, J. Fluorine Chem., 2004, 125, 1585 CrossRef CAS.
- T. S. Cameron, I. Dionne, H. D. B. Jenkins, S. Parsons, J. Passmore and H. K. Roobottom, Inorg. Chem., 2000, 39, 2042 CrossRef CAS PubMed.
- K. O. Christe and H. D. B. Jenkins, J. Am. Chem. Soc., 2003, 125, 9457 CrossRef CAS PubMed.
- K. O. Christe and H. D. B. Jenkins, J. Am. Chem. Soc., 2003, 125, 14210 CrossRef CAS.
- A. Decken, H. D. B. Jenkins, G. B. Nikiforov and J. Passmore, Dalton Trans., 2004, 2496 RSC.
- D. A. Dixon, D. Feller, K. O. Christe, W. W. Wilson, A. Vij, V. Vij, H. D. B. Jenkins, R. M. Olson and M. S. Gordon, J. Am. Chem. Soc., 2004, 126, 834 CrossRef CAS PubMed.
- K. O. Christe, A. Vij, W. W. Wilson, V. Vij, D. A. Dixon, D. Feller and H. D. B. Jenkins, Chem. Br., 2003, 39, 17 Search PubMed.
- D. R. Rosseinsky, L. Glasser and H. D. B. Jenkins, J. Am. Chem. Soc., 2004, 126, 10472 CrossRef CAS PubMed.
- A. Decken, H. D. B. Jenkins, C. Knapp, G. B. Nikiforov, J. Passmore and J. M. Rautiainen, Angew. Chem., Int. Ed., 2005, 44, 7958 CrossRef CAS PubMed.
- H. S. Elliott, J. F. Lehmann, H. P. A. Mercier, H. D. B. Jenkins and G. J. Schrobilgen, Inorg. Chem., 2010, 49, 8504 CrossRef CAS PubMed.
- K. K. Bhasin, M. J. Crawford, H. D. B. Jenkins and T. M. Klapötke, Z. Anorg. Allg. Chem., 2006, 632, 897 CrossRef CAS.
- S. Brownridge, L. Calhoun, H. D. B. Jenkins, R. S. Laitinen, M. P. Murchie, J. Passmore, J. Pietikainen, J. M. Rautiainen, J. C. P. Sanders, G. J. Schrobilgen, R. J. Suontamo, H. M. Tuononen, J. U. Valkonen and C. M. Wong, Inorg. Chem., 2009, 48, 1938 CrossRef CAS PubMed.
- H. D. B. Jenkins, L. Glasser and J. F. Liebman, J. Chem. Eng. Data, 2010, 55, 4369 CrossRef CAS.
- L. Glasser and F. Jones, Inorg. Chem., 2009, 48, 1661 CrossRef CAS PubMed.
- K. O. Christe, R. Haiges, J. A. Boatz, H. D. B. Jenkins, E. B. Garner and D. A. Dixon, Inorg. Chem., 2011, 50, 3752 CrossRef CAS PubMed.
- A. Vegas, J. F. Liebman and H. D. B. Jenkins, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 511 CrossRef CAS PubMed.
- H. D. B. Jenkins, D. Holland and A. Vegas, Thermochem. Acta., 2016, 633, 24 CrossRef CAS.
- D. W. M. Hofmann, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 57, 489 Search PubMed.
- H. D. B. Jenkins and L. Glasser, J. Am. Chem. Soc., 2004, 126, 15809 CrossRef CAS PubMed.
- L. Glasser and H. D. B. Jenkins, Inorg. Chem., 2007, 46, 9768 CrossRef CAS PubMed.
- H. D. B. Jenkins and J. F. Liebman, J. Chem. Eng. Data, 2009, 54, 351 CrossRef CAS.
- H. D. B. Jenkins and L. Glasser, J. Chem. Eng. Data, 2010, 55, 4231 CrossRef CAS.
- H. D. B. Jenkins, L. Glasser and J. F. Liebman, J. Chem. Eng. Data, 2010, 55, 4369 CrossRef CAS.
- H. D. B. Jenkins and C. E. Housecraft, J. Chem. Thermodyn., 2017 Search PubMed , submitted for publication.
- L. Glasser, H. D. B. Jenkins and T. M. Klapotke, Z. Anorg. Allg. Chem., 2014, 640, 1297 CrossRef CAS.
- A. Vegas, J. F. Liebman and H. D. B. Jenkins, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 511 CrossRef CAS PubMed.
- A. Vegas and H. D. B. Jenkins, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 94 CrossRef CAS.
- S. V. Makarov, S. Sal'nikov and A. S. Pogorelova, Russ. J. Inorg. Chem., 2010, 55, 301 CrossRef CAS.
- S. V. Makarov, D. S. Sal'nikov and A. S. Pogorelova, Zh. Neorg. Khim., 2010, 55, 309 Search PubMed.
- S. A. Svarovsky, R. H. Simoyi and S. V. Makarov, J. Chem. Soc., Dalton Trans., 2000, 511 RSC.
- F. A. LeBlanc, A. Decken, T. S. Cameron, J. Passmore, J. M. Rautiainen and T. K. Whidden, Inorg. Chem., 2017, 56, 974 CrossRef CAS PubMed.
- K. K. Bhasin, M. J. Crawford, H. D. B. Jenkins and T. M. Klapotke, Z. Anorg. Allg. Chem., 2016, 632, 897 CrossRef.
- D. Srinivas, V. Ghule, K. Muralidharan and H. D. B. Jenkins, Chem.–Asian. J., 2013, 8, 1023 CrossRef CAS PubMed.
- P. Bruna, A. Decken, S. Greer, F. Grein, H. D. B. Jenkins, B. Mueller, J. Passmore, T. A. P. Paulose, J. M. Rautiainen and S. Richardson, Inorg. Chem., 2013, 52, 13651 CrossRef CAS PubMed.
- E. Zintl, Angew. Chem., 1939, 52, 1 CrossRef CAS.
- W. Klemm, Proc. R. Soc. London, Ser. A, 1958, 329 CAS.
- H. D. B. Jenkins and A. Vegas, Acta Crystallogr., Sect. B, 2017, eb5061 Search PubMed.
- H. D. B. Jenkins and A. Vegas, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, eb5062 Search PubMed.
- A. Vegas, New Models in Inorganic Structures – from elements to compounds, International Union of Crystallography/Oxford University Press, 2017, MS in preparation Search PubMed.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2006, 110, 16066 CrossRef CAS PubMed.
- M. D. Tissendier, K. A. Cowen, W. Y. Feng, E. Grundlach, M. H. Cohen, A. D. Earhart, J. V. Coe and T. R. Tuttle Jr, J. Phys. Chem. A, 1998, 102, 7787 CrossRef.
- J. V. Coe, Chem. Phys. Lett., 1994, 229, 161 CrossRef CAS.
- http://kinetics.nist.gov/janaf/.
- M. Born, Zeitschrift für Physik, 1920, 1, 45 CrossRef CAS.
- Y. Marcus, Ion Properties, Marcel Dekker, New York, 1997 Search PubMed.
- P. Vieillard, Acta Crystallogr., Sect. B: Struct. Sci., 1987, 43, 513 CrossRef.
- V. M. Goldschmidt, Geochemische Verteilungsgesetze der Elemente, Skrifter Norske Videnskapp-Akad, Oslo, I, Mat, -Naturv. Kl, 1926 Search PubMed.
- L. Pauling, Nature of the Chemical Bond, Oxford University Press, 3rd edn, 1960 Search PubMed.
- E. J. King, J. Phys. Chem., 1970, 74, 4590 CrossRef CAS.
- D. W. M. Hofmann, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 57, 489 Search PubMed.
- D. M. Camaioni and C. A. Schwerdtfeger, J. Phys. Chem. A, 2005, 109, 10795 CrossRef CAS PubMed.
- D. R. Lide, Handbook of Chemistry & Physics, CRC Press, Boca Raton, 80th edn, 1999–2000, pp. 5–85 Search PubMed.
- D. D. Wagman, W. H. Evans, V. B. Parker, R. H. Schumm, I. Halow, S. M. Bailey, K. L. Churney and R. L. Nutall, NBS Tables of Chemical Thermodynamic Properties, 1982, J. Phys. Chem. Ref. Data, vol. 11, Supplement 2 Search PubMed.
- J. F. Zemaitis, D. M. Clark, M. Rafal and N. C. Scrivner, Handbook of Aqueous Electrolyte Thermodynamics, American Institute of Chemical Engineers, New York, 1986 Search PubMed.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2005, 1, 1133 CrossRef CAS PubMed.
- J. R. Pliego Jr and J. M. Riveros, Chem. Phys. Lett., 2000, 332, 597 CrossRef.
- G. J. Tawa, I. A. Topol, S. K. Burt, R. A. Cladwell and A. A. Rashin, J. Chem. Phys., 1998, 109, 4852 CrossRef CAS.
- J. R. Pliego Jr and J. M. Riveros, J. Chem. Phys., 2000, 112, 4045 CrossRef.
- J. R. Pliego Jr and J. M. Riveros, J. Phys. Chem. B, 2000, 104, 5155 CrossRef.
- J. R. Pliego Jr and J. M. Riveros, Phys. Chem. Chem. Phys., 2002, 4, 1622 RSC.
- O. L. Davies and P. L. Goldsmith, Statistical Methods in Research and Production, Oliver & Boyd, 4th edn, 1972 Search PubMed.
- http://Surfstat.anu.edu.au/serfstat-home/tables/t.php.
Footnote |
| † Electronic supplementary information (ESI) available: Tables S1–S5; Fig. S1–S2. See DOI: 10.1039/c6ra25804b |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a and
H. Donald Brooke Jenkins*bc
a and
H. Donald Brooke Jenkins*bc
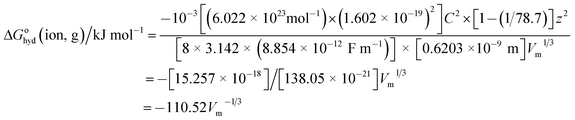


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1) salts using latest data
1) salts using latest data![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) salts by:
1) salts by:

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2NH3+
CHCH2NH3+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2)2NH2+
CHCH2)2NH2+


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(n) − 117.05 (N = 6; R2 = 0.9924)
ln(n) − 117.05 (N = 6; R2 = 0.9924)


