DOI:
10.1039/C6RA25807G
(Paper)
RSC Adv., 2017,
7, 3078-3088
Spontaneous supersaturation of calcium citrate from simultaneous isothermal dissolution of sodium citrate and sparingly soluble calcium hydroxycarboxylates in water
Received
25th October 2016
, Accepted 22nd December 2016
First published on 13th January 2017
Abstract
Strongly supersaturated homogeneous calcium citrate solutions are formed spontaneously when solid sodium citrate and solid calcium hydroxycarboxylates are dissolved simultaneously in water or when solid sodium citrate is dissolved in an already saturated aqueous solution of the calcium hydroxycarboxylate at ambient conditions. Maximal supersaturation of calcium citrate was found to decrease for an increasing value of the stability constant for calcium binding: L-lactate < D-gluconate < citrate, indicating citrate assisted dissolution through competitive complex formation as a thermodynamic factor controlling spontaneous supersaturation for up to a factor of more than twenty. Time elapsing prior to initiation of precipitation of calcium citrate was found to be shorter for a higher degree of supersaturation and lasted between hours and days. During subsequent precipitation equilibrium solubility of calcium citrate was approached with a simultaneous increase in water activity. Both thermodynamic and kinetic factors are suggested to be important for the spontaneous supersaturation, which seems to explain the paradoxal but well-stablished high bioavailability of calcium from the sparingly soluble calcium citrate and the high mobility of calcium in the presence of citrate during biomineralization.
Introduction
Citrate as a vehicle for calcium ions has been demonstrated to increase the bioavailability of calcium from food or from supplements under various conditions despite the low solubility of calcium citrate.1,2 Milk and other dairy products, known as important calcium sources in human nutrition, have a significant content of citrate.3
Calcium citrate as a calcium source with an equilibrium release of 5 mM calcium to an aqueous environment also enhances bone regeneration by bone morphogenetic proteins by affecting osteoblast differentiation and proliferation.4 A high production of citrate by osteoblasts was also identified as important for bone formation and an optimal structure of apatite nanocrystals for improved bone resistance to fracture.5 A more specific role of citrate in apatite crystallization has now also been recognized during bone mineralization.6–8
A common factor for these observations from experimental human nutrition and from medical treatment of osteoporosis may be related to the solubility overshooting phenomena recently observed for dissolution of calcium citrate tetrahydrate in aqueous solutions of sodium citrate but not in pure water.9 Notably, the initial solubility of calcium citrate in aqueous sodium citrate was higher by approximately 10% than the equilibrium solubility established after 48 hours of isothermal equilibration of solutions with solid calcium citrate in the temperature interval from 0 to 100 °C.9 Similarly spontaneous supersaturation of calcium D-gluconate in water by up to a factor of seven was observed by isothermal continuing dissolution of calcium L-lactate in an already saturated aqueous calcium L-lactate solution after addition of solid sodium D-gluconate.10 Notably, both calcium L-lactate and calcium D-gluconate find widespread use for calcium fortification of food and beverages.11,12
Non-equilibrium conditions may also explain the increased bioavailability of calcium from mixtures of citric acid and calcium hydroxide compared to calcium citrate found in human intervention studies.1 Likewise, a suspension of calcium citrate in aqueous potassium citrate had superior calcium bioavailability compared to tablet formulation of calcium citrate for patients after Roux-en-Y gastric bypass operations.13
The mechanism behind spontaneous formation of supersaturated aqueous solutions of sparingly soluble calcium hydroxycarboxylates under isothermal condition accordingly deserves more attention not only in relation to improvement of bioavailability of calcium from foods and supplements but also in relation to biomineralization and mineral mobility in calcified tissue. Most mammalian biofluids are supersaturated with respect to calcium hydroxyapatite but calcium phosphate deposition in various tissues is strictly controlled by specific crystallization inhibitors.14 The dissolution process resulting in spontaneous supersaturation under isothermal conditions is less understood. We now report the results of investigations, which points towards a special role of citrate and possibly other hydroxycarboxylates in mineral mobility involving spontaneous isothermal supersaturation.
Experimental
Materials
Tricalcium dicitrate tetrahydrate, calcium L-lactate pentahydrate, calcium D-gluconate monohydrate, ammonium purpurate 5,5-nitrilodibarbituric acid (murexid), and trisodium citrate dihydrate were all from Sigma Aldrich (Steinheim, Germany). Purity of all calcium salts was of analytical grade. Ethylenediaminetetraacetic acid disodium salt dihydrate (EDTA), calcium chloride dihydrate, and sodium hydroxide were from Merck (Darmstadt, Germany). All aqueous solutions were made from purified water from Milli-Q Plus (Millipore Corporation, Bedford, MA).
Total calcium determination
Standardization of 0.0100 mol L−1 and 0.0500 mol L−1 solution of EDTA used for titration was obtained against a 0.0100 mol L−1 aqueous solution of CaCl2 prepared by weighing of calcium chloride dihydrate. An aliquot of the 1.000 mL of sample was transferred to a titration flask and subsequently diluted with 25 mL of water. To maintain basic pH, 0.50 mL of 2.0 mol L−1 solution of NaOH was added to each sample, and 0.20 mL of 0.50% murexid solution was used as an indicator.
Electrochemical measurement of calcium ion activity
Calcium ion activity, aCa2+, was measured using a calcium ion selective electrode ISE25Ca with a reference REF251 electrode from Radiometer (Copenhagen, Denmark). The calibration of the electrode was obtained using aqueous 1.00 × 10−4, 1.00 × 10−3, 1.00 × 10−2 mol L−1 CaCl2 standard solutions prepared from a 1.000 mol L−1 CaCl2 stock solution at 25 °C. Calcium ion activity, aCa2+, in the standard solutions was calculated from the relationship between activity and calcium concentration, cCa2+, according towhere γ2+ is the activity coefficient calculated from the Davies' equation as described previously15| |
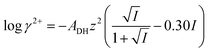 | (2) |
where ADH is the Debye–Hückel constant with the numerical value of ADH = 0.510 at 25 °C, I is the ionic strength, and z is the charge of the ion, i.e., 2 for calcium ions.16 The calcium ion activity in the test solutions was calculated from a linear standard curve between electrode potential (mV) measured for the calibration solutions and −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aCa2+ of the calibration solutions according to the Nernst equation at 25 °C.
aCa2+ of the calibration solutions according to the Nernst equation at 25 °C.
Water activity
Water activity, aw, was determined using an Aqua lab CX-2 (Aqua lab, Pullman, WA, USA) at 25.0 ± 0.2 °C. The water activity was determined as the mean of measurements for two separate solutions. For measurement under conditions of supersaturation, solutions were prepared by mixing 16.00 g and 20.00 g of solid calcium L-lactate with 12.00 g and 24.00 g of solid sodium citrate, respectively, and 16.00 g of solid calcium D-gluconate with 24.00 g of solid sodium citrate, dissolved in 100 mL of water. Water activity was measured in the transparent solutions and after 96 h in the solution with precipitate, which was filtered off prior to measurement.
Dissolution experiments
1. Solid sodium citrate in saturated aqueous calcium L-lactate. (a) Saturated solutions of calcium L-lactate were prepared by adding 12.00 g (0.0389 mol) to 100 mL of water and equilibrating for two hours under constant stirring at 25 °C. The saturated solution contained 10.5 g (0.340 M) of calcium L-lactate in equilibrium with a precipitate of 1.5 g (0.0049 mol) of calcium L-lactate. Aliquots of 13.00 g (0.0442 mol) or 6.00 g (0.0204 M) of solid sodium citrate were added to the saturated calcium L-lactate solutions. Supersaturated homogeneous solutions appeared within approximately 10 minutes of moderate stirring at 25 °C. The homogeneous solutions were analysed for total calcium concentration and after 2, 24, 48, and 72 hours under constant stirring during which period precipitation occurred, and calcium ion activity was determined.(b) Saturated solutions of calcium L-lactate were prepared by adding 16.00 g (0.0519 mol) to 100 mL of water and equilibrating for two hours under constant stirring at 25 °C. The saturated solution contained 10.5 g (0.340 M) of calcium L-lactate in equilibrium with a precipitate of 5.5 g (0.0178 mol). Aliquots of 12.00 g (0.0408 mol), or 24.00 g (0.0816 mol) of solid sodium citrate were added to the saturated calcium L-lactate solutions. Supersaturated homogeneous solutions appeared within approximately 12 minutes of moderate stirring at 25 °C for the conditions of 12.00 g and 24.00 g added solid sodium citrate. The homogeneous solutions were analysed for total calcium concentration and after 2, 24, 48, and 72 hours under constant stirring during which period precipitation occurred, and calcium ion activity was determined.
2. Solid sodium citrate in saturated aqueous calcium D-gluconate. (a) Saturated solutions of calcium D-gluconate were prepared by adding 5.00 g (0.0111 mol) to 100 mL of water and equilibrating for two hours under constant stirring at 25 °C. The saturated solution contained 4.3 g (0.096 M) of calcium D-gluconate in equilibrium with a precipitate of 0.70 g (0.0015 mol) of calcium D-gluconate. Aliquots of 13.00 g (0.0442 mol) or 6.00 g (0.0204 mol) of solid sodium citrate were added to the saturated calcium D-gluconate solutions. Supersaturated homogeneous solutions appeared within approximately 10 minutes of moderate stirring at 25 °C. The homogeneous solutions were analysed for total calcium concentration and after 2, 24, 48, and 72 hours under constant stirring during which period precipitation occurred, and calcium ion activity was determined.(b) Saturated solution of calcium D-gluconate was prepared by adding 6.50 g (0.0145 mol) to 100 mL of water and equilibrating for two hours under constant stirring at 25 °C. The saturated solution contained 4.3 g (0.096 M) of calcium D-gluconate in equilibrium with a precipitate of 2.2 g (0.0049 mol). An aliquot of 12.00 g (0.0408 mol) of solid sodium citrate was added to the saturated calcium D-gluconate solution. Supersaturated homogeneous solutions appeared within approximately 30 minutes of moderate stirring at 25 °C. The homogeneous solution was analysed for total calcium concentration and after 2, 24, 48, and 72 hours under constant stirring during which period precipitation occurred, and calcium ion activity was determined.
3. Solid calcium L-lactate and solid sodium citrate. To 16.00 g (0.0519 mol) of solid calcium L-lactate and 12.00 g (0.0408 mol) of solid sodium citrate was added 100 mL of water. A supersaturated homogeneous solution appeared within approximately 30 minutes of moderate stirring at 25 °C. The homogeneous solution was analysed for total calcium concentration and after 2, 24, 48, and 72 hours under constant stirring during which period precipitation occurred, and calcium ion activity was determined.
4. Solid calcium D-gluconate and solid sodium citrate. To 6.50 g (0.0145 mol) of solid calcium D-gluconate and 12.00 g (0.0408 mol) of solid sodium citrate was added 100 mL of water. A supersaturated homogeneous solution appeared within approximately 30 minutes of moderate stirring at 25 °C. The homogeneous solution was analysed for total calcium concentration and after 2, 24, 48, and 72 hours under constant stirring during which period precipitation occurred, and calcium ion activity was determined.
5. Solid sodium citrate in saturated aqueous calcium citrate. Saturated solution of calcium citrate was prepared by adding 2.00 g (0.0035 mol) to 100 mL of water and equilibrating for two hours under constant stirring at 25 °C. The saturated solution contained 0.100 g (0.00175 M) of calcium citrate in equilibrium with a precipitate of 1.9 g (0.0033 mol) of calcium citrate. Aliquot of 24.00 g (0.0816 mol) of solid sodium citrate was added to the saturated calcium citrate solution. A supersaturated homogeneous solution appeared within approximately 45 minutes of moderate stirring at 25 °C. The homogeneous solution was analysed for total calcium concentration and after 2, 24, 48, 72, 96, and 168 hours under constant stirring during which period precipitation occurred, and calcium ion activity was determined.
6. Minimum sodium citrate to dissolve calcium L-lactate. Various combinations of calcium L-lactate and sodium citrate have been investigated in order to find the minimum sodium citrate concentration required to dissolve a specified amount of calcium L-lactate to form maximal supersaturation. The following combinations of sodium citrate and calcium L-lactate were found to result in maximal supersaturation: 16.00 g (0.0519 mol), 18.00 g (0.0584 mol), or 20.00 g (0.0649 mol) of solid calcium L-lactate combined with 12.00 g (0.0408 mol), 18.00 g (0.0612 mol), and 24.00 g (0.0816 mol) of solid sodium citrate, respectively, when for each of these combinations of calcium L-lactate and sodium citrate, 100 mL of water was added. The solutions were stored under moderate stirring at 25 °C for a period of 72 hours and analysed for total dissolved calcium and calcium ion activity was determined. During the period of 72 hours all solutions were inspected visually and it was noted when solutions temporally became clear and again unclear and time was noted for initiation of precipitation.
7. Minimum sodium citrate to dissolve calcium D-gluconate. Various combinations of calcium D-gluconate and sodium citrate have been investigated in order to find the minimum sodium citrate concentration required to dissolve a specified amount of calcium D-gluconate to form maximal supersaturation. The following combinations of sodium citrate and calcium D-gluconate have been found to result in maximal supersaturation: 6.50 g (0.0145 mol), 8.00 g (0.0178 mol), or 16.00 g (0.0357 mol) of solid calcium D-gluconate combined with 6.00 g (0.0204 mol), 8.00 g (0.0272 mol), and 24.00 g (0.0816 mol) of solid sodium citrate, respectively, when for each of these combinations of calcium D-gluconate and sodium citrate, 100 mL of water was added. The solutions were stored under moderate stirring at 25 °C for a period of 72 hours and analysed for total dissolved calcium and calcium ion activity was determined. During the period of 72 hours all solutions were inspected visually and it was noted when solutions temporally became clear and again unclear and time was noted for initiation of precipitation.
Association constant and solubility product of calcium citrate in aqueous solution of unity ionic strength
Association constant for calcium and citrate, and solubility product for calcium citrate, corrected for complex formation, were determined for a saturated solution of calcium citrate in aqueous solution with unity ionic strength, prepared by saturation of 3.0 g in 100 mL of water with ionic strength adjusted to 1.0 with KCl. The solution was stored under moderate stirring at 25.0 °C for a period of 48 hours and analysed for total calcium and calcium ion activity was determined. The sample was prepared in duplicate.
Calculation of the association constant and the solubility product of calcium citrate at ionic strength 1.0 at 25 °C was based on electrochemically determined calcium ion activity converted to calcium ion concentration, [Ca2+], by eqn (1). The complex concentration, [CaCitr−], was calculated according to
| | |
[CaCitr−] = cCa2+ − [Ca2+]
| (3) |
where
cCa2+ is total calcium concentration, determined by EDTA titration and [Citr
3−], the free citrate concentration was calculated according to
| | |
[Citr3−] = cCitr3− − [CaCitr−]
| (4) |
where
cCitr3− is total citrate concentration. The association constant,
Kc, based on concentration defined as
| |
 | (5) |
was calculated using the iterative procedure already described
9 resulting in a value of (2.2 ± 0.3) × 10
3 M
−1, which is in good agreement with the value of (2.95 ± 0.03) × 10
3 M
−1 found for aqueous 0.020 M sodium citrate at 25 °C.
9
The solubility product, Ksp, for calcium citrate at ionic strength 1.0 at 25 °C corrected for complex formation was calculated according to
| | |
Ksp = [Ca2+]3[Citr3−]2
| (6) |
resulting in a value of (7 ± 2) × 10
−14 M
5.
Precipitate from supersaturated solutions of calcium citrate
Precipitates were collected by filtration from equilibrated solutions for all conditions and washed with water and ethanol prior to air-drying overnight and in an oven at 105 °C until constant weight. Water loss was calculated as the percentage difference between the weight of air dried and oven-dried precipitate.
Infrared spectra
Infrared spectra Fourier Transform Infrared (FT-IR) – Attenuated Total Reflection (ATR) Spectroscopy FT-IR of the precipitates collected from equilibrated mixed solutions were recorded with a FT-IR spectrometer (Bomem MB100, ABB, Quebec, Canada) equipped with an ATR attachment. All the spectra were obtained by accumulation of 64 scans, with resolution of 4 cm−1, at 500–4000 cm−1.
Results and discussion
Supersaturated aqueous solutions were found to be formed within a few minutes by dissolution of excess calcium L-lactate or of excess calcium D-gluconate in already saturated aqueous solutions by addition of solid sodium citrate to each of the two saturated solutions at a constant temperature of 25 °C. Similarly, for a saturated solution of calcium citrate in water at 25 °C, addition of solid sodium citrate resulted in continuing dissolution of calcium citrate. A significant supersaturation was evident in each case, since a precipitate identified by infrared spectroscopy as calcium citrate was formed subsequently in the solution with lag phase ranging from 30 min to 2 days for L-lactate and D-gluconate solutions. For solid calcium citrate, a similar spontaneous supersaturation has previously been reported for isothermal dissolution in aqueous solutions of sodium citrate.9 The supersaturation of calcium citrate was studied with respect to calcium speciation for a moderate supersaturation of approximately 15% and also for approximately 50% supersaturation in two series of experiments, both series including calcium L-lactate and calcium D-gluconate. For all three hydroxycarboxylates, i.e. L-lactate, D-gluconate, and citrate, the maximal supersaturation obtained by dissolution of the solid calcium salts mixed with solid sodium citrate was determined in separate experiments.
In a saturated solution of calcium L-lactate three ionic species are dominating according to the dissolution established as a two-step process
| | |
CaLact2 → CaLact+ + Lact−
| (7) |
| | |
CaLact+ ⇌ Ca2+ + Lact−
| (8) |
where Lact
− is the lactate ion and CaLact
+ is the 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1 complex between calcium and lactate. The addition of sodium citrate will lower the concentration of calcium ions due to a stronger complex formation by citrate:
| | |
Ca2+ + Citr3− ⇌ CaCitr−
| (9) |
in effect increasing the solubility of calcium lactate. Citr
3− is the citrate ion and CaCitr
− is the 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1 complex. Notably, the dissolution of excess calcium
L-lactate in saturated aqueous solution by an increasing concentration of citrate from dissolving sodium citrate will result in supersaturation with respect to calcium citrate either as the hexahydrate or tetrahydrate depending on temperature:
9,17| | |
3Ca2+ + 2Citr3− ⇌ Ca3Citr2(s)
| (10) |
No immediate precipitation of any of the calcium citrate hydrates was observed from these solutions supersaturated in calcium citrate. However, precipitate was formed with a lag phase ranging for up to 2 hours depending on the degree of supersaturation. The speciation of calcium in these supersaturated solutions depends on the chemical equilibria of eqn (8) and (9). Since citrate has a thermodynamic association constant of 3.6 × 104 at 25 °C for binding calcium compared to 49 for lactate, citrate can be assumed to control the free calcium ion concentration. The thermodynamic association constants are valid for ion activities as they were determined by extrapolation to zero ionic strength.9,15 For the supersaturated solutions with ionic strength higher than unity concentration based association constants will have to replace the activity based association constants for quantitative calculations. The use of equilibrium constants determined for 1.0 M KCl or NaCl seems an acceptable approximation, since ionic strength in most of the supersaturated and the equilibrated solutions are close to unity. For the solutions with ionic strength higher than unity the same constants were used as it has been shown that calcium salts like calcium nitrate and calcium chloride have activity coefficients rather constant with values around 0.33 in the concentration range between 0.7 to 2.0 (molal scale) corresponding to the ionic strength interval of relevance for the supersaturated calcium hydroxycarboxylate solutions.18,19 The association constant determined at ionic strength 1.0 for calcium citrate, KaCaCitr = (2.2 ± 0.3) × 103 M−1 in the present study and in 1.0 M NaCl for calcium lactate, KaCaLact = 8 ± 2 M−1,9,20 both based on concentrations, were accordingly used for the calculation of calcium speciation in the supersaturated solutions:
| | |
Ca2+ + Citr3− ⇌ CaCitr−
| (11) |
corresponding to the equilibrium constant
| |
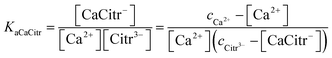 | (12) |
in which
cCa2+ is the total calcium ion concentration and
cCitr3− is the total citrate concentration originating from added citrate. Total calcium ion concentration as determined by EDTA titration and shown in
Tables 1,
2 and
5 is thus equal to the final calcium concentration in the supersaturated solutions.
Table 1 Supersaturated aqueous solutions of calcium citrate as formed at 25 °C by dissolution of calcium L-lactate in an already saturated solution of calcium L-lactate by addition of solid sodium citrate (sat/solid), or by simultaneous dissolution of solid calcium L-lactate and solid sodium citrate in water (solid/solid)
| |
Total Ca2+ in supersat. solution/M |
Total lactate/M |
Total citrate/M |
Calcium ion activity |
Free [Ca]2+/M |
[CaLact+]/M |
[CaCitr−]/M |
[Lact−]/M |
[Citr3−]/M |
I |
QCaLact = [Ca2+][Lact−]2 |
QCaCitr = [Ca2+]3[Citr−]2 |
| Sat/solid |
0.366 ± 0.002 |
0.778 |
0.442 |
(1.2 ± 0.1) × 10−3 |
(2.1 ± 0.1) × 10−3 |
(1.05 ± 0.03) × 10−2 |
0.354 ± 0.001 |
0.722 ± 0.003 |
(8.8 ± 0.1) × 10−2 |
1.608 ± 0.004 |
(1.11 ± 0.04) × 10−3 |
(7.6 ± 0.4) × 10−11 |
| Sat/solid |
0.379 ± 0.001 |
0.778 |
0.204 |
(3.92 ± 0.03) × 10−3 |
(2.89 ± 0.03) × 10−2 |
0.149 ± 0.001 |
0.201 ± 0.001 |
0.609 ± 0.002 |
(3.00 ± 0.01) × 10−3 |
0.857 ± 0.002 |
(1.07 ± 0.02) × 10−2 |
(2.17 ± 0.05) × 10−10 |
| Sat/solid |
0.50 ± 0.01 |
1.038 |
0.408 |
(2.3 ± 0.2) × 10−3 |
(1.0 ± 0.1) × 10−2 |
(9 ± 1) × 10−2 |
0.394 ± 0.001 |
0.90 ± 0.01 |
(1.4 ± 0.1) × 10−2 |
1.39 ± 0.01 |
(8 ± 1) × 10−3 |
(2.0 ± 0.3) × 10−10 |
| Sat/solid |
0.467 ± 0.001 |
1.038 |
0.816 |
(6.4 ± 0.1) × 10−4 |
(6.09 ± 0.04) × 10−4 |
(4.43 ± 0.04) × 10−3 |
0.462 ± 0.001 |
0.930 ± 0.003 |
0.354 ± 0.001 |
3.516 ± 0.004 |
(5.3 ± 0.1) × 10−4 |
(2.84 ± 0.04) × 10−11 |
| Solid/solid |
0.491 ± 0.001 |
1.038 |
0.408 |
(2.32 ± 0.04) × 10−3 |
(9.5 ± 0.1) × 10−3 |
(8.77 ± 0.05) × 10−2 |
0.3934 ± 0.0001 |
0.893 ± 0.001 |
(1.46 ± 0.01) × 10−2 |
1.384 ± 0.001 |
(7.5 ± 0.1) × 10−3 |
(1.81 ± 0.3) × 10−10 |
For the ligand exchange reaction
| | |
Citr3− + CaLact+ ⇌ CaCitr− + Lact−
| (13) |
the ligand equilibrium constant is defined as
| |
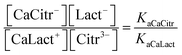 | (14) |
This equation together with three mass balance equations
| | |
[CaCitr−] + [CaLact+] = cCa2+ − [Ca2+]
| (15) |
| | |
[Lact−] = 2cCa2+ − [CaLact+]
| (16) |
| | |
[Citr3−] = cCitr3− − [CaCitr−]
| (17) |
and the equation for electroneutrality
| | |
[Na+] + [CaLact+] + 2[Ca2+] = [CaCitr−] + 3[Citr3−] + [Lact−]
| (18) |
contains five unknowns. The five unknowns, [Ca
2+], [CaLact
+], [CaCitr
−], [Lact
−], and [Citr
3−] were determined for each experiment from the five
eqn (14)–(18) by an iterative procedure starting with an initial estimate of [Ca
2+] similar to the calculations preformed for the calcium saccharate/gluconate equilibria.
21 The equilibrium concentrations for the supersaturated, homogeneous solutions not taking the precipitation equilibria into account, are presented in
Table 1. The ionic products,
Q, for each of the two salts
| | |
QCaLact = [Ca2+][Lact−]2
| (19) |
| | |
QCaCitr = [Ca2+]3[Citr3−]2
| (20) |
calculated for each solutions are included in
Table 1 together with ionic strength calculated from
| | |
I = 1/2(22[Ca2+] + [Na+] + [CaLact+] + [CaCitr−] + [Lact−] + 32[Citr3−])
| (21) |
Similar calculations were done for the supersaturated solutions emerging from continuing dissolution of calcium D-gluconate in already saturated aqueous solutions of calcium D-gluconate or by simultaneous dissolution of calcium D-gluconate and sodium citrate in water see Table 2, using KaCaGl = 14 ± 3 M−1 as determined in 1.0 M NaCl.20
Table 2 Supersaturated aqueous solutions of calcium citrate as formed at 25 °C by dissolution of calcium D-gluconate in an already saturated solution by addition of solid sodium citrate (sat/solid), or by simultaneous dissolution of solid calcium D-gluconate and solid sodium citrate in water (solid/solid)
| |
Total Ca2+ in supersat. solution/M |
Total gluconate/M |
Total citrate/M |
Calcium ion activity |
Free [Ca]2+/M |
[CaGl+]/M |
[CaCitr−]/M |
[Gl−]/M |
[Citr3−]/M |
I |
QCaGl = [Ca2+][Gl−]2 |
QCaCitr = [Ca2+]3[Citr−]2 |
| Sat/solid |
0.102 ± 0.001 |
0.223 |
0.442 |
(7.1 ± 0.2) × 10−5 |
(1.37 ± 0.01) × 10−4 |
(3.9 ± 0.1) × 10−4 |
0.102 ± 0.001 |
0.204 ± 0.001 |
0.340 ± 0.001 |
2.347 ± 0.002 |
(5.7 ± 0.1) × 10−6 |
(3.0 ± 0.1) × 10−13 |
| Sat/solid |
0.107 ± 0.001 |
0.223 |
0.204 |
(2.33 ± 0.02) × 10−4 |
(5.0 ± 0.1) × 10−4 |
(1.4 ± 0.1) × 10−3 |
0.105 ± 0.001 |
0.213 ± 0.003 |
(9.9 ± 0.1) × 10−2 |
0.912 ± 0.004 |
(2.3 ± 0.1) × 10−5 |
(1.2 ± 0.1) × 10−12 |
| Sat/solid |
0.144 ± 0.002 |
0.290 |
0.408 |
(1.12 ± 0.02) × 10−4 |
(2.5 ± 0.1) × 10−4 |
(9.8 ± 0.4) × 10−4 |
0.142 ± 0.002 |
0.286 ± 0.004 |
0.266 ± 0.004 |
2.02 ± 0.01 |
(2.0 ± 0.1) × 10−5 |
(1.07 ± 0.06) × 10−12 |
| Solid/solid |
0.140 ± 0.001 |
0.290 |
0.408 |
(1.030 ± 0.003) × 10−4 |
(2.4 ± 0.1) × 10−4 |
(9.23 ± 0.01) × 10−4 |
0.139 ± 0.001 |
0.279 ± 0.001 |
0.269 ± 0.001 |
2.03 ± 0.01 |
(1.85 ± 0.01) × 10−5 |
(9.77 ± 0.01) × 10−13 |
It should be evident from Table 1, by a comparison of the values of QCaCitr with the solubility product, KspCaCitr = (7 ± 2) × 10−14 M5, determined for unity ionic strength, that all solutions are strongly supersaturated in calcium citrate. The solutions are to a varying degree saturated with calcium L-lactate as seen by a comparison of QCaLact with KspCaLact = (5.8 ± 0.2) × 10−3 M3 valid for unity ionic strength.20
The robustness of supersaturated solutions of the calcium salts, important for biomineralization dynamics, was quantified by the length of the lag phase prior to initiation of precipitation. For the most robust solutions precipitation occurred within 24 or 48 hours, while for the less robust solutions, the precipitation occurred following 30 min of storage. All the supersaturated solutions showed precipitation after some time and in each case the precipitate isolated from the solution was identified as calcium citrate by infrared spectroscopy. The calcium content in solution was followed by EDTA titration and when constant, the iterative calculations were repeated for the equilibrium conditions with the adjusted calcium concentration and corrected citrate concentration. Citrate concentration, 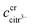 , was corrected for the part of the total citrate precipitated as calcium citrate
, was corrected for the part of the total citrate precipitated as calcium citrate
| |
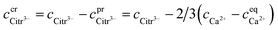 | (22) |
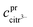
is precipitated citrate and
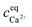
is total calcium in the equilibrated solution determined by EDTA titration. All equilibrium concentrations of the calcium
L-lactate sodium citrate solutions with precipitation of calcium citrate are shown in
Table 3, and for the calcium
D-gluconate sodium citrate solutions in
Table 4.
Table 3 Equilibrated aqueous solutions of calcium citrate as formed at 25 °C by dissolution of calcium L-lactate in an already saturated solution by addition of solid sodium citrate (sat/solid) or by simultaneous dissolution of solid calcium L-lactate and solid sodium citrate in water (solid/solid)
| |
Total Ca2+ in equilib./M |
Total lactate/M |
Total citrate/M |
Correc. citrate/M |
Calcium ion activity |
Free [Ca]2+/M |
[CaLact+]/M |
[CaCitr−]/M |
[Lact−]/M |
[Citr3−]/M |
I |
QCaLact = [Ca2+][Lact−]2 |
QCaCitr = [Ca2+]3[Citr3−]2 |
| Sat/solid |
(2.81 ± 0.01) × 10−2 |
0.778 |
0.442 |
0.217 ± 0.001 |
(1.27 ± 0.02) × 10−4 |
(6.8 ± 0.1) × 10−5 |
(3.0 ± 0.1) × 10−5 |
(2.80 ± 0.01) × 10−2 |
(5.62 ± 0.01) × 10−2 |
0.189 ± 0.001 |
1.56 ± 0.01 |
(2.14 ± 0.01) × 10−7 |
(1.1 ± 0.1) × 10−14 |
| Sat/solid |
0.121 ± 0.001 |
0.778 |
0.204 |
0.168 ± 0.002 |
(1.84 ± 0.02) × 10−3 |
(1.13 ± 0.03) × 10−3 |
(2.0 ± 0.1) × 10−3 |
0.118 ± 0.001 |
0.239 ± 0.002 |
(5.1 ± 0.1) × 10−2 |
0.715 ± 0.002 |
(6.4 ± 0.3) × 10−5 |
(3.6 ± 0.2) × 10−12 |
| Sat/solid |
(6.81 ± 0.04) × 10−2 |
1.038 |
0.408 |
0.123 ± 0.005 |
(5.3 ± 0.3) × 10−4 |
(5.6 ± 0.1) × 10−4 |
(5.9 ± 0.1) × 10−4 |
(6.70 ± 0.04) × 10−2 |
0.136 ± 0.001 |
(5.60 ± 0.04) × 10−2 |
0.967 ± 0.001 |
(1.02 ± 0.03) × 10−5 |
(5.4 ± 0.1) × 10−13 |
| Sat/solid |
(2.8 ± 0.4) × 10−2 |
1.038 |
0.816 |
0.523 ± 0.003 |
(2.6 ± 0.5) × 10−5 |
(2.6 ± 0.5) × 10−5 |
(1.1 ± 0.4) × 10−5 |
(2.8 ± 0.5) × 10−2 |
(6 ± 1) × 10−2 |
0.495 ± 0.005 |
3.49 ± 0.02 |
(8 ± 5) × 10−8 |
(4 ± 2) × 10−15 |
| Solid/solid |
(6.87 ± 0.04) × 10−2 |
1.038 |
0.408 |
0.127 ± 0.001 |
(5.4 ± 0.1) × 10−4 |
(5.3 ± 0.1) × 10−4 |
(5.7 ± 0.1) × 10−4 |
(6.76 ± 0.04) × 10−2 |
0.137 ± 0.001 |
(5.94 ± 0.04) × 10−2 |
0.983 ± 0.001 |
(9.9 ± 0.3) × 10−6 |
(5.2 ± 0.1) × 10−13 |
Table 4 Equilibrated aqueous solutions of calcium citrate as formed at 25 °C by dissolution of calcium D-gluconate in an already saturated solution by addition of solid sodium citrate (sat/solid) or by simultaneous dissolution of solid calcium D-gluconate and sodium citrate in water (solid/solid)
| |
Total Ca2+ in equilib./M |
Total gluconate/M |
Total citrate/M |
Correc. citrate/M |
Calcium ion activity |
Free [Ca]2+/M |
[CaGl+]/M |
[CaCitr−]/M |
[Gl−]/M |
[Citr3−]/M |
I |
QCaGl = [Ca2+][Gl−]2 |
QCaCitr = [Ca2+]3[Citr3−]2 |
| Sat/solid |
(4.68 ± 0.01) × 10−2 |
0.223 |
0.442 |
0.405 ± 0.001 |
(2.43 ± 0.03) × 10−5 |
(6.0 ± 0.1) × 10−5 |
(7.8 ± 0.4) × 10−5 |
(4.7 ± 0.1) × 10−2 |
(9.4 ± 0.2) × 10−2 |
0.358 ± 0.001 |
2.346 ± 0.003 |
(5.2 ± 0.4) × 10−7 |
(2.7 ± 0.2) × 10−14 |
| Sat/solid |
(4.7 ± 0.2) × 10−2 |
0.223 |
0.204 |
0.164 ± 0.001 |
(8.303 ± 0.001) × 10−5 |
(1.8 ± 0.1) × 10−4 |
(2.4 ± 0.2) × 10−4 |
(4.7 ± 0.2) × 10−2 |
(9.4 ± 0.4) × 10−2 |
0.117 ± 0.002 |
0.904 ± 0.005 |
(1.6 ± 0.2) × 10−6 |
(9 ± 1) × 10−14 |
| Sat/solid |
(5.67 ± 0.04) × 10−2 |
0.290 |
0.408 |
0.350 ± 0.001 |
(3.38 ± 0.03) × 10−5 |
(8.8 ± 0.1) × 10−5 |
(1.40 ± 0.02) × 10−4 |
(5.65 ± 0.04) × 10−2 |
0.113 ± 0.001 |
0.2935 ± 0.0004 |
2.018 ± 0.001 |
(1.13 ± 0.03) × 10−6 |
(5.9 ± 0.1) × 10−14 |
| Solid/solid |
(5.27 ± 0.04) × 10−2 |
0.290 |
0.408 |
0.3498 ± 0.0003 |
(2.9 ± 0.1) × 10−5 |
(8.1 ± 0.1) × 10−5 |
(1.19 ± 0.02) × 10−4 |
(5.25 ± 0.04) × 10−2 |
0.105 ± 0.001 |
0.2973 ± 0.0004 |
2.029 ± 0.001 |
(9.0 ± 0.2) × 10−7 |
(4.7 ± 0.1) × 10−14 |
The supersaturation of the calcium L-lactate sodium citrate solutions was confirmed in all cases since precipitation of calcium citrate was found to be initiated in a few hours. The ionic product QCaCitr as defined in eqn (20) should accordingly be compared with the solubility product, which is not known for the actual high ionic strengths conditions. The value Ksp = 7 × 10−14 M5 for calcium citrate determined for unity ionic strength at 25 °C in the present study will probably be higher than the solubility product valid in these solutions with insignificant water for hydration of ions. A similar conclusion is reached for the equilibrium calcium D-gluconate sodium citrate solution. For both calcium L-lactate and calcium D-gluconate solutions supersaturated through dissolution of sodium citrate, precipitation of calcium citrate will lower the ionic product QCaCitr, which for both the L-lactate and D-gluconate solution becomes comparable with the solubility product for calcium citrates as may be seen from Tables 3 and 4, respectively. It should also be noted, that the ionic product of calcium L-lactate is less than the solubility product, which is ∼1 × 10−3 M−3 for the equilibrated solutions, see Table 3. From Table 4 it may further be seen, that the ionic product also is lower than the solubility product for calcium D-gluconate, which is 5 × 10−5 M−3. The solutions with calcium citrate precipitation are accordingly not supersaturated with calcium L-lactate or with calcium D-gluconate. Presence of other hydrates or polymorph forms prior to equilibrium could also be established.22 However, for calcium citrate, the other hydrate of relevance is calcium citrate hexahydrate, which has a lower not higher solubility.9
For a saturated solution of calcium citrate in water, addition of sodium citrate results in a continuing dissolution of calcium citrate. This somewhat surprising observation is, however, in agreement with previous findings9 and is in parallel to the observations for calcium L-lactate and calcium D-gluconate. The stoichiometry of citrate assisted dissolution
| | |
Ca3Citr2(s) → 2CaCitr− + Ca2+
| (23) |
| | |
Ca2+ + Citr3− ⇌ CaCitr−
| (24) |
| | |
Ca3Citr2(s) + Citr3− ⇌ 3CaCitr−
| (25) |
helps to identify the critical step for the supersaturation. The free calcium ion concentration needs now to be calculated according to the equilibrium
| |
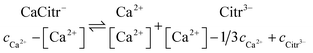 | (26) |
where again
cCitr3− is added sodium citrate concentration. For the equilibrium constant
| |
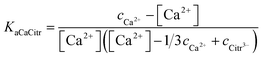 | (27) |
with
cCa2+ as the total calcium ion concentration, the free calcium [Ca
2+] ion concentration was calculated from the resulting quadratic equation
| | |
Ka[Ca2+]2 + [Ca2+](1 − 1/3cCa2+Ka + KacCitr3−) − cCa2+ = 0
| (28) |
From the mass balance equations
| | |
[CaCitr−] = cCa2+ − [Ca2+]
| (29) |
| | |
[Citr3−] = cCitr3− − [CaCitr−] = 2/3cCa2+ + cCitr3− − [CaCitr−]
| (30) |
the two other equilibrium concentrations, [CaCitr
−], and [Citr
3−], were now calculated from
eqn (29) and
(30), followed by calculation of the ionic product
QCaCitr from
eqn (20). The calculations were identical for the supersaturated solutions and the equilibrated solutions with reprecipitated calcium citrate except for the corrected total calcium concentration determined by titration. The ionic product is clearly larger than the solubility product showing that the homogeneous solutions formed after addition of sodium citrate is becoming supersaturated with respect to calcium citrate. After reprecipitation, the ionic product is comparable to the solubility product previously determined, see
Table 5, and the solution accordingly saturated.
Table 5 Supersaturated aqueous solutions of calcium citrate at 25 °C as formed by dissolution of calcium citrate in an already saturated solution of calcium citrate by addition of solid sodium citrate, and equilibrated solutions after subsequent precipitation of calcium citrate
| |
Total Ca2+ in solution/M |
Total citrate/M |
Citrate added/M |
Calcium ion activity |
[Ca2+]/M |
[CaCit−]/M |
[Citr3−]/M |
I |
Q = [Ca2+]3[Citr3−]2 |
| Calcium citrate supersaturated |
0.086 ± 0.001 |
0.8730 ± 0.0005 |
0.816 |
(2.15 ± 0.02) × 10−5 |
(4.96 ± 0.04) × 10−5 |
(8.5 ± 0.1) × 10−2 |
0.7875 ± 0.0002 |
4.811 ± 0.001 |
(7.5 ± 0.2) × 10−14 |
| Calcium citrate equilibrium |
0.052 ± 0.001 |
0.828 ± 0.001 |
0.816 |
(1.08 ± 0.02) × 10−5 |
(3.0 ± 0.1) × 10−5 |
(5.1 ± 0.1) × 10−2 |
0.7762 ± 0.0001 |
4.743 ± 0.001 |
(1.7 ± 0.1) × 10−14 |
Citrate has been found to dissolve excess of the calcium L-lactate, calcium D-gluconate, and calcium citrate in already saturated solutions of these calcium hydroxycarboxylates forming strongly supersaturated solutions in calcium citrate. From the supersaturated solutions, calcium citrate precipitates reaching solubility equilibrium, see Fig. 1. The precipitation results in an over-all increase in water activity, see Fig. 2. The increase in water activity may be explained simply by the less dissolved ion concentration for water binding. The calcium citrate supersaturation depends on two factors: (i) the relative strength of complex binding between citrate as ligand assisting the dissolution and the other hydroxycarboxylate ligand, and (ii) the initiation of precipitation of calcium citrate. This balance was investigated by a determination of the minimum amount of sodium citrate required for dissolution of a fixed amount of calcium L-lactate or calcium D-gluconate. Under specified conditions described in Experimental section, the degree of supersaturation for increasing added sodium citrate may be seen in Fig. 3. As may be seen from this figure, the supersaturation is rather significant especially for calcium L-lactate. For calcium D-gluconate the supersaturation was found less dependent on excess citrate due to the smaller difference between the association constant for binding of calcium to gluconate relative to binding to citrate compared to the difference between the association constant for binding of calcium to lactate relative to binding to citrate. For calcium citrate this thermodynamic factor almost vanishes, and the supersaturation depends on kinetics as from the smaller degree of supersaturation.
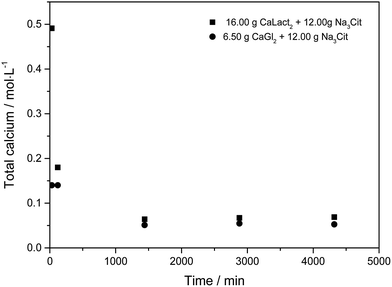 |
| | Fig. 1 Calcium concentration in 100 mL of water during dissolution of 16.00 g of solid calcium L-lactate mixed with 12.00 g of sodium citrate, and of 6.50 g of calcium D-gluconate mixed with 12.00 g of sodium citrate under constant stirring at 25 °C, followed by precipitation of calcium citrate. | |
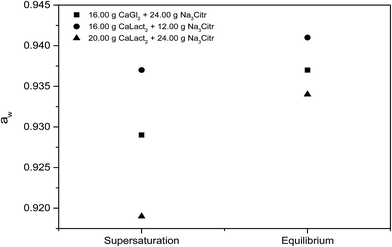 |
| | Fig. 2 Water activity, aw of supersaturated and equilibrated solutions of calcium citrate at 25 °C made by dissolution of calcium L-lactate and sodium citrate or by dissolution of calcium D-gluconate and sodium citrate in 100 mL of water. | |
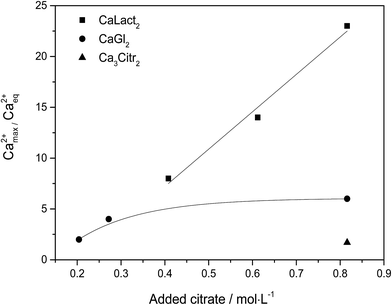 |
| | Fig. 3 Calcium citrate supersaturation expressed as a degree of supersaturation Ca2+max/Ca2+eq after adding solid sodium citrate to calcium L-lactate, calcium D-gluconate, or to calcium citrate. | |
The lag phase for initiation of precipitation was studied by visual inspection for calcium L-lactate, for which the largest supersaturation was detected, see Fig. 3. The length of the lag phase seems to decrease exponentially with an increasing degree of supersaturation, see Fig. 4. For extrapolation to infinity supersaturation the length of the lag phase gets close to zero with an extrapolated value of 0.4 ± 0.1 hours, as would be expected. Similarly an extrapolation to little or no supersaturation yield a very long lag phase tending to approach infinity as also is to be expected. For calcium D-gluconate sodium citrate solutions, the length of the lag phase was larger and apparently less dependent on the degree of supersaturation. This observation, which could indicate formation of mixed D-gluconate/citrate complexes of calcium could be important for formulation of supplements with high bioavailability and will later be studied in more details.
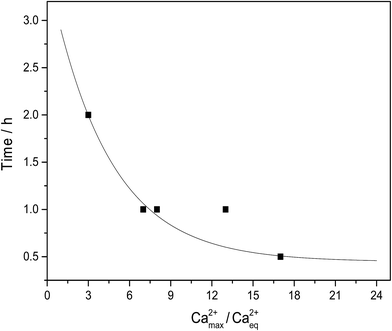 |
| | Fig. 4 Lag phase for initiation of precipitation of calcium citrate in supersaturated solutions made by dissolution of calcium L-lactate by sodium citrate in water at 25 °C. Ca2+max/Ca2+eq is the degree of supersaturation determined by titration of Ca2+ in maximal supersaturated solution. Curve is based on fitting to an exponential equation to yield: time = 3.09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ca2+max/Ca2+eq/4.33) + 0.44 (all points except point for supersaturation degree of 12). exp(−Ca2+max/Ca2+eq/4.33) + 0.44 (all points except point for supersaturation degree of 12). | |
The maximal supersaturation of calcium citrate found for dissolution of calcium L-lactate by citrate depends linearly on the concentration of sodium citrate used for the dissolution, see Fig. 3. Dissolution of calcium L-lactate by citrate is suggested to depend on a mechanism entailing binding of citrate to the surface of solid calcium L-lactate and accordingly to appear as a zero-order reaction with a constant rate depending on the excess concentration of sodium citrate used
| | |
CaLact2(s) + Citr3− → CaCitr− + 2Lact−
| (31) |
The total calcium concentration, cCa2+, accordingly increases linearly from the initial calcium concentration, 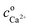 , with time as
, with time as
| |
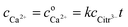 | (32) |
where
k is an unknown constant depending on surface properties of the calcium salt and
t is a time of dissolution. The length of the lag phase for initiation of precipitation of calcium citrate decreases exponentially with increasing total calcium dissolved, see
Fig. 4. The initiation of precipitation will limit the degree of supersaturation. The information from
Fig. 3 combined with the information from
Fig. 4 in a more qualitative way yields the over-all picture as shown in
Fig. 5. In this figure the linear increase of calcium in citrate assisted dissolution above the initial solubility of calcium lactate,
, is depicted for three citrate concentrations. The time for initiation of precipitation increasing with decreasing calcium concentration intersect with the dissolution curves defining the maximal supersaturation possible for this specific citrate concentration. To a fair approximation, this supersaturation depends linearly on the citrate concentration as confirmed by the experimental data shown in
Fig. 3 for calcium
L-lactate. The situation for calcium
D-gluconate is different as the lag time for initiation of precipitation is longer and the supersaturation seems to be less dependent on the added citrate concentration, see
Fig. 3.
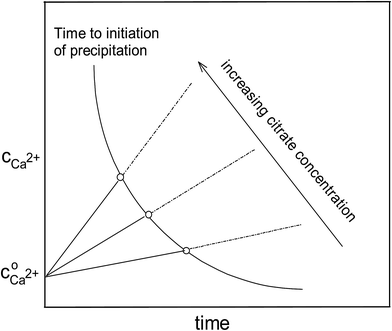 |
| | Fig. 5 Increasing calcium concentration during dissolution of calcium L-lactate in aqueous solution of sodium citrate with three different concentrations. The intersection with the time curve for initiation of precipitation as dependent on calcium concentration indicates the maximal supersaturation for each concentration of citrate. | |
Conclusions
Citrate has been shown to assist dissolution of calcium hydroxycarboxylates forming supersaturated solution of calcium citrate. This effect is most remarkable for dissolution of calcium citrate and helps to explain the high bioavailability of calcium from this sparingly soluble calcium salt. The effect is, however, more dramatic for dissolution of calcium L-lactate and calcium D-gluconate for which very high degrees of robust supersaturation were demonstrated. The robustness of the supersaturated solutions seems to depend on a slow precipitation of calcium citrate. The presence of citrate in calcified tissue has now been recognized.7,8 The demonstration of the assistance of citrate in spontaneous supersaturation phenomena occurring by isothermal dissolution against a concentration gradient explains important part of biomineralization dynamics. This perspective of spontaneous supersaturation needs also to be studied for higher temperatures as they are relevant for physiological conditions in the human body. The temperature dependence for these phenomena should also be extended to the elevated temperatures as are used during dairy processing. Other factors could also be considered and further investigated such as pH as they could affect solubility of calcium salts.22 The recognition of this unique role of citrate also opens up for novel design of better calcium supplements and foods for special needs for individuals with low calcium uptake, like elderly with high risk of developing osteoporosis.
Acknowledgements
Danish Dairy Research Foundation and Arla Foods Ingredients are thanked for supporting the project “Calcium during whey processing. Technology and Products”. This study was also financially supported by grant from Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) to ACG (process number 12963/13-5 CAPES/Science Without Borders).
References
- C. Y. C. Pak, J. A. Harvey and M. C. Hsu, Enhanced Calcium Bioavailability from A Solubilized Form of Calcium Citrate, J. Clin. Endocrinol. Metab., 1987, 65(4), 801–805 CrossRef CAS PubMed.
- P. Tondapu, D. Provost, B. Adams-Huet, T. Sims, C. Chang and K. Sakhaee, Comparison of the Absorption of Calcium Carbonate and Calcium Citrate after Roux-en-Y Gastric Bypass, Obes. Surg., 2009, 19(9), 1256–1261 CrossRef CAS PubMed.
- J. M. Hess, S. S. Jonnalagadda and J. L. Slavin, Dairy Foods: Current Evidence of their Effects on Bone, Cardiometabolic, Cognitive, and Digestive Health, Compr. Rev. Food Sci. Food Saf., 2016, 15, 251–268 CrossRef.
- L. M. Wang, W. Wang, X. C. Li, L. Peng, Z. Q. Lin and H. Z. Xv, Calcium citrate: a new biomaterial that can enhance bone formation in situ, Chin. J. Traumatol., 2012, 15(5), 291–296 CAS.
- L. C. Costello, R. B. Franklin, M. A. Reynolds and M. Chellaiah, The Important Role of Osteoblasts and Citrate Production in Bone Formation: ‘Osteoblast Citration’ as a New Concept for an Old Relationship, Open Bone J., 2013, 4, 1–17 Search PubMed.
- M. Iafisco, G. B. Ramirez-Rodriguez, Y. Sakhno, A. Tampieri, G. Martra, J. Gomez-Morales and J. M. Delgado-Lopez, The growth mechanism of apatite nanocrystals assisted by citrate: relevance to bone biomineralization, CrystEngComm, 2015, 17(3), 507–511 RSC.
- Y. Y. Hu, A. Rawal and K. Schmidt-Rohr, Strongly bound citrate stabilizes the apatite nanocrystals in bone, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(52), 22425–22429 CrossRef CAS PubMed.
- D. G. Reid, M. J. Duer, G. E. Jackson, R. C. Murray, A. L. Rodgers and C. M. Shanahan, Citrate Occurs Widely in Healthy and Pathological Apatitic Biomineral: Mineralized Articular Cartilage, and Intimal Atherosclerotic Plaque and Apatitic Kidney Stones, Calcif. Tissue Int., 2013, 93(3), 253–260 CrossRef CAS PubMed.
- M. Vavrusova and L. H. Skibsted, Aqueous solubility of calcium citrate and interconversion between the tetrahydrate and the hexahydrate as a balance between endothermic dissolution and exothermic complex formation, Int. Dairy J., 2016, 57, 20–28 CrossRef CAS.
- M. Vavrusova and L. H. Skibsted, Spontaneous supersaturation of calcium D-gluconate during isothermal dissolution of calcium L-lactate in aqueous sodium D-gluconate, Food Funct., 2014, 5(1), 85–91 CAS.
- A. L. Márquez, G. N. Salvatore, R. G. Otero, J. R. Wagner and G. G. Palazolo, Impact of freeze–thaw treatment on the stability of calcium-fortified soy beverages, LWT–Food Sci. Technol., 2015, 62(1), 474–481 CrossRef.
- A. Irshad, B. D. Sharma, S. R. Ahmed, S. Talukder, O. P. Malav and A. Kumar, Effect of incorporation of calcium lactate on physico-chemical, textural, and sensory properties of restructured buffalo meat loaves, Vet. World, 2016, 9(2), 151–159 CrossRef CAS PubMed.
- K. Sakhaee and C. Pak, Superior calcium bioavailability of effervescent potassium calcium citrate over tablet formulation of calcium citrate after Roux-en-Upsilon gastric bypass, Surg. Obes. Relat. Dis., 2013, 9(5), 743–748 CrossRef PubMed.
- C. Holt, S. Lenton, T. Nylander, E. S. Sorensen and S. C. Teixeira, Mineralisation of soft and hard tissues and the stability of biofluids, J. Struct. Biol., 2014, 185(3), 383–396 CrossRef CAS PubMed.
- M. Vavrusova, R. Liang and L. H. Skibsted, Thermodynamics of Dissolution of Calcium Hydroxycarboxylates in Water, J. Agric. Food Chem., 2014, 62(24), 5675–5681 CrossRef CAS PubMed.
- C. W. Davies, Ion Association, Butterworth & Co, Ltd, London, UK, 1962 Search PubMed.
- K. P. Chatterjee and N. R. Dhar, Studies of sparingly soluble salts, readily obtained from hot solutions of reacting substances I, J. Phys. Chem., 1924, 28, 1009–1028 CrossRef CAS.
- R. H. Stokes and R. A. Robinson, Ionic Hydration and Activity in Electrolyte Solutions, J. Am. Chem. Soc., 1948, 70(5), 1870–1878 CrossRef CAS PubMed.
- R. G. Bates, B. R. Staples and R. A. Robinson, Ionic Hydration and Single Ion Activities in Unassociated Chlorides at High Ionic Strengths, Anal. Chem., 1970, 42(8), 867–871 CrossRef CAS.
- M. Vavrusova, M. B. Munk and L. H. Skibsted, Aqueous Solubility of Calcium L-Lactate, Calcium D-Gluconate, and Calcium D-Lactobionate: Importance of Complex Formation for Solubility Increase by Hydroxycarboxylate Mixtures, J. Agric. Food Chem., 2013, 61(34), 8207–8214 CrossRef CAS PubMed.
- A. C. Garcia, M. Vavrusova and L. H. Skibsted, Calcium D-Saccharate: Aqueous Solubility, Complex Formation, and Stabilization of Supersaturation, J. Agric. Food Chem., 2016, 64(11), 2352–2360 CrossRef CAS PubMed.
- S. L. Goss, K. A. Lemons, J. E. Kerstetter and R. H. Bogner, Determination of calcium salt solubility with changes in pH and P-CO2, simulating varying gastrointestinal environments, J. Pharm. Pharmacol., 2007, 59(11), 1485–1492 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a
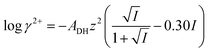
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aCa2+ of the calibration solutions according to the Nernst equation at 25 °C.
aCa2+ of the calibration solutions according to the Nernst equation at 25 °C.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex between calcium and lactate. The addition of sodium citrate will lower the concentration of calcium ions due to a stronger complex formation by citrate:
1 complex between calcium and lactate. The addition of sodium citrate will lower the concentration of calcium ions due to a stronger complex formation by citrate:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. Notably, the dissolution of excess calcium L-lactate in saturated aqueous solution by an increasing concentration of citrate from dissolving sodium citrate will result in supersaturation with respect to calcium citrate either as the hexahydrate or tetrahydrate depending on temperature:9,17
1 complex. Notably, the dissolution of excess calcium L-lactate in saturated aqueous solution by an increasing concentration of citrate from dissolving sodium citrate will result in supersaturation with respect to calcium citrate either as the hexahydrate or tetrahydrate depending on temperature:9,17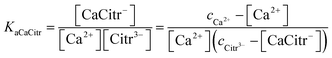

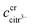 , was corrected for the part of the total citrate precipitated as calcium citrate
, was corrected for the part of the total citrate precipitated as calcium citrate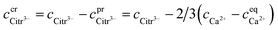
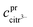 is precipitated citrate and
is precipitated citrate and 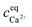 is total calcium in the equilibrated solution determined by EDTA titration. All equilibrium concentrations of the calcium L-lactate sodium citrate solutions with precipitation of calcium citrate are shown in Table 3, and for the calcium D-gluconate sodium citrate solutions in Table 4.
is total calcium in the equilibrated solution determined by EDTA titration. All equilibrium concentrations of the calcium L-lactate sodium citrate solutions with precipitation of calcium citrate are shown in Table 3, and for the calcium D-gluconate sodium citrate solutions in Table 4.
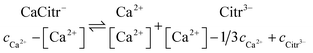
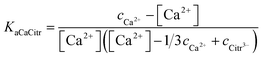

 , with time as
, with time as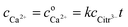
 , is depicted for three citrate concentrations. The time for initiation of precipitation increasing with decreasing calcium concentration intersect with the dissolution curves defining the maximal supersaturation possible for this specific citrate concentration. To a fair approximation, this supersaturation depends linearly on the citrate concentration as confirmed by the experimental data shown in Fig. 3 for calcium L-lactate. The situation for calcium D-gluconate is different as the lag time for initiation of precipitation is longer and the supersaturation seems to be less dependent on the added citrate concentration, see Fig. 3.
, is depicted for three citrate concentrations. The time for initiation of precipitation increasing with decreasing calcium concentration intersect with the dissolution curves defining the maximal supersaturation possible for this specific citrate concentration. To a fair approximation, this supersaturation depends linearly on the citrate concentration as confirmed by the experimental data shown in Fig. 3 for calcium L-lactate. The situation for calcium D-gluconate is different as the lag time for initiation of precipitation is longer and the supersaturation seems to be less dependent on the added citrate concentration, see Fig. 3.




