Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Separation of cyanide from an aqueous solution using armchair silicon carbide nanotubes: insights from molecular dynamics simulations
Alireza Khataee *,
Golchehreh Bayat and
Jafar Azamat
*,
Golchehreh Bayat and
Jafar Azamat
Research Laboratory of Advanced Water and Wastewater Treatment Processes, Department of Applied Chemistry, Faculty of Chemistry, University of Tabriz, 51666-16471 Tabriz, Iran. E-mail: a_khataee@tabrizu.ac.ir; ar_khataee@yahoo.com; Fax: +98 4133340191; Tel: +98 4133393165
First published on 23rd January 2017
Abstract
Separation of cyanide, as a model contaminant, from aqueous solution was investigated using molecular dynamics simulations. In this research, cyanide separation was investigated using armchair silicon carbide (SiC) nanotubes of four different diameters at different applied pressures. The systems included (5,5), (6,6), (7,7) and (8,8) SiC nanotubes placed between two graphene sheets, and an external pressure was applied to the system. The ion permeability, the radial distribution function of nanotube–water and ion–water, the retention time of the cyanide ions, the density of water and water flux and the hydrogen bonding between inner water molecules were investigated. The results showed that all four studied nanotubes accepted water molecules into their interiors, and the (5,5) SiC nanotube could provide high rejection (100%) of cyanide ions.
1. Introduction
Cyanide is a damaging and poisonous pollutant, which threatens the environment and human health. Cyanide is widely used in diverse industries including electroplating, mining, photoprocessing, fertilizer production, gas production, pharmaceuticals and plating.1 The existence of cyanides in wastewater poses a high risk and hence, it should be removed from wastewaters before release.2 Cyanides cause extensive fish death and affect the microscopic and invertebrate organisms in water. It is also toxic and damaging for human health, causes neurological effects (quick breathing, tremors), weight loss, nerve injury and disease. Skin contact with cyanides may produce irritation and sores.3–5There are different ways of treating cyanide-containing wastewaters, including chemical oxidation, physical methods and biological processes.6–10 For example, Simsek et al. conducted column and batch studies with a Purolite resin in order to remove cyanide ions from aqueous solutions.1 Moreover, Hijosa-Valsero et al. tested plasma discharge technology for cyanide removal from water with an initial concentration of 1 mg L−1.11 They proposed a coaxial DBD plasma reactor only for the treatment of dilute solutions such as drinking water. In another study, Sarla and coworkers studied the oxidation process of cyanide in aqueous solutions with H2O2 as the oxidant and Cu2+ as the catalyst. They found that chemical oxidation by H2O2 is slow, whereas by UV/H2O2 it is much faster, and in both cases, Cu2+ accelerated the oxidation process, acting as a catalyst.12 In a similar study, the oxidation process of free cyanide with H2O2 catalyzed by activated alumina was studied by Chergui et al. They claimed that their proposed method had advantages over the method based on copper catalyst.13
Akcil et al. investigated the biological degradation of cyanide by specific bacteria. These bacteria could efficiently degrade cyanide into less toxic compounds, namely ammonia and carbonate.14 In addition, various biodegradation methods for cyanide removal were introduced in a review by Ibrahim et al.15
Some of these methods are not economical or environmentally friendly because of the application of dangerous chemical reagents. Moreover, they produce poisonous residues and cannot completely reduce all cyanide complexes.1,16
In this regard, for water purification and to meet qualification requirements, nanotechnology has emerged as a novel and powerful tool.17,18 Nanotubes are an excellent and appropriate choice as ion selective materials.19–21 Although carbon nanotubes have received more attention,22,23 other materials, such as boron nitride (BN)24–26 and silicon carbide (SiC),27 can also be used to fabricate nanotubes. SiC nanotubes were first synthesized in 2001.28 They exhibit better reactivity than carbon nanotubes due to their polar nature.29 For example, theoretical studies have shown that SiC nanotubes are an excellent material for hydrogen storage.30 According to these studies, SiC nanotubes exhibit a H2 binding energy that is 20% greater than that of carbon nanotubes. In another study, the capability of SiC nanotubes as a sensor for formaldehyde detection was demonstrated. CH2O molecules were chemisorbed to SiC nanotubes with a more noticeable adsorption energy, relative to that of carbon nanotubes. Zhao et al. studied the catalytic behavior of SiC nanotubes. Their theoretical calculations showed that SiC nanotubes can efficiently break the N–H bond of ammonia and the O–H bond of H–OX (X = H, CH3, and C2H5).31 Moreover, some researchers have shown the ion selectivity of SiC nanotubes.21,32 In our previous study, separation of nitrate ions was studied using armchair SiC nanotubes. We found that (8,8) SiC nanotubes can remove nitrate ions from aqueous solutions.32 In a similar study, Hilder and coworkers demonstrated the ion-selectivity of (6,6) and (7,7) SiC nanotubes. They found that no sodium ions were able to pass through the nanotubes, whereas chloride ions were able to pass.21
Fluid-particle dynamics simulations consist of computational methods for macroscale (smoothed particle hydrodynamics (SPH)),33 mesoscale (dissipative particle dynamics (DPD)),34 and microscale (molecular dynamics (MD)) systems.32 In the field of computational chemistry, MD simulation is an invaluable method for studying the atom flow through nanopores.35,36 The atom resolution can be simulated accurately via MD, and therefore it is possible to investigate the transport characteristics because of the tunable long timescale of MD, which allows researchers to collect adequate statistics. Moreover, numerous permeation events for single ions and water molecules through nanopores can be studied via MD.37 Thus, in this study, the passage of cyanide ions through SiC nanotubes under pressure was studied via MD simulations.
2. Simulation details
Four types of armchair SiC nanotubes, including (5,5), (6,6), (7,7) and (8,8) nanotubes with a length of 20 Å were selected. The system domain contained an armchair SiC nanotube placed between two graphene sheets, potassium and cyanide ions, and water molecules. The concentration of dissolved potassium and cyanide ions was 0.3 M. The dimensions of the simulation box were (x × y × z) 30 × 30 × 80 Å3. The periodic boundary conditions were used in all three directions. The short-range Lennard–Jones interaction parameters are summarized in Table 1. Long-range electrostatic interactions were calculated using the PME (Particle Mesh Ewald)38 method with a 12 Å cut-off for van der Waals interactions. The optimized geometries of these nanotubes were obtained at the B3LYP level of theory with the 6-31G** basis set using the GAMESS program.39 The value of 1.8 Å was obtained for the optimized Si–C bond length. This amount of bond length was used in other researchers, too.40,41 For water molecules, the TIP3P water model42 was used to exactly reproduce the entropic and hydrogen bonding behavior of water.NAMD 2.10 (ref. 43) was used for performing MD simulations, similar to previous study,44–47 and visualized via VMD1.9.2.48 The van der Waals interaction energies (ELJ) are defined by eqn (1) as follows:49
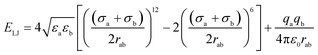 | (1) |
The simulation box was exposed to zero-temperature energy minimization for 40 ps, then equilibrated at 298 K for 10 ps and finally, MD simulation was performed for 5 ns. The temperature was fixed at 298 K using the Langevin dynamics method. External constant forces perpendicular to the cross-section of the nanotube were applied to the water molecules in a selected area of the system (within a distance of 9 Å to the left or right boundary of the system).
The applied forces generate a pressure difference through the SiC nanotubes that forces the fluid to flow, which is known as pressure-driven flow.52,53 The applied force was defined as F = ΔPA/n, where F is the force exerted to the chosen section of the box (in pN), ΔP is the pressure difference (in Pa), A is the cross sectional area of the system (in m2), and n is the number of water molecules in the selected region (see Fig. 1). Pressure ranged from 10 to 200 MPa and was applied to nearly 542 water molecules.
3. Results and discussion
In this study, single-walled (5,5), (6,6), (7,7) and (8,8) SiC nanotubes with a length of 20 Å, fixed between two graphene sheets were studied for the separation of cyanide ions from a potassium cyanide (KCN) aqueous solution. In order to study the ion selectivity of this system, the following properties were evaluated: arrangement of the inner water molecules, number of hydrogen bonds between water molecules, ion retention time, density of the inner water, water flux, and radial distribution functions (RDF) of the water–nanotube and water–ion.3.1. Water conduction
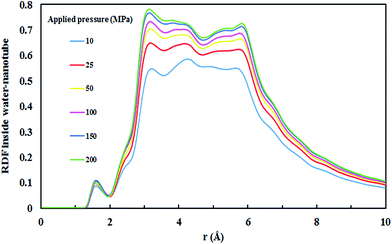
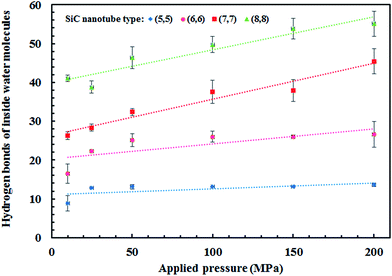
All four SiC nanotubes accepted water molecules into their interior. The arrangement of the water molecules inside the nanotubes changed on increasing the nanotube diameter. The arrangement of the water molecules, illustrated in Fig. 2, was verified by the RDF between inner water molecules and the nanotube (see Fig. 3). It was found that for the (5,5) SiC nanotube, at low pressure (10 MPa), inner water molecules formed a two-chain structure. This structure was similar to that formed inside the (6,6) SiC nanotube, and changed to a cylindrical arrangement at higher pressures. In the (7,7) SiC nanotube, inner water molecules were arranged into the form of a cylinder, with a single-file structure inside it. Finally, inside the (8,8) SiC nanotube, water molecules were arranged forming an structure with two concentric cylinders. RDFs between inner water molecules and the nanotube confirmed the arrangements of the water molecules. Likewise, Fig. 4 displays the RDF between the inner water molecules and the (5,5) SiC nanotube at the different studied pressures. In this figure, the differences in the water molecule arrangements between low and high pressure were evident.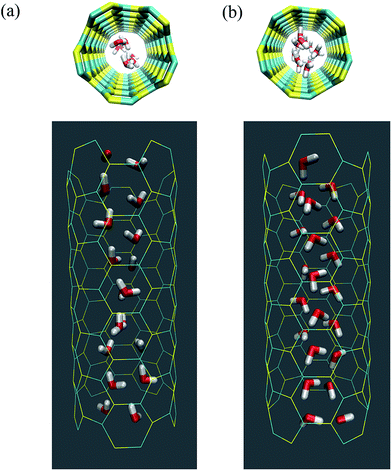 | ||
| Fig. 2 Arrangement of the water molecules inside a (5,5) SiC nanotube under different pressures, namely (a) at 10 MPa and (b) 25 MPa. | ||
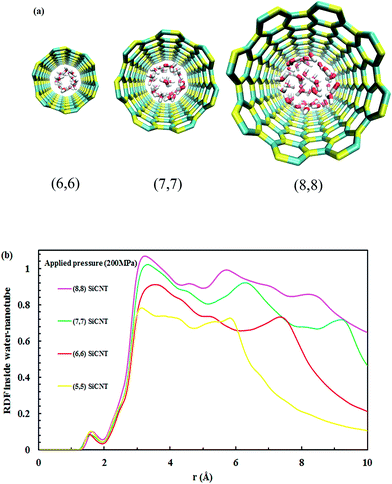 | ||
| Fig. 3 (a) Water arrangement inside SiC nanotubes of different diameter and (b) RDF of inner water molecules–SiC nanotubes at 200 MPa. | ||
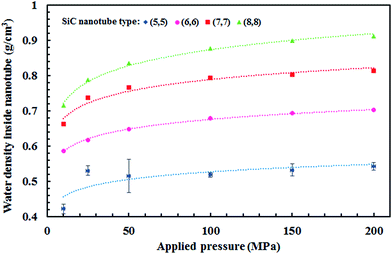
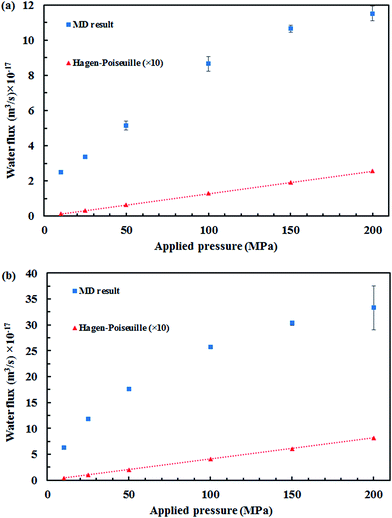
Fig. 5 displays the density of the inner water molecules in the four types of SiC nanotubes at the applied pressures during the 5 ns MD simulations. As it can be seen, the water density increased upon increasing the applied pressure because of the high transport of water molecules at high pressures. Water density also increased as the nanotube diameter became larger. The effect of nanotubes diameter on water density was stronger than that of applied pressure. Fig. 6 shows the water flux values through (6,6) and (8,8) SiC nanotubes for the different applied pressures. These values were obtained using MD simulations and the Hagen–Poiseuille (HP) equation as described below:54
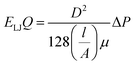 | (2) |
The water network structure inside the nanotubes led to the formation of hydrogen bonds. The number of water molecules that entered the nanotube was directly proportional to the applied pressure, i.e., the number of water molecules was higher at higher pressures. Thus, the number of hydrogen bonds also increased, as can be observed in Fig. 7.
3.2. Ion transportation
The number of cyanide ions that passed through the SiC nanotubes of various diameters under the applied pressure was counted during the simulation time to investigate the cyanide rejection ability. Indeed, for the passage of ions through the nanotube, ion size should be smaller than the diameter of the nanotube. Therefore, the water molecules that form the hydration shell of the cyanide ion should be removed. This dehydration requires a large amount of energy that is known as the energy barrier. The applied pressure to the system provided the required energy to overcome this barrier. Fig. 8 shows the effect of SiC nanotube diameter and applied pressure on cyanide ion rejection. As can be seen, rejection ability decreased when both the SiC nanotube diameter and applied pressure increased. The ion rejection rate decreased when increasing the pressure mainly because the large force applied on the ions helped to overcome the energy barrier. On the other hand, rejection rate was greater than 78% in the (5,5) SiC nanotube (100% at 10 MPa). This is due to the limited diameter of the (5,5) SiC, which causes a high energy barrier for cyanide permeation at low pressure. Indeed, at low pressure, the applied force is not enough to separate water molecules from the ion hydration shell. SiC nanotubes with larger diameters allowed ions to pass through them more easily; subsequently, they had a lower rejection rate, with the rejection rate for the (8,8) SiC nanotube being 0%. This was because the energy barrier for ions to enter larger nanotubes was lower.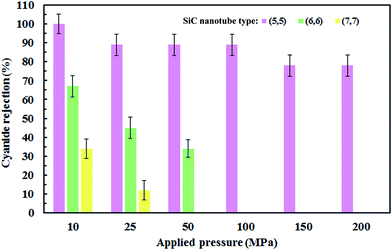 | ||
| Fig. 8 Ion rejection percentages for different applied pressures (MPa) and (SiC) nanotube diameters. Error bars represent uncertainty of the corresponding data. | ||
Fig. 9 shows the pressure effect on the separation time of the ions. Cyanide ions separated from the aqueous solution at the beginning of the simulation time at higher pressures, whereas at lower pressures, it took a longer time for them to be removed from the aqueous solution. Pressure force exerted to the flowing fluid through a distance resulted in a kind of work called flow work, which is defined as follows:56
| eflowwork = P/ρ | (3) |
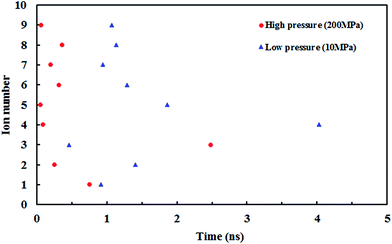
Fig. 10 shows the z position of the cyanide ions inside the (8,8) SiC nanotube during the simulations. The results did not show any overlap between the retention time of ions at high and low pressures. If the applied driving force to the system is a type of high energy (such as pressure) the ions traverse through the nanotube independently, i.e., the first ion does not need the assistance from the second ion to push it outwards through the nanotube. On the other hand, if the applied driving force is smaller (such as a small electrical field) the first ion needs a second ion to help it to move outside the nanotube.32
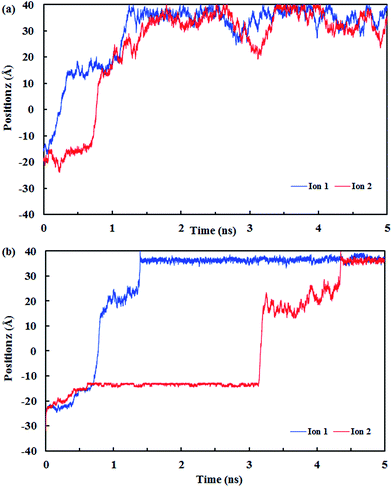 | ||
| Fig. 10 The z positions of the CN− ions at each simulation time at (a) low pressure (10 MPa) and (b) high pressure (150 MPa). | ||
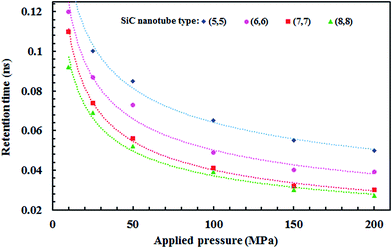
Fig. 11 illustrates the effect of the applied pressure on the retention time of the ions (time of passing one ion through the nanotube) in each SiC nanotubes. The retention time is shorter if the ions pass faster through the SiC nanotube, thus accelerating the separation process. The retention time was observed to decrease proportionally to the square root of the applied pressure. Furthermore, for large nanotubes the retention time was lower than for smaller nanotubes.
3.3. Radial distribution functions between cyanide ions and water molecules
The RDF is defined as:57
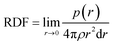 | (4) |
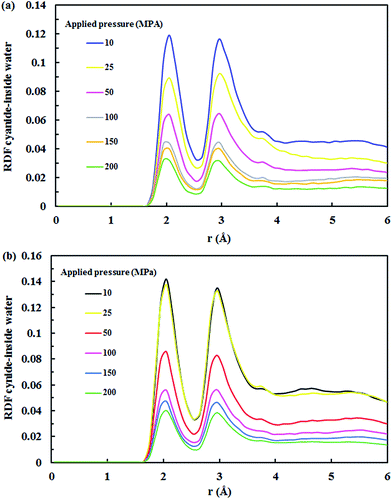 | ||
| Fig. 12 RDF for cyanide ions–water at various applied pressures in the (a) (7,7) SiC nanotube and (b) (8,8) SiC nanotube. | ||
4. Conclusion
The separation of cyanide ions from aqueous solution with SiC nanotubes was studied via MD simulations, and (5,5), (6,6), (7,7) and (8,8) SiC nanotubes were used. The results showed that a high rejection was achieved by (5,5) SiC nanotubes, which was 100% at 10 MPa. This rejection ability decreased when both the diameter of SiC nanotubes and the applied pressures increased. Moreover, it was found that the four types of SiC nanotubes accepted water molecules into their interior. The transportation of water molecules increased in the large nanotubes when applying high pressures, which compared with the theoretical HP equation. The large deviation of the MD result and macroscopic HP equation was a result of the inability of the HP equation for calculating fluid flows at a nanoscale.Acknowledgements
Authors thank the University of Tabriz for the support provided. We also acknowledge the support of the Iran Science Elites Federation.References
- H. Simsek, M. Kobya, E. Khan and A. N. Bezbaruah, Environ. Technol., 2015, 36, 1612–1622 CrossRef CAS PubMed.
- C. A. P. Arellano and S. S. Martínez, Int. J. Hydrogen Energy, 2007, 32, 3163–3169 CrossRef.
- M. Goncalves, A. Pinto and M. Granato, Environ. Technol., 1998, 19, 133–142 CrossRef CAS.
- T. Mudder and M. Botz, Eur. J. Miner. Process. Environ. Prot., 2004, 4, 62–74 Search PubMed.
- M. A. Acheampong, R. J. Meulepas and P. N. Lens, J. Chem. Technol. Biotechnol., 2010, 85, 590–613 CrossRef CAS.
- K. Baek, B.-K. Kim, H.-J. Cho and J.-W. Yang, J. Hazard. Mater., 2003, 99, 303–311 CrossRef CAS PubMed.
- R. R. Dash, C. Balomajumder and A. Kumar, Chem. Eng. J., 2009, 146, 408–413 CrossRef CAS.
- S. Sirianuntapiboon and C. Chuamkaew, Bioresour. Technol., 2007, 98, 266–272 CrossRef CAS PubMed.
- G. Hassani, S. Nasseri and H. Gharibi, Anal. Bioanal. Electrochem., 2011, 3, 625–634 Search PubMed.
- R. Roshan Dash, C. Balomajumder and A. Kumar, Eng. Life Sci., 2009, 9, 53–59 CrossRef.
- M. Hijosa-Valsero, R. Molina, H. Schikora, M. Müller and J. M. Bayona, Water Res., 2013, 47, 1701–1707 CrossRef CAS PubMed.
- M. Sarla, M. Pandit, D. Tyagi and J. Kapoor, J. Hazard. Mater., 2004, 116, 49–56 CrossRef CAS PubMed.
- S. Chergui, A. R. Yeddou, A. Chergui, F. Halet, H. Amaouche, B. Nadjemi and A. Ould-Dris, Toxicol. Environ. Chem., 2015, 97, 1289–1295 CrossRef CAS.
- A. Akcil, A. Karahan, H. Ciftci and O. Sagdic, Miner. Eng., 2003, 16, 643–649 CrossRef CAS.
- K. K. Ibrahim, M. A. Syed, M. Y. Shukor and S. A. Ahmad, BIOTROPIA, 2016, 22, 151–163 Search PubMed.
- S. C. Cheng, M. Gattrell, T. Guena and B. MacDougall, Electrochim. Acta, 2002, 47, 3245–3256 CrossRef CAS.
- T. Humplik, J. Lee, S. O'Hern, B. Fellman, M. Baig, S. Hassan, M. Atieh, F. Rahman, T. Laoui and R. Karnik, Nanotechnology, 2011, 22, 292001 CrossRef CAS PubMed.
- J. Theron, J. Walker and T. Cloete, Crit. Rev. Microbiol., 2008, 34, 43–69 CrossRef CAS PubMed.
- T. A. Hilder, D. Gordon and S.-H. Chung, Small, 2009, 5, 2183–2190 CrossRef CAS PubMed.
- Y. M. Kim, H. Ebro and J. H. Kim, Desalin. Water Treat., 2016, 1–8 CrossRef.
- T. A. Hilder, R. Yang, D. Gordon, A. P. Rendell and S.-H. Chung, J. Phys. Chem. C, 2012, 116, 4465–4470 CAS.
- P. S. Goh, A. F. Ismail and B. C. Ng, Desalination, 2013, 308, 2–14 CrossRef CAS.
- T. Bora and J. Dutta, J. Nanosci. Nanotechnol., 2014, 14, 613–626 CrossRef CAS PubMed.
- N. G. Chopra, R. Luyken, K. Cherrey, V. H. Crespi, M. L. Cohen, S. G. Louie and A. Zettl, Science, 1995, 269, 966–967 CrossRef CAS PubMed.
- L. Li, C. P. Li and Y. Chen, Phys. E, 2008, 40, 2513–2516 CrossRef CAS.
- D. Golberg, Y. Bando, W. Han, K. Kurashima and T. Sato, Chem. Phys. Lett., 1999, 308, 337–342 CrossRef CAS.
- X.-H. Sun, C.-P. Li, W.-K. Wong, N.-B. Wong, C.-S. Lee, S.-T. Lee and B.-K. Teo, J. Am. Chem. Soc., 2002, 124, 14464–14471 CrossRef CAS PubMed.
- C. Pham-Huu, N. Keller, G. Ehret and M. J. Ledoux, J. Catal., 2001, 200, 400–410 CrossRef CAS.
- R. Q. Wu, M. Yang, Y. H. Lu, Y. P. Feng, Z. G. Huang and Q. Y. Wu, J. Phys. Chem. C, 2008, 112, 15985–15988 CAS.
- G. Mpourmpakis, G. E. Froudakis, G. P. Lithoxoos and J. Samios, Nano Lett., 2006, 6, 1581–1583 CrossRef CAS PubMed.
- J.-X. Zhao, B. Xiao and Y.-H. Ding, J. Phys. Chem. C, 2009, 113, 16736–16740 CAS.
- A. Khataee, J. Azamat and G. Bayat, Comput. Mater. Sci., 2016, 119, 74–81 CrossRef CAS.
- R. Saghatchi, J. Ghazanfarian and M. Gorji-Bandpy, J. Offshore Mech. Arct. Eng., 2014, 136, 031801 CrossRef.
- A. Yazdani, M. Deng, B. Caswell and G. E. Karniadakis, J. Comput. Phys., 2016, 305, 906–920 CrossRef CAS.
- H. J. Berendsen, Simulating the physical world: hierarchical modeling from quantum mechanics to fluid dynamics, Cambridge University Press, 2007 Search PubMed.
- N. Modi, M. Winterhalter and U. Kleinekathoefer, Nanoscale, 2012, 4, 6166–6180 RSC.
- M. Thomas, B. Corry and T. A. Hilder, Small, 2014, 10, 1453–1465 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen and S. Su, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- M. Menon, E. Richter, A. Mavrandonakis, G. Froudakis and A. N. Andriotis, Phys. Rev. B: Condens. Matter, 2004, 69, 115322 CrossRef.
- Y. Zhang and H. Huang, Comput. Mater. Sci., 2008, 43, 664–669 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- J. Azamat, A. Khataee and S. W. Joo, Chem. Eng. Sci., 2015, 127, 285–292 CrossRef CAS.
- J. Azamat, A. Khataee and S. W. Joo, J. Mol. Struct., 2016, 1108, 144–149 CrossRef CAS.
- J. Azamat, A. Khataee and S. W. Joo, J. Mol. Model., 2016, 22, 1–8 CrossRef CAS PubMed.
- J. Azamat, J. Phys. Chem. C, 2016, 120, 23883–23891 CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. Azamat, J. J. Sardroodi and A. Rastkar, Desalin. Water Treat., 2015, 56, 1090–1098 CrossRef CAS.
- B. J. Bucior, D.-L. Chen, J. Liu and J. K. Johnson, J. Phys. Chem. C, 2012, 116, 25904–25910 CAS.
- J. Azamat, A. Khataee and S. W. Joo, J. Mol. Model., 2014, 20, 2468 CrossRef PubMed.
- F. Zhu, E. Tajkhorshid and K. Schulten, Biophys. J., 2002, 83, 154–160 CrossRef CAS PubMed.
- F. Zhu, E. Tajkhorshid and K. Schulten, Biophys. J., 2004, 86, 50–57 CrossRef CAS PubMed.
- D. F. Young, B. R. Munson, T. H. Okiishi and W. W. Huebsch, A brief introduction to fluid mechanics, John Wiley & Sons, 2010 Search PubMed.
- R. Saghatchi and J. Ghazanfarian, Applied Mathematical Modelling, 2015, 39, 1063–1073 CrossRef.
- Y. A. Cengel and M. A. Boles, Sea, 1994, 1000, 8862 Search PubMed.
- A. Kalinichev and R. Kirkpatrick, Eur. J. Soil Sci., 2007, 58, 909–917 CrossRef CAS.
- A. A. Dezfoli, M. Mehrabian and H. Hashemipour, Chem. Eng. Commun., 2015, 202, 1685–1692 CrossRef CAS.
- F. Taghavi, S. Javadian and S. M. Hashemianzadeh, J. Mol. Graphics Modell., 2013, 44, 33–43 CrossRef CAS PubMed.
- D. Cohen-Tanugi and J. C. Grossman, Nano Lett., 2012, 12, 3602–3608 CrossRef CAS PubMed.
- A. D. MacKerell Jr, D. Bashford, M. Bellott, R. L. Dunbrack Jr, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo and S. Ha, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed.
- M. W. Lee and M. Meuwly, J. Phys. Chem. A, 2011, 115, 5053–5061 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |