Molecular dynamic simulations on TKX-50/HMX cocrystal

Abstract

Dihydroxylammonium 5,5′-bistetrazole-1,1′-diolate (TKX-50) is a newly synthesized explosive with excellent comprehensive properties. Cyclotetramethylenetetranitramine (HMX) is currently one of the highest energy explosives used around the world. TKX-50/HMX cocrystal can improve the defects of TKX-50 and HMX and vastly expand their application scope. TKX-50 and HMX supercell structures and TKX-50/HMX cocrystal structures were established based on their crystal cell parameters and the formation mechanism of the cocrystals, respectively. The binding energy, radial distribution function (RDF), X-ray powder diffraction (XRD), cohesive energy density (CED) and mechanical properties were simulated based on the equilibrium structures of models via molecular dynamics (MD) simulations. The calculated results indicate that the TKX-50/HMX cocrystal forms as a new structure under the intermolecular forces, and the cocrystal structures of TKX-50 substituted by HMX on its slow-growing facets are more stable. Moreover, the cocrystal structure has greatly improved the high sensitivity defect of HMX and the mechanical properties of TKX-50 and HMX; thus the cocrystal will be more likely to be used widely in the energetic materials field.

---

1. Introduction

Developing high energy, low sensitivity explosives and designing high security, low vulnerability weapons are new requests of the modern war.^1–7 Dihydroxylammonium 5,5′-bistetrazole-1,1′-diolate (TKX-50) was first synthesized in 2012 and possesses favorable application prospects in energetic materials field considering its excellent comprehensive properties: high energy storage, low impact sensitivity and low toxicity.^8–19 Cyclotetramethylenetetranitramine (HMX),^20–22 which possesses high density and high energy, is typically an eight-membered heterocyclic nitramine explosive and it is currently the most widely used explosive in the world; however, high mechanical sensitivity defect has limited its application.

A cocrystal refers to two or more than two different molecules combined into the same lattice by intermolecular interactions with a fixed stoichiometric ratio, which forms a special multicomponent molecular crystal structure.^23–26 Due to the formation of a new structure and possible improvement of the comprehensive performance of materials, cocrystals have been widely studied in pharmaceutical, chemical and other fields.^27,28 Therefore, using cocrystal technology to induce non-covalent interactions, if TKX-50 and HMX can be made a unique structure with high energy and low sensitivity, it will vastly expand the application scope of TKX-50 and HMX.

We simulated the crystal morphology of TKX-50 using a growth morphology method and established TKX-50 and HMX supercell structures and TKX-50/HMX cocrystal structures by Material Studio software. We carried out molecular dynamics (MD) simulations^29,30 on these models to balance their structures and then calculated the binding energy (E_bind), radial distribution function (RDF), X-ray diffraction (XRD), cohesive energy density (CED) and mechanical properties based on their equilibrium structures to deduce the formation mechanism and the characteristics of the cocrystal, which provides theoretical calculation support for the formation of the cocrystal.

2. Computational methods

2.1 Crystal morphology prediction of TKX-50

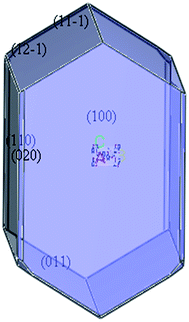
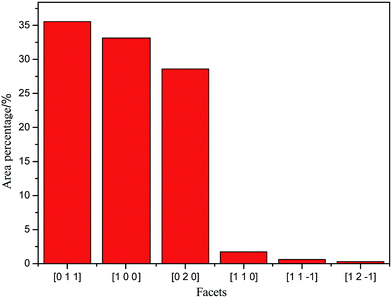
According to the single crystal diffraction data of TKX-50 (ref. 8) (monoclinic syngony, P₂₁/c space group, Z = 2.), the crystal structure of TKX-50, which consists of two hydroxylammonium cations (NH₃OH⁺) and a bistetrazole anion (C₂N₈O₂₂⁻), was established via PCFF force field, and the crystal morphology was simulated using the morphology growth method (see Fig. 1). TKX-50 possesses six stable facets; [011], [100], and [020] facets occupy larger area and are the slow-growing facets, whereas [11−1], [12−1], [110] facets occupy a smaller area and are the fast-growing facets (see Fig. 2).

Fig. 1 Crystal growth morphology of TKX-50.

Fig. 2 Area percentage of different facets.

2.2 Construction of supercell and cocrystal models

The intermolecular forces (e.g., van der Waals force, hydrogen bond, π–π accumulation) play an important role in the formation of a cocrystal. Among them, the bond energy of the hydrogen bond is in the range of 4–120 kJ mol⁻¹, which is far larger than that of other intermolecular forces. Moreover, with directionality, saturability and rich bonding mode characteristics, hydrogen bonding is the most important supramolecular force in the formation of a cocrystal. According to the compound structures of TKX-50 and HMX, they can form hydrogen bond types of N–H⋯O, O–H⋯O, etc. (see Fig. 3(a)). The intermolecular interactions in the cocrystal structure are shown in Fig. 3(b). Based on this, we predict that the TKX-50/HMX cocrystal may form as a new structure under the intermolecular forces, which will improve the defects of TKX-50 and HMX, and thereby possess better comprehensive properties of a stable structure with lower sensitivity, better thermal stability, better mechanical properties, etc. Thus we constructed the (3 × 2 × 1) supercell structures of TKX-50 and HMX and several TKX-50/HMX cocrystal models with a molar ratio of 1 : 1.

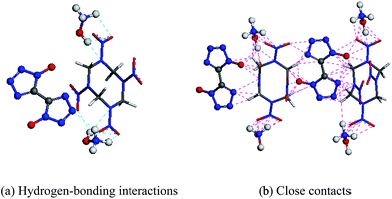Fig. 3 Molecular structures of TKX-50 and HMX (C, H, O, N are represented by gray, white, red, and blue colors, respectively. TKX-50 and HMX are represented by ball and stick models, respectively).

2.3 MD simulations

TKX-50 and HMX supercell models and TKX-50/HMX cocrystal models were optimized by the smart minimizer method to obtain reasonable configurations. Then, we carried out MD simulation on these optimized structures. We used NVT system and scale velocity temperature control method for the subsequent simulations, while the electrostatic and van der Waals interactions were calculated by Ewald's and atom-based methods, respectively. An MD simulation with a total simulation time of 100 ps was performed to equilibrate the system. After the system proceeded at an equilibration stage, another MD simulation with a period of 100 ps was performed, during which a total number of 2000 frames of data were collected finally in the trajectory at an interval of 50 fs. The final equilibrium structures are shown in Fig. 4.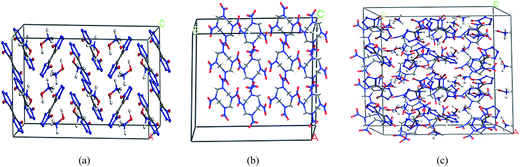

Fig. 4 Equilibrium structures of (a) TKX-50 supercell, (b) HMX supercell and (c) TKX-50/HMX cocrystal.

2.4 RDF simulation

RDF refers to the ratio of the area density around the investigated atom and the average density of the entire system, which mainly investigates the distance of a given particle from other particles in the system. Thus, we can speculate the interactions between molecules by analyzing the distribution of particles in the space. To clarify the interactions in TKX-50/HMX cocrystal molecules, we carried out the RDF simulation on the hydrogen atom of TKX-50 and the oxygen atom of HMX in the cocrystal system.

2.5 XRD simulation

XRD is a common method used to characterize the cocrystal. By analyzing and comparing the diffraction patterns of the cocrystal and single-compound explosives, we can judge whether diffraction peaks disappear and new peaks appear as well as confirm the position and intensity of diffraction peaks; thus we can deduce whether the cocrystal forms as a new crystallographic structure. We carried out XRD simulation on the equilibrium structures with a scanning range of 5–45° and a step size of 0.02 fs.

2.6 CED simulation

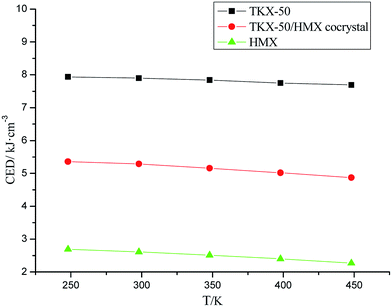
CED refers to the energy required by 1 mol of condensates to overcome intermolecular forces and turn into gas in unit volume. This technique can measure the magnitude of intermolecular forces in the system, and it can also be used as the theoretical criterion of thermal sensitivity magnitude in a high energy system under certain conditions. Therefore, we carried out CED simulation on the equilibrium structures under different temperatures (248 K, 298 K, 348 K, 398 K, 448 K).

2.7 Mechanical properties simulation

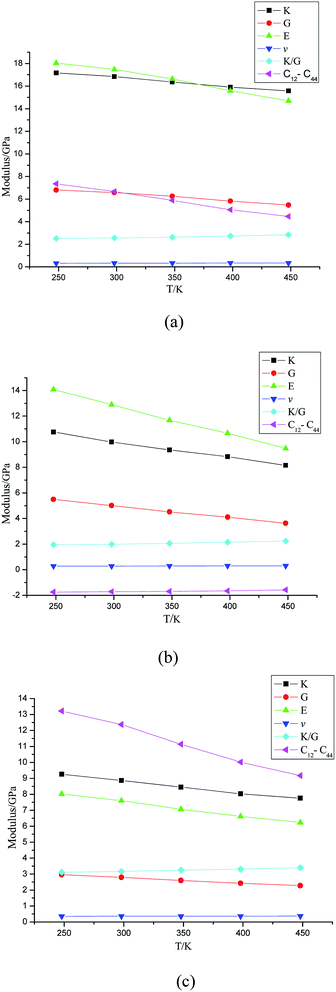
Mechanical properties are quite important to the application process of energetic materials; the parameters of the mechanical properties include strength, hardness, plasticity, and ductility. Shear modulus (G) and modulus of elasticity (E) usually refer to the ability to prevent plastic deformation of materials; the larger the value, the greater the hardness. The bulk modulus (K) refers to the fracture strength of materials; the larger the value, the greater the fracture strength. Poisson ratio (v) is an elastic constant that reflects the transverse deformation of materials. The ratio of K and G (K/G) and Cauchy pressure (C₁₂–C₄₄) is mainly used to predict the ductility of materials; the larger the value, the better the ductility. Therefore, we carried out mechanical properties simulations on the equilibrium structures under different temperatures (248 K, 298 K, 348 K, 398 K, 448 K). The calculated methods of E and v are presented in formula (1).

E = 2G(1 + v) = 3K(1 − v) (1)

3. Results and discussion

3.1 Energy calculation

The binding energy (E_bind) of the cocrystal system is the quantitative marker of the interaction strength between components. It is the negative value of the intermolecular interaction energy; the larger the value, the stronger the interaction strength, and the better the thermal stability of the system. As the calculated results show in Table 1, the E_bind values of cocrystal structures of TKX-50 substituted by those of HMX on its slow-growing facets ([011], [100], [020]) are larger, which indicates that these cocrystal structures are more stable.

Table 1 E_bind of the cocrystal models

Cocrystal models	[011]/HMX	[100]/HMX	[020]/HMX	[110]/HMX	[11−1]/HMX	[12−1]/HMX
Ebind/(kcal mol^−1)	2445.59	2505.33	2351.11	2259.26	2215.85	1924.97

---

3.2 RDF analysis

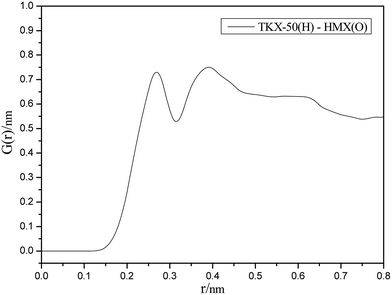
As can be seen from the RDF spectrum in Fig. 5, there are strong diffraction peaks appearing in the range of 0.20–0.30 nm and 0.31–0.50 nm. Due to the varying lengths of hydrogen bond and strong van der Waals forces ranging from 0.11–0.31 nm and 0.31–0.50 nm, we can deduce that hydrogen bonds and strong van der Waals forces exist in the cocrystal model and they possess important influences in the formation of the cocrystal.

Fig. 5 RDF spectrum of the cocrystal model.

3.3 XRD analysis

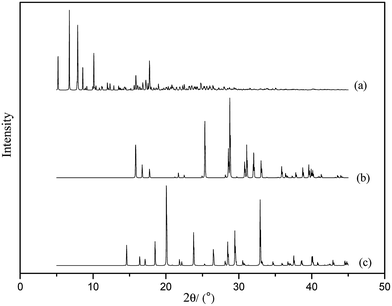
From the XRD spectra (see Fig. 6) we can see that the original characteristic peaks of HMX and TKX-50 disappeared or declined, and new peaks appeared at 2θ = 5–15° in the TKX-50/HMX cocrystal spectrum, which indicates that the intermolecular forces have destroyed the crystal structures of HMX and TKX-50 during the formation of the cocrystal, and a new structure is formed finally.

Fig. 6 XRD spectra of the (a) TKX-50/HMX cocrystal, (b) TKX-50 and (c) HMX.

3.4 CED analysis

It can be seen from the simulation results that the CED value decreased gradually with increasing temperature in all models, that is, the energy required by the systems turning into vapor decreased and the corresponding sensitivity increased gradually (shown in Fig. 7). For the different systems, the CED value of TKX-50 is far larger than that of HMX, indicating that TKX-50 possesses much lower sensitivity than HMX, which provides quite good agreement with the experiment.

Fig. 7 CED spectra of different models.

Moreover, the CED value of the cocrystal system is between the values of TKX-50's and HMX's, and is much larger than the value for HMX's, indicating that the cocrystal structure has greatly improved the high sensitivity defect of HMX and shows better thermal stability.

3.5 Mechanical properties analysis

From the mechanical properties spectra, it can be seen that the modulus of the crystal models have all changed evidently under different temperatures (shown in Fig. 8). The E, G, K values showed a downward trend with the increasing temperature in all systems; thus the rigidity, hardness and fracture strength of the models decreased at the same time.

Fig. 8 Mechanical properties of (a) TKX-50, (b) HMX and (c) TKX-50/HMX cocrystal.

In addition, the E, K, G values of the cocrystal system were lower than those of TKX-50's and HMX's, and the K/G and C₁₂–C₄₄ values were higher than those of TKX-50's and HMX's at the same temperature, indicating that the hardness and rigidity of the cocrystal decreased and ductility increased. Hence, the cocrystal structure has improved the mechanical properties of TKX-50 and HMX, which makes it more attractive for widespread use.

4. Conclusion

The cocrystal structures of TKX-50 substituted by HMX on its slow-growing facets ([011], [100], [020]) were more stable. Hydrogen bonds and van der Waals forces were proven to exist in the cocrystal model and they possessed important influences on the formation of the cocrystal. The original characteristic peaks of HMX and TKX-50 disappeared or declined, and new peaks appeared in the XRD spectrum of the cocrystal model. This is because the intermolecular forces destroyed the crystal structures of HMX and TKX-50 and controlled the formation of a new cocrystalline structure.

Moreover, the cocrystal structure has greatly improved the high sensitivity defect of HMX and the mechanical properties of TKX-50 and HMX. The simulated characteristics of TKX-50/HMX cocrystal are consistent with the theoretical prediction; hence, the cocrystal will more likely be widely used in the energetic materials field.

Acknowledgements

This study was financially supported by the National Special Plan Project (3090020121115). The authors express their sincere thanks to the financial supporter.

Notes and references

1. T. M. Klapötke, A. Preimesser and J. Stiertorfer, Z. Anorg. Allg. Chem., 2012, 638, 1278–1286.
2. R. Wang, H. Xu, Y. Guo, R. Sa and J. M. Shreeve, J. Am. Chem. Soc., 2010, 132, 11904–11905.
3. A. A. Dippold and T. A. Klapötke, J. Am. Chem. Soc., 2013, 135, 9931–9938.
4. O. Bolton and A. J. Matzger, Angew. Chem., Int. Ed., 2011, 50, 8960–8963.
5. M. B. Talawar, R. Sivabalan, T. Mukundan, H. Muthurajan, A. K. Sikder, B. R. Gandhe and A. S. Rao, J. Hazard. Mater., 2009, 161, 589–607.
6. R. Duddu, P. R. Dave, R. Damavarapu, N. Gabler and D. Parrish, Tetrahedron Lett., 2010, 51, 399–401.
7. M. B. Talawar, R. Sivabalan, M. Anniyappan, G. M. Gore, S. N. Asthana and B. R. Gandhe, Combust., Explos. Shock Waves, 2007, 43, 62–72.
8. N. Fischer, D. Fischer, T. M. Klapötke, D. G. Piercey and J. Stierstorfer, J. Mater. Chem., 2012, 22, 20418–20422.
9. N. Fischer, T. M. Klapötke, M. Reymann and J. Stierstorfer, Eur. J. Inorg. Chem., 2013, 12, 2167–2180.
10. N. Fischer, T. M. Klapötke, M. A. Matecic, J. Stierstorfer and M. Sucesca, New Trends Res. Energ. Mater., Proc. Semin., 16th, 2013, 16, 574–585.
11. V. K. Golubev and T. M. Klapötke, New Trends Res. Energ. Mater., Proc. Semin., 17th, 2014, 1, 220–227.
12. V. K. Golubev and T. M. Klapoetke, New Trends Res. Energ. Mater., Proc. Semin., 17th, 2014, 2, 672–676.
13. Q. An, T. Cheng, W. A. Goddard and S. V. Zybin, J. Phys. Chem. C, 2015, 119, 2196–2207.
14. B. Yuan, Z. J. Yu and E. R. Bernstein, J. Phys. Chem. A, 2015, 119, 2965–2981.
15. Z. A. Dreger, Y. C. Tao, B. B. Averkiev, Y. M. Gupta and T. M. Klapötke, J. Phys. Chem. B, 2015, 119, 6836–6847.
16. S. H. Xiong, S. S. Chen, S. H. Jin and C. Y. Zhang, RSC Adv., 2016, 6, 4421–4426.
17. Q. An, W. G. Liu, W. A. Goddard, T. Cheng, S. V. Zybin and H. Xiao, J. Phys. Chem. C, 2014, 118, 27175–27181.
18. S. H. Xiong, S. S. Chen, S. H. Jin and L. J. Li, J. Energ. Mater., 2016, 34, 384–394.
19. H. F. Hang, Y. M. Shi, J. Yang and B. P. Li, J. Energ. Mater., 2015, 33, 66–72.
20. K. F. Grebenkin, Combust., Explos. Shock Waves, 2009, 45, 78–87.
21. F. Käser and M. A. Bohn, J. Therm. Anal. Calorim., 2009, 96, 687–695.
22. K. Hartmut, Propellants, Explos., Pyrotech., 2008, 33, 33–36.
23. F. Lara-Ochoa and G. Espinosa-Perez, Supramol. Chem., 2007, 19, 553–557.
24. K. B. Landenberger and A. J. Matzger, Cryst. Growth Des., 2010, 10, 5341–5347.
25. C. Guo, H. Zhang, X. Wang, J. Xu, Y. Liu and J. Sun, J. Mol. Struct., 2013, 1048, 267–273.
26. Z. Yang, H. Li, X. Zhou, C. Zhang, H. Huang, J. S. Li and F. D. Nie, Cryst. Growth Des., 2012, 12, 5155–5188.
27. O. Bolton and A. J. Matzger, Angew. Chem., Int. Ed., 2011, 50, 8960–8963.
28. A. V. Trask, W. D. S. Motherwell and W. Jones, Cryst. Growth Des., 2005, 5, 1013–1021.
29. K. Lindorff-Larsen, N. Trobvic, P. Maragakis, S. Piana and D. E. Shaw, J. Am. Chem. Soc., 2012, 134, 3787–3791.
30. W. Zhu, J. J. Xiao, W. H. Zhu and H. M. Xiao, J. Hazard. Mater., 2009, 164, 1082–1088.

---