Preferred cell alignment along concave microgrooves

Abstract

Geometrical cues in the extracellular environment are essential for guiding the direction of cells and tissue architectures. For example, nano/micro-scale topography such as grooves and fibrous scaffolds induces cell alignment and migration through contact guidance. However, previous research has focused on patterns with scales ranging from nanometers to several microns. It remains unclear how cell behavior is affected by geometric cues at larger scales, such as the cylindrical curvature in the interior surface of blood vessels. Here, using microfabricated concave microgrooves to culture vascular endothelial cells, we examine how the radius of curvature affects cell body characteristics including shape, spreading area, and preferred alignment along the microgroove direction. Furthermore, analysis of subcellular actin filaments reveals that subcellular stress fibers play an essential role in such morphological response. Together, our findings not only broaden the knowledge basis of surface curvature as a biophysical factor but also offer cell characterization and contact guidance strategies for future cell and tissue engineering applications.

---

I. Introduction

Interactions between cells and their surrounding extracellular matrix (ECM)^34,35 play important roles in cell and tissue behaviors.^1–3 ECM physical factors such as stiffness,^4–8 geometrical cues,^9–16 and force stimulation^17–21 can regulate cell migration, proliferation, differentiation, and so on. In particular, it has been reported that the topology of ECM^22–24 can also direct the alignment and migration of cells through contact guidance.²⁵ On the other hand, cell morphology including cell spreading and alignment has been proven to be crucial to cell growth and tissue formation and functioning. Taking the endothelial cells as an example, the morphology of endothelial cells correlates to the nucleus shape and alignment, and even the gene expressions,^11,26–28 which govern cell fate. As the major component of vessel interiors, the alignment of endothelial cells also determines endothelial conformity and formation of new blood capillaries.^29,30 Notably, the abnormal cell behaviors may lead to endothelial dysfunctions and vascular diseases such as atherosclerosis.^20,31,32

However, most previous studies focused on cell behaviors in response to ECM topography in the range of nanometers to several microns.^23,33 The ECM topology with larger feature sizes, i.e. tens of microns, which is equally important and prominent in the human body, were rarely addressed. Considering the endothelial cells growing on vessel interiors, the ECM of tunica media confines the biophysical conditions including the cylindrical curvatures of vessels, which should affect the cell behaviors. As such, investigations on how cells behave on the micro-scale topology could provide new insights on the roles of environmental cues from ECM.

Microfabrication techniques have been widely applied to engineer cell environment for investigating cell behaviors and physiological mechanisms. Micro-contact printing was employed to pattern different micro-adhesion islands confining cell shape and demonstrated that cell shape can influence individual cell viability and morphological behaviors.¹⁰ Subcellular actin filaments, focal adhesions and nucleus can also be affected by micro-topographical features including the shape³⁴ and aspect ratio^35,36 of adhesion islands. Nevertheless, most of these techniques focus on controlling topographical factors of planar substrates. As cells in three-dimensional matrices can behave distinctly compared to those on planar substrates,³⁷ how the non-planar topographical cues affect cell behaviors is worth to be investigated quantitatively but remains elusive.

Researchers have employed several methods to fabricate non-planar microstructures for cell studies. Nikkhah et al. fabricated microchambers by reactive ion etching (RIE)³⁸ to examine the cytoskeletal properties. However, the rough edges left after fabrication caused the radii of curvature undefined. Park et al. applied suction pressure to fabricate silicone micro-chambers, yet the research focus remained on comparison of convex and concave surfaces for their effects to cell adhesion and proliferation.³⁹ Lee et al. manufactured scaffolds embedded with micro-pores with a controlled concave curvature,⁴⁰ but the accessibility and detailed cell analysis were challenging because the micro-pores were located inside the scaffold material.

In this study, we characterize the vascular endothelial cells growing on an array of concave microgrooves with different micro-scale curvatures. Owing to the geometric similarity between the microgrooves and vessel interiors, these results could exhibit key cell properties in the vascular endothelium. We examine the effect of microgroove dimensions on cell morphology and alignment. As cell morphology reflects the intracellular properties^41,42 including the architecture of cytoskeletal stress,^36,43 we also investigate the roles of stress fibers in such alignment processes through analysis of subcellular actin filaments. Overall, our study of surface curvature in determining cell alignment and morphology will provide new insights for tissue formation and the related mechanistic processes.

II. Results

Microgroove curvature mediates cell morphology and orientation

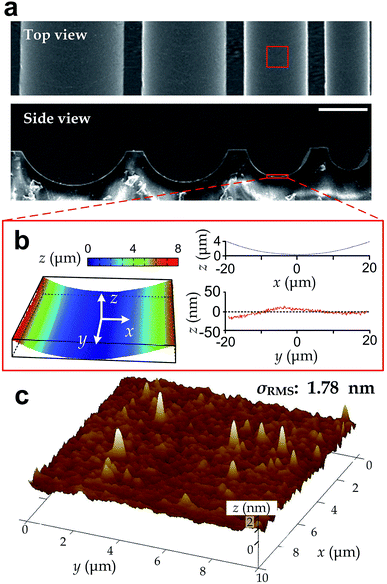
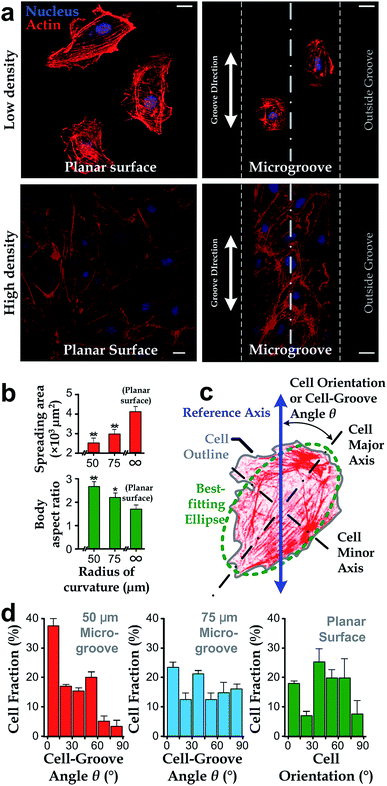
We manufactured arrays of concave microgrooves (Fig. 1) with different radii of curvature (50 μm, 75 μm and infinity (flat surface)) using replica molding of polydimethylsiloxane (PDMS).^44,45 Notably, the surface roughness of all the substrate surfaces is negligible (<5 nm) as indicated in Fig. 1c, which indicates that the radius of curvature is the only variable in our experiments. After seeding human vascular endothelial cells (hVECs) on the substrates and culturing them for 4 h, we fixed the cells and conducted immunofluorescence staining on cytoskeletal actin and nuclei (Fig. 2a) to visualize spreading areas, orientations and body aspect ratios of the cell bodies. Using low density for visualizing single cells and high density for a cell layer, we found that cell alignment is apparent in microgrooves with 50 μm radius of curvature regardless of cell densities. Moreover, through quantitative analysis, the cell spreading areas increased with the radii of curvature, while the body aspect ratios decreased with the radii (Fig. 2b). Of note, hVECs in the microgrooves with a 50 μm radius of curvature exhibited a halved average spreading area and a two-fold average body aspect ratio compared to those on the planar surface.

Fig. 1 Structure characterization of the microgrooves. (a) Top view and side view SEM images of a series of microgrooves with different radii of curvature captured. Scale bar: 100 μm. (b) Surface profile of a microgroove region (top view size: 40 μm × 40 μm). (c) Surface root-mean-square roughness (σ_RMS) measured by AFM over an area of 10 μm × 10 μm.

Fig. 2 Cell morphology and orientation in microgrooves. (a) Representative fluorescence microscopy images of hVECs at low and high densities on a planar surface (left) and in a microgroove with a radius of curvature of 50 μm (right). Scale bar: 20 μm. (b) The average cell spreading area and body aspect ratio for cells in microgrooves and the planar surface. Each data point is calculated based on at least 40 cells. (c) The schematic showing θ defined by an intersection angle between the major axis of cells and the microgroove direction. (d) θ of hVECs on microgrooves with 50 μm and 75 μm radii of curvature (n₅₀ = 96, n₇₅ = 87) and cell orientation on the planar surface exhibited as in micrographs (n = 53).

To test whether cell alignment was also effected, we analyzed the orientation of each single cell by applying a best-fitting ellipse to the cell body boundary in the fluorescence micrographs (Fig. 2c). The cell orientation in microgrooves was defined by a cell-groove angle θ as the intersection angle between the major axis of the ellipse and the groove direction to quantify the cell alignment tendency. For the flat substrates, the cell orientation was defined as an intersection angle between the major axis and the vertical direction of the micrograph. We can observe that cell orientations tended to align with the groove direction, i.e. θ → 0°, when cultured in microgrooves with 50 μm radius of curvature (Fig. 2d), suggesting a preferred cell body alignment along the microgroove direction. In contrast, there was not obvious alignment when cultured in microgrooves with radius of curvature 75 μm or on planar substrate. Moreover, as θ can be viewed as the ‘misalignment error’ between major axes of the cell body and groove directions, the level of alignment can be further quantified based on the standard deviation of such ‘misalignment error’ using the root-mean-squares of θ (θ_RMS). Our results showed that θ_RMS were 19.3° ± 2.1°, 30.1° ± 1.9° and 48.57° ± 0.17° for 50 μm microgrooves, 75 μm microgrooves and planar surfaces, respectively. A smaller ‘misalignment error’ reveals that substrates with a smaller radius of curvature would induce the more coherent cell-groove alignment.

Alignment of actin filaments with cell body is independent of microgroove curvatures

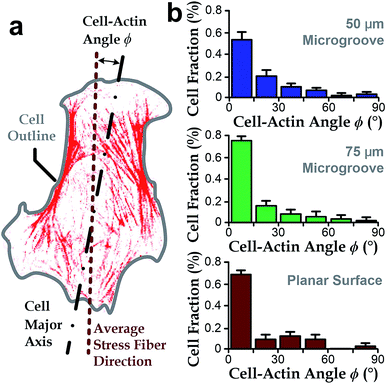
Intracellular stress fibers can modulate ranges of cell behaviors including cell shape and orientation.^36,43,46,47 Here, we investigated the intersection angle between the dominant direction of stress fibers (represented by actin filaments) and the major axis of cell body, ϕ (Fig. 3a). Results showed that stress fibers tended to align with the cell body when cultured either in microgrooves or on planar surfaces (ϕ → 0°, Fig. 3b). Similar with the analyses in the previous section, we quantified the standard deviations of the ‘misalignment error’ between the major axis of cell body and dominant actin directions using the root-mean-squares of ϕ (ϕ_RMS). We found that the ϕ_RMS values were comparable for all the chosen cases: 28.57° ± 2.5° on 50 μm microgrooves, ϕ_RMS = 23.43° ± 3.5° on 75 μm microgrooves, and ϕ_RMS = 24.31° ± 3.2° on planar surfaces. It suggests that stress fibers are always aligned with cell body and may underlie the cell's directionality.

Fig. 3 The cell-actin intersection angle ϕ between the major axis of cells and average stress fiber direction inside a cell. (a) The schematic showing ϕ defined by an intersection angle between the average orientation of stress fibers and the major axis of cells. (b) ϕ of hVECs in microgrooves with a radius of curvature as 50 (n = 96) and 75 μm (n = 87) and on a planar surface (n = 53).

Stress fibers are involved in cell alignment to microgrooves

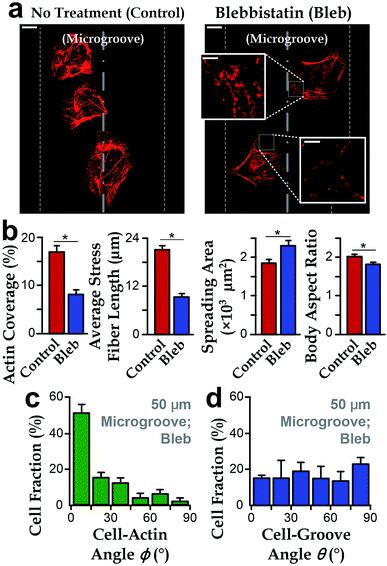
To further investigate the roles of stress fibers, we employed the stress-fiber-targeting reagent, blebbistatin, to inhibit formation of stress fibers.^48,49 In the experiments, we chose microgrooves with a radius of 50 μm because of the significant alignment between cell body and groove directions. As shown in Fig. 4a and b, cells treated with blebbistatin in microgrooves have lower total contents and reduced lengths of stress fibers as compared to the control group. We also observed increased spreading area and the reduced body aspect ratio after the blebbistatin treatment (Fig. 4b). Collectively, as the drug-treated cell morphology was analogous to that on planar substrates, it is interesting to further examine whether the suppressed stress fiber content may abrogate the influence of concave microgrooves, resulting in the more randomly distributed cell-groove angles θ.

Fig. 4 Blebbistatin inhibition revealing the role of stress fibers in cell morphology and preferred alignment along microgroove directions. (a) In a microgroove with a radius of curvature as 50 μm, fluorescence microscopy images showing that the reduced actin filament after blebbistatin inhibition. Scale bar: 10 μm. Insets show the disrupted actin filaments by blebbistatin. Scale bar: 2 μm. (b) The change of cell morphology and actin filament in microgrooves with the presence of blebbistatin. Left to right: actin coverage; average stress fiber length; cell spreading area; cell body aspect ratio; (n = 60 for the control group and n = 57 for the group treated with blebbistatin). (c) Cell-groove angle θ (n = 57) and (d) cell-actin angle ϕ of hVECs treated with blebbistatin in the microgrooves with a radius of curvature as 50 μm (n = 57).

We then investigated the cell orientation on concave microgrooves in response to the blebbistatin treatment. It should be noted that the stress fibers were still aligned with the cell body for those cells treated with blebbistatin (ϕ → 0°, Fig. 4c), which is consistent with previous report on the maintained cell-actin alignment for cells with inhibited actin contents.^11,50 More importantly, the drug-treated cell orientation relative to the direction of microgrooves showed a random distribution from 0 to 90° (Fig. 4d), suggesting the important role of stress fibers in the preferred cell alignment to microgrooves.

III. Discussions

In this work, we employed the photolithography with reflow of photoresist microstructures and the replica molding of PDMS to obtain microgroove substrates. Notably, the surface roughness of the microgroove substrate is the same as the unstructured PDMS material. As the roughness is less than 5 nm (Fig. 1), which is far less than the range known capable for influencing cell behaviors (dozens to hundreds of nanometers),¹⁶ the effect of surface roughness can be disregarded. Therefore, the fabricated microgroove should reduce to only one defined environmental factor – the surface radius of curvature.

In a microgroove, cells encounter an environment with anisotropic geometries. That is, the radius of curvature is minimum when orthogonal to the microgroove direction and becomes infinity when parallel to it. On such substrates, our results showed that cells in microgrooves with smaller nominal radius of curvature exhibited less spreading (Fig. 2b). Given the anisotropic geometries of microgrooves, the preferred alignment of cells along the microgrooves (Fig. 2d) and increased body aspect ratios (Fig. 2b) may be all due to the intention of spreading along the direction with larger even or infinite radius of curvature – the microgroove direction. This may explain why the alignment preferences of cell body and intracellular actin reduce as the radius of curvature increases (Fig. 2d).

Cells can respond to their environment via the force interactions between the cells and the biophysical cues of substrates.⁴³ Among different intracellular components, stress fibers play a key role in such force interaction and associated with cell morphology.^46,47 Prior to this study, cell characteristics including morphology, migration and cytoskeletal architecture have been reported sensitive to many other directional physical cues. For instance, vascular endothelial cells tended to align with the direction of shear stress under a liquid flow.^51,52 With a unidirectional cyclic stretching, fibroblasts reoriented to the stretch direction.^53–55 Of note, the alignment of cell behaviors to directional physical cues correlated with the cytoskeletal activities. When stress fibers were inhibited by related reagents, endothelial cells no longer displayed the shear-stress-induced alignment.⁵¹ Likewise, after blebbistatin treatment, the phenomenon of stretch-induced reorientation in fibroblasts disappeared.⁵⁴ Here, through the quantitative analysis (Fig. 3), we found that the stress fibers' average direction is consistent with the cell body orientation, for both the cells on a planar surface or in a microgroove. Moreover, on the blebbistatin-treated hVECs with a suppressed cell-groove alignment (Fig. 4) suggest good agreements with those previous findings for the other physical cues. In such processes, stress fibers were proven to play an essential role in sensing and responding to those stimulations.

As stress fibers are the main source of cell contractility and responsible for cell-ECM force interaction,⁴³ it is very likely that the cell alignment along microgrooves is due to the force balance between cell contractility and the force from the ECM. On a flat surface (roughness: <5 nm), there is no dominating anisotropic cues; arrange isotopically; and the cells exhibit a random orientation distributed accordingly. Differently, in microgrooves contains micro-curvatures orthogonal to the groove direction, which might lead to the biased distribution of cell contractility represented by stress fibers and cells alignment along microgrooves analogous to the effect of shear stress⁵¹ and stretching.⁵⁵ When being treated with the blebbistatin (stress fibers inhibitor), cell contractility is inhibited and its role in cell alignment along microgrooves is reduced. Thus, the effect cell alignment along microgrooves becomes insignificant compared with cells without any treatment.

In a nutshell, the underlying mechanism behind these results may lie in the role of stress fibers in the force interaction between cells and such concave micro-curvature. Considering the micro-curvature is a biophysical factor affecting cell alignment and morphology, it should be worthwhile to further investigate its effect together with the other well-studied biophysical factors (e.g. substrate stiffness,^4,7,8 shear stress^21,55 and external stretch^53,54) on the integrative effects to a broad range of cell behaviors in the future. It will be interesting to discover possible roles of the substrates stiffness in cell alignment along microgrooves by regulating rigidity of PDMS substrates using different ratios of PDMS monomer and curing agent as the substrate materials. The shear stress along the microgroove direction can be produced by driving culture media along the desired direction, mimicking the blood flow. Additionally, stretching the substrates carrying the adherent cells along one direction can generate the tensile stress/strain, which might be induced from blood pressure or muscular movements in the human body. Collectively, the results reported here provide insightful information about morphological characteristics of cells growing on micro-curved surfaces present in scaffolds as well as other tissue engineering applications.

IV. Methods

Fabrication of microgrooves

Substrates containing an array of microgrooves were fabricated by replica molding of polydimethylsiloxane (PDMS). To fabricate the molds, photolithography was used to pattern positive photoresist (AZ 50XT, AZ electronics) containing rectangular stripes on a silicon wafer. The photoresist with 60 μm thickness was first spin-coated on a silicon wafer, followed by soft-baking at 95 °C for 2 min. After UV exposure, the photoresist was developed using diluted AZ400K (1 : 2 dilution by deionized water) and dried by air flow. For the planar substrates, neither UV exposure nor development was performed. In order to obtain the quasi-semi-cylindrical structures in the microgroove geometries, the developed photoresist was baked at 120 °C for 1 min to allow photoresist reflowing. Due to the surface tension of photoresist, the cross-section of photoresist patterns turns round, which is the targeted microgrooves. The mold was then silanized with trichloro(1H,1H,2H,2H-perfluorooctyl)silane (Sigma-Aldrich) to reduce the adhesion of PDMS to the mold to facilitate the demolding processes.

To perform replica molding, the PDMS pre-polymer was prepared by mixing the PDMS base with a curing agent (Sylgard 184, Dow Corning Corporation) at a weight ratio of 10 : 1. After the PDMS pre-polymer was poured onto the molds and fully degassed, we baked the PDMS at 70 °C for 24 h. The PDMS was then peeled off and the pattern regions were cut out. For physical supports, the PDMS substrate was bonded onto glass slides (microgroove structures facing outward) using air plasma (energy 1 kJ; Harrick Plasma, Ithaca, NY). Before plating cells, a 50 mg ml⁻¹ human fibronectin solution (cat#33016-015, Life Technologies) was applied onto these PDMS substrates for cell culture. Then, the substrates were rinsed with phosphate-buffered saline (PBS) and submerged in fresh cell culture media.

Characterization of substrate surface

After fabricating the substrates, we applied light reflection and interference between interfaces to visualize and examine surface curvatures using the optical surface profiler (NT9300, Veeco). Then, we quantified roughness of the groove surfaces using an atomic force microscope (DMI, Bruker) with the tapping mode (Fig. 1c). To facilitate SEM imaging, we coated a 20 nm thick layer of Aurum on the surface of microstructures with a sputter-coating machine (Q150T, Quorum). The coated microgrooves were then observed in the high vacuum mode of SEM machine (FEI 250, Quanta). We took SEM for the top view and side view of the microgrooves.

Cell preparation

Primary human vascular endothelial cells (hVECs; C2517A, Lonza, Walkersvilla, MD) were cultured in supplemented endothelial cell growth medium (CC-3162, Lonza). The cells were cultured in standard 5% CO₂, 37 °C humidified incubator (Forma Steri-Cycle CO₂ incubator, Thermo Scientific). Once the cells reached 80% confluence, they were washed with hydroxyethyl piperazineethanesulfonic acid-buffered saline solution (CC-5022, Lonza), trypsinized (CC-5012, Lonza), and neutralized with a trypsin neutralization solution (CC-5002, Lonza). The resuspended cells were reseeded at two cell densities (3000 cell per cm² and 10 000 cell per cm²) in fresh media for subculture. Only cells within 5 passages were used in all experiments in this research.⁵⁶

Drug treatment

After seeding hVECs in the microgrooves, we randomly selected samples to treat with reagents. The cells were treated at the fourth hour after cell seeding and incubation for 30 min. Afterwards, the reagents were removed by replacing with PBS for follow-up experiments. For control groups, cells were added with equal amount of corresponding reagents solvent (PBS or dimethyl sulfoxide) to cell media for 30 min.

Fluorescence staining

For all cell samples, actin filaments and nuclei were stained with Alexa Fluor 555 conjugated phalloidin (A34055, ThermoFisher) and 40,6-diamidino-2-phenylindole (DAPI; D1306, ThermoFisher) respectively for 1 h. The samples were washed to remove unbounded staining agents with PBS. Finally, we applied a mounting solution (17984-25, Electron Microscopy Sciences) to the stained cells for microscopic imaging.

Image characterization

For determining the cell body aspect ratio, we used the projection images (along the direction normal to substrates' flat surface, same below) of image stacks of actin filaments. The body aspect ratio was defined based on the ratio of the major axis and minor axis for each cell's most fitted ellipse calculated based on ImageJ software (NIH, US). With those projection images of actin filaments, we used ImageJ software with FibrilTool plugin⁵⁷ to quantify the overall average orientation of actin filaments (stress fibers) in a cell. The stress fibers coverage was calculated by dividing the projection area of actin filaments with the cell's projection area.

Statistics

All values in this paper are each expressed as mean ± standard error of the mean (S.E.M) unless otherwise specified. Samples for quantification were from three independent, repeated experiments. Each cell group in this study contains >50 cells for promising comparison. To calculate the significance of the difference between two groups of data, we conducted a student's t-test with a two-tailed distribution and a two-sample unequal variance for these two data sets. An asterisk in charts represents the significant difference with the p-value < 0.05.

V. Conclusion

In this work, we applied concave microgrooves to characterize the morphology and alignment of vascular endothelial cells in response to the direction and radius of curvature. Importantly, the results demonstrate that the substrate curvature causes significant influence on cell spreading areas, body aspect ratios and preferred alignment along the microgroove direction. Furthermore, the weakened stress fibers mediated by blebbistatin underlie the reduced spreading area, enhanced body aspect ratio, and indifferent cell orientation along microgrooves, suggesting the essential role of stress fiber in such preferred directionality. Altogether, our results about the effects of the surface curvature of ECM on cells offer further insights about cell behaviors on ECM topology at the micro-scale, e.g. morphology, alignment and cytoskeletal structures, and enlighten relative application on engineering tissue formation/regeneration processes in the future.

Acknowledgements

We thank the financial supports from City University of Hong Kong (project# 9678100 and 7004540), Croucher Foundation Startup Grant (CityU project# 9500017), National Natural Science Foundation of China (NSFC 31500758), General Research Fund (project# RGC11206014), and Collaborative Research Fund (project# C1013-15GF) of Hong Kong Research Grant Council.

References

1. T. Rozario and D. W. DeSimone, Dev. Biol., 2010, 341, 126–140.
2. C. Frantz, K. M. Stewart and V. M. Weaver, J. Cell Sci., 2010, 123, 4195–4200.
3. A. D. Theocharis, S. S. Skandalis, C. Gialeli and N. K. Karamanos, Adv. Drug Delivery Rev., 2016, 97, 4–27.
4. A. Zemel, F. Rehfeldt, A. E. X. Brown, D. E. Discher and S. A. Safran, Nat. Phys., 2010, 6, 468–473.
5. J. R. Garcia and A. J. Garcia, Nat. Mater., 2014, 13, 539–540.
6. S. V. Plotnikov, A. M. Pasapera, B. Sabass and C. M. Waterman, Cell, 2012, 151, 1513–1527.
7. A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Cell, 2006, 126, 677–689.
8. T. Yeung, P. C. Georges, L. A. Flanagan, B. Marg, M. Ortiz, M. Funaki, N. Zahir, W. Ming, V. Weaver and P. A. Janmey, Cell Motil. Cytoskeleton, 2005, 60, 24–34.
9. M. J. Dalby, N. Gadegaard, P. Herzyk, H. Agheli, D. S. Sutherland and C. D. Wilkinson, Biomaterials, 2007, 28, 1761–1769.
10. C. S. Chen, M. Mrksich, S. Huang, G. M. Whitesides and D. E. Ingber, Science, 1997, 276, 1425–1428.
11. M. Versaevel, T. Grevesse and S. Gabriele, Nat. Commun., 2012, 3, 671.
12. K. Mandal, I. Wang, E. Vitiello, L. A. C. Orellana and M. Balland, Nat. Commun., 2014, 5, 5749.
13. M. Théry, J. Cell Sci., 2010, 123, 4201–4213.
14. B. Geiger, J. P. Spatz and A. D. Bershadsky, Nat. Rev. Mol. Cell Biol., 2009, 10, 21–33.
15. W. Chen, L. G. Villa-Diaz, Y. Sun, S. Weng, J. K. Kim, R. H. Lam, L. Han, R. Fan, P. H. Krebsbach and J. Fu, ACS Nano, 2012, 6, 4094–4103.
16. Y. Shao and J. Fu, Adv. Mater., 2014, 26, 1494–1533.
17. K. Kurpinski, J. Chu, C. Hashi and S. Li, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16095–16100.
18. N. Ziegler, A. Alonso, T. Steinberg, D. Woodnutt, A. Kohl, E. Müssig, S. Schulz and P. Tomakidi, BMC Cell Biol., 2010, 11, 1.
19. J. H.-C. Wang and B. P. Thampatty, Biomech. Model. Mechanobiol., 2006, 5, 1–16.
20. C. Hahn and M. A. Schwartz, Nat. Rev. Mol. Cell Biol., 2009, 10, 53–62.
21. J. Ando and K. Yamamoto, Circ. J., 2009, 73, 1983–1992.
22. A. D. Doyle, F. W. Wang, K. Matsumoto and K. M. Yamada, J. Cell Biol., 2009, 184, 481–490.
23. Y. Li, G. Huang, X. Zhang, L. Wang, Y. Du, T. J. Lu and F. Xu, Biotechnol. Adv., 2014, 32, 347–365.
24. M. K. Driscoll, X. Sun, C. Guven, J. T. Fourkas and W. Losert, ACS Nano, 2014, 8, 3546–3555.
25. P. Weiss, J. Exp. Zool., 1945, 100, 353–386.
26. C. H. Thomas, J. H. Collier, C. S. Sfeir and K. E. Healy, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 1972–1977.
27. R. P. Jean, D. S. Gray, A. A. Spector and C. S. Chen, J. Biomech. Eng., 2004, 126, 552–558.
28. C. Lanctôt, T. Cheutin, M. Cremer, G. Cavalli and T. Cremer, Nat. Rev. Genet., 2007, 8, 104–115.
29. R. M. Merks, S. V. Brodsky, M. S. Goligorksy, S. A. Newman and J. A. Glazier, Dev. Biol., 2006, 289, 44–54.
30. H. Parsa, R. Upadhyay and S. K. Sia, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5133–5138.
31. D. B. Cines, E. S. Pollak, C. A. Buck, J. Loscalzo, G. A. Zimmerman, R. P. McEver, J. S. Pober, T. M. Wick, B. A. Konkle and B. S. Schwartz, Blood, 1998, 91, 3527–3561.
32. A. Lerman and A. M. Zeiher, Circulation, 2005, 111, 363–368.
33. A. I. Teixeira, G. A. Abrams, P. J. Bertics, C. J. Murphy and P. F. Nealey, J. Cell Sci., 2003, 116, 1881–1892.
34. K. A. Kilian, B. Bugarija, B. T. Lahn and M. Mrksich, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4872–4877.
35. M. Thery, A. Pepin, E. Dressaire, Y. Chen and M. Bornens, Cell Motil. Cytoskeleton, 2006, 63, 341–355.
36. J. James, E. D. Goluch, H. Hu, C. Liu and M. Mrksich, Cell Motil. Cytoskeleton, 2008, 65, 841–852.
37. M. A. Schwartz and C. S. Chen, Science, 2013, 339, 402–404.
38. M. Nikkhah, J. S. Strobl, R. De Vita and M. Agah, Biomaterials, 2010, 31, 4552–4561.
39. J. Y. Park, D. H. Lee, E. J. Lee and S.-H. Lee, Lab Chip, 2009, 9, 2043–2049.
40. Y.-h. Lee, J.-r. Huang, Y.-k. Wang and K.-h. Lin, Integr. Biol., 2013, 5, 1447–1455.
41. V. Vogel and M. Sheetz, Nat. Rev. Mol. Cell Biol., 2006, 7, 265–275.
42. F. Pampaloni, E. G. Reynaud and E. H. Stelzer, Nat. Rev. Mol. Cell Biol., 2007, 8, 839–845.
43. M. Murrell, P. W. Oakes, M. Lenz and M. L. Gardel, Nat. Rev. Mol. Cell Biol., 2015, 16, 486–498.
44. Y. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153–184.
45. F. T. O'Neill and J. T. Sheridan, Optik, 2002, 113, 391–404.
46. D. E. Ingber, J. Cell Sci., 2003, 116, 1397–1408.
47. S. Kumar, I. Z. Maxwell, A. Heisterkamp, T. R. Polte, T. P. Lele, M. Salanga, E. Mazur and D. E. Ingber, Biophys. J., 2006, 90, 3762–3773.
48. M. Kovacs, J. Toth, C. Hetenyi, A. Malnasi-Csizmadia and J. R. Sellers, J. Biol. Chem., 2004, 279, 35557–35563.
49. S. Shu, X. Liu and E. D. Korn, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 1472–1477.
50. N. Gadhari, M. Charnley, M. Marelli, J. Brugger and M. Chiquet, Biochim. Biophys. Acta, 2013, 1833, 3415–3425.
51. B. Wojciak-Stothard and A. J. Ridley, J. Cell Biol., 2003, 161, 429–439.
52. J. T. Butcher, A. M. Penrod, A. J. García and R. M. Nerem, Arterioscler., Thromb., Vasc. Biol., 2004, 24, 1429–1434.
53. D. Wang, W. Zheng, Y. Xie, P. Gong, F. Zhao, B. Yuan, W. Ma, Y. Cui, W. Liu, Y. Sun, M. Piel, W. Zhang and X. Jiang, Sci. Rep., 2014, 4, 6160.
54. A. M. Greiner, H. Chen, J. P. Spatz and R. Kemkemer, PLoS One, 2013, 8, e77328.
55. A. Livne, E. Bouchbinder and B. Geiger, Nat. Commun., 2014, 5, 3938.
56. R. H. Lam, S. Weng, W. Lu and J. Fu, Integr. Biol., 2012, 4, 1289–1298.
57. A. Boudaoud, A. Burian, D. Borowska-Wykręt, M. Uyttewaal, R. Wrzalik, D. Kwiatkowska and O. Hamant, Nat. Protoc., 2014, 9, 457–463.

---