Open Access Article
Open Access ArticleTheoretical investigation on the balance between large band gap and strong SHG response in BMO4 (M = P and As) crystals†
Yanzhou Sun,
Zhihua Yang*,
Dianwei Hou and
Shilie Pan*
Key Laboratory of Functional Materials and Devices for Special Environments of CAS, Xinjiang Key Laboratory of Electronic Information Materials and Devices, Xinjiang Technical Institute of Physics & Chemistry of CAS, 40-1 South Beijing Road, Urumqi 830011, China. E-mail: zhyang@ms.xjb.ac.cn
First published on 12th January 2017
Abstract
Nonlinear optical (NLO) materials with outstanding performances are particularly important in laser science. To design an efficient NLO material with an optimal balance between the optical band gap and the NLO coefficient is still a huge challenge. In this paper, the electronic structures and optical properties of two isostructural non-centrosymmetric BMO4 (M = P and As) crystals exclusively containing tetrahedral groups have been studied by the first-principles method. Our calculated results show the compounds exhibit excellent properties with a suitable balance of large band gap and large NLO coefficient for BPO4 (10.4 eV and 0.64 pm V−1) and BAsO4 (7.8 eV and 1.58 pm V−1). The unanticipated large second-harmonic generation (SHG) response can be understood by the relatively strong s–p hybridization in BMO4 (M = P and As). It is found that substitution of PO4 groups for AsO4 groups can increase the SHG effect and the birefringence but decrease the band gap. Whether the redshift of bandgap will be responsible for the change of SHG effect between BMO4 (M = P and As) is explored by energy correction method. The increased polarizability anisotropy of tetrahedral groups explained the enhanced birefringence.
Introduction
Nonlinear optical (NLO) crystals have attracted much attention because they can be used to extend the working wavelength range of a solid state laser through frequency conversion.1,2 For ultraviolet (UV) or deep-UV NLO applications, ideal NLO materials require a strict combination of properties that need to be satisfied simultaneously in a non-centrosymmetric crystal: a wide transparency window down to the deep-UV region, relatively strong effective second-harmonic generation (SHG) response, and suitable birefringence to realize phase matching. Borate and phosphate crystals have attracted much interest for their excellent performance as NLO crystals, such as, KH2PO4 (KDP),3 CsB3O5,4 LiB3O5 (LBO),5 SrB4O7,6 LiCs2PO4,7 Ba3P3O10Cl,8 Ba5P6O20,9 and RbBa2(PO3)5.10 The tetrahedral BO4 or PO4 groups existing in the above mentioned crystals enlarge the band gaps of the crystals shifting the cutoff edge to the deep-UV region. However, the crystals with BO4 or PO4 groups as building blocks are usually labeled by small NLO coefficients and/or small birefringence. The combination of the π-conjugated planar BO3 groups into the structures is away to improve the birefringence and optical nonlinearities of these crystals.11–16 Especially, KBe2BO3F2 (KBBF) has a short deep-UV cutoff wavelength about 150 nm, a relatively large SHG tensor d11 about 0.47 pm V−1, and a moderate birefringence of 0.077. And it is the sole NLO crystal, which can generate coherent light of wavelength below 200 nm by the direct SHG at room temperature.17 However, KBBF crystal is very difficult to grow in thickness due to its strong layering growth habit, which severely hinders its practical applications.18In 1934, the cristobalite like forms of the ternary silica analogues BPO4 were first discovered by solid-state synthesis at high temperature.19 The theoretical or experimental researches of BPO4 on its growth and optical properties have been in progress for many years.20–24 They measured BPO4 has a NLO coefficient d36 = 0.76 pm V−1, which is larger than that of KBBF (d11 = 0.47 pm V−1). BPO4 also has a short deep-UV cutoff wavelength ∼134 nm, 16 nm shorter than that of KBBF.24 BPO4 should have a smaller NLO coefficient resulting from the larger band gap because the possibility of quantum transition between valence and conduction bands is ratio to the reciprocal of diverse energy at each momentum point. Until 2016, Li et al. explained the mechanism of its large NLO coefficient.25 Unsatisfactorily, BPO4 has a smaller birefringence (approximately 0.007) than KBBF, which makes it non-phase matched in ultraviolet SHG progress, limiting its application in ultraviolet output. Therefore, the issue of how to improve the birefringence of the available frequency conversion material should be focused on. Previous studies have promised strain engineering and ion-doping methods could modulate or even enhance the birefringence of relevant materials both theoretically and experimentally.26–30 Following this idea, we “look away” to arsenic, which is similar to phosphorus can coordinate with four oxygen atoms to form the tetrahedral groups. Curiously, does the combination of the BO4 and AsO4 groups result in an optimal balance between large band gap and strong SHG response? Does the value of birefringence also increase compared to BPO4? To the best of our knowledge, theoretical or experimental reports about the optical properties of BAsO4 are still absent after it was discovered due to the difficulty in growth.31–33
In this paper, in order to explore the influence on optical properties by the substitution of NLO-active PO4 groups for AsO4 groups, BMO4 (M = P and As) crystals exclusively containing tetrahedral groups are studied. We first introduced the optical properties obtained by ab initio method. Then, the gap-determination factor was discussed to explain the mechanism of large band gaps in BMO4 (M = P and As) crystals. BAsO4 has a stronger SHG response with 2.5 times than that of BPO4. The origin and enhancement of the large SHG effect of BAsO4 was explored by combining the band structures and the energy correction analysis. Finally, we systemically discussed the polarizability anisotropy of tetrahedral groups to explain why the birefringence of BAsO4 is 2.6 times than that of BPO4.
Calculation methods
The first-principles calculations for electronic structure employed the planewave pseudopotential method in the CASTEP.34–36 The calculations was performed using the crystallographic information files BPO4: ICSD-4132434; BAsO4: ICSD-413438. During the calculation, geometry optimization was performed using the BFGS minimization technique. The converged criterions for the geometry optimization are that the residual forces on the atoms, the displacements of atoms and the energy change were less than, 5.0 × 10−6 eV per atom, 0.01 eV Å−1 and 5 × 10−4 Å, respectively. Two exchange and correlation functionals, local density approximation/Ceperley–Alder–Perdew–Zunger (LDA/CA–PZ)37,38 and generalized gradient approximation/Perdew–Burke–Ernzerhof (GGA/PBE)39 were adopted to calculate the electronic structures and NLO coefficients. After a series of successful tests, the LDA/CA–PZ functional with ultrasoft pseudopotentials (USP)40 was finally selected, giving the best agreement with the experimental data of BPO4. The valence electrons were B-2s22p1, O-2s22p4, P-3s23p3 and As-4s24p3, respectively. The number of plane waves was determined by a cutoff energy of 380 eV and the k-point sampling was set as 7 × 7 × 8.Based on the electronic structures, the imaginary part of the dielectric constant ε2 (ω) can be obtained by
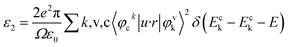 | (1) |
In which Ω is the volume of the elemental cell, v, and c represent the valence and conduction bands, respectively, and u is the vector defining the polarization of the electric field of the incident light. The real part of the dielectric constant, and then the refractive index n and birefringence Δn = nmax − nmin can be obtained using the Kramers–Kronig transform.41 It is well known that although the LDA functional always underestimates the bandgap, after the scissors corrections were employed, reliable refractive indices and birefringence can still be got from the LDA calculations.42–45 To get suitable scissors corrections of these two compounds, the modified Becke–Johnson (mBJ) exchange potential46,47 and implemented in WIEN2k48 was used to calculate the optical band gap because the mBJ method can get similar accuracy comparison with very expensive GW calculations49,50 and experimental values.22 Besides above methods, PBE0 hybridization functional has also been utilized to estimate the bandgaps in this work.
In addition, Becke three-parameter Lee–Yang–Parr (B3LYP) exchange correlation functional with the Lee–Yang–Parr correlation functional at the 6-31G basis set in Gaussian 09W program51 were employed to calculate the polarizability of the tetrahedra groups MO4 (M = B, P and As). The anisotropic polarizabilities (Δα) are defined by the following equation:
| Δα = (1/2)1/2[(αxx − αyy)2 + (αxx − αzz)2 + (αzz − αyy)2]1/2 | (2) |
SHG coefficients were calculated at a zero frequency limit by the length-gauge formalism derived by Aversa and Sipe,52 and later developed by Zhang et al.27
| χ(2)αβγ = χ(2)αβγ(VE) + χ(2)αβγ(VH) | (3) |
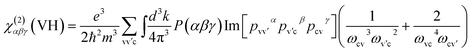 | (4) |
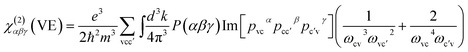 | (5) |
Results and discussion
Structure and optical properties
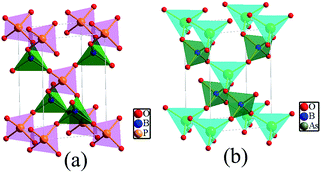
BPO4 and BAsO4 crystallize in the tetragonal space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) (no. 82), with a = b = 4.3401 Å, c = 6.6470 Å, Z = 2 for BPO4, a = b = 4.4658 Å, c = 6.8139 Å, Z = 2 for BAsO4, respectively. As sketched in Fig. 1, a continuous 3D framework of BMO4 (M = P and As) crystals is built by sharing the corner of the BO4 and MO4 (M = P, As) tetrahedra.
(no. 82), with a = b = 4.3401 Å, c = 6.6470 Å, Z = 2 for BPO4, a = b = 4.4658 Å, c = 6.8139 Å, Z = 2 for BAsO4, respectively. As sketched in Fig. 1, a continuous 3D framework of BMO4 (M = P and As) crystals is built by sharing the corner of the BO4 and MO4 (M = P, As) tetrahedra.
The band gaps, SHG coefficients in static limit and the birefringences for BMO4 (M = P and As) were obtained (shown in Table 1). As compared with the experimental results, the PBE0 functional gives reliable values that are estimated of 10.4 eV and 7.8 eV, respectively. It is well known that although the LDA and GGA functional always underestimates the bandgap, after the scissors corrections were employed, reliable SHG coefficient and birefringence can still be got from the LDA calculations. It is clearly shown that the largest calculated NLO coefficient d36 = 1.58 pm V−1 of BAsO4 also is larger than that d36 = 0.64 pm V−1 of BPO4, which is very closed to the experimentally measured value of about two times of KDP.22 And the calculated birefringences are 0.011 for BPO4, and 0.029 for BAsO4 at 589 nm. The calculated birefringence about 0.011 is consistent well with the experimental value 0.007 at 589 nm.24 It should be noticed that the band gap and NLO coefficient of BAsO4 are comparable to these of the commercial NLO crystals LBO (7.8 eV and 1.17 pm V−1), β-BaB2O4 (6.6 eV and 2.26 pm V−1) and KTiOPO4 (3.2 eV and 3.24 pm V−1).53 A subtle balance is obtained between large band gap and strong SHG response in BAsO4 crystal. It indicates that BAsO4 may have a promising potential to be a NLO material in UV or even DUV region.
| Gap (eV) | SHG (pm V−1) | Δn | |
|---|---|---|---|
| BPO4 | 10.4 | 0.64 | 0.011 |
| BAsO4 | 7.8 | 1.58 | 0.029 |
Role of AsO4 in band gap
LDA and GGA functionals are performed to calculate the band gap of BMO4 (M = P and As), as shown in Table 2. The LDA and GGA results are smaller than the experimental data 9.25 eV (corresponding to the measured optical cutoff edge of 134 nm). It is not strange at all because the Kohn–Sham schemes based on LDA and GGA usually underestimate the band gap of materials primarily owning to the discontinuity of exchange–correlation energy. For comparison, the experimental optical bandgaps, the PBE0 and mBJ methods are also employed. It is found that PBE0 result is close to the experimental one. The results clearly indicate the validity of the method used here, so the optical bandgaps of BMO4 (M = P and As) are very large (10.4 eV and 7.8 eV), comparable to the crystals aimed in deep-UV region such as Ba3P3O10Cl (6.9 eV),8 Li4Sr(BO3)2 (6.5 eV)14 and KBBF (8.3 eV),17 NaSr3Be3B3O9F4 (7.2 eV)54 and can be used in the UV region as NLO materials.| BPO4 | BAsO4 | |
|---|---|---|
| LDA | 7.62 | 5.32 |
| GGA | 7.22 | 4.75 |
| PBE0 | 10.35 | 7.77 |
| mBJ | 10.62 | 7.55 |
| Exp. | 9.25 (ref. 22) | — |
To explore the reason for the large band gaps, the partial density of states (PDOS) for BMO4 (M = P and As) are plotted in Fig. 2a and b. For BPO4, the upper of the valence band (VB) is mainly occupied by the non-bonding 2p orbitals of O; the bottom of the conduction band (CB) mainly consists of the hybridization orbitals of B–O and P–O. Similar to BPO4, the contributions of O 2p orbitals primarily dominate the upper VB of BAsO4. However, the bottom of CB of BAsO4 mainly consists of As-s, B-p, O-p. To gain a deeper understanding of the electric structure features and check the band-gap determiner, we plotted slices of orbital density of CB minimum and VB maximum as shown in Fig. 2c–f. From Fig. 2c and e, it concludes that the VB maximum in BMO4 (M = P and As) is mainly occupied by the nonbonding oxygen orbitals. While CB minimum exhibits totally different characters for the title compounds. It is clearly shown that the orbitals from P atoms, O atoms and B atoms dominate VB maximum of BPO4 (see Fig. 2d). However, for BAsO4, the VB maximum is primarily only controlled by orbitals from As and O atoms without B atoms as shown in Fig. 2f. Therefore, one can make a conclusion that the band gap determiner is nonbonding 2p of O under Fermi level and hybridization orbitals of B/P–O in CB for BPO4 crystal, and As–O in CB for BAsO4 crystal. In addition, the orbital density also reveals a strong hybridization between As-s and O-p in Fig. 2e. Such strong sp hybridization in BAsO4 leads to a slight red-shift of the deep-UV cutoff edge compared with BPO4.
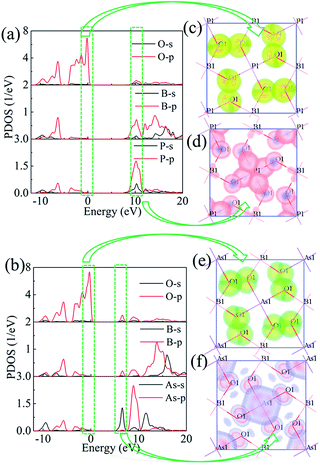 | ||
| Fig. 2 The partial density of states (PDOS) for BPO4 (a) and BAsO4 (b). The energy range of the specific orbitals of the BPO4 crystals (c), (d) and the BAsO4 crystals (e), (f). | ||
In the light of the frontier molecular orbitals theory, the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) of MO4 (M = B, P and As) and BO3 groups were also obtained (Table 3). Evidently, the band gaps ΔEg of the MO4 (M = B, P and As) tetrahedral groups and BO3 groups obey the following relative orders: ΔEg (BO4) > ΔEg (PO4) > ΔEg (AsO4) ≈ ΔEg (BO3). It should pay attention to that the band gaps of AsO4 groups is comparable with that of BO3 groups revealing AsO4 to be as a NLO active unit which is also beneficial to the large band gap.
| Units | HOMO (a.u.) | LUMO (a.u.) | Gap (a.u.) |
|---|---|---|---|
| BO4 | 1.064 | 1.459 | 0.395 |
| PO4 | 0.443 | 0.775 | 0.332 |
| AsO4 | 0.424 | 0.729 | 0.305 |
| BO3 | 0.578 | 0.898 | 0.311 |
Mechanism for strong and enhanced SHG response
SHG coefficients dij were estimated by the sum-over-states under the static limit within the length gauge.27 BMO4 (M = P and As) both belong to I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) space group, owing to the restriction of Kleinman's symmetry, there are two independent elements: d36 and d15. The calculated results are listed in Table 4. It is clearly shown that the largest SHG tensor for BPO4 is d36 = 0.64 pm V−1 which is comparable to the reported value d36 = 0.78 pm V−1.22 As for BAsO4, the SHG coefficients d36 = 1.58 pm V−1 and d15 = 1.04 pm V−1 are obtained, respectively.
space group, owing to the restriction of Kleinman's symmetry, there are two independent elements: d36 and d15. The calculated results are listed in Table 4. It is clearly shown that the largest SHG tensor for BPO4 is d36 = 0.64 pm V−1 which is comparable to the reported value d36 = 0.78 pm V−1.22 As for BAsO4, the SHG coefficients d36 = 1.58 pm V−1 and d15 = 1.04 pm V−1 are obtained, respectively.
| Compound | d36 | d15 |
|---|---|---|
| BPO4 | 0.64 | −0.07 |
| BAsO4 | −1.58 | 1.04 |
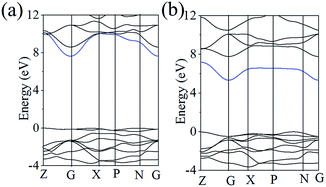
As mentioned above, BMO4 (M = P and As) should have a weaker NLO response resulting from the large band gap. Curiously, SHG response is 2 × KDP for BPO4 and 4 × KDP for BAsO4, which is larger than many crystals with equivalent bang gap like KBBF (1.2 × KDP, 8.3 eV). To illuminate this question, we carefully check the band structures of BMO4 (M = P and As) (shown in the Fig. 3). We mainly focused on the electric structure around the Fermi energy level because the optical properties of the crystal are particularly determined by the states close to the Fermi level. Evidently, the lowest conducting band is only dispersive around the G point (dyed by blue), and valence bands are clearly dispersive. It implies a relatively strong hybridization between the O 2p orbitals and the 4s orbitals from As which can enhance the interband Berry connection, and contribute a relatively large SHG effect in BAsO4. The same situation (see the Fig. 3a) also occurs in the BPO4 crystal.25
To identify the contribution of each atom in the SHG processes in real space, the SHG-density method was analyzed for both compounds. The SHG process contains the two virtual transition processes, namely virtual electron (VE) and virtual hole (VH) processes. Here we will just show the SHG-density of the largest SHG tensors d36 to discuss the origin of the SHG effect. The obtained SHG-densities of the two compounds are shown in Fig. S1† and 4. More attention will be paid on that the SHG-density of BMO4 (M = P and As) mainly distributes around the BO4 and MO4 groups (especially on O2− anions) for unoccupied states and occupied states, illustrating their dominant contributions to the SHG.
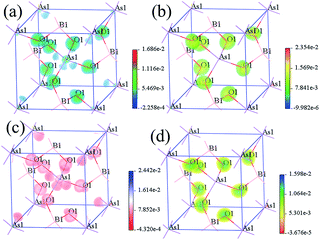 | ||
| Fig. 4 SHG-density of BAsO4: (a) VE occupied states; (b) VE unoccupied states; (c) VH occupied states; (d) VH unoccupied states. | ||
It is worth to notice that BAsO4 has SHG response about 2.5 × BPO4. Curiously what is the origin of the largely enhanced SHG coefficients of BAsO4? It is well known that band gap has a significant influence on SHG effect that the small gap can change the SHG response dramatically. To check the influence of the decrease of band gap in BAsO4, we use the scissor operator corrections to the experimental band gaps of BPO4. It turns out that the band-gap-corrected SHG coefficient d36 is 0.79 pm V−1 for BAsO4, which is close to that of BPO4 (d36 = 0.64 pm V−1). Compared with 1.58 pm V−1, we found that the contribution induced by band gap reduction is around 85%. And we know from the electronic structure that the band gap reduction or the red-shift of UV-cutoff from BPO4 to BAsO4 attributes to the strong hybridization interaction between As and O. Therefore, the stronger covalent interaction of As–O is a significant factor to the enhanced SHG response in BAsO4 compared that of BPO4.
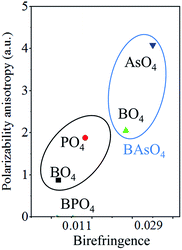
Origin of enhanced birefringence
The obtained birefringence of BAsO4 is about 2.6 × BPO4. In order to figure out the enhancement, we calculate the polarizability anisotropy of BO4, PO4 and AsO4 groups in BMO4 (M = P and As) using the DFT implemented via the Gaussian09 package at the 6-31 G level. The polarizability anisotropy Δα of BO4, PO4 and AsO4 groups are shown in the Fig. 5. It is clearly the Δα of tetrahedral groups of BAsO4 are larger than those of BPO4. The sequence of the calculated polarizability anisotropy is in good agreement with the sequence of birefringence.Conclusion
In this paper, the electronic structures and optical properties of BMO4 (M = P and As) were calculated by DFT method. The band gap of BAsO4 is still large after a substitution of NLO active PO4 groups for AsO4 groups. The band gaps ΔEg of the groups MO4 (M = B, P and As) and BO3 groups obey the following relative orders: ΔEg (BO4) > ΔEg (PO4) > ΔEg (AsO4) ≈ ΔEg (BO3). It implies AsO4 groups to be as a NLO active unit which is also in favour of the large band gap. We also found BMO4 (M = P, As) have large SHG responses. A relatively strong hybridization between the O 2p orbitals and the orbitals from B/P or As contributes a relatively large SHG effect in BMO4 (M = P, As). The strong s–p hybridization influence between As and O gives the band gap reduction and the 85% enhancement of SHG response from BPO4 to BAsO4. The calculated birefringence of BAsO4 is about 2.6 × BPO4 due to the stronger polarizability anisotropy of tetrahedral groups in BAsO4 than those of BPO4. The results show the replacing PO4 tetrahedra by AsO4 groups do not only achieve an optimal balance between large band gap and strong SHG response but also are helpful to increase birefringence. And one may be able to design new compounds with the adjustment effect of tetrahedral groups.Acknowledgements
This work is supported by the National Key Basic Research Program of China (Grant No. 2014CB648400), the “National Natural Science Foundation of China” (Grant No. 51425206, 11474353), the Xinjiang International Science & Technology Cooperation Program (20146001).References
- D. Cyranoski, Nature, 2009, 457, 953–955 CrossRef CAS PubMed.
- P. Becker, Adv. Mater., 1998, 10, 979–992 CrossRef CAS.
- J. De Yoreo, A. Burnham and P. Whitman, Int. Mater. Rev., 2002, 47, 113–152 CrossRef CAS.
- Y. C. Wu, T. Sasaki, S. Nakai, A. Yokotani, H. G. Tang and C. T. Chen, Appl. Phys. Lett., 1993, 62, 2614–2615 CrossRef CAS.
- C. T. Chen, Y. C. Wu, A. D. Jiang, B. C. Wu, G. M. You, R. K. Li and S. J. Lin, J. Opt. Soc. Am. B, 1989, 6, 616–621 CrossRef CAS.
- A. I. Zaitsev, A. S. Aleksandrovskii, A. V. Zamkov and A. M. Sysoev, Inorg. Mater., 2006, 42, 1360–1362 CrossRef CAS.
- L. Li, Y. Wang, B. H. Lei, S. J. Han, Z. H. Yang, K. R. Poeppelmeier and S. L. Pan, J. Am. Chem. Soc., 2016, 138, 9101–9104 CrossRef CAS PubMed.
- S. G. Zhao, P. F. Gong, S. Y. Luo, L. Bai, Z. S. Lin, Y. Y. Tang, Y. L. Zhou, M. C. Hong and J. H. Luo, Angew. Chem., Int. Ed., 2015, 54, 4217–4221 CrossRef CAS PubMed.
- S. G. Zhao, P. F. Gong, S. Y. Luo, L. Bai, Z. S. Lin, C. M. Ji, T. L. Chen, M. C. Hong and J. H. Luo, J. Am. Chem. Soc., 2014, 136, 8560–8563 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- C. T. Chen, G. L. Wang, X. Y. Wang and Z. Y. Xu, Appl. Phys. B: Lasers Opt., 2009, 97, 9–25 CrossRef CAS.
- C. T. Chen, Y. B. Wang, B. C. Wu, K. C. Wu, W. L. Zeng and L. H. Yu, Nature, 1995, 373, 322–324 CrossRef CAS.
- S. C. Wang, N. Ye, W. Li and D. Zhao, J. Am. Chem. Soc., 2010, 132, 8779–8786 CrossRef CAS PubMed.
- S. G. Zhao, P. F. Gong, L. Bai, X. Xu, S. Q. Zhang, Z. H. Sun, Z. S. Lin, M. C. Hong, C. T. Chen and J. H. Luo, Nat. Commun., 2014, 5, 4019 CAS.
- H. P. Wu, S. L. Pan, K. R. Poeppelmeier, H. Y. Li, D. Z. Jia, Z. H. Chen, X. Y. Fan, Y. Yang, J. M. Rondinelli and H. S. Luo, J. Am. Chem. Soc., 2011, 133, 7786–7790 CrossRef CAS PubMed.
- S. G. Zhao, P. F. Gong, S. Y. Luo, S. J. Liu, L. Li, M. Adnan, T. Khan, M. C. Hong, Z. S. Lin and J. H. Luo, J. Am. Chem. Soc., 2015, 137, 2207–2210 CrossRef CAS PubMed.
- L. Kang, S. Luo, H. Huang, T. Zheng, Z. S. Lin and C. T. Chen, J. Phys.: Condens. Matter, 2012, 24, 335503 CrossRef PubMed.
- P. Yu, L. M. Wu, L. J. Zhou and L. Chen, J. Am. Chem. Soc., 2014, 136, 480–487 CrossRef CAS PubMed.
- G. E. R. Schulze, Z. Phys. Chem., Abt. B, 1934, 24, 215–218 Search PubMed.
- Z. H. Li, Y. C. Wu, P. Z. Fu, S. L. Pan and C. T. Chen, J. Cryst. Growth, 2004, 270, 486–490 CrossRef CAS.
- Z. H. Li, Z. S. Lin, Y. C. Wu, P. Z. Fu, Z. Z. Wang and C. T. Chen, Chem. Mater., 2004, 16, 2906–2908 CrossRef CAS.
- S. F. Zhang, E. P. Zhang, P. Z. Fu and Y. C. Wu, J. Cryst. Growth, 2009, 311, 2433–2436 CrossRef CAS.
- G. G. Xu, J. Li, S. J. Han, Y. J. Guo and J. Y. Wang, Kristallografiya, 2010, 55, 1242–1244 CrossRef CAS.
- X. Zhang, L. R. Wang, S. F. Zhang, G. L. Wang, S. G. Zhao, Y. Zhu, Y. C. Wu and C. T. Chen, J. Opt. Soc. Am. B, 2011, 28, 2236–2239 CrossRef CAS.
- Z. Li, Q. Liu, S. J. Han, T. Iitaka, H. B. Su, T. Tohyama, H. D. Jiang, Y. J. Dong, B. Yang, F. F. Zhang, Z. H. Yang and S. L. Pan, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 245125 CrossRef.
- Z. J. Ma, K. C. Wu, R. J. Sa, K. N. Ding and Q. H. Li, AIP Adv., 2012, 2, 032170 CrossRef.
- B. B. Zhang, M.-H. Lee, Z. H. Yang, Q. Jing, S. L. Pan, M. Zhang, H. P. Wu, X. Su and C.-S. Li, Appl. Phys. Lett., 2015, 106, 031906 CrossRef.
- J. Li, Z. J. Ma, C. He, Q. H. Li and K. C. Wu, J. Mater. Chem. C, 2016, 4, 1926–1934 RSC.
- J. Y. Hu, Z. J. Ma, J. Li, C. He, Q. H. Li and K. C. Wu, J. Phys. D: Appl. Phys., 2016, 49, 185103 CrossRef.
- L. Yang, Y. C. Yue, F. Yang and Z. Y. Xu, Opt. Lett., 2016, 41, 1598–1600 CrossRef PubMed.
- J. Haines, C. Chateau, J. M. Leger and R. Marchand, Ann. Chim. Sci. Mater., 2001, 26, 209–215 CrossRef CAS.
- J. Haines, O. Cambon, R. Aster, P. Fertey and C. Chateau, Z. Kristallogr., 2004, 219, 32–38 CAS.
- A. Baykal and A. Evren, Turk. J. Chem., 2006, 30, 723–730 CAS.
- V. Vildosola, L. Pourovskii, R. Arita, S. Biermann and A. Georges, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 064518 CrossRef.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- B. G. Pfrommer, M. Cote, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233–240 CrossRef CAS.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. S. Lin, A. Qteish, M. C. Payne and V. Heine, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 4174–4180 CrossRef.
- F. Wooten, Optical properties of solids, Academic, New York, 1972 Search PubMed.
- L. J. Sham and M. Schluter, Phys. Rev. Lett., 1983, 51, 1888–1891 CrossRef.
- A. J. Cohen, P. Mori-Sanchez and W. T. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115123 CrossRef.
- P. Mori-Sanchez, A. J. Cohen and W. T. Yang, Phys. Rev. Lett., 2008, 100, 146401 CrossRef PubMed.
- R. He, H. W. Huang, L. Kang, W. J. Yao, X. X. Jiang, Z. S. Lin, J. G. Qin and C. T. Chen, Appl. Phys. Lett., 2013, 102, 231904 CrossRef.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2006, 124, 221101 CrossRef PubMed.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, an Augmented Plane Search PubMed.
- D. Koller, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195134 CrossRef.
- D. Koller, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 55109 Search PubMed.
- M. J. Frisch, et al., Gaussian 09, Gaussian, Wallingford, CT, 2009 Search PubMed.
- C. Aversa and J. E. Sipe, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 14636 CrossRef CAS.
- (a) A. H. Reshak, V. Kityk and S. Auluck, J. Phys. Chem. B, 2010, 114, 16705–16712 CrossRef CAS PubMed; (b) I. I. Tordjman, R. Masse and J. C. Guitel, Z. Kristallogr., 1974, 139, 103–115 CrossRef CAS.
- (a) A. H. Reshak, H. W. Huang, H. Kamarudin and S. Auluck, J. Appl. Phys., 2015, 117, 085703 CrossRef; (b) X. S. Wang, L. J. Liu, X. Y. Wang, L. Bai and C. T. Chen, CrystEngComm, 2015, 17, 925–929 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra26568e |
| This journal is © The Royal Society of Chemistry 2017 |