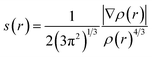Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Systematic analysis of structural and topological properties: new insights into PuO2(H2O)n2+ (n = 1–6) complexes in the gas phase
Peng Li *a,
Wenxia Niu*b and
Tao Gaoc
*a,
Wenxia Niu*b and
Tao Gaoc
aCollege of Physics and Electronic Engineering, Shanxi University, Taiyuan, 030006, China. E-mail: lip@sxu.edu.cn
bDepartment of Physics, Taiyuan Normal University, Taiyuan, 030031, China. E-mail: nwx_ky@163.com
cInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu, 610065, China
First published on 16th January 2017
Abstract
The equilibrium structure, stabilities, electronic structures, chemical bonding and topological properties of PuO2(H2O)n2+ (n = 1–6) complexes in the gas phase have been systematically investigated by different levels of theory. The results indicate that all the ground states of these complexes are triplet. The five water molecules of PuO2(H2O)m2+ (m = 1–5) are arranged on the equatorial plane of plutonyl. Reactivity analysis of PuO2(H2O)52+ shows that the oxygen atom of the sixth water molecule is connected by hydrogen-bonds to the two water molecules which are on the equatorial plane of PuO2(H2O)52+. The optimized geometries are in agreement with available theoretical and experimental results. The weak covalent interactions of Pu–ligand bonds were evaluated by the electron localization function and atoms in molecules analyses. The orbital interactions were investigated by analysis of total, partial, and overlap population density of state diagrams. Besides, a reduced density gradient approach was implemented to analyze the weak interactions and steric repulsions present in PuO2(H2O)52+ and PuO2(H2O)62+ complexes.
1 Introduction
The chemistry of dipositive actinyl ions, particularly plutonyl complexes, is of major importance in nuclear waste reprocessing cycles and safe storage.1–6 It is worth mentioning that Pu ions have a higher-valence above +4 (e.g., +5, +6, and +7), and can easily form a variety of complexes with other ligands. Another interesting topic of this area is the active effects of the 5f electrons, due to the f elements having a high oxophilicity feature.7 Therefore, the interactions of plutonyl with other ligand molecules have attracted considerable attention.8–18 In particular, researches have focused on the interaction of plutonyl with H2O molecules, which is a major issue in secure nuclear storage, because H2O plays a catalytic role in plutonium corrosion.19,20Theoretical research in this area is more common than experimental; this may be due to the high activity and radioactivity which causes difficulties for experimental studies. In a recent experimental study,11 the hydration and oxidation of gas-phase plutonyl monovalent ions were investigated by electrospray ionization mass spectrometry (ESI-MS), and the ESI mass spectra of PuO2(H2O)n+ (n = 0–5) were obtained. In contrast, tremendous theoretical works have been performed to exploring the properties of PuO2(H2O)n2+ complexes.10,12,16,17,21–24 Cao et al. have utilized density functional theory (DFT) methods to investigate the structural properties and vibrational frequencies of PuO2(H2O)m2+ complexes (m = 4–6).10 Most of the previous studies predicted that plutonyl(VI) ions will be the favorable structure, therefore, the equilibrium structure of PuO2(H2O)52+ has been well studied.12,16,17,20–23 On the other hand, these theoretical studies significantly suggest that DFT is an appropriate and successful method to access the nature of PuO2(H2O)n2+ complexes.
As seen from the above survey of PuO2(H2O)n2+ complexes, there are uncertainties of the bonds characterization, bonding mechanism and the effect of plutonyl orbitals in the interaction. Therefore, detailed interaction mechanisms and the topological properties as well as orbitals information need to be systematically examined.
The main focus of the present work is to perform a new thorough investigation of the PuO2(H2O)n2+ complexes (n = 1–6). The optimized geometries and electronic state properties of these complexes are reported. The covalent interactions were evaluated for Pu–ligand bonds in these complexes with electron localization function (ELF) and atoms in molecules (AIM) analyses. The roles of plutonyl orbitals were analyzed by total and partial density of state (TDOS and PDOS), and overlap population density of state (OPDOS) analysis. In addition, the weak interactions and steric repulsions exist in these complexes were studied by reduced density gradient (RDG) approach.
2 Computational details
Geometry optimization and frequency calculation of the stable structures were performed at the B3LYP,25,26 B3PW91,27 PBE0 (ref. 28) and PW91PW91 (ref. 29) methods, along with Stuttgart–Dresden–Bonn relativistic effective core potential (RECP)30 for Pu atom. This small core RECP, named as SDD, replaces 60 electrons in inner shells,1–4 leaving the 5s, 5p, 5d, 5f, 6s, 6p, 6d and 7s shells as the valence electrons. For O and H atoms, the 6-311++G(d,p) basis sets by Pople and coworkers were employed.31 Calculations were carried out by using the Gaussian 03 programs.32 The geometry structures of these complexes were identified to be one minimum in potential energy, and their stability were examined by molecular dynamics. The current computational scheme has been successfully performed in actinide systems.6,33–40 Specifically, previous works show that B3LYP/SDD and PW91/SDD methods have good performance in the structure and frequencies computation for Pu–H2O system.6With the aim of deeply investigate the nature of the bonding, a systematic topological description of these complexes was performed. The wavefunction files (.wfn) which obtained from geometry optimization and frequency calculation were used as input files of the Multiwfn41 package to perform the ELF42,43 and AIM44 analysis. In order to gathering insights about the participation of plutonyl orbitals in the chemical bonds of complexes, TDOS, PDOS, and OPDOS45,46 analysis were also performed. In addition, the reduced density gradient proposed by Yang et al.47 was used to obtain a deep insight into the weak interactions and steric repulsions in titled complexes.
3 Results and discussion
To evaluate the accuracy of current computational schemes for plutonyl systems, first, we calculated the bond distances and vibrational frequencies of PuO, PuO2 and PuO22+ molecule. The results are listed in Table 1 along with the corresponding available experimental values and previous theoretical results. As can be seen, our results are in agreement with available experimental values, and have good consistency with other theoretical results.| Methods | Methods | r(Pu–O) | Vibrational frequencies |
|---|---|---|---|
| a This work, SDD for Pu and 6-311++G(d,p) for O atoms.b Ref. 48.c Ref. 49.d Ref. 50.e Ref. 10.f Ref. 51.g Ref. 52. | |||
| PuO | B3LYP/SDDa | 1.832 | 792.73 |
| B3PW91/SDDa | 1.817 | 814.97 | |
| PBE0/SDDa | 1.813 | 816.41 | |
| PW91/SDDa | 1.832 | 768.92 | |
| CASPT2b | 1.818 | ||
| PW91/SDDc | 1.828 | ||
| Expt.d | 822.28 (Ar), 817.27 (Kr) | ||
| PuO2 | B3LYP/SDDa | 1.816 | 808.41, 757.01, 160.11 |
| B3PW91/SDDa | 1.801 | 833.03, 778.24, 170.32 | |
| PBE0/SDDa | 1.794 | 844.90, 789.74, 173.52 | |
| PW91/SDDa | 1.804 | 823.57, 709.59, 173.61 | |
| M06/SDDc | 1.786 | ||
| PW91/SDDc | 1.802 | ||
| Expt.d | 794.2 (Ar), 786.8 (Kr) | ||
| PuO22+ | B3LYP/SDDa | 1.673 | 1101.36, 237.98, 250.20, 980.20 |
| B3PW91/SDDa | 1.662 | 1127.62, 244.23, 255.84, 1010.96 | |
| PBE0/SDDa | 1.653 | 1153.99, 257.02, 263.77, 1041.14 | |
| PW91/SDDa | 1.695 | 1039.55, 207.96, 210.55, 915.67 | |
| B3LYP/RECP78e | 1.663 | ||
| MP2/RECP78e | 1.686 | ||
| Expt. | 1.74f | 1043, 218 × 2, 1020g | |
3.1 Geometric structures and electronic properties
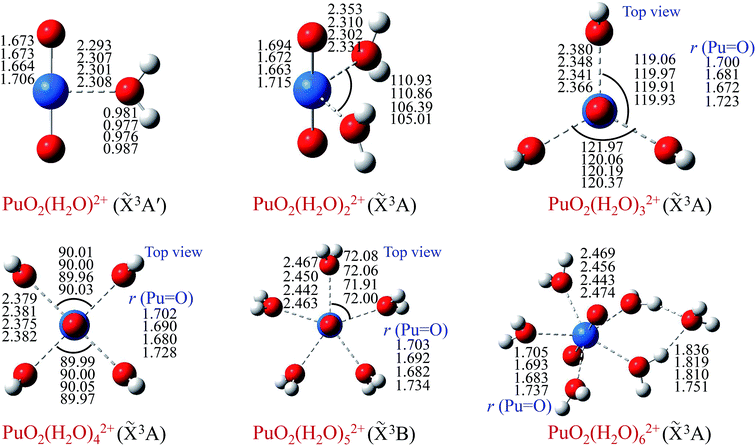
In order to obtain minimum energy structures, dozens of possible structures of PuO2(H2O)n2+ complexes (n = 1–6) were constructed, and taking into account different possible spin states. Geometry optimization was performed without symmetry constrain, and their corresponding ground state geometries in the gas phase were located. Moreover, the stability of these stable structures was confirmed by Born–Oppenheimer molecular dynamics (BOMD)53 simulations at 300 K. Geometric parameters are reported in Fig. 1 for different levels of theory.As can been seen from Fig. 1, the optimized geometries show little dependence on the level of theory. Our results indicate that the ground electronic state of these complexes are triplet. In terms of geometry, we can see that water molecules of PuO2(H2O)m2+ (m = 1–5) are arranged on the equatorial plane of the plutonyl group. In particular, water molecules wherein PuO2(H2O)32+ and PuO2(H2O)42+ are almost in the equivalent position.
To evaluate the sites of six water molecules in PuO2(H2O)62+, we performed the reactivity analysis by using electrostatic potential (ESP) on molecular vdW surface of PuO2(H2O)52+. ESP on vdW surface has been proved as a critical for studying intermolecular interaction, and widely used for prediction of nucleophilic and electrophilic sites. More negative ESP signifies this region has the stronger ability to attract electrophiles, on the contrary, more positive ESP site has the stronger ability to attract nucleophiles.54 The ESP-mapped vdW surface of PuO2(H2O)52+ is shown in Fig. 2. It can be seen that, the surface maximum of ESP present at the H atoms of water molecule. Therefore, from ESP point of view, these H atoms of the PuO2(H2O)52+ are the primary bonding site of O atom. After optimization, as seen from Fig. 1, we found that the oxygen atom of sixth water molecule is connected to the two water molecules which on the equatorial plane of PuO2(H2O)52+ by hydrogen-bonds.
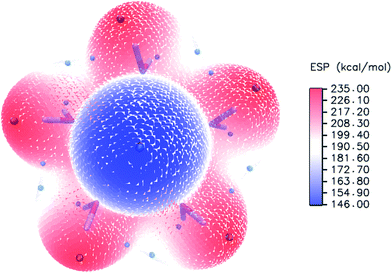 | ||
| Fig. 2 ESP-mapped molecular vdW surface of PuO2(H2O)52+. The unit is in kcal mol−1. Surface local minima and maxima of ESP are represented as green and orange spheres, respectively. | ||
In terms of bond length, with the increase of water molecules, the bond length of Pu–Oyl and Pu![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O increased slightly. Taking the calculation result of B3LYP/SDD as an example, for bond length of Pu–Oyl, 2.293 Å for PuO2(H2O)2+ and 2.469 Å for PuO2(H2O)62+; for bond length of Pu
O increased slightly. Taking the calculation result of B3LYP/SDD as an example, for bond length of Pu–Oyl, 2.293 Å for PuO2(H2O)2+ and 2.469 Å for PuO2(H2O)62+; for bond length of Pu![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, 1.673 Å for PuO2(H2O)2+ and 1.705 Å for PuO2(H2O)62+, respectively.
O, 1.673 Å for PuO2(H2O)2+ and 1.705 Å for PuO2(H2O)62+, respectively.
3.2 Bonding features
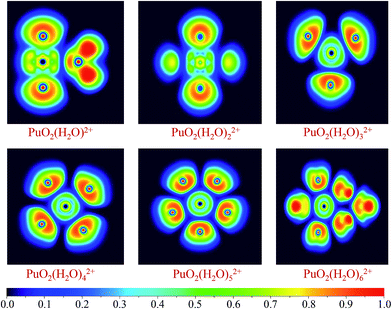
The bonding nature of Pu–O for these complexes have been investigated using ELF and AIM analytical method. It is worth mentioned that ELF and AIM are appropriate and successful tools to analyzing bonding mechanism and have been applied in many actinides complexes investigations. In addition, ELF obtained from small-core RECP has been proven to correctly analyze the topological properties.55,56The ELF shaded-surface-projection map of the titled complexes are displayed in Fig. 3. As can be seen, these are disynaptic valence basins between the Pu and Oyl atoms, which indicate that there are covalent bonds formation between plutonyl and H2O molecules.
In order to further exploring the chemical-bonding natures of these complexes, we employ a more quantitative method, the atoms in molecules (AIM) analysis. The different topological properties including electron density ρ(r) and its Laplacian ∇2ρ(r), kinetic electron energy density G(r), potential energy density V(r) and the total energy density H(r) of the (3, −1) bond critical points (BCP) were calculated. The corresponding results are shown in Table 2.
| Complexes | Species | ρ(r) | ∇2ρ(r) | G(r) | V(r) | H(r) |
|---|---|---|---|---|---|---|
| a Two special water molecules of PuO2(H2O)52+, which connected with the sixth water molecule.b Hydrogen-bonds. | ||||||
| PuO2H2O2+ | Pu–O | 0.388 | 0.211 | 0.476 | −0.900 | −0.424 |
| Pu–Oyl | 0.074 | 0.314 | 0.085 | −0.093 | −0.008 | |
| PuO2(H2O)22+ | Pu–O | 0.384 | 0.187 | 0.466 | −0.885 | −0.419 |
| Pu–Oyl | 0.072 | 0.302 | 0.081 | −0.087 | −0.006 | |
| PuO2(H2O)32+ | Pu–O | 0.375 | 0.191 | 0.448 | −0.849 | −0.401 |
| Pu–Oyl | 0.065 | 0.280 | 0.074 | −0.077 | −0.003 | |
| PuO2(H2O)42+ | Pu–O | 0.366 | 0.199 | 0.432 | −0.815 | −0.383 |
| Pu–Oyl | 0.060 | 0.257 | 0.066 | −0.068 | −0.002 | |
| PuO2(H2O)52+ | Pu–O | 0.364 | 0.200 | 0.428 | −0.806 | −0.378 |
| Pu–Oyl | 0.051 | 0.215 | 0.054 | −0.0543 | −0.0003 | |
| PuO2(H2O)62+ | Pu–O | 0.323 | 0.326 | 0.377 | −0.673 | −0.296 |
| Pu–Oyl | 0.049 | 0.203 | 0.0511 | −0.0513 | −0.0002 | |
| Pu–Oyla | 0.054 | 0.212 | 0.054 | −0.056 | −0.002 | |
| H–Ob | 0.039 | 0.121 | 0.032 | −0.034 | −0.002 | |
As the criterion proposed by Cremer and Kraka:57 |V(r)| > G(r), H(r) is negative, corresponds to covalent interactions; conversely, for closed-shell interactions, |V(r)| < G(r), H(r) is positive. This criterion was proved to be very sufficient to explore the bonding characteristics for actinide system.37–39 As shown in Table 2, the H(r) values of all calculated BCPs in the PuO2(H2O)n2+ are negative, the corresponding |V(r)|/G(r) ratio exceeds 1.0. The H(r) values of Pu–Oyl bonds are relatively small (around −0.003), and with the increase of water molecules, this value is decreasing. These quantities suggest that the Pu–Oyl bonds belong to weak covalent interaction. This conclusion is consistent with the ELF analysis. In term of the connection of sixth water molecule, there are two (3, −1) BCPs between the oxygen atom of sixth water molecule and two water molecules in the vertical plane of PuO2(H2O)52+. The corresponding ρ(r) = 0.039, H(r) = −0.002, indicating that these two bonds are hydrogen bonds.
3.3 Orbital interactions
As can be seen from the above discussion, on the basis of PuO2(H2O)52+ complex, the additional water molecules will no longer bonding with the main PuO22+ molecule directly. To get more in-depth information about the roles that plutonyl orbitals play in the formation of plutonyl–water complexes, the TDOS, PDOS and OPDOS of PuO2(H2O)52+ and PuO2(H2O)62+ were calculated and plotted with Gaussian curves, the corresponding full width at half maximum (FWHM) is 0.05 a.u. The TDOS, PDOS and OPDOS graphics are depicted in Fig. 4. The vertical dashed line indicates the position of the HOMO level. Fragment 1 is defined as the plutonyl orbitals and fragment 2 is defined as the oxygen and hydrogen atom orbitals.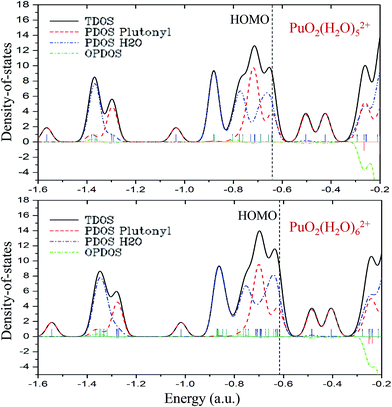 | ||
| Fig. 4 The TDOS, PDOS, and OPDOS curves of PuO2(H2O)52+ and PuO2(H2O)62+ at the B3PW91/SDD levels of theory. | ||
As seen in Fig. 4, at the position of the HOMO level, the H2O orbitals approached the TDOS line, which means that most of the contributions to the HOMO came from the H2O orbitals. The OPDOS values of plutonyl and H2O orbitals are almost zero, which means that there are weak covalent characters in PuO2(H2O)52+ and PuO2(H2O)62+ complex. Comparing the two subgraphs, we found that the addition of the sixth water molecule had little effect on the overall DOS.
3.4 Weak interactions
With the aim of investigating the weak interactions of the PuO2(H2O)52+ and PuO2(H2O)62+ complexes, we performed reduced density gradient (RDG) analysis. The RDG was defined as follows:46where ρ(r) is electron density. The RDG s(r) isosurfaces are mapped with values of ρ(r)·sgn(λ2), where sgn is the signum function, and λ2 is the sign of the second eigenvalue of the Hessian of the ρ(r).
Fig. 5 shows the 3D isosurfaces (s = 0.5) and scatter plots of the RDG vs. ρ(r)sign(λ2) were generated for PuO2(H2O)52+ and PuO2(H2O)62+ complexes. From the isosurfaces, we can see that the Pu–Oyl interaction in PuO2(H2O)62+ is slightly weaker than that in the PuO2(H2O)52+. The ρ(r)·sgn(λ2) value of Pu–Oyl interaction in the PuO2(H2O)52+ is −0.0335 a.u., and the corresponding value in PuO2(H2O)62+ is −0.034 a.u. In addition, there are two spikes in RDG vs. ρ(r)sign(λ2) of PuO2(H2O)52+, one is around −0.01 a.u. corresponding the van der Waals interaction between the adjacent water molecules; the other one is around 0.01 a.u., represents the steric repulsion effects between Pu and H2O molecules which on both sides of Pu–Oyl. Differently, the RDG vs. ρ(r)sign(λ2) of PuO2(H2O)62+ is one more spike than that of PuO2(H2O)52+ in the region of 0 to −0.4 a.u. This spike around −0.034 is corresponds to the hydrogen-bond interaction of the sixth H2O molecule and two water molecules in the vertical plane of PuO2(H2O)52+.
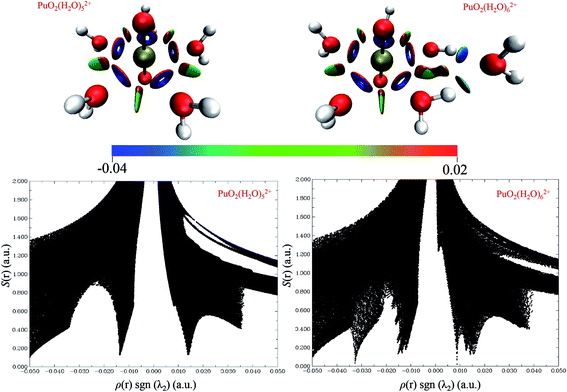 | ||
| Fig. 5 3D isosurfaces (s = 0.5) and scatter plots of the RDG vs. ρ(r)sign(λ2) were generated for PuO2(H2O)52+ and PuO2(H2O)62+ complexes. | ||
In order to quantitatively gauge the bond strengths, in Table 3, we computed bond dissociation energies (BDE) of Pu–Oyl bond for PuO2(H2O)32+, PuO2(H2O)42+ and PuO2(H2O)52+ as well as hydrogen-bond for PuO2(H2O)62+ complexes. It can be clearly seen that, as the H2O number increases, the BDE of Pu–Oyl bond decrease. Taking PW91/SDD results as an example, the BDE of Pu–Oyl for PuO2(H2O)32+ as much as 49.788 kcal mol−1, which is larger than that computed for the PuO2(H2O)42+ (36.675 kcal mol−1) and more larger than that for the PuO2(H2O)52+ (27.145 kcal mol−1). In the case of O–H hydrogen-bond for PuO2(H2O)62+, by contrast, the BDE is smaller (12.287 kcal mol−1 in PW91/SDD method).
| Complex | B3LYP/SDD | B3PW91/SDD | PBE0/SDD | PW91/SDD | |
|---|---|---|---|---|---|
| PuO2(H2O)32+ | r(Pu–Oyl) | 2.351 | 2.310 | 2.302 | 2.331 |
| BDE | 42.586 | 49.903 | 45.973 | 49.788 | |
| PuO2(H2O)42+ | r(Pu–Oyl) | 2.379 | 2.381 | 2.375 | 2.382 |
| BDE | 40.330 | 39.143 | 40.941 | 36.675 | |
| PuO2(H2O)52+ | r(Pu–Oyl) | 2.467 | 2.450 | 2.442 | 2.463 |
| BDE | 21.150 | 20.413 | 22.967 | 27.145 | |
| PuO2(H2O)62+ | r(O6yl–H′) | 1.836 | 1.819 | 1.810 | 1.751 |
| BDE | 11.133 | 10.794 | 11.637 | 12.287 |
4 Conclusions
The equilibrium structure, stabilities, electronic structures, chemical bonding and topological properties of PuO2(H2O)n2+ (n = 1–6) complexes in gas phase have been systematically investigated by different levels of theory. The following conclusions were refined from the present results.(1) The ground state geometry of these complexes was found, and our results show that all the ground states of these complexes are triplet. The water molecules of PuO2(H2O)m2+ (m = 1–5) are arranged on the equatorial plane of plutonyl. Reactivity analysis and optimization results of PuO2(H2O)62+ show that, the oxygen atom of sixth water molecule connected with two water molecules in the vertical plane of PuO2(H2O)52+ by hydrogen-bonds. These optimized geometries are in agreement with available theoretical and experimental results.
(2) The properties of the chemical-bonding of these complexes were evaluated with ELF, AIM and TDOS, PDOS and OPDOS analyses. The ELF and AIM analyses indicate the Pu–Oyl bonds have weak covalent interaction. This conclusion is consistent with the OPDOS analysis. The TDOS results show that most of the contributions to the HOMO of PuO2(H2O)52+ and PuO2(H2O)62+ came from the H2O orbitals.
(3) The RDG approach was implemented to analyze the weak interactions and steric repulsions existed in PuO2(H2O)52+ and PuO2(H2O)62+ complexes. In addition to explaining weak covalent interactions of Pu–Oyl, the RDG results also suggest that the interactions of the sixth H2O molecule and two water molecules in the vertical plane of PuO2(H2O)52+ are hydrogen-bonds.
Acknowledgements
This work is supported by National Natural Science Foundation of China (NSFC) (Grant No. 11604187 and No. 11647040). We are very grateful to Dr Sobereva for many helpful discussions and providing us with the Multiwfn package. We would like to thank the reviewers for the valuable suggestions on improving our paper.References
- R. G. Denning, J. Phys. Chem. A, 2007, 111, 4125 CrossRef CAS PubMed.
- U. Wahlgren, H. Moll, I. Grenthe, B. Schimmelpfennig, L. Maron, V. Vallet and O. Gropen, J. Phys. Chem. A, 1999, 103, 8257 CrossRef CAS.
- J. M. Haschke, T. H. Allen and J. L. Stakebake, J. Alloys Compd., 1996, 243, 23 CrossRef CAS.
- J. M. Haschke, T. H. Allen and L. A. Morales, Science, 2000, 287, 285 CrossRef CAS PubMed.
- J. M. Haschke, T. H. Allen and L. A. Morales, J. Alloys Compd., 2001, 314, 78 CrossRef CAS.
- P. Li, W. X. Niu, T. Gao and H. Y. Wang, ChemPhysChem, 2014, 15, 3078 CrossRef CAS PubMed.
- H. H. Cornehl, R. Wesendrup, M. Diefenbach and H. Schwarz, Chem.–Eur. J., 1997, 3, 1083 CrossRef CAS.
- C. Madic, G. M. Begun, D. E. Hobart and R. L. Hahn, Inorg. Chem., 1984, 23, 1914 CrossRef CAS.
- S. D. Conradson, K. D. Abney, B. D. Begg, E. D. Brady, D. L. Clark, C. den Auwer, M. Ding, P. K. Dorhout, F. J. Espinosa-Faller and P. L. Gordon, Inorg. Chem., 2004, 43, 116 CrossRef CAS PubMed.
- Z. Cao and K. Balasubramanian, J. Chem. Phys., 2005, 123, 114309 CrossRef PubMed.
- D. Rios, M. C. Michelini, A. F. Lucena, J. Marcalo, T. H. Bray and J. K. Gibson, Inorg. Chem., 2012, 51, 6603 CrossRef CAS PubMed.
- K. A. Maerzke, G. S. Goff, W. H. Runde, W. F. Schneider and E. J. Maginn, J. Phys. Chem. B, 2013, 117, 10852 CrossRef CAS PubMed.
- J. P. Austin, M. Sundararajan, M. A. Vincent and I. H. Hillier, Dalton Trans., 2009, 5902 RSC.
- L. H. Jones and R. A. Penneman, J. Chem. Phys., 1953, 21, 542 CrossRef CAS.
- G. A. Shamov and G. Schreckenbach, J. Phys. Chem. A, 2006, 110, 12072 CrossRef CAS.
- A. Kovács, R. J. M. Konings, J. K. Gibson, I. Infante and L. Gagliardi, Chem. Rev., 2015, 115, 1725 CrossRef PubMed.
- S. E. Horowitz and J. B. Marston, J. Chem. Phys., 2011, 134, 064510 CrossRef CAS PubMed.
- J. G. Du, X. Y. Sun and G. Jiang, Int. J. Mol. Sci., 2016, 17, 414 CrossRef PubMed.
- J. M. Haschke, J. Alloys Compd., 1998, 278, 149 CrossRef CAS.
- J. M. Haschke, T. H. Allen and L. A. Morales, Los Alamos Sci., 2000, 26, 252 CAS.
- P. J. Hay, R. L. Martin and G. Schreckenbach, J. Phys. Chem. A, 2000, 104, 6259 CrossRef CAS.
- G. A. Shamov and G. Schreckenbach, J. Phys. Chem. A, 2005, 109, 10961 CrossRef CAS PubMed.
- V. Vallet, P. Macak, U. Wahlgren and I. Grenthe, Theor. Chem. Acc., 2006, 115, 145 CrossRef CAS.
- G. Schreckenbach and G. A. Shamov, Acc. Chem. Res., 2010, 43, 19 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- A. D Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef.
- A. D. Becke, Phys. Rev. A, 1998, 38, 3098 CrossRef.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533 CrossRef CAS.
- W. Kuchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535 CrossRef.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb and J. R. Cheeseman, et al., Gaussian 03, Revision E.01., Gaussian, Inc., Wallingford, CT, USA, 2004 Search PubMed.
- M. C. Michelini, N. Russo and E. Sicilia, Angew. Chem., Int. Ed., 2006, 45, 1095 CrossRef CAS PubMed.
- M. E. Alikhani, M. C. Michelini, N. Russo and B. Silvi, J. Phys. Chem. A, 2008, 112, 12966 CrossRef CAS PubMed.
- J. Zhou and H. B. Schlegel, J. Phys. Chem. A, 2010, 114, 8613 CrossRef CAS PubMed.
- K. J. De Almeida and H. A. Duarte, Organometallics, 2010, 29, 3735 CrossRef CAS.
- X. F. Wang, L. Andrews and C. J. Marsden, Chem.–Eur. J., 2007, 13, 5601 CrossRef CAS PubMed.
- P. Li, W. X. Niu and T. Gao, RSC Adv., 2014, 4, 29806 RSC.
- P. Li, W. X. Niu and T. Gao, J. Radioanal. Nucl. Chem., 2015, 304, 489 CrossRef CAS.
- P. Li, W. X. Niu and T. Gao, J. Mol. Model., 2015, 21, 316 CrossRef PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397 CrossRef CAS.
- A. Savin, R. Nesper, S. Wengert and T. R. Fassler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808 CrossRef CAS.
- R. F. W. Bader, Atoms in molecules. A quantum theory, Clarendon, Oxford, 1990 Search PubMed.
- R. Hoffmann, Solids and surfaces: a chemist's view of bonding in extended structures, VCH, New York, 1988 Search PubMed.
- J. G. Malecki, Polyhedron, 2010, 29, 1973 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed.
- A. Kovács and R. J. M. Konings, J. Phys. Chem. A, 2011, 115, 6646 CrossRef PubMed.
- W. Küchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535 CrossRef.
- D. W. Green and G. T. Reedy, J. Chem. Phys., 1978, 69, 544 CrossRef CAS.
- S. D. Conradson, Appl. Spectrosc., 1998, 52, 252A CrossRef CAS.
- L. V. Moskaleva, A. V. Matveev, J. Dengler and N. Rösch, Phys. Chem. Chem. Phys., 2006, 8, 3767 RSC.
- V. Bakken, J. M. Millam and H. B. Schlegel, J. Chem. Phys., 1999, 111, 8773 CrossRef CAS.
- T. Lu and F. Chen, J. Mol. Graphics Modell., 2012, 38, 314 CrossRef CAS PubMed.
- E. Di Santo, M. C. Michelini and N. Russo, Organometallics, 2009, 28, 3716 CrossRef CAS.
- S. F. Vyboishchikov, A. Sierraalta and G. Frenking, J. Comput. Chem., 1996, 18, 416 CrossRef.
- D. Cremer and E. Kraka, Angew. Chem., Int. Ed. Engl., 1984, 23, 627 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |