Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermal decomposition of isolated and crystal 4,10-dinitro-2,6,8,12-tetraoxa-4,10-diazaisowurtzitane according to ab initio molecular dynamics simulations†
Dong Xiang and
Weihua Zhu *
*
Institute for Computation in Molecular and Materials Science, Department of Chemistry, Nanjing University of Science and Technology, Nanjing 210094, China. E-mail: zhuwh@njust.edu.cn
First published on 25th January 2017
Abstract
We performed ab initio molecular dynamics simulations to study the initiation chemical reaction and subsequent decomposition mechanism of a 4,10-dinitro-2,6,8,12-tetraoxa-4,10-diazaisowurtzitane (TEX) crystal at 2160 K. It was found that there are three different initial reactions involved in the decomposition of an isolated TEX molecule. The activation energy barriers for the initial decomposition reactions indicate that among the three initial reaction paths, cleavage of the nitrogen–nitro bond is the easiest path to be triggered. The decomposition of the TEX crystal is triggered by the unimolecular C–H bond breaking to form a hydrogen radical. The generated H radicals can prompt other unreacted TEX molecules to decompose. Moreover, there are many multimolecular reactions during the decomposition of the TEX crystal. Overall, after the decomposition of TEX was triggered, some long chains and complicated carbon-rich heterocyclic rings were formed, and then they split to form small fragments. This study may provide useful information to understand the decomposition mechanism of cage explosives and develop new high-energy explosives.
1. Introduction
In recent years, 4,10-dinitro-2,6,8,12-tetraoxa-4,10-diazaisowurtzitane (TEX) has attracted attention as a novel energy material with a cage structure due to its high performance, high thermal stability, and insensitivity towards external stimuli.1 TEX (Fig. 1a) possesses the same isowurtzitane cage structure as CL-20 (2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane or HNIW), which is one of the most powerful high explosives that have been synthesized to date, and it also has a relatively high ambient temperature density of 1.99 g cm−3.2 The absence of sterically demanding nitramine groups in the TEX structure greatly reduces its sensitivity greatly and makes it an interesting insensitive energetic material (h50 > 177 cm).3 Its heat of formation, detonation velocity, and detonation pressure were calculated to be −541 kJ mol−1, 8665 m s−1, and 41.03 GPa, respectively.4 To understand the complex behavior of explosives, to control risk during their usage and storage, and to develop new high-energy explosives, it is necessary to study the structure and properties of TEX as it has a special structure and exhibits excellent performance under extreme conditions.It is known that information on the thermal decomposition mechanisms of explosives is useful for understanding their behavior at high temperatures. However, it is extremely difficult to obtain a clear molecular-level picture of the thermal decomposition of explosives through experimental measurements due to their complex behavior and the risks associated with them. An alternative approach is atomistic simulation, which is an effective way to model the physical and chemical properties of complex solids at the atomic level under high temperature conditions. The advances in ab initio molecular dynamics (AIMD) methodology5,6 make it possible to study the complex chemical phenomena of explosives at high temperatures. Recently, AIMD has been successfully applied to study the thermal decomposition of explosives.7–11 For example, Isayev et al.8 performed a series of ab initio molecular dynamics simulations to improve the atomistic understanding of the thermal decomposition of gaseous and solid CL-20 at high temperatures. Wu et al.9 performed ab initio molecular dynamics simulations to investigate the thermal decomposition of 3,6-di(azido)-1,2,4,5-tetrazine (DiAT) at 3000 K. Ye et al.10 unraveled the initial decomposition reactions of bicyclic-HMX via ab initio molecular dynamics simulations. Although these studies provide important information for understanding the initial decomposition reactions of the explosives, full picture of their decomposition mechanisms is as complex as far from completion.
In this study, we performed AIMD simulations to study the chemical events involved in the initial decomposition reactions of unimolecular and crystalline TEX at high temperatures.
2. Computational methods
AIMD simulations were performed within the framework of density functional theory (DFT)12,13 based on the CASTEP code14 using Troullier–Martins norm-conserving pseudopotentials15 and a plane-wave expansion of the wave functions. Moreover, the Perdew–Burke–Ernzerhof16 (PBE) exchange–correlation function was employed. We applied a plane wave cut-off of 500 eV for the MD simulations and 900 eV for geometry optimizations and energy calculations. In addition, the ionic temperature was controlled using a Nosé thermostat in the NVT ensemble.17 The initial positions of the simulation supercell were obtained from the experimentally determined X-ray crystal structure.18 The convergence criteria were as follows: an energy difference of 1 × 10−5 eV for solving the electronic wave functions and a force of 1 × 10−3 eV for structural optimizations. We used bond length and lifetime criteria to identify the changes in the geometry during the simulations. It was observed that a new bond is formed between two atoms when the smallest distance between them is larger than 0.6 times the ideal bond length, whereas a bond is ruptured when the largest distance between them is greater than 1.15 times the ideal bond length. For atoms bonded to hydrogen, the lifetime criterion must be met for at least 20 fs, whereas atoms that are not bonded to hydrogen (e.g. C–C, N–N, N–O, etc.) must survive for 45 fs.To study the unimolecular decomposition of an isolated TEX molecule, one optimized TEX molecule at 0 K was placed in the center of a 18.0 Å cubic periodic cell. The 18.0 Å cubic box is large enough to prevent interactions between the periodic images.8 The system was first equilibrated at 298.15 K for 15 ps with a time step of 1.0 fs using the NVT ensemble, and then heated to 2160 K. After this, ab initio MD simulations were carried out using a time step of 1.0 fs at 2160 K for 15 ps. To provide appropriate statistical sampling and obtain more reliable results, we performed 10 independent simulations of the unimolecular decomposition process. The Mulliken bond orders of TEX were calculated in the gas phase at the B3LYP/6-311+G(d,p) level. We located the nearby transition states (TSs), which were confirmed to have exactly one negative eigenvalue of the Hessian, in the gas phase at UB3LYP/6-311+g(d,p) level. The geometries and energies of the reactants and products were calculated at the B3LYP/6-311+G(d,p) level. In our previous studies, this method has been demonstrated to be reliable for studying organic explosive molecules.9,19 Then, we followed the reaction path by intrinsic reaction coordinate (IRC) scans to connect the structures of the reactants and products.
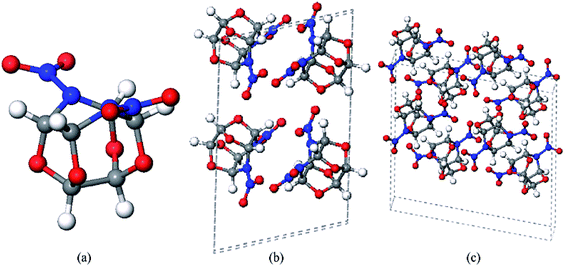
The thermal decomposition of crystalline TEX was simulated using a 2 × 1 × 1 unit cell (4 TEX molecules, 96 atoms, as shown in Fig. 1b). After the system was equilibrated at 298.15 K for 15 ps with a time step of 1.0 fs, ab initio MD simulations were carried out at 2160 K with a time step of 1.0 fs for 130 ps. Moreover, to verify the size dependence of the system, we performed one additional large-scale simulation with a larger 3 × 1 × 1 supercell (8 TEX molecules, 144 atoms, as shown in Fig. 1c) at 2160 K for 15 ps with a 1.0 fs time step after the system was equilibrated at 298.150 K for 15 ps.
3. Results and discussion
TEX crystallizes in a monoclinic lattice with a P1 space group and contains two molecules per unit cell (48 atoms). Our optimized lattice parameters are a = 82.12, b = 74.94, and c = 78.91 Å, which are in agreement with the experimental lattice parameters (a = 82.37, b = 75.05, and c = 79.46 Å),20 with an average error of 0.6%. The density of TEX was calculated to be 1.91 g cm−3, 4% smaller than the experimental density. In addition, the calculated bond lengths, bond angles, and dihedral angles of TEX compare well with the experimental values, as shown in Table 1. All the results validate the reliability of our calculations and indicate that PBE-G06 is appropriate to study the TEX crystal.| Bond lengths | Expt.20 | Cal. | Bond angles | Expt.20 | Cal. |
|---|---|---|---|---|---|
| a The values in parentheses correspond to the percentage differences relative to the experimental data. | |||||
| N4–O4 | 1.225 | 1.236 (−0.89) | O4–N4–N3 | 117.073 | 116.436 (0.54) |
| N4–N3 | 1.396 | 1.432 (−2.58) | N3–C3–O7 | 112.183 | 112.117 (0.06) |
| C2–N3 | 1.448 | 1.458 (−0.69) | C2–C1–N1 | 109.161 | 109.209 (−0.04) |
| C3–O7 | 1.421 | 1.423 (−0.14) | O4–N4–N3–C2 | −167.774 | −168.930 (−0.69) |
| C5–C6 | 1.557 | 1.600 (−2.76) | C1–N1–C4–O8 | −57.907 | −58.518 (−1.06) |
3.1. Decomposition mechanism of the isolated TEX molecule
Table 2 lists the bond orders of five different types of bonds in a single TEX molecule at B3LYP/6-311+G(d,p) level. It was found that among these bonds, the N1–N2 bond has the smallest bond order. This indicates that it may be the weakest bond and its cleavage will trigger the decomposition of the TEX molecule.| Bond | N1–N2 | C1–O5 | C1–C2 | C5–C6 | C1–N1 |
| Bond order | 0.177 | 0.227 | 0.288 | 0.211 | 0.288 |
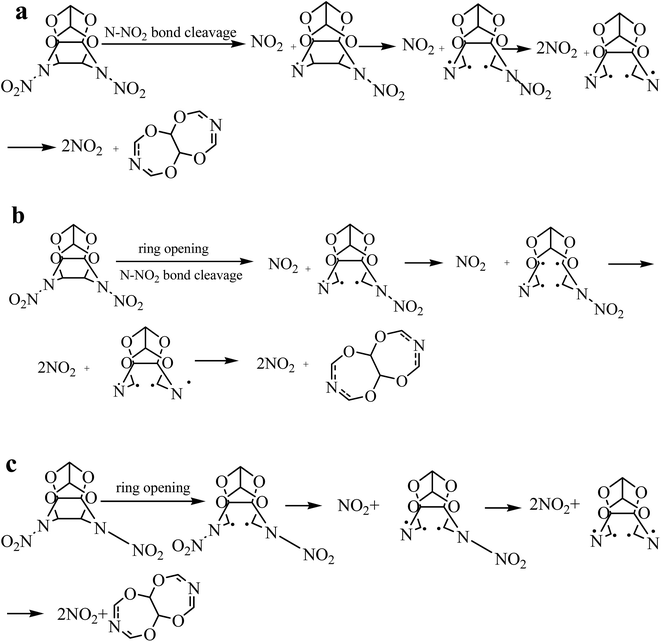
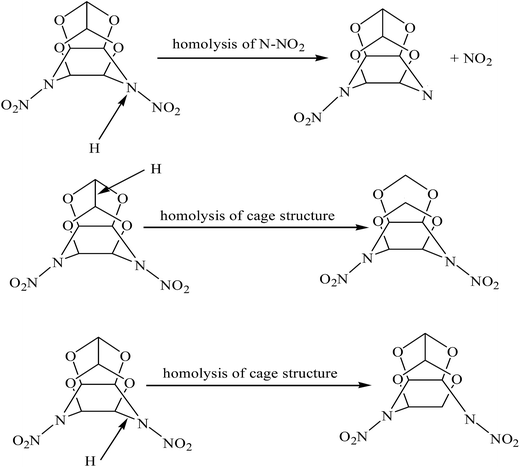
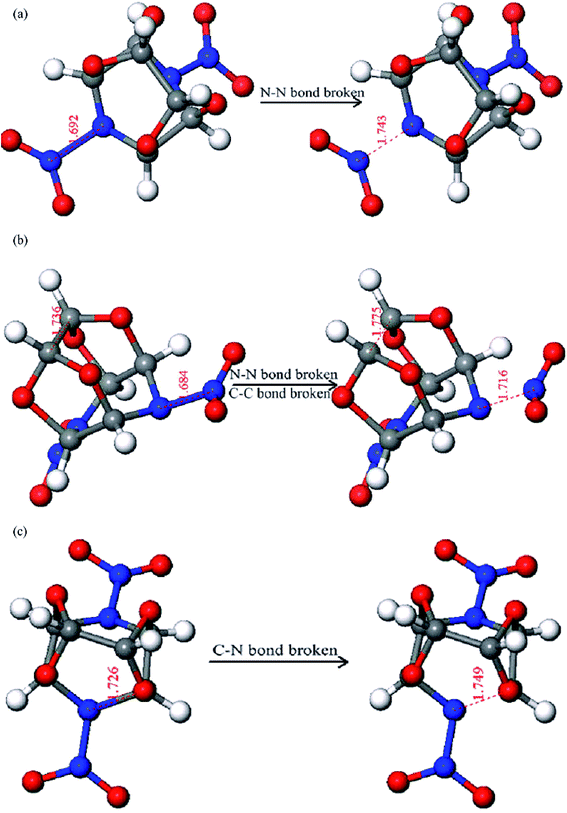
From the ten independent simulations conducted on the isolated TEX molecule at 2160 K, three different initial decomposition reactions were observed and the corresponding snapshots are shown in Fig. 2. These include (a) the N–NO2 bond cleavage to release NO2, (b) the N–NO2 bond cleavage and ring opening in the concerted step, and (c) the ring opening via the cleavage of a C–C bond. It can be seen in Fig. 2a that the N–NO2 bond length changes from 1.692 to 1.743 Å. In addition, the N–NO2 cleavage has a lifetime of approximately 0.6 ps. Fig. 2b indicates that the N–NO2 bond length changes from 1.684 to 1.716 Å and the C–C bond length changes from 1.736 to 1.775 Å. Moreover, the C–N bond length varies from 1.726 to 1.749 Å, as shown in Fig. 2c. The bond cleavages shown in Fig. 2b and c have a slightly smaller lifetime at a given temperature than that shown in Fig. 2a. Compared with path (a), as shown in Fig. 2a, the appearance incidence of paths (b), as shown in Fig. 2b, and (c), as shown in Fig. 2c, is very low. Therefore, the N–NO2 fission predominated in the early thermal decomposition stages of the TEX molecule. The homolysis of all N–NO2 bonds took place within the time range of 0.085–0.152 ps, which is in agreement with the conclusion drawn from the bond order analysis. Isayev et al.8 reported only one distinct initial reaction in the thermal decomposition of CL-20: the cleavage of the N–NO2 bond before a cage-opening reaction.7 This is similar to the initial decomposition reaction for the TEX molecule studied herein. The paths (b) and (c) have not been reported in the thermal decomposition of other nitramine explosives (e.g., CL-20, RDX, HMX, etc.).21,22 Moreover, subsequently generated intermediates during these three initial decomposition paths are different from those in the unimolecular decomposition of the isolated TEX molecule. This should be confirmed by further experimental studies.
 | ||
| Fig. 2 Snapshots of three different initiation reactions in the thermal decomposition of the isolated TEX molecule. | ||
More detailed decomposition processes that occur after the three initiation reactions are shown in Fig. 3. After the TEX explosion was triggered by the three different initial decomposition reactions, the subsequent decomposition intermediates were examined. It was found that the cage-opening mechanisms of the TEX molecules are different: the cage breaking by the C1–C2 cleavage predominates, whereas that by the C3–C4 fission is occasional. After cage opening, subsequent decomposition processes are accompanied by the cleavage of the C–O and C–N bonds to form various types of radicals and release NO2. Most of the radicals are very unstable. For example, one TEX molecule rapidly decomposed into two nitrogen molecules and one heterocyclic radical. The heterocyclic radical further decomposed to form several different small fragments. Some small intermediates decomposed in a stepwise manner to produce HCN molecules. Others were oxidized by NO2 that lead to further decomposition, forming one to two HCN molecules (depending on bond length) and yielding simpler methyleneformamide carbenes. Although our AIMD simulations were performed on an isolated TEX, the results provided an important qualitative picture for understanding its initial thermal decomposition.
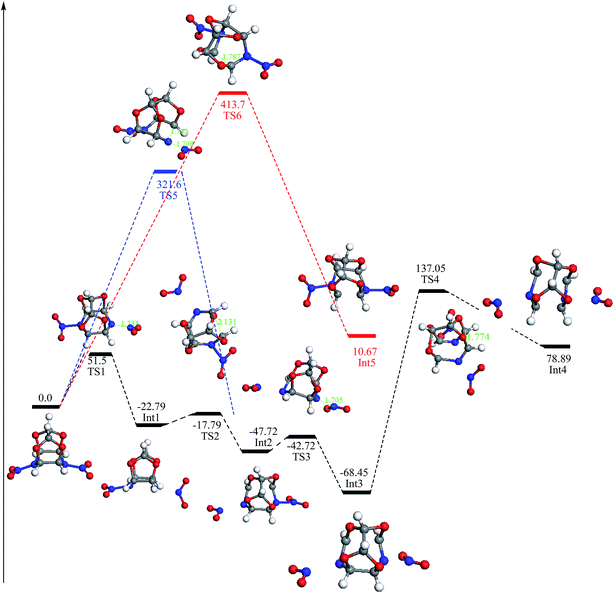
To further understand the mechanisms of these initial decomposition paths for the TEX molecule, we extracted the activated intermediates from the condensed phase simulations and searched the TS for each pathway in the gas-phase unimolecular reactions. The potential energy profiles for the three initial decomposition paths calculated in the gas phase are shown in Fig. 4. Calculated relative energies and entropies of TEX, intermediates, and transition states are listed in the Table S1 of the ESI.† Calculated frequencies and IRC calculation results of the transition states are listed in Table S2 and Fig. S1 of the ESI,† respectively. The reaction path (a) is the cleavage of the N–NO2 bond via TS1 to form an intermediate Int1 with an energy barrier of 51.5 kcal mol−1. Then, the C1–C2 bond of the intermediate Int1 breaks via TS2 to form an intermediate Int2, which has an energy barrier of 5 kcal mol−1. Thus, the total energy barrier is 56.5 kcal mol−1. Moreover, there is another path to form Int2 that is the simultaneous cleavage of the nitrogen–nitro bond and ring opening via TS5. This decomposition reaction has a high energy barrier (321.6 kcal mol−1) to produce Int2 than the former path. Subsequently, the N–NO2 bond in Int2 breaks via TS3 (5 kcal mol−1) to give an intermediate Int3 and release one molecule of NO2. The cage structure of Int3 is opened by the cleavage of N–NO2 bond via TS4 (205.5 kcal mol−1) to give an intermediate Int4, which has a fused cyclic structure. The third decomposition path is the ring opening at the C1–C2 bond via TS6 to form an intermediate Int5, which has an energy barrier of 413.5 kcal mol−1. The energy barrier values increase in the following order: nitrogen–nitro cleavage < the nitrogen–nitro cleavage and ring opening in the concerted step < ring opening. This indicates that at high temperatures, among these three initial reactions, the nitrogen–nitro cleavage is the easiest path to trigger the decomposition of the TEX molecule.
3.2. Decomposition mechanism of crystalline TEX
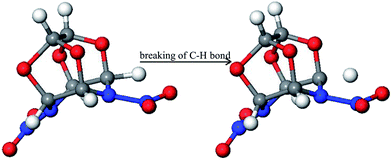
Fig. 5 presents the initial decomposition mechanism of the TEX crystal. It was found that the initial decomposition is triggered by the unimolecular cleavage of the C–H bond to form a hydrogen radical. This is different from the initial decomposition paths of the isolated TEX molecule: (a) N–NO2 bond cleaves to release NO2; (b) the N–NO2 bond cleavage and ring opening in the concerted step; and (c) ring opening through the cleavage of the C–C bond. The local molecular packing and external condition (high temperature) for the decomposition of crystalline TEX are completely different from those for the decomposition of isolated TEX. This may be the main cause for the difference in their decomposition mechanisms.The generated H radicals are very active and can prompt other unreacted TEX molecules to decompose. This catalytic role mainly occur through three interesting paths, as shown in Fig. 6: (1) the H radical attacks the N atoms in the cage, leading to the N–NO2 bond homolysis, (2) the H radical attacks the C–C bond, opening the cage structure, and (3) the H radical attacks the C–N bond, opening the cage structure. The catalytic behavior of the hydrogen radical is similar to that described in previous reports, such as studies on the thermal decompositions of PETN23 and crystalline furoxan19 by ab initio MD simulations.
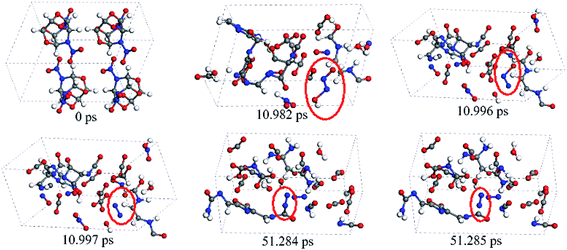
Fig. 7 presents the snapshots for the release mechanism (slow formation and disintegration of polycyclic networks) of nitrogen gas in the later decomposition stage of crystal TEX molecules. Note that the equilibrium established herein (for all the later species) is dynamic, i.e., previously formed molecules can further react and undergo rearrangements. After the initial decomposition reaction took place, there were many chain reactions occurring in the TEX molecules. At 10.982 ps, one NO combined with one HNO to form one HON![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NO. Then, HON
NO. Then, HON![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NO decomposed to produce N
NO decomposed to produce N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NO and OH radicals at 10.996 ps. Next, the O–N bond of N
NO and OH radicals at 10.996 ps. Next, the O–N bond of N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NO broke down to rapidly release N2 and an oxygen radical at 10.997 ps. After this, TEX molecules continued to decompose to form long chains and complicated carbon-rich heterocyclic rings. As the simulation continued, they split to form small fragments after 50 ps. At 51.243 ps, the carbon-rich heterocyclic rings broke down to form R–N–NOH. Subsequently, R–N–NOH rearranged to form N
NO broke down to rapidly release N2 and an oxygen radical at 10.997 ps. After this, TEX molecules continued to decompose to form long chains and complicated carbon-rich heterocyclic rings. As the simulation continued, they split to form small fragments after 50 ps. At 51.243 ps, the carbon-rich heterocyclic rings broke down to form R–N–NOH. Subsequently, R–N–NOH rearranged to form N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NC–R, which further decomposed to produce N2 and a fragment. Despite the different paths leading to R1–N
NC–R, which further decomposed to produce N2 and a fragment. Despite the different paths leading to R1–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–R2, the release mechanism of nitrogen gas was found to be the same during the whole decomposition stage. Our findings are different from the mechanism for the nitrogen release during the thermal decompositions of the high-energy crystal DiAT.9 This may be due to their structural differences.
N–R2, the release mechanism of nitrogen gas was found to be the same during the whole decomposition stage. Our findings are different from the mechanism for the nitrogen release during the thermal decompositions of the high-energy crystal DiAT.9 This may be due to their structural differences.
The abovementioned observations were obtained from the simulations on a 2 × 1 × 1 supercell. To validate the reliability of these simulations, we performed one additional simulation on a larger 3 × 1 × 1 supercell. Fig. 8 presents the snapshots for the release mechanism of nitrogen gas during the decomposition of crystal TEX molecules using the 3 × 1 × 1 supercell. Overall, after the decomposition of TEX was triggered, some long chains and complicated carbon-rich heterocyclic rings were formed, and then they split to form small fragments. At 3.204 ps, the carbon-rich heterocyclic ring broke to produce N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NC–R. After this, N
NC–R. After this, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NC–R rapidly decomposed to form N2 and a fragment. In addition, HON–NH radicals were observed in the system. At 13.448 ps, HON–NH decomposed to release N2. The release mechanism of nitrogen gases observed in the 3 × 1 × 1 supercell is the same as that observed in the 2 × 1 × 1 supercell. Although enlarging the system size can produce more decomposition and combination reactions and lead to the formation of larger and more complicated polycyclic networks, we did not observe significant differences in the release mechanism of nitrogen gas between the simulations on the two supercells. Therefore, a 2 × 1 × 1 supercell is sufficient to observe the most important features of the decomposition process.
NC–R rapidly decomposed to form N2 and a fragment. In addition, HON–NH radicals were observed in the system. At 13.448 ps, HON–NH decomposed to release N2. The release mechanism of nitrogen gases observed in the 3 × 1 × 1 supercell is the same as that observed in the 2 × 1 × 1 supercell. Although enlarging the system size can produce more decomposition and combination reactions and lead to the formation of larger and more complicated polycyclic networks, we did not observe significant differences in the release mechanism of nitrogen gas between the simulations on the two supercells. Therefore, a 2 × 1 × 1 supercell is sufficient to observe the most important features of the decomposition process.
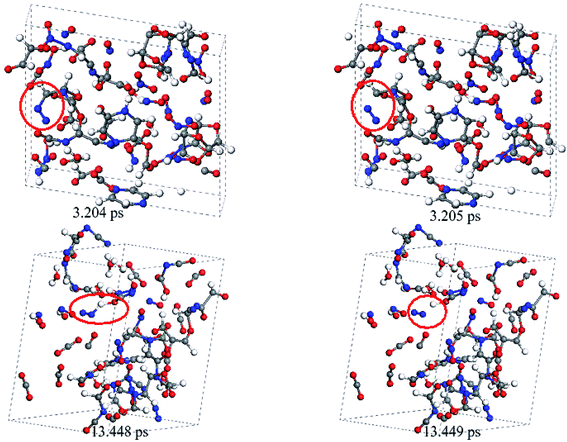 | ||
| Fig. 8 Snapshots for the release mechanism of nitrogen gas in crystal TEX molecules, obtained from the simulations performed on a 3 × 1 × 1 supercell. | ||
The release of carbon dioxide as a main product is very fast during the whole decomposition stage of crystal TEX molecules. It is seen in Fig. 9 that R1–CO2–R2 could be formed by two different mechanisms: one is through 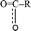 fragments, and the other one is through O
fragments, and the other one is through O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–R fragments. Then, R1–CO2–R2 breaks to produce CO2 and other small radicals. At 3.237 ps, the cage of one TEX molecule rapidly breaks to form a
O–R fragments. Then, R1–CO2–R2 breaks to produce CO2 and other small radicals. At 3.237 ps, the cage of one TEX molecule rapidly breaks to form a 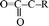 fragment and CO2. In the
fragment and CO2. In the 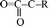 fragment, the C–C bond opened to release another CO2 molecule at 14.524 ps. The subsequent four CO2 molecules were rapidly released by the same decomposition mechanism, with the
fragment, the C–C bond opened to release another CO2 molecule at 14.524 ps. The subsequent four CO2 molecules were rapidly released by the same decomposition mechanism, with the 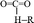 fragments cleaving the C–H bonds at 4.082, 4.605, 6.128, and 20.216 ps, respectively. At 9.423 ps, one CO2 was released by the cleavage of the O–H bond in the O
fragments cleaving the C–H bonds at 4.082, 4.605, 6.128, and 20.216 ps, respectively. At 9.423 ps, one CO2 was released by the cleavage of the O–H bond in the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–H–R fragment. Finally, the other three CO2 were produced by the cleavage of the C–N bond in the
O–H–R fragment. Finally, the other three CO2 were produced by the cleavage of the C–N bond in the 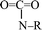 fragments at 10.335, 14.518, and 15.556 ps, respectively. Only two mechanisms for the release of carbon dioxide gas were found during the whole decomposition process. One decomposition mechanism occurs via the C–R bond cleavage and the other via the O–R bond cleavage.
fragments at 10.335, 14.518, and 15.556 ps, respectively. Only two mechanisms for the release of carbon dioxide gas were found during the whole decomposition process. One decomposition mechanism occurs via the C–R bond cleavage and the other via the O–R bond cleavage.
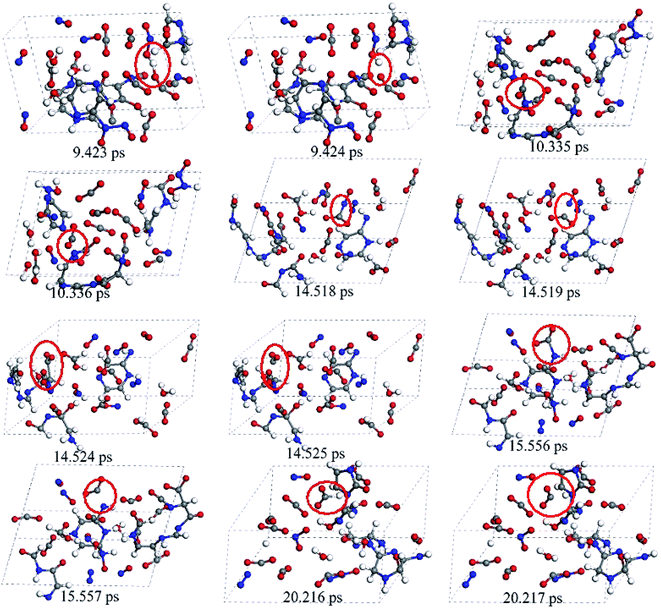 | ||
| Fig. 9 Snapshots for the release mechanism of carbon dioxide throughout the decomposition process of the crystal TEX molecules. Red ovals mark the key steps for the formation of CO2. | ||
It was observed that there are many multimolecular reactions during the decomposition of TEX. Fig. 10 displays the snapshots of the ring cleavage and the unstable long chain and heterocyclic formation throughout the decomposition process of the crystal TEX molecules. At 2.210 ps, one TEX molecule decomposed to form a six-membered heterocycle and other small molecules. Then, three TEX molecules reacted to form three unstable small chains at 2.67 ps. Two small chains linked to form a longer chain at 2.938 ps. At 34.402 ps, the whole molecular cage had decomposed to form an unstable ten-membered heterocycle. Then, at 35.730 ps, this heterocycle further decomposed to form a tricycle that also decomposed to finally produce various gases and small fragments at 50 ps.
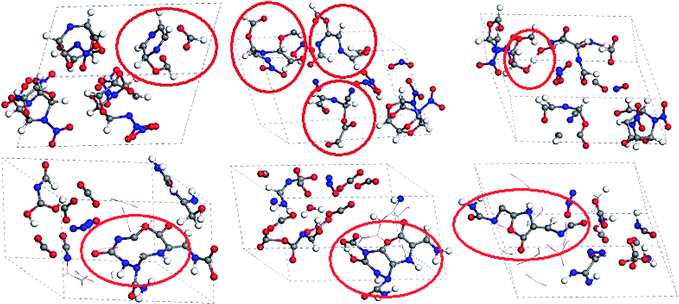 | ||
| Fig. 10 Snapshots for the formation of rings, unstable long chains, and heterocyclic clusters throughout the decomposition process of the crystal TEX molecules. Red ovals mark the key steps. | ||
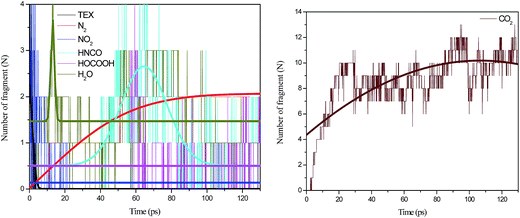
Fig. 11 presents the time evolution of the population of the main fragments during the decomposition of the crystal TEX molecules. The decomposition of TEX completed in 20 ps. Therefore, the 130 ps simulation time is almost sufficient to reach the equilibrium concentrations of the decomposition products. Since the unimolecular N–NO2 cleavage is the main step in the decomposition of the TEX crystal, the release of nitro groups is very fast. This is supported by our observations that the completion of the N–NO2 cleavage only requires 1 ps. Most of the NO2 molecules were formed at about 20 ps. After this, the formation of NO2 requires about 50 ps. Further, during the decomposition, neither NO nor N2 reached the equilibrium concentrations, and moreover, the lifetimes for NO2 and NO were significantly prolonged. The decrease in the concentration of NO was hardly noticeable but still faster than that of N2. The formation of molecular nitrogen was expected to be delayed for 0.5 ps. CO2 was mostly produced during the latter decomposition stage, reaching a concentration of nine to twelve molecules. The concentration of HOCOOH was from one to four molecules per unit cell by the end of the simulation. HNCO was formed after 10 ps. The concentration of HNCO reached its peak at about 75 ps, and then smoothly decreased. Water was produced at 4.1 ps, amounting to about four H2O molecules per unit cell. The concentration of H2O reached its peak at about 65 ps, and then smoothly decreased. HOCOOH, HNCO, and H2O disappeared due to their reactive lone pair electrons. The primary decomposition products of the TEX crystal are nitrogen and various carboxyl derivatives.
4. Conclusions
In this study, AIMD simulations were performed to study the chemical events in the decomposition of isolated and crystal TEX molecules at high temperatures. It was found that there are three different initial reactions involved in the decomposition of the isolated TEX molecule: (a) the N–NO2 bond cleavage to release NO2; (b) the N–NO2 bond cleavage and ring opening in the concerted step; and (c) the ring opening through the C–C bond cleavage. The activation energy barriers for the initial decomposition reactions indicate that at high temperatures, among the three initial reactions, the nitrogen–nitro cleavage is the easiest path to trigger the decomposition of the TEX molecule.The decomposition of the crystal TEX molecules is triggered by the breaking of the unimolecular C–H bond to form a hydrogen radical. The generated H radicals can promote the decomposition of other unreacted TEX molecules. Moreover, there are many multimolecular TEX reactions during the decomposition. Overall, after the decomposition of the crystal TEX molecules was triggered, some long chains and complicated carbon-rich heterocyclic rings were formed, and then they split to form small fragments: N2, NO2, NO, HNCO, HOCOOH, H2O, and CO2.
This study may provide useful information for understanding the decomposition mechanisms of cage explosives and for developing new high-energy explosives.
Acknowledgements
This work was supported by the NSAF Foundation of the National Natural Science Foundation of China and the China Academy of Engineering Physics (Grant No. U1530104), the National Natural Science Foundation of China (Grant No. 21273115), and a Project Funded by the Priority Academic Program Development of the Jiangsu Higher Education Institutions.References
- Y. Bayat and V. Azizkhani, J. Energ. Mater., 2012, 30, 209–219 CrossRef CAS.
- E. C. Koch, Propellants, Explos., Pyrotech., 2015, 40, 374–387 CrossRef CAS.
- J. A. Vagenknecht, P. Marecek and W. A. Trzcinski, J. Energ. Mater., 2002, 20, 245–253 CrossRef CAS.
- M. B. Talwar, J. K. Nair, R. S. Palaiah, T. Mukundan and S. P. Gejji, Def. Sci. J., 2002, 52, 157–163 CrossRef CAS.
- D. M. Badgujar, M. B. Talawar, S. N. Asthana and P. P. Mahulikar, J. Hazard. Mater., 2008, 151, 289–305 CrossRef CAS PubMed.
- A. E. Mattsson, P. A. Schultz, M. P. Desjarlais, T. R. Mattsson and K. Leung, Modell. Simul. Mater. Sci. Eng., 2005, 13, R1–R13 CrossRef CAS.
- R. Iftimie, P. Minary and M. E. Tuckerman, Proc. Natl. Acad. Sci., 2005, 102, 6654–6659 CrossRef CAS PubMed.
- O. Isayev, L. Gorb, M. Qasim and J. Leszczynski, J. Phys. Chem. B, 2008, 112, 11005–11013 CrossRef CAS PubMed.
- Q. Wu, W. H. Zhu and H. M. Xiao, Phys. Chem. Chem. Phys., 2014, 16, 21620–21628 RSC.
- C. C. Ye, Q. An, W. A. Goddard III, T. heng, S. Zybin and X. H. Ju, J. Phys. Chem. C, 2015, 119, 2290–2296 CAS.
- Q. Wu, H. Chen, G. L. Xiong, W. H. Zhu and H. M. Xiao, J. Phys. Chem. C, 2015, 119, 16500–16506 CAS.
- Q. Wu, G. L. Xiong, W. H. Zhu and H. M. Xiao, Phys. Chem. Chem. Phys., 2015, 17, 22823–22831 RSC.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133–1138 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev. [Sect.] B, 1964, 136, B864–B871 CrossRef.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- N. Troullier and J. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Nose, J. Chem. Phys., 1984, 81, 511–519 CrossRef CAS.
- Q. Wu, W. H. Zhu and H. M. Xiao, RSC Adv., 2014, 4, 34454–34459 RSC.
- M. H. V. Huynh, M. A. Hiskey, J. G. Archuleta, E. L. Roemer and R. Gilardi, Angew. Chem., Int. Ed., 2004, 43, 5658–5661 CrossRef CAS PubMed.
- L. Turker, Def. Technol., 2014, 10, 328–333 CrossRef.
- D. Chakraborty, R. P. Muller, S. Dasgupta and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 1302–1314 CrossRef CAS.
- C. J. Wu, L. E. Freid, L. H. Yang, N. Goldman and S. Bastea, Nat. Chem., 2009, 1, 57–62 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Calculated relative energies and entropies of the TEX molecule, intermediates, and transition states, calculated frequencies and IRC calculation results of the transition states. See DOI: 10.1039/c6ra27255j. |
| This journal is © The Royal Society of Chemistry 2017 |