Theoretical study on crystal polymorphism and electronic structure of lead(II) phthalocyanine using model dimers

Abstract

Lead(II) phthalocyanine (PbPc) crystallises into two modifications of monoclinic and triclinic systems. In order to investigate the solid state electronic structures, we calculated three model dimers and two model trimers of PbPc using the M06 method of density functional theory (DFT). The geometries of these models for the crystal polymorphs were optimised, and the stability of each model was discussed along with the Gibbs free energy when comparing with the case of the triclinic system of tin(II) phthalocyanine. The optimised geometries of these models simulated well the molecular structures and orientations in the crystalline solids of PbPc. The time-dependent DFT (TD-DFT) calculation has been applied to these model dimers and trimers in order to investigate the excited states. The results also reproduced well the observed UV-vis spectra of PbPc in the solid state.

---

Introduction

Phthalocyanines (MPc: Pc = phthalocyaninato anion C₃₂H₁₆N₈²⁻, M = H₂ or divalent metals) are compounds possessing a macrocyclic ring with a large π-conjugated aromatic system. They generally have highly symmetrical square planar D_4h structures,^1–4 and show high thermal and chemical stability.

Among many MPc compounds, lead(II) phthalocyanine (PbPc) has a peculiar structure with C_4v symmetry like a shuttlecock. It has been reported that there exists two polymorphs in PbPc crystals, the monoclinic system with space group P2₁/b⁵ and the triclinic one with P1̄.⁶ Thin films with both crystalline polymorphs showed different sensitivity against air, nitrogen oxide, and water vapour.⁷ PbPc has been also used as non-linear optical materials,⁸ organic solar cells,⁹ and so on. Tin(II) phthalocyanine (SnPc) also has a C_4v shuttlecock-shaped structure; however, the triclinic polymorph has been only reported for SnPc^10,11 up to now to our knowledge.

Density functional theory (DFT) methods have been applied to investigate various physical properties of several MPc compounds.^12–19 The time-dependent DFT (TD-DFT) calculations have been especially used to discuss the UV-vis spectra of them. These works showed that DFT methods are efficient, reliable and effective to investigate the molecular and electronic structures of MPcs for the present. In the previous report, we successfully investigated physical properties for the triclinic solid of SnPc with these methods using the dimer models.²⁰

In this study, we extended the same approach as SnPc to investigating the electronic structures of two polymorphic PbPc solids. Three types of dimers were extracted from the two crystal systems; Type 1 from the monoclinic polymorph, Types 2 and 3 from the triclinic one (see Scheme 1). The geometries of these dimers were optimised using the DFT method, and the results were compared to the observed molecular structures in solids. We conducted an investigation into electronic structures of both ground and excited states for crystals with using these model dimers. The results of the TD-DFT calculations were examined carefully with comparing to the observed electronic absorption spectra for thin solid films. In order to check the propriety of the dimer model, we also compared the same calculation results for the model trimers of Types 4 and 5 (see Scheme 1) for monoclinic and triclinic polymorphs, respectively, as those for the dimers. Through these investigations, we will give an insight into the origin of polymorphs in SnPc and PbPc.

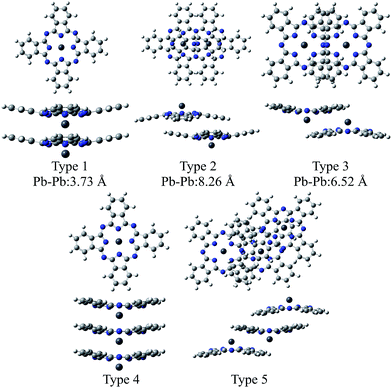Scheme 1 Structures of the model dimers and trimers of PbPc. The distances between Pb atoms are referred from ref. 5 (Type 1) and 6 (Types 2 and 3) for monoclinic and triclinic crystals, respectively.

Experimental section

Computational detail

Geometry optimization and excitation energies of the PbPc monomer, dimers and trimers were carried out using DFT and TD-DFT methods. To investigate the solvent effect of chloroform, we used the CPCM method.^21,22 It has been shown that the M06 functional would give the most reliable results for investigating the geometric and electronic structures of the weakly bound systems such as MPc molecules in solids;^23–25 therefore, we employed the M06 functional for the exchange correlation term.^26–29 We also compared the results obtained by the M06-2X functional,²⁹ which gives the relatively good results for fullerene complexes with π–π interactions.^30,31 The LANL2DZ(d,p) basis set was used for Pb and Sn atoms, where the effective core potentials (ECPs) were employed to replace core electrons. For C, N and H atoms, the 6-311G(d) basis set was employed. All calculations were performed using the Gaussian09 program package,³² and the results were visualised by the GaussView program package.³³

In order to give insight into the electronic structures of PbPc polymorphic solids, we optimised the geometries of the model dimers (Types 1–3) and trimers (Types 4 and 5) in Scheme 1 under the following conditions: (1) the structural parameters of each PbPc moiety were fixed as those of the PbPc monomer, which were optimised under constraint to keep C_4v symmetry using the parameter shown in Fig. 1. (2) The distance between the PbPc moieties was optimised with the dimer of Type 1 to keep C_4v symmetry, and the distance and the tilt angle between them were optimised simultaneously with those of Types 2 and 3 under constraint to keep C_2h symmetries. (3) We calculated the trimers under constraint to keep C_4v and C₁ symmetries for Types 4 and 5, respectively. The two distances between the PbPc moieties were optimised independently with the trimer of Type 4, and the distances and tilt angles between them were optimised with the trimer of Type 5.

Fig. 1 Optimised geometries of PbPc monomer.

All these models had vibration modes with small negative frequency. Our purpose is to reproduce molecular orientations in PbPc solids for investigating their electronic structures; therefore, we proceeded with this study using these geometries. The differences of the total energy between the models and the corresponding components are listed in Table S1 of the ESI.†

Experiments

The commercially available powdery sample of PbPc was purified by vacuum sublimation (see Table S2 of the ESI† for the results of the elemental analysis). The thin film of PbPc was prepared by vapour deposition on a quartz substrate kept at room temperature under vacuum of 10⁻² Pa. The deposition rate and the film thickness were monitored with a quartz thickness monitor, and were controlled at 0.03 nm min⁻¹ and about 80 nm, respectively. The thin film was annealed at 170 °C for 7 days in vacuum of 10⁻¹ Pa. The electronic absorption spectra were measured for the thin film before and after annealing. The absorption spectrum of PbPc was also measured in a chloroform solution. The thin film was characterised by Raman spectroscopy and X-ray diffraction measurements at each step during a course of absorption measurements, and infrared spectroscopy was also applied to characterise the film after the electronic absorption measurements. The X-ray powder patterns for the as-synthesized film were similar to those expected for a monoclinic system,⁵ showing that the evaporated film consisted mainly of monoclinic crystals. The X-ray diffraction measurements also showed that the film changed its crystalline system into a triclinic system⁶ after annealing (see Fig. S1 of the ESI†).

Results and discussion

Optimised geometry of PbPc monomer

First, we will discuss briefly on the result of the optimised geometry for the PbPc monomer. The optimised geometric parameters and the observed bond lengths are compared in Fig. S2 of the ESI,† and were summarised in Table S3 of the ESI.† The data for SnPc are also shown in the figure and table for a comparison. The M06 and M06-2X methods gave nearly similar results to each other. Although there existed a small difference in the parameters of the optimised geometries among the present and previous works^12,16,18,19 depending on the method used for the calculations; all showed a similar tendency to each other. As pointed previously,^16,18 the optimised geometry showed a better consistency with the observed molecular structures in a triclinic crystal than those in a monoclinic one. Particularly, the optimised distance between Pb and isoindole nitrogen atoms differed larger from a monoclinic structure than in a triclinic one. It would be concluded that PbPc molecules are placed under a stronger crystal field in monoclinic crystal than that in a triclinic one making molecules in monoclinic solids deformed especially in a region of the central metal as compared to isolated molecule. On the other hand, this could imply that PbPc molecules can be deformed easily to adjust their molecular structures to circumstances. Actually, it has been reported that hydrostatic pressure makes the PbPc molecules take the planar structure.³⁴

Here, we would like to compare the optimised structures of PbPc and SnPc with the M06 and M06-2X methods. The Pc rings of both compounds have a saucer-shaped structure, where the central metal atom sticks out of the molecule on the opposite side of its curvature. The calculation results showed that the Mulliken charge of the Pb atom in PbPc is estimated to be +1.1 e and +1.2 e by the M06 and M06-2X methods, respectively, which are similar to the value of +0.9 e and +1.0 e for the Sn atom of SnPc by the M06 and M06-2X methods, respectively. It should be noted, as pointed out in the previous work,¹² that there exist little differences of the bond lengths and bond angles in the region of the Pc rings between SnPc and PbPc, where the curvature of the Pc ring differs just a little. Contrary to this similarity in the atomic charges and molecular structures, the dipole moments were quite different between PbPc and SnPc, where both methods gave the same values of 1.0 and −0.6 Debye for PbPc and SnPc, respectively, along the four-fold rotational axis. This might be originated from the small difference of about 0.2 e in the atomic charges of the central metal atoms and in the atomic distances between the central metal and its neighbour nitrogen atoms. The distances were estimated to be 2.340 and 2.334 Å for PbPc by the M06 and M06-2X methods, respectively, where those of SnPc were to be 2.272 and 2.270 Å by these two methods, respectively. These values were similar to the value of 2.279 Å obtained by the previous work.¹²

Optimised geometry and electronic structures of PbPc dimers and trimers

Fig. 2 illustrates the optimised structures of the model dimers of PbPc using the M06 method. The Gibbs free energies of the optimised dimers were lower than the sum of the monomers by about 4–8 kcal mol⁻¹ at 298.15 K as shown in parentheses of the figure. Interestingly, all three dimers under investigation would be preferable to two independent molecules. It has been reported that these values for the SnPc dimers are calculated to be −10.3 and −8.8 kcal mol⁻¹ for the dimers of Types 2 (concave) and 3 (convex), respectively, with using the same method and basis sets as this work.¹² Comparing the relative stability of these dimers between PbPc and SnPc, the Type 2 dimer of PbPc was less stable than the corresponding one of SnPc in marked contrast to the Type 3 dimers, which showed a nearly same stability between PbPc and SnPc. This might be originated from the fact that the overlap of Pc rings is less effective in the case of PbPc than SnPc due to a small difference in the molecular structures between them.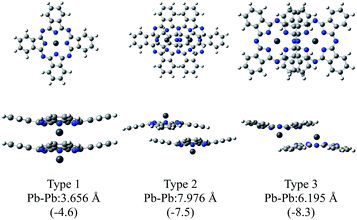

Fig. 2 Optimised geometries of the model dimers of PbPc. The relative Gibbs free energies (kcal mol⁻¹) to the sum of the monomers are shown in parentheses.

There is no report on the SnPc dimer similar to Type 1; therefore, we additionally calculated for the Type 1 dimer of SnPc using the same method with this study. The relative Gibbs free energy was interestingly estimated to be +2.2 kcal mol⁻¹. This value shows clearly that the model dimer of the monoclinic crystal is unstable as compared, at least, to those of the triclinic crystal for SnPc.

The distances between two Pb atoms were evaluated to be 3.656, 7.976 and 6.195 Å for the optimised geometries of Types 1–3, respectively. These values were consistent with the corresponding experimental values of 3.73 Å for the monoclinic crystal⁵ and of 8.26 and 6.52 Å for the triclinic one.⁶

The M06-2X method gave nearly similar results to the M06 one in stabilities of the dimers. The differences between the Gibbs free energies of the dimers and two monomers were estimated to be −5.9, −8.3 and −12.9 kcal mol⁻¹ for Types 1–3, respectively. The distances between Pb atoms were evaluated to be 3.748, 7.815 and 6.278 Å for Types 1–3, respectively, for the optimised geometries with the M06-2X method. These values are similar to those obtained by the M06 method; therefore, we chose the M06 method in the following discussion for the simple reason to compare the present results with those reported previously for SnPc.¹²

Fig. 3 illustrates the optimised structures of the two model trimers, Types 4 and 5. The relative Gibbs free energies of these trimers were much lower than the sum total of three monomers by 15.2 and 17.8 kcal mol⁻¹ for the trimers of Types 4 and 5, respectively. It should be noted that the relative energies of these two trimers become closer to each other as compared to those of the dimers. It was also shown that the Type 5 trimer is less stable about 5 kcal mol⁻¹ than the corresponding trimer of SnPc, for which the relative Gibbs free energy was estimated to be −23.4 kcal mol⁻¹.²⁰ In addition, we also performed the calculations for the similar SnPc trimer to the Type 4 one, and the relative Gibbs free energy was estimated to be −0.9 kcal mol⁻¹. These results showed clearly that the PbPc molecules are much stable in a columnar structure of the monoclinic crystal, contrary to SnPc. This is consistent with the experimental facts that PbPc crystallises in both triclinic and monoclinic crystal systems, but the triclinic crystal system was only reported on SnPc up to now. This remarkable difference between SnPc and PbPc might be originated from the small differences in the curvature of the molecules and the projection of the metal atoms. It might also be thought that a charge distribution on the molecule will affect the stable arrangement for each pair of the PbPc molecules in solids.

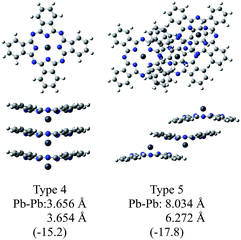Fig. 3 Optimised geometries of the model trimers of PbPc. The relative Gibbs free energies (kcal mol⁻¹) to the sum of the monomers are shown in parentheses.

The distances between two Pb atoms of the optimised geometries were evaluated to be 3.656 and 3.654 Å for the Type 4 trimer and 8.034 and 6.272 Å for the Type 5 one. It would be mentioned that these values for the Type 5 trimer become much closer to the distances of 8.26 and 6.52 Å in the triclinic crystal⁶ as compared to those calculated for the dimers. In contrast with this, the distances between the Pb atoms for the Type 4 trimer were calculated to be nearly the same value to that of the dimer and the value of 3.73 Å observed in the monoclinic crystal.⁵ These facts, in conjunction with the relative Gibbs free energy, might indicate that the dimer is sufficient to investigate the molecular and electronic structures in the monoclinic system theoretically. On the other hand, it would be concluded properly from the crystal structure that the triclinic crystal of PbPc requires at least the trimer for investigation. In passing, the differences between the observed and calculated values may be due to the effect of the crystal packing.

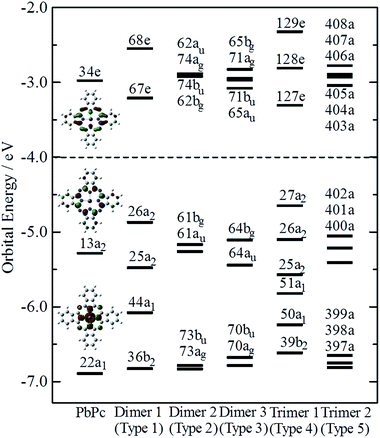
Fig. 4 indicates the energy diagrams of the monomer, the three dimers and the two trimers in the region of the highest occupied (HOMO) and the lowest unoccupied (LUMO) molecular orbitals. The orbital symmetries are labelled under the C_4v symmetry group for the monomer, the Type 1 dimer and the Type 4 trimer, under the C_2h symmetry group for the dimers of Types 2 and 3, and under the C₁ symmetry group for the Type 5 trimer. The energy diagrams of the dimers basically consisted of two orbitals in pairs, which were constructed of interactions between two moieties in bonding and anti-bonding ways. In the case of the trimers, there existed the non-bonding type molecular orbital in addition to each pair of bonding and anti-bonding type orbitals. The energy values of these molecular orbitals are compiled in Table S3 of the ESI,† where the corresponding molecular orbitals are indicated in the same colour. The atomic contributions to the several molecular orbitals near the frontier orbitals are shown schematically in Fig. S3–S7 of the ESI† for the model dimers and trimers of Types 1–5, respectively.

Fig. 4 Orbital energies near the frontier orbital of PbPc. The orbital symmetries are labelled under the C_4v, C_4v, C_2h, C_2h, C_4v and C₁ symmetry groups for the monomer, the three model dimers (Types 1–3), and the two model trimers (Types 4 and 5), respectively.

The HOMO of the PbPc monomer has a large contribution from carbon atoms of the inner C₈N₈ ring and the next occupied orbital to the HOMO (HOMO − 1) has a strong contribution from s-type atomic orbital of a Pb atom as shown in Fig. 4. It would be reasonable to think that the energy splitting between the bonding and anti-bonding type orbitals depends on the strength of the interaction between PbPc moieties of the dimers. From the calculation results, the energy differences between the HOMO and HOMO − 1 were estimated to be 0.61, 0.09 and 0.34 eV for the dimers of Types 1–3, respectively. It has been reported that the values for SnPc are estimated to be 0.30 and 0.34 eV for the Type 2 (concave) and Type 3 (convex) dimers, respectively.²⁰ In the case of the trimers, these energy differences between the bonding and anti-bonding type orbitals were evaluated to be 0.92 and 0.36 eV for the trimers of Types 4 and 5, respectively, which were a little larger than those of the corresponding dimers. The value of the Type 5 PbPc trimer was a little smaller than that of the SnPc trimer, which has been reported as to be 0.43 eV.²⁰

We also calculated the ionisation potentials and the electron affinities by the ΔSCF method, and the results are compiled in Table 1. For comparison, the values for SnPc are also shown in parenthesis, where the ionisation potentials are based on the previous work²⁰ for the monomer, the dimers of Types 2 and 3, and the trimer of Type 5. It has been reported³⁵ that the bilayer film of PbPc shows two bands split with about 0.35 eV in the top region of the valence band, while the monolayer film has a single peak in the same energy region of the photoelectron spectra. The energy difference of 0.34 eV between the HOMO and the HOMO − 1 of the Type 3 dimer is fairly consistent to their conclusions. The calculation results would give an interesting indication that the ionisation threshold of the PbPc solids will be affected strongly by their polymorphic systems. Even in the thin films of PbPc such as the bilayer one, a molecular arrangement is crucial to photoelectric properties of the film. The molecular arrangement of Type 1 will give the most small ionisation energy, while those of Types 2 and 3 will affect slightly on the first ionisation energy but strongly on the second ionisation one. In contrast with this, the photoelectric properties for the thin films of SnPc would be insensitive to the molecular arrangement.

Table 1 Ionisation-potential and electron affinity obtained by the ΔSCF method for PbPc (SnPc) in eV

		Ionisation potential^a	Electron affinity^a
a Vertical ionisation potential and electron affinity by the ΔSCF.b Ref. 20.
Monomer		6.19 (6.26)^b	2.02 (2.12)
Dimer	Type 1	5.66 (5.76)	2.39 (2.42)
	Type 2	5.91 (5.87)^b	2.15 (2.29)
	Type 3	5.82 (5.84)^b	2.36 (2.45)
Trimer	Type 4	5.37 (5.49)	—
	Type 5	5.69 (5.68)^b	—

---

Electronic absorption spectra of PbPc model dimers and trimers

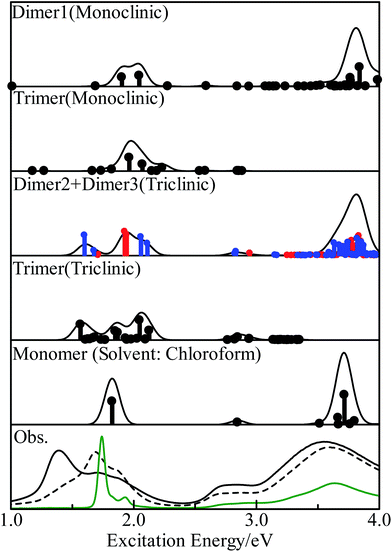
We calculated the excitation energies of three PbPc dimers and two trimers using the TD-DFT method. The optically allowed excited states obtained by the TD-M06/LANL2DZ(d,p)+6-311G(d) method are shown as vertical lines in Fig. 5. In order to investigate the solid state effects, we also calculated the excited states for the PbPc monomer with the solvent effects, and the results are shown in the figure. We calculated the 40 optically allowed excited states for the trimers in order to investigate an absorption profile in the Q-band region below 2.5 eV by reason of reducing computational time. The height of each vertical line represents the oscillator strength of excitation. The solid line of each panel shows the theoretical absorption spectrum obtained by convoluting each excited state with a Gaussian function, where the FWHM was assumed to be 0.06 eV and the oscillator strength was used as the pre-exponential factor. The experimentally obtained absorption spectra for the thin film and a chloroform solution are also shown in the figure. As for the triclinic polymorph, the unit cell consists of two different configurations between two adjacent molecules which are similar to those of the dimers of Types 2 and 3; therefore, we depict the sum of the absorption spectra of these dimers in the figure. The spectrum of each dimer is also shown individually in Fig. S8 of the ESI.† The excitation energy of the dimers are summarised in Table 2 for the optically-allowed excitations with oscillator strength over 0.05. The important components of the one electron transition, in which the coefficient is larger than 0.3, are also presented in the tables. The excitation energies and the important components for all optically allowed states of the monomer, dimers and trimers are shown in Tables S5–S10 of the ESI.†

Fig. 5 Excited states of the PbPc monomer, model dimers and trimers obtained by the TD-M06 calculations. The vertical line depicts the oscillator strength of each state. The theoretical spectra were obtained by convoluting each excited state with a Gaussian function with the FWHM of 0.06 eV and with the oscillator strength as the pre-exponential factor. In order to simulate a spectrum of the triclinic system, the sum of the results for the dimers of Types 2 (red lines) and 3 (blue lines) is shown in the third panel. The experimental absorption spectra for the thin films before and after annealing and a chloroform solution are shown in the bottom panel by broken, solid and green curves, respectively.

Table 2 Symmetry-allowed TD-M06 excited state of the dimers

		State	Main configuration (|C| ≧ 0.30)	E^a	f^b	p^c
a Excitation energy in eV.b Oscillator strength.c Transition moment direction.
Type 1	C4v	3E	±0.47(44a1 → 67e)[45%] − 0.40(26a2 → 68e)[32%]	1.90	0.219	x + y
		4E	+0.46(44a1 → 67e)[42%] ± 0.32(26a2 → 68e)[20%]	2.05	0.256	x + y
Type 2	C2h	2Bu	+0.54(61au → 62bg)[58%] + 0.43(61bg → 62au)[36%]	1.93	0.568	x + y
		2Au	+0.58(61au → 74ag)[66%] − 0.37(61bg → 74bu)[28%]	1.94	0.492	z
		3Au	+0.43(73ag → 62au)[37%] + 0.52(73bu → 62bg)[55%]	2.94	0.049	z
		3Bu	−0.46(73ag → 74bu)[43%] + 0.50(73bu → 74ag)[50%]	2.95	0.057	x + y
Type 3	C2h	1Bu	+0.70(64bg → 65au)[98%]	1.60	0.481	x + y
		1Au	+0.67(64bg → 71bu)[90%]	1.68	0.116	z
		2Au	+0.66(64au → 71ag)[87%]	2.06	0.441	z
		2Bu	+0.69(64au → 65bg)[95%]	2.11	0.287	x + y
		3Au	+0.58(70ag → 65au)[66%] − 0.37(70bu → 65bg)[27%]	2.83	0.050	z
		3Bu	+0.43(70ag → 71bu)[37%] + 0.53(70bu → 71ag)[56%]	2.83	0.094	x + y

---

The electronic ground states of the monomer, and the model dimers and trimers under investigation are all totally symmetric singlet states, which are labelled as ¹A₁, ¹A_g and ¹A under the C_4v, C_2h and C₁ point groups, respectively; therefore, the optical allowed excited states belong to the ¹A₁ or ¹E, ¹A_u or ¹B_u, and ¹A (all states) representations, respectively. The results for the monomer were similar to those of the previous work¹² in spite of the different functional used. The calculated results showed clearly that the solid state effects would be observed obviously in the Q-band region as broadening with some features, but not in the B-band region.

In the case of the monoclinic models (Types 1 and 4), there would exist low energy excitations in the region below 1.7 eV with small oscillator strengths. These states consisted of one-electron transitions between the molecular orbitals originated from the HOMO and LUMO of the monomer, which could be assigned as the π–π* transitions. Contrary to these small oscillator strengths of these states, the excited states around 2 eV had relatively strong oscillator strengths. These states contained one-electron transitions from the molecular orbitals with large contribution from the s-type atomic orbital of the central metal atom in addition to the π–π* transitions; therefore these excited states would be assigned to the mixed states with the π–π* and the metal to ligand charge-transfer (MLCT) transitions. A series of the excited states would contribute together to a strong absorption profile over 3.5 eV, which generates the B-band. It would be concluded from these results that the Q-band observed for the monoclinic system has a strong contribution of the MLCT. This result differs remarkably from those discussed for the free molecules.^12,18

The triclinic models (Types 2, 3 and 5) showed a different excitation profile as compared to the monoclinic ones. The excited states below 2.1 eV consisted of one-electron transitions between the molecular orbitals originated from the HOMO and LUMO of the monomer. These states could be assigned to the π–π* transition states. On the contrary, the excited states with contributions of the MLCT transition showed small oscillator strengths, and their excitation energies were estimated to be about 2.9 eV. It would be concluded for the triclinic system that the Q-band has the π–π* transition states as a main component, and the MLCT band be observed at the region between the Q- and B-band with a small intensity as compared to the Q-band. These excitation features for the triclinic solid are similar to those of the free molecule except the band broadening due to interactions between molecules in solids.

Fig. 5 shows the observed absorption spectra of the thin PbPc film before and after annealing by broken and solid curves, respectively, in the bottom panel. The absorption spectrum for a chloroform solution is also shown in the figure by a green curve. As expected by the calculations, the absorption features of the thin film differ remarkably from those of a solution especially in the Q-band region. Before annealing, the film showed an absorption band at 1.7 eV with a shoulder at about 1.9 eV in the Q-band region, and the broad absorption band around 3.6 eV as the B-band. The weak feature around 2.8 eV was also observed in the region between the Q- and B-bands. After annealing, the thin film exhibited three absorption features at 1.40, 1.74 and 1.85 eV in the Q-band region, where the feature at 1.4 eV had the strongest intensity among them. The position of the B-band was independent of annealing. It should be noted that the feature at 2.8 eV was intensified by annealing as compared to the others. These experimental results were the same as those reported previously.^36–38 Particularly, Miyamoto et al. have also reported that the monoclinic crystalline film of PbPc changes its crystalline form to the triclinic system by annealing through the detailed investigation.³⁶ The present calculation results with the model dimers represented well all of the experimental results. The present work would also show that the electronic structure in a solid state can be investigated sufficiently with using the relatively small models chosen appropriately.

Conclusions

In this study, we reported optimised geometric and electronic structures, and excitation energies of the monomer and the model dimers and trimers of PbPc for the monoclinic and triclinic polymorphs using the M06 method. The optimised geometry of the monomer agreed much better with the experimental structure in the triclinic crystal than that in the monoclinic one. The Pb–Pb distances in the model dimers and trimers corresponded well to the experimental values of both monoclinic and triclinic polymorphs. The calculation results would also show that these model dimers and trimers simulate well the molecular structures and orientations in the crystalline solids of PbPc.

The stabilities of the model dimers and trimers were estimated from the differences in the Gibbs free energies between them and the corresponding components. The results revealed clearly that PbPc would show a possibility to take both molecular orientations of the monoclinic and triclinic crystal systems. Contrary to this, SnPc may prefer the triclinic molecular orientation strongly to the monoclinic one.

The excitation energies of the three dimers and two trimers were calculated by the TD-DFT method. The theoretical absorption spectra could explain well the experimental results observed for the thin film including its evolution along with polymorphic change. The calculated results would solid state effects were obviously observed especially in the Q-band region. It would be interestingly concluded from the calculation results that the π–π* and MLCT transitions contribute differently to the excited states of the monoclinic and triclinic solids of PbPc. Particularly, the main contribution to the Q-band could be assigned as the π–π* and MLCT transitions for the triclinic and monoclinic systems, respectively.

Finally, this work has been shown that the electronic structures in the solid state can also be investigated theoretically with using the small models properly selected.

Acknowledgements

Theoretical calculations were partly performed using Research Centre for Computational Science, Okazaki, Japan.

Notes and references

1. T. Kobayashi, F. Kurokawa, N. Uyeda and E. Suito, Spectrochim. Acta, Part A, 1970, 26, 1305.
2. E. A. Lukyanets and V. N. Nemykin, J. Porphyrins Phthalocyanines, 2010, 14, 1.
3. A. B. P. Lever, Adv. Inorg. Chem. Radiochem., 1965, 7, 28.
4. W. R. Scheidt and W. Dow, J. Am. Chem. Soc., 1977, 99, 1101.
5. K. Ukei, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 2290.
6. Y. Iyechika, K. Yakushi, I. Ikemoto and H. Kuroda, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 29, 766.
7. R. A. Collins and A. Belghachi, Mater. Lett., 1989, 8, 349.
8. Q. Yang, T. Chen, J. Si, T. Lin, X. Hou, G. Qian and J. Guo, Opt. Commun., 2008, 281, 831.
9. K. Vasseur, K. Broch, A. L. Ayzner, B. P. Rand, D. Cheyns, C. Frank, F. Schreiber, M. F. Toney, L. Froyen and P. Heremans, ACS Appl. Mater. Interfaces, 2013, 5, 8505.
10. R. Kubiak and J. Janczak, J. Alloys Compd., 1992, 189, 107.
11. A. Yamashita, S. Matsumoto, S. Sakata, T. Hayashi and H. Kanbara, J. Phys. Chem. B, 1998, 102, 5165.
12. M. Sumimoto, T. Honda, Y. Kawashima, K. Hori and H. Fujimoto, Dalton Trans., 2012, 41, 7141.
13. J. D. Baran and J. A. Larsson, Phys. Chem. Chem. Phys., 2010, 12, 6179.
14. A. S. Nixovtsev and S. G. Kozlova, J. Phys. Chem. A, 2013, 117, 481.
15. Y. Zhang, X. Cai, X. Zhang, H. Xu, Z. Liu and J. Jiang, Int. J. Quantum Chem., 2007, 107, 952.
16. Y. Zhang, X. Zhang, Z. Liu, H. Xu and J. Jiang, Vib. Spectrosc., 2006, 40, 289.
17. A. Irfan, A. G. Al-sehemi, A. M. Asiri, M. Nadeem and K. A. Alamry, Comput. Theor. Chem., 2011, 977, 9.
18. Y. Zhang, X. Zhang, Z. Liu, Y. Bian and J. Jiang, J. Phys. Chem. A, 2005, 109, 6363.
19. N. Papageorgiou, Y. Ferro, E. Salomon, A. Allouche, J. M. Layet, L. Giovanelli and G. Le Lay, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 235105.
20. M. Sumimoto, T. Honda, Y. Kawashima, K. Hori and H. Fujimoto, RSC Adv., 2012, 2, 12798.
21. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995.
22. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669.
23. M. Sumimoto, Y. Kawashima, D. Yokogawa, K. Hori and H. Fujimoto, J. Comput. Chem., 2011, 32, 3062.
24. M. Sumimoto, Y. Kawashima, D. Yokogawa, K. Hori and H. Fujimoto, Int. J. Quantum Chem., 2013, 113, 272.
25. M. Sumimoto, D. Yokogawa, Y. Kawashima, K. Hori and H. Fujimoto, Spectrochim. Acta, Part A, 2012, 91, 118.
26. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454.
27. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439.
28. R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218.
29. Y. Zhao and D. G. Truhlar, Theor. Chim. Acta, 2008, 120, 215.
30. Y. Zhao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2008, 10, 2813.
31. G. Casella and G. Saielli, New J. Chem., 2011, 35, 1453.
32. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2010.
33. R. Dennington, T. Keith and J. Millam, Gauss View, Version 5, Semichem Inc., Shawnee Mission, KS, 2009.
34. M. Sakata, M. Sumimoto, M. Gushima, H. Fujimoto and S. Matsuzaki, Solid State Commun., 2002, 121, 363.
35. S. Kera, H. Fukagawa, T. Kataoka, S. Hosoumi, H. Yamane and N. Ueno, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 121305R.
36. A. Miyamoto, K. Nichogi, A. Taomoto, T. Nambu and M. Murakami, Thin Solid Films, 1995, 256, 64.
37. M. Simonyan, E. A. Kafadaryan, M. C. Murijanyan, A. K. Petrosyan and E. G. Sharoyan, Phys. Status Solidi A, 1987, 101, 143.
38. R. A. Collins, A. Krier and A. K. Abass, Thin Solid Films, 1933, 229, 113.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates, several molecular orbitals and all calculated excitation energies for all species, and the results of elemental analysis for sublimed PbPc samples and X-ray powder pattern recorded with the evaporated thin film of PbPc. See DOI: 10.1039/c6ra27269j

---