Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ideal strength and elastic instability in single-layer 8-Pmmn borophene†
Junhui Yuana,
Niannian Yub,
Kanhao Xue *a and
Xiangshui Miaoa
*a and
Xiangshui Miaoa
aSchool of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan, Hubei 430074, China. E-mail: xkh@hust.edu.cn
bSchool of Science, Wuhan University of Technology, Wuhan, Hubei 430070, China
First published on 27th January 2017
Abstract
Using first principle calculations based on density functional theory (DFT), we have investigated the mechanical properties of monolayer 8-Pmmn borophene, including ideal strength and critical strain. It was found that monolayer 8-Pmmn borophene can withstand stress up to 21.59 N m−1 and 27.79 N m−1 in a and b directions, respectively. The ultimate tensile strain along the a direction is about 0.155, and 0.16 along the b direction, which is larger than that of stripe borophene. Furthermore, the phonon dispersions under the three applied strains indicate that the mechanical failure in 8-Pmmn borophene is likely to originate from the elastic instability. Our study shows that 8-Pmmn borophene is a hard but flexible 2D material, and may potentially be useful in high-strain engineering applications.
1 Introduction
Beyond the scope of group-IV and group-V elementary two-dimensional (2D) materials,1–10 a novel 2D material of group-III named borophene (2D boron sheet) has been grown successfully on Ag (111) substrates very recently.11,12 Three types of borophene sheets are have been fabricated in the experiments, i.e. stripe, β12, and χ3 borophene. The variety of the geometric structures of borophene stems from boron's unique physical properties. For example, the monolayer borophene exhibits highly anisotropic metallic characteristic and unique mechanical properties, such as high ideal strength and critical strain.13–15 On the other hand, the stripe borophene possesses an extremely large Young's modulus of 398 GPa nm along the a direction, much larger than that of graphene.11,15 More interestingly, the stripe borophene has an out-of-plane negative Poisson's ratio, similar to black phosphorus (BP).15Although most forms of borophene are good metals, striped borophene exhibits a direction-dependent Dirac cone when fully hydrogenated. In addition, the intrinsic band structure of 8-Pmmn borophene also has a Dirac cone.16 8-Pmmn borophene has been predicted to be highly stable by several theoretical studies,17,18 but has not been synthesized experimentally yet. Previous calculations reveal that strong structural anisotropy exists in 8-Pmmn borophene, similar to the cases of stripe, β12, and χ3 borophene. Hence, 8-Pmmn borophene may be transformed into an indirect band gap semiconductor by means of external shear stress.17 These discoveries make 8-Pmmn borophene a very promising candidate for next generation flexible electronics. Moreover, due to the lattice mismatch between the materials and the substrates or external environmental factors, an adventitious strain is almost unavoidable experimentally. Thus, to investigate the failure mechanisms of 2D materials under tension strain is very important for the research and application.19,20 Also as different applications fields have different performance requirements for materials, thus it is necessary to selectively control the properties of the two-dimensional material before it is prepared as an electronic device.21 Meanwhile, apply strains have been confirmed to be an efficient way to adjust the electronic structure of 2D materials.22–25 Although the elastic constants and the intrinsic electronic structure of the 8-Pmmn borophene have been studied by very few studies, the mechanical properties of 8-Pmmn borophene have not been comprehensive investigated, especially the elastic limit, how its electronic structure varies with strain and failure mechanisms under tension strain. Therefore, it is essential to investigate the mechanical properties of 8-Pmmn borophene.
In this work, we have conducted a comprehensive investigation on the strain-induced mechanical properties of monolayer 8-Pmmn borophene based on density functional theory (DFT). The ultimate stress and critical strain, as well as the failure mechanism when approaching the limit strain have been discussed. Our calculation shows that the 8-Pmmn borophene exhibit superior mechanical properties. The monolayer 8-Pmmn borophene can withstand up to 21.59 N m−1 and 27.79 N m−1 in a and b directions, which is much higher than that of stripe borophene, β12 borophene, χ3 borophene, silicene, MoS2 and BP, indicating 8-Pmmn borophene a promising flexible material. The calculated Young's moduli of 8-Pmmn borophene are 241.08 N m−1 (a direction) and 305.20 N m−1 (b direction), respectively, which is comparable to that of steel, make it a hard and flexible 2D material which can withstand strong strains compared with other 2D materials. The strain also has a significant effect on the electronic structure of 8-Pmmn borophene.
2 Method and computational details
All DFT calculations were performed using plane-wave-based Vienna Ab initio Simulation Package (VASP) code.26,27 The generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) functional form was used for the exchange–correlation energy,28 and projector augmented-wave (PAW) pseudopotentials were used to replace the core electrons.29,30 The plane wave energy cutoff was fixed to 500 eV. For all structural relaxations, the convergence criteria for total energy was set to 1.0 × 10−7 eV, and structural optimization was carried out until the Hellmann–Feynman force acting on each atom was less than 0.001 eV Å−1. A 15 × 20 × 1 k-point mesh generated by the scheme of Monkhorst–Pack was chosen for Brillouin zone sampling.31 In order to reduce the interaction between neighboring layers, a vacuum slab of 15 Å along the z-axis was introduced. The phonon dispersion was calculated with the density functional perturbation theory, using the phonopy code.32The theoretical stress–strain relation was predicted by following a standard method as follows.33,34 To compute the stress–strain relation as defined in Fig. 1, we applied a series of incremental tensile strains to the monolayer 8-Pmmn borophene and relaxed on the rectangular directions until the corresponding conjugate stress components were less than 0.01 GPa. The engineering tensile strain is defined as ε = −(l − l0)/l0, where l is the strained lattice constants and l0 is the original lattice constants, respectively. Since the interlayer distance of borophene has not been determined experimentally, we used the in-plane stress f (2D force per length with a unit of N m−1) to represent the strength of the structure.35 The 2D stress can be expressed by multiplying the Cauchy stresses and the thickness of the unit cell.
3 Results and discussion
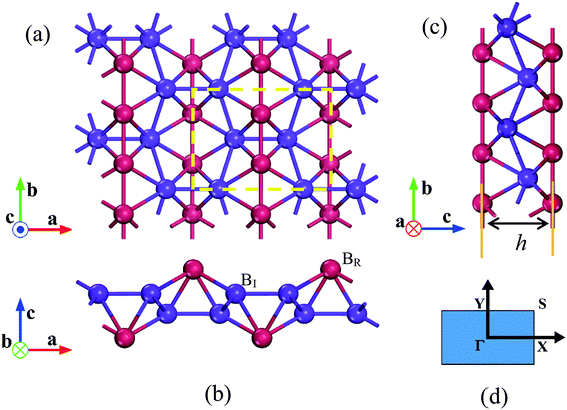
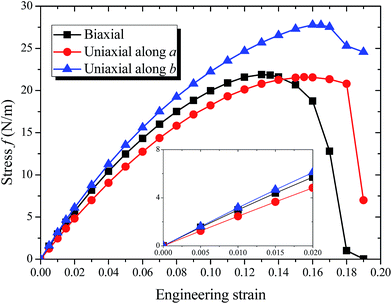
The optimized structures of 8-Pmmn borophene are shown in Fig. 1. Compared with the other three types of borophene (stripe, β12 and χ3, see ESI, Fig. ESI1†), the 8-Pmmn borophene has a much different geometric structure with four boron atomic layers. The calculated lattice constants and buckling height are a = 4.523 Å, b = 3.258 Å and h = 2.18 Å, in good agreement with the previous theoretical results.16–18 8-Pmmn borophene has a highly anisotropic crystal structure with two types of nonequivalent B atoms in a unit cell, namely ridge atoms (BR) and inner atoms (BI), as shown in Fig. 1b. The distinct local environments of BR and BI atoms lead to different local physical and chemical properties.17 As the 8-Pmmn borophene has not been experimentally realized for now, so we firstly discussed the relative stability of the four types of borophene (8-Pmmn, stripe, β12 and χ3 borophene) by comparing the total energy (see ESI, Table ESI1†). The calculated total energy E of 8-Pmmn, stripe, β12 and χ3 borophene are −6.325, −6.187, −6.232 and −6.244 eV per atom, respectively, which is in line with the previous theory studies.13,36 Remarkably, the calculated results show that 8-Pmmn borophene is 0.138, 0.093 and 0.081 eV per atom, respectively, lower in energy than that of the most recently synthesized stripe, β12 and χ3 borophene, indicating its high possibility for experimental realization. The calculated cohesive energies (Ec) confirmed the previous results as well (see ESI, Table ESI1†). Therefore, the 8-Pmmn structure of borophene is more energetic favourable than other three forms of borophene.Fig. 2 shows the calculated ideal tensile stress–strain relations for 8-Pmmn borophene under both biaxial and uniaxial strains. By fitting the initial stress–strain curves based on linear regression up to 2% along the a and b directions (Fig. 2, inset), we obtained the corresponding elastic moduli. The Young's moduli are Ea = 241.08 N m−1 and Eb = 305.20 N m−1, in line with the previous theoretical results.37 The stiffness of 8-Pmmn borophene along a direction is substantially lower than that along b direction, indicating the strong anisotropy of the crystal structure. In addition, the stiffness of 8-Pmmn borophene is much higher than that of χ3 and β12 borophene,13 as shown in Table 1. Compared with the stripe borophene, though the Young's modulus along a direction (Ea) of 8-Pmmn borophene is lower than that of stripe borophene, the Young's modulus along b direction (Eb) is much higher than that of stripe borophene. Compared to other 2D materials, such as graphene,39 BN,40 silicene,41 and MoS2,42 the Young's moduli of graphene are higher than that of 8-Pmmn borophene in both directions, but the Young's moduli of silicene and MoS2 are much lower than that of 8-Pmmn borophene. The Young's moduli of BN is slightly higher than that of 8-Pmmn borophene along a-axis, but lower than that of 8-Pmmn borophene along b-axis. In addition, our calculated Poisson's ratios of 8-Pmmn borophene (as listed in Table 1) are around 0.042 and 0.062 along the a and b directions, respectively, also in good agreement with the previous study.37 Compared with the other two types of borophenes, the Poisson's ratios of 8-Pmmn borophene is much smaller than that of χ3 and β12 borophene, indicating the higher stiffness of 8-Pmmn borophene in consistent with its Young's modulus.
| a (Å) | b (Å) | h (Å) | Ea (N m−1) | Eb (N m−1) | νa | νb | |
|---|---|---|---|---|---|---|---|
| 8-Pmmn borophene | 4.523 | 3.258 | 2.18 | 241.08 | 305.20 | 0.042 | 0.062 |
| Ref. 18 | 4.52 | 3.25 | 2.21 | — | — | — | — |
| Ref. 17 | 4.51 | 3.25 | 2.20 | — | — | — | — |
| Ref. 37 | — | — | — | 248.26 | 321.54 | 0.048 | 0.062 |
| Stripe borophene15 | 1.614 | 2.866 | 0.911 | 389 | 166 | −0.012 | −0.005 |
| χ3 borophene13 | 4.45 | 4.45 | 0 | 187.8 | 180.8 | 0.19 | 0.19 |
| β12 borophene13 | 5.07 | 2.93 | 0 | 182.0 | 207.5 | 0.17 | 0.19 |
| Graphene39 | — | — | — | 342.2 | 342.2 | 0.175 | 0.175 |
| BN40 | — | — | — | 275.8 | 275.8 | — | — |
| Silicene41 | — | — | — | 60.6 | 60.6 | — | — |
| MoS2 (ref. 42) | — | — | — | 197.9 | 200.3 | — | — |
The calculated strain–stress relation becomes nonlinear as the applied strain increases, as shown in Fig. 2. The stress–strain curve under the uniaxial strain in a or b direction follows the similar tendency as that under the biaxial strain until epsilon > 0.12. The maximum stress for biaxial strain is 21.89 N m−1, and the corresponding critical strain is 0.13. The tensile strength value is much larger than that of stripe borophene,15 silicene,41 and MoS2 (also shown in Table 2).42 When the biaxial strain exceeds 0.13, the stress curve decreased rapidly. Along the a and b directions, the critical tensile strains are 0.155 and 0.16, respectively. The corresponding ideal strengths are 21.59 and 27.79 N m−1, both higher than that of stripe borophene,15 β12 borophene,38 χ3 borophene,38 silicene,41 MoS2,42 and BP,43 but much lower than that of graphene.39 Compared to the biaxial strain or uniaxial strain along a direction, 8-Pmmn borophene shows superior flexibility when tension is applied along the b direction. The high ultimate strains make 8-Pmmn borophene potentially useful in high-strain engineering applications.
| Direction | f (N m−1) | ε | Failure mechanism | |
|---|---|---|---|---|
| 8-Pmmn borophene | a | 21.59 | 0.155 | Elastic instability |
| b | 27.79 | 0.165 | Elastic instability | |
| Biaxial | 21.89 | 0.13 | Elastic instability | |
| Stripe borophene15 | a | 20.26 | 0.08 | Phonon instability |
| b | 12.98 | 0.15 | Elastic instability | |
| Biaxial | 14.75 | 0.08 | Phonon instability | |
| β12 borophene38 | Armchair | 19.97 | 0.2 | — |
| Zigzag | 20.38 | 0.21 | — | |
| χ3 borophene38 | Armchair | 19.91 | 0.11 | — |
| Zigzag | 20.18 | 0.21 | — | |
| Graphene39 | Armchair | 40.41 | 0.266 | Elastic instability |
| Zigzag | 36.74 | 0.194 | Elastic instability | |
| Silicene41 | Armchair | 7.59 | 0.17 | Elastic instability |
| Zigzag | 5.26 | 0.136 | Elastic instability | |
| Biaxial | 6.76 | 0.16 | Elastic instability | |
| MoS2 (ref. 42) | Armchair | 14.75 | 0.256 | Phonon instability |
| Zigzag | 9.59 | 0.18 | Elastic instability | |
| Biaxial | 14.63 | 0.195 | Phonon instability | |
| BP43 | Armchair | 9.99 | 0.27 | — |
| Zigzag | 4.44 | 0.33 | — |
Fig. 3 shows the dependence of buckling height h of 8-Pmmn borophene on the three types of tensions, where the tension dependent buckling heights are monotonic. For the biaxial strain, the buckling height decreased significantly, especially when the strain ε > 0.13. On the other hand, when the tension is applied along the a or b direction, the buckling height decreased monotonously and almost linearly before the strain approaches the critical value. Note that the buckling height of the 8-Pmmn borophene does not decrease to zero within the applied strain range, in contrast to stripe borophene, which turns from buckled structure to planar structure when a biaxial strain of 0.13 is applied.15
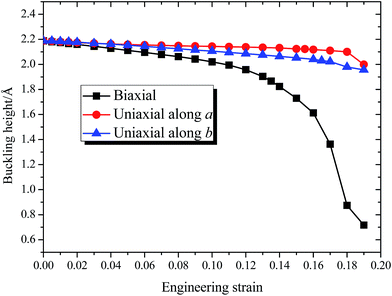 | ||
| Fig. 3 The calculated dependence of buckling height of 8-Pmmn borophene on the three types of tensions. | ||
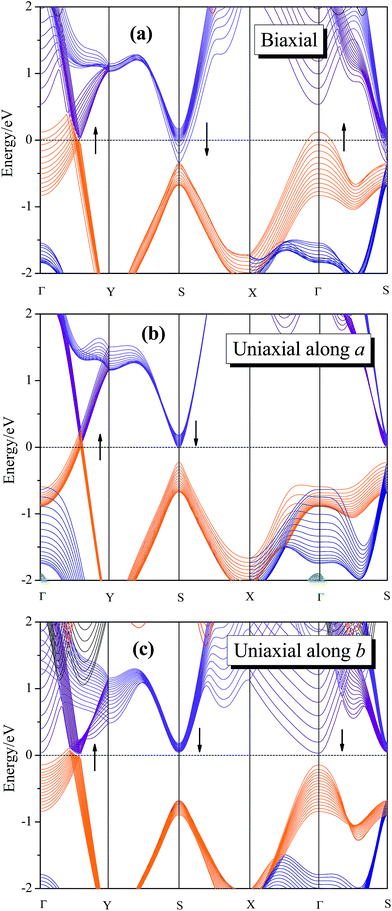
Applying mechanical strain is proved to be a powerful method for modulating the electronic properties of 2D materials.22–25 The intrinsic band structure of 8-Pmmn borophene has a Dirac cone located along Γ–Y direction.16–18 The spatial inversion symmetry is of great significance for the sake of Dirac cone formation, and the broken of the spatial inversion symmetry may have great effects on characteristic of the Dirac fermion in the system. For example, graphene will break its symmetry after applying a certain strain, which yields a band gap and destroys its Dirac cone.44 Therefore, it is important to study the electronic structure of 8-Pmmn borophene under strain. The calculated dependence of band structure of 8-Pmmn borophene on the three types of tensions are shown in Fig. 4. Fig. 4a shows the band structure of 8-Pmmn borophene under biaxial strain range from 0.01 to 0.13. According to our calculation, 8-Pmmn borophene will open a tiny energy gap (about 44 meV) with a small (ε = 0.02) strain along Γ–Y direction. However, within the increase of strain, the valence band maximum (VBM) along Γ–Y direction will cross over the Fermi level. Meanwhile, the conduction band at high symmetry point S and the valence band located at Γ will also pass through the Fermi energy, as marked by the arrows in the Fig. 4a. Thus, the metallic characteristics of 8-Pmmn borophene will be enhanced by applying a large biaxial strain. When the applied uniaxial strain increases along the a direction, similar to the biaxial strain condition, the VBM located at Γ–Y direction will cross the Fermi level, and the conduction band located at S will gradually decrease, approaching the Fermi surface (as drawn in Fig. 4b), both tend to enhance the metallic behavior of 8-Pmmn borophene. Finally, when the applied uniaxial strain is along the b direction, 8-Pmmn borophene will open a small energy gap (about 23 to 48 meV), in contrast to the case of a-axis strain. However, when the b-axis strain reach 7%, the VBM along Γ–Y direction will cross the Fermi level, which transforms 8-Pmmn borophene from a semiconductor to a metal (Fig. 4c).
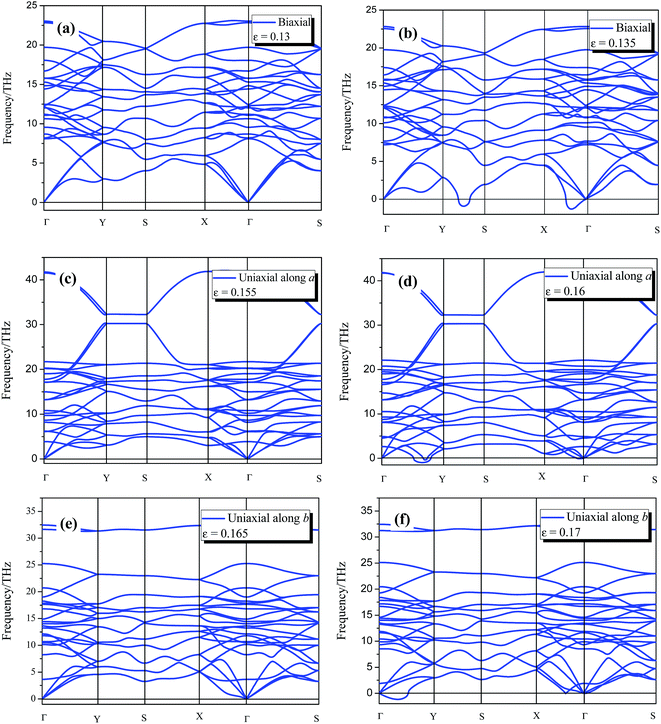
The 8-Pmmn borophene possesses good mechanical properties with relatively high critical strain under the three types of strain. Thus, it is important to verify whether the monolayer 8-Pmmn borophene remains stable before approaching the maximum stress. Phonon dispersion is an effective way to estimate structural stability of crystal structures. Accordingly, we performed phonon dispersion calculations for the systems in order to examine the kinetic stability. The calculated phonon dispersions of 8-Pmmn borophene under the three types of applied strains are shown in Fig. 5. Under the biaxial strain ε = 0.13, the system exhibits good stability due to the phonon dispersion without imaginary frequencies. Nevertheless, as the biaxial strain increases to 0.135, imaginary frequencies appear in the Y–S and Γ–X direction. Under the uniaxial strain in the a-direction, the imaginary frequencies appear when the strain reaches εa = 0.16. We also noticed that top-most phonon branches are extremely flat between Y and S, as shown in Fig. 5c and d. These phonon dispersion curves (flat phonon dispersion) mean the localization of phonons and may cause the low thermal conductivity.45–48 Under b-axis uniaxial strain, imaginary frequencies appear at εb = 0.17. The phonon dispersions of 8-Pmmn borophene under tensile strains indicate that 8-Pmmn borophene can withstand up to 15.5% and 16.5% uniaxial tensile strains along the a and b directions, respectively, and 13% biaxial tensile strain. It is generally accepted that imaginary frequencies of phonon dispersion are signs of instability. Hence, 8-Pmmn borophene would remain stable when reaching the ultimate tensile strain limits. In other words, the failure mechanisms of 8-Pmmn borophene under biaxial and uniaxial tensions are elastic instability.
To understand the chemical bonding of 8-Pmmn borophene under three types of strains, we calculated its bond lengths (see ESI, Fig. ESI2†) and valence charge density (see ESI, Fig. ESI3a–d†) as well. The B–B bond lengths (l1–l5, see ESI, Fig. ESI2d†) show a linear variation under the biaxial (ε < 0.13) and uniaxial strains. As the biaxial strain goes beyond 0.13, the bond lengths change rapidly, which explains the change of the buckling height h (as drawn in Fig. 3). The applied strain has a great influence on the B–B bond of 8-Pmmn borophene. As the strain increases, the electron around boron atom becomes more localized (especially in the case of biaxial strain, see ESI, Fig. ESI3b†) and the B–B bonds are transformed from a strong covalent bond to a weak ionic bond, as shown in ESI, Fig. ESI3.† The weakening of the B–B bonding also led to the structural instability of 8-Pmmn borophene under sufficiently large strain, as shown in Fig. 5.
Within the context of novel 2D materials, we also compared the mechanical responses of 8-Pmmn borophene with stripe borophene,15 β12 borophene,38 χ3 borophene,38 graphene,39 silicene,41 MoS2,42 and BP,43 as shown in Table 2. Compared with the other three types of borophene, silicene, MoS2 or BP, the ideal tensile strengths of monolayer 8-Pmmn borophene are substantially larger, but much smaller than that of graphene, due to the C–C bonds are stronger than the B–B bonds. The corresponding strain along the a direction (15.5%) is also much larger than that of stripe (8%) and χ3 borophene (11%), but slightly smaller than that of β12 borophene. For the tension applied in b direction, the 8-Pmmn borophene shows superior mechanical flexibility as well, just like the other three types of borophene. The failure mechanisms of 8-Pmmn borophene are similar to graphene and silicene, i.e., under uniaxial and biaxial tensions their failure mechanism is elastic instability. Such is quite different from the failure mechanisms of stripe borophene and MoS2 upon tensions, where in one direction (b or zigzag direction) attributed to elastic instability, while in the other direction (a or armchair direction) due to phonon instability.
4 Conclusion
We have investigated the ideal strength and critical strain of monolayer 8-Pmmn borophene by first-principles calculations. The monolayer 8-Pmmn borophene can withstand up to 21.59 N m−1 and 27.79 N m−1 stresses in a and b directions, respectively. The corresponding critical strains are 15.5% (a direction) and 16.5% (b direction). For biaxial tension, it also can withstand up to 21.89 N m−1 and the corresponding critical strain is 13%. The calculated Young's moduli are 241.08 N m−1 (a direction) and 305.20 N m−1 (b direction), respectively, revealing that 8-Pmmn borophene is a hard but also flexible 2D material compared with other common 2D materials. It has been found that the tensile strains have a significant effect on the electronic structures of 8-Pmmn borophene. Furthermore, phonon dispersions under various applied strains imply that the mechanical failure in 8-Pmmn borophene is likely to originate from the elastic instability. Our calculation indicates that 8-Pmmn borophene may find its applications in high-strain engineering electronics area.Acknowledgements
This work was financially supported by the MOST of China under Grant No. 2016YFA0203800, the Natural Science Foundation of Hubei Province under Grant No. 2016CFB223, the National Natural Science Foundation of China (No. 11504281), and the Fundamental Research Funds for the Central Universities of China under Grant No. HUST:2016YXMS212.Notes and references
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- P. Vogt, P. P. De, C. Quaresima, J. Avila, F. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. L. Lay, Phys. Rev. Lett., 2012, 108, 155501 CrossRef PubMed.
- L. F. Li, S. Z. Lu, J. B. Pan, Z. H. Qin, Y. Q. Wang, Y. L. Wang, G. Y. Cao, S. X. Du and H. J. Gao, Adv. Mater., 2014, 26, 4820–4824 CrossRef CAS PubMed.
- F. F. Zhu, W. J. Chen, Y. Xu, C. L. Gao, D. D. Guan, C. H. Liu, D. Qian, S. C. Zhang and J. F. Jia, Nat. Mater., 2015, 14, 1020–1025 CrossRef CAS PubMed.
- L. K. Li, Y. J. Yu, G. J. Ye, Q. Q. Ge, X. D. Ou, H. Wu, D. L. Feng, X. H. Chen and Y. B. Zhang, Nat. Nanotechnol., 2014, 9, 372–377 CrossRef CAS PubMed.
- S. L. Zhang, Z. Yan, Y. F. Li, Z. F. Chen and H. B. Zeng, Angew. Chem., Int. Ed., 2015, 54, 3112–3115 CrossRef CAS PubMed.
- C. Kamal and M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 085423 CrossRef.
- H. S. Tsai, S. W. Wang, C. H. Hsiao, C. W. Chen, H. Ouyang, Y. L. Chueh, H. C. Kuo and J. H. Liang, Chem. Mater., 2016, 28, 425–429 CrossRef CAS.
- T. Lei, C. Liu, J. L. Zhao, J. M. Li, Y. P. Li, J. Q. Wang, R. Wu, H. J. Qian, H. Q. Wang and K. Ibrahim, J. Appl. Phys., 2016, 119, 015302 CrossRef.
- C. H. Chen, K. D. Kepler, A. A. Gewirth, B. M. Ocko and J. Wang, J. Phys. Chem., 1993, 97, 7290–7294 CrossRef CAS.
- A. J. Mannix, X. F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago, J. R. Guest, M. J. Yacaman, A. Ponce, A. R. Oganov, M. C. Hersam and N. P. Guisinger, Science, 2015, 350, 1513–1516 CrossRef CAS PubMed.
- B. J. Feng, J. Zhang, Q. Zhong, W. B. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. H. Wu, Nat. Chem., 2016, 8, 563–568 CrossRef CAS PubMed.
- B. Peng, H. Zhang, H. Z. Shao, Z. Y. Ning, Y. F. Xu, H. L. Lu, D. W. Zhang and H. Y. Zhu, 2016, arXiv:1608.05877.
- B. Peng, H. Zhan, H. Z. Shao, Y. F. Xu, R. J. Zhang and H. Y. Zhua, J. Mater. Chem. C, 2016, 4, 3592–3598 RSC.
- H. F. Wang, Q. F. Li, Y. Gao, F. Miao, X. F. Zhou and X. G. Wan, New J. Phys., 2016, 18, 073016 CrossRef.
- X. F. Zhou, X. Dong, A. R. Oganov, Q. Zhu, Y. J. Tian and H. T. Wang, Phys. Rev. Lett., 2014, 112, 085502 CrossRef.
- A. Lopez-Bezanilla and P. B. Littlewood, Phys. Rev. B, 2016, 93, 241405 CrossRef.
- J. Carrete, W. Li, L. Lindsay, D. A. Broido, L. J. Gallego and N. Mingo, Mater. Res. Lett., 2016, 4, 204–211 CrossRef.
- C. A. Marianetti and H. G. Yevick, Phys. Rev. Lett., 2010, 105, 245502 CrossRef CAS PubMed.
- E. B. Isaacs and C. A. Marianetti, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 89, 184111 CrossRef.
- Y. F. Sun, S. Gao and Y. Xie, Chem. Soc. Rev., 2013, 43, 530–546 RSC.
- A. S. Rodin, A. Carvalho and A. H. C. Neto, Phys. Rev. Lett., 2014, 112, 176801 CrossRef CAS PubMed.
- H. Pan and Y. W. Zhang, J. Phys. Chem. C, 2012, 116, 11752–11757 CAS.
- F. Guinea, M. I. Katsnelson and A. K. Geim, Nat. Phys., 2009, 6, 30–33 CrossRef.
- H. J. Zhang, Y. D. Ma and Z. F. Chen, Nanoscale, 2015, 7, 19152–19159 RSC.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and J. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- T. Li, J. W. Morris and D. C. Chrzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 054107 CrossRef.
- T. Li, J. W. Morris and D. C. Chrzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 024105 CrossRef.
- J. Zhou and R. Huang, J. Mech. Phys. Solids, 2008, 56, 1609 CrossRef CAS.
- F. X. Ma, Y. L. Jiao, G. P. Gao, Y. T. Gu, A. Bilic, Z. F. Chen and A. J. Du, Nano Lett., 2016, 16, 3022 CrossRef CAS PubMed.
- Z. Q. Wang, T. Y. Lv, H. Q. Wang and J. C. Zheng, Phys. Chem. Chem. Phys., 2016, 18, 31424 RSC.
- B. Mortazavi, O. Rahaman, A. Dianat and T. Rabczuk, Phys. Chem. Chem. Phys., 2016, 18, 27405 RSC.
- F. Liu, P. D. Ming and J. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 064120 CrossRef.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- C. H. Yang, Z. Y. Yu, P. F. Lu, Y. M. Liu, H. Ye and T. Gao, Comput. Mater. Sci., 2014, 95, 420–428 CrossRef CAS.
- T. S. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 167402 CrossRef.
- Q. Wei and X. H. Peng, Appl. Phys. Lett., 2014, 104, 251915 CrossRef.
- R. M. Ribeiro, V. M. Pereira, N. M. R. Peres, P. R. Briddon and A. H. C. Neto, New J. Phys., 2009, 11, 115002 CrossRef.
- J. F. Rodriguez-Nieva, R. Saito, S. D. Costa and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 245406 CrossRef.
- A. J. H. Mcgaughey, M. I. Hussein, E. S. Landry, M. Kaviany and G. M. Hulbert, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 104304 CrossRef.
- R. Mittal, M. Zbiri, H. Schober, E. Marelli, S. J. Hibble, A. M. Chippindale and S. L. Chaplot, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 83, 024301 CrossRef.
- Y. Xie, H. Y. Cao, Y. Zhou, S. Y. Chen, H. J. Xiang and X. G. Gong, Sci. Rep., 2015, 5, 10011 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra28454j |
| This journal is © The Royal Society of Chemistry 2017 |