Defect-sensitive performance of silicene sheets under uniaxial tension: mechanical properties, electronic structures and failure behavior

Abstract

As a silicon analog of graphene, silicene has attracted considerable attention due to its unique physical and chemical properties. Pioneering studies have demonstrated that defects in graphene-like two-dimensional materials are considered tools for tuning the physical properties of these materials. In this work, the influence of defects on the mechanical properties and failure behavior of silicene sheets were investigated using molecular mechanics and molecular dynamics methods. The results showed that the intrinsic strength of the silicene sheets decreased with increased linear density for vacancies, width ratio for cracks, and inflection angle for grain boundaries. The elastic properties of the silicene sheets were affected by not only the defects but also their corrugated structure. Fracture failure of the silicene sheet with defects usually started from the Si–Si bond, which was located at the defect edge. The stretching strain could tune the electronic structure of the silicene sheets. This study demonstrated the defect-sensitive performance of silicene under uniaxial tension and thus helped evaluate and extend the application of this material.

---

1. Introduction

Silicene is a two-dimensional (2D) hexagonal structure, which has attracted significant interest from both academia and industry due to its unique physical and chemical properties.^1–5 Unlike the planar structure of graphene, silicene exhibits a low-buckle structure owing to the weakening of the π–π overlaps induced by its large atom–atom distance.^6,7 After the prediction of the silicene structure based on ab initio calculations in 1994,⁸ numerous studies were carried out to fabricate silicene using experimental methods.^9–13 Recently, silicene was synthesized by epitaxial growth on metal substrates, such as Ag,^9,10 ZrB₂,¹¹ and Au.¹² Silicene has considerable potential in electronic, thermoelectric and photovoltaic applications.^14–16 In addition to its electronic properties, the mechanical characteristics of silicene should also be understood. Very recently, the stiffness and strength of pristine silicene under uniaxial strain were studied using density functional theory (DFT)^17–20 and molecular dynamics (MD) methods.^21–23 In 2013, Peng and coworkers demonstrated that silicene exhibits a nonlinear elastic deformation with large strains using a DFT method.¹⁹ In addition, the strength and fracture strains of silicene were higher than those of bulk silicon, but the Young's modulus of silicene was lower than that of bulk silicon.²²

For the application of silicene in various devices, defects are often the first concern. Recently, Shaikhutdinov's experimental research showed that patterned defect structures that were predicted for graphene were observed on single-layer silica films on Ru(0001).²⁴ In their work, defects such as vacancies, pentagon–heptagon pairs, and square–octagon pairs were clearly observed by scanning tunneling microscopy. Pioneering works have pointed out that structural imperfections play an important role in tuning the physical properties of low-dimensional materials.^25–27 “Defect engineering” via patterning the defects on the 2D materials as a tool to control the performance of such materials become a hot topic. Until now, effects of point (vacancies^28,29) and line (grain boundaries^30–33 and cracks^34–38) defects on the mechanical properties and fracture of graphene and hexagonal boron nitride have been systematically studied. It was detected using DFT method that the intrinsic strength of graphene might be either enhanced or reduced depending on the distribution of pentagon–heptagon pair grain boundaries (GBs).³¹

Studies on the defects in silicene sheets have also attracted much attention.^39–44 However, most of these studies focus on the structural, electronic, and thermal properties of the defects. To the best of our knowledge, the influence of these defects (including point, line, and planar defects) on the mechanical properties and failure behavior of silicene has rarely been reported. Distinct properties may be introduced by the defects in the low-buckled structure of silicene. In addition, due to the practical difficult in experiments to identify the exact affection induced by a particular type of defects, it was a useful and feasible way to study the affection of defects on the silicene sheet by theoretic methods.

In the present work, typical types of point, line, and patterned planar defects in the surface of silicene were studied by molecular mechanics (MM) and MD methods. The structure, in-plane stiffness, intrinsic strength, and critical failure strain of silicene with and without defects were obtained and compared. Similar to a piece of paper, a silicene sheet usually takes tensile load only. If it is used in a part of material system, there must be something in the system that can resist the expected compressive load. So this work is about the behavior of silicene in the tensile sense, with and without defects. The issues we focused on include the possible relationships among the mechanical properties of silicene sheets, the defect parameters, as well as their fracture behaviors.

2. Computational details and models

2.1 Computational details

The MM and MD methods were employed to perform the tensile test of silicene models with and without defects by using the Discover module of Materials Studio. The condensed phase optimization molecular potentials for atomistic simulation studies (COMPASS) force field was chosen to describe the silicene systems.^45,46 COMPASS is a powerful force field which supports atomistic simulations of condensed phase materials. The COMPASS force field has been extended and covered most common organic molecules, organic and inorganic polymers, zeolites, and metal/transition-metal oxides.^47,48 It has been also verified by several previous simulation works that COMPASS force field^49,50 could be used to study the dynamical behaviors of Si sheets. Details of the COMPASS force field parameters are available and embedded in Materials Studio for Si–Si interactions.⁵¹ The periodic boundary condition was imposed in the computational unit cell. A vacuum with a height of 100 Å was placed above the silicene surface to minimize the influence of adjacent layers.

To investigate the influence of defects on the in-plan mechanical properties of silicene sheet, a series of uniaxial tensile tests along the tangential direction of the silicene surface was carried out. The tensile test was accomplished by applying an atomic strain on the armchair (am) direction or the zigzag (zz) direction of the 2D surface with a strain step of 0.5%. For each configuration, an energy minimization was carried out, and a 100 ps MD simulation with NVT ensemble was performed on the system. The strain rate of the tensile tests was 5 × 10⁷ s⁻¹. The equations of atomic motion were integrated with a time step of 1 fs, and the simulation was carried out at a temperature of 1 K to eliminate the influence of temperature on the systems.

2.2 Nomenclature and silicene models

To reflect the influence of defects on the mechanical behavior of such materials, silicene models with point defects (vacancies and Stone–Wales defects), line defects (initial cracks and GBs) and patterned planar defects in the silicene surface were constructed based on the experimental observations. For vacancies, a zz_V (am_V) system denotes a silicene sheet with a vacancy defect, and the tensile test was performed along the zz (am) direction of the system. Similarly, a zz_SW (am_SW) system refers to a silicene sheet with a Stone–Wales defect, and the tensile test was performed along its zz (am) direction.

Turning to the cracks in the silicene surface, a zz_crack (am_crack) system is a silicene system with an initial crack perpendicular to the zz (am) direction; during the tensile test, the external force was applied along the zz (am) direction. The GB models selected in this work comprised pentagon–heptagon (5|7) pairs. These systems were name as “(5|7) pairs_1” to “(5|7) pairs_6” corresponding to different arrangements and linear densities of (5|7) pairs. The external force was applied perpendicular to the GBs. Upon encountering a planar defect, three systems with different planar defect density, which were named as “am_P1” to “am_P3” systems, were considered as probes. For the tensile test on these systems, the external force was added along the am direction.

3. Results and discussion

The mechanical properties and failure behaviors of the silicene systems under uniaxial strain were analyzed in this section. The stress–strain curves of the silicene models with and without defects were plotted based on the relationship between strain energy and stress. The in-plane stiffness which reflected the rigidity of the 2D sheet was calculated. In addition, the intrinsic strength which was defined as the highest stress point along the stress–strain curve was obtained to evaluate the mechanical performance of the silicene sheets. The thickness of such 2D sheet was difficult to be determined experimentally;²³ thus, a controversy concerning the value of the sheet thickness arose. A previous discussion of this parameter suggested that it is better to report the stress and elastic moduli of monolayer systems in force per unit length (N m⁻¹) rather than force per unit area (Pa), especially for the buckled silicene structure. As such, the results of in-plane stiffness and intrinsic strength obtained in the present work were expressed using the unit of N m⁻¹.

3.1 Structures and mechanical properties of the pristine silicene

A defect-free silicene model was constructed and optimized with all the atomic structure parameters fully relaxed to obtain the equilibrium configuration (Fig. 1(a)). The lattice constant of the equilibrium silicene model was 3.80 Å, and the Si–Si bond length was 2.25 Å. This model showed a low buckling structure with a buckled distance of 0.58 Å. These parameters were consistent with the previous DFT and MD calculation results reported in the literature (see Table 1).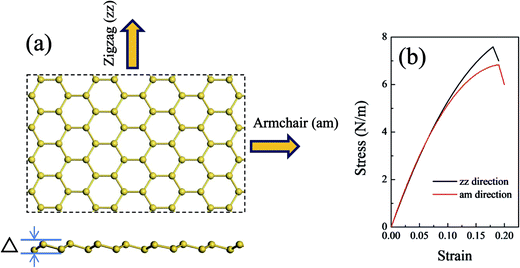

Fig. 1 (a) Atomic structures of the silicene sheet. The upper image shows the top view, and the bottom image shows the side view; (b) stress–strain curves of the defect-free silicene.

Table 1 Parameters of the pristine silicene including the lattice constant a₀, buckled distance Δ, Si–Si bond length d_Si–Si, in-plane stiffness Y, intrinsic strength τ and critical failure strain δ

System	Methods	a0 (Å)	Δ (Å)	dSi–Si (Å)	In-plane stiffness Y (N m^−1)	Intrinsic strength τ (N m^−1)	Critical failure strain δ (%)
Pristine silicene	MD-Compass-ours	3.80	0.58	2.25	66.2(zz)/68.7(am)	7.7(zz)/6.8(am)	19(zz)/20(am)
	DFT-LDA^17	3.83	0.42	2.25	63.0	—	20
	DFT-GGA^18	—	0.45	2.28	60.06(zz)/63.51(am)	5.66(zz)/7.07(am)	14(zz)/18(am)
	MD-ReaxFF^21	3.80	0.67	2.30	—	—	—
	MD--ReaxFF^23	3.76	0.69	2.11	50.44(zz)/62.31(am)	5.85(zz)/4.78(am)	—

---

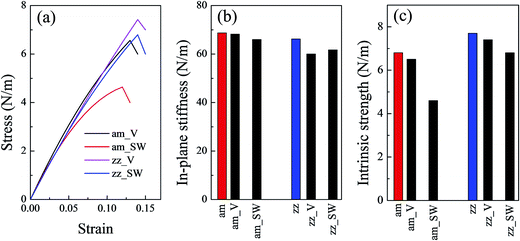
Fig. 1(b) shows the stress–strain relationship of a silicene sheet along its zz and am directions. The in-plane stiffness obtained for the defect-free silicene sheet were 66.2 N m⁻¹ and 68.7 N m⁻¹ for zz and am directions, respectively (see Table 1). At the same time, this silicene sheet possessed an intrinsic strength of 7.7 N m⁻¹ and 6.8 N m⁻¹ along the zz and am directions, respectively. These values indicated a slight anisotropism property in the silicene sheet. Compared with graphene, the values of the mechanical characteristics of silicene were about 25% those of graphene. The dramatic decrease in silicene stiffness and strength has been pointed out due to the buckled structure and the relatively weak interaction of the Si–Si bond.²³ The critical failure strains of silicene obtained in our work (19% for zz direction and 20% for am direction) were comparable with those of graphene. As shown in Table 1, the values of mechanical properties obtained by COMPASS force field were in good agreement with those obtained by ReaxFF force field and DFT method.

3.2 Mechanical properties of defects in silicene surface

3.2.1 Vacancies and Stone–Wales defects. A small energy barrier needs to be overcome to form vacancies or Stone–Wales defects in the silicene surface.^41,42 Thus, these two types of point defects might occur frequently during the silicene growth process. Fig. S1 (in the ESI†) shows the typical models of a vacancy (with a Si atom lost) and a Stone–Wales defect (with a pair of conjoint Si atoms rotating at 90°). To reveal the effect of these two defect types on the mechanical properties of the silicene sheet, tensile tests were performed along either the zz or am directions. Fig. 2(a) shows the various relationships between stress and the atomic strain. As shown in Fig. 2(b), only a slight decrease in the in-plane stiffness was induced by the defect compared with the defect-free silicene system. The silicene sheet possessed a corrugated structure; thus, the system underwent unfolding instead of direct bond stretching in the elastic region of the tensile test. The influence of the point defect on this “unfolding” process was minor. Fig. 2(c) shows that for both the vacancy and Stone–Wales defects, the single point defect reduced the intrinsic strength of the silicene sheet. The am_SW system exhibited an intrinsic strength of 4.6 N m⁻¹, which was just 68% that of the defect-free silicene along the am direction. These results were in accord with the previous reports about the role of the point defects in silicene,⁴² i.e. Young's modulus of the defective silicene sheets only reduces a little from that of the pristine one. However, a single point defect could reduce the fracture stress and fracture strain of the silicene sheets to a large degree. For each tensile direction (zz or am), the intrinsic strength of the silicene system with a vacancy defect was higher than that of the silicene system with a Stone–Wales defect (Table 2 and Fig. 2(c)).

Fig. 2 (a) Stress–strain curves, (b) in-plane stiffness, and (c) intrinsic strength of the silicene sheets with point defects. The red and blue bars denote the pristine silicene along the am and zz directions, respectively.

Table 2 Parameters of the silicene sheet with point defects including the linear density ρ_l, in-plane stiffness Y, intrinsic strength τ and critical failure strain δ

Systems	Linear density ρl (Å^−1)	In-plane stiffness Y (N m^−1)	Intrinsic strength τ (N m^−1)	Critical failure strain δ (%)
zz_V	—	60.0	7.4	14.0
zz_SW	—	61.7	6.8	14.0
am_SW	—	66.0	4.6	12.0
am_V (am_V1)	0.017	68.2	6.5	13.0
am_V2	0.034	67.0	5.3	13.0
am_V3	0.069	66.0	5.0	11.0
am_V4	0.086	54.8	4.4	10.0

---

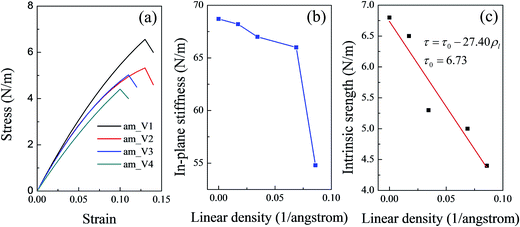
As the defects in a line increased, the point defects might be converted into a line defect. The linear density of point defects was defined to denote the degree of the defect. To further discuss the influence of the defect degree on the mechanical properties of silicene, several more systems with different linear densities of vacancies were constructed. The relationship between the in-plane stiffness (the intrinsic strength) and the linear density of the vacancies in the silicene surface was studied. With limited computing resource, mechanical characteristics along the am direction were selected for the comparison. Fig. 3(a) shows the stress–strain curves for the vacancy systems with different linear densities. All the values of the mechanical properties of the four systems (am_V1–am_V4) were collected and are shown in Table 2. As shown in Fig. 3(b), the in-plane stiffness showed a slight decrease during the initial increase of the linear density (by near 0.07 Å⁻¹). However, as the linear density continued to increase, a sudden drop in the in-plane stiffness was observed. As mentioned above, in the elastic deformation region of the tensile test the system underwent unfolding of the buckled surface instead of direct bond stretching. When the defect degree was relatively low, the in-plane stiffness was slightly affected at the initial increase of the vacancy linear density. However, when the linear density of the vacancies increased to a certain degree, damages on the integral structure could not be ignored. Thus a sudden drop in the in-plane stiffness appeared.

Fig. 3 (a) Stress–strain curves of vacancies in the silicene sheet with different linear densities; (b) in-plane stiffness and (c) intrinsic strength as functions of the linear density of vacancies in the silicene surface. The linear density was defined as the number of vacancies per angstrom.

Owing to the damage of the vacancies to the integral structure, the intrinsic strength along the am direction decrease as the vacancy density increased; this trend showed a linear relationship unlike that of the in-plane stiffness (shown in Fig. 3(c)). The fitted line in Fig. 3(c) shows that the relationship between the intrinsic strength and the vacancy linear density can be expressed as

τ = τ₀ − 27.40ρ_l (1)

where τ₀ = 6.4 N m⁻¹ is approximately equal to the intrinsic strength of the defect-free silicene along the am direction. The lost of Si atoms at the vacancy introduced dangling bonds around the vacancy defect on the interface, which destroyed the integrity of the whole surface. Thus, the increasing defect degree led to a more detrimental effect on the silicene surface and induced a decrease in the intrinsic strength of the system.

3.2.2 Initial cracks in the silicene surface. Recently, crack initiation and propagation on graphene surface was studied using linear elastic theory, molecular dynamics or couple quantum/continuum mechanics approaches.^35–38 In these studies, the characterizations of crack propagation in the graphene surface were detailed discussed. For example, Batra and co-workers investigated the propagation speed^35,37 and the stress intensity factor³⁸ of the crack tip in the graphene surface. These results indicated that the crack width is a sensitive parameter for the crack propagation in graphene surface. In view of these, in the present work, we focused on the influence of initial cracks on the mechanical properties of silicene, especially on the relationship between the mechanical properties and the crack width. Both types of initial cracks which were perpendicular to the zz or am directions were studied. Fig. S2(a) and (b)† show the models of an initial crack perpendicular to the zz and am directions, respectively. The tensile load was performed perpendicular to the initial cracks.

For each crack types, six models with different crack widths in the silicene surface were considered; that is, ‘zz_crack1’ to ‘zz_crack6’ for the cracks perpendicular to the zz direction and ‘am_crack1’ to ‘am_crack6’ for the cracks perpendicular to the am direction. After the tensile testing of the systems with initial cracks, the stress versus axial strain relationship was plotted and shown in Fig. S2(c) and (d)† for the cracks perpendicular to the zz and am directions, respectively. The values of the mechanical properties including in-plane stiffness, intrinsic strength, and critical failure strain for all the systems with initial cracks are summarized in Table 3.

Table 3 Parameters of the silicene sheet with cracks including the crack width w, width ratio of the crack, in-plane stiffness Y, intrinsic strength τ and critical failure strain δ

Systems	Crack width w (Å)	Width ratio of the crack (%)	In-plane stiffness Y (N m^−1)	Intrinsic strength τ (N m^−1)	Critical failure strain δ (%)
zz direction without defects	0	0	66.2	7.7	19.0
zz_crack1	7.58	13.38	62.9	7.7	12.0
zz_crack2	10.41	18.37	60.0	6.9	11.0
zz_crack3	16.65	29.40	59.3	5.2	9.0
zz_crack4	19.81	34.99	59.3	4.4	8.0
zz_crack5	22.85	40.35	59.2	4.0	7.5
zz_crack6	29.13	51.44	51.7	3.7	6.5
am direction without defects	0.00	0.00	68.7	6.8	20.0
am_crack1	7.31	12.56	66.7	5.5	11.5
am_crack2	10.97	18.84	66.7	3.0	9.0
am_crack3	14.62	25.12	66.7	2.7	8.0
am_crack4	18.28	31.40	64.3	2.2	7.0
am_crack5	21.80	37.45	60.0	2.2	7.0
am_crack6	29.07	49.93	59.6	1.5	5.0

---

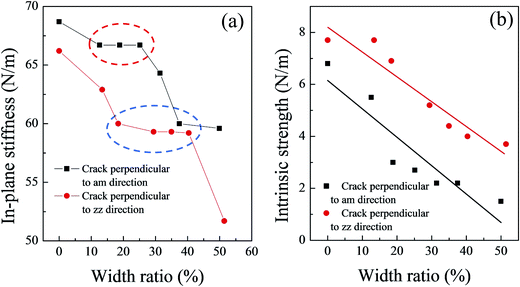
The in-plane stiffness of these models basically decreased as the initial crack width increased (Fig. 4(a)). However, a platform is present on the in-plane stiffness curve for each type of silicene models with initial cracks (see the red and blue circles for the cracks perpendicular to the am and zz directions in Fig. 4(a)); the platform might be also caused by the corrugated structure of the silicene sheet. Only when the initial width of the crack reached a certain degree, the elastic deformation region was affected dramatically. The critical value of the crack width ratio could cause a sudden drop in the in-plane stiffness of the system, and this value was estimated to be about 40% for the zz direction and 25% for the am direction.

Fig. 4 (a) In-plane stiffness and (b) intrinsic strength as functions of the width ratio of cracks in the silicene surface. The width ratio was defined as the ratio of the crack width to the whole width of the unit cell.

The values of the intrinsic strength for the silicene sheet with initial cracks ranged from 7.7 N m⁻¹ to 3.7 N m⁻¹ for cracks perpendicular to the zz direction and 5.5 N m⁻¹ to 1.5 N m⁻¹ for cracks perpendicular to the am direction. Fig. 4(b) shows the intrinsic strength as a function of the width ratio of the cracks. A clear linear relationship was observed between the intrinsic strength and the width ratio of both crack types. The fitting equation can be obtained as:

τ = τ_zz0 − 0.10R (for cracks perpendicular to the zz direction) (2)

and

τ = τ_am0 − 0.11R (for cracks perpendicular to the am direction) (3)

where τ_zz0 = 8.2 and τ_am0 = 6.2 are the approximate intrinsic strengths along the zz and am directions, respectively. These results demonstrated that cracks could introduce a detrimental effect on the silicene surface by breaking the integrity of the whole surface. When the width ratio of the crack reached about 30%, the intrinsic strength was reduced to half of that of the defect-free silicene sheet.

3.2.3 Grain boundaries with pentagon–heptagon pairs in the silicene surface. GBs are topological line defects in the silicene surface that possess complex structures and usually affect its mechanical properties significantly. Previous studies have shown that GBs formed by pentagon–heptagon (5|7) pairs are one of the most typical structures in low-dimensional materials.^30–33 Differences in the arrangement and distribution of (5|7) pair dislocations may bring totally distinct mechanical properties in such materials. To determine the effect of GBs with (5|7) pairs on the mechanical properties of silicene sheets in this study, six silicene models with different (5|7) pair distributions and linear densities were constructed and explored (named ‘(5|7) pairs_1’ to ‘(5|7) pairs_6’). The misorientation and inflection angles were defined to describe the mismatching degree between the two domains separated by the GB line, as well as the inflection degree of the silicene sheet with GBs (Fig. S3†). All the angle parameters of the GB models are shown in Table 4. Fig. S4(a)† shows one of the GB models with (5|7) pairs ((5|7) pairs_4). Formation energy was used to describe the stability of GBs in silicene surface, which can be calculated by the follow equation⁵²where E_total and E_pristine are the energies of the silicene sheet with and without grain boundaries, respectively. μ_i is the increased (n_i > 0) or decreased (n_i < 0) chemical potential of silicon atoms. L is the periodic length along the GB line. Formation energies of all GB models are shown in Table 4. Values of the formation energies for all the GBs ranged from 23.0 (kcal mol⁻¹ nm⁻¹) to 82.6 (kcal mol⁻¹ nm⁻¹).

Table 4 Parameters of the silicene sheet with GBs including the linear density of (5|7) pairs ρ_l, formation energy E_f, inflection angle α, misorientation angle θ, in-plane stiffness Y, intrinsic strength τ and critical failure strain δ

Systems	Linear density ρl (Å^−1)	Formation energy Ef (kcal mol^−1 nm^−1)	Inflection angle α (deg)	Misorientation angle θ (deg)	In-plane stiffness Y (N m^−1)	Intrinsic strength τ (N m^−1)	Critical failure strain δ (%)
zz direction without defects	0.00	—	0.0	0.0	66.2	7.7	19.0
(5|7) pairs_1	0.04	35.7	10.0	9.0	71.9	5.5	8.0
(5|7) pairs_2	0.05	40.5	30.0	10.5	65.7	3.3	5.5
(5|7) pairs_3	0.08	55.0	18.5	19.5	30.0	4.6	8.0
(5|7) pairs_4	0.10	82.6	20.0	20.0	56.7	4.4	7.0
(5|7) pairs_5	0.11	23.0	5.0	3.0	56.8	7.6	11.5
(5|7) pairs_6	0.17	35.4	8.0	2.0	51.6	6.7	11.0

---

As shown in Fig. S4(b),† the stress–strain curves for all six GBs with (5|7) pairs exhibited brittle fracture characteristic. The values of the in-plane stiffness and intrinsic strength were ranged from 71.9 N m⁻¹ to 30.0 N m⁻¹ and 7.6 N m⁻¹ to 3.3 N m⁻¹, respectively. Accordingly, the critical failure strain ranged from 11.5% to 5.5%. Notably, the in-plane stiffness of some of the GB models were close to or even higher than those of the defect-free silicene sheets (Table 4). On the other hand, the intrinsic strength of (5|7) pairs_6 was 7.6 N m⁻¹, which was very close to that of the defect-free silicene along the zz direction. These results indicate that the GBs can enhance or weaken of the rigidity and strength of the silicene sheets, which relied on the detailed arrangement of the (5|7) pairs. Similar properties of GBs have also been found and reported in graphene surfaces.³² These characteristics are important in tuning the mechanical properties by engineering GBs in a 2D material surface, thereby providing an effective application in future nano-devices.

As shown in Fig. S5,† neither the in-plane stiffness nor the intrinsic strength showed a clear relationship with the linear density of the (5|7) pairs. Fig. 5 shows the mechanical properties of GBs as a function of either the inflection angle or the misorientation angle. As the buckling structure of the silicene sheet plays a very important role in the elastic deformation region, the in-plane stiffness did not show a clear relationship with the inflection angles (Fig. 5(a)). However, the relationship between the in-plane stiffness and the misorientation angle from 0° to 20° (Fig. 5(b)) was approximately a downward opening parabolic. The increasing misorientation angle corresponded to the planar rotation of the hexatomic rings in the silicene surface.^33,53 The misorientation angle between the two domains on the sides of the GB resulted in different buckling directions of the two domains. With the initial increase of the misorientation angle (up to about 10° in Fig. 5(b)), the buckling structures with different directions served as mutual support; as a result, the silicene sheet was not easily deformed, and the in-plane stiffness increased accordingly. However, as the misorientation angle increased, corresponding changes in the buckling directions occurred. Then, such mutual support might disappear, and the in-plane stiffness would decrease.

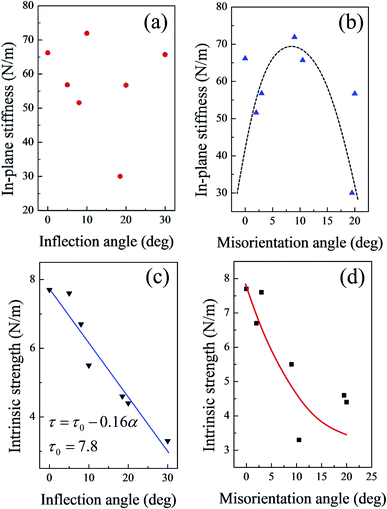Fig. 5 In-plane stiffness of GBs as functions of (a) inflection angle and (b) misorientation angle; intrinsic strength of GBs as functions of (c) inflection angle and (d) misorientation angle.

Fig. 5(c) shows that the intrinsic strength of the silicene sheets with GBs exhibited a clear linear degressive relationship with the increasing inflection angle. When the inflection angle of the silicene sheets reached 20°, the intrinsic strength of the system decreased to about 60% that of the defect-free silicene. The fitted line in Fig. 5(a) shows that the linear relationship between the intrinsic strength and inflection angles can be expressed as

τ = τ₀ − 0.16α (5)

where τ₀ = 7.8 N m⁻¹ is approximately the intrinsic strength of the defect-free silicene sheet along the zz direction. The intrinsic strength also decreased along with the misorientation angles in the range of 0° to 20° (Fig. 5(d)). However, the relationship was not exactly linear.

3.2.4 Patterned planar defects in the silicene surface. When point and line defects form a network of domain boundaries, the situation becomes more complex. These boundaries might be formed by relatively large depressions.²⁴ Such an extended defect is regarded as a planar defect rather than a line or point defect. These types of defects should introduce complex distributions of stress fields in the 2D surface, which gives rise to the complex mechanical behavior of the surface. Fig. 6(a) shows the typical structure of a planar defect, which has been identified by TEM in a single silica layer.²⁴

Fig. 6 (a) Atomic structure and (b) stress–strain curves of the silicene sheet with planar defects.

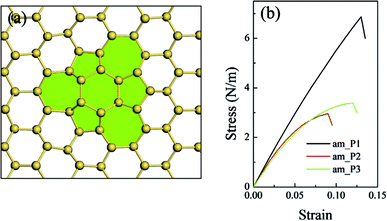
In the present work, we give a predict study on the planar defects of the silicene sheet. Three types of planar defects with defect area ratios ranging from 1.2% to 5.5% were constructed and compared with the defect-free silicene sheet (along the am direction). When the area ratio was just 1.2%, the planar defect did not considerably affect the in-plane stiffness and the intrinsic strength (Fig. 6(b) and Table 5). The in-plane stiffness slightly decreased as the area ratio of defects increased, whereas the intrinsic strength dramatically decreased to about half of that of the defect-free silicene as the area ratio of defects increased. The critical failure strain of the silicene sheet with planar defects decreased correspondingly. However, the complex stress field in the planar defects complicated the relationship between the mechanical properties and the parameters of the planar defects compared with that of the point and line defects. This issue is further investigated in our ongoing related studies.

Table 5 Parameters of the silicene sheet with planar defects including the area ratio of defects, in-plane stiffness Y, intrinsic strength τ and critical failure strain δ. The area ratio of defects was defined as the ratio of defective area to the whole area of the unit cell

Systems	Area ratio of defects (%)	In-plane stiffness Y (N m^−1)	Intrinsic strength τ (N m^−1)	Critical failure strain δ (%)
am direction without defects	0.00	68.7	6.8	20.0
am_P1	1.17	63.0	6.8	13.0
am_P2	3.13	59.9	3.0	9.0
am_P3	5.47	53.8	3.4	12.0

---

3.3 Failure behavior of the silicene surface

During the tensile progress, the buckling structure of silicene trend to a more flat surface. For a pristine silicene sheet, the buckled distance changed from 0.58 Å to about 0.29 Å when it was fractured. To reveal the fracture process of the silicene sheets caused by the tensile load, the configuration of the interfaces with different strains was observed. The fracture process for three typical defect units was collected in Fig. 7. The fracture of the silicene sheets usually started from the defect unit because of the stress concentration near the irregular rings. Fig. 7(a) and (b) show the fracture process of a single vacancy defect along the am and zz directions, respectively. Along the am direction, the silicene sheet was fractured with the elongation of the Si–Si bonds at the vacancy. The two initially elongated Si–Si bonds (labeled as a₁ and a₂) were parallel to the tensile load and at the upper and bottom edges of the vacancy (Fig. 7(a)). As the atomic strain increased, the adjacent Si–Si bonds in the same line were fractured one by one, and a crack perpendicular to the tensile load was formed. After the stress release, a new Si–Si bond formed between the two Si atoms (labeled in red) at the center of the initial vacancy, which resulted in a five-member ring in the silicene surface.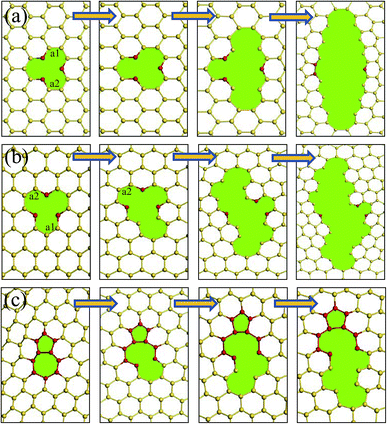

Fig. 7 Fracture failure processes of (a) a vacancy defect along the am direction; (b) a vacancy defect along the zz direction; and (c) an isolated (5|7) pair in the silicene surface.

For the fracture process of the silicene sheet with a vacancy defect along the zz direction, the first broken Si–Si bond a₁ (with an initial bond length of 2.23 Å) was located around the vacancy and at one of the vacancy tips. The Si–Si bond a₂ which was parallel to and at the opposite position of the first broken bond was fractured subsequently. Owing to the breakage of these two bonds, the initial direction of the crack propagation showed an angle of about 60° with the tensile load, which made it easier to release energy. When the crack continued to propagate, the growth direction became perpendicular to the tensile direction. This phenomenon was similar to that observed in a graphene surface with a vacancy along the zz direction.²⁸

As the (5|7) pair was usually subjected to the highest tension among the atomic rings, the fracture of a (5|7) pair started at a 7–6 Si–Si bond (shared by a heptagon and a hexagon) (shown in Fig. 7(c)). After breaking the 7–6 Si–Si bond, a meta-Si–Si bond in the same hexagonal ring was elongated and broken. The fracture was then transferred to the regular hexagonal rings along the same line, and complete failure occurred subsequently.

3.4 Electronic properties of silicene under the applied mechanical stain

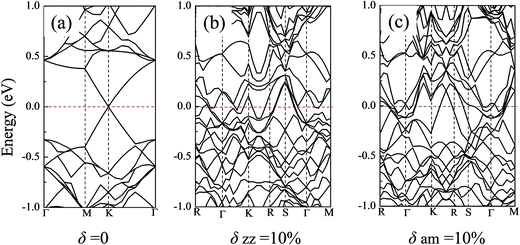
Strain induced energy band dispersion has been studied and verified in Si nanosheets along the (100) and (110) directions by R. Q. Zhang group.⁵⁴ Their research results showed that under some particular conditions, a direct-to-indirect transition of the band gap was observed in the (100) Si nanosheet. In the present work, the electronic band structure of the silicene sheets and their changes during the tensile process along both the zz and am directions were studied. Considering the limitation of the computing resource, just three typical silicene models were selected: (i) the defect-free silicene system; (ii) the silicene system with a vacancy defect; (iii) the silicene system with a Stone–Wales defect. For each model, the original band structure, the energy band under a high stretching strain (i.e. 10% atomic strain) along the zz or am directions were analyzed.

Fig. 8 shows the energy bands of the defect-free silicene sheets. As shown in Fig. 8(a), without the stretching strain, the defect-free silicene sheet showed a clear Dirac point at the high symmetry point, which reflected the semi-metal property of silicene. When under a high atomic strain near its fracture point, the Dirac point disappeared and the silicene sheet exhibited metallic character. For the free silicene system with a vacancy or a Stone–Wales defect, the systems showed a band gap of 0.16 eV and 0.10 eV in the absence of strain, respectively (shown in Fig. S6(a) and S7(a)†). However, along both the zz or the am direction, the 10% atomic strain made the band gap disappear and the silicene sheet show obvious metallic property (Fig. S6(b), (c), S7(b) and (c)†). For example, for the silicene system with a vacancy defect, the 10% atomic strain along the zz direction introduce a significantly up-shift in the conduction bands near the high-symmetric points of the first Brillouin zone and bands over the Fermi level appeared in silicene. Thus, mechanical stretching, which would lead to the electron redistribution, is an effective way to tune the electrical properties of silicene sheets.

Fig. 8 Energy band for the pristine silicene systems with (a) 0% atomic strain; (b) 10% atomic strain along the zz direction; and (c) 10% atomic strain along the am direction. The Fermi level is set to be zero.

4. Conclusions

In summary, three representative types of defects including point, line, and planar defects in the silicene sheet were studied by MM and MD methods. Mechanical properties such as rigidity, strength, and fracture behaviors of defective silicene sheets were found to be significantly affected by the defects. The intrinsic strength of the silicene sheet showed a clear linear degressive relationship with the increasing defect parameters, namely, the linear density for vacancies, the width ratio for cracks, and the inflection angle for GBs. However, the in-plane stiffness of silicene sheets was affected not only by the defects but also by its corrugated structure. The silicene sheet with different types of defects showed varied failure behaviors because of the distinct stress distribution in the surface; however, the fracture started from the Si–Si bond located at the edge of the defect. Mechanical strain induced changes in the electronic band structure would be an effective way to tuning the material property. The information obtained in this work would be useful for the potential use of silicene in future nano-devices.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 11404192), the Shandong Province Special Grant for High-Level Overseas Talents (Grant No. tshw20120745), the Research Award Fund for Outstanding Young and Middle-aged Scientists of Shandong Province, China (Grant No. BS2014CL002), the Key Research and Development Project of Shandong Province, China (Grant No. 2015GSF120002), the Science and Technology Activities Foundation of China for Returned Personnel and the research fund of Shandong Academy of Sciences (2015QN003).

References

1. D. Jose and A. Datta, Acc. Chem. Res., 2014, 47, 593–602.
2. C. Grazianetti, E. Cinquanta and A. Molle, 2D Materials, 2016, 3, 012001.
3. M. S. Xu, T. Liang, M. M. Shi and H. Z. Chen, Chem. Rev., 2013, 113, 3766–3798.
4. W. F. Tsai, C. Y. Huang, T. R. Chang, H. Lin, H. T. Jeng and A. Bansil, Nat. Commun., 2013, 4, 1–6.
5. M. Ezawa, Phys. Rev. Lett., 2012, 109, 055502.
6. S. Cahangirov, V. O. Özçelik, L. Xian, J. Avila, S. Y. Cho, M. C. Asensio, S. Ciraci and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035448.
7. E. F. Sheka, Int. J. Quantum Chem., 2013, 113, 612–618.
8. K. Takeda and K. Shiraishi, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 14916–14922.
9. P. Vogt, P. De Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. Le Lay, Phys. Rev. Lett., 2012, 108, 155501.
10. B. J. Feng, Z. J. Ding, S. Meng, Y. G. Yao, X. Y. He, P. Cheng, L. Chen and K. H. Wu, Nano Lett., 2012, 12, 3507–3511.
11. A. Fleurence, R. Friedlein, T. Ozaki, H. Kawai, Y. Wang and Y. Yamada-Takamura, Phys. Rev. Lett., 2012, 108, 245501.
12. R. T. Mohamed, E. Hanna, M. Andrew, K. Abdelkader, R. Silvan, S. Mathieu, G. B. Azzedine, S. Fausto, G. Thomas, A. Bernard, D. Gérald, A. A. Mustapha and O. Hamid, Appl. Phys. Lett., 2013, 102, 083107.
13. L. Meng, Y. L. Wang, L. Z. Zhang, S. X. Du, R. G. Wu, L. F. Li, Y. Zhang, G. Li, H. T. Zhou, W. A. Hofer and H. J. Gao, Nano Lett., 2013, 13, 685–690.
14. L. Pan, H. J. Liu, X. J. Tan, H. Y. Lv, J. Shi, X. F. Tang and G. Zheng, Phys. Chem. Chem. Phys., 2012, 14, 13588–13593.
15. Q. X. Pei, Y. W. Zhang, Z. D. Sha and V. B. Shenoy, J. Appl. Phys., 2013, 114, 033526.
16. S. Cahangirov, M. Topsakal, E. Aktürk, H. Şahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804.
17. H. J. Zhao, Phys. Lett. A, 2012, 376, 3546–3550.
18. R. Qin, C. H. Wang, W. J. Zhu and Y. L. Zhang, AIP Adv., 2012, 2, 022159.
19. Q. Peng, X. D. Wen and S. De, RSC Adv., 2013, 3, 13772–13781.
20. Q. Qin, W. J. Zhu, Y. L. Zhang and X. L. Deng, Nanoscale Res. Lett., 2014, 9, 521–527.
21. T. Botari, E. Perim, P. A. S. Autreto, A. C. T. Van Duin, R. Paupitz and D. S. Galvao, Phys. Chem. Chem. Phys., 2014, 16, 19417–19423.
22. Q. X. Pei, Z. D. Sha, Y. Y. Zhang and Y. W. Zhang, J. Appl. Phys., 2014, 115, 023519.
23. R. E. Roman and S. W. Cranford, Comput. Mater. Sci., 2014, 82, 50–55.
24. B. Yang, J. A. Boscoboinik, X. Yu, S. Shaikhutdinov and H. J. Freund, Nano Lett., 2013, 13, 4422–4427.
25. M. T. Lusk and L. D. Carr, Phys. Rev. Lett., 2008, 100, 175503.
26. L. D. Carr and M. T. Lusk, Nat. Nanotechnol., 2010, 5, 316–317.
27. G. B. Xie, R. Yang, P. Chen, J. Zhang, X. Z. Tian, S. Wu, J. Zhao, M. Cheng, W. Yang, D. M. Wang, C. L. He, X. D. Bai, D. X. Shi and G. Y. Zhang, Small, 2014, 10, 2280–2284.
28. X. Y. Sun, Z. G. Fu, M. T. Xia and Y. J. Xu, Theor. Appl. Mech. Lett., 2014, 4, 051002–051003.
29. M. Dewapriya and R. Rajapakse, J. Appl. Mech., 2014, 81, 081010.
30. O. V. Yazyev and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195420.
31. J. F. Zhang, J. J. Zhao and J. P. Lu, ACS Nano, 2012, 6, 2704–2711.
32. Y. J. Wei, J. T. Wu, H. Q. Yin, X. H. Shi, R. G. Yang and M. Dresselhaus, Nat. Mater., 2012, 11, 759–763.
33. N. Ding, C.-M. L. Wu and H. Li, Phys. Chem. Chem. Phys., 2014, 16, 23716–23722.
34. T. Zhang, X. Y. Li, S. Kadkhodaei and H. Gao, Nano Lett., 2012, 12, 4605–4610.
35. M. Q. Le and R. C. Batra, Comput. Mater. Sci., 2014, 84, 238–243.
36. I. A. Ovid'ko and A. G. Sheinerman, J. Phys. D: Appl. Phys., 2013, 46, 345305–345309.
37. M. Q. Le and R. C. Batra, Comput. Mater. Sci., 2013, 69, 381–388.
38. M. Q. Le and R. C. Batra, Comput. Mater. Sci., 2016, 118, 251–258.
39. M. P. Lima, A. Fazzio and A. J. R. da Silva, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 235413–235417.
40. S. Li, Y. F. Wu, Y. H. Wang, T. Jiang, W. Liu and Y. H. Zhao, Sci. Rep., 2015, 5, 7881–7887.
41. H. Sahin, J. Sivek, S. Li, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045434.
42. J. Gao, J. Zhang, H. Liu, Q. Zhang and J. Zhao, Nanoscale, 2013, 5, 9785–9792.
43. M. R. Chávez-Castillo, M. A. Rodríguez-Meza and L. Meza-Montes, RSC Adv., 2015, 5, 96052–96061.
44. M. Q. Le and D. T. Nguyen, Appl. Phys. A, 2015, 118, 1437–1445.
45. H. Sun, Comput. Theor. Polym. Sci., 1998, 8, 229–246.
46. H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364.
47. K. Y. Yan, Q. Z. Xue, D. Xia, H. J. Chen, J. Xie and M. D. Dong, ACS Nano, 2009, 3, 2235–2240.
48. C. F. Wu, Polymer, 2010, 51, 4452–4460.
49. S. D. Liu, X. Y. Zhou, W. K. Wu, X. Z. Zhu, Y. R. Duan, H. Li and X. Wang, Nanoscale, 2016, 8, 4520–4528.
50. S. L. Yuan, Y. Zhang, Y. Li and G. Y. Xu, Colloids Surf., A, 2004, 242, 129–135.
51. From “Materials studio online help, COMPASS forcefield”.
52. C. G. Van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851–3879.
53. Y. Y. Liu, X. L. Zou and B. I. Yakobson, ACS Nano, 2012, 6, 7053–7058.
54. C. Zhang, A. De Sarkar and R. Q. Zhang, J. Phys. Chem. C, 2011, 115, 23682–23687.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27291f

---