Open Access Article
Open Access ArticleToward a uniform description of hydrogen bonds and halogen bonds: correlations of interaction energies with various geometric, electronic and topological parameters†
Jian-Wei Zou *a,
Meilan Huangb,
Gui-Xiang Hua and
Yong-Jun Jianga
*a,
Meilan Huangb,
Gui-Xiang Hua and
Yong-Jun Jianga
aSchool of Biological and Chemical Engineering, Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China. E-mail: jwzou@nit.zju.edu.cn
bSchool of Chemistry and Chemical Engineering, Queen's University Belfast, David Keir Building, Stranmillis Road, Belfast BT9 5AG, UK
First published on 7th February 2017
Abstract
Halogen bonds, which are specific non-covalent interactions similar to hydrogen bonds, play crucial roles in fields as diverse as supramolecular assemblies, crystal engineering, and biological systems. A total of 108 halogen-bonded and hydrogen-bonded complexes formed by different electron acceptors and NH3, namely, R–A⋯NH3 (A = H, Cl, Br or I), have been investigated at the MP2(full)/aug-cc-pVDZ(-PP) level of theory. The relationships between the interaction strengths and various geometric and electronic structures, as well as topological properties, were established, with a particular focus on the uniformity of these two types of interaction. The dependence of the BSSE-corrected interaction energy (ΔEcor) on the interatomic distance (rA⋯N) appeared to be nonlinear for both halogen-bonded and hydrogen-bonded systems; the relationship between ΔEcor and the difference between rA⋯N and the sum of the van der Waals radii (ΔrA⋯N) can be fitted to a combined quadratic regression equation. Furthermore, we demonstrated that the linear correlations between ΔEcor and ρb(BCP) (the electron density at bond critical points in the A⋯N bond) and its Laplacian ∇2ρb(BCP) can be used to provide a combined description of hydrogen bonds and halogen bonds, with correlation coefficients of 0.964 and 0.956, respectively. The dependence of the interaction strength on the electrostatic potential corresponding to an electron density of 0.002 a.u. along the R–A bond vector (ESP0.002), the amount of charge transferred (QCT) and the second-order perturbation stabilization energies of n(NH3) → σ*(R–A) (E(2)) were also examined. Strong halogen-bonded complexes were found to exhibit different linear correlations from weak halogen-bonded and hydrogen-bonded systems. Nevertheless, for the latter two types of system, a uniform regression equation can be constructed. These relationships not only improve our understanding of the nature of halogen bonding but also provide a feasible approach for predicting or determining the relative strengths of hydrogen bonds and halogen bonds, in particular when both types of non-covalent interaction coexist and compete with each other.
1. Introduction
Intermolecular interactions play important roles in many aspects of physics, chemistry, the life sciences and materials science.1 Hydrogen bonding is undoubtedly the most important and comprehensively studied example. Halogen bonding, which is a form of non-covalent interaction between halogen atoms and electronegative atoms with a lone pair of electrons (frequently N or O), has elicited much interest during the last decade owing to its importance in the fields of supramolecular assemblies2,3 and crystal engineering,4–6 as well as biochemistry7–9 and medicinal chemistry.10–12The similarity between hydrogen bonds and halogen bonds has long been noted; in fact, the term “halogen bond” stems from their resemblance to a great extent.13 It has been revealed that both are directional interactions in which the electrostatic contribution is generally thought to be dominant, and existing explanations of the characteristics of hydrogen bonds can also be applied to those of halogen bonds, and vice versa. Moreover, some concepts have been extended from hydrogen bonding, e.g., blue-shifting hydrogen bonds, charge-assisted hydrogen bonds, single-electron hydrogen bonds, and hydrogen bond cooperativity, and have all found their corresponding counterparts in halogen bonding.14–17
The determination of the strength of intermolecular interactions is critical in the study of physical, chemical and biochemical processes. Halogen bonds are comparable in strength to hydrogen bonds and thus may compete with and, in some cases, interfere with the latter.18–22 It has even been demonstrated that compounds that are capable of co-crystallizing with both hydrogen bond donors and halogen bond donors, when dissolved in a mixture of both only form co-crystals with the latter.23
The existence and strength of weak interactions can be determined by several techniques. Crystal structures determined by X-ray data, measurements of thermodynamic complexation constants, red shifts in infrared spectra and the chemical shift in nuclear magnetic resonance (NMR) have often been used to characterize the existence and strength of hydrogen bonds.24–26 Theoretical calculations can not only provide optimized geometries of hydrogen-bonded complexes and the interaction energies of two approaching monomers but also shed light on variations in electronic structures during the bonding process and have therefore become an essential method for studying hydrogen bonds.27
In view of the importance of hydrogen bonds, it is of great interest to study the relationships between different measures of the strength of hydrogen bonds, and this topic has been presented in many recent publications.28–39 These relationships fall mainly into two categories. One is the connection between experimentally determined hydrogen bond strengths and theoretically derived quantities. For instance, several studies have aimed at predicting scales of hydrogen bond basicity/acidity (hydrogen-bond-donating/accepting ability) using the minima (Vmin) and maxima (Vs,max) of electrostatic potentials (ESPs) or computed interaction energies.28–30 The other category comprises the correlation of interaction energies with various geometric, electronic and topological descriptors, among which Bader's “atoms in molecules” (AIM) topological parameters and ESP values are frequently used.31–39 In a series of studies, Grabowski31–33 investigated various conventional and unconventional hydrogen-bonded complexes and established several excellent linear relationships between interaction energies and AIM topological parameters. In a recent communication, Rozenberg34 summarized two dozen excellent linear relationships between calculated interaction energies and electron densities at critical points and disclosed that the relationships reported by different authors are, in fact, close to one another (the slopes differ by less than 30%). In addition to the above-mentioned Vmin and Vs,max, other ESPs at a given site in the molecule have been used for measuring hydrogen bond strengths. For example, Galabov et al.35–37 found a strong correlation between hydrogen bonding energies and ESPs at the nuclei of electron donor atoms (VN–D). Suresh et al.38 conducted an analysis of ESPs for a group of 26 hydrogen-, halogen- and dihydrogen-bonded complexes with diverse donor and acceptor molecules and showed that the difference in the change in the ESP at the sites of donor and acceptor atoms due to the formation of the complex (ΔΔVN) was strongly correlated with the binding strength of the complex. In a more recent study39 they demonstrated that such a correlation could be extended to a wider range of electron donor–acceptor complexes. Similar correlation analyses have also been performed for halogen bonds, either separately or together with other electron donor–acceptor interactions; however, these have not been as systematic as those for hydrogen bonds.40–42 Because there are great similarities between halogen bonds and hydrogen bonds, it is interesting to speculate whether a combined description can be given of the relationships between different indicators of the interaction strength of hydrogen bonds and halogen bonds. As the understanding of halogen bonds is far from sufficient, besides enabling a more thorough comparison between these two forms of non-covalent interaction such a study may also provide us with an insight into the nature of halogen bonds.
In addition, because hydrogen bonds and halogen bonds may coexist and compete with each other in certain specific systems,18–22 it would be important to determine whether there is a possibility of predicting the predominant interactions using relatively simple theoretical calculations. In the present work, we have investigated the relationships between interaction strengths and various geometric and electronic structures, as well as topological properties, with a particular focus on the uniformity of hydrogen bonds and halogen bonds.
2. Computational details
The geometries of hydrogen bond and halogen bond donors and acceptors, as well as the corresponding complexes, including all electrons, were fully optimized using the Møller–Plesset second-order perturbation theory (MP2) method. Dunning's aug-cc-pVDZ correlation-consistent basis set was adopted for all atoms except iodine. The Stuttgart-Koln MCDHF RSC effective core potential (ECP, 28 core electrons) basis set (aug-cc-pVDZ-PP43), which was obtained from the EMSL Basis Set Exchange, was used for iodine atoms. To ensure the reliability of the calculated results, hydrogen-bonded and bromine-bonded systems were further considered at a higher level of theory, namely, MP2(full)/aug-cc-pVTZ. The interaction energy of each complex was defined as the difference between the total energy of the complex and the sum of the total energies of the monomers. Basis set superposition error (BSSE) was incorporated into the calculations in order to obtain corrected interaction energies using the counterpoise (CP) technique developed by Boys and Bernardi.44 Atomic charges and second-order perturbation stabilization energies (E(2)) were computed by means of natural population analysis (NPA) and natural bond orbital (NBO) analysis, respectively. The former was used to calculate the amount of charge transferred from the electron donor to the acceptor, and the latter provided a measurement of the contribution of charge transfer from the viewpoint of local orbital interactions. Electrostatic potentials (ESPs) and electron densities along the R–A (A = H, Cl, Br or I) bond vector were calculated for the hydrogen bond and halogen bond donors in order to determine the electrostatic contribution to the non-covalent interactions. All the above computations were performed with the Gaussian 09 suite of programs.45 The topological properties of the electron density (ρc) and its Laplacian (∇2ρc) at bond critical points in each complex were characterized using the atoms in molecules (AIM) methodology with AIM 2000 software.463. Results and discussion
3.1 General description of the systems studied, the interaction energies and the computation method
Table S1 (ESI†) summarizes the systems and interaction energies calculated at the MP2(full)/aug-cc-pVDZ(-PP) level of theory. A total of 34 hydrogen-bonded complexes formed by different electron acceptors and NH3, which was chosen as a representative electron donor, and 74 halogen-bonded complexes were considered. To avoid confusion, henceforth R–H⋯NH3 and R–X⋯NH3 (X = Cl, Br or I) represent hydrogen- and halogen-bonded complexes, respectively, whereas R–A⋯NH3 refers to both types. The types of hydrogen bond and halogen bond donors were diversified and the atoms connected to H or X in the R groups included nitrogen, oxygen, halogens, sulfur and carbon in different hybridization states.We found that the optimized R–A⋯N angles in all the complexes studied are larger than 160° (most are >170°). The approximate linearity of this angle ensures that the interaction between the electron acceptor and NH3 in each complex is primarily attributed to monodentate hydrogen bonds or halogen bonds (i.e., other secondary interactions can be ignored).
The interaction strengths span a broad range, with the interaction energies (ΔE) ranging from approximately 2.0 to 13.3 kcal mol−1 for hydrogen bonds and from 0.3 to 19.9 kcal mol−1 for halogen bonds. After BSSE was taken into account, the interaction energies (ΔEcor) were predicted to be 1.1–11.6 kcal mol−1 and −0.3–16.5 kcal mol−1 for the hydrogen- and halogen-bonded systems, respectively. The ΔEcor values are negative for CH3CH2Cl, (CH3)2CHCl and (CH3)3CCl, which implies that the chlorine-containing molecules and NH3 are weakly bound. According to a recent comparison47 of different binding energies used for benchmarking non-covalent interactions, the counterpoise correction was safe for general use and therefore ΔEcor would be adopted in subsequent discussions. In fact, both ΔE values are strongly correlated (the correlation coefficient is 0.994), which indicates that there is little difference between the use of corrected and uncorrected interaction energies for the purpose of comparison.
A comparison of complexes containing the same attached R group indicates that the halogen bond strengths in R–X⋯NH3 decrease in the order of R–I > R–Br > R–Cl, and the hydrogen bond strengths in R–H⋯NH3 are slightly lower than or roughly equal to the halogen bond strengths in the R–Br⋯NH3 complexes. Furthermore, the effects of the R group on the hydrogen bond or halogen bond strengths were examined. We found that the interaction strengths of various R groups with different electron-accepting atoms follow the order: F > Cl > Br > O > N > C(sp) > C(sp2) > C(sp3) for both hydrogen-bonded and halogen-bonded complexes.
Regarding the computation method, the MP2/aug-cc-pVDZ level of theory has been widely used for studying reasonably weak non-covalent interactions.48–50 This level is believed to represent a good compromise between accuracy and calculation cost, in particular for more than one hundred systems, as studied in the present work. Nevertheless, to ensure the reliability of the calculated results two series of complexes, namely, R–A⋯NH3 (A = H or Br), were further examined at the MP2(full)/aug-cc-pVTZ level of theory using the MP2(full)/aug-cc-pVDZ optimized geometries. Table S2 (ESI†) lists the calculated interaction energies and some parameters relevant to the interaction strength, which will be presented in the following discussion. We noted that the results calculated by the two different computation methods are close to each other and, moreover, are strongly correlated, with a correlation coefficient R of nearly unity (Fig. S1†).
3.2 Dependence of interaction energies on geometric parameters
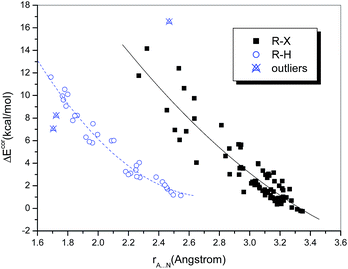
One of the most important geometric characteristics of hydrogen bonds and halogen bonds is that the distance between the donor and acceptor atoms is shorter than the sum of their van der Waals (vdW) radii. Table S1† lists the interatomic distances rA⋯N. It can be seen that the intermolecular distances range from 1.689 to 3.349 Å. These separations are generally less than the sums of the Bondi's vdW radii of the atoms involved, except for the three above-mentioned weakly bound chlorine-containing complexes, in which the Cl⋯N distance is slightly longer than the sum of the vdW radii of Cl and N (3.30 Å).Plots of the interaction energy versus the interatomic distance are displayed in Fig. 1. It is observed that the hydrogen-bonded and halogen-bonded systems exhibit different dependences. This is not surprising, because the vdW radius of a halogen atom is significantly larger than that of a hydrogen atom. The dependences for both types of system (in particular, the halogen-bonded systems) appear to be nonlinear. Quadratic polynomial fitting of the values of ΔEcor and rA⋯N yielded strong correlations, with correlation coefficients (R) of 0.920 and 0.980, respectively, for the halogen-bonded and hydrogen-bonded systems (Fig. 1), which means that the interaction energies become dramatically higher with a reduction in rA⋯N.
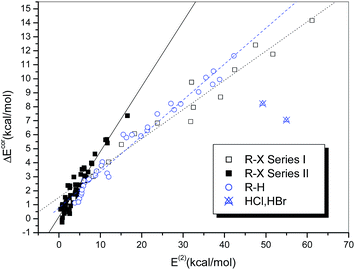
It is noteworthy that the two hydrogen-bonded complexes that contain hydrogen halides (HX, X = Cl or Br) as the hydrogen bond donor deviate significantly from the regression lines. Moreover, we observed that the interaction strengths of these two complexes, in comparison with that of the homologous complex (HF⋯NH3), do not increase but decline with an increase in the acidity of HX, i.e., ΔE(HF) > ΔE(HCl) > ΔE(HBr). The same results were also reported in previous studies of the hydrogen bonding interactions of HX with ammonia51,52 and water,53 as well as methanol derivatives.54 However, for the hydrogen-bonded complexes formed between HX and benzene, which is a much weaker hydrogen bond acceptor, the calculated binding energies follow the opposite order, i.e., ΔE(HBr) > ΔE(HCl) > ΔE(HF).55,56 This anomalous behavior can be ascribed to the high Brønsted acidities of HCl and HBr (HF is a weak acid) and the ion-pair character of XH⋯NH3, i.e., the complexes not only exist in the form of neutral hydrogen-bonded structures, namely, X–H⋯NH3, but also display some attributes of ion pairs, namely, X−⋯[NH4]+.57 According to the classification of hydrogen bonds in chemical leitmotifs (CLs) proposed by Gilli et al.,58 they are classed as double charge-assisted hydrogen bonds (CL#2), in contrast to all the other hydrogen-bonded systems (ordinary hydrogen bonds, CL#1). Similarly, the complex formed between iodine monofluoride and NH3 (F–I⋯NH3) exhibits a relatively large deviation owing to substantial charge transfer (it is classed as an inner complex according to the Mulliken notation59). The corresponding data points for these three complexes were therefore identified as outliers and excluded from the curve fittings and correlation analyses.
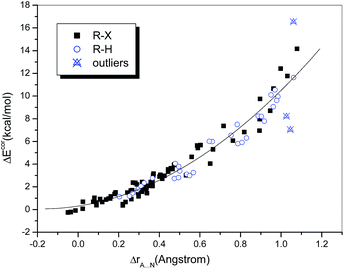
The difference between the sums of the vdW radii of the approaching atoms and the interatomic distance, namely, ΔrA⋯N (ΔrA⋯N = rA + rN − rX⋯N), may also be used as a measure of interaction strength. Grabowski33 investigated several conventional and unconventional hydrogen-bonded systems containing HF as a fixed proton donor and showed that the relationship between the interaction energy and ΔrH⋯Y can be well fitted by a quadratic polynomial regression (R = 0.971). He also demonstrated that this nonlinear dependence holds for samples containing unrelated complexes and even with a range of proton donors.31 Accordingly, we investigated the dependence of ΔEcor on ΔrA⋯N (Fig. 2). It was found that the data points corresponding to hydrogen-bonded and halogen-bonded systems were interspersed and could even be completely fitted by the same quadratic regression equation. The fit was satisfactory (R = 0.978) when the above-mentioned outliers were omitted. In other words, the dependences of the interaction strength on the difference in distance ΔrA⋯N were similar for hydrogen bonds and halogen bonds.
In addition, the formation of hydrogen bonds and halogen bonds led to a slight variation in the R–A bond and a small shift in the corresponding frequency.60 For the hydrogen-bonded systems considered here, in only one case it was observed that the R–A bond contracted (or led to a blue shift), whereas for the halogen-bonded systems, it was found that the R–A bond contracted in 29 cases (almost one-third of the systems investigated). Blue shifting is much more common in the halogen-bonded systems in comparison with that in the hydrogen-bonded systems.
3.3 Relationship between interaction energies and electrostatic potentials
It has been well documented that electrostatic interactions are predominant in hydrogen bonds and most halogen bonds. The molecular ESP is a rigorously defined quantum mechanical property. It not only enables a qualitative understanding of the distribution of electrostatic charge within a molecule, but also provides a very effective tool for the quantitative prediction of various non-covalent interactions, including hydrogen bonds and halogen bonds.38,48,61,62The relationships between halogen bond strengths and quantities derived from ESPs were investigated.48 It was suggested that the ESP corresponding to an electron density of 0.002 a.u. along the R–X axis, namely, ESP0.002, is the optimal descriptor of the electrostatic contribution for correlation with the binding energy. A similar conclusion has been reached for hydrogen bonds.63 It was found that strong correlations exist between the hydrogen bond acidities of solutes and the ESPs on surfaces defined by the 0.002 a.u. contour of electron density, although these are family-dependent.
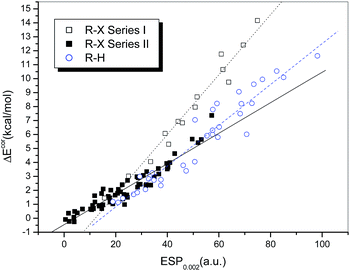
Fig. 3 presents a plot of ΔEcor versus the calculated value of ESP0.002 (Table S1†). The 73 halogen-bonded complexes were divided into two different series according to the type of electron acceptor. Series I includes 14 strongly bound complexes (represented by empty squares and with relatively large interaction energies), which contain dihalogens, HOX, and NH2X as electron acceptors. The other 59 weakly bound complexes (filled squares), which contain HCl, HBr and carbon-bonded halogen molecules as electron acceptors, are classified as Series II.
Obvious linear relationships between the interaction energies and the ESPs were observed for the complexes in both series. The correlation coefficients are 0.983 and 0.952 for Series I and II, respectively. The slope of the linear regression line is 0.215 for Series I, which is significantly larger than that for Series II (0.109). This means that the interaction energy is proportional to the electrostatic potential, but the slope of the correlation line is dependent on the type of halogen bond, i.e., the interaction energies for complexes with strong halogen bonds will be underestimated if the correlation established for complexes with relatively weak halogen bonds is used, which implies that charge transfer may play a more significant role in complexes with strong halogen bonds.
For hydrogen-bonded complexes, no evident family dependence was observed. It was shown that their interaction strengths display a linear correlation with the values of ESP0.002 (empty circles in Fig. 3). The correlation coefficient was found to be 0.960 after two outliers (HCl and HBr) were excluded. The slope of the regression line is 0.126, which lies between those of the regression lines for the halogen-bonded complexes in Series I and II but is apparently closer to the latter. This indicates that the electrostatic contribution is more dominant in hydrogen bonds and weak halogen bonds in comparison with strong halogen bonds. Moreover, because the slopes of the regression lines for the complexes with hydrogen bonds and weak halogen bonds are similar to each other, it is possible to establish a combined linear correlation for both systems. The resulting regression equation (eqn (1)) exhibits a high correlation coefficient (R = 0.965), which even exceeds the individual correlation coefficients.
| ΔEcor = 0.1252 × ESP0.002 − 0.9053 |
| N = 93, R = 0.9654, Sd = 0.7268, F = 1248.5 | (1) |
Because ESP0.002 is a monomer-based quantity that corresponds to the electron-accepting abilities of R–H and most R–X molecules but does not relate to the complexity of the entire complex, it provides us with a convenient means of predicting the relative interaction strengths of hydrogen bonds and halogen bonds (see below).
It is worth mentioning that the ESP at the site of an electron donor atom (VN) has been successfully used as a descriptor of reactivity for the study of hydrogen bonds.35–37 For the hydrogen-bonded complexes studied here, our results indicate that the linear correlation between this descriptor and the interaction energy (R = 0.935) is not stronger than that between ESP0.002 and ΔEcor (R = 0.960). Moreover, because different atomic nuclei have distinctly different VN values, it is undoubtedly the case that this descriptor cannot be used to provide a combined description of hydrogen bonds and halogen bonds. Similarly, we investigated the relationship between ΔEcor and ΔΔVN, which is a parameter based on VN as mentioned above, for hydrogen-bonded and bromine-bonded systems and obtained a strong combined correlation (R = 0.956) (Table S3 and Fig. S1, ESI†), which further supports the wide-ranging applicability of this descriptor for quantifying the strength of non-covalent interactions.38 Nevertheless, because the determination of ΔΔVN is dependent on calculations on both the monomer and the complex it is not a good descriptor from the perspective of prediction.
In addition, the atomic charge can also be used for the quantitative estimation of the electrostatic contribution of a molecule. For instance, Famini et al.64 proposed a set of computational parameters for constructing a so-called theoretical linear solvation energy relationship (TLSER), in which the magnitude of the most negative charge in the molecule was used to describe the electrostatic basicity of the hydrogen bond. In addition, partial atomic charges calculated by fitting the respective ESPs in the vdW region are often used to simulate the electrostatic interactions in molecular mechanical (MM) force fields65 (e.g., the AMBER force field). However, it was shown that almost all the halogen atoms studied bear negative NPA or CHelpG charges. The results indicate that the interactions of halogen-containing molecules with electronegative atoms are repulsive, but this is evidently inconsistent with the fact that a halogen bond is an attractive interaction. Therefore, the relationships between interaction energies and partial atomic charges were not considered further.
3.4 Relationship between interaction energies and amounts of charge transferred
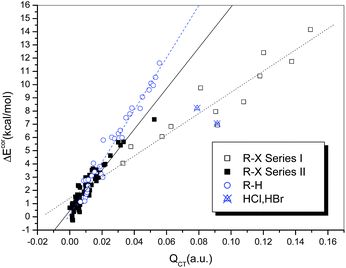
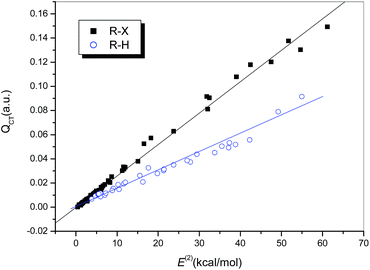
It is generally accepted that hydrogen bonds have electrostatic as well as covalent components, and the latter are more prominent for strong hydrogen bonds.24 Similarly, covalent-type components are dominant in strong halogen bonds, and, before the concept of the halogen bond was widely recognized, halogen-bonded complexes, typically those formed between electron donors and dihalogen molecules, were classified as charge-transfer complexes.66 In other words, charge redistribution occurs upon the formation of hydrogen-bonded or halogen-bonded complexes, and the interaction strength is closely related to the amount of charge transferred (QCT) from the electron donors to the acceptors.Table S1† summarizes the values of QCT for all the hydrogen-bonded and halogen-bonded systems, and the dependence of ΔEcor on QCT is shown in Fig. 4. For the strongly halogen-bonded complexes (Series I), our calculated results indicate that the values of QCT are in the range of 9–149 me, and there is an excellent linear correlation (R = 0.962) between the interaction energy and QCT, as indicated in Fig. 4 (dotted line). A similar correlation can also be established for the complexes of hydrogen halides with carbon-bonded halogen molecules (Series II), although it is somewhat weaker than that for the complexes in series I (solid line in Fig. 4, R = 0.939). However, the slope of the linear regression line for Series II is larger than that for Series I (154.21 versus 80.20), which is in contrast to the relationship between ΔEcor and ESP0.002.
For the hydrogen-bonded systems, the values of QCT were calculated to be 7–91 me. Abnormally large amounts of charge (79 and 91 me) were observed to be transferred in the Br–H⋯NH3 and Cl–H⋯NH3 complexes. Again, these were considered as outliers and excluded from the subsequent regression analysis. The resulting linear correlation is fairly satisfactory, with a correlation coefficient of 0.983. The slope of the regression line is again closer to that for the weakly halogen-bonded complexes (Series II), which means that the sensitivities of ΔEcor to the value of QCT are comparable for hydrogen bonds and weak halogen bonds, and therefore the linear dependence of ΔEcor on QCT can be expressed by a combined regression equation (R = 0.972).
Considering the obvious correlations between both charge transfer and electrostatic contribution and the interaction strength and their complementary effects in determining the interaction energy, it is expected that a combination of QCT and ESP0.002 can be used to better interpret the variations in the interaction strengths of hydrogen bonds and halogen bonds. The resulting linear regression equation for the entire data set excluding the three outliers is expressed as follows:
| ΔEcor = 51.5099QCT + 0.0920ESP0.002 − 0.6745 |
| N = 105, R = 0.990, Sd = 0.4614, F = 2534.8 | (2) |
The multiple correlation coefficient is as high as 0.990, i.e., 98.0% of the variation in the interaction energy can be explained by using QCT and ESP0.002 as descriptors. Fig. 5 illustrates the consistency between the values of ΔEcor calculated directly and those predicted by eqn (2). We found that the data points, whether these corresponded to weak or strong halogen bonds or to hydrogen bonds, fit the regression line perfectly, which indicates that the interaction strengths of both hydrogen- and halogen-bonded complexes can be described in the same way via a combination of QCT and ESP0.002.
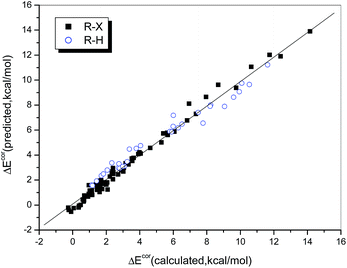 | ||
| Fig. 5 Relationship between the values of ΔEcor calculated directly and those predicted from eqn 2. | ||
3.5 Relationship between interaction energies and second-order stabilization energies
Natural bond orbital (NBO) analysis provides an alternative valuable tool for our understanding of the formation of a molecular complex with respect to local orbital interactions.67 In particular, the second-order perturbation stabilization energy (E(2)) has been used to correlate the strengths of hydrogen bonds and halogen bonds.41,68 This describes the charge transfer interactions between a pair of donor–acceptor orbitals and is calculated as follows:| E(2) = ΔEij = qiF(i,j)2/(εi − εj) | (3) |
Fig. 6 illustrates the dependence of the interaction strength on E(2), which exhibits some similarity with the relationship between ΔEcor and QCT. The hydrogen-bonded complexes and the halogen-bonded complexes in Series I and II display three different linear correlations with correlation coefficients of 0.986, 0.977 and 0.947, respectively. The halogen-bonded complexes of HCl and HBr deviate significantly from the correlation and therefore were excluded from the regression analysis. The regression line of the hydrogen-bonded systems in Fig. 6 is closer to that of the strongly halogen-bonded systems (Series I) than that of the weakly bonded systems (Series II), which is different from the case observed in Fig. 4.
In fact, the second-order stabilization energy not only represents the intrinsic connection between the pair of donor–acceptor orbitals, but is also correlated with the amount of charge transferred. Plots of E(2) versus QCT are illustrated in Fig. 7. Strong correlations were observed for the hydrogen-bonded complexes (R = 0.986, dotted line), as well as for the halogen-bonded complexes (R = 0.996, solid line), among which weak and strong halogen bonds are no longer distinguished. The slope of the regression line for the halogen-bonded complexes is larger than that for the hydrogen-bonded complexes, which indicates that the amount of charge transferred in the complexes with halogen bonds is more sensitive to orbital interactions.
It is worth mentioning that although variations in electron density and NBO have been extensively used to analyze the formation of hydrogen and halogen bonds, correlations between the interaction strength and the values of QCT and E(2), in contrast to geometric, topological and ESP-derived parameters, are uncommon. Moreover, most previous works deal with either specific complexes (e.g., base pairs69) or only a few simple and homogeneous hydrogen-bonded complexes.70–72 Therefore, it is difficult (or seems meaningless) to make a comparison with these results.
3.6 Relationship between interaction energies and AIM topological parameters
The atoms in molecules (AIM) theory developed by Bader73 represents a very important means of studying various non-covalent interactions. Several typical topological parameters derived from AIM analyses, such as the electron density at bond critical points (BCPs) (ρb(BCP)), and its Laplacian (∇2ρb(BCP)) have been proven to be very effective in describing the existence and strength of hydrogen bonds and halogen bonds.41,74–79Here, AIM analyses were performed for each of the hydrogen- and halogen-bonded complexes, in which there was one BCP between the hydrogen or halogen atom of the acceptor R–A and the N atom of the donor NH3. The values of ρb(BCP) and ∇2ρb(BCP) at this BCP are listed in Table S1.† The values of ρb(BCP) are within the range of 0.0064–0.0538 a.u. for the halogen-bonded systems and 0.0094–0.0533 a.u. for the hydrogen-bonded systems. Their Laplacians (∇2ρb(BCP)) span the ranges of 0.0151–0.1585 a.u. and 0.0267–0.1506 a.u. for the halogen-bonded and hydrogen-bonded systems, respectively.
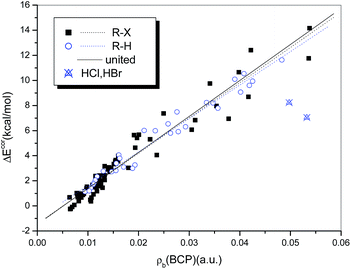
It has been suggested that the interaction strength, whether the system is halogen-bonded or hydrogen-bonded, is strongly correlated with the value of ρb(BCP).76,78 Rozenberg34 summarized in a recent publication 24 linear correlations between interaction energies and values of ρb(BCP) for hydrogen bonds that were calculated at the MP2 level of theory. He observed that these high-quality relations are close and can be expressed as a general linear relationship. Strong correlations between ΔEcor and ρb(BCP) also exist for the complexes studied in the present work. The correlation coefficients are 0.982 and 0.966 for the hydrogen-bonded (with the exception of HCl and HBr) and halogen-bonded systems, respectively. Moreover, the two regression lines overlap perfectly, so that a single regression equation can be used to describe them in combination (eqn (4) and Fig. 8).
| ΔEcor (kJ mol−1) = −5.595 + 1159.6 × ρb(BCP) (a.u.) |
| N = 105, R = 0.973, Sd = 3.139, F = 1852.8 | (4) |
The quality of eqn (4), although inferior to those of the relations established for homogeneous samples of hydrogen- or halogen-bonded complexes, is significantly high, with a correlation coefficient of R = 0.973. Moreover, both the intercept and the slope in eqn (4) are very close to those in the general relationship proposed by Rozenberg34 for hydrogen bonds (−6.6 and 1215, respectively), which further supports the theory that ρb(BCP) can be used to describe hydrogen and halogen bonds in combination.
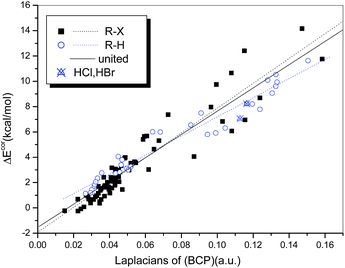
A similar analysis was also conducted to establish the relationship between ΔEcor and ∇2ρb(BCP). We found that the general qualities of the regression models used for the hydrogen-bonded (R = 0.974) and halogen-bonded systems (R = 0.942) (Fig. 9) are inferior to those of the regression models of ΔEcor versus ρb(BCP). Although the two regression lines are not as similar as they appear in Fig. 8, a uniform regression model that encompasses complexes with hydrogen bonds and those with halogen bonds was obtained with significantly high quality (R = 0.950).
3.7 Applications of the relationships
Because theoretical studies of halogen bonds are much less extensive than those of hydrogen bonds, the establishment of dependences between the interaction strength and various physical quantities and a comprehensive comparison of these two types of non-covalent interaction may improve our understanding of the nature of halogen bonding. Besides, the relationships established in the current research may also find practical applications.One practical application is the prediction of the electron-accepting abilities of hydrogen bond or halogen bond donors. This is particularly important in systems in which hydrogen bonds and halogen bonds coexist or compete with each other. Aakeröy et al.20 studied the structural competition between hydrogen-bonded and halogen-bonded supramolecular synthons. Two molecules A and B were selected carefully to co-crystallize with 1-methyl-2-(pyridin-4-yl)-1H-benzimidazole (C), which is a molecule with two electron donor sites (Fig. 10). The proton in the oxime –OH group in both A and B was shown to bind to the N site of the imidazole moiety in C during co-crystallization. The imine proton and halogen atom in A and B competed for the other N site, namely, that in the pyridine moiety, in C via hydrogen bonding and halogen bonding interactions. We propose that it is possible to determine which type of interaction is predominant by estimating the electron-accepting abilities of these three sites in A and B on the basis of ESP calculations. The calculated values of ESP0.002 of the bromine atom (A) and the iodine atom (B) at the MP2(full)/aug-cc-pVDZ(-PP) level of theory are 35.04 and 47.73 kcal mol−1, respectively. The corresponding value of the imine proton (33.99 kcal mol−1) is close to that of the bromine atom in A, but significantly lower than that of the iodine atom in B. This result is consistent with the experimental observation of an N⋯I halogen bond in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal of B and C.20 A similar N⋯Br interaction was not observed in a co-crystal of A and C, which was in part because the strength of a N⋯Br halogen bond is comparable with that of a C–H⋯N hydrogen bond on the basis of their ESP0.002 values, and it is certain that the final crystal structure is the result of a balance between numerous weak interactions.
1 co-crystal of B and C.20 A similar N⋯Br interaction was not observed in a co-crystal of A and C, which was in part because the strength of a N⋯Br halogen bond is comparable with that of a C–H⋯N hydrogen bond on the basis of their ESP0.002 values, and it is certain that the final crystal structure is the result of a balance between numerous weak interactions.
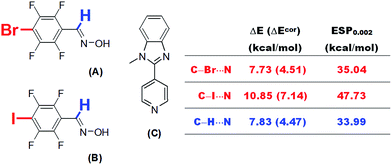 | ||
| Fig. 10 Supramolecular synthons A and B bearing donor sites of both a hydrogen bond and a halogen bond. | ||
It is worth noting that direct calculations of the interaction strengths for such systems at a reasonably high level of theory, although time-consuming, are not infeasible. We calculated the BSSE-corrected and uncorrected interaction energies for complexes of A and B with pyridine at the MP2(full)/aug-cc-pVDZ(-PP) level of theory. The N⋯I interaction energy between B and pyridine was calculated to be 7.14 kcal mol−1 (BSSE-corrected), which is higher than the C–H⋯N interaction energy by ca. 2.7 kcal mol−1. However, the difference between the latter and the N⋯Br interaction energy in the complex of A with pyridine, with or without the correction for BSSE, is less than 0.1 kcal mol−1. These results are in excellent agreement with the predictions from our ESP calculations (Fig. 10).
Another potential application is the utilization of the AIM topological properties to determine the relative strengths of hydrogen bonds and halogen bonds in complex systems. In fact, the parameter ρb(BCP) has been extensively used to study intramolecular hydrogen bonds and hydrogen bond cooperativity.79–82 Similar studies of halogen bonds have also been reported sporadically.83–86 Hydrogen bonds and halogen bonds were, however, considered separately in previous studies.
In view of the strong uniform dependence between ΔEcor and ρb(BCP), as was established above, when hydrogen bonds and halogen bonds coexist and, in particular, when they are competitive and unavoidably entangled with other weak interactions, this provides a feasible approach to the determination of the relative strengths of the two types of interaction via the examination of their ρb(BCP) values.
4. Conclusions
Ab initio calculations were performed for a series of hydrogen-bonded and halogen-bonded complexes formed between various electron acceptors and NH3, namely, R–A⋯NH3 (A = H, Cl, Br or I). The relationships between the interaction strength (expressed in terms of the BSSE-corrected interaction energy, ΔEcor) and the interatomic distance (rA⋯N), the difference between the interatomic distance and the sum of the respective van der Waals radii (ΔrA⋯N), the electrostatic potential corresponding to an electron density of 0.002 a.u. along the R–A bond vector (ESP0.002), the amount of charge transferred (QCT), the second-order perturbation stabilization energy of n(NH3) → σ*(R–A) (E(2)), the electron density at bond critical points of the A⋯N bond (ρb(BCP)) and its Laplacian (∇2ρb(BCP)) were established to clarify the similarities and differences between these two types of intermolecular interaction.We found that the dependences of ΔEcor on rA⋯N and ΔrA⋯N are nonlinear for both hydrogen bonds and halogen bonds, and the latter (ΔEcor versus ΔrA⋯N) can be fitted to a combined quadratic regression equation. Linear correlations between the interaction strength and the values of ESP0.002, QCT and E(2), although family-dependent, have been successfully constructed, with correlation coefficients ranging from 0.939 to 0.986. The sensitivities of the interaction strength to the values of ESP0.002 and QCT for weakly halogen-bonded systems are significantly different from those for strongly halogen-bonded systems but are close to those for hydrogen-bonded systems. This result suggests that linear relationships established separately for complexes with hydrogen bonds and weak halogen bonds can be integrated using uniform regression equations. Moreover, owing to the complementary effects of ESP0.002 and QCT in determining the interaction strength, an excellent biparametric equation that combined these two properties was obtained. Because the value of ESP0.002 corresponds to the electron-accepting ability of R–H and most R–X molecules and is independent of the entire complex, it provides us with a convenient means of predicting the relative strengths of hydrogen bonds and halogen bonds.
Finally, two uniform linear regression models of ΔEcor versus ρb(BCP) and ∇2ρb(BCP) that encompass complexes with hydrogen bonds and those with halogen bonds were obtained. The topological properties of hydrogen bonds and halogen bonds provide alternative descriptors for determining their relative strengths, in particular when these two types of interaction are competitive with each other and direct calculations of the interaction energies are not feasible.
Acknowledgements
The authors are grateful to the Natural Science Foundation of China (Project No. 21272211) for financial support.Notes and references
- A. J. Stone, The Theory of Intermolecular Forces, Oxford University Press, Oxford, 1996 Search PubMed.
- P. Metrangolo and G. Resnati, Chem.–Eur. J., 2001, 7, 2511–2519 CrossRef CAS.
- T. Shirman, T. Arad and M. E. Van Der Boom, Angew. Chem., Int. Ed., 2010, 49, 926–929 CrossRef CAS PubMed.
- P. Metrangolo, T. Pilati, G. Terraneo, S. Biella and G. Resnati, CrystEngComm, 2009, 11, 1187–1196 RSC.
- A. Mukherjee, S. Tothadi and G. R. Desiraju, Acc. Chem. Res., 2014, 47, 2514–2524 CrossRef CAS PubMed.
- R. B. Walsh, C. W. Padgett, P. Metrangolo, G. Resnati, T. W. Hanks and W. T. Pennington, Cryst. Growth Des., 2001, 1, 165–175 CAS.
- Y. Lu, Y. Wang and W. Zhu, Phys. Chem. Chem. Phys., 2010, 12, 4543–4551 RSC.
- M. R. Scholfield, C. M. V. Zanden, M. Carter and P. S. Ho, Protein Sci., 2013, 22, 139–152 CrossRef CAS PubMed.
- P. Auffinger, F. Hays, E. Westhof and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16789–16794 CrossRef CAS PubMed.
- Y. Lu, T. Shi, Y. Wang, H. Yang, X. Yan, X. Luo, H. Jiang and W. Zhu, J. Med. Chem., 2009, 52, 2854–2862 CrossRef CAS PubMed.
- R. Wilcken, M. O. Zimmermann, A. Lange, A. C. Joerger and F. M. Boeckler, J. Med. Chem., 2013, 56, 1363–1388 CrossRef CAS PubMed.
- M. Z. Hernandes, S. M. Cavalcanti, D. R. Moreira, W. F. de Azevedo Jr and A. C. Leite, Curr. Drug Targets, 2010, 11, 303–314 CrossRef CAS PubMed.
- G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713 CrossRef CAS.
- J. S. Murray, M. C. Concha, P. Lane, P. Hobza and P. Politzer, J. Mol. Model., 2008, 14, 699–704 CrossRef CAS PubMed.
- S. J. Grabowski and E. Bilewicz, Chem. Phys. Lett., 2006, 427, 51–55 CrossRef CAS.
- J. Lieffrig, O. Jeannin, A. Frackowiak, I. Olejniczak, R. Swietlik, S. Dahaoui, E. Aubert, E. Espinosa, P. Auban-Senzier and M. Fourmigue, Chem.–Eur. J., 2013, 19, 14804–14813 CrossRef CAS PubMed.
- Y.-H. Wang, J.-W. Zou, Y.-X. Lu, Q.-S. Yu and H.-P. Xu, Int. J. Quantum Chem., 2007, 107, 501–506 CrossRef CAS.
- I. Alkorta, F. Blanco, M. Solimannejad and J. Elguero, J. Phys. Chem. A, 2008, 112, 10856–10863 CrossRef CAS PubMed.
- Q. Li, X. Xu, T. Liu, B. Jing, W. Li, J. Cheng, B. Gong and J. Sun, Phys. Chem. Chem. Phys., 2010, 12, 6837–6843 RSC.
- C. B. Aakeröy, M. Fasulo, N. Schultheiss, J. Desper and C. Moore, J. Am. Chem. Soc., 2007, 129, 13772–13773 CrossRef PubMed.
- F. F. Awwadi, D. Taher, S. F. Haddad and M. M. Turnbull, Cryst. Growth Des., 2014, 14, 1961–1971 CAS.
- N. Nagels, Y. Geboes, B. Pinter, F. De Proft and W. A. Herrebout, Chem.–Eur. J., 2014, 20, 8433–8443 CrossRef CAS PubMed.
- E. Corradi, S. V. Meille, M. T. Messina, P. Metrangolo and G. Resnati, Angew. Chem., Int. Ed., 2000, 39, 1782–1786 CrossRef CAS PubMed.
- G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, New York, 1997 Search PubMed.
- F. Weinhold and R. A. Klein, Mol. Phys., 2012, 110, 65–579 CrossRef.
- M. H. Abraham, Chem. Soc. Rev., 1973, 22, 73–83 RSC.
- S. Scheiner, Hydrogen Bonding: A Theoretical Perspective, Oxford University Press, New York, 1997 Search PubMed.
- M. Nocker, S. Handschuh, C. Tautermann and K. R. Liedl, J. Chem. Inf. Model., 2009, 49, 2067–2076 CrossRef CAS PubMed.
- P. W. Kenny, C. A. Montanari, I. M. Prokopczyk, J. F. R. Ribeiro and G. R. Sartori, J. Med. Chem., 2016, 59, 4278–4288 CrossRef CAS PubMed.
- A. J. Green and P. L. A. Popelier, J. Chem. Inf. Model., 2014, 54, 553–561 CrossRef CAS PubMed.
- S. J. Grabowski, J. Phys. Chem. A, 2001, 105, 10739–10746 CrossRef CAS.
- S. J. Grabowski, Chem. Phys. Lett., 2001, 338, 361–366 CrossRef CAS.
- S. J. Grabowski, J. Phys. Org. Chem., 2004, 17, 18–31 CrossRef CAS.
- M. Rozenberg, RSC Adv., 2014, 4, 26928–26931 RSC.
- B. Galabov and P. Bobadova-Parvanova, J. Phys. Chem. A, 1999, 103, 6793–6799 CrossRef CAS.
- V. Dimitrova, S. Ilieva and B. Galabov, J. Phys. Chem. A, 2002, 106, 11801–11805 CrossRef CAS.
- B. Galabov, P. Bobadova-Parvanova, S. Ilieva and V. Dimitrova, J. Mol. Struct.: THEOCHEM, 2003, 630, 101–112 CrossRef CAS.
- N. Mohan and C. H. Suresh, J. Phys. Chem. A, 2014, 118, 1697–1705 CrossRef CAS PubMed.
- P. V. Bijina and C. H. Suresh, J. Chem. Sci., 2016, 128, 1677–1686 CrossRef CAS.
- I. Alkorta, G. Sanchez-Sanz and J. Elguero, CrystEngComm, 2013, 15, 3178–3186 RSC.
- Y.-X. Lu, J.-W. Zou, Y.-H. Wang, Y.-J. Jiang and Q.-S. Yu, J. Phys. Chem. A, 2007, 111, 10781–10788 CrossRef CAS PubMed.
- M. G. Chudzinski and M. S. Taylor, J. Org. Chem., 2012, 77, 3483–3491 CrossRef CAS PubMed.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–577 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 09 (Revision A.02), Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- F. Biegler-König, AIM 2000 version 1.0, University of Applied Science, Bielefeld, Germany, 2000 Search PubMed.
- L. A. Burns, M. S. Marshall and C. D. Sherrill, J. Chem. Theory Comput., 2014, 10, 49–57 CrossRef CAS PubMed.
- J.-W. Zou, Y.-J. Jiang, M. Guo, G.-X. Hu, B. Zhang, H.-C. Liu and Q.-S. Yu, Chem.–Eur. J., 2005, 11, 740–751 CrossRef CAS PubMed.
- K. E. Riley and K. M. Merz, J. Phys. Chem. A, 2007, 111, 1688–1694 CrossRef CAS PubMed.
- P. K. Sahu and S.-L. Lee, J. Chem. Phys., 2005, 123, 044308 CrossRef PubMed.
- B. Cherng and F.-M. Tao, J. Chem. Phys., 2001, 114, 1720–1726 CrossRef CAS.
- J. A. Snyder, R. A. Cazar, A. J. Jamka and F.-M. Tao, J. Phys. Chem. A, 1999, 103, 7719–7724 CrossRef CAS.
- W. Zierkiewicz, D. Michalska, Z. Havlas and P. Hobza, ChemPhysChem, 2002, 3, 511–518 CrossRef CAS PubMed.
- H. Raissi, M. Yoosefian and F. Mollania, Int. J. Quantum Chem., 2012, 112, 2782–2786 CrossRef CAS.
- P. Tarakeshwar, S. J. Lee, J. Y. Lee and K. S. Kim, J. Chem. Phys., 1998, 108, 7217–7222 CrossRef CAS.
- L. T. Ji, L. P. Meng, S. J. Zheng and Y. L. Zeng, Acta Chimica Sinica, 2011, 69, 889–897 CAS.
- R. L. DeKock, L. A. Schipper, S. C. Dykhouse, L. P. Heeringa and B. M. Brandsen, J. Chem. Educ., 2009, 86, 1459–1464 CrossRef CAS.
- P. Gilli, L. Pretto, V. Bertolasi and G. Gilli, Acc. Chem. Res., 2009, 42, 33–44 CrossRef CAS PubMed.
- R. S. Mulliken and W. B. Person, Molecular Complexes: A Lecture and Reprint Volume, Wiley-Interscience, New York, 1969 Search PubMed.
- W. Wang, Y. Zhang and B. Ji, J. Phys. Chem. A, 2010, 114, 7257–7260 CrossRef CAS PubMed.
- P. W. Kenny, J. Chem. Inf. Model., 2009, 49, 1234–1244 CrossRef CAS PubMed.
- J. Graton, J. Y. Le Questel, P. Maxwell and P. Popelier, J. Chem. Inf. Model., 2016, 56, 322–334 CrossRef CAS PubMed.
- H. Hagelin, T. Brinck, M. Berthelot, J. S. Murray and P. Politzer, Can. J. Chem., 1995, 73, 483–488 CrossRef CAS.
- G. R. Famini, C. A. Penski and L. Y. Wilson, J. Phys. Org. Chem., 1992, 5, 395–408 CrossRef CAS.
- Y. Duan, C. Wu, S. Chowdhury, M. C. Lee, G. Xiong, W. Zhang, R. Yang, P. Cieplak, R. Luo and T. Lee, J. Comput. Chem., 2003, 24, 1999–2012 CrossRef CAS PubMed.
- I. Alkorta, I. Rozas and J. Elguero, J. Phys. Chem. A, 1998, 102, 9278–9285 CrossRef CAS.
- A. E. Reed, L. A. Curtius and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- M. G. Siskos, A. G. Tzakos and I. P. Gerothanassis, Org. Biomol. Chem., 2015, 13, 8852–8868 CAS.
- H. Szatylowicz, A. Jezierska and N. Sadlej-Sosnowska, Struct. Chem., 2016, 27, 367–376 CrossRef CAS.
- N. Sadlej-Sosnowska, Int. J. Quantum Chem., 2009, 109, 294–300 CrossRef CAS.
- B. G. Oliveira, F. S. Pereira, R. C. M. U. de Araújo and M. N. Ramo, Chem. Phys. Lett., 2006, 427, 181–184 CrossRef CAS.
- V. Umadevi, L. Senthilkumar and P. Kolandaivel, Mol. Simul., 2013, 39, 908–921 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- W. D. Arnold and E. Oldfield, J. Am. Chem. Soc., 2000, 122, 12835–12841 CrossRef CAS.
- Q.-Z. Li, B. Jing, R. Li, Z.-B. Liu, W.-Z. Li, F. Luan, J.-B. Cheng, B.-A. Gong and J.-Z. Sun, Phys. Chem. Chem. Phys., 2011, 13, 2266–2271 RSC.
- B. G. Oliveira, F. S. Pereira, R. C. M. U. de Araujo and M. N. Ramos, Chem. Phys. Lett., 2006, 427, 181–184 CrossRef CAS.
- V. Tognetti and L. Joubert, Theor. Chem. Acc., 2015, 134, 90 CrossRef.
- Y.-X. Lu, J.-W. Zou, Y.-H. Wang and Q.-S. Yu, J. Mol. Struct.: THEOCHEM, 2006, 776, 83–87 CrossRef CAS.
- A. Shahi and E. Arunan, Phys. Chem. Chem. Phys., 2014, 16, 22935–22952 RSC.
- S. J. Grabowski, J. Mol. Struct., 2001, 562, 137–143 CrossRef CAS.
- M. Mandado, A. M. Grana and R. A. Mosquera, Chem. Phys. Lett., 2003, 381, 22–29 CrossRef CAS.
- M. Solimannejad, M. Malekani and I. Alkorta, Mol. Phys., 2011, 109, 1641–1648 CrossRef CAS.
- Y. Lu, J. Zou, H. Wang, Q. Yu, H. Zhang and Y. Jiang, J. Phys. Chem. A, 2005, 109, 11956–11961 CrossRef CAS PubMed.
- M. Palusiak and S. J. Grabowski, Struct. Chem., 2008, 19, 5–11 CrossRef CAS.
- C. Estarellas, A. Frontera, D. Quinonero and P. M. Deya, ChemPhysChem, 2011, 12, 2742–2750 CrossRef CAS PubMed.
- B. V. Pandiyan, P. Deepa and P. Kolandaivel, Phys. Chem. Chem. Phys., 2015, 17, 17496–27508 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27590g |
| This journal is © The Royal Society of Chemistry 2017 |