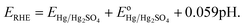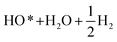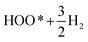Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fluorine substituted (Mn,Ir)O2:F high performance solid solution oxygen evolution reaction electro-catalysts for PEM water electrolysis†
Shrinath Dattatray Ghadge‡
a,
Prasad Prakash Patel‡a,
Moni Kanchan Dattabc,
Oleg I. Velikokhatnyibc,
Ramalinga Kurubab,
Pavithra M. Shanthia and
Prashant N. Kumta *abcde
*abcde
aChemical and Petroleum Engineering, Swanson School of Engineering, University of Pittsburgh, PA 15261, USA
bDepartment of Bioengineering, Swanson School of Engineering, University of Pittsburgh, 815C Benedum Hall, 3700 O'Hara Street, Pittsburgh, PA 15261, USA. E-mail: pkumta@pitt.edu; Fax: +1-412-624-3699; Tel: +1-412-648-0223
cCenter for Complex Engineered Multifunctional Materials, University of Pittsburgh, PA 15261, USA
dMechanical Engineering and Materials Science, University of Pittsburgh, Pittsburgh, PA 15261, USA
eSchool of Dental Medicine, University of Pittsburgh, PA 15217, USA
First published on 20th March 2017
Abstract
Identification and development of high performance with reduced overpotential (i.e. reduced operating electricity cost) oxygen evolution reaction (OER) electrocatalysts for proton exchange membrane (PEM) based water electrolysis with ultra-low noble metal content (i.e. reduced materials cost) is of significant interest for economic hydrogen production, thus increasing the commercialization potential of PEM water electrolysis. Accordingly, a novel electrocatalyst should exhibit low overpotential, excellent electrochemical activity and durability superior to state of the art noble metal based electro-catalysts (e.g. Pt, IrO2, RuO2). Herein, for the very first time to the best of our knowledge, exploiting first-principles theoretical calculations of the total energies and electronic structures, we have identified a reduced noble metal content fluorine doped solid solution of MnO2 and IrO2, denoted as (Mn1−xIrx)O2:F (x = 0.2, 0.3, 0.4), OER electrocatalyst system exhibiting lower overpotential and higher current density than the state of the art IrO2 and other previously reported systems for PEM water electrolysis. The doped solid solution displays an excellent electrochemical performance with a lowest reported onset potential to date of ∼1.35 V (vs. RHE), ∼80 mV lower than that of IrO2 (∼1.43 V vs. RHE) and ∼15 fold (x = 0.3 and 0.4) higher electrochemical activity compared to pure IrO2. In addition, the system displays excellent long term electrochemical durability, similar to that of IrO2 in harsh acidic OER operating conditions. Our study therefore demonstrates remarkable, ∼60–80% reduction in noble metal content along with lower overpotential and excellent electrochemical performance clearly demonstrating the potential of the (Mn1−xIrx)O2:F system as an OER electro-catalyst for PEM water electrolysis.
1. Introduction
The inherent unceasing global energy demand, accelerating the diminution of fossil fuels and the continuing upsurge of our carbon footprint causing potentially perilous damage to the global climate are the primary thrusts for the pursuit of renewable and non-carbonaceous clean energy sources.1–4 In this milieu, hydrogen has garnered immense attention for transportation and stationary applications on the grounds of its high energy density and low carbon footprint.5–9 However, the efficient and economic production of hydrogen from a non-carbonaceous clean source along with cost-effective storage and distribution are major challenges that need to be addressed before hydrogen can be commercially developed as an energy carrier for transportation at industrial scales.10,11 In this direction, hydrogen production from water splitting, via water electrolysis is considered as a promising approach due to its non-toxic and non-carbonaceous nature.12,13 In specific, water electrolysis operation in acidic media, known as proton exchange membrane (PEM) water electrolysis, is considered to be more advantageous than that in neutral and basic media due to higher efficiency, superior production rates, more compact design and increased product purity for operation in acidic media.14–16 Oxygen evolution reaction (OER) for efficient hydrogen production is the major driver for water electrolysis under PEM conditions.The slow reaction kinetics as well as the concomitant high reaction overpotential (i.e. high operating electricity cost) of OER electrocatalyst (∼200 mV overpotential for IrO2) and the high materials cost due to need of expensive and precious noble metals OER electro-catalysts (Pt, IrO2, RuO2) has thwarted the progress and commercialization of PEM based water electrolysis.17–20 Therefore, the OER reaction (Eo = 1.23 V vs. NHE), which occurs at the anode of PEM water electrolysis cells, is an important, challenging and energy intensive process.12,21–23 Hence, the identification and development of high performance, faster reaction kinetics, highly active and low overpotential OER electro-catalyst with ultra-low noble metal content will considerably aid in achieving high efficiency and also help reduce the materials and electricity costs of PEM based water electrolysis cells.24–26
In the pursuit of identifying low noble metal content electro-catalysts as a replacement of currently used expensive pure IrO2 or RuO2 electro-catalysts, one of the widely adopted approaches is mixing of robust and cheap transition metal oxides (e.g. SnO2, Ta2O5, Nb2O5, TiO2) with IrO2 and/or RuO2 (e.g. IrO2–SnO2, RuO2–SnO2, IrO2–Ta2O5, IrO2–SnO2–Nb2O5, etc.) maintaining the electronic conductivity and catalytic activity similar to IrO2 and/or RuO2 and improving the durability of IrO2 and/or RuO2.12,23,27,28 However, in this approach, with increase in the content of non-noble metal oxides above 50 wt%, there is deterioration in catalytic activity due to a decrease in the electrochemical active surface area and electronic conductivity.12,23,27 We29,30 have recently identified several F doped binary and ternary solid solution oxides [(M,M′,Ir)O2:F; M,M′ = Sn, Nb] with significant reduction in IrO2 (∼70–80 mol% reduction) content albeit exhibiting similar electrochemical performance to pure IrO2 electro-catalyst, thus offering significant reduction in materials cost of the PEM water splitting process. However, all these developed [(M,M′,Ir)O2:F; M,M′ = Sn, Nb] electro-catalysts show similar electrochemical performance (i.e. overpotential and activity) to that of pure IrO2.29,30 In addition to lowering the materials cost, a novel electro-catalyst offering lower operating electricity cost with significantly improved electrochemical performance (lower overpotential and faster kinetics) with respect to IrO2 needs to be identified in order to commercialize PEM water electrolysis technology. The focus of the current work is thus not only on the identification and development of novel electro-catalyst with reduced noble metal content but more importantly, identifying reduced noble metal containing systems that exhibit faster reaction kinetics, low overpotential, superior electrochemical performance than that of pure IrO2 utilizing the prudent two pronged theoretical and experimental approach.
In this work, for the very first time to the best of our knowledge, exploiting first-principles theoretical calculations of the total energies and electronic structures, we have identified fluorine doped solid solution of MnO2 and IrO2, denoted as (Mn1−xIrx)O2:F electro-catalyst system exhibiting lower overpotential and higher current density than state of the art IrO2 and also superior electrochemical performance as compared to other solid solution based OER electro-catalyst systems in PEM water electrolysis.25,29–32 These results will portend significant reduction in noble metal content in electro-catalyst aiding in achieving significantly reduced material's cost as well as operating electricity cost. In addition, in the current study, a thorough investigation of total energies, electronic structure and density of electronic states of the as-synthesized electro-catalysts, employing the density functional theory has been implemented. The present study also determines the free energy (ΔG) values of (Mn,Ir)O2 electro-catalyst system which successfully shows the significant decrease in the onset potential of (Mn,Ir)O2 electro-catalyst system.
In the present study, fluorine (F) is chosen as an anionic dopant for the (Mn1−xIrx)O2 solid solution due to its pivotal role in improving the electrochemical activity of [(M,M′,Ir)O2:F; M,M′ = Sn, Nb] for OER in acidic media as already demonstrated by us previously following experiments and first principles calculations.29,30 The results of the theoretical studies are experimentally verified by synthesizing thin film architectures of (Mn1−xIrx)O2 (x = 0, 0.3, 1) and (Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4) electro-catalysts on Ti foil (substrate). Thus, for the very first time, we document the theoretical studies, synthesis, physical characteristics, and electrochemical performance of nanostructured (Mn1−xIrx)O2 (x = 0, 0.3, 1) and (Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4) thin film electro-catalysts for OER in PEM water electrolysis.
2. Computational methodology
The overall electro-catalytic activity and the overpotential of (Mn,Ir)O2:F OER electro-catalyst is expected to depend on the electronic structure and thermodynamics of the four elementary steps (eqn (1)) of OER under acidic conditions.
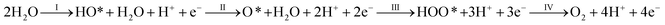 | (1) |
To study the influence of compositions on the electronic structure as well as the activity of the electro-catalyst, theoretical analysis has been performed. The computational component of the current study is to understand the electronic structure of (Mn,Ir)O2:F oxides with the following chemical compositions: (Mn1−xIrx)O2, with x = 0.17, 0.33, 0.5 and (Mn0.83Ir0.17)O1.33F0.67, corresponding approximately to 10 wt% of F. Also, for comparison purposes pure IrO2 oxide has been considered as a standard electro-catalyst for PEM based water electrolysis.
In order to determine the electric potentials at which a certain specific reaction would occur, the free energies (ΔG) of all the four anodic intermediate reactions (I–IV) have been considered. Therefore, a methodical analysis of all the calculated free energies may explain the rate determining step of the oxygen evolution reaction. This systematic analysis is essential for the knowledge of electro-catalytic activity of the specific material used as an electro-catalyst in water electrolysis reaction.
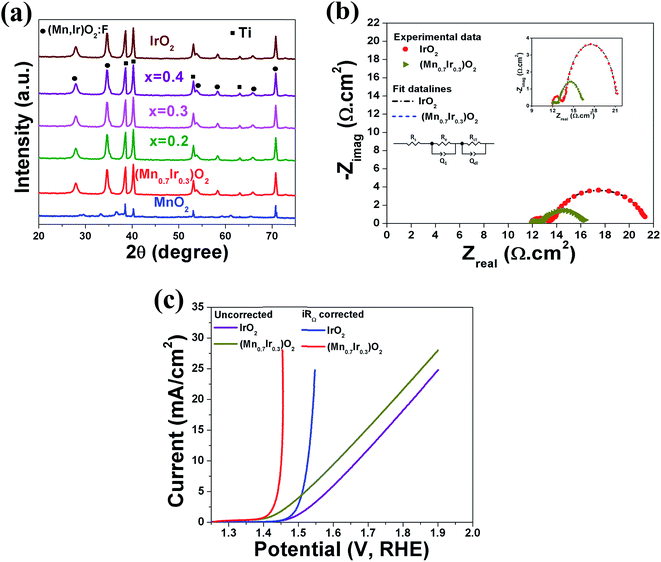
For comparison purposes two different materials have been chosen for calculation of the OER elementary steps: pure IrO2 and IrO2 doped with small amount of Mn as a substituent of Ir at the corresponding Ir-type lattice sites. For calculations of the total energies and electronic structure of the above mentioned oxides bulk and (110) surface rutile structure with a tetragonal unit cell and space group P42/mnm have been utilized. The rutile structure of IrO2 and (Mn,Ir)O2:F have been experimentally confirmed from XRD analysis which will be presented in the Experimental results section to follow.
For bulk calculations [1 × 1 × 3] supercell containing three elementary unit cells stacked in c direction has been chosen as the basis for construction of different Ir, Mn, and F concentrations of the oxide solid solution. Such a supercell contains 6 transition metal atoms and 12 atoms of oxygen/fluorine. Thus, for convenience of calculations the basic composition has been chosen i.e. several different atomic ratios of Mn/Ir, such as 5/1 corresponds to (Mn0.83Ir0.17)O2 formula unit, while 4/2 and 3/3 correspond to (Mn0.67Ir0.33)O2 and (Mn0.5Ir0.5)O2 formula units, respectively. For simulation of 10 wt% of fluorine, 4 atoms of oxygen were randomly replaced with corresponding number of fluorine atoms generating the following formula unit: (Mn0.83Ir0.17)O1.33F0.67. Such composition has been chosen for smaller representative super-cells for all the calculation of bulk and surface electronic structures employed in the present study.
For calculation of the (110) surface electronic properties of the materials, a two-dimensional slab repeated in [1, −1, 0] direction with 24 atom unit cell containing four oxygen layers with three oxygen–metal mixed layers in between them. A vacuum distance ∼12 Å between adjacent images of the slab was selected.
Following the previous studies,33,34 for the calculation of the free energies of all the elementary reactions i.e. (I)–(IV) for IrO2 with and without Mn atoms located at the surface, the rutile type (110) preferred surface which is covered with oxygen has been selected. The 2 × 2 surface unit cell for a symmetric 7-layer slab of ∼10.3 Å thickness which is separated between its images perpendicular to the surface direction by vacuum space of ∼20 Å has been taken which will prevent the interaction between the slab and its adjacent images. On the coordinated unsaturated sites of both sides of the chosen slab, all intermediate species involved in the OER i.e. O*, OH*, and OOH* have been attached. Three middle layers of the slab were fixed with the lattice parameter corresponding to the bulk IrO2. Apart from these three middle layers, all other layers of the slab together with the intermediate species were fully relaxed and therefore, all the mathematical data obtained from such model should be divided by two.
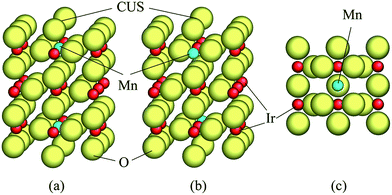
A unit cell chosen for the calculations in the present study has been shown in Fig. 1. Two different atomic positions of Mn as a replacement of Ir in the unit cell have been considered to investigate the difference between the electronic structures of pure and doped IrO2 compounds as well as to assess the role of Mn on lowering of the overpotential of the (Mn,Ir)O2. The first Mn-atomic distribution consists of one Mn-atom located in place of Ir just below the coordinatively unsaturated site (CUS) with an oxygen vacancy shown on Fig. 1a. The second distribution is characterized by introduction of Mn-atom at the lower part of the unit cell while the CUS locates above the Ir atom [Fig. 1b]. In order to calculate the free energies of all the four elementary reaction steps discussed above, such two different unit cells which have been covered by adsorbed oxygen monolayers in conjunction with intermediate species at the surface have been used.
For calculating the total energies, electronic structure and density of electronic states of the studied materials, the density functional theory implemented in Vienna Ab initio Simulation Package (VASP) was used within the projector-augmented wave (PAW) method35–37 and the spin-polarized generalized gradient approximation (GGA) for the exchange–correlation energy functional in a form described by Perdew and Yue.38 This computational package analyses the electronic structure and via Hellmann–Feynman theorem, the inter-atomic forces are determined from first-principles. The standard PAW potentials were utilized for the elemental components and the Ir, Mn, O and F potentials thus contained nine, seven, six and seven valence electrons, respectively. In the present theoretical analysis, to maintain the high precision for total energy calculations for all the electro-catalyst compositions, the plane wave cutoff energy of 520 eV has been chosen. By employing the double relaxation procedure, the internal positions as well as the lattice parameters of atoms have been completely optimized.
Moreover, the minima of the total energies with respect to the lattice parameters and internal ionic positions have been determined. Also, by minimizing the Hellman–Feynman forces via a conjugate gradient method, the geometry optimization was achieved. This will cause the net forces applied on every ion in the lattice close to zero. The total electronic energies were converged within 10−5 (i.e. 0.00001) eV per unit cell which result into the residual force components on each atom to be lower than 0.01 eV per Å per atom. This allows the accurate determination of the internal structural parameters. Herein, the Monkhorst–Pack scheme has been used to sample the Brillouin Zone (BZ) and create the k-point grid for the solids and the different isolated atoms used in the current study. The selection of an appropriate number of k-points in the irreducible part of the BZ was made on the grounds of the convergence of the total energy to 0.1 meV per atom.
It is noteworthy to mention that, for Mn–Ir–O–F compositions, the corresponding atomic distributions are uncertain and thus, different spatial configurations can be used for exemplification of the atomic distributions. This uncertainty has been eliminated by assembling the various atomic configurations for each selected composition and the configurations which correspond to the minimum total energy, have been selected for conducting further numerical analysis of these specific compositions of the binary oxides.
3. Experimental methodology
3.1. Synthesis of (Mn1−xIrx)O2 (x = 0, 0.3, 1) and (Mn1−xIrx)O2:10 wt% F (x = 0.2, 0.3, 0.4)
Iridium tetrachloride (IrCl4, 99.5%, Alfa Aesar), manganese chloride (MnCl2, 99.5%, Aldrich) and ammonium fluoride (NH4F, 98%, Alfa Aesar) were used as the sources for Ir, Mn and F respectively. Stock solutions of IrCl4, MnCl2 and NH4F of the desired compositions were prepared in deionized (D.I.) water (18 MΩ cm, MilliQ Academic, Millipore). These stock solutions were mixed together according to the desired composition of the electro-catalyst material and then spin coated onto titanium foils (Alfa Aesar) of ∼1 cm2 area (0.5 cm × 2 cm) (used as a substrate). The spin coating (Speciality coating Systems Inc., Model P6712) was performed employing a rotating speed of 500 rpm for 10 s with suitable amount of the precursors selected to achieve a desired total loading of ∼0.3 mg cm−2 of (Mn1−xIrx)O2 and (Mn1−xIrx)O2:10F oxide electro-catalyst. The precursors spin coated on Ti foil were then thermally treated at 400 °C for 4 h in air to initiate decomposition and adequate reaction of the precursors to form (Mn1−xIrx)O2 and (Mn1−xIrx)O2:10F solid solutions on the Ti foil to achieve a total electro-catalyst loading of ∼0.3 mg cm−2. It should be noted that the same chemical approach was used to generate IrO2 thin films on the Ti foil serving as the control for comparing the electrochemical activity of the Mn substituted IrO2 solid solutions and F-doped Mn substituted IrO2 solid solutions.3.2. Electro-catalyst materials characterization
X-ray photoelectron spectroscopy (XPS) was used to investigate the oxidation states of Mn and Ir in (Mn1−xIrx)O2 and (Mn1−xIrx)O2:10F electro-catalysts. XPS analysis was carried out using the ESCALAB 250 Xi system (Thermo Scientific) equipped with a monochromated Al Kα X-ray source. The standard analysis spot of 400 × 400 μm2 was defined by the micro-focused X-ray source. The system is operated at a room temperature in an ultra-high vacuum chamber with a base pressure less than 5 × 10−10 mbar. The binding energy (BE) scale of the analyzer was calibrated to produce <50 meV deviations of the three standard peaks from their standard values. The aliphatic C 1s peak was observed at 284.6 eV. High-resolution elemental XPS data in C 2p, S 2p, Mg 2p, and Zn 2p regions were acquired with the analyzer pass energy set to 20 eV (corresponding to energy resolution of 0.36 eV) and the step size set to 0.1 eV. The Avantage software package (Thermo Fisher Scientific) was used to fit the elemental spectra based on the calibrated analyzer transmission functions, Scofield sensitivity factors, and effective attenuation lengths for photoelectrons from the standard TPP-2M formalism.
Where, ERHE is the potential versus RHE. EHg/Hg2SO4 is the potential measured against the Hg/Hg2SO4 reference electrode.
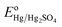 is the standard electrode potential of Hg/Hg2SO4 reference electrode (+0.65 V vs. NHE).
is the standard electrode potential of Hg/Hg2SO4 reference electrode (+0.65 V vs. NHE).Electrochemical impedance spectroscopy (EIS): The EIS was conducted to determine the solution resistance (Rs), the electrode resistance (Re), the ohmic resistance (RΩ) (RΩ = Rs + Re) and the charge transfer resistance (Rct) of the synthesized electro-catalyst materials.7,43 The ohmic resistance (RΩ) obtained from the EIS was further utilized for iRΩ (iRs + iRe) correction7,43 in the polarization curves of the electro-catalysts. The EIS was performed in the frequency range of 100 mHz to 100 kHz (amplitude = 10 mV) using the electrochemical work station (Versa STAT 3, Princeton Applied Research) in 1 N H2SO4 electrolyte solution at 40 °C, at the constant applied potential of ∼1.45 V (vs. RHE, iRΩ corrected) using a total loading of 0.3 mg cm−2 for (Mn1−xIrx)O2 (x = 0.3 and 1) and (Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4). Impedance data for OER has been modeled by using the ZView software from Scribner Associates employing the Rs(ReQ1)(RctQdl) equivalent circuit model. In the present circuit model (similar to that of used in earlier reports25,29) Rs is in series with the parallel combination of the Re and Q1 and further in series with the parallel combination of the Rct and Qdl. The components of this model are given as below:7,43
Rs = solution resistance faced at high frequency due to charge transfer in the electrolyte solution.
Re = electrode resistance for electron transfer from the electrode to current collector (Ti foil).
Rct = charge transfer resistance (i.e., polarization resistance).
Q1 = constant phase element.
Qdl = contribution from both double layer capacitance and pseudocapacitance.
Linear scan polarization: The electrochemical activity of the electro-catalysts for OER was determined by conducting linear scan polarization in 1 N H2SO4 electrolyte solution employing a scan rate of 10 mV s−1 at 40 °C. Polarization curves of different electro-catalysts were iRΩ corrected (RΩ, the ohmic resistance was determined from electrochemical impedance spectroscopy analysis). The current density at ∼1.45 V (vs. RHE, which is the typical potential used for assessing the electrochemical activity of the electro-catalyst for OER44) in iRΩ corrected polarization curves was used for comparison of the electrochemical performance of the different electro-catalyst materials. The Tafel plot after iRΩ correction given by the equation η = a + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i (plot of overpotential η vs. log
i (plot of overpotential η vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) current, log
current, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i) was used to determine the Tafel slope (b), which was further used to study the reaction kinetics for all the synthesized electro-catalysts.
i) was used to determine the Tafel slope (b), which was further used to study the reaction kinetics for all the synthesized electro-catalysts.
Electrochemical stability test: The electrochemical stability of (Mn1−xIrx)O2:10F electro-catalyst for possible long term operation in an electrolyzer was studied by conducting chronoamperometry (CA) test (current vs. time), wherein, the electrode was maintained for 24 h in the electrolyte solution of 1 N H2SO4 at 40 °C under a constant potential of ∼1.45 V (vs. RHE, iRΩ corrected). For comparison, the CA test was also conducted for the in-house synthesized IrO2 electro-catalyst used as the control.
4. Results and discussion
4.1. Computational study to predict the high electrochemical activity of (Mn1−xIrx)O2 and (Mn1−xIrx)O2:10F
In the present study, we have continued to adopt the concept proposed by J. K. Nørskov and his group45,46 and accordingly, we have used it for qualitative evaluation of the electrochemical activity of (Mn,Ir)O2 and (Mn,Ir)O2:10F. The concept shows the existence of a simple descriptor for determining the surface catalytic activity of the two electro-catalyst systems. This descriptor has been defined as a gravity center of the transition metal d-band εd usually located in the vicinity of the Fermi level. An optimal position of the d-band center thus, provides an optimal interaction between the catalytic surface and various species participating in the catalytic reactions predominantly occurring on the surface leading to the expected maximum catalytic activity. Thus, such an interaction should be considered optimal allowing the reactants and products to both adsorb at the surface and desorb most efficiently. Hence, an adjustment of the d-band center position with respect to the Fermi level may likely play a critical role in designing the novel highly active and electrochemically stable electro-catalysts discussed herein. As mentioned earlier in the present study, the electronic structure of the stable surfaces for all the electro-catalysts have been calculated and the positions of the corresponding d-band centers have been obtained as a first moment of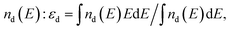 where nd(E) is the projected d-band density of states of the corresponding materials.
where nd(E) is the projected d-band density of states of the corresponding materials.
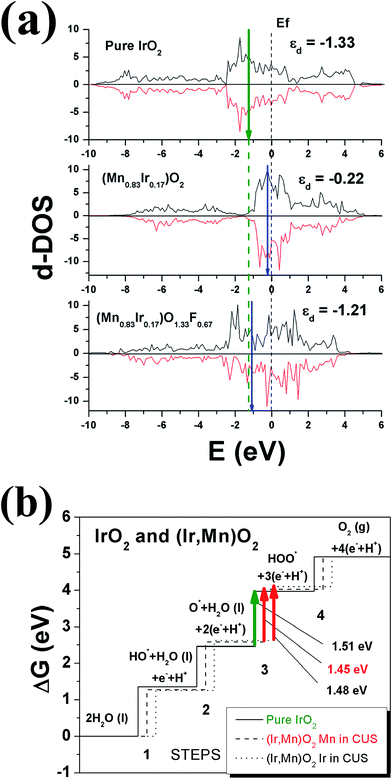
Fig. 2a thus accordingly shows the projected d-band densities of states together with the corresponding centers of these zones marked with vertical arrows on the graphs for pure IrO2, Ir substituted MnO2, (Mn0.83Ir0.17)O2, as well as F doped Mn substituted MnO2, (Mn0.83Ir0.17)O1.33F0.67. Since, IrO2 is a recognized OER electro-catalyst, the d-band positions for IrO2, marked with a dashed vertical line throughout the whole graph, could serve as a reference point or a benchmark attesting to the optimal catalytic activity for the designed electro-catalysts. Our calculations have showed that IrO2 is characterized by the d-band centers located at ∼(−1.33 eV). The closer the corresponding d-band center of the solid solution electro-catalyst studied herein to IrO2 d-band center position, it can be considered as the likely indication of the substituted solid solution exhibiting electrochemical activity matching that of IrO2 and thus, an indicator of expected improvement in overall catalytic activity of the electro-catalyst. Such an approach can thus help in understanding the effect of fluorine on the electro-catalytic activity of (Mn,Ir)O2:F.
It can be seen from Fig. 2a that the projected density of d-electronic states for (Mn0.83Ir0.17)O2 can be presented as a sum of Mn 3d and Ir 5d electrons characterized by the d-band center position located at −0.22 eV vs. the Fermi level. However, an introduction of F into (Mn0.83Ir0.17)O2 changes the overall electronic structure in such a way that formation of the hybridized F 2p–Mn 3d and F 2p–Ir 5d electronic states shifts the d-band center downward to −1.21 eV very close to that of IrO2 (−1.33 eV). Of course, it should be noted that this approach is very qualitative and does not provide exact chemical compositions demonstrating the optimal catalytic activity of the material. Nevertheless, it provides a basic understanding of the effect of F doping and its likely influence on the electro-catalytic activity of (Mn0.83Ir0.17)O2:F. An identical effect of F on the electronic structure has also been seen earlier and reported by us in the study of (Sn,Ir)O2:F electro-catalysts.29 Similar to (Mn0.83Ir0.17)O2:F, formation of F 2p–Ir 5d hybridized electronic states shifts the d-band center of (Ir,Sn)O2:F down towards the optimal position, and thus, improves the overall catalytic activity of (Ir,Sn)O2:F with substantial reduction of ∼70–80% in the noble metal content.29 The theoretical calculations were also validated experimentally and reported by us in the corresponding reports.29
Although the d-band center concept can provide a qualitative explanation of the basic origins of high catalytic activity of (Mn,Ir)O2:F, it does not provide insights to elucidate effect of Mn introduction into the IrO2 lattice on the overpotential of the (Ir,Mn)O2 solid solution oxide. To study this effect, it is imperative to consider all the four elementary steps involved in the oxygen evolution reaction discussed in Fig. 2b and also outlined in the earlier section (eqn (1)).
Fig. 2b demonstrates the free energies of all the four elementary steps of OER calculated for pure IrO2 and the two different Ir–Mn atomic configurations discussed above and illustrated in Fig. 1. Also, some of the data used for plotting these graphs are collected in the Table 1. One can see that the most energetically challenging step for all the three materials is step 3, resulting in the formation of the hydroperoxide HOO* from the second water molecule. This step determines the major overpotential that is required to be overcome to meet the four steps outlined in Fig. 2b, leading to the evolution of oxygen. For pure IrO2 the overpotential is 1.51–1.23 = 0.28 V, while for (Ir,Mn)O2 it is 0.22 V and 0.25 V for the two different positions of Mn in the unit cell, thus indicating that the presence of Mn is critical to lower the overpotential for the electrolysis reaction in comparison with pure IrO2. Such a decrease in the energy difference for the third elementary step in the case of Mn-doped IrO2 is due to the stronger interaction between the adsorbed oxygen O* and the surface resulting in a decrease in the total energy of the system in comparison with pure IrO2; making it more feasible for the species to adsorb at the surface and thus, resulting in a reduction in the overpotential of the overall OER for (Mn,Ir)O2 oxide. From Table 1, it can also be seen that the ΔG values for all the intermediates in the case of both the Mn-configurations of (Mn,Ir)O2 are consistently lower than those for pure IrO2 indicating a stronger binding of the intermediates to the Mn-containing surface. Such an enhancement in adsorption is indirectly confirmed by the d-band calculations discussed above, when the introduction of Mn shifts the resulted d-band center upward towards the Fermi level, thus making the effective interactions between the intermediate species and the catalytic surface stronger in comparison to pure IrO2. The more close the d-band center to the Fermi level of the material, the larger is the overlap between the d-orbitals of the surface and oxygen s,p-orbitals in O*, HO*, and HOO* intermediate species leading to a stronger overall interaction between the surface and the adsorbed species. These results clearly demonstrate that the coordinatively unsaturated sites (CUS) on the oxidized surface could serve as the main active sites for water oxidation regardless of the local distribution of the Mn-ions with the difference in the over-potential of 0.03 V for the different surface configurations (see Fig. 2b).
As demonstrated in various previous studies, introduction of F into the different solid solutions of IrO2 with SnO2 and/or NbO2 oxides did not result in decreasing the overpotential for OER.29,30 The onset potential remained the same for all the materials ∼1.43 V (the corresponding overpotential was ∼0.20 V), while the kinetic properties (e.g. exchange current density) strongly depended on the F-content of the material.29,30 In light of this, computational investigation into the effect of F on the overpotential of (Mn,Ir)O2 oxide was therefore deemed redundant and hence, has not been conducted in the current study.
Thus, the present theoretical study has demonstrated different effects of introduction of Mn and F into the IrO2 lattice: an introduction of Mn makes interactions between the surface and intermediate species more strong thus decreasing the overpotential and increasing the propensity for the overall OER, while F-doping modifies the electronic structure of the material in a such way, that the d-band center moves towards the ideal position corresponding to the optimal electro-catalytic activity. Also, fluorine introduces more free electrons into the system resulting in improving the overall electronic conductivity of (Mn,Ir)O2:F and, in turn, the overall catalytic activity. These theoretical findings correlate very well with experimental observations discussed in the present study.
4.2. Experimental characterization of (Mn1−xIrx)O (x = 0, 0.3, 1) electro-catalyst
| Composition | Lattice parameter (Å) | Molar volume (cm3 mol−1) | |
|---|---|---|---|
| a = b | c | ||
| MnO2 | 9.88 ± 0.07 | 2.82 ± 0.02 | 20.72 |
| (Mn0.7Ir0.3)O2 | 4.64 ± 0.04 | 3.07 ± 0.03 | 19.77 |
| (Mn0.8Ir0.2)O2:10F | 4.63 ± 0.06 | 3.06 ± 0.04 | 19.75 |
| (Mn0.7Ir0.3)O2:10F | 4.64 ± 0.06 | 3.08 ± 0.04 | 19.96 |
| (Mn0.6Ir0.4)O2:10F | 4.65 ± 0.06 | 3.06 ± 0.04 | 19.92 |
| IrO2 | 4.63 ± 0.06 | 3.06 ± 0.04 | 19.75 |
| Composition | Onset potential (V vs. RHE) | Current density at ∼1.45 V (vs. RHE) (mA cm−2) | Rs (Ω cm2) | Re (Ω cm2) | RΩ (Ω cm2) | Rct (Ω cm2) | Tafel slope (mV dec−1) |
|---|---|---|---|---|---|---|---|
| (Mn0.7Ir0.3)O2 | ∼1.35 | ∼9.09 | ∼11.73 | ∼1.85 | ∼13.58 | ∼3.6 | ∼67 |
| (Mn0.8Ir0.2)O2:10F | ∼1.35 | ∼5.45 | ∼11.72 | ∼2.4 | ∼14.12 | ∼4 | ∼68 |
| (Mn0.7Ir0.3)O2:10F | ∼1.35 | ∼10.65 | ∼11.68 | ∼1.78 | ∼13.46 | ∼2.6 | ∼65 |
| (Mn0.6Ir0.4)O2:10F | ∼1.35 | ∼11.03 | ∼11.71 | ∼1.7 | ∼13.41 | ∼2.1 | ∼62 |
| IrO2 | ∼1.43 | ∼0.75 | ∼11.73 | ∼2.5 | ∼14.23 | ∼8.5 | ∼71 |
In order to analyze the electrochemical activity of (Mn0.7Ir0.3)O2 electro-catalyst, linear scan polarization has also been performed in the electrolyte solution of 1 N H2SO4 at 40 °C with the scan rate of 10 mV s−1. The electrolyte solution resistance (Rs), electrode resistance (Re) and bubble resistance (Rbub) are mainly responsible for the linear nature of polarization curve and non-linearity in the Tafel plot.54,55 Thus, to study the inherent electrochemical activity of the electro-catalysts, ohmic resistance (RΩ) correction (iRΩ = iRs + iRe)6,7,43,56 has been performed in the polarization curves as well as in Tafel plots of (Mn0.7Ir0.3)O2 and IrO2. Fig. 3c shows the uncorrected and iRΩ corrected polarization curves of pure IrO2 and (Mn0.7Ir0.3)O2 electro-catalyst. The electrochemical activity of pure MnO2 has not been performed due to the inherent instability of MnO2 in the acidic electrolyte solution.57–59 As shown in Fig. 3c and Table 3, the onset potential of OER for (Mn0.7Ir0.3)O2 is ∼1.35 V (vs. RHE) with ∼120 mV overpotential (w.r.t. the standard potential for OER i.e. 1.23 V vs. RHE) which is much lower than that of IrO2 which shows an onset potential of ∼1.43 V (vs. RHE) with ∼200 mV overpotential similar to earlier reports.29,34,60 The significant decrease in the overpotential, lowest reported to date, measured for (Mn0.7Ir0.3)O2 electro-catalyst is in good agreement with the results of the theoretical calculation discussed in the earlier section and shown in (Fig. 2a and b, Table 1). The current density obtained at ∼1.45 V for (Mn0.7Ir0.3)O2 (total loading = 0.3 mg cm−2) is ∼9.09 mA cm−2 which is ∼12 fold higher than that of IrO2 (0.75 mA cm−2 at 1.45 V with an identical loading = 0.3 mg cm−2) (Table 3). The excellent electrochemical performance (i.e. low over-potential and higher current density) of (Mn0.7Ir0.3)O2 is due to the improved reaction kinetics (i.e. low Rct as seen earlier in Fig. 3b and Table 3) for OER of (Mn0.7Ir0.3)O2 than that of IrO2 as predicted by the theoretical calculations (Fig. 2a and b, Table 1).
In order to further improve the reaction kinetics of (Mn,Ir)O2 electro-catalyst, 10 wt% F has been introduced as a dopant in the (Mn,Ir)O2 electro-catalyst as proposed from the theoretical studies discussed earlier (Fig. 2a and b). In addition, a higher (x = 0.4) and lower (x = 0.2) IrO2 content solid solution electro-catalysts [(Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4)] has also been explored to identify the nominal composition with an excellent electrochemical activity towards OER in PEM based water electrolysis.
4.3. Characterization of (Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4) electro-catalyst
SEM/EDX analysis: The SEM micrograph combined with the EDX pattern of the representative composition, (Mn1−xIrx)O2:10F (x = 0.2) shows the presence of Ir, Mn and O (Fig. 4a). The quantitative elemental composition analysis of (Mn1−xIrx)O2:10F (x = 0.2) obtained from EDX shows the measured elemental composition of Ir and Mn close to the nominal composition. The elemental X-ray maps of Ir, Mn and O for (Mn1−xIrx)O2:10F (x = 0.2) (Fig. 4b) show the homogeneous distribution of elements within the particles indicating absence of any segregation at any specific site.
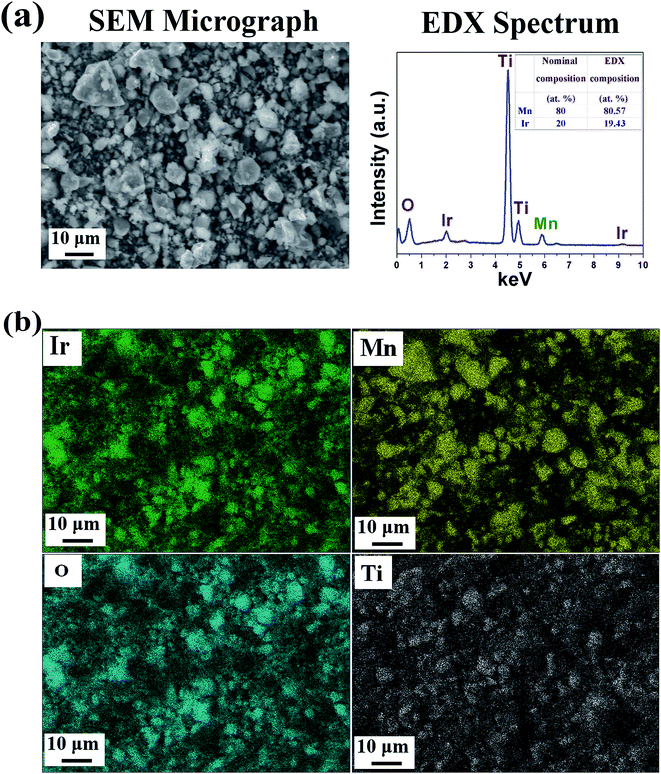 | ||
| Fig. 4 (a) The SEM micrograph and EDX spectrum, (b) elemental X-ray mapping of (Mn1−xIrx)O2:10F (x = 0.2). | ||
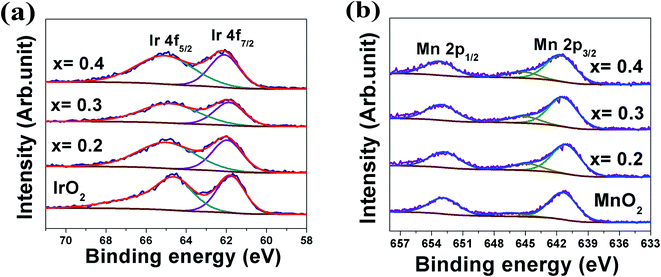
X-ray photoelectron spectroscopy (XPS) analysis: XPS analysis has been performed on (Mn1−xIrx)O2:10F electro-catalysts with different Mn content to study the valence states of Ir and Mn. The XPS analysis has been plotted in the Fig. 5a and b for Ir and Mn, respectively. The deconvoluted XPS spectrum of Ir in pure IrO2 (Fig. 5a) shows the presence of Ir 4f doublet centered at binding energy of ∼61.7 eV and ∼64.6 eV (similar to earlier report62) which corresponds to Ir 4f7/2 and Ir 4f5/2 respectively, consistent with that of pure IrO2.48 Fig. 5b shows the XPS spectra of Mn 2p doublet for MnO2 centered at ∼641.6 eV and ∼653.8 eV (similar to earlier report63–65) for Mn 2p3/2 and Mn 2p1/2, respectively, which corresponds to that of pure MnO2.63,66 As can be seen in Fig. 5b, deconvoluted XPS spectra of (Mn1−xIrx)O2:10F (for x = 0.2, 0.3, 0.4) exhibit an additional peak centered near ∼645.5 eV, similar to the previous studies, which may be a shake-up peak and can be referred as a satellite peak.63,64 However, the positive shift in Ir 4f doublet and Mn 2p doublet positions of (Mn1−xIrx)O2:10F after incorporation of F in the solid solution lattice as well as with increase in Ir content (Fig. 5a and b) suggests modification of the electronic structure of (Mn1−xIrx)O2:10F for the different compositions upon formation of solid solution and due to the presence of fluorine in the solid solution lattice leading to stronger binding due to the higher electronegativity of fluorine.29,67 The presence of F in (Mn1−xIrx)O2:10F of different compositions could not be unequivocally ascertained by the XPS analysis similar to our earlier publications on Sn substituted IrO2,29,30 probably due to the low concentration of F actually retained within the lattice. Nevertheless, F incorporation has indeed beneficial effect on the electrochemical activity (as witnessed in the polarization curve, Fig. 6b, discussed later) of (Mn,Ir)O2:F solid solution most likely due to the improved electronic conductivity.29
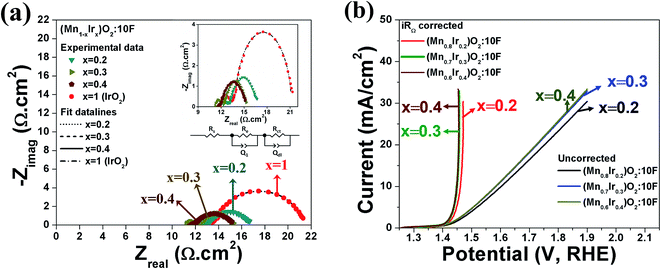
Based on the above results, it is anticipated that (Mn1−xIrx)O2:10F (x = 0.3 and 0.4) will show enhanced reaction kinetics as well as electrochemical activity than (Mn0.7Ir0.3)O2 and pure IrO2. The uncorrected and iRΩ corrected linear scan polarization curves of (Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4) obtained in the electrolyte solution of 1 N H2SO4 at 40 °C with the scan rate of 10 mV s−1 are shown in Fig. 6b. The onset potential of OER for (Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4) is ∼1.35 V (vs. RHE) which is comparable to (Mn0.7Ir0.3)O2 with ∼120 mV overpotential and lower than IrO2 which shows ∼200 mV overpotential (Fig. 3c and Table 3). The current density obtained at ∼1.45 V (vs. RHE) for (Mn0.7Ir0.3)O2:10F, (Mn0.6Ir0.4)O2:10F is ∼10.65 mA cm−2 and ∼11.03 mA cm−2 respectively (Table 3), which is ∼14 and ∼15 fold higher than that of IrO2 (0.75 mA cm−2 at 1.45 V), respectively. Although the current density obtained at ∼1.45 V for (Mn0.8Ir0.2)O2:10F electro-catalyst (i.e. ∼5.45 mA cm−2) is lower than that of (Mn0.7Ir0.3)O2:10F, (Mn0.6Ir0.4)O2:10F and (Mn0.7Ir0.3)O2, (Mn0.8Ir0.2)O2:10F shows a significantly higher current density (∼7 fold) than that of pure IrO2 observed at ∼1.45 V with a hallmark 80% reduction in noble metal content and even ∼11 fold higher current density than (Mn0.87Ir0.13)O2 solid solution system reported in a recent publication.32 The Tafel slope of (Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4) is ∼68 ± 0.0001 mV dec−1, ∼65 ± 0.0001 mV dec−1 and ∼62 ± 0.0001 mV dec−1, respectively (Fig. 7a–d). Thus, the Tafel slope of (Mn1−xIrx)O2:10F decreases with increase in Ir content with the lowest obtained for (Mn0.6Ir0.4)O2:10F indicating increase in the reaction kinetics and higher electrochemical activity with the largest value obtained for (Mn0.6Ir0.4)O2:10F. In addition, the Tafel slope of (Mn1−xIrx)O2:10F does reflect the desired two electron pathway for OER in accordance with published reports (Table 3).13
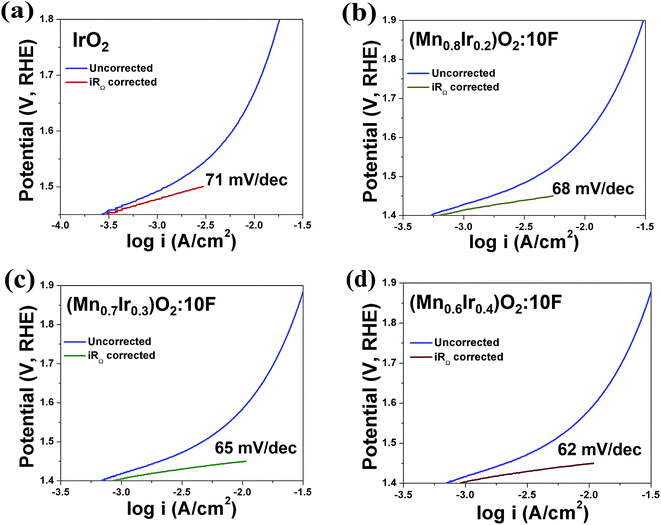 | ||
| Fig. 7 The Tafel plot of (a) IrO2 (b) (Mn0.8Ir0.2)O2:10F (c) (Mn0.7Ir0.3)O2:10F and (d) (Mn0.6Ir0.4)O2:10F, before and after iRΩ correction. | ||
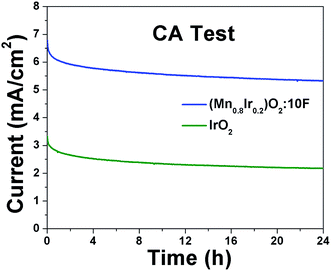
Electrochemical stability/durability test: It is extremely important for electro-catalyst to exhibit excellent long term electrochemical durability in harsh acidic operating conditions of OER, which will aid in efficient continuous long term operation when implemented in PEM water electrolysis cells. Therefore, to assess the electrochemical stability/durability of (Mn1−xIrx)O2:10F electro-catalyst, chronoamperometry (CA) test has been performed at the constant applied potential of ∼1.45 V (iRΩ corrected, i.e., ∼1.55 V in the uncorrected polarization curve) in 1 N H2SO4 at 40 °C. The CA curve obtained for the higher Mn content electro-catalyst (Mn0.8Ir0.2)O2:10F, shown in Fig. 8, displays minimal loss in current density, indicating the superior long term electrochemical stability, similar to that of in-house synthesized IrO2. The initial decrease in current density seen in CA curves of both in-house synthesized IrO2 and (Mn1−xIrx)O2:10F (x = 0.2) can possibly be due to dissolution of irregular electro-catalyst coating and/or diffusion controlled reaction, similar to earlier reports.29,68 Thus, excellent long term electrochemical stability of (Mn1−xIrx)O2:10F (x = 0.2) can possibly be due to good alloying of IrO2 and MnO2 and beneficial modification in the electronic structure upon formation of F-doped solid solution, resulting in unique active phase exhibiting superior electrochemical stability.
The above results clearly suggest that the incorporation of IrO2 in the framework of MnO2 along with incorporation of F in the lattice offers a unique opportunity to tailor the electronic, physical, chemical and electro-catalytic properties of (Mn,Ir)O2:10F. The formation of a single phase solid solution (Mn,Ir)O2:10F offers modified electro-catalytic properties due to a change in the d-band center energy leading to change in adsorption strength of the corresponding adsorbed species on the electro-catalyst surface. Additionally, significant decrease in overpotential and improvement in electrochemical performance contributes to efficient OER electro-catalytic activity for PEM water electrolysis. The present study also demonstrates remarkable, ∼60–80% reduction in the noble metal content along with substantial reduction in over-potential for the (Mn1−xIrx)O2:F solid solution systems indicative of the excellent electrochemical performance. The study thus clearly demonstrates the potential of (Mn1−xIrx)O2:F system as an efficient OER electro-catalysts for PEM water electrolysis. However, it should be noted that the true potential of the electro-catalyst can only be realized when tested in a full PEM based water electrolyzer. Although electrolyzer evaluation of these electro-catalysts is beyond the scope of the current study, it can be mentioned that the present electro-catalyst system displays superior electrochemical response compared to F-doped IrO2 when evaluated in a half-cell configuration. Our evaluation of F-doped IrO2 in a full PEM electrolyzer was also reported in a previous publication.69 It is therefore likely, that if the current system were tested in a full PEM based electrolyzer system, the electro-catalyst would also potentially exhibit superior electrochemical response. These studies will nevertheless, be planned in the near future and reported in subsequent publications.
5. Conclusions
The present study successfully demonstrates nanostructured solid solution of 10 wt% F doped IrO2 and MnO2 solid solutions denoted as (Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4) with thin film architecture coated on Ti foil as potential anode electro-catalysts for OER in PEM based water electrolysis. The corresponding solid solutions (Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4) with unique electronic/molecular structure showed excellent electrochemical activity with the lowest reported to date, onset potential of ∼1.35 V (vs. RHE) with ∼120 mV overpotential (w.r.t 1.23 V vs. RHE, which is the standard potential for OER), lower than that of IrO2 (∼1.43 V vs. RHE, i.e. ∼200 mV overpotential). In addition, remarkable ∼7, ∼14 and ∼15 fold higher electrochemical activity was obtained for (Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4) than that of pure IrO2, respectively. Additionally, (Mn0.8Ir0.2)O2:10F displayed excellent long term stability in acidic media, similar to that of IrO2. Hence, (Mn1−xIrx)O2:10F (x = 0.2, 0.3, 0.4) indeed shows excellent promise for replacing state of the art OER electro-catalyst (IrO2) based on the excellent electrochemical performance demonstrated in this study. Moreover, this study portends significant reduction in noble metal content for OER electro-catalyst and thus, can likely lead to new electrocatalysts development with significant reduction in capital costs of water electrolysis cells for economic and efficient hydrogen production from acid based PEM water electrolysis.Author contributions
The original concept of the present work is conceived by S. D. G., P. P. P. and P. N. K. based on the earlier project conceived by P. N. K. along with M. K. D. and O. I. V. S. D. G. and P. P. P. performed the synthesis, structural and electrochemical characterization and analyzed the results of structural and electrochemical characterization of electro-catalyst materials. Theoretical study is conducted by O. I. V. P. M. S. performed XPS. S. D. G. and P. P. P. performed analysis of XPS results. S. D. G., P. P. P. and R. K. performed and analyzed SEM-EDX-elemental X-ray mapping results. M. K. D. and P. N. K. made important suggestions in the draft components. S. D. G., P. P. P., M. K. D., O. I. V. and P. N. K. composed first draft of the present paper. All authors contributed extensively in the manuscript revision. The current project was conceived by P. N. K. and was prudently supervised by P. N. K., M. K. D. and O. I. V.Acknowledgements
Authors gratefully acknowledge the support of the National Science Foundation, CBET – Grant 0933141 and CBET – Grant 1511390 for the current research. Acknowledgement is also due to the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award DE-SC0001531 for supporting the early work on substituted IrO2. PNK acknowledges the Edward R. Weidlein Chair Professorship funds, the Center for Complex Engineered Multifunctional Materials (CCEMM) for acquiring the electrochemical equipment and facilities used in the present research work and the Pittsburgh Supercomputing Center for providing the computational resources. P. N. K. and O. I. V. also gratefully acknowledge the Extreme Science and Engineering Discovery Environment (XSEDE)70 supported by National Science Foundation grant number ACI-1053575, for providing the computational resources needed to complete the theoretical component of the present study.References
- M. Ball and M. Wietschel, Int. J. Hydrogen Energy, 2009, 34, 615–627 CrossRef CAS
.
- I. Katsounaros, S. Cherevko, A. R. Zeradjanin and K. J. J. Mayrhofer, Angew. Chem., Int. Ed., 2014, 53, 102–121 CrossRef CAS PubMed
.
- K. Zeng and D. Zhang, Prog. Energy Combust. Sci., 2010, 36, 307–326 CrossRef CAS
.
- J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385 CrossRef CAS PubMed
.
- P. P. Patel, P. J. Hanumantha, O. I. Velikokhatnyi, M. K. Datta, B. Gattu, J. A. Poston, A. Manivannan and P. N. Kumta, J. Mater. Sci. Eng. B, 2016, 208, 1–14 CrossRef CAS
.
- P. P. Patel, P. J. Hanumantha, O. I. Velikokhatnyi, M. K. Datta, D. Hong, B. Gattu, J. A. Poston, A. Manivannan and P. N. Kumta, J. Power Sources, 2015, 299, 11–24 CrossRef CAS
.
- P. P. Patel, M. K. Datta, O. I. Velikokhatnyi, P. Jampani, D. Hong, J. A. Poston, A. Manivannan and P. N. Kumta, J. Mater. Chem. A, 2015, 3, 14015–14032 CAS
.
- M. Fischer, M. Werber and P. V. Schwartz, Energy Policy, 2009, 37, 2639–2641 CrossRef
.
- P. P. Patel, M. K. Datta, O. I. Velikokhatnyi, R. Kuruba, K. Damodaran, P. Jampani, B. Gattu, P. M. Shanthi, S. S. Damle and P. N. Kumta, Sci. Rep., 2016, 6, 28367 CrossRef CAS PubMed
.
- K. Shimura and H. Yoshida, Energy Environ. Sci., 2011, 4, 2467–2481 CAS
.
- N. Himeshima and Y. Amao, Green Chem., 2005, 7, 742–746 RSC
.
- A. T. Marshall, S. Sunde, M. Tsypkin and R. Tunold, Int. J. Hydrogen Energy, 2007, 32, 2320–2324 CrossRef CAS
.
- A. H. A. Rahim, A. S. Tijani, S. K. Kamarudin and S. Hanapi, J. Power Sources, 2016, 309, 56–65 CrossRef
.
- P. Millet, N. Mbemba, S. A. Grigoriev, V. N. Fateev, A. Aukauloo and C. Etiévant, Int. J. Hydrogen Energy, 2011, 36, 4134–4142 CrossRef CAS
.
- S. A. Grigoriev, V. I. Porembsky and V. N. Fateev, Int. J. Hydrogen Energy, 2006, 31, 171–175 CrossRef CAS
.
- A. S. Aricò, V. Baglio, N. Briguglio, G. Maggio and S. Siracusano, Fuel Cells: Data, Facts and Figures, 2016 Search PubMed
.
- X. Lu and C. Zhao, Nat. Commun., 2015, 6, 6616 CrossRef CAS PubMed
.
- J. Xu, M. Wang, G. Liu, J. Li and X. Wang, Electrochim. Acta, 2011, 56, 10223–10230 CrossRef
.
- A. Skulimowska, M. Dupont, M. Zaton, S. Sunde, L. Merlo, D. J. Jones and J. Rozière, Int. J. Hydrogen Energy, 2014, 39, 6307–6316 CrossRef CAS
.
- S. A. Grigoriev, P. Millet and V. N. Fateev, J. Power Sources, 2008, 177, 281–285 CrossRef CAS
.
- Y. Matsumoto and E. Sato, Mater. Chem. Phys., 1986, 14, 397–426 CrossRef CAS
.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed
.
- E. Mayousse, F. Maillard, F. Fouda-Onana, O. Sicardy and N. Guillet, Int. J. Hydrogen Energy, 2011, 36, 10474–10481 CrossRef CAS
.
- K. Kadakia, M. K. Datta, P. H. Jampani, S. K. Park and P. N. Kumta, J. Power Sources, 2013, 222, 313–317 CrossRef CAS
.
- K. S. Kadakia, P. Jampani, O. I. Velikokhatnyi, M. K. Datta, S. J. Chung, J. A. Poston, A. Manivannan and P. N. Kumta, J. Electrochem. Soc., 2014, 161, F868–F875 CrossRef CAS
.
- T. Reier, Z. Pawolek, S. Cherevko, M. Bruns, T. Jones, D. Teschner, S. R. Selve, A. Bergmann, H. N. Nong and R. Schlögl, J. Am. Chem. Soc., 2015, 137, 13031–13040 CrossRef CAS PubMed
.
- J. M. Hu, H. M. Meng, J. Q. Zhang and C. N. Cao, Corros. Sci., 2002, 44, 1655–1668 CrossRef CAS
.
- C. P. De Pauli and S. Trasatti, J. Electroanal. Chem., 1995, 396, 161–168 CrossRef
.
- M. K. Datta, K. Kadakia, O. I. Velikokhatnyi, P. H. Jampani, S. J. Chung, J. A. Poston, A. Manivannan and P. N. Kumta, J. Mater. Chem. A, 2013, 1, 4026–4037 CAS
.
- K. Kadakia, M. K. Datta, O. I. Velikokhatnyi, P. H. Jampani and P. N. Kumta, Int. J. Hydrogen Energy, 2014, 39, 664–674 CrossRef CAS
.
- R. G. Gonzalez-Huerta, G. Ramos-Sanchez and P. B. Balbuena, J. Power Sources, 2014, 268, 69–76 CrossRef CAS
.
- W. Sun, L. Cao and J. Yang, J. Mater. Chem. A, 2016, 4, 12561–12570 CAS
.
- J. Rossmeisl, Z. W. Qu, H. Zhu, G. J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS
.
- O. I. Velikokhatnyi, K. Kadakia, M. K. Datta and P. N. Kumta, J. Phys. Chem. C, 2013, 117, 20542–20547 CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS
.
- J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800–8802 CrossRef
.
- G. N. Murshudov, A. A. Vagin and E. J. Dodson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1997, 53, 240–255 CrossRef CAS PubMed
.
- P. R. Zafred, J. T. Dederer, J. E. Gillett, R. A. Basel and A. B. Antenucci, Google Patents, 1996
.
- H. Hu, Y. Fan and H. Liu, Int. J. Hydrogen Energy, 2009, 34, 8535–8542 CrossRef CAS
.
- J. A. V. Butler, Proc. R. Soc. London, Ser. A, 1936, 157, 423–433 CrossRef CAS
.
- P. P. Patel, M. K. Datta, P. H. Jampani, D. Hong, J. A. Poston, A. Manivannan and P. N. Kumta, J. Power Sources, 2015, 293, 437–446 CrossRef CAS
.
- K. S. Kadakia, P. H. Jampani, O. I. Velikokhatnyi, M. K. Datta, S. K. Park, D. H. Hong, S. J. Chung and P. N. Kumta, J. Power Sources, 2014, 269, 855–865 CrossRef CAS
.
- B. Hammer and J. K. Nørskov, Adv. Catal., 2000, 45, 71–129 CAS
.
- T. Bligaard and J. K. Nørskov, Electrochim. Acta, 2007, 52, 5512–5516 CrossRef CAS
.
- V. Subramanian, H. Zhu, R. Vajtai, P. M. Ajayan and B. Wei, J. Phys. Chem. B, 2005, 109, 20207–20214 CrossRef CAS PubMed
.
- P. P. Patel, P. H. Jampani, M. K. Datta, O. I. Velikokhatnyi, D. Hong, J. A. Poston, A. Manivannan and P. N. Kumta, J. Mater. Chem. A, 2015, 3, 18296–18309 CAS
.
- J. Xu, G. Liu, J. Li and X. Wang, Electrochim. Acta, 2012, 59, 105–112 CrossRef CAS
.
- D. J. Davis, T. N. Lambert, J. A. Vigil, M. A. Rodriguez, M. T. Brumbach, E. N. Coker and S. J. Limmer, J. Phys. Chem. C, 2014, 118, 17342–17350 CAS
.
- M. Sugantha, P. A. Ramakrishnan, A. M. Hermann, C. P. Warmsingh and D. S. Ginley, Int. J. Hydrogen Energy, 2003, 28, 597–600 CrossRef CAS
.
- C. S. Johnson, D. W. Dees, M. F. Mansuetto, M. M. Thackeray, D. R. Vissers, D. Argyriou, C. K. Loong and L. Christensen, J. Power Sources, 1997, 68, 570–577 CrossRef CAS
.
- K. Kadakia, M. K. Datta, O. I. Velikokhatnyi, P. H. Jampani and P. N. Kumta, Int. J. Hydrogen Energy, 2014, 39, 664–674 CrossRef CAS
.
- N. Krstajic and S. Trasatti, J. Appl. Electrochem., 1998, 28, 1291–1297 CrossRef CAS
.
- A. Minguzzi, F.-R. F. Fan, A. Vertova, S. Rondinini and A. J. Bard, Chem. Sci., 2012, 3, 217–229 RSC
.
- P. P. Patel, P. H. Jampani, M. K. Datta, O. I. Velikokhatnyi, D. Hong, J. A. Poston, A. Manivannan and P. N. Kumta, J. Mater. Chem. A, 2015, 3, 18296–18309 CAS
.
- A. M. Mohammad, M. I. Awad, M. S. El-Deab, T. Okajima and T. Ohsaka, Electrochim. Acta, 2008, 53, 4351–4358 CrossRef CAS
.
- F. Cheng, Y. Su, J. Liang, Z. Tao and J. Chen, Chem. Mater., 2009, 22, 898–905 CrossRef
.
- M. Morita, C. Iwakura and H. Tamura, Electrochim. Acta, 1977, 22, 325–328 CrossRef CAS
.
- K. Kadakia, M. K. Datta, P. H. Jampani, S. K. Park and P. N. Kumta, J. Power Sources, 2013, 222, 313–317 CrossRef CAS
.
- R. H. Blessing, Crystallogr. Rev., 1987, 1, 3–58 CrossRef
.
- C. Zhao, H. Yu, Y. Li, X. Li, L. Ding and L. Fan, J. Electroanal. Chem., 2013, 688, 269–274 CrossRef CAS
.
- H. W. Nesbitt and D. Banerjee, Am. Mineral., 1998, 83, 305–315 CrossRef CAS
.
- X. Liang, C. Hart, Q. Pang, A. Garsuch, T. Weiss and L. F. Nazar, Nat. Commun., 2015, 6, 5682 CrossRef PubMed
.
- Z. Li, Y. Mi, X. Liu, S. Liu, S. Yang and J. Wang, J. Mater. Chem., 2011, 21, 14706–14711 RSC
.
- M. A. Stranick, Surf. Sci. Spectra, 1999, 6, 31–38 CrossRef CAS
.
- M. Sathish, B. Viswanathan, R. P. Viswanath and C. S. Gopinath, Chem. Mater., 2005, 17, 6349–6353 CrossRef CAS
.
- K. Kadakia, M. K. Datta, O. I. Velikokhatnyi, P. Jampani, S. K. Park, S. J. Chung and P. N. Kumta, J. Power Sources, 2014, 245, 362–370 CrossRef CAS
.
- K. S. Kadakia, P. H. Jampani, O. I. Velikokhatnyi, M. K. Datta, S. K. Park, D. H. Hong, S. J. Chung and P. N. Kumta, J. Power Sources, 2014, 269, 855–865 CrossRef CAS
.
- J. Towns, T. Cockerill, M. Dahan, I. Foster, K. Gaither, A. Grimshaw, V. Hazlewood, S. Lathrop, D. Lifka and G. D. Peterson, Comput. Sci. Eng., 2014, 16, 62–74 CrossRef
.
Footnotes |
| † This is an abstract presented at the AIChE Annual Meeting, San Francisco, CA, USA (November 14–18, 2016). |
| ‡ The authors have contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2017 |