Open Access Article
Open Access ArticleSpatial summation of the short-term plasticity of a pair of organic heterogeneous junctions†
C. T. Changab,
F. Zeng *ab,
J. X. Liab,
W. S. Dongab,
Y. D. Huab and
G. Q. Lib
*ab,
J. X. Liab,
W. S. Dongab,
Y. D. Huab and
G. Q. Lib
aKey Laboratory of Advanced Materials (MOE), School of Materials Science and Engineering, Tsinghua University, Beijing, 100084, China. E-mail: zengfei@mail.tsinghua.edu.cn
bCenter for Brain Inspired Computing Research (CBICR), Tsinghua University, Beijing 100084, People's Republic of China
First published on 16th January 2017
Abstract
Recent studies have found that responses to electrical stimulations in organic semiconductor and/or electrolyte heterogeneous junctions possess features in common with synaptic plasticity in neural networks. Spatial summation of short-term plasticity was then studied using a pair of such junctions, i.e., Pt/Mg-doped polyethylene oxide (PEO)/Pt and Pt/Mg-doped PEO/poly(3-hexylthiophene-2,5-diyl) (P3HT)/Pt devices. The former displayed short-term depression for charging peaks and short-term facilitation (STF) for discharging peaks, while the latter displayed STF for both the charging and discharging peaks. A simple integration of parallel connection showed that the system displayed frequency selectivity in the weight modification of the charging peaks, i.e., it facilitated below a frequency threshold but depressed at a higher frequency. The frequency threshold varied with input numbers from about 60 Hz to 100 Hz. In contrast, only STF was observed in the weight modifications of the discharging peaks. In addition, the weight modification could be linearly summed from those of the two source devices though the absolute peak currents could not. Our study demonstrates that synaptic computation are feasible for parallel connection system, depending on both input frequency and linear summation of weight modifications. Finally, we suggest that directional selectivity might be realized using the parallel system.
1. Introduction
Recent studies have found that ionic migrations in organic semiconductor and/or electrolyte heterogeneous junctions possess features in common with those in the macromolecules of biological neural networks, particularly in the aspect of responses to electrical stimulations.1–8 Frequency selectivity was found in an organic semiconducting polymer/electrolyte hetero-junction device, i.e., the semiconducting polymer/electrolyte device responded to low-frequency pulses in depression and to high-frequency pulses in potentiation.9,10 A modulation of the semiconducting layer could realize long-term plasticity (memory) from short-term plasticity,6,11 i.e., conventional spike-rate-dependent plasticity (SRDP), a widely discussed learning protocol in neuroscience.12–14 This is because the ionic doping and de-doping at the semiconducting polymer/electrolyte interface is regarded to be modulated by the periodic pulses. If only an ion-doped electrolyte is used as a device, the pulse response varies monotonically with input frequency.8 Since the ionic type can be changed easily in macromolecules, the difference in ionic kinetics becomes the basis of computation. Subsequently, both the charging and discharging peaks of a Ba-doped polyethylene oxide (PEO) electrolyte can be used to mimic two types of short term plasticity (STP) of biological synapses.8 Moreover, both the charging and discharging peaks displayed frequency selectivity in the pulse responses of the Pt/Mg-doped polyethylene oxide (PEO)/poly(3-hexylthiophene-2,5-diyl) (P3HT)/Pt devices.15 On the whole, these studies demonstrate clearly that the ionic kinetics in organic macromolecules relates greatly to signal encoding and handling. Consequently, in one aspect, it is significant to find elemental materials to construct artificial synapses for brain-like computation. In another aspect, it is helpful for establishing a simple system composed of several such elementary devices to explore the principles of computing.Neuroscientists considered that not only the specific synaptic plasticity but also their integration results dominate the operation of the bio-neural system. Enabled by single synapse units in the first place, the synaptic plasticity characteristics are subsequently integrated into a synthetic form by spatial summation through a synaptic net.16 At the same time, the transmitted excitatory post-synaptic currents (EPSCs) are integrated together and diversified into several weight-modified forms as new inputs to the post-synapses.17 They strongly affect the behaviours of the post-synapses, especially in the case of short-term plasticity,16,18,19 which is the basis of signal-processing in a neural system. The short-term plasticity displays two forms, i.e., short-term facilitation (STF) and short-term depression (STD). Facilitation reflects an increase in the probability of neurotransmitter release, while depression reflects a decrease. They could last even for up to hundreds of milliseconds to seconds and could be recorded in the variations of EPSCs. They have inverse impacts on the weights of EPSCs, i.e., either the increase or decrease of EPSCs comparing with those before external stimulations, after the synapses are triggered by the input trains in a neural system. The former and the latter give rise to increasing and decreasing EPSC weights, respectively, along with both the input number and the input frequency.16,20,21 The spatial summation results of STF–STD, STF–STF, and STD–STD generate a variety of weight-modified EPSCs as new inputs to post-synapses, and make them burst differently.16,22 They crucially modify the signal-transmitting process in the bio-synaptic net.16,18,19 Hence, the interactive frame of STP and EPSCs, based on spatial summation has been a vital concern for synaptic computation,16 and should be likewise for simulation of synaptic plasticity.6
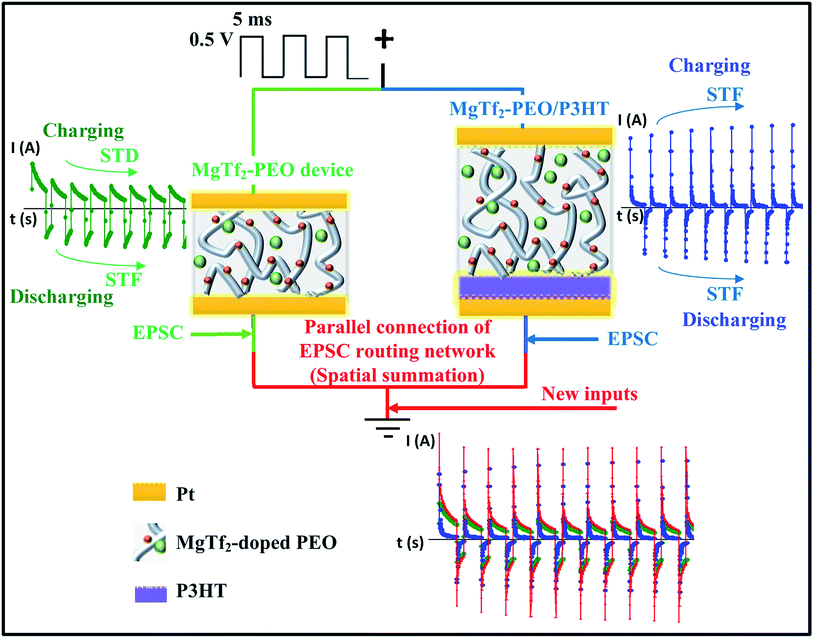
To implement an STP spatial summation, we thought a simple parallel connection between synaptic devices would be a feasible approach to integrate organic STP devices into an EPSC routing network and transform the source signals into a syncretic form in both “strength” and “plasticity” aspects. Following our previous works, we adopted Pt/Mg-doped PEO/Pt and Pt/Mg-doped PEO/P3HT/Pt devices as the sources of the STD and STF synaptic device units, respectively, and integrated them together by parallel connections to study the synaptic spatial summation of STP.
2. Experimental details
Magnesium trifluoromethanesulfonate (Mg(CF3SO3)2, ∼MgTf2, Product no. 337986) was purchased from Sigma-Aldrich Co. Ltd. Polyethylene oxide (PEO, MW = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Product no. 42236) was purchased from Alfa Aesar. Poly(3-hexylthiophene-2,5-diyl) (P3HT, Product no. PT-500C6, MW = 30
000, Product no. 42236) was purchased from Alfa Aesar. Poly(3-hexylthiophene-2,5-diyl) (P3HT, Product no. PT-500C6, MW = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, purity 95%) was purchased from Beijing Synwit Tech Co Ltd. The products were used directly as they were. A 2 wt% MgTf2–PEO aqueous solution was prepared in a 1
000, purity 95%) was purchased from Beijing Synwit Tech Co Ltd. The products were used directly as they were. A 2 wt% MgTf2–PEO aqueous solution was prepared in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 molar ratio with ether oxygen (EO) and Mg. The P3HT was dissolved into a 2-dichlorobenzene as solvent as a 0.5 wt% solution. The solutions were both reserved in sealed containers, subsequently stirred at 40 °C for about 8 h until the chemicals were completely dissolved, and then hermetically preserved in a N2-filled glove box at 28 °C. We conducted the following series of device fabricating processes in the N2-filled glove box with 86 ppm moisture content and 43 ppm oxygen content at about 28 °C. Regarding the MgTf2–PEO device, a MgTf2–PEO single-layered film was prepared by drop-casting a 3 μL MgTf2–PEO solution on the bottom electrode (BE), i.e., a 100 nm-Pt-deposited Si substrate and baked at 100 °C for 20 min before naturally cooling to room temperature (28 °C). With respect to the MgTf2–PEO/P3HT double-layered device, a 3 μL P3HT solution was spin-coated onto the BE at 500, 3000, and 1500 rpm for 10, 30, and 20 s, respectively, in sequence. It was then baked at 140 °C on the heating platform for 1 h and naturally cooled to the 28 °C box temperature. Afterward, a 6 μL MgTf2–PEO solution was drop-casted onto the P3HT layer and baked at 100 °C on the heating platform for 20 min, followed by natural cooling to the 28 °C box temperature. Both the coated MgTf2–PEO/P3HT devices were subsequently removed from the glove box and sent to the ultra-high vacuum facility. They were finalized by an electron-beam depositing Pt (300 μm-diam and 70 nm thick) on top of them as the top electrodes (TEs). Thus, the device is a sandwiched structure with the infinite area of BE and 300 μm-diam of TE, which has been plotted schematically in the previous works.6,8,11
32 molar ratio with ether oxygen (EO) and Mg. The P3HT was dissolved into a 2-dichlorobenzene as solvent as a 0.5 wt% solution. The solutions were both reserved in sealed containers, subsequently stirred at 40 °C for about 8 h until the chemicals were completely dissolved, and then hermetically preserved in a N2-filled glove box at 28 °C. We conducted the following series of device fabricating processes in the N2-filled glove box with 86 ppm moisture content and 43 ppm oxygen content at about 28 °C. Regarding the MgTf2–PEO device, a MgTf2–PEO single-layered film was prepared by drop-casting a 3 μL MgTf2–PEO solution on the bottom electrode (BE), i.e., a 100 nm-Pt-deposited Si substrate and baked at 100 °C for 20 min before naturally cooling to room temperature (28 °C). With respect to the MgTf2–PEO/P3HT double-layered device, a 3 μL P3HT solution was spin-coated onto the BE at 500, 3000, and 1500 rpm for 10, 30, and 20 s, respectively, in sequence. It was then baked at 140 °C on the heating platform for 1 h and naturally cooled to the 28 °C box temperature. Afterward, a 6 μL MgTf2–PEO solution was drop-casted onto the P3HT layer and baked at 100 °C on the heating platform for 20 min, followed by natural cooling to the 28 °C box temperature. Both the coated MgTf2–PEO/P3HT devices were subsequently removed from the glove box and sent to the ultra-high vacuum facility. They were finalized by an electron-beam depositing Pt (300 μm-diam and 70 nm thick) on top of them as the top electrodes (TEs). Thus, the device is a sandwiched structure with the infinite area of BE and 300 μm-diam of TE, which has been plotted schematically in the previous works.6,8,11
The electrical characteristics of the devices were examined by using a semiconductor device analyzer (Agilent B1500A) and an arbitrary function generator (Agilent B1530). Rectangle pulses with an amplitude of 0.5 V, width of 5 ms, and sampling interval of 50 μs were adopted. The testing was performed on a Cascade 150 platform. The compliant current was set at 1 μA and the corresponding bandwidth was 80 kHz. The samples were both preserved and tested in an atmosphere of about 24 °C and 26% humidity. The morphology of the polymer films was examined by crystalline phase images and scanning electrical microscopy.
3. Results and discussions
Fig. 1 shows the responses to 142 Hz, i.e., treated as EPSCs or inhibitory postsynaptic current (IPSCs) in biology,12,20 of the MgTf2–PEO and MgTf2–PEO/P3HT devices, and the parallel connection. The responses of the MgTf2–PEO device varied following trends similar to those reported in previous work. This device possessed a vermiform morphology rather than a general spherulite morphology (Fig. S1†).8 The charging peak decreased gradually with the pulse number to a stable value, while in contrast, the discharging peak increased. The stable value of the charging peaks decreased with the frequency, and that of the discharging peaks increased with the frequency (as shown in Fig. 2(a)). To a great extent, this makes the device a candidate for a short-term depression (STD) device in the charging condition and for a short term facilitate (STF) device in the discharging condition. We fitted both the charging peaks and the discharging peaks using capacitive exponential functions (Fig. S2†),6,8 and found that the time constant varied greatly when the Ba2+ ion was substituted by the Mg2+ ion. For the first charging peak, responding to the 142 Hz pulse, the time constant of τ1 was about 9.81 × 10−5 s and τ2 is about 1.38 × 10−3 s.8 These two values changed to 4.20 × 10−4 s and 3.99 × 10−3 s after the Ba ions were replaced by Mg ions. For the first discharging peak responding to the 142 Hz pulse, the time constant of τ1 varied from 9.54 × 10−5 s to 2.81 × 10−4 s and that of τ2 varied from 1.52 × 10−3 to 4.24 × 10−3 s.8 The larger time constant indicated that the migration length was longer for the Mg ions because of the smaller atomic size and vermiform morphology of MgTf2–PEO (Fig. S1†).The responses of the MgTf2–PEO/P3HT device differed from those of the MgTf2–PEO device. Both the charging peaks and the discharging peaks increased with the pulse number as shown in Fig. 1 and 2(b), which makes it a reasonably suitable STF device candidate in the above two loading conditions.8,20 The discharging peaks potentiated but the charging peaks depressed under the consecutive pulse stimulations, though the discharging relaxation differed from the charging relaxation in both strength and time constant.8 The potentiation of the charging peaks was once observed at certain frequencies or voltage amplitudes for the MgTf2–PEO/P3HT device,15 which was thought to result from the ionic-pair effect at the interface, elongating the charging time and enhancing the charging voltage. However, since the MgTf2–PEO/P3HT device in this study did not crystallize fully (Fig. S1†), the negative differential resistance (NDR) effect disappeared during the positive loading process.15 The laterally ionic diffusion at the interface weakened the reverse electric field.15 Thus, the ionic-pair effect still played a main roles in the potentiation of the charging peaks for this MgTf2–PEO/P3HT device, which needs to be characterized using an effective method.
When connected together in parallel (Fig. 1), the transmitting signals from the MgTf2–PEO device and the MgTf2–PEO/P3HT device immediately overlapped without any time lag, which fairly equates to the biological situation when two synapses burst simultaneously, transmitting new inputs toward a common post-synapse.16,23 Meanwhile, the charging and discharging conditions could be treated as signals responding to the pre- and the post-directions, respectively. The former represents the spatial summation of the STD and STF synapses, and the latter the two STF synapses.8 To examine the strength and variation of the response pulses, the values of the charging and discharging peaks were transformed into weight modification values, with the formulae Wci,f = Ici,f/Ic1,f and Wdi,f = Idi,f/Id1,f, respectively, where i represents the input number, f represents the input frequency, and I represents the value of the peak current. Wc1,f and Wd1,f are equal to 1 and regarded as the baseline weights. Thus, the objective was to simulate the operation of spatial summation in both “signal strength” and “plasticity” aspects.
3.1 Charging system: spatial summation of STD and STF devices
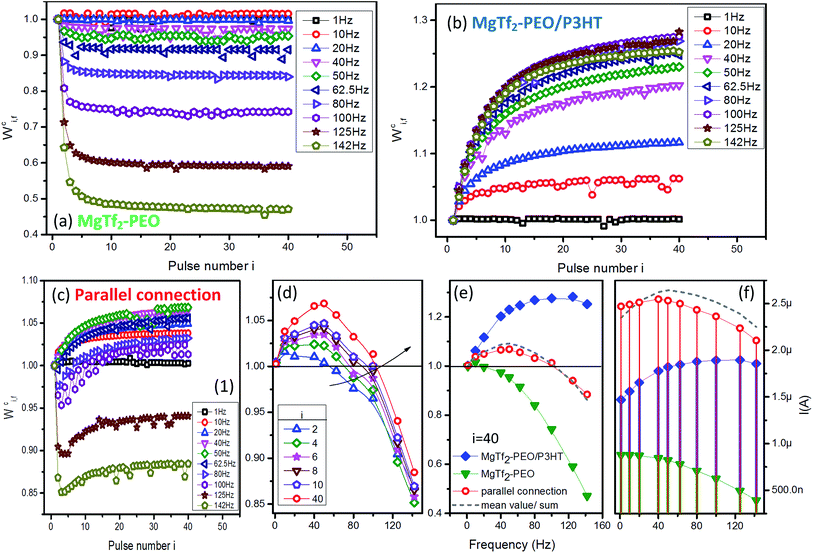
The weight modification forms of the charging peaks for various frequencies are demonstrated in Fig. 2. Regarding the MgTf2–PEO device, the peak weight value Wci,f>1 Hz decayed rapidly during the first few input pulses (Fig. 2(a)) and Wc40,142 Hz left less than half of the baseline weight (Fig. 2(e) green-triangular line). On the other hand, Wci,f>1 Hz of the MgTf2–PEO/P3HT device increased gradually along with the pulse number (Fig. 2(b)) accompanied by Wc40,80 Hz, reaching a significantly larger value than that of the baseline weight, and descending slightly at 142 Hz (Fig. 2(e), blue-diamond line).With the paralleled connection, the plasticity of the two opposite source, i.e., STD and STF, predominated the weight modifications in the specific frequency sections and response ordinals. On the one hand, for the STF effect of the source MgTf2–PEO/P3HT device, the larger the input number was, the wider the facilitation effect toward the high-frequency section. The facilitation zone (Wci,f > 1) was broadened from the 1–62.5 Hz section (i = 2) to 1–100 Hz section (i = 40) within 40 inputs (Fig. 2(d), where Wc40,50 Hz reached the highest potentiating weight value). Wc40,f>50 Hz sequentially declined toward the baseline weight with the frequency (Fig. 2(d), red-circle line). On the other hand, for the STD effect of the source MgTf2–PEO device, the depression effect worked quite well at the input frequency above 100 Hz, as well as the first few responses above 62.5 Hz. Wci,f>100 Hz was not capable of recovering back to the baseline weight with the pulse number, similar to Wci,f>62.5 Hz staying in the depression zone (Wci,f < 1) during the first few input pulses (Fig. 2(c) to (e)). On the whole, the STD–STF routing network featured conspicuous “frequency selectivity” – STD and STF respectively predominated the plasticity of certain frequency sections, whose range were changeable until the input ordinal was large enough for the responses to saturate.
Comparing weight value Wc40,f before and after the parallel connection (Fig. 2(e)), the values examined in the parallel connection (red-circle line) were approximately identical to the mean values of the two source devices (grey-dash line). The mean-value idea introduced a new, meaningful angle for analysis: it is reasonable to regard the weight of the paralleled signal as the “offset result” of those of the source STD and STF signals. However, the actual current values of the artificial synapses (Fig. 2(c) and (f)), the paralleled one (red-circle line) and the sum of the source individuals (grey-dash line) were apparently different although they shared the same current magnitude. This phenomenon demonstrated that the paralleled current did not result from the simple linear overlap of the source currents, but from a nonlinear overlap,24,25 which could be attributed to the inductance effect of the ionic capacitance. It is consistent with the signal-processing work of a bio-synaptic network: the new input propagating into the post-synapse is nonlinearly transformed from the spatial summation of the pre-synaptic signals.26–28
Overall, the parallel-connected system constructed a charging routing network of spatially-summed EPSCs in both “strength” and “plasticity” aspects; it not only generated new signals using nonlinear overlap, but made the source STD and STF experience distinct offset processes according to the input ordinals. The characteristics of the source STPs ended up being reversed for the new input with a connotative, novel outlook: frequency selectivity, i.e., facilitating in the low-frequency section and depressing in the high-frequency section. Consequently, the parallel-connection measure could be regarded as a promising approach to create new inputs with diverse frequency selectivity as long as the source synaptic devices characterized STD and STF properties with the appropriate weight magnitude and variation. Such weight modifications depend greatly on the type of ions, as shown in Fig. S3.† The frequency selectivity also appeared, but its threshold varied with the doping ions. Several models of the operable frequency selectivity are categorized in Fig. S5.†
3.2 Discharging system: spatial summation of STF devices
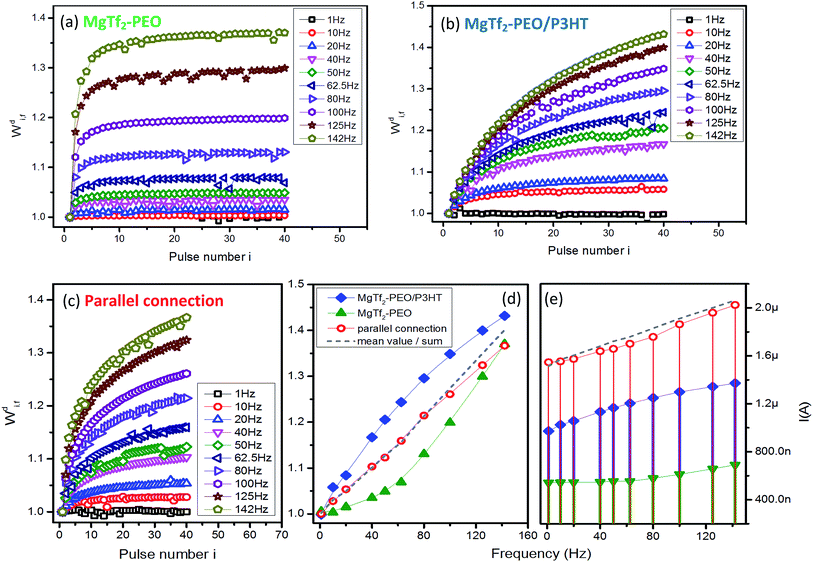
The responding results of source devices MgTf2–PEO and MgTf2–PEO/P3HT and their parallel routing network in the discharging system are demonstrated in Fig. 3. The two STFs responded in a distinct facilitating rate; the signals of the former enhanced instantly to saturation in the first few input pulses (Fig. 3(a)) and those of the latter varied gradually with the pulse number instead (Fig. 3(b)). Since the two individual devices responded in the facilitation, the parallel connection simply regulated their mean value in the weight modification and response current (Fig. 3(d) and (e)), and did not induce the frequency selectivity as in the case of the STD-STF synaptic pair. The results in Fig. 3(d) indicate that the offset concept is still valid, because the mean value (grey-dash) is compatible with that of the parallel connection (red-circle). However, the response current (red-dot in Fig. 3(e)) deviates from the linear average value (grey-dash in Fig. 3(e)).The results in Fig. 2 and 3 demonstrate clearly and further that the systems might be useful in transferring signal bi-directionally. The results in Fig. 2(e) and 3(d) also demonstrate that the synaptic computation is feasible on the basis of diversity of the weight modifications.16 However, it is unknown how the computation is processed and what computing principal is. Superlinear and sublinear summation, of which the current summation deviates from linear overlapping of individual source devices, have been reported in neuroscience.24,29 Such a current overlapping cannot be described by using definite function, suggesting the difficulty to obtain precise quantitative calculation. Our results indicate that the linear summation of synaptic weight might be an elementary computation principal, which need to be examined in more systems and measurement situations.
3.3 Directional selectivity
For the ion-migration dominate system, the resistance, capacitance and inductance all vary with the input stimulation, which is a problem for analysis. However, the features resembling those observed in biology suggest great potential in application. Considering that the weight modifications can linearly overlap in certain condition as shown in Fig. 2 and 3, we simply handle the data to examine the possibility that whether the system has the directional selectivity discussed intensively in neuroscience. Normally, the bursting time lag between the source synapses critically determines the spatial summation and the resulting new inputs in the bio-neuron system,30 which is called direction selectivity and functions by staggering the overlap timing of the EPSCs from different sources.The new analogue inputs generated by staggering the overlap are demonstrated in Fig. 4. The 142 Hz charging peaks of the MgTf2–PEO/P3HT device were held back 1–6 pulses, i.e., 1–6 lag units, and were linearly overlapped with those of the MgTf2–PEO device. It was equivalent to the situation when an STF synapse bursts before an STD synapse during spatial summation (Fig. 4(a) and (b)). Compared with the new inputs without any lag unit (Fig. 4(b), black line), the ones with 1–6 lag units stayed in the facilitation zone rather than the depression one. Their Wci,142 Hz not only varied more drastically with the response number but also experienced an instant hunch, which was beneficial for reaching the bursting threshold of the post-synapse, before saturation.16
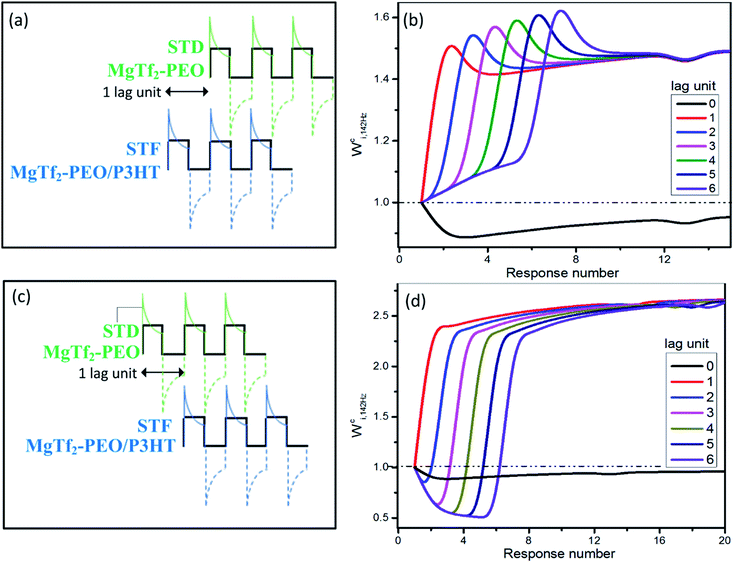 | ||
| Fig. 4 The new analogue inputs generated by staggered overlapping for directional selectivity. The 142 Hz charging responses in Fig. 2(a) and (c) were linearly integrated together with 0–6 lag units. ((a) and (b)) The responses of the MgTf2–PEO device (STD device) lagged 0–6 units behind those of the MgTf2–PEO/P3HT device (STF device). This corresponds to the situation when an STD synapse bursts after an STF synapse. ((c) and (d)) The responses of the MgTf2–PEO/P3HT device (STF device) lagged 0–6 units behind those of the MgTf2–PEO device (STD device). It corresponds to the situation when an STF synapse bursts after an STD synapse. | ||
On the other hand, Fig. 4(c) and (d) demonstrate the situation when an STD synapse (MgTf2–PEO device) bursts before an STF synapse (MgTf2–PEO/P3HTdevice). The Wci,142 Hz of the new charging inputs (2–6 lag units) varied dramatically. It first stayed in the depression zone, then instantaneously rose toward the facilitation zone, and eventually saturated to a value more than twice that of the weight baseline. Such a variegated weight variation assisted the post-synapse to behave diversely.18,19,31 Though the above results had some reference value for simulating directional selectivity, deviations still existed, since the real parallel routing network and the neurobiological spatial summation were nonlinear systems in the current value rather than the linear one in this analogue. Therefore, concrete experiments should be conducted for further verification.
4. Conclusions
We fabricated Pt/Mg-doped PEO/Pt and Pt/Mg-doped PEO/P3HT/Pt devices, and studied their pulse responses and synaptic plasticity. The former displayed STD for the charging peaks and STF for the discharging peaks, while the latter displayed STF for both the charging and discharging peaks. We integrated them together simply by a parallel connection to study the synaptic spatial summation of STP. Frequency selectivity appeared in the weight modification of the charging peaks, i.e., it facilitated below a frequency threshold but depressed at a higher frequency. The threshold of the frequency selectivity varied with the input numbers from about 60 Hz to 100 Hz. In contrast, only facilitate was observed in the weight modification of the discharging peaks. In addition, we found that the weight modification could be linearly summed from those of the source devices but the absolute peak currents could not. The synaptic computation depends on both the frequency and linear summation of the weight modifications. Finally, we suggest that directional selectivity might be realized using the parallel system.Acknowledgements
This work was supported by National Natural Science foundation of China (Grant No. 51371103 and 51231004), Brain Inspired Computing Research, Tsinghua University (20141080934) and Fund of Key Laboratory of Advanced Materials (MOE).References
- V. E. Shashoua, Nature, 1967, 215, 846–847 CrossRef CAS.
- G. E. Wnek, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 7–14 CrossRef CAS.
- A. Gonzalez-Perez, R. Budvytyte, L. D. Mosgaard, S. Nissen and T. Heimburg, Phys. Rev. X, 2014, 4, 031047 Search PubMed.
- Q. X. Lai, L. Zhang, Z. Y. Li, W. F. Stickle, R. S. Williams and Y. Chen, Adv. Mater., 2010, 22, 2448–2453 CrossRef CAS PubMed.
- A. E. Hady and B. B. Machta, Nat. Commun., 2015, 6, 6697 CrossRef PubMed.
- W. S. Dong, F. Zeng, S. H. Lu, A. Liu, X. J. Li and F. Pan, Nanoscale, 2015, 7, 16880–16889 RSC.
- A. Liu, F. Zeng, Y. D. Hu, S. H. Lu, W. S. Dong, X. J. Li, C. T. Chang and D. Guo, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 831–837 CrossRef CAS.
- C. T. Chang, F. Zeng, X. J. Li, W. S. Dong, S. H. Lu, S. Gao and F. Pan, Sci. Rep., 2016, 5, 18915 CrossRef PubMed.
- F. Zeng, S. H. Lu, S. Z. Li, X. J. Li and F. Pan, PLoS One, 2014, 9, e108316 Search PubMed.
- S. H. Lu, F. Zeng, W. S. Dong, A. Liu, X. J. Li and J. T. Luo, Nano-Micro Lett., 2015, 7, 121–126 CrossRef.
- W. S. Dong, F. Zeng, S. H. Lu, X. J. Li, C. T. Chang, A. Liu, F. Pan and D. Guo, RSC Adv., 2015, 5, 98110–98117 RSC.
- S. M. Dudek and M. F. Bear, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 4363–4367 CrossRef CAS.
- G. Rachmuth, H. Z. Shouval, M. F. Bear and C. S. Poon, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, E1266–E1274 CrossRef CAS PubMed.
- L. N. Cooper and M. F. Bear, Nat. Rev. Neurosci., 2012, 13, 798–810 CrossRef CAS PubMed.
- F. Zeng, S. H. Lu, W. S. Dong, A. Liu, X. J. Li and C. T. Chang, Solid State Ionics, 2016, 287, 42–47 CrossRef CAS.
- L. F. Abbott and W. G. Regehr, Nature, 2004, 431, 796 CrossRef CAS PubMed.
- J. H. Byrne and T. U. o. T. H. S. C. a. H., UTHealth, 1997, vol. 2015.
- S. D. Brenowitz and W. G. Regehr, Neuron, 2005, 45, 419–431 CrossRef CAS PubMed.
- D. V. Buonomano and M. M. Merzenich, J. Neurophysiol., 1998, 80, 1765–1774 CAS.
- J. S. Dittman, A. C. Kreitzer and W. G. Regehr, J. Neurosci., 2000, 20, 1374–1385 CAS.
- R. S. Zucker and W. G. Regehr, Annu. Rev. Physiol., 2002, 64, 355–405 CrossRef CAS PubMed.
- W. Rall, J. Neurophysiol., 1967, 30, 1138–1168 CAS.
- S. H. Chung, X. Li and S. B. Nelson, Neuron, 2002, 34, 437–446 CrossRef CAS PubMed.
- A. Polsky, B. W. Mel and J. Schiller, Nat. Neurosci., 2004, 7, 621–627 CrossRef CAS PubMed.
- C. J. Wan, L. Q. Zhu, Y. H. Liu, P. Feng, Z. P. Liu, H. L. Cao, P. Xiao, Y. Shi and Q. Wan, Adv. Mater., 2016, 28, 3557–3563 CrossRef CAS PubMed.
- Y. Zheng, J. J. Luo, S. Harris, A. Kennerley, J. Berwick, S. A. Billings and J. Mayhew, NeuroImage, 2012, 63, 81–94 CrossRef PubMed.
- J. Hao, X. D. Wang, Y. Dan, M. M. Poo and X. H. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 21906–21911 CrossRef CAS PubMed.
- W. Rall, J. Neurophysiol., 1967, 30, 1138–1168 CAS.
- N. Spruston and W. L. Kath, Nat. Neurosci., 2004, 7, 567–569 CrossRef CAS PubMed.
- S. Carver, E. Roth, N. J. Cowan and E. S. Fortune, PLoS Comput. Biol., 2008, 4, e32 Search PubMed.
- W. G. Regehr, Cold Spring Harbor Perspect. Biol., 2012, 4, a005702 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27406d |
| This journal is © The Royal Society of Chemistry 2017 |