Open Access Article
Open Access ArticleField-induced formation and growth of pillars on films of bisphenol-A-polycarbonate
Yu-Fan Chuanga,
Jyun-siang Penga,
Fuqian Yangb,
Donyau Chiangc and
Sanboh Lee *a
*a
aDepartment of Materials Science and Engineering, National Tsing Hua University, Hsinchu 300, Taiwan. E-mail: sblee@mx.nthu.edu.tw; Fax: +886-3-5719677; Tel: +886-3-5719677
bDepartment of Chemical and Materials Engineering, University of Kentucky, Lexington, KY 40506, USA
cInstrument Technology Research Center, National Applied Research Laboratories, Hsinchu, 30076, Taiwan
First published on 30th January 2017
Abstract
An electric field is used to construct pillars on films of bisphenol-A-polycarbonate (BPAPC) between two parallel electrodes. Both the size and density of the pillars are dependent on the film thickness. For the same experimental conditions, thicker films will lead to the formation of pillars of larger sizes and smaller densities. The time dependence of the average diameter of the pillars is found to be a linear function of the square root of the difference between the annealing time and incubation time. The temperature dependence of the temporal evolution of the pillars follows the Arrhenius relation with an activation enthalpy of 121.5 kJ mol−1. Increasing the film thickness and electric field intensity leads to the decrease of the characteristic wavenumber for the surface patterns at the same annealing temperature. There is a larger change in the film thickness for a thinner film than that of a thicker film after the formation of pillars under the same experimental conditions.
1. Introduction
Surface instability of polymer films on relatively rigid substrates can lead to the phenomenon of self-organization via a dewetting process. The self-organization generally involves four steps:1 (1) formation of local defects/holes (local rupture of polymer films), (2) growth of defects/holes, (3) coalescence of holes, and (4) formation of isolated islands/droplets. The driving force for the dewetting process is the decrease of resultant surface energy. To assist and control the surface instability of polymer films in forming well-organized surface structures, various techniques, including evaporation,2,3 electric field,4–6 thermal gradient,7,8 acoustic dispersion force,9 LISA,10,11 and surface stress and surface tension,12,13 have been developed. All of these techniques have led to the change of the driving force for the dewetting process, which determines the motion of contact line and formation of well-organized surface structures.Using the structure of parallel plates of small gaps, Chou and Zhang10 observed the self-formation of well-organized supramolecular (micrometer scale) pillar arrays from a thin, single-homopolymer film melt, and suggested that the pillar formation is due to the surface instability induced by the electric charges on the surface of initially smooth single-homopolymer film melt. Instead of using the structure of parallel plates, Schäffer et al.14 constructed a wedge-like structure with one plate coated with a polymer film (PMMA, PS, and PBrS) of liquid state, and studied the surface instability of the polymer film under the action of electric field. Leach et al.5 constructed closed-cell structures from field-induced instability of PMMA/PS. Forming a capacitor-like structure from parallel plates of a patterned plate and a p-type silicon substrate and using field-induced surface instability, Tian et al.15 constructed “irregular” surface patterns on mr-NIL 6000E. They observed three possible surface patterns: (1) spatially under-modulated, (2) spatially fine-modulated, and (3) spatially over-modulated. Wu et al.16 studied the effect of electric field on the coarsening of PDMS pillars and found that there are two regimes for the coarsening of the PDMS pillars; a linear growth regime and a logarithmic growth regime for the average diameter of the PDMS pillars. Most studies have been focusing on the field-induced formation of pillars, and there are few reports on the growth behavior of the pillars formed between two parallel plates under the action of an electric field.
The field-assisted formation of well-organized surface structures on polymer films is due to electromechanical interaction between electric field and polymer films, which exerts electric stresses onto the surface of the polymer films and introduces local surface instability, as observed first by Tonks17 in studying the field-induced surface rupture of liquid. The competition among electric stresses, disjoining pressure and surface tension on the polymer films plays an important role in the initiation and growth of local instability. There are various studies on the field-induced surface instability from the framework of viscous flow16,18–21 and viscoelasticity22,23 in order to understand the mechanisms controlling the formation of well-organized surface structures. Wu and Chou22 concluded that the resonant phenomenon associated with field-induced surface instability of viscoelastic films is dependent on electrostatic force and polymer elasticity. Recently, Peng et al.24 developed a simple model for field-induced growth of a liquid pillar between two parallel electrodes, and obtained a quadratic relationship between time and the diameter of the pillar.
Using thermal-induced dewetting of Au nanofilms on poly(methyl methacrylate) underlying layers, Ruffino et al.25 constructed Au nanostructures on PMMA films. Considering the progress in flexible electronics and the potential applications of metallic surface structures on polymer substrates in automobile and aerospace, the field-induced formation and growth of pillars on BPAPC (bisphenol-A-polycarbonate) films between two parallel plates is investigated. The study is focused on the temporal evolution of the diameter of the pillars. The effects of temperature and electric field intensity are studied, and the temporal evolution of the film thickness is also examined.
2. Experimental detail
The material used in this work was BPAPC (Lexan™ 9030-112, General Electric Company, San Diego, CA, USA) with average molecular weight of 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 and the polydispersity index of 1.65. BPAPC was dissolved in chloroform to form BPAPC solutions of different concentrations. The BPAPC solutions were continuously stirred for 2 h at 25 °C, and PTFE (polytetrafluoroethylene) membranes (Pall Corp., Port Washington, New York) with the pore size of ∼200 nm was used to remove un-dissolved impurity in the solutions.
000 g mol−1 and the polydispersity index of 1.65. BPAPC was dissolved in chloroform to form BPAPC solutions of different concentrations. The BPAPC solutions were continuously stirred for 2 h at 25 °C, and PTFE (polytetrafluoroethylene) membranes (Pall Corp., Port Washington, New York) with the pore size of ∼200 nm was used to remove un-dissolved impurity in the solutions.
Si (100) wafers of p-type with a thickness of 525 μm (Summit-Tech, Hsinchu, Taiwan) were used as the substrates for parallel capacitors. Spacers of dielectric SiO2 with 670 nm in thickness and 1 mm in width were formed on Si wafers, which were sliced into Si plates of 1 × 1 cm2 with the spacers of 0.5 cm apart. An Au film of ∼40 nm in thickness was coated on the rear side of the Si plates using a Pelco SC-6 sputter coater (Ted Pella Inc., Redding, CA, USA) at a pressure of 0.5 mbar and an electric current of 0.5 mA.
Using a spin-coating process, BPAPC thin films were coated on the surface of the Si plates at 25 °C. The spin-coating was performed on a spin coater (SWIENCO PM-490) at 4000 ± 50 rpm for 20 s. The thicknesses of the BPAPC thin films were obtained from different solution concentrations. Parallel capacitors were made from the Si plates, in which the Si plates with the BPAPC thin films were used as the bottom-electrode.
Surface treatment of the Si plates, which were used as the top-electrodes of the parallel capacitors, was performed to form a self-assembled monolayer. For detailed information of the surface treatment, see the work by Peng et al.24 A single molecular layer of n-octadecyltrichlorosilane was formed on the surface of the Si plates after the surface treatment to reduce the adhesion between the top electrode and the BPAPC pillars induced by electric field for easy separation. An Au film of ∼40 nm in thickness was also coated on the rear side of the Si plates after the surface treatment at a pressure of 0.5 mbar and an electric current of 0.5 mA.
An electrostatic field was applied to the parallel capacitors made from the Si plates with the BPAPC films as the bottom electrode (cathode) and the Si plates with a single molecular layer of n-octadecyltrichlorosilane as the top electrode (anode) using a DC power (PPS-2018A, Taiwan). The parallel capacitors were placed in a furnace (DV-303 Channel, Taiwan) in air with the temperature ranging from 180 to 210 °C. After finishing the field-assisted process, the parallel capacitors were removed immediately from the furnace and quenched by spreading cold air. This process avoided the possible effects of the flow of BPAPC at high temperatures on the geometrical changes of the pillars.
The surface topology of the field-induced surface structures was examined, using an optical microscope (Olympus Optical Co., Tokyo, Japan) and an atomic force microscope (AFM) (Dimension ICON®, Bruker, Billerica, MA, USA) at a tapping mode. The spring constant of the AFM tips was ∼42 N m−1, and the resonance frequency was 330 kHz. The AFM software, Gwyddion (Czech Metrology Institute, Brno, Czech Republic), and Image J (National Institute of Health, Bethesda, MD, USA) were used to analyze the surface patterns. The functional group in bulk BPAPC, which was prepared by hot press at 200 °C, was analyzed using FTIR (Fourier transform infrared spectroscopy) (Nicolet Nexus 320 FTIR, Thermo Fisher Scientific, Waltham, MA, USA).
3. Results and discussion
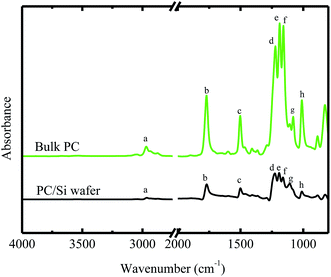
Fig. 1 shows the FTIR spectra of the bulk BPAPC. A number of characteristic bands were assigned and listed in Table 1. The wavenumbers for the peaks presented in the FTIR spectra of bulk BPAPC are 2968 cm−1, 1772 cm−1, 1502 cm−1, a group of 1222, 1188 and 1158 cm−1, 1080 cm−1, and 1010 cm−1, which correspond to the stretching mode of single C–H bond, the stretching mode of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, the stretching mode of aromatic C
O, the stretching mode of aromatic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, the asymmetrical stretching mode of O–C–O bond, the ring mode of aromatic C–H bond, and symmetrical stretching mode of O–C–O bond, respectively. According to the work of Apai and McKenna,26 the wavenumbers for the peaks in FTIR spectra are 2874 and 2970 cm−1 for the stretching mode of C–H bond, 1775 cm−1 for C
C bond, the asymmetrical stretching mode of O–C–O bond, the ring mode of aromatic C–H bond, and symmetrical stretching mode of O–C–O bond, respectively. According to the work of Apai and McKenna,26 the wavenumbers for the peaks in FTIR spectra are 2874 and 2970 cm−1 for the stretching mode of C–H bond, 1775 cm−1 for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration of carbonate group, 1505 cm−1 for the stretching mode of aromatic C
O stretching vibration of carbonate group, 1505 cm−1 for the stretching mode of aromatic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, a group of 1165, 1195, and 1235 cm−1 for asymmetrical stretching mode of O–C–O bond, 1080 cm−1 for ring mode of aromatic C–H bond, and 1015 cm−1 for symmetrical O–C–O stretching vibration of carbonate group. The results listed in Table 1 are compatible with the results given by Apai and McKenna for pure BPAPC,26 confirming that the received polymer is chemically the same as pure BPAPC. Fig. 1 also shows the FT-IR spectra of BPAPC coated with silicon wafer with the characteristic wavenumbers being listed in Table 1. From Table 1, one can note that, for the same band, the characteristic wavenumbers for the BPAPC are different from those for the BPAPC coated on silicon wafer. This is attributed to the surface interaction between the BPAPC and the silicon wafer.
C bond, a group of 1165, 1195, and 1235 cm−1 for asymmetrical stretching mode of O–C–O bond, 1080 cm−1 for ring mode of aromatic C–H bond, and 1015 cm−1 for symmetrical O–C–O stretching vibration of carbonate group. The results listed in Table 1 are compatible with the results given by Apai and McKenna for pure BPAPC,26 confirming that the received polymer is chemically the same as pure BPAPC. Fig. 1 also shows the FT-IR spectra of BPAPC coated with silicon wafer with the characteristic wavenumbers being listed in Table 1. From Table 1, one can note that, for the same band, the characteristic wavenumbers for the BPAPC are different from those for the BPAPC coated on silicon wafer. This is attributed to the surface interaction between the BPAPC and the silicon wafer.
| Peak code | Bulk BPAPC | BPAPC with Si wafer | Band assignments |
|---|---|---|---|
| a | 2968 | 2964 | Antisymmetric methyl group C–H stretch |
| b | 1772 | 1770 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration of carbonate group O stretching vibration of carbonate group |
| c | 1502 | 1500 | Aromatic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching C stretching |
| d | 1222 | 1226, 1192, 1162 | Asymmetrical O–C–O stretching vibrations of carbonate group |
| e | 1188 | ||
| f | 1158 | ||
| g | 1080 | 1108 | Aromatic C–H and ring vibrations |
| h | 1010 | 1012 | Symmetrical O–C–O stretching vibration of carbonate group |
AFM was used to examine the surface roughness of the prepared BPAPC films without the action of electric filed. For the film thickness in the range of 30 to 60 nm, the root mean square roughness was in the range of 1.4 to 1.6 nm, suggesting that there were no significant surface features on the surface of the prepared BPAPC films and the films were relatively smooth. One can approximately assume that the field-induced surface structures formed on the smooth surfaces of the prepared BPAPC films.
The surface topologies of the BPAPC films after being subjected to the action of an electric voltage of 30 V at a temperature of 200 °C with different heating times were examined by an optical microscope and an atomic force microscope. Fig. 2 shows optical images of the surface topologies of the BPAPC films of 30, 40, 50, and 60 nm in thickness, respectively, which reveals the field-induced formation of pillars on the BPAPC films.
Both the densities and radii of the pillars increase with increasing the annealing time, similar to the observation by Peng et al.24 and Wu et al.16 Such a trend reveals that BPAPC continuously flows into the pillars after the pillars reach the top electrode, resulting in the radial growth of the pillars, and the driving force is larger than the configuration force associated with the increase in surface energy for the radial growth of the pillars. Also, the field-induced formation and growth of the pillars are dependent on both the film thickness and temperature. At the same temperature, the size of the pillars increases with the increase of the film thickness while the density decreases with the increase of the film thickness for the same heating time.
Fig. 3 shows the corresponding AFM images of the surface topologies of the BPAPC films shown in Fig. 2. The AFM images confirm that the densities and radii of the pillars increase with increasing the annealing time, which were revealed by the optical images. The cross sections of the pillars can be approximated as circular, and there is no significant difference in the radii of the cross section near the bottom electrode and that near the top electrode due to the ultra-small gap between two parallel electrodes. The initial thickness of the BPAPC films has no effect on the height of the formed pillars, which ranges from 180 to 200 nm.
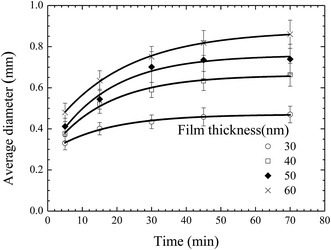
From the AFM images, one can evaluate the time-dependence of the average diameter of the pillars. Fig. 4 shows the temporal evolution of the average diameter of the pillars formed on the BPAPC films of 30, 40, 50 and 60 nm in thickness, respectively, under the action of an electric voltage of 30 V at a temperature of 200 °C. It is evident that the average diameter of the pillars increase nonlinearly with the increase of the annealing time. The electromechanical interaction provides the driving force for the growth of the pillars, which is large enough to force the BPAPC to flow into the pillars and cause the increase of the radii of the pillars.
Fig. 5 shows the temporal evolution of the average diameter of the pillars formed on the BPAPC films of 70 nm in thickness under the action of an electric voltage of 30 V at different temperatures. Increasing the annealing temperature leads to the increase of the average diameter of the pillars for the same annealing time. Such behavior suggests that the growth of the pillars is temperature-dependent in accord with the temperature dependence of the mobility of polymer chains and the viscosity of polymer.
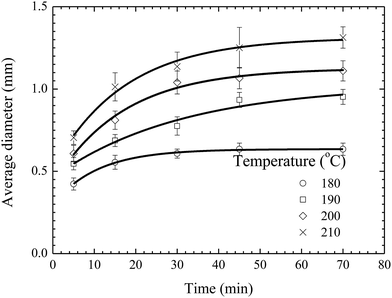 | ||
| Fig. 5 Temporal evolution of the pillars formed on BPAPC films of 70 nm under the action of an electric voltage of 30 V at different temperatures. | ||
Peng et al.24 recently derived an approximate relationship between the average diameter of the pillars and the annealing time as
| 〈D〉 = 〈D0〉 + α(t − t0)1/2 | (1) |
As discussed above, the incubation time is determined by the time interval between the formation of a pillar sandwiched between two electrodes and the onset of the radial growth of the pillar. Increasing temperature will lead to fast formation of a pillar sandwiched between two electrodes, while it may not have a substantial effect on the onset of the radial growth of the pillar. The onset of the radial growth of the pillar is controlled by the electric field and the pressure in the pillar if the surface energy of the pillar is negligible. The electric field is independent of temperature, and the pressure in the pillar is likely weakly-dependent on temperature for a quasi-stationary pillar. Thus, it is reasonable to assume that the temperature dependence of the incubation time is negligible for the experimental configuration and conditions used in this work.
Using eqn (1) with the incubation time of 4 min to curve-fit the experimental data given in Fig. 5, one can obtain the values of the constant α for different temperatures. Note that the fitting curves are included in Fig. 5. From Fig. 4 and 5, one can conclude that eqn (1) can be used to describe the temporal evolution of the pillars formed on BPAPC films of different thicknesses at different temperatures for the experimental conditions used in this work.
Fig. 6 shows the dependence of the average diameter of the pillars with the incubation time of 4 min on the film thickness. The average diameter of the pillars with the incubation time of 4 min linearly increases with the increase of the film thickness. More BPAPC is driven into the pillars for thick films under the action of electric field, leading to the formation of the pillars of large diameters. The constant of α in a range of 0.02 to 0.074 μm min−1/2 is proportional to power 3/2 of the film thickness as expected by Peng et al.24 This result suggests that there exists surface interaction between the polymer films and the substrate, which limits the motion of the polymer chains. Such behavior is similar to the decrease of the glass transition temperature of PMMA thin films with decreasing the film thickness on the native oxide of silicon, as observed by Keddie et al.;27 the hydrogen bonding at the interface between the BPAPC and the silicon substrate restricts the motion of the polymer chains. Comparing the FT-IR spectra of bulk BPAPC and BPAPC coated with the silicon wafer shown in Fig. 1 with the corresponding bands listed in Table 1, the different characteristic wavenumbers of the same band for bulk BPAPC and BPAPC coated with silicon substrate are attributed to the hydrogen bonding between BPAPC and silicon wafer.
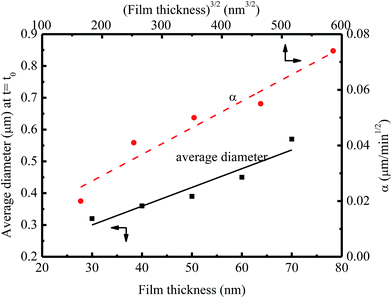 | ||
| Fig. 6 Dependence of the average diameter of the pillars with the incubation time of 4 min on the film thickness at a temperature of 200 °C. | ||
From the theory of thermal activation process, the temperature dependence of the viscosity of polymer can be described by Arrhenius relation as28
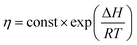 | (2) |
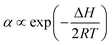 | (3) |
Fig. 7 shows the temperature dependence of the constant of α. Using eqn (3) to curve-fit the experimental data given in Fig. 7, one obtains
α = 3.57 × 105![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−60.75/RT e−60.75/RT
| (4) |
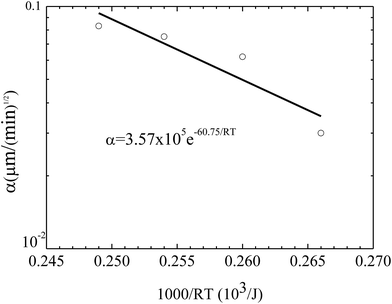 | ||
| Fig. 7 Temperature dependence of the constant α for the growth of the pillars on the BPAPC films of 70 nm under the action of an electric voltage of 30 V. | ||
As shown in Fig. 2 and 3, well-ordered surface patterns were formed on the surface of the BPAPC films under the action of electric field. The spatial characteristics of the surface patterns were analyzed using 2D fast Fourier transform via the software of Image J (National Institute of Health). The FFT diffraction patterns of the surface patterns are depicted in Fig. 8 for the pillars formed on the BPAPC films of four different thicknesses at four different temperatures under the action of an electric field of 30 V. There are only ring-like patterns presented in the FFT diffraction patterns, suggesting that the spatial distribution of the pillars is narrow.
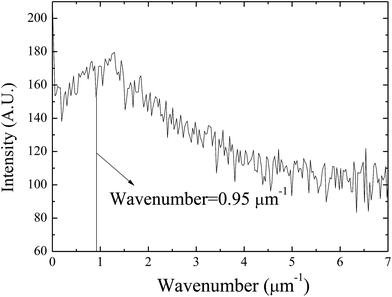
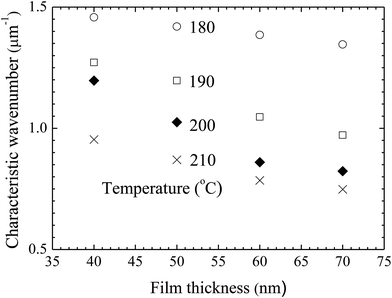
Using the FFT diffraction patterns to calculate the variation of the intensity with wavenumber of the surface patterns, as shown in Fig. 9, for the surface patterns formed on the BPAPC film of 40 nm in thickness at a temperature of 210 °C under the action of an electric field of 30 V, one can determine the characteristic wavenumber for the formed surface structures. The variation of the characteristic wavenumber with the film thickness is shown in Fig. 10 for the surface patterns formed under the action of an electric field of 30 V at four different temperatures with the annealing time of 70 min. For the same electric voltage, the increase of the film thickness and the increase of the annealing temperature cause the decrease of the characteristic wavenumber, qualitatively in accord with the variation of the average density of the pillars on the film thickness. The thicker the film, the larger is the characteristic wavelength.
As discussed above, the formation of the pillars is controlled by the electric field applied to the BPAPC films. It is expected that there exists field-dependence of the geometric characteristics of the formed pillars. Fig. 11 shows the field-dependence of the characteristic wavenumber for the pillars formed on the BPAPC films of 70 nm at four different temperatures with the annealing time of 70 min. Here, the electric field intensity of E was calculated as
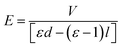 | (5) |
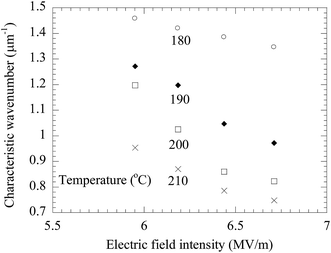 | ||
| Fig. 11 Variation of the characteristic wavenumber with electric field for the surface patterns formed on the BPAPC films of 70 nm at four different temperatures with the annealing time of 70 min. | ||
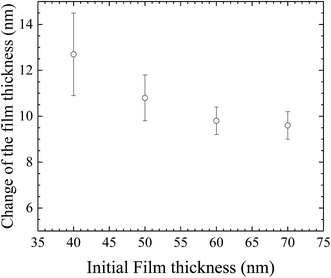
In general, the formation of the pillars between two parallel electrodes will cause the thinning of the film over the space where there are no pillars. Small pieces of the BPAPC films with the pillars were sliced away from the silicon substrates, using a razor blade. AFM was used to measure the thickness of the remained films, at which there are no pillars. Fig. 12 shows the variation of the thickness change with the initial film thickness for the surface patterns formed on the BPAPC films under the action of an electric field of 30 V at a temperature of 200 °C with the annealing time of 70 min. It is evident that there is a larger change in the film thickness for a thinner film than that of a thicker film. Such behavior is due to the limited amount of polymer available for the formation and growth of the pillars. To limit the change of the film thickness due to the formation and growth of the pillars, a relatively thick film is needed.
4. Summary
In summary, the configuration of a parallel capacitor has been used to construct the BPAPC pillars on BPAPC films. Both the size and density of the pillars are dependent on the film thickness. For the same experimental conditions, thicker films will lead to the formation of pillars of larger sizes and smaller densities. Increasing the annealing time allows more BPAPC to flow into the root of the pillars and increase the average diameter of the pillars formed on all BPAPC films of different thicknesses. The time dependence of the average diameter of the pillars is found to be a linear function of the square root of the difference between the annealing time and an incubation time, in accord with the simple relation derived by Peng et al.24 The temperature dependence of the temporal evolution of the pillars follows the Arrhenius relation with an activation enthalpy of 121.5 kJ mol−1. The FFT analysis of the formed pillars reveals the ring-like patterns of the FFT diffraction patterns. There is narrow distribution of the pillar sizes. The characteristic wavenumber of the surface patterns are dependent on the film thickness, annealing time and electric field intensity. Increasing the film thickness and electric field intensity lead to the decrease of the characteristic wavenumber for the surface patterns formed at the same annealing temperature. There is a larger change in the film thickness for a thinner film than that of a thicker film due to the formation of the pillars under the same experimental conditions.Acknowledgements
This work was financially supported by the Ministry of Science and Technology, Taiwan.References
- A. Sharma and G. Reiter, J. Colloid Interface Sci., 1996, 178, 383–399 CrossRef CAS.
- W. Sun and F. Q. Yang, J. Phys. Chem. C, 2014, 118, 10177–10182 CAS.
- W. Sun and F. Q. Yang, Langmuir, 2014, 30, 6548–6555 CrossRef CAS PubMed.
- N. Wu, L. F. Pease and W. B. Russel, Adv. Funct. Mater., 2006, 16, 1992–1999 CrossRef CAS.
- K. A. Leach, S. Gupta, M. D. Dickey, C. G. Willson and T. P. Russell, Chaos, 2005, 15, 047506 CrossRef PubMed.
- N. E. Voicu, S. Harkema and U. Steiner, Adv. Funct. Mater., 2006, 16, 926–934 CrossRef CAS.
- E. Schäffer, S. Harkema, R. Blossey and U. Steiner, Europhys. Lett., 2002, 60, 255–261 CrossRef.
- J. Peng, H. F. Wang, B. Y. Li and Y. C. Han, Polymer, 2004, 45, 8013–8017 CrossRef CAS.
- M. D. Morariu, E. Schäffer and U. Steiner, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, 375–379 CrossRef CAS PubMed.
- S. Y. Chou, L. Zhuang and L. J. Guo, Appl. Phys. Lett., 1999, 75, 1004–1006 CrossRef CAS.
- S. Y. Chou and L. Zhuang, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 1999, 17, 3197–3202 CrossRef CAS.
- C. C. Lin, F. Q. Yang and S. Lee, Langmuir, 2008, 24, 13627–13631 CrossRef CAS PubMed.
- P. Y. Liang, F. Q. Yang and S. Lee, Mater. Chem. Phys., 2012, 135, 168–173 CrossRef CAS.
- E. Schäffer, T. Thurn-Albrecht, T. P. Russell and U. Steiner, Europhys. Lett., 2001, 53, 518–524 CrossRef.
- H. M. Tian, Y. C. Ding, J. Y. Shao, X. M. Li and H. Z. Liu, Soft Matter, 2013, 9, 8033–8040 RSC.
- N. Wu, M. E. Kavousanakis and W. B. Russel, Phys. Rev. E, 2010, 81, 026306 CrossRef PubMed.
- L. Tonks, Phys. Rev., 1935, 48, 562–568 CrossRef.
- D. Bandyopadhyay and A. Sharma, J. Phys. Chem. C, 2010, 114, 2237–2247 CAS.
- K. Mondal, P. Kumar and D. Bandyopadhyay, J. Chem. Phys., 2013, 138, 024705 CrossRef PubMed.
- G. Amarandei, P. Beltrame, I. Clancy, C. O'Dwyer, A. Arshak, U. Steiner, D. Corcoran and U. Thiele, Soft Matter, 2012, 8, 6333–6349 RSC.
- L. F. Pease and W. B. Russel, J. Chem. Phys., 2006, 125, 184716 CrossRef PubMed.
- L. Wu and S. Y. Chou, J. Non-Newtonian Fluid Mech., 2005, 125, 91–99 CrossRef CAS.
- G. Tomar, V. Shankar, A. Sharma and G. Biswas, J. Non-Newtonian Fluid Mech., 2007, 143, 120–130 CrossRef CAS.
- J.-S. Peng, F. Q. Yang, D. Chiang and S. Lee, Langmuir, 2016, 32, 4602–4609 CrossRef CAS PubMed.
- F. Ruffino, V. Torrisi, G. Marletta and M. Grimaldi, J. Appl. Phys., 2012, 112, 124316 CrossRef.
- G. Apai and W. P. McKenna, Langmuir, 1991, 7, 2266–2272 CrossRef CAS.
- J. L. Keddie, R. A. L. Jones and R. A. Cory, Faraday Discuss., 1994, 98, 219–230 RSC.
- F. Q. Yang, Polym. Eng. Sci., 1997, 37, 101–104 CAS.
- G. F. Baumann and S. Steingiser, J. Polym. Sci., Part A: Gen. Pap., 1963, 1, 3395–3406 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |