Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reaction of the hydrogen atom with nitrous oxide in aqueous solution – pulse radiolysis and theoretical study†
Lukasz Kazmierczak ,
Dorota Swiatla-Wojcik
,
Dorota Swiatla-Wojcik * and
Marian Wolszczak
* and
Marian Wolszczak
Institute of Applied Radiation Chemistry, Faculty of Chemistry, Lodz University of Technology, Zeromskiego 116, 90-924 Lodz, Poland. E-mail: swiatlad@p.lodz.pl
First published on 27th January 2017
Abstract
UB3LYP/cc-pVTZ computations using C-PCM, IEF-PCM, and SMD water-solvent models have been performed for the reaction of the H˙ atom with nitrous oxide (N2O) producing N2 and ˙OH in aqueous solution. The H˙ atom attacks the oxygen atom in the N2O molecule resulting in the formation of the [H–ONN]‡ transition state and its decomposition into ˙OH and N2. This direct path requires 54.2 kJ mol−1 (PCM) or 54.6 kJ mol−1 (SMD) compared to 53.0 kJ mol−1 in a vacuum. The H˙ atom addition to the nitrogen end leads to the [H–NNO]‡ transition state decaying to a cis-HNNO intermediate that after transformation to [NNOH]‡ finally produces ˙OH and N2. The total energy expense associated with the indirect mechanism, 67.6 kJ mol−1 (PCM) or 65.5 kJ mol−1 (SMD), is slightly smaller compared to 67.7 kJ mol−1 computed for the reaction in vacuum. The temperature dependence of the reaction rate constant obtained based on the pulse radiolysis measurements in N2O-saturated 0.1 M HCl solution over the temperature range of 296–346 K shows the activation energy (62.6 ± 2.1) or (59.9 ± 2.1) kJ mol−1 depending on a form of the pre-exponential factor in the Arrhenius equation, A or A′ × T, respectively. The activation energy, almost three times higher than observed in gases at temperatures below 500 K, indicates predominance of the direct reaction path via [H–ONN]‡. The indirect mechanism may also contribute, but in contrast to the gas phase reaction neither tunnelling from [H–NNO]‡ to [NNOH]‡ nor collisional stabilization of [H–NNO]‡ occurs in solution.
1. Introduction
Rate and mechanism of reactions initiated by N2O in aqueous solutions are of growing interests because of the environmental impact of N2O and its various applications in chemistry, biology, and medicine. Emissions of N2O due to industrial processes and extensive use of fertilizers1 contribute either to ozone depletion in the stratosphere2 or to the greenhouse effect.3 Medicinal, technical and industrial applications of N2O result from its anaesthetic and analgesic effects, an inert character and the ability to be a donor of nitrogen and oxygen atoms in chemical reactions. Synthetic chemistry with N2O in homogenous solution,4 utilization of N2O as a whipping agent or fuel additive,5 and its role in water remediation by the electron beam treatment6 have been recently reviewed. In a class of advanced oxidation processes (AOPs) ionising radiation has been successfully used to generate hydroxyl radicals for degradation of such hazardous pollutants as chlorpyrifos,7 4-chloroaniline,8 or primidone.9 Saturation of water with N2O is used to transform the main reducing radiolytic products, hydrated electrons (eaq−) into ˙OH radicals, thus increasing their concentration in solution.The reaction of H˙ with N2O was thoroughly examined in the gas phase in view of its occurrence in combustion chemistry.10–14 Compilation of evaluated kinetic data in the temperature range of 350–2500 K, was provided by Baulch et al.15 In contrast to the gas phase, very little is known on the reaction occurring in aqueous solution. The kinetic data on this reaction in solution are available for ambient conditions only, and the reported values of the room temperature rate constant are very divergent, ranging from 1 × 103 to 2 × 106 M−1 s−1. In our earlier paper a critical test of the room temperature data was carried out.16 In a series of pulse radiolysis experiments we traced the decay of dichloride radical ion (Cl2˙−) in N2- and N2O-saturated 0.1 M HCl aqueous solution, attributing the slower decay in N2O-saturated system to the reaction of H˙ with N2O. The obtained room temperature value of the reaction rate constant, (9 ± 2) × 104 M−1 s−1, is about ten times higher than kg = 6.2 × 103 M−1 s−1 calculated from eqn (1), which is recommended for the gas phase reaction.15
kg [M−1 s−1] = 3.31 × 107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2560/T) + 7.83 × 1011 exp(−2560/T) + 7.83 × 1011![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−9750/T) exp(−9750/T)
| (1) |
The quantum chemical computations of the reaction in vacuum shows two reaction paths13 described by eqn (2) and (3). Path (2) refers to the H˙ atom attack on the oxygen atom in the N2O molecule and leads to the formation of the [H–ONN]‡ transition state decomposing into ˙OH and N2.
| H˙ + N2O → [H–ONN]‡ → ˙OH + N2 | (2) |
Path (3) corresponds to the H˙ atom addition to the nitrogen end to form [H–NNO]‡ and then cis-HNNO, which may either isomerise to stable trans-HNNO, or produce N2 and ˙OH via the [NNOH]‡ transition state.
 | (3) |
Given the above the following questions arise: (i) what is the temperature dependence of the reaction rate constant in solution and (ii) what is the solvent effect on the reaction mechanism. To the best of our knowledge these problems have never been discussed. With the aim to fill this gap, our kinetic measurements have been extended here up to 346 K and combined with quantum chemical calculations carried out for the reaction in vacuum and in solution. The experimental procedure is presented in Sec. 2 and processing of the acquired kinetic data is described in Sec. 3. The DFT computations at the UB3LYP/cc-pVTZ level of theory assuming C-PCM, IEF-PCM, and SMD solvent models are described in Sec. 4, and the solvent effect on the reaction kinetics and mechanism is discussed in Sec. 5. The summary and conclusions are given in Sec. 6.
2. Pulse radiolysis measurements
Pulse radiolysis measurements were carried out using the same experimental setup as before.16 The duration of electron beam pulses delivered from the 6 MeV ELU-6 linear accelerator was 7 or 17 ns, giving the dose of (14.0 ± 0.4) Gy or (46.5 ± 1.4) Gy respectively, as evaluated using N2O-saturated 0.01 M solution of potassium thiocyanate (KSCN) as the dosimeter and taking Gε475 = 5.28 × 10−4 m2 J−1.17 The stock 0.1 M HCl aqueous solutions were deoxygenated by purging with high purity N2O and then irradiated. In this system the hydroxyl radical is rapidly converted to Cl2˙−.18 Comparative measurements have been also carried out for N2-saturated solutions. The decay of Cl2˙− absorbance was traced over the temperature range of 296–346 K at 340 nm being the absorption maximum of Cl2˙−. The molar absorption coefficient ε340 = 960 m2 mol−1 (ref. 19) was assumed for all temperatures. The optical absorption was recorded using a monochromator ARC SpectraPro275, a photomultiplier R 928 Hamamatsu Photonics and an oscilloscope Tektronix TDS 500 MHz. The optical path of the cell was 1 cm.3. Kinetic data processing
Diffusion-kinetic modelling of spur chemistry
The ionization of aqueous solutions by high energy electrons results in the ultrafast formation of highly reactive hydrated electrons (eaq−) and ˙OH radicals, which are non-homogeneously distributed in isolated spherical spurs formed along the radiation track. We simulate evolution of the radiolytic species during the spur expansion in N2O saturated aqueous solution of 0.1 M HCl using the extended diffusion-kinetic approach,20 successfully adopted to reproduce the pH effect on spur chemistry in irradiated aqueous solutions.21 The computations have been based on the numerical algorithm, developed by Burns et al.,22 which divides the reaction space into a number of concentric zones and treats reactions in each zone and simultaneous mass flow between adjoining zones according to the Fick's law of diffusion. The reactants were placed into each zone according to the initial Gaussian distributions. Following the extended diffusion-kinetic model the initial species distributions have been described by the properly chosen set of parameters accounting for the early track events, occurring within ca. 10−12 s. The parameters and the reaction scheme assumed to simulate evolution of the average radiation spur in N2O saturated 0.1 M HCl solution are given in ESI.† A set of coupled differential equations describing, the mutual second order reactions of the transient species, the first order reactions with the dissolved scavengers (N2O, hydronium and chloride ions), and simultaneous diffusion of the radiolytic species has been solved numerically using FACSIMILE 4 software package.‡ Simulation has been also carried out for N2-saturated 0.1 M HCl solution. A temporal evolution of the main radiolytic species is presented in Fig. 1. Solid and dashed lines refer to N2O- and N2-saturated solution, respectively. Numerical integration of the diffusion-kinetic equations up to the time limit of 0.1 μs, corresponding to decay of spatial correlations, provides the G-values or the primary yields. In N2O-saturated solution scavenging of the hydrated electron by N2O in reaction (4), competes with the H˙ atom formation in the reaction with the H3O+ ion. At ambient temperature about 13% of eaq− is scavenged by N2O, resulting in a partial restoration of ˙OH and in a lower primary yield of the H˙ atom.
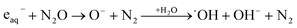 | (4) |
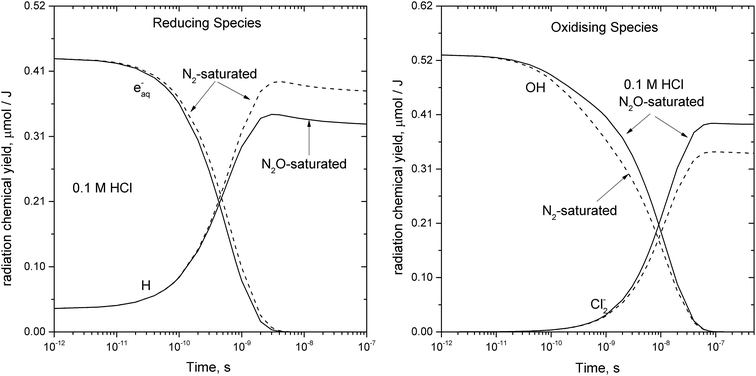 | ||
| Fig. 1 Simulated evolution of the average radiation spur in 0.1 M HCl aqueous solution at ambient temperature: solid – N2O-saturated and dash – N2-saturated system. | ||
Within ca. 70 ns the hydroxyl radical is converted to Cl2˙− via complex reaction (R6) given in Table 2. Therefore, in N2O-saturated system reaction (4) contributes to the higher yield of Cl2˙−.
The primary yields of the radical and molecular products computed for the high energy electron radiolysis of N2O-saturated solution at different temperatures are given in Table 1. A small amount of H2O2 results from the recombination of ˙OH radicals prior to the scavenging by Cl− anions. The temperature dependence for the rate of reaction (R6) in Table 2 has been modelled as diffusion controlled because in 0.1 M HCl solution all the equilibria are shifted to the right. The calculated G-values showed low sensitivity either to the value of the activation energy assumed for the overall rate of reaction (R6) or to the examined temperature dependence for the reaction rate constant of the title reaction, denoted as R1 in Table 2.
| T (K) | G(H˙) | G(Cl2˙−) | G(H2O2) | G(H2) |
|---|---|---|---|---|
| a Details on the temperature dependence for the reaction rate constants and model parameters are given in ESI. The temperature dependence for reaction of eaq− with N2O was taken from ref. 40. | ||||
| 298 | 0.331 | 0.398 | 0.064 | 0.042 |
| 313 | 0.346 | 0.406 | 0.056 | 0.042 |
| 333 | 0.371 | 0.409 | 0.052 | 0.044 |
| 353 | 0.393 | 0.408 | 0.047 | 0.046 |
| No. | Reaction | k25, M−1 s−1 | Ref. |
|---|---|---|---|
| a Calculated for the ionic strength of 0.1 M.b See ref. 18.c Calculated assuming the rate determining diffusional encounter of ˙OH and Cl− and the activation energy of 18 kJ mol−1. | |||
| R1 | H˙ + N2O → ˙OH + N2 | (9 ± 2) × 104 | This work |
| R2 | H˙ + H˙ → H2 | (5.6 ± 1.3) × 109 | 41 |
| R3 | H˙ + Cl2˙− → H+ + 2Cl− | (6.1 ± 0.6) × 109 | 18 |
| R4 | Cl2˙− + Cl2˙− → Cl2 + 2Cl− | (1.27 ± 0.13) × 109a | 42 |
| R5 | H˙ + Cl2 → H+ + Cl2˙− | (7.6 ± 1.9) × 109 | 18 |
| R6 | 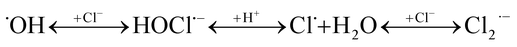 |
7.4 × 107 s−1b | c |
Fitting of kinetic traces
The concentration profiles of Cl2˙− recorded in pulse radiolysis experiments have been fitted using FACSIMILE software. As seen from Table 1 the main transient species produced by high energy electron radiolysis in our systems are Cl2˙− and H˙. The amount of H2O2 is too small to contribute to the decay of Cl2˙−. Therefore, a set of differential kinetic equations has been limited to the reactions listed in Table 2.The primary yields G(Cl2˙−) and G(H˙) resulting from the diffusion-kinetic modelling have been used to estimate the initial concentration of hydrogen atom cH(0) from the following formula:
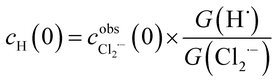 | (5) |
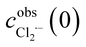 has been obtained from the maximum absorbance at a given temperature.
has been obtained from the maximum absorbance at a given temperature.
The fitted first order rate constant, k′R1, depends on the concentration of dissolved N2O, cN2O. Since in our system cN2O decreases with the increasing temperature, the second order rate constant, kR1, has been calculated using eqn (6):
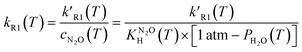 | (6) |
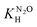 , and the pressure of saturated water vapour, PH2O were respectively taken from ref. 23 and 24.
, and the pressure of saturated water vapour, PH2O were respectively taken from ref. 23 and 24.
4. DFT computations and results
The reaction of the H˙ atom with N2O has been modelled in vacuum and in aqueous solution. Although the potential energy surface of the reaction H˙ + N2O in the gas phase was computed previously by various methods,13,25–30 to the best of our knowledge the reaction path in aqueous solution is studied here for the first time. The density functional theory (DFT) calculation have been performed using GAUSSIAN 09W.31 The unrestricted hybrid three-parameter functional UB3LYP including the Becke 88 exchange functional, the correlation functional of Lee, Yang and Parr, and the Dunning's correlation-consistent triple-zeta basis set cc-pVTZ32 have been chosen. The calculation procedure started with the optimization of stationary points geometries. The self-consistent field (SCF) procedure has been controlled by the quadratically convergent method, involving linear searches when far from convergence, and Newton–Raphson steps otherwise. After the optimization, the force constants and the resulting vibrational frequencies have been computed to specify the thermodynamic output. Geometries and vibrational frequencies of the stationary points are given in ESI.† The energies have been corrected to zero-point energy (ZPE). In Table 3 the energies obtained for the reaction in vacuum are presented along with the literature reports from previous computational studies. Our UB3LYP results agree with the B3LYP energy values. Both approaches use the spin-unrestricted formalism for open shelled structures, which assigns different spatial orbitals to the α and β electrons of unlike spin. A slight difference in the [H–NNO]‡ and [NNOH]‡ energies is possibly due to the use of spin-unrestricted functional in our UB3LYP calculations for all the structures, and the spin-restricted functional set as default for the closed shelled N2O molecule in B3LYP calculations. In comparison with more accurate methods, the [H–NNO]‡ and [H–ONN]‡ energies predicted by UB3LYP or B3LYP computations are lower. However, according to all the methods the [H–ONN]‡ transition state energy is about two times higher than the [H–NNO]‡ one. It is consistent with the quasi-classical trajectory calculations indicating that the trajectories associated with the direct path via the H˙ atom attack on the oxygen atom and the formation of the [H–ONN]‡ transition state has shorter collision times than those corresponding to the H˙ atom attachment to the nitrogen end of the N2O molecule.26| Species | QCISD(T) cc-pVTZ | CCSD(T) CBS{Q, 5} | CASSCF/ICCI cc-pVTZ | G3X | G2 | B3LYP cc-pVTZ | G2//QCISD | BAC MP4 | MRD-CI//HF 4-31G(d,p) | UB3LYP cc-pVTZ |
| [H–ONN]‡ | 0.84 | 0.78 | 0.69 | 0.55 | 0.86 | 0.55 | ||||
| [H–NNO]‡ | 0.49 | 0.31 | 0.45 | 0.42 | 0.40 | 0.25 | 0.40 | 0.16 | 0.82 | 0.24 |
| cis-HNNO | −0.59 | −0.75 | −0.63 | −0.51 | −0.67 | −0.88 | −0.62 | −0.63 | −1.27 | −0.88 |
| [NNOH]‡ | 0.72 | 0.75 | 0.71 | 0.83 | 0.81 | 0.71 | 0.72 | 0.72 | 0.99 | 0.70 |
| cis/trans-[HNNO]‡ | −0.13 | −0.16 | −0.095 | −0.13 | ||||||
| trans-HNNO | −0.84 | −1.00 | −0.86 | −0.90 | −0.93 | −1.12 | −0.93 | −0.93 | −1.28 | −1.12 |
| N2 + OH | −2.73 | −2.77 | −2.72 | −2.71 | −2.56 | −2.71 | −2.87 | −2.67 | −2.51 | |
| Ref. | 26 | 27 | 28 | 28 | 26 | 25 | 29 | 13 | 30 | (This work) |
The UB3LYP/cc-pVTZ computations of the reaction path in water have been carried out assuming two values of the dielectric constant ε = 78.355 and ε = 63.677, corresponding to the solvent at 298 and 343 K, respectively. We employed two polarizable continuum models (PCMs), C-PCM and IEF-PCM, and SMD model.33 The IEF-PCM self-consistent reaction field method uses the integral equation formalism variant34 and the conductor-like solvation C-PCM model.35 In the SMD approach the free energy of solvation is separated into the bulk electrostatic component and the short-range interaction energy between a solute and solvent molecules in the first solvation shell. Calculation of the long-range electrostatic component is based on the solution of the Poisson equation in terms of the IEF-PCM method. The short-range component includes dispersion energies and a cavitation energy associated with the formation of a cavity in the liquid solvent.
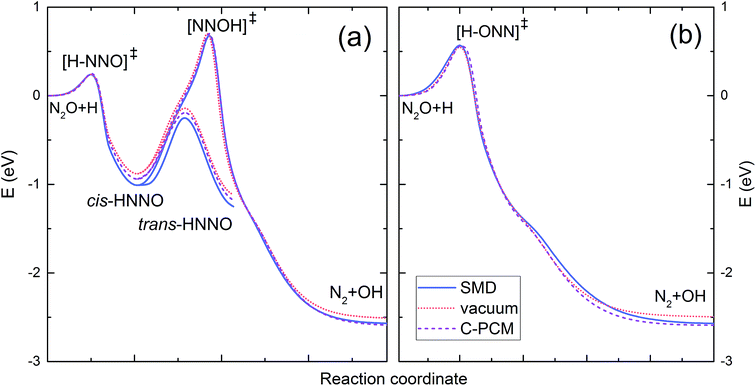
Fig. 2 shows the intrinsic reaction coordinate (IRC) diagram computed for the reaction H˙ + N2O in vacuum and in solution. Part (a) shows the reaction path resulting from the H˙ atom attack on the nitrogen end of the N2O molecule, whereas part (b) refers to the attack on the oxygen atom. The attack on the N atom leads to the [H–NNO]‡ transition state followed by the formation of cis-HNNO intermediate, which may either isomerise to trans-HNNO or transform to the [NNOH]‡ intermediate decomposing into ˙OH and N2. The attack on the O atom leads to the formation of the [H–ONN]‡ transition state directly decomposing to the products. The energies of the stationary points in solution are presented in Table 4 along with the UB3LYP results obtained for vacuum. Geometries and vibrational frequencies of the stationary points in solution are given in ESI.† Within the considered range of temperature, all the solvent models are insensitive to the value of ε. Compared to vacuum, the PCM models show slightly higher energy barriers for [H–ONN]‡ and [NNOH]‡, but clearly lower energy levels of cis/trans[HNNO]‡, cis-HNNO, trans-HNNO, and N2 + OH, all calculated relative to the energy level of the reactants. The SMD model predicts better stabilization of cis/trans[HNNO]‡, cis-HNNO, trans-HNNO, a slightly higher energy barrier for [H–ONN]‡, but a lower one for the [NNOH]‡ transition state. Unlike the PCM models, the SMD energy barrier for the formation of [NNOH]‡ is slightly below that in vacuum.
| Species | Vacuum | 298 K, ε = 78.355 | 343 K, ε = 63.677 | ||||
|---|---|---|---|---|---|---|---|
| C-PCM | IEF-PCM | SMD | C-PCM | IEF-PCM | SMD | ||
| a The energies expressed in eV include ZPE correction. The values in kJ mol−1 are given in parentheses. | |||||||
| [H–ONN]‡ | 0.55 (53.0) | 0.56 (54.2) | 0.56 (54.2) | 0.57 (54.6) | 0.56 (54.2) | 0.56 (54.2) | 0.57 (54.6) |
| [H–NNO]‡ | 0.24 (23.5) | 0.25 (24.1) | 0.25 (24.1) | 0.24 (22.8) | 0.25 (24.1) | 0.25 (24.1) | 0.24 (22.8) |
| cis-HNNO | −0.88 (−85.1) | −0.94 (−90.7) | −0.94 (−90.6) | −1.01 (−97.4) | −0.94 (−90.6) | −0.94 (−90.6) | −1.01 (−97.3) |
| [NNOH]‡ | 0.70 (67.7) | 0.70 (67.6) | 0.70 (67.6) | 0.68 (65.5) | 0.70 (67.6) | 0.70 (67.6) | 0.68 (65.5) |
| cis/trans-[HNNO]‡ | −0.13 (−12.4) | −0.18 (−17.5) | −0.18 (−17.5) | −0.24 (−23.5) | −0.18 (−17.5) | −0.18 (−17.5) | −0.24 (−23.5) |
| trans-HNNO | −1.12 (−108.0) | −1.18 (−114.1) | −1.18 (−114.0) | −1.25 (−120.9) | −1.18 (−114.0) | −1.18 (−114.0) | −1.25 (−120.8) |
| N2 + OH | −2.51 (−242.6) | −2.59 (−250.1) | −2.59 (−250.1) | −2.57 (−247.7) | −2.59 (−250.1) | −2.59 (−250.0) | −2.57 (−247.6) |
5. Discussion
The reaction in solution – pulse radiolysis results
Fig. 3 presents selected absorption traces of Cl2˙− decay in N2O- and N2-saturated 0.1 M HCl solution. The FACSIMILE fits obtained taking into account the reaction set from Table 2 and allowing the first order rate constant k′R1 to vary are shown in Fig. 3 by solid lines through the experimental traces. The decay of Cl2˙− in N2O-saturated solution is significantly slower. Numerical simulation shows that in N2O-saturated solution contribution of reaction (R3) to the decay of Cl2˙− is more limited because the H˙ atom is partially consumed in reaction with N2O. The role of reaction (R1) is confirmed by more striking slow-down of the Cl2˙− decay observed in 7 ns pulse (lower dose) experiments. A noticeable difference between the kinetic traces shown for 313 and 343 K indicates that the significance of the reaction H˙ + N2O rapidly increases with temperature.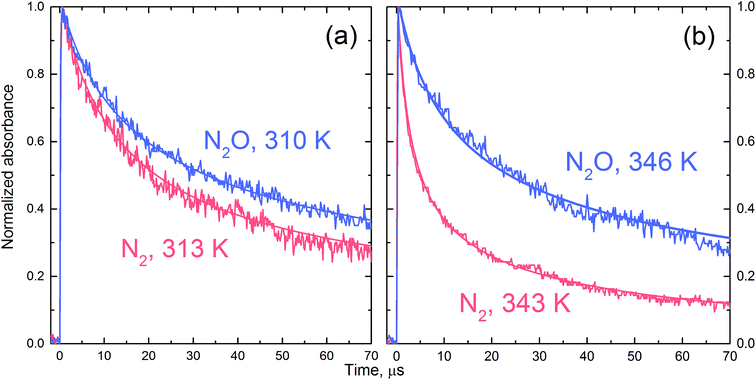 | ||
| Fig. 3 The normalized-to-maximum transient absorbance of Cl2˙− in pulse irradiated aqueous 0.1 HCl solution saturated with N2 (pink) and N2O (blue) recorded at 340 nm after 7 ns pulse at ca. 313 K (a) and 343 K (b). The solid lines through the experimental traces present FACSIMILE fits obtained taking into account the reaction set from Table 2, and allowing k′R1 to vary. | ||
Fig. 4 shows the Arrhenius plot of the rate constant of reaction (R1) calculated based on the fitted rate constants k′R1 and eqn (6). The error bars include uncertainty in both the fitted values of k′R1 and in N2O-concentration. The latter has been estimated to be ±10% at each temperature. The activation energy Ea = (62.6 ± 2.1) kJ mol−1 has been obtained from a weighted nonlinear regression using the Marquardt–Levenberg method and OriginPro 2016 software. Inset in Fig. 4 presents the nonlinear regression fit to eqn (7), which results from the transition state theory and thus is more appropriate for comparison with our DFT computations. Fit to eqn (7) results in a slightly lower value of the activation energy, E′a = (59.9 ± 2.1) kJ mol−1.
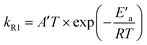 | (7) |
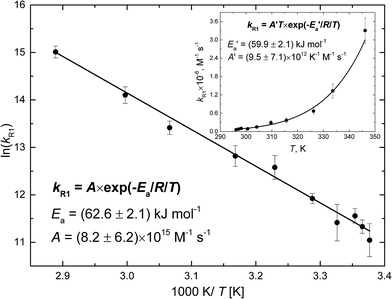 | ||
| Fig. 4 The measured rate constant of reaction (R1) as a function of temperature (points). The error bars include uncertainty in both k′R1 and cN2O (see text). The solid line shows the nonlinear regression fit to the Arrhenius equation (the correlation coefficient is 0.986). The inset presents the nonlinear regression fit to eqn (7) resulting from the transition state theory. | ||
The value of E′a is very close to the [H–ONN]‡ transition state energy predicted by SMD and PCM models (see Table 4). It indicates the predominance of the direct reaction path shown in Fig. 2b, but does not exclude the indirect path through the H˙ atom attachment to the N atom of the N2O molecule. As seen in Fig. 2a the total energy expense associated with the formation of [H–NNO]‡, subsequent relaxation to cis-HNNO, and transformation to [NNOH]‡ is equal to the [NNOH]‡ transition state energy relative to the reactants. As seen from Table 4 the energy values of [NNOH]‡ in solution are only slightly higher than E′a. Taking the PCM barrier heights of 54.2 and 67.6 kJ mol−1 corresponding to the direct and indirect paths, respectively, the value of E′a can be reproduced by the weighted sum assuming 57.5% contribution of the direct mechanism. Taking the respective SMD barrier heights, 54.6 and 65.5 kJ mol−1, the contribution of the direct path is 51.2%. Thus, in agreement with all the solvent models, the measured value of the activation energy indicates two mechanisms for the reaction H˙ + N2O in solution: (i) formation of [H–ONN]‡ directly decaying into N2 and ˙OH, and (ii) less contributing indirect path through the formation of [H–NNO]‡, relaxation to cis-HNNO, and subsequent transformation to the [NNOH]‡ transition state finally decomposing to the products.
Solvent effect on the reaction mechanism
Our pulse radiolysis measurements over the temperature range of 296–346 K show that the reaction of H˙ with N2O in solution requires almost three times higher activation energy than the reaction in the gas phase (see the first Arrhenius term in eqn (1)). Since Bozzelli et al.36 confirmed that at temperatures below 500 K loss of the reactants in the gas phase leads to the formation of N2 and ˙OH, two hypothesis were considered to explain unexpectedly weak temperature dependence of the reaction rate constant. Marshall et al. suggested the H˙ atom addition to the nitrogen end of the N2O molecule and the quantum mechanical tunnelling through the barrier to produce [NNOH]‡ dissociating into N2 and ˙OH.13 An alternative hypothesis assumed the collisional stabilisation of the H–NNO adduct and its rapid diffusion to the wall followed by the decay into N2 and ˙OH.36–38 Whichever hypothesis is true, our pulse radiolysis measurements indicate that the suggested processes do not occur in solution. The quantum mechanical tunnelling from [H–NNO]‡ to [NNOH]‡ or the collisional stabilization and decay of [H–NNO]‡ are probably specific for the gas phase reaction below 500 K since at higher temperatures the increase in the reaction rate constant is more rapid. The activation energy 62.8 kJ mol−1 observed by Hidaka et al. in shock-tube experiments over the temperature range of 1450–2200 K (ref. 39) is close to the value of Ea measured in solution. It may suggest that, like in aqueous solution, the reaction of the H˙ atom with N2O in high temperature gases may proceed via two paths: directly through the formation of [H–ONN]‡ or indirectly through the H˙ attack on the N atom followed by relaxation to cis-HNNO and subsequent transformation to [NNOH]‡ dissociating into N2 and ˙OH.6. Summary and conclusion
To the best of our knowledge, in contrast to the gas phase, the temperature dependence for the reaction H˙ + N2O → ˙OH + N2 has never been studied in solution. To fill this gap we have combined here pulse radiolysis kinetic measurements and DFT computations with the aim to measure the activation energy and indicate the reaction mechanism. Comparative observations of the decay of Cl2˙− in pulse-irradiated 0.1 M HCl solution saturated with N2 and N2O showed particularly slower decay in the latter system at 7 ns pulse (lower dose) confirming the contribution of the H˙ atom reaction with the dissolved N2O. The observed slow-down was significantly enhanced by the increasing temperature. The kinetic measurements over the temperature range of 296–346 K and numerical simulation showed the Arrhenius dependence of the reaction rate constant with the activation energy established to be (62.6 ± 2.1) kJ mol−1 or (59.9 ± 2.1) kJ mol−1 depending on a form of the pre-exponential factor in the Arrhenius equation, A or A′ × T, respectively.The UB3LYP/cc-pVTZ computations have been performed for the reaction H˙ + N2O → ˙OH + N2 in vacuum and in solution using three water-solvent models: C-PCM, IEF-PCM, and SMD. We have showed that the reaction initiated by the H˙ atom attack on the oxygen atom in the N2O molecule results in the formation of the [H–ONN]‡ transition state directly decomposing into ˙OH and N2. According to SMD model the energy barrier associated with this direct path is 54.6 kJ mol−1 in comparison with 54.2 kJ mol−1 predicted by the PCM models and 53.0 kJ mol−1 corresponding to the reaction in vacuum. Computations assuming the H˙ atom attack on the N atom revealed the indirect reaction mechanism including the formation of [H–NNO]‡, the adduct decay to cis-HNNO intermediate, transformation of cis-HNNO to [NNOH]‡, and decomposition to ˙OH and N2. In contrast to the direct path, the total energy expense associated with the indirect mechanism, 65.5 and 67.6 kJ mol−1 as predicted by SMD and PCM models, is slightly smaller than 67.7 kJ mol−1 computed in vacuum. The energy expense associated with the direct and indirect paths is similar and show good agreement with the activation energy obtained from the pulse radiolysis experiments. As the measured value is in-between the computed energy barriers we conclude that both mechanisms may occur in solution, but with a slight predominance of the direct one. This is in contrast to the literature reports on the gas phase reaction at temperatures below 500 K indicating almost three times lower activation energy and suggesting either the quantum mechanical tunnelling from [H–NNO]‡ to [NNOH]‡ or the collisional stabilisation and decay of the H–NNO adduct into N2 and ˙OH.
Acknowledgements
The financial support from the Lodz University of Technology is greatly acknowledged. Dr Michał Rostkowski is thanked for a discussion of the DFT results obtained for the gas phase reaction.References
- D. S. Reay, E. A. Davidson, K. A. Smith, P. Smith, J. M. Melillo, F. Dentener and P. J. Crutzen, Nat. Clim. Change, 2012, 2, 410–416 CrossRef CAS.
- M. Dameris, Angew. Chem., Int. Ed., 2010, 49, 489–491 CrossRef CAS PubMed.
- W. C. Wang, Y. L. Yung, A. A. Lacis, T. Mo and J. E. Hansen, Science, 1976, 194, 685–690 CAS.
- K. Severin, Chem. Soc. Rev., 2015, 44, 6375–6386 RSC.
- D. Zuck, P. Ellis and A. Dronsfield, Educ. Chem., 2012, 26–29 CAS.
- S. S. Emmi and E. Takács, in Radiation chemistry. From basics to applications in material and life sciences, ed. M. Spotheim-Maurizot, M. Mostafavi, T. Douki and J. Belloni, EDP Sciences, 2008, vol. 6, pp. 79–95 Search PubMed.
- M. Ismail, H. M. Khan, M. Sayed and W. J. Cooper, Chemosphere, 2013, 93, 645–651 CrossRef CAS PubMed.
- M. Sanchez, H. Wolfger and N. Getoff, Radiat. Phys. Chem., 2002, 65, 611–620 CrossRef CAS.
- N. Liu, T. Wang, M. Zheng, J. Lei, L. Tang, G. Hu, G. Xu and M. Wu, Chem. Eng. J., 2015, 270, 66–72 CrossRef CAS.
- J. A. Miller and C. T. Bowman, Prog. Energy Combust. Sci., 1989, 15, 287–338 CrossRef CAS.
- C. P. Fenimore and G. W. Jones, J. Phys. Chem., 1959, 63, 1154–1158 CrossRef CAS.
- H. Henrici and S. H. Bauer, J. Phys. Chem., 1969, 50, 1333–1342 CrossRef CAS.
- P. Marshall, A. Fontijn and C. F. Melius, J. Chem. Phys., 1987, 86, 5540–5549 CrossRef CAS.
- P. Marshall, T. Ko and A. Fontijn, J. Chem. Phys., 1989, 93, 1922–1927 CrossRef CAS.
- D. L. Baulch, C. T. Bowman, C. J. Cobos, R. A. Cox, Th. Just, J. A. Kerr, M. J. Philling, D. Stocker, J. Troe, W. Tsang, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 2005, 34, 757–1397 CrossRef CAS.
- L. Kazmierczak, D. Swiatla-Wojcik, J. Szala-Bilnik and M. Wolszczak, Radiat. Phys. Chem., 2016, 125, 156–159 CrossRef CAS.
- G. V. Buxton and C. R. Stuart, J. Chem. Soc., Faraday Trans., 1995, 91, 279–281 RSC.
- L. Kazmierczak, J. Szala-Bilnik, M. Wolszczak and D. Swiatla-Wojcik, Radiat. Phys. Chem., 2015, 117, 7–11 CrossRef CAS.
- D. J. Adams, S. Barlow, G. V. Buxton, T. N. Malone and G. A. Salmon, J. Chem. Soc., Faraday Trans., 1995, 91, 3303–3305 RSC.
- D. Swiatla-Wojcik and G. V. Buxton, Phys. Chem. Chem. Phys., 2000, 2, 5113–5119 RSC.
- D. Swiatla-Wojcik, Nukleonika, 2008, 53, 31–37 Search PubMed.
- W. G. Burns, H. E. Sims and J. A. Goodall, Radiat. Phys. Chem., 1984, 23, 143–180 CrossRef CAS.
- S. Ma'mun and H. F. Svendsen, Energy Procedia, 2009, 1, 837–843 CrossRef.
- W. Wagner and A. Pruß, J. Phys. Chem. Ref. Data, 2002, 31, 387–535 CrossRef CAS.
- J. F. Castillo, M. A. Collins, F. J. Aoiz and L. Banares, J. Chem. Phys., 2003, 118, 7303–7312 CrossRef CAS.
- J. F. Castillo, F. J. Aoiz, L. Banares and M. A. Collins, J. Phys. Chem. A, 2004, 108, 6611–6623 CrossRef CAS.
- N. L. Haworth, J. C. Mackie and G. B. Bacsay, J. Phys. Chem. A, 2003, 107, 6792–6803 CrossRef CAS.
- S. P. Walch, J. Chem. Phys., 1993, 98, 1170–1177 CrossRef CAS.
- J. L. Durant Jr, J. Phys. Chem., 1994, 98, 518–521 CrossRef.
- T. Fueno, M. Fukuda and K. Yokoyama, Chem. Phys., 1988, 124, 265–272 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- A. V. Marenich, Ch. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and E. Cancés, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- J. W. Bozzelli, A. Y. Chang and A. M. Dean, 25th Symp. (Int.) Combustion, 1994, pp. 965–974 Search PubMed.
- N. L. Arthur, I. A. Cooper and Y. M. Gershenzon, J. Chem. Soc., Faraday Trans., 1997, 93, 3485–3490 RSC.
- E. W. G. Diau and M. C. Lin, J. Phys. Chem., 1995, 99, 6589–6594 CrossRef CAS.
- Y. Hidaka, H. Takuma and M. Suga, Bull. Chem. Soc. Jpn., 1985, 58, 2911–2916 CrossRef CAS.
- K. Takahashi, S. Ohgami, Y. Koyama, S. Sawamura, T. W. Marin, D. M. Bartels and C. D. Jonah, Chem. Phys. Lett., 2004, 383, 445–450 CrossRef CAS.
- K. Sehested and H. Christensen, Radiat. Phys. Chem., 1999, 36, 499–500 Search PubMed.
- J. Szala-Bilnik, P. Pierscieniewska, M. Wolszczak and D. Swiatla-Wojcik, Radiat. Phys. Chem., 2014, 97, 184–187 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27793d |
| ‡ Facsimile 4 for Windows, MCPA software, version 4.2.50. |
| This journal is © The Royal Society of Chemistry 2017 |