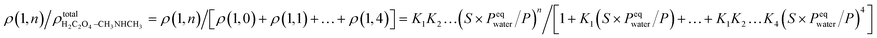Interaction of oxalic acid with dimethylamine and its atmospheric implications

Abstract

Oxalic acid and dimethylamine are the most common organic acid and base in the atmosphere, and are recognized as significant precursor species in atmospheric new particle formation. However, the interaction between oxalic acid and dimethylamine in the presence of hydration is not yet understood. In this study, the most stable geometric structures and thermodynamics of (C₂H₂O₄)_m(CH₃NHCH₃)(H₂O)_n (m = 1–2, n = 0–4) clusters are investigated using M06-2X coupled with the 6-311+G(2d,p) basis set. A high level explicitly corrected CCSD(T)-F12/VDZ-F12 method is utilized to benchmark the density functional theory (DFT) methods. Hydration promotes proton transfer from oxalic acid to dimethylamine for (C₂H₂O₄)(CH₃NHCH₃)(H₂O)_n (n = 0–4) clusters, while proton transfer from oxalic acid to dimethylamine occurs without hydration for (C₂H₂O₄)₂(CH₃NHCH₃)(H₂O)_n (n = 0–4) clusters. With regards to the isomer distribution at the potential energy surface, temperature seems not to be an important parameter, since almost all of the global minima for the investigated size range dominate within the investigated temperature range, except for in the (C₂H₂O₄)_m(CH₃NHCH₃)(H₂O)₂ clusters. Under atmospheric conditions, the peak hydration distribution shifts from unhydrated clusters to trihydrates for the (C₂H₂O₄)(CH₃NHCH₃)(H₂O)_n (n = 0–4) clusters, while for the (C₂H₂O₄)₂(CH₃NHCH₃)(H₂O)_n (n = 0–4) clusters, unhydrated clusters clearly dominate the cluster distribution, irrespective of whether the humidity is low or high. Finally, the formation free energies obtained from quantum calculations are used to calculate the evaporation rates. We find that evaporation of dimethylamine is preferred compared to oxalic acid for the (C₂H₂O₄)(CH₃NHCH₃)(H₂O)_n clusters, while the results are reversed for the (C₂H₂O₄)₂(CH₃NHCH₃)(H₂O)_n clusters.

---

1. Introduction

Aerosols have a tremendous impact on the Earth's radiation budget, cloud formation, photochemical chemistry, human health, and the climate system.^1–10 New particle formation (NPF) contributes significantly to the number of aerosol particles and cloud condensation nuclei (CCN).¹¹ Although a large amount of research has been conducted, the mechanisms of aerosol nucleation are still not well understood,^8,12,13 especially in terms of measuring the chemical composition of newly nucleated clusters.^14–19 Sulfuric acid (SA) has been identified as a critical nucleation precursor. However, binary homogeneous nucleation of sulfuric acid and water is insufficient to explain the nucleation events under actual atmospheric conditions measured in the field, due to the low concentration of SA in the range of 10⁵ to 10⁷ cm⁻³,^8,12,13 which indicates that other species may participate in nucleation.^20–22 So far, several nucleation mechanisms have been proposed to account for new particle formation under different atmospheric environments, such as ternary nucleation by sulfuric acid/water and ammonia/amines,^23–30 ion induced nucleation,^31,32 organic acids,^33–37 and iodine oxides.¹²

Numerous atmospheric observations have shown that amines^38–41 and organic acids¹² participate in nucleation. Theoretical calculations on the interaction of carboxylic acids and amines with sulfuric acid show that sulfuric acid can connect strongly with both carboxylic acids and amines via hydrogen bonding.^36,42–46 Dicarboxylic acids have been frequently found in significant concentrations, and participate in ice nucleation,^47–49 cloud condensation,⁵⁰ and the production of fine particulate matter.^32,51 In particular, oxalic acid (OA) is the most common dicarboxylic acid in the atmosphere and a major constituent of aerosol particles, present at concentrations 2–3 orders of magnitude higher than NH₃.^15,52,53 In addition, another study has shown that dicarboxylic acids have lower saturation vapor pressures than monocarboxylic acids, indicating that dicarboxylic acids may play a more significant role in new particle formation.⁵⁴ A theoretical investigation by Xu et al. predicted that oxalic acid binds strongly with sulfuric acid.³⁶ Furthermore, density functional theory (DFT) calculations revealed that oxalic acid could enhance the stability of ionic clusters, promoting the formation of positively charged clusters.⁴⁵ Another DFT study by Ehn et al. indicated that oxalic, malonic, and succinic acids stabilize anionic bisulfate clusters.⁵⁵ In addition, the subsequent hydration of the (C₂H₂O₄)(NH₃) core has been found to be energetically favorable, indicating that oxalic acid and ammonia can participate in atmospheric aerosol nucleation.^56,57

Amines have been reported to participate in nucleation during new particle formation events.³⁸ Various quantum calculations have revealed that amines stabilize sulfuric acid clusters more efficiently than ammonia.^42,43,58 Additionally, laboratory studies and recent field observations have suggested that the presence of amines has a considerable effect on new particle formation.^39–41 Dimethylamine (DMA) is the strongest and most common base in the atmosphere,^59,60 and it can rapidly undergo acid–base reactions, which enhance neutral and ion-induced sulfuric acid–water nucleation.^42,58,61,62 Experiments using the CLOUD chamber at CERN have demonstrated that DMA concentrations exceeding three parts per trillion by volume are able to increase the new particle formation rate by more than 3 orders of magnitude relative to that seen with ammonia.⁴¹ However, the concentration of amines in the atmosphere is several orders of magnitude lower than the concentration of dicarboxylic acids. It has been indicated that molecular complexes containing amines and dicarboxylic acids may play an important role in atmospheric conditions.^36,63

Although a larger number of theoretical calculations have investigated the effect of carboxylic acid and amines on sulfuric acid nucleation,^37,64,65 the influence of the interaction between oxalic acid and dimethylamine in the presence of hydration has not yet been studied. Here, we investigate the possibility of oxalic acid behaving in a similar manner to the ternary sulfuric acid, dimethylamine and water system. The subsequent hydration of OA–DMA is studied using DFT at the M06-2X/6-311+G(2d,p) level. We benchmark and utilize high level coupled cluster analysis to accurately determine the binding energies of the clusters. We also discuss the atmospheric implications of the present results for nucleation. In addition, the effects of temperature on the formation of (C₂H₂O₄)_m(CH₃NHCH₃)(H₂O)_n (m = 1–2, n = 0–4) clusters, and the atmospheric relevance of these effects are also studied. Finally, the formation free energies obtained from quantum calculations are used to calculate the evaporation rates.

2. Theoretical methods

The initial geometries of the (C₂H₂O₄)_m(H₂O)_n (m = 1–2, n = 0–4) and (C₂H₂O₄)_m(CH₃NHCH₃)(H₂O)_n (m = 1–2, n = 0–4) clusters were obtained using the Basin–Hopping (BH) algorithm⁶⁶ coupled with DFT. In previous studies, this method has been successfully applied to atomic and molecular systems.^66–74 In this method, a new structure is generated through the random displacement of atoms, and then the structure is optimized to a local minimum. The optimized local energy minimum is used as a criterion for accepting the structure spaces that were initially generated with Boltzmann weight at a finite temperature. The initial geometries were optimized with PW91/DND implemented in the DMol³ software package.⁷⁵ Then the identified conformations within 10 kcal mol⁻¹ of the lowest binding energy were calculated at the M06-2X/6-311+G(2d,p) level of theory. Frequency calculations were executed to ensure that there were no imaginary frequencies for each stationary point. Geometry and frequency calculations were performed using the Gaussian09 program.⁷⁶ The thermochemistry was calculated using the harmonic-oscillator and rigid-rotor approximations at 298.15 K and 1 atm. Finally, single-point energy calculations were performed at the DF-LMP2-F12/VDZ-F12 level of theory, based on the optimized geometries at the M06-2X/6-311+G(2d,p) level of theory, using Molpro 2010.1.⁷⁷ Structural information was provided by Chemcraft 1.6 (http://www.chemcraftprog.com).

In previous studies, the M06-2X, PW91PW91 and ωB97X-D DFT functionals have presented good performance in modeling the formation of atmospheric nucleation clusters.^78–82 Thus, a sensitivity analysis on the performance of these three DFT methods was conducted. The detailed information is presented in the ESI.† According to the results, we find that the maximum error in the DFT binding energy reaches 2.94 kcal mol⁻¹ for PW91PW91/6-311+G(2d,p), which results from the formation of (OA)₁(W)₁ clusters. Although there is a relatively larger scatter in the DFT binding energy, the thermal contribution to the Gibbs free energy varies significantly less, within 1 kcal mol⁻¹. When the basis set is changed from a large 6-311++G(3df,3pd) basis set to a smaller 6-311+G(2d,p) basis set, a small effect (within 0.9 kcal mol⁻¹) on the Gibbs free energy is obtained. This indicates that the electronic binding energy is the largest source of error when using DFT for these systems. Comparing CCSD(T)-F12a/VDZ-F12 with DF-LMP2-F12/VDZ-F12, whether the geometries have been optimized using the 6-31++G(d,p) or 6-311++G(3df,3pd) basis set, we find a minor effect on the calculation of the Gibbs free energies.

In conclusion, our results indicate that the DF-LMP2-F12/VDZ-F12//M06-2X/6-311+G(2d,p) basis set can be used as a good compromise between accuracy and computational efficiency.

3. Results and discussion

3.1 Structures

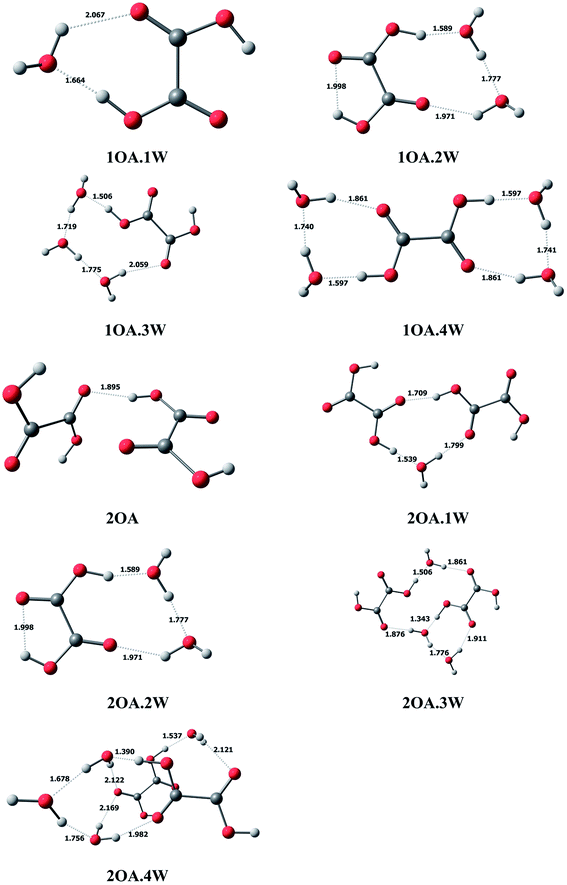
In this study, we use mOA·1DMA·nW-j notation to present the (C₂H₂O₄)_m(CH₃NHCH₃)(H₂O)_n (m = 1–2, n = 0–4) conformations. Here, “m” denotes the number of oxalic acid molecules, “n” denotes the number of water molecules, and “j” (j = a − j) is used to differentiate various isomers with the same number of oxalic acid, dimethylamine and water molecules, arranged in order of increasing relative single-point energy.

Clusters with C₂H₂O₄ and H₂O.
C₂H₂O₄(H₂O)_n (n = 1–4). The optimized global minimum clusters of oxalic acid with water are presented in Fig. 1. For monohydrated clusters, the water molecule is bound to oxalic acid by two new hydrogen bonds formed between water and oxalic acid. The COH angle of the acid group binding to water increases from 108° to 115°, allowing the O–H⋯O hydrogen bond angle to increase linearly up to 173°, and the hydrogen bond formed between the oxalic OH group and the oxygen of water has a short H⋯O bond distance of 1.664 Å. For the dihydrated oxalic acid clusters, the two water molecules bound to oxalic acid create a single ring, which is found to be the most stable conformation. In this cluster, the bonding of the carboxylic acid to the oxygen of water appears to be the strongest, with the shortest bond distance of 1.589 Å. Then, the acid bound water binds to the second water, forming a H⋯O bond with a distance of 1.777 Å. The second bound water connects with the carbonyl group forming a hydrogen bond with a distance of 1.971 Å. In the case of the trihydrate global minimum, the three water molecules are arranged in a chain, binding the external acid OH group and the carbonyl group forming a cyclic ring structure. The hydrogen bond distances to the water are 1.506 Å, 1.719 Å, 1.775 Å and 2.059 Å successively. For the tetrahydrate cluster, two water molecules bind on opposing sides of the exterior acid group forming two rings.

Fig. 1 The global minima for (C₂H₂O₄)_m(H₂O)_n (m = 1–2, n = 0–4) optimized at the M06-2X/6-311+G(2d,p) level.

(C₂H₂O₄)₂(H₂O)_n (n = 0–4). In the case of clusters with two oxalic acid molecules, the most stable structure is found to be the two oxalic acid molecules binding through the adjacent carbonyl group and the interior acid OH group, with a bond distance of 1.895 Å. From Fig. 1, the two oxalic acid molecules hydrated with one to three water molecules formed nearly planar ring structures, which are the most stable conformations. For monohydrated clusters, the water molecule acts as a bridge and interacts with the external carboxylic acid group of one oxalic acid molecule with the shortest bond distance of 1.539 Å, and binds the carbonyl group of the other oxalic acid molecule with a bond distance of 1.799 Å. When a second water molecule is added, the bonding is approximately symmetrical with an acidic proton bonding to an oxygen of water with the same distance of 1.501 Å. The water also binds to the carbonyl group, and the hydrogen bond distances are also the same at 1.864 Å. For the trihydrated cluster, the third water molecule inserts into the dihydrated cluster by connecting with the hydrogen of one water molecule, with a bond distance of 1.776 Å, and the adjacent carbonyl group, with a bond distance of 1.911 Å. The addition of a fourth water molecule changes the most stable configuration from a planar ring structure to a cage-like structure, where the two oxalic acid molecules form a parallel double layer structure.

Clusters with C₂H₂O₄, CH₃NHCH₃ and H₂O.
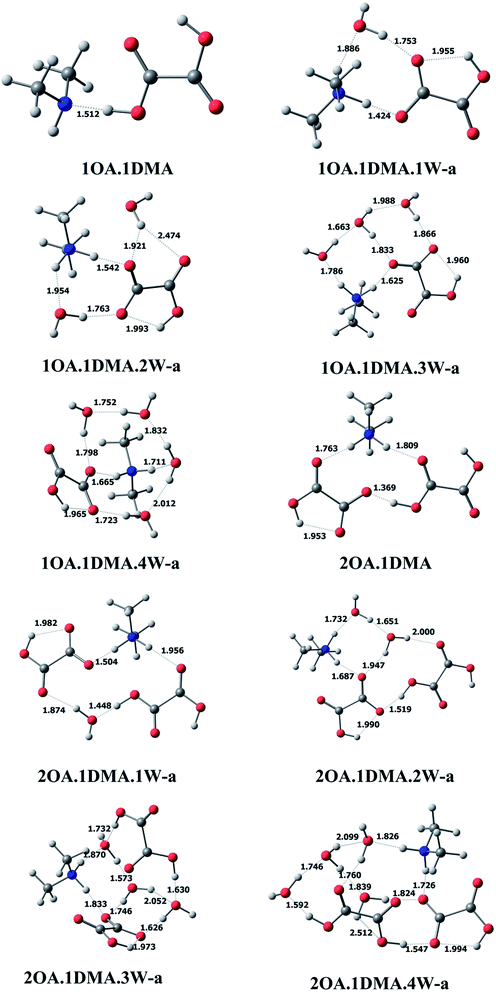
C₂H₂O₄(CH₃NHCH₃)(H₂O)_n (n = 0–4). The most stable clusters of oxalic acid with dimethylamine are presented in Fig. 2. One hydrogen bond is formed between one of the acid groups and the nitrogen of ammonia, with a distance of 1.512 Å and a nearly linear bond angle. For the (C₂H₂O₄)_m(CH₃NHCH₃)(H₂O)_n (m = 1–2, n = 0–4) conformations, among the different structures obtained, the ten lowest energy configurations were chosen. Here, only the global minimum structures are shown in Fig. 2 and described in detail, the other low energy isomers are presented in the ESI.† For (C₂H₂O₄)₁(CH₃NHCH₃)₁(H₂O)₁, a total of six isomers of the monohydrated cluster were characterized in Fig. 2 and S1.† All of the isomers exhibit proton transfer from oxalic acid to dimethylamine, except for the least stable cluster. The OH bond length in a free oxalic acid monomer is 0.973 Å, and after bonding with dimethylamine and water, the OH bond is elongated to 1.424 Å, indicating proton transfer from the oxygen of oxalic acid to the nitrogen of dimethylamine. Seven stable isomers of (C₂H₂O₄)₁(CH₃NHCH₃)₁(H₂O)₂ are identified in this work. In the most stable conformation, the second water interacts with the deprotonated oxygen of oxalic acid, and the OH hydrogen bond distance appears to be slightly increased from 1.424 Å to 1.542 Å. As the number of water molecules increases up to two, proton transfer exists in all isomers. The resulting ion pair is stabilized by water molecules through hydrogen bonding interactions. The 7 most stable clusters of oxalic acid with dimethylamine and three water molecules are shown in Fig. 2 and S2.† The most stable cluster has two adjacent cyclic hydrogen bonded networks. The intramolecular hydrogen bond between the carbonyl group and the OH group of the adjacent carboxylic acid group appears to be little affected, as evidenced by a slightly shortened hydrogen bonding distance of 1.960 Å, compared to 2.120 Å in the monomer. As the number of water molecules increases up to four, the number of possible conformers and the complexity of the configurations increases significantly, and all of the clusters were found to spontaneously ionize.

Fig. 2 The global minima for (C₂H₂O₄)_m(CH₃NHCH₃)(H₂O)_n (m = 1–2, n = 0–4) optimized at the M06-2X/6-311+G(2d,p) level.

(C₂H₂O₄)₂(CH₃NHCH₃)(H₂O)_n (n = 0–4). For the (C₂H₂O₄)₂(CH₃NHCH₃) cluster without water, proton transfer could happen. The two oxalic acid molecules interact through the carbonyl group and the adjacent carboxylic acid group, completing the circuit with the shortest bond distance of 1.369 Å, with one intramolecular interaction also present. Seven conformers of (C₂H₂O₄)₂(CH₃NHCH₃)₁(H₂O)₁ are depicted in Fig. 2 and S3.† The global minimum conformation has a similar bonding pattern to (C₂H₂O₄)₂(H₂O)₂. Eight stable clusters of (C₂H₂O₄)₂(CH₃NHCH₃)₁(H₂O)₂ were identified in this work. The two water molecules bind to the dimethylamine and two oxalic acids forming two closed rings. The bonding of the two oxalic acid molecules appears to be the strongest, having the shortest bond distance of 1.519 Å. A total of ten and seven isomers of (C₂H₂O₄)₂(CH₃NHCH₃)₁(H₂O)₃ and (C₂H₂O₄)₂(CH₃NHCH₃)₁(H₂O)₄ are shown in Fig. 2 and S4.† The hydrogen bond network changes from a nearly planar ring structure to a cage-like configuration. Increasing the number of water molecules tends to promote proton transfer from oxalic acid to dimethylamine, even though the oxalic acid molecule does not connect with dimethylamine directly.

3.2 Thermochemical analysis

The relative single-point energy, ΔE (0 K), the intermolecular enthalpy, ΔH (298.15 K) and the Gibbs free energy, ΔG (298.15 K), of the global minima for the (C₂H₂O₄)_m(CH₃NHCH₃)(H₂O)_n (m = 1–2, n = 0–4) (in kcal mol⁻¹) structures are displayed in Tables 1–4.

Table 1 Energy changes associated with the reaction of oxalic acid and dimethylamine with water. The energies are in kcal mol⁻¹, and were calculated at the DF-LMP2-F12/VDZ-F12//M06-2X/6-311+G(2d,p) level of theory

Reactions	ΔE (0 K)	ΔH (298.15 K)	ΔG (298.15 K)
OA + W ⇔ (OA)(W)	−10.09	−8.67	0.03
OA + 2W ⇔ (OA)(W)2	−19.64	−16.66	1.00
OA + 3W ⇔ (OA)(W)3	−28.84	−24.22	2.35
OA + 4W ⇔ (OA)(W)4	−39.62	−33.23	2.87
DMA + W ⇔ (DMA)(W)	−7.91	−6.10	2.14
DMA + 2W ⇔ (DMA)(W)2	−16.98	−13.48	4.29
DMA + 3W ⇔ (DMA)(W)3	−27.56	−22.30	4.84
DMA + 4W ⇔ (DMA)(W)4	−36.28	−29.43	6.73
OA + OA ⇔ (OA)2	−6.33	−5.09	3.59
2OA + W ⇔ (OA)2(W)	−17.13	−14.65	3.27
2OA + 2W ⇔ (OA)2(W)2	−33.33	−29.42	−0.65
2OA + 3W ⇔ (OA)2(W)3	−43.94	−38.92	0.09
2OA + 4W ⇔ (OA)2(W)4	−48.65	−41.74	7.33

---

Table 2 Energy changes associated with the formation of (C₂H₂O₄)(CH₃NHCH₃)(H₂O)_n (n = 0–4). The energies are in kcal mol⁻¹, and were calculated at the DF-LMP2-F12/VDZ-F12//M06-2X/6-311+G(2d,p) level of theory

Reactions	ΔE (0 K)	ΔH (298.15 K)	ΔG (298.15 K)
OA + DMA ⇔ (OA)(DMA)	−15.06	−14.2	−4.16
OA + DMA + W ⇔ (OA)(DMA)(W)	−27.99	−25.14	−5.73
(OA)(DMA) + W ⇔ (OA)(DMA)(W)	−12.93	−10.94	−1.58
OA + (DMA)(W) ⇔ (OA)(DMA)(W)	−20.08	−19.04	−7.87
(OA)(W) + DMA ⇔ (OA)(DMA)(W)	−17.90	−16.47	−5.79
OA + DMA + 2W ⇔ (OA)(DMA)(W)2	−39.74	−34.35	−5.31
(OA)(DMA) + 2W ⇔ (OA)(DMA)(W)2	−24.68	−20.15	−1.15
OA + (DMA)(W)2 ⇔ (OA)(DMA)(W)2	−22.76	−20.87	−9.60
(OA)(W) + (DMA)(W) ⇔ (OA)(DMA)(W)2	−21.75	−19.82	−7.48
(OA)(W)2 + DMA ⇔ (OA)(DMA)(W)2	−20.10	−17.69	−6.31
OA + DMA + 3W ⇔ (OA)(DMA)(W)3	−53.88	−46.53	−8.66
(OA)(DMA) + 3W ⇔ (OA)(DMA)(W)3	−38.86	−32.33	−4.50
OA + (DMA)(W)3 ⇔ (OA)(DMA)(W)3	−26.36	−24.23	−13.50
(OA)(W) + (DMA)(W)2 ⇔ (OA)(DMA)(W)3	−26.85	−24.38	−12.98
(OA)(W)2 + (DMA)(W) ⇔ (OA)(DMA)(W)3	−26.36	−23.77	−11.80
(OA)(W)3 + DMA ⇔ (OA)(DMA)(W)3	−25.08	−22.31	−11.01
OA + DMA + 4W ⇔ (OA)(DMA)(W)4	−63.65	−54.34	−5.61
(OA)(DMA) + 4W ⇔ (OA)(DMA)(W)4	−48.59	−40.14	−1.45
OA + (DMA)(W)4 ⇔ (OA)(DMA)(W)4	−27.37	−24.91	−12.34
(OA)(W) + (DMA)(W)3 ⇔ (OA)(DMA)(W)4	−26.01	−23.37	−10.48
(OA)(W)2 + (DMA)(W)2 ⇔ (OA)(DMA)(W)4	−27.02	−24.20	−10.90
(OA)(W)3 + (DMA)(W) ⇔ (OA)(DMA)(W)4	−26.90	−24.02	−10.01
(OA)(W)4 + DMA ⇔ (OA)(DMA)(W)4	−24.02	21.11	−8.48

---

Table 3 Energy changes associated with the formation of (C₂H₂O₄)₂(CH₃NHCH₃)(H₂O)_n (n = 0–2). The energies are in kcal mol⁻¹, and were calculated at the DF-LMP2-F12/VDZ-F12//M06-2X/6-311+G(2d,p) level of theory

Reactions	ΔE (0 K)	ΔH (298.15 K)	ΔG (298.15 K)
2OA + DMA ⇔ (OA)2(DMA)	−34.27	−31.51	−10.80
OA + (DMA)(OA) ⇔ (OA)2(DMA)	−19.21	−17.31	−6.65
(OA)2 + DMA ⇔ (OA)2(DMA)	−27.94	−26.41	−14.39
2OA + DMA + W ⇔ (OA)2(DMA)(W)	−46.79	−42.62	−11.60
2OA + (DMA)(W) ⇔ (OA)2(DMA)(W)	−38.88	−36.52	−13.77
OA + (DMA)(OA) + W ⇔ (OA)2(DMA)(W)	−31.73	−28.42	−7.47
OA + (DMA)(OA)(W) ⇔ (OA)2(DMA)(W)	−18.80	−17.48	−5.90
(OA)(W) + (DMA)(OA) ⇔ (OA)2(DMA)(W)	−21.64	−19.76	−7.45
(OA)2 + DMA + W ⇔ (OA)2(DMA)(W)	−40.46	−37.52	−15.22
(OA)2(DMA) + W ⇔ (OA)2(DMA)(W)	−12.52	−11.11	−0.83
(OA)2 + (DMA)(W) ⇔ (OA)2(DMA)(W)	−32.55	−72.56	−17.36
(OA)2(W) + DMA ⇔ (OA)2(DMA)(W)	−29.65	−27.96	−14.90
2OA + DMA + 2W ⇔ (OA)2(DMA)(W)2	−59.20	−52.63	−12.90
2OA + (DMA)(W)2 ⇔ (OA)2(DMA)(W)2	−42.22	−39.15	−17.15
OA + (DMA)(OA) + 2W ⇔ (OA)2(DMA)(W)2	−44.14	−38.44	−8.70
OA + (DMA)(OA)(W)2 ⇔ (OA)2(DMA)(W)2	−19.46	−18.28	−7.55
(OA)(W) + (DMA)(OA)(W) ⇔ (OA)2(DMA)(W)2	−21.12	−18.83	−7.15
(OA)(W)2 + (DMA)(OA) ⇔ (OA)2(DMA)(W)2	−24.49	−21.78	−9.70
(OA)2 + DMA + 2W ⇔ (OA)2(DMA)(W)2	−52.87	−47.54	−16.45
(OA)2(DMA) + 2W ⇔ (OA)2(DMA)(W)2	−24.93	−21.13	−2.05
(OA)2 + (DMA)(W)2 ⇔ (OA)2(DMA)(W)2	−35.89	−34.06	−20.73
(OA)2(W) + (DMA)(W) ⇔ (OA)2(DMA)(W)2	−34.16	−31.88	−18.26
(OA)2(W)2 + DMA ⇔ (OA)2(DMA)(W)2	−25.86	−23.22	−12.21

---

Table 4 Energy changes associated with the formation of (C₂H₂O₄)₂(CH₃NHCH₃)(H₂O)_n (n = 3–4). The energies are in kcal mol⁻¹, and were calculated at the DF-LMP2-F12/VDZ-F12//M06-2X/6-311+G(2d,p) level of theory

Reactions	ΔE (0 K)	ΔH (298.15 K)	ΔG (298.15 K)
2OA + DMA + 3W ⇔ (OA)2(DMA)(W)3	−68.44	−59.59	−6.54
2OA + (DMA)(W)3 ⇔ (OA)2(DMA)(W)3	−40.89	−37.28	−11.38
OA + (DMA)(OA) + 3W ⇔ (OA)2(DMA)(W)3	−53.38	−45.39	−2.39
OA + (DMA)(OA)(W)3 ⇔ (OA)2(DMA)(W)3	−14.52	−13.06	2.12
(OA)(W) + (DMA)(OA)(W)2 ⇔ (OA)2(DMA)(W)3	−18.61	−16.57	−1.26
(OA)(W)2 + (DMA)(OA)(W) ⇔ (OA)2(DMA)(W)3	−20.80	−17.79	−1.81
(OA)(W)3 + (DMA)(OA) ⇔ (OA)2(DMA)(W)3	−24.54	−21.17	−4.74
(OA)2 + DMA + 3W ⇔ (OA)2(DMA)(W)3	−62.11	−54.49	−10.13
(OA)2(DMA) + 3W ⇔ (OA)2(DMA)(W)3	−34.17	−28.08	4.26
(OA)2 + (DMA)(W)3 ⇔ (OA)2(DMA)(W)3	−34.55	−32.19	−14.97
(OA)2(W) + (DMA)(W)2 ⇔ (OA)2(DMA)(W)3	−34.32	−31.45	−14.10
(OA)2(W)2 + (DMA)(W) ⇔ (OA)2(DMA)(W)3	−27.20	−24.07	−8.03
(OA)2(W)3 + (DMA) ⇔ (OA)2(DMA)(W)3	−24.49	−20.66	−6.63
2OA + DMA + 4W ⇔ (OA)2(DMA)(W)4	−78.79	−68.66	−6.09
2OA + (DMA)(W)4 ⇔ (OA)2(DMA)(W)4	−42.51	−39.23	−12.81
OA + (DMA)(OA) + 4W ⇔ (OA)2(DMA)(W)4	−63.73	−54.47	−1.93
OA + (DMA)(OA)(W)4 ⇔ (OA)2(DMA)(W)4	−15.14	−14.32	−0.48
(OA)(W) + (DMA)(OA)(W)3 ⇔ (OA)2(DMA)(W)4	−14.78	−13.47	2.55
(OA)(W)2 + (DMA)(OA)(W)2 ⇔ (OA)2(DMA)(W)4	−19.40	−17.66	−1.78
(OA)(W)3 + (DMA)(OA)(W) ⇔ (OA)2(DMA)(W)4	−21.96	−19.31	−2.70
(OA)(W)4 + (DMA)(OA) ⇔ (OA)2(DMA)(W)4	−24.10	−21.24	−4.80
(OA)2 + DMA + 4W ⇔ (OA)2(DMA)(W)4	−72.46	−63.57	−9.68
(OA)2(DMA) + 4W ⇔ (OA)2(DMA)(W)4	−44.52	−37.16	4.72
(OA)2 + (DMA)(W)4 ⇔ (OA)2(DMA)(W)4	−36.18	−34.14	−16.40
(OA)2(W) + (DMA)(W)3 ⇔ (OA)2(DMA)(W)4	−34.10	−31.71	−14.19
(OA)2(W)2 + (DMA)(W)2 ⇔ (OA)2(DMA)(W)4	−28.47	−25.77	−9.73
(OA)2(W)3 + (DMA)(W) ⇔ (OA)2(DMA)(W)4	−26.93	−23.64	−8.31
(OA)2(W)4 + DMA ⇔ (OA)2(DMA)(W)4	−30.13	−26.92	−13.42

---

The Gibbs free energy changes of oxalic acid hydration and dimethylamine hydration in our study are summarized in Table 1, and the results are almost all positive except for the cluster with two oxalic acids and two water molecules, which has a value of −0.65 kcal mol⁻¹. The dimethylamine hydration conformations are explained in our earlier study.⁷¹ It may be deduced from Table 1 that the (C₂H₂O₄)_m(H₂O)_n (m = 1–2, n = 0–4) and (CH₃NHCH₃)(H₂O)_n (n = 0–4) clusters may not be favorable in the atmosphere.

The Gibbs free energy changes of the formation of the clusters containing one oxalic acid molecule along with dimethylamine and water are presented in Table 2. The Gibbs free energy of the interaction of oxalic acid with dimethylamine is −4.16 kcal mol⁻¹, while the Gibbs free energy of the interaction of oxalic acid with dimethylamine hydrated with one to four water molecules is −7.87 kcal mol⁻¹, −9.60 kcal mol⁻¹, −13.50 kcal mol⁻¹ and −12.34 kcal mol⁻¹, respectively, 3.71 kcal mol⁻¹, 5.44 kcal mol⁻¹, 9.34 kcal mol⁻¹ and 8.18 kcal mol⁻¹ larger than the unhydrated interaction. In contrast, the free energy of the interaction between oxalic acid hydrated with one to four water molecules and dimethylamine is −5.79 kcal mol⁻¹, −6.31 kcal mol⁻¹, −11.01 kcal mol⁻¹ and −8.48 kcal mol⁻¹, respectively, indicating that the hydration of oxalic acid decreases its reactivity with dimethylamine, while the hydration of dimethylamine enhances its reactivity with oxalic acid. For each cluster size, when unhydrated oxalic acid reacts with hydrated dimethylamine, the maximum free energy of the interaction for oxalic acid and dimethylamine is reached. Compared with a previous study,³⁷ this conclusion is consistent with clusters of SA–DMA–W, but inconsistent with SUA (succinic acid)–DMA–W clusters. The difference of the two dicarboxylic acids likely comes from the hydrophilic properties.⁸³ However, the minimum free energy is observed for the cluster where (C₂H₂O₄)₁(CH₃NHCH₃)₁ interacts with water.

The energy changes for the (C₂H₂O₄)₂(CH₃NHCH₃)₁(H₂O)_n (n = 0–4) clusters are summarized in Table 3. In the case of (C₂H₂O₄)₂(CH₃NHCH₃)₁, the maximum free energy of the interaction of (C₂H₂O₄)₂ with dimethylamine is −14.39 kcal mol⁻¹, 10.23 kcal mol⁻¹ higher than that in (C₂H₂O₄)₁(CH₃NHCH₃)₁. This is consistent with the conformational analysis, since proton transfer occurs readily for the (C₂H₂O₄)₂(CH₃NHCH₃)₁ cluster, while for the (C₂H₂O₄)₁(CH₃NHCH₃)₁ cluster, proton transfer requires water molecules for hydration. When the cluster of (C₂H₂O₄)₂ interacts with (CH₃NHCH₃)₁(H₂O)_n (n = 0–4), the Gibbs free energy changes reached the maximum for each cluster size, −17.36 kcal mol⁻¹, −20.23 kcal mol⁻¹, −14.79 kcal mol⁻¹ and −16.40 kcal mol⁻¹, respectively. This conclusion is in agreement with the interactions of (OA)₁(DMA)₁(W)_n (n = 1–4), where the Gibbs free energies of the (OA)₂(DMA)₁(W)_n (n = 1–4) clusters are larger than those of the (OA)₁(DMA)₁(W)_n (n = 1–4) clusters by 9.49 kcal mol⁻¹, 10.63 kcal mol⁻¹, 1.29 kcal mol⁻¹ and 4.06 kcal mol⁻¹, respectively. For the (C₂H₂O₄)₂(CH₃NHCH₃)₁(H₂O)_n (n = 0–4) clusters, the maximum Gibbs free energy change of the interaction is reached when the number of water molecules is up to two, while for the (C₂H₂O₄)₁(CH₃NHCH₃)₁(H₂O)_n (n = 0–4) clusters the maximum Gibbs free energy change is observed when the number of water molecules is three. This is consistent with the structural explanation, in which the planar ring structure may be more favorable than the cage-like configuration. Furthermore, hydration of the oxalic acid and dimethylamine clusters promotes proton transfer from the oxygen of the carboxylic acid group to the nitrogen of the dimethylamine, indicating the formation of a stabilized dicarboxylate aminium ion pair.

3.3 Temperature dependence of cluster formation

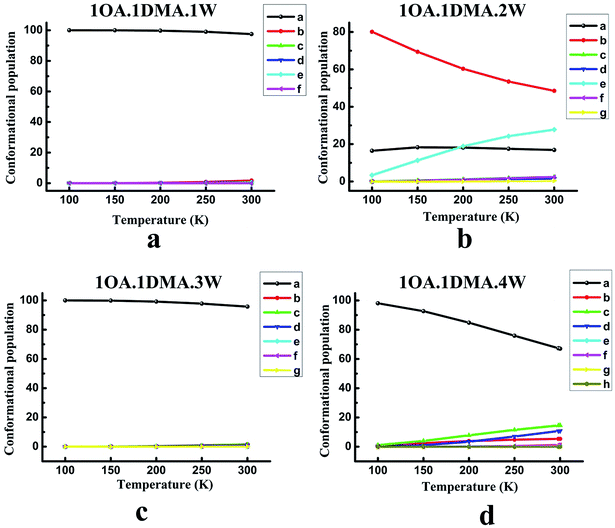
The contribution from the global minimum is important for the ensemble of energetically accessible conformations because it is the most common conformer in the population. However, as the cluster systems become larger and the configurations more complex, the energetic difference between the global minimum and low local minima gets smaller due to the flexible hydrogen bond networks. This would suggest that the presence of local minima in the population might also be significant. Previous studies have revealed that the thermodynamic properties and the stability order of isomers may change at different temperatures.^65,71,84 Thus, understanding the temperature dependence of cluster formation is important, especially at atmospheric temperature. However, because the wall loss of the clusters increases as the temperature decreases, it is hard to perform the relevant experiments at low temperature. Here, theoretical calculations can provide such data. The relevant computational methods have been given in our previous work.⁸⁵

For (OA)(DMA)(W)_n (n = 0–4), the variation of the population distribution of the isomers versus the temperature, ranging from 100 K to 300 K, is presented in Fig. 3. For monohydrates, our calculations predicted that the proportion of isomer-a in the population remained almost constant in the temperature range of 100–300 K. Isomer-a was the most prevalent conformer with a share of practically 100 percent. It is also interesting to notice from Fig. 3(b) that the changes in weighting for the (OA)(DMA)(W)₂ isomers with respect to temperature are very pronounced, especially for isomer-b and isomer-e. The second most stable isomer, isomer-b, is the most common, but its proportion in the population drops significantly from 80% to 49% as the temperature increases from 100 to 300 K. Meanwhile, the proportion of isomer-e increases from 3% to 28% as the temperature increases. Below 200 K, isomer-a is the second most common isomer, but it is replaced by isomer-e when the temperature is above 200 K. However, in the temperature range of 100–300 K, the weighting of isomer-a almost remained constant at about 18%. The other isomers are negligible. In the case of n = 3, given in Fig. 3(c), the results show that the isomer distribution follows a similar trend to the (OA)(DMA)(W)₁ clusters with respect to temperature, as discussed above. For the (OA)(DMA)(W)₄ clusters, our results predict a very smooth decrease in the proportion of isomer-a from 98% to 67% with increasing temperature. The proportion of isomer-b, isomer-c and isomer-d increases slightly, and the growth rate of isomer-c and isomer-d is clearly higher than that of isomer-b.

Fig. 3 The conformational population changes for the low energy isomers of (C₂H₂O₄)(CH₃NHCH₃)(H₂O)_n (n = 1–4) versus the temperature. The top left a, top right b, bottom left c, and bottom right d panels give the results for 1OA.1DMA.1W, 1OA.1DMA.2W, 1OA.1DMA.3W, and 1OA.1DMA.4W clusters, respectively.

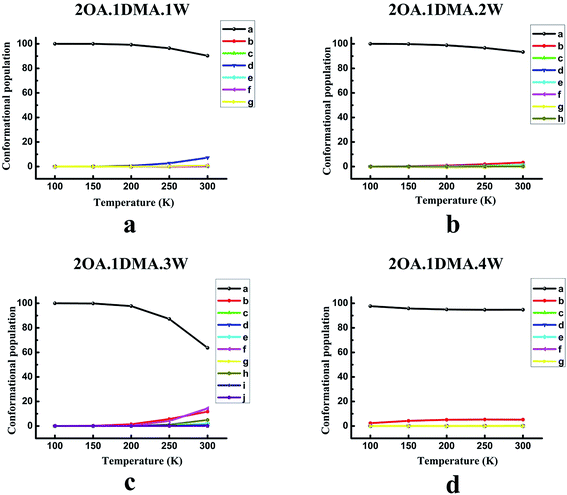
The temperature dependence of the isomer distribution for (OA)₂(DMA)(W)_n (n = 0–4) is displayed in Fig. 4. Fig. 4(a) shows that isomer-a plays a dominant role at temperatures below 200 K, and then diminishes very slightly. As the temperature increases up to 200 K, there is a slight rise in the proportion of isomer-d. It is interesting to find that the population distribution of the isomers of (OA)₂(DMA)(W)_2–3 changes in a similar way to the population distribution of the (OA)₂(DMA)(W)₁ isomers with rising temperature. However, for (OA)₂(DMA)(W)₃, the proportion of isomer-a falls significantly when the temperature is above 200 K, and there is an obvious increase in isomer-b, isomer-f and isomer-h. According to the results in Fig. 4(d), our calculations predict a slight decrease in isomer-a below 200 K, and then the proportion of isomer-a remains approximately constant. Meanwhile, the proportion of isomer-b increases slightly below 200 K, and then remains constant.

Fig. 4 The conformational population changes for the low energy isomers of (C₂H₂O₄)₂(CH₃NHCH₃)(H₂O)_n (n = 1–4) versus the temperature. The top left a, top right b, bottom left c, and bottom right d panels give the results for 2OA.1DMA.1W, 2OA.1DMA.2W, 2OA.1DMA.3W, and 2OA.1DMA.4W clusters, respectively.

In conclusion, at low temperature, the weightings of the global minima are approximately 100%, except for the (OA)(DMA)(W)₂ clusters, which indicates that the structure of all the clusters is the same at low temperature. For the (OA)(DMA)(W)_1,3 clusters, the most stable isomers remain predominant at close to 100% in the temperature range of 100–300 K, due to the considerably different Gibbs free energy values between their global minimum and local minima. The effects of temperature contribute to the alternation of the stability order of the isomers of (OA)(DMA)(W)₂. Our calculation results predict that, for the (OA)₂(DMA)(W)_n (n = 0–4) clusters, 200 K is a turning point. As seen in Fig. 4(a–c), the proportion of isomer-a is almost unchanged below 200 K, and then decreases to a different extent for each cluster size, while isomers of (OA)₂(DMA)(W)₄ vary in the opposite way.

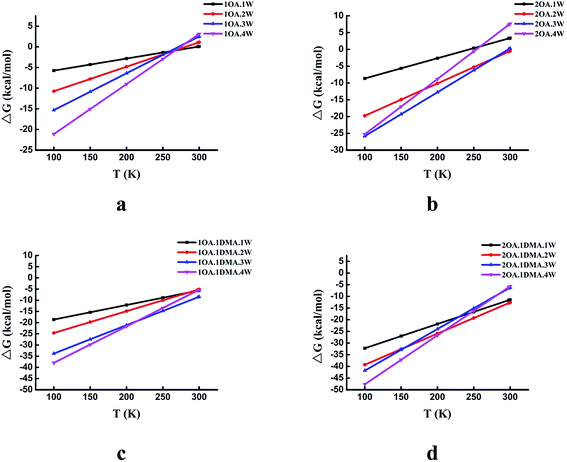
The temperature dependence of the thermodynamic properties is an important parameter that is crucial to understanding how a specific nucleation mechanism plays roles at different temperatures in the atmosphere. Fig. 5 shows the Gibbs free energy changes (in kcal mol⁻¹) for the global minima clusters at different temperatures (100–300 K). The Gibbs free energy changes by approximately 25 kcal mol⁻¹ for the (OA)(W)_n (n = 0–4) clusters, 35 kcal mol⁻¹ for the (OA)₂(W)_n (n = 0–4) clusters, 33 kcal mol⁻¹ for the (OA)(DMA)(W)_n (n = 0–4) clusters, and 43 kcal mol⁻¹ for the (OA)₂(DMA)(W)_n (n = 0–4) clusters from 100 K to 300 K. For the (OA)(W)_n (n = 0–4) and (OA)₂(W)_n (n = 0–4) clusters, all of the clusters may be favored at low temperature, while at room temperature, all of the clusters are unfavorable except for (OA)₂(W)₂. Meanwhile, for the (OA)(DMA)(W)_n (n = 0–4) and (OA)₂(DMA)(W)_n (n = 0–4) clusters, cluster formation is favored at temperatures from 100 K to 300 K. There is a similar trend for all complexes, in which cluster formation becomes unfavorable as the temperature gradually increases. The different temperature dependence behaviors between oxalic acid hydrate and oxalic acid–dimethylamine could be explained by the enhanced stability from acid–base binding for the latter.

Fig. 5 The Gibbs free energy changes (in kcal mol⁻¹) for the global minima clusters at different temperatures. The top left (a), top right (b), bottom left (c), and bottom right (d) panels give the results for 1OA·nW, 2OA·nW, 1OA·1DMA·nW, and 2OA·1DMA·nW, respectively.

3.4 Atmospheric relevance

In previous studies,^37,56 it was shown that hydration plays an important role in the interaction of amines and dicarboxylic acids, indicating that dicarboxylic acids can contribute to aerosol nucleation. The formation energies and structures of oxalic acid with dimethylamine show that oxalic acid combines with dimethylamine in the atmosphere by forming aminium dicarboxylate ion pairs, which contribute to the nucleation of atmospheric nanoparticles. In addition, hydration affects proton transfer from oxalic acid to dimethylamine. However, the number of water molecules in the clusters is affected by the relative humidity (RH). To get further results, the hydrate distributions of the “core” (C₂H₂O₄)₁(CH₃NHCH₃) and (C₂H₂O₄)₂(CH₃NHCH₃) were estimated at different RHs. As an n-hydrate in this study, the relative concentration can be given as:
where K_n is the equilibrium constant for the formation of an n-hydrate from one water molecule and an (n − 1)-hydrate. ρ represents the concentration of different species and S is the saturation ratio, defined as the ratio of the proper partial pressure of the water vapor to the saturation vapor pressure, and thus the relative humidity is defined as RH = 100% × S, and the reference pressure P is 1 atm. The hydration level, n, can be any value between 1 and 4.

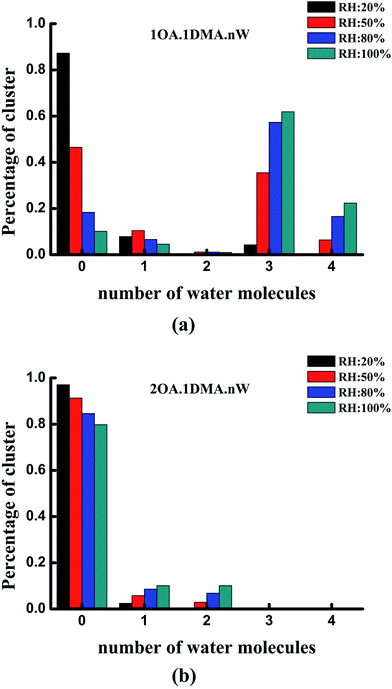
The hydrate distributions for all of the studied core clusters are presented in Fig. 6 for four values of RH (20%, 50%, 80% and 100%) with a constant temperature of 298.15 K. As shown in Fig. 6(a), the total concentration of the (C₂H₂O₄)₁(CH₃NHCH₃)₁ cluster was mainly dispersed as the un-, tri- and tetrahydrates. As RH increases, the most prevalent species changes from unhydrated clusters to trihydrates. When the RH is close to 50%, more than 50% of the clusters are hydrated. The dihydrated cluster almost does not exist at 20%, but is present at a proportion of as much as 6% at a relative humidity of 80%. The hydration patterns of the clusters containing two oxalic acid molecules with one dimethylamine are revealed in Fig. 6(b). The unhydrated cluster clearly dominates the cluster distribution, irrespective of whether the humidity is low or high. With increasing RH, the percentage of unhydrated clusters gradually decreases slightly from 91% to 80%, while the percentage of mono- and dihydrates increases gradually from 2% to 10%, and 0.5% to 10%, respectively. The larger hydrated clusters are virtually nonexistent at the various relative humidities.

Fig. 6 Hydrate distributions of clusters with one oxalic acid molecule and dimethylamine (a), and clusters with two oxalic acid molecules and dimethylamine (b) at four different relative humidities. In all cases, the temperature is 298.15 K.

Under the most tropospherically reasonable conditions, the peak hydration distribution shifts from unhydrated clusters to trihydrates for the (OA)(DMA)(W)_n (n = 0–4) clusters. This behavior can probably be explained by analyzing the conformation of the (OA)(DMA)(W)_n (n = 0–4) clusters: here the oxalic acid is still intact for the unhydrated cluster, as opposed to the hydrated clusters where the acid has dissociated forming a dicarboxylate aminium ion pair, creating stronger bonding. Meanwhile, for the (OA)₂(DMA)₁(W)_n (n = 0–4) clusters, the distribution peak stays at the unhydrated level. Similar reasoning also explains the distribution of the clusters containing two oxalic acid molecules with dimethylamine, since the proton transfer reaction that occurs forms the most strongly bound of all the two acid–dimethylamine clusters. At the same relative humidity, the distribution of the hydrates may not only be influenced by the relative humidity, but may also be related to the stability of the clusters under atmospherically relevant conditions.

3.5 Evaporation rates

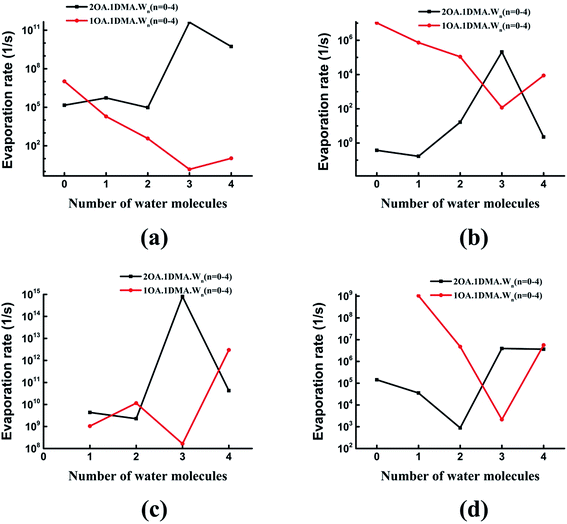
Recently, the cluster evaporation rates based on the formation free energy gained by quantum chemical calculation have been identified to be a significant parameter to investigate the very early stages of particle formation.^86,87 As can be seen in Fig. 7(a), for hydrated clusters just containing one oxalic acid and one dimethylamine molecule, the evaporation of DMA will be more preferred than evaporation of OA. The reason for this high DMA evaporation rate is that the hydrated oxalic acid cluster is more stable than the hydrated dimethylamine cluster. As hydration of the neutral clusters significantly affects the collision rate, the presence of water qualitatively changes the effect of OA and DMA on the evaporation rates. The stability of the clusters increases as the number of water molecules increases up to three, due to a marked drop in the evaporation rate of both oxalic acid and dimethylamine molecules. Obviously, the evaporation of water is more significant than the evaporation of oxalic acid and dimethylamine. This is due to the very simple reason that proton transfers from oxalic acid to dimethylamine play an important role in stabilizing the acid–base cluster. The evaporation rates after adding a second oxalic acid molecule are shown in Fig. 7(b). The evaporation of oxalic acid starts to be more important than the evaporation of DMA, around 3–9 orders of magnitude higher. The (OA)₂(DMA)(W)_n (n = 0–4) ⇔ (OA)(DMA) + (OA)(W)_n (n = 0–4) fission rate is smaller than the evaporation rate of one oxalic acid molecule, but higher than the evaporation rate of the dimethylamine molecule, so the cluster's lifetime will be determined by the evaporation rate of oxalic acid rather than the fission process. When the number of water molecules is increased to four, the evaporation rate of oxalic acid is considerably close to the evaporation rate of water. For all clusters, evaporation of the water molecules is always preferred. Hydration of the (OA)(DMA) clusters has a more important effect on the acid or base evaporation rate than hydration of the (OA)₂(DMA) clusters. This is because water molecules promote proton transfer for the (OA)(DMA) clusters, while for the (OA)₂(DMA) clusters, protons transfer without water molecules.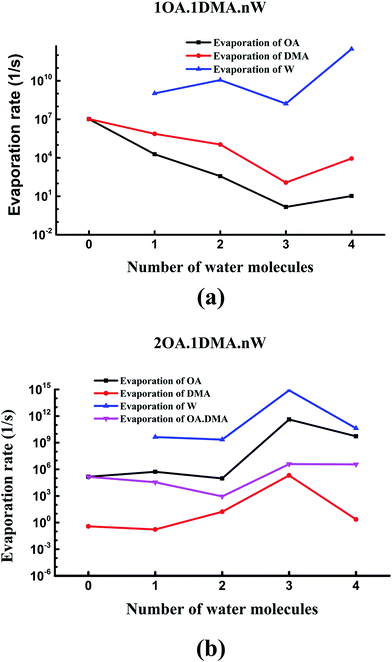

Fig. 7 Evaporation rates of oxalic acid, dimethylamine and water molecules from (C₂H₂O₄)(CH₃NHCH₃)(H₂O)_n (n = 0–4) clusters (a), and (C₂H₂O₄)₂(CH₃NHCH₃)(H₂O)_n (n = 0–4) clusters (b).

Fig. 8 shows the difference in the evaporation rates of the clusters containing one or two oxalic acid molecules. For the unhydrated clusters, the evaporation of OA is higher for (OA)(DMA) than for (OA)₂(DMA) by two orders of magnitude. The reason for this high OA evaporation rate is that the formation of the dicarboxylate aminium ion pair for the (OA)₂(DMA) cluster stabilizes the cluster. As the clusters are hydrated, our results, shown in Fig. 8(a), show that the evaporation rate of OA from (OA)₁(DMA)(W)_n (n = 1–4) is low compared to that from (OA)₂(DMA)(W)_n (n = 1–4). For the clusters containing the same DMA molecule, it can be seen in Fig. 8(b) that the evaporation rate of dimethylamine from the (OA)(DMA)(W)_n clusters is larger than that from the (OA)₂(DMA)(W)_n clusters, except for the clusters with three water molecules. For the clusters with one or two water molecules, the evaporation rate of water from (OA)(DMA)(W)_n is close to that from (OA)₂(DMA)(W)_n. However, the difference in the evaporation rate of water changes significantly after adding a third water molecule, by around six orders of magnitude. In addition to the evaporation of the monomers, we also investigated cluster fission, as shown in Fig. 8(d). Our results show that the (OA)_m(DMA)(W)_n ⇔ (OA)(DMA) + (W)_n/(OA)(W)_n fission rate follows a similar trend to the DMA evaporation rate with respect to the number of water molecules, as discussed above. A discrepancy in the trend of the evaporation rate for the clusters with three water molecules is that (OA)(DMA)(W)₃ is the most stable cluster for the (OA)(DMA)(W)_n clusters.

Fig. 8 Evaporation rates from (C₂H₂O₄)(CH₃NHCH₃)(H₂O)_n (n = 1–4) and (C₂H₂O₄)₂(CH₃NHCH₃)(H₂O)_n (n = 0–4) clusters. The top left (a), top right (b), bottom left (c), and bottom right (d) panels give the results for evaporation of OA, DMA, W, and 1OA·1DMA, respectively.

Comparing the evaporation rates, we can see that the evaporation reactions of water molecules are more important than the evaporation reactions of the acid and base molecules. For the (OA)(DMA)(W)_n clusters, hydration can decrease the evaporation rates of oxalic acid and dimethylamine, which contributes to the formation of the dicarboxylate aminium ion pair, promoted by water molecules. For clusters containing one OA and one DMA molecule, evaporation of DMA is preferred compared to OA, while the results are reversed for the (OA)₂(DMA)(W)_n clusters.

4. Conclusions

In this study, the hydration of oxalic acid and dimethylamine has been investigated to reveal the interaction between oxalic acid and dimethylamine. For studying larger clusters, we have benchmarked the commonly used DFT methods and DF-LMP2-F12/VDZ-F12 method against CCSD(T)-F12/VDZ-F12. We find that the DF-LMP2-F12/VDZ-F12//M06-2X/6-311+G(2d,p) method is a good compromise between efficiency and accuracy. The clusters containing one or two oxalic acid molecules with dimethylamine and up to 4 water molecules are studied. The results show that hydration promotes proton transfer from oxalic acid to dimethylamine for (C₂H₂O₄)(CH₃NHCH₃)(H₂O)_n (n = 0–4), while proton transfer occurs without hydration when the number of oxalic acid molecules increases up to two. The Gibbs free energy values show that the interaction between oxalic acid and dimethylamine is strongly dependent on the degree of hydration of the acids and dimethylamine. The maximum free energy change of the reaction is reached for the different cluster sizes, when oxalic acid is unhydrated while dimethylamine is hydrated. The interaction energy of oxalic acid with dimethylamine suggests that oxalic acid combines with dimethylamine by forming aminium dicarboxylate ion pairs, which may participate in the nucleation of atmospheric new particle formation. In view of the isomer distribution at the potential energy surface, temperature seems not to be an important parameter since almost all of the global minima for the investigated size range dominate within the temperature range studied, except for the (C₂H₂O₄)_m(CH₃NHCH₃)(H₂O)₂ clusters. The hydration distribution changes significantly as the relative humidity increases for (C₂H₂O₄)(CH₃NHCH₃)(H₂O)_n, while for the (C₂H₂O₄)₂(CH₃NHCH₃)(H₂O)_n clusters, the hydration of the (C₂H₂O₄)₂(CH₃NHCH₃) core is insignificant. Finally, the formation free energies obtained from quantum calculations were used to calculate the evaporation rates. We found that the evaporation of dimethylamine is preferred compared to oxalic acid for the (C₂H₂O₄)(CH₃NHCH₃)(H₂O)_n clusters, while the results are reversed for the (C₂H₂O₄)₂(CH₃NHCH₃)(H₂O)_n clusters.

Our results tentatively provide a reference for further study of nucleation from clusters containing dimethylamine and oxalic acid in the atmosphere. Further experimental and theoretical studies are required to investigate the synergetic effect of oxalic acid and dimethylamine on the nucleation system involving sulfuric acid, oxalic acid, dimethylamine and water.

Acknowledgements

This study was supported by grants from the National Natural Science Foundation of China (Grant No. 21403244, 21133008, 21573241, 41527808 and 41505114), the Director Foundation of AIOFM (AGHH201505, Y23H161131), the National Key Research and Development Program of China (Grant No. 2016YFC0202203, 2016YFC0203703), the National High Technology Research and Development Program of China (863 Program) (Grant No. 2014AA06A501), and the program of Formation Mechanism and Control Strategies of Haze in China (Grant No. XDB05000000). We also appreciate the “Interdisciplinary and Cooperative Team” of CAS and the “Thousand Youth Talents” program. The computation was performed at EMSL, a national scientific user facility sponsored by the Department of Energy's Office of Biological and Environmental Research, which is located at Pacific Northwest National Laboratory (PNNL). PNNL is a multi-program national laboratory operated for the DOE by Battelle. Part of the computation was performed at the Supercomputing Center of USTC.

References

1. R. Zhang, G. Li, J. Fan, D. L. Wu and M. J. Molina, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 5295–5299.
2. M. J. Molina, L. T. Molina, R. Zhang, R. F. Meads and D. D. Spencer, Geophys. Res. Lett., 1997, 24, 1619–1622.
3. R. Zhang, M.-T. Leu and M. J. Molina, Geophys. Res. Lett., 1996, 23, 1669–1672.
4. G. Li, R. Zhang, J. Fan and X. Tie, J. Geophys. Res., 2005, 110, D23206.
5. R. Makkonen, A. Asmi, V. M. Kerminen, M. Boy, A. Arneth, P. Hari and M. Kulmala, Atmos. Chem. Phys., 2012, 12, 1515–1524.
6. J. Kazil, P. Stier, K. Zhang, J. Quaas, S. Kinne, D. O'Donnell, S. Rast, M. Esch, S. Ferrachat, U. Lohmann and J. Feichter, Atmos. Chem. Phys., 2010, 10, 10733–10752.
7. M. B. Baker and T. Peter, Nature, 2008, 451, 299–300.
8. M. Kulmala, H. Vehkamäki, T. Petäjä, M. Dal Maso, A. Lauri, V. M. Kerminen, W. Birmili and P. H. McMurry, J. Aerosol Sci., 2004, 35, 143–176.
9. A. Saxon and D. Diaz-Sanchez, Nat. Immunol., 2005, 6, 223–226.
10. G. Oberdörster and M. J. Utell, Environ. Health Perspect., 2002, 110, A440.
11. J. Merikanto, D. V. Spracklen, G. W. Mann, S. J. Pickering and K. S. Carslaw, Atmos. Chem. Phys., 2009, 9, 8601–8616.
12. R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2012, 112, 1957–2011.
13. B. R. Bzdek, M. R. Pennington and M. V. Johnston, J. Aerosol Sci., 2012, 52, 109–120.
14. F. L. Eisele and D. R. Hanson, J. Phys. Chem., 2000, 104, 830–836.
15. D. R. Hanson and F. L. Eisele, J. Geophys. Res., 2002, 107, AAC10.
16. H. Junninen, M. Ehn, T. Petäjä, L. Luosujärvi, T. Kotiaho, R. Kostiainen, U. Rohner, M. Gonin, K. Fuhrer, M. Kulmala and D. R. Worsnop, Atmos. Meas. Tech., 2010, 3, 1039–1053.
17. T. Jokinen, M. Sipilä, H. Junninen, M. Ehn, G. Lönn, J. Hakala, T. Petäjä, R. L. Mauldin, M. Kulmala and D. R. Worsnop, Atmos. Chem. Phys., 2012, 12, 4117–4125.
18. J. Zhao, F. L. Eisele, M. Titcombe, C. Kuang and P. H. McMurry, J. Geophys. Res., 2010, 115, D08205.
19. J. Jiang, J. Zhao, M. Chen, F. L. Eisele, J. Scheckman, B. J. Williams, C. Kuang and P. H. McMurry, Aerosol Sci. Technol., 2011, 45, ii–v.
20. J. N. Smith, M. J. Dunn, T. M. VanReken, K. Iida, M. R. Stolzenburg, P. H. McMurry and L. G. Huey, Geophys. Res. Lett., 2008, 35, L04808.
21. C. Kuang, I. Riipinen, S. L. Sihto, M. Kulmala, A. V. McCormick and P. H. McMurry, Atmos. Chem. Phys., 2010, 10, 8469–8480.
22. M. Kulmala and V.-M. Kerminen, Atmos. Res., 2008, 90, 132–150.
23. J. Herb, Y. Xu, F. Yu and A. B. Nadykto, J. Phys. Chem. A, 2013, 117, 133–152.
24. M. E. Erupe, A. A. Viggiano and S. H. Lee, Atmos. Chem. Phys., 2011, 11, 4767–4775.
25. D. R. Benson, J. H. Yu, A. Markovich and S. H. Lee, Atmos. Chem. Phys., 2011, 11, 4755–4766.
26. D. R. Benson, L.-H. Young, F. R. Kameel and S.-H. Lee, J. Geophys. Res., 2008, 35, L11801.
27. T. Kurtén, L. Torpo, C.-G. Ding, H. Vehkamäki, M. R. Sundberg, K. Laasonen and M. Kulmala, J. Geophys. Res., 2007, 112, D04210.
28. N. Bork, J. Elm, T. Olenius and H. Vehkamäki, Atmos. Chem. Phys., 2014, 14, 12023–12030.
29. J. W. DePalma, D. J. Doren and M. V. Johnston, J. Phys. Chem. A, 2014, 118, 5464–5473.
30. I. K. Ortega, T. Olenius, O. Kupiainen-Määttä, V. Loukonen, T. Kurtén and H. Vehkamäki, Atmos. Chem. Phys., 2014, 14, 7995–8007.
31. E. R. Lovejoy, J. Curtius and K. D. Froyd, J. Geophys. Res., 2004, 109, D08204.
32. F. Yu and R. P. Turco, J. Geophys. Res., 2000, 27, 883–886.
33. R. Zhang, I. Suh, J. Zhao, D. Zhang, E. C. Fortner, X. Tie, L. T. Molina and M. J. Molina, Science, 2004, 304, 1487–1490.
34. R. Zhang, Science, 2010, 328, 1366–1367.
35. J. Elm and K. V. Mikkelsen, Chem. Phys. Lett., 2014, 615, 26–29.
36. W. Xu and R. Zhang, J. Phys. Chem. A, 2012, 116, 4539–4550.
37. W. Xu and R. Zhang, J. Chem. Phys., 2013, 139, 064312.
38. J. M. Mäkelä, S. Yli-Koivisto, V. Hiltunen, W. Seidl, E. Swietlicki, K. Teinila, M. Sillanpää, I. K. Koponen, J. Paatero, K. Rosman and K. Hameri, Tellus, Ser. B, 2001, 53, 380–393.
39. J. N. Smith, K. C. Barsanti, H. R. Friedli, M. Ehn, M. Kulmala, D. R. Collins, J. H. Scheckman, B. J. Williams and P. H. McMurry, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6634–6639.
40. J. Zhao, J. N. Smith, F. L. Eisele, M. Chen, C. Kuang and P. H. McMurry, Atmos. Chem. Phys., 2011, 11, 10823–10836.
41. J. Almeida, S. Schobesberger, A. Kurten, I. K. Ortega, O. Kupiainen-Maatta, A. P. Praplan, A. Adamov, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, N. M. Donahue, A. Downard, E. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, H. Henschel, T. Jokinen, H. Junninen, M. Kajos, J. Kangasluoma, H. Keskinen, A. Kupc, T. Kurten, A. N. Kvashin, A. Laaksonen, K. Lehtipalo, M. Leiminger, J. Leppa, V. Loukonen, V. Makhmutov, S. Mathot, M. J. McGrath, T. Nieminen, T. Olenius, A. Onnela, T. Petaja, F. Riccobono, I. Riipinen, M. Rissanen, L. Rondo, T. Ruuskanen, F. D. Santos, N. Sarnela, S. Schallhart, R. Schnitzhofer, J. H. Seinfeld, M. Simon, M. Sipila, Y. Stozhkov, F. Stratmann, A. Tome, J. Trostl, G. Tsagkogeorgas, P. Vaattovaara, Y. Viisanen, A. Virtanen, A. Vrtala, P. E. Wagner, E. Weingartner, H. Wex, C. Williamson, D. Wimmer, P. Ye, T. Yli-Juuti, K. S. Carslaw, M. Kulmala, J. Curtius, U. Baltensperger, D. R. Worsnop, H. Vehkamaki and J. Kirkby, Nature, 2013, 502, 359–363.
42. V. Loukonen, T. Kurtén, I. K. Ortega, H. Vehkamäki, A. A. H. Pádua, K. Sellegri and M. Kulmala, Atmos. Chem. Phys., 2010, 10, 4961–4974.
43. A. Nadykto, F. Yu, M. Jakovleva, J. Herb and Y. Xu, Entropy, 2011, 13, 554–569.
44. T. Kurtén, Entropy, 2011, 13, 915–923.
45. Y. Xu, A. B. Nadykto, F. Yu, L. Jiang and W. Wang, J. Mol. Struct.: THEOCHEM, 2010, 951, 28–33.
46. Y. Xu, A. B. Nadykto, F. Yu, J. Herb and W. Wang, J. Phys. Chem. A, 2010, 114, 387–396.
47. A. J. Prenni, P. J. DeMott, S. M. Kreidenweis, D. E. Sherman, L. M. Russell and Y. Ming, J. Phys. Chem. A, 2001, 105, 11240–11248.
48. B. Kärcher and T. Koop, Atmos. Chem. Phys., 2005, 5, 703–704.
49. B. Zobrist, C. Marcolli, T. Koop, B. P. Luo, D. M. Murphy, U. Lohmann, A. A. Zardini, U. K. Krieger, T. Corti, D. J. Cziczo, S. Fueglistaler, P. K. Hudson, D. S. Thomson and T. Peter, Atmos. Chem. Phys., 2006, 6, 3115–3129.
50. H. Giebl, A. Berner, G. Reischl, H. Puxbaum, A. Kasper-Giebl and R. Hitzenberger, J. Aerosol Sci., 2002, 33, 1623–1634.
51. A. B. Nadykto and F. Yu, Phys. Rev. Lett., 2004, 93, 016101.
52. A. Limbeck, H. Puxbaum, L. Otter and M. C. Scholes, Atmos. Environ., 2001, 35, 1853–1862.
53. P. K. Martinelango, P. K. Dasgupta and R. S. Al-Horr, Atmos. Environ., 2007, 41, 4258–4269.
54. P. A. Makar, Atmos. Environ., 2001, 35, 961–974.
55. M. Ehn, H. Junninen, T. Petäjä, T. Kurtén, V. M. Kerminen, S. Schobesberger, H. E. Manninen, I. K. Ortega, H. Vehkamäki, M. Kulmala and D. R. Worsnop, Atmos. Chem. Phys., 2010, 10, 8513–8530.
56. X.-Q. Peng, T. Huang, S.-K. Miao, J. Chen, H. Wen, Y.-J. Feng, Y. Hong, C.-Y. Wang and W. Huang, RSC Adv., 2016, 6, 46582–46593.
57. K. H. Weber, Q. Liu and F. M. Tao, J. Phys. Chem. A, 2014, 118, 1451–1468.
58. T. Kurtén, V. Loukonen, H. Vehkamäki and M. Kulmala, Atmos. Chem. Phys., 2008, 8, 4095–4103.
59. X. Ge, A. S. Wexler and S. L. Clegg, Atmos. Environ., 2011, 45, 561–577.
60. X. Ge, A. S. Wexler and S. L. Clegg, Atmos. Environ., 2011, 45, 524–546.
61. W. A. Glasoe, K. Volz, B. Panta, N. Freshour, R. Bachman, D. R. Hanson, P. H. McMurry and C. Jen, J. Geophys. Res.: Atmos., 2015, 120, 1933–1950.
62. C. N. Jen, P. H. McMurry and D. R. Hanson, J. Geophys. Res.: Atmos., 2014, 119, 7502–7514.
63. J. Zhao, A. Khalizov, R. Y. Zhang and R. McGraw, J. Phys. Chem. A, 2009, 113, 680–689.
64. Y. P. Zhu, Y. R. Liu, T. Huang, S. Jiang, K. M. Xu, H. Wen, W. J. Zhang and W. Huang, J. Phys. Chem. A, 2014, 118, 7959–7974.
65. S.-K. Miao, S. Jiang, J. Chen, Y. Ma, Y.-P. Zhu, Y. Wen, M.-M. Zhang and W. Huang, RSC Adv., 2015, 5, 48638–48646.
66. W. Huang, R. Pal, L. M. Wang, X. C. Zeng and L. S. Wang, J. Chem. Phys., 2010, 132, 054305.
67. W. Huang and L. S. Wang, Phys. Rev. Lett., 2009, 102, 153401.
68. W. Huang, M. Ji, C.-D. Dong, X. Gu, L.-M. Wang, X. G. Gong and L.-S. Wang, ACS Nano, 2008, 2, 897–904.
69. K.-M. Xu, T. Huang, H. Wen, Y.-R. Liu, Y.-B. Gai, W.-J. Zhang and W. Huang, RSC Adv., 2013, 3, 24492–24502.
70. L. L. Yan, Y. R. Liu, T. Huang, S. Jiang, H. Wen, Y. B. Gai, W. J. Zhang and W. Huang, J. Chem. Phys., 2013, 139, 244312.
71. J. Chen, S. Jiang, S.-K. Miao, X.-Q. Peng, Y. Ma, C.-Y. Wang, M.-M. Zhang, Y.-R. Liu and W. Huang, RSC Adv., 2015, 5, 91500–91515.
72. S. Jiang, T. Huang, Y. R. Liu, K. M. Xu, Y. Zhang, Y. Z. Lv and W. Huang, Phys. Chem. Chem. Phys., 2014, 16, 19241–19249.
73. S. Jiang, Y. R. Liu, T. Huang, H. Wen, K. M. Xu, W. X. Zhao, W. J. Zhang and W. Huang, J. Comput. Chem., 2014, 35, 159–165.
74. Y.-R. Liu, H. Wen, T. Huang, X.-X. Lin, Y.-B. Gai, C.-J. Hu, W.-J. Zhang and W. Huang, J. Phys. Chem. A, 2014, 118, 508–516.
75. B. Delley, J. Chem. Phys., 1990, 92, 508–517.
76. M. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision A. 02, Wallingford, CT, 2009, vol. 270, p. 271.
77. H. Werner, P. Knowles, G. Knizia, F. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov and G. Rauhut, MOLPRO, version 2010.1, Cardiff University, Cardiff, UK, 2010.
78. J. Elm, M. Bilde and K. V. Mikkelsen, J. Chem. Theory Comput., 2012, 8, 2071–2077.
79. H. R. Leverentz, J. I. Siepmann, D. G. Truhlar, V. Loukonen and H. Vehkamäki, J. Phys. Chem. A, 2013, 117, 3819–3825.
80. N. Bork, L. Du and H. G. Kjaergaard, J. Phys. Chem. A, 2014, 118, 1384–1389.
81. N. Bork, L. Du, H. Reiman, T. Kurten and H. G. Kjaergaard, J. Phys. Chem. A, 2014, 118, 5316–5322.
82. J. Elm, M. Bilde and K. V. Mikkelsen, Phys. Chem. Chem. Phys., 2013, 15, 16442–16445.
83. R. Zhang, L. Wang, A. F. Khalizov, J. Zhao, J. Zheng, R. L. McGraw and L. T. Molina, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17650–17654.
84. A. Vargas-Caamal, J. L. Cabellos, F. Ortiz-Chi, H. S. Rzepa, A. Restrepo and G. Merino, Chem.–Eur. J., 2016, 22, 2812–2818.
85. X.-Q. Peng, Y.-R. Liu, T. Huang, S. Jiang and W. Huang, Phys. Chem. Chem. Phys., 2015, 17, 9552–9563.
86. I. K. Ortega, O. Kupiainen, T. Kurtén, T. Olenius, O. Wilkman, M. J. McGrath, V. Loukonen and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 225–235.
87. M. J. McGrath, T. Olenius, I. K. Ortega, V. Loukonen, P. Paasonen, T. Kurtén, M. Kulmala and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 2345–2355.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra27945g

---