Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polymorphism of a hexadecane–heptadecane binary system in nanopores
Jian Suia,
Shi Qi Zhanga,
Min Zhaia,
Fang Tiana,
Jian Zhangb and
Xiao Zheng Lan *a
*a
aCollege of Chemistry and Materials Science, Shandong Agricultural University, Tai'an 271018, Shandong, China. E-mail: lanxzh@sdau.edu.cn; Fax: +86-538-8242251; Tel: +86-538-8247753
bDalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, China
First published on 8th February 2017
Abstract
Inspired by the interest in the confinement effect on polymorphism of alkane mixtures, phase behaviors of a hexadecane–heptadecane (n-C16H34–C17H36, C16–C17) binary system in the bulk and in nanopores of controlled porous glasses (CPGs) are investigated using differential scanning calorimetry (DSC) and temperature-dependent powder X-ray diffraction (XRD). As reported, bulk C16–C17 mixtures form two intermediate phases with monoclinic (Mdci) and orthorhombic (Op) structures in a low temperature range and rotator phase RI in high temperature range. In the pores of CPG (300 nm), these solid phases appear in the temperatures slightly below the bulk system. The RI one-phase region extends a bit in temperature range in the mixtures of high C17 components. In CPG (8.1 nm), the solid phases come up in much lower temperatures than the bulk. The rotator RI is found in a larger range of the temperature and composition than the bulk and in CPG (300 nm). A new phase, the rotator RII, is observed in a narrow temperature range of high C17 composition just before melting. XRD analysis shows diffractions from the alkane layered ordering in CPG (300 nm) with a more roughened layer surface than the bulk. Lamellar stacking of the solids in CPG (8.1 nm) is heavily perturbed. The variation in the polymorphism of C16–C17 mixtures in the nanopores is associated with the reduced ordering of the molecule arrangements. These results can help to understand the influence of confinement effect on binary mixtures of alkanes, the chain molecules.
Introduction
Since Jackson and McKenna's first work in 1990, the nanoconfinement effect on physical properties of materials has been investigated in many fields such as adsorption, intrusion, catalysis, design and drug delivery and fabrication of energy-related nanomaterials.1–7 It is found that the freezing/melting points of many pure fluids as water, organic liquids confined in nanopores follow the Gibbs–Thomson equation.3,8–11 In a more general model, the transition temperature of a confined fluid can be estimated from the size, the relative interface interactions of fluid–fluid to fluid-wall, and pore geometries.5,12–14 Basically, the existing states of the molecules in nanopores determine the properties of the confined fluids. As a common case, the molecules can form a non-freezing layer near the pore wall and a freezable core which also may be in a heterogeneous state. For the crystalline phase, the non-polymorphic fluid normally takes the same structure as the bulk, for example water inside SBA-15 in a defective hexagonal crystal.4 Polymorphic materials in nanopores, like glycine or acetaminophen in CPGs or anodic aluminum oxide film (AAO),6 may show much different crystallization behaviour to the bulk. The metastable or uncommon forms are stabilized under nanoconfinement, which might be favoured by nucleation mechanism, competition among growing crystal species and free path length.6,15–17 Although with the previous efforts, it is still a challenge to predict the nanoconfinement effect such as the influence to the heterogeneous distribution of molecules in the pores, the preference of a structure in polymorphic materials. It therefore needs more experiments to reveal new physical phenomena in confined space.Polymorphism of normal alkanes (Cn) in nanopores provides an interesting system for observation of nanoconfinement effect on polymorphs and phase transitions of chain molecules.18 According to Huber's work, pure C12 in CPG (10 nm) shows a same phase sequence between triclinic structure and liquid phase, T12 ↔ L, as the bulk on both cooling and heating. In the same porous matrix, a new phase rotator RI, one of specific plastic solids of the chain-molecule alkanes, appears on cooling of C14, and both on cooling and heating of C16.19 Besides rotator RI and stable orthorhombic phase (O19) as in the bulk, a new phase rotator RII was observed in C19 in CPG (∼7 nm) upon cooling and heating.20 In our work, C16 displays new rotators RI, and RII on cooling and RI on heating in CPG (8.1 nm), new RI and RII on cooling and heating in SBA-15 (7.8 nm) and carbon-filmed C-SBA-15 (15.6 nm), new RI on cooling and heating in SBA-15 (17.2 nm) and KIT-6 (8.6 nm).21 C18 in CPG (8.1 nm) exhibits new rotators RI and RII on heating.22 C16–C18 binary system in CPG (8.1 nm) varies largely compared to the bulk.22 A new rotator phase RII in mixtures is found in a range of several degrees before melting. These results present a general more complicated polymorphism of the normal alkanes under nanoconfinement.
Normal alkanes are not only useful model systems in investigation of crystallization of polymers and bio-membranes but the important products in petroleum industry.23 As an even-numbered member, bulk C16 has a stable crystalline form of triclinic structure T16 with unit cell parameters a = 4.29 Å, b = 4.82 Å, c = 22.36 Å, α = 84.57°, β = 67.31°, γ = 72.73°,24 space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) .25 The T16 phase melt directly into isotropic liquid after heated to melting point. As an odd-numbered member, bulk C17 owns a stable orthorhombic crystal (Oi) (a = 7.432 Å, b = 4.956 Å, c = 46.87 Å, space group Pbcm24,25), and a stable rotator RI. The C16–C17 mixtures possess intermediate phases Op and Mdci in low temperatures, and a wide scope of RI phase in high temperature range.26 Research of phase behaviour of C16–C17 system in nanopores can provide more information of confinement effect on binary system, which is little known at present and cannot be predicted as the Gibbs–Thomson equation for a pure material. Although the phase behaviour of C16–C18 system in some nanopores is investigated, those results are highly expected not to be the same for C16–C17 binary mixtures. It is because the two systems in bulk have completely different phase regions in the structure of solid phases, especially in temperature and mole fraction boundaries, which shows even–even and even–odd effect in the binary alkanes. The difference in the phase behaviours of the two systems at nanoscale will display the effect of the average chain length of the alkane mixtures and stabilities of alkane solids, whether/how the possible new phase appears.
.25 The T16 phase melt directly into isotropic liquid after heated to melting point. As an odd-numbered member, bulk C17 owns a stable orthorhombic crystal (Oi) (a = 7.432 Å, b = 4.956 Å, c = 46.87 Å, space group Pbcm24,25), and a stable rotator RI. The C16–C17 mixtures possess intermediate phases Op and Mdci in low temperatures, and a wide scope of RI phase in high temperature range.26 Research of phase behaviour of C16–C17 system in nanopores can provide more information of confinement effect on binary system, which is little known at present and cannot be predicted as the Gibbs–Thomson equation for a pure material. Although the phase behaviour of C16–C18 system in some nanopores is investigated, those results are highly expected not to be the same for C16–C17 binary mixtures. It is because the two systems in bulk have completely different phase regions in the structure of solid phases, especially in temperature and mole fraction boundaries, which shows even–even and even–odd effect in the binary alkanes. The difference in the phase behaviours of the two systems at nanoscale will display the effect of the average chain length of the alkane mixtures and stabilities of alkane solids, whether/how the possible new phase appears.
In this paper, we report the phase behaviours C16–C17 mixtures in nanopores of CPG (8.1 nm, and 300 nm) characterized by DSC and temperature-dependent powder X-ray diffractions. In CPG (300 nm), the solid phases are almost the same as those in the bulk. In CPG (8.1 nm), the solid phases appear in much lower temperatures with different compositions. A new phase rotator RII was observed in a narrow temperature range before melting. The confinement effect on polymorphism of C16–C17 binary system is discussed from the point of the size effect, and the defect-driven mechanism.
Experimental
Materials
Normal alkanes hexadecane, heptadecane and tricosane used in the experiments are products from Aladdin Reagents Co. with a purity in mass fractions larger than 0.99 controlled pore glasses (Millipore) with pore diameter of d = 8.1–300 nm are used as confinement matrix. The specifications of the CPGs are listed in Table 1, as provided by the manufacturer. Here the pore size distribution means 80% of the pores of CPG have a pore diameter within +/− the value shown on certificate of analysis of the nominal diameter. For example, if the pore size distribution for a particular lot of CPG3000 is shown on the certificate of analysis as 6%, then it means that 80% of the pores have a pore diameter within 6% of 3000 Angstrom. Before use, the glass powder was cleaned with concentrated nitric acid according to a method recommended by the supplier. The treatment was reported to result in negligible influence on the pore diameter and distributions.27| Product name | Mean pore diameter (nm) | Pore size distribution (%) | Specific pore volume (cm3 g−1) | Specific surface area (m2 g−1) |
|---|---|---|---|---|
| CPG3000 | 300 | 6 | 1.08 | 10 |
| CPG1000 | 107.6 | 5 | 1.59 | 31 |
| CPG500 | 46.4 | 3 | 1.31 | 64 |
| CPG240 | 25.2 | 3.9 | 0.89 | 79 |
| CPG120 | 11.5 | 7.3 | 0.49 | 119.5 |
| CPG75 | 8.1 | 9 | 0.49 | >120 |
DSC and XRD analysis
In experiments, C16, C17 and C23 were used as obtained; the mixtures of C16 and C17 were obtained by accurate weighing them together to specific molar ratios. Preparation of samples CPG filled with C16, C17 or the mixtures, and C23 were as follows. In one sample, CPG powder (>10 mg for DSC, ∼60 mg for XRD measurement) was put into a piece of glass tube and outgassed under a vacuum of 10−1 Pa for 2 h at 50 °C. After cooled to room temperature, the alkane liquid was transferred into the glass tube by a clean glass capillary under protection of dried nitrogen atmosphere. The pore fillingness of the alkane is less than the total pore volume of CPG, 90–95%, to avoid interference of excess liquid. After sealed, the sample in the glass tube was equilibrated for more than 2 h at room temperature to 30 °C, after stored in a refrigerator for some time. The bulk alkanes were also posed to such a same thermal treatment before analysis.DSC analysis of the sample was performed on Q10 (TA Instruments) under a high purity nitrogen atmosphere. In a typical way, the sample was cooled to a temperature 30–50 °C below the transition temperature at a rate of around 2 °C min−1. Then heat flow signals were recorded in heating process with a scanning rate of 5 °C min−1. The temperature scale of the DSC instrument was calibrated using high purity indium, water and adamantane. In most cases, transition temperatures of the bulk and confined alkanes were reproducible to within 0.5 °C.
Temperature-dependent powder X-ray diffraction analysis was done on a Philips X'Pert Pro MPD type diffractometer in the same temperature range as those for the DSC measurements. The diffractometer uses Cu Kα (1.54 Å) radiation source at a power of 40 mA/40 kV. The sample was placed in an aluminum vessel with a size of 2 × 1.6 × 1 mm3. After the sample was cooled to expected temperature at a rate of 2 °C min−1, diffraction patterns were recorded in rotating angle 2θ = 5–40° at selected temperatures in heating process. Before each scan, the sample was equilibrated for 10 minutes. The Cu Kα backgrounds were subtracted from the raw data in presentation of the diffraction patterns.
Diffraction patterns of C23 in CPG (nominal d = 12–300 nm) were scanned on the station (4B9A) of Beijing Synchrotron Radiation Facility (BSRF) at room temperature (∼24 °C), using the six circle diffractometer Huber 5020 and the scintillation crystal detector Huber 9910, with a synchrotron radiation wavelength of 1.54 Å. Data were collected in steps of Δ(2θ) = 0.02°.
Results and discussion
DSC analysis
Thermal analysis was performed for three series of samples: C16–C17 binary mixtures in the bulk, and that confined in nanopores of CPG (8.1, and 300 nm). DSC curves of representative compositions of xC17 = 0–1 in the heating scans are shown in Fig. 1. Endothermic thermal anomalies are solid–liquid (s–l) and solid–solid (s–s) transitions of the alkane solids in pure component or mixtures. In the left panel, the bulk system shows clear transition peaks in every composition, which is in agreement with the previous results.28 In the middle, the transitions of the pore mixtures in CPG (300 nm) get a bit weak and widened in most cases, appearing at close temperatures with the bulk. In the right panel, the melting peaks of the mixtures in CPG (8.1 nm) are still fairly strong but the s–s transitions are so weak to be seen. They happen at temperatures almost 25 °C lower than those in the bulk and in CPG (300 nm). Depression of s–l or s–s transition temperature of pure C16 and C17 may be qualitatively understood from the Gibbs–Thomson equation under the condition of a middle strength interface interactions between the alkane molecules and the glass pore wall.6,29 As the two components only have difference of one –CH2– unit in the chains, their mixtures have the similar compositions as them and also follow lowering in the transition temperatures. The smaller transition peaks or enthalpies in the nanopores together with the depressed transition temperatures are the common phenomena observed in nanoparticles, because of the defective crystal structures.30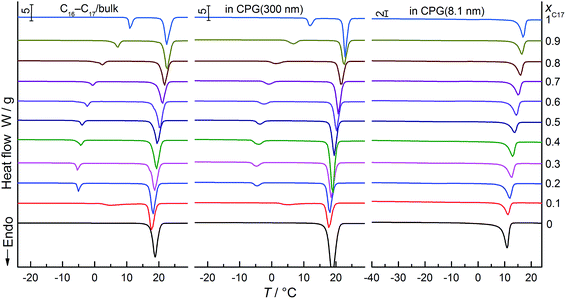 | ||
| Fig. 1 DSC curves of C16, C17 and the mixtures (molar fraction interval of xC17 = 0.1) in the bulk, and confined in CPG (8.1, and 300 nm), recorded in heating processes. | ||
Table 2 lists s–l and s–s transition temperatures of the alkane solids from the DSC analysis for the bulk, and confined in CPG (8.1, and 300 nm), which are defined as the onset point of the DSC curve extrapolated from the leading edge of the peak to intersection with the base line. It includes some transition temperatures determined from XRD measurements in the following sections. These data are used to depict diagram of phase boundary as a function of mole fraction. The crystal structures of the solid phases of the bulk and under confinement will be decided by XRD measurements afterward. Normally, the solids can be well recognized before and after a certain temperature the transition taken place on the DSC curves, especially in nanopores of CPG (300 nm). However, most of the s–s transitions of the mixtures in CPG (8.1 nm) can be found in the diffraction scans but not in the thermal analysis. In the case, the thermal effect is very weak to be detected. Therefore, the combined DSC and XRD analysis are reliable to probe the nano-sized phases in the low temperature range.
| Mole fraction of C17 | Temperature of the phase transition (°C) | |||||||
|---|---|---|---|---|---|---|---|---|
| Bulk | CPG (d/nm) | |||||||
| 300 | 8.1 | |||||||
| s–l | s–s | s–l | s–s | s–l | SLT–RI | RI–RIIb | ||
| a The average deviations are mostly within 0.5 °C.b The range refers to the highest temperature of RI to the lowest temperature of RII detected in X-ray diffractions. The rest of data are obtained from DSC analysis. LT refers to low temperature (phase). | ||||||||
| 0 | 17.4 | 16.7 | 8.6 | |||||
| 0.05 | 16.5 | 13.0 | 16.2 | 7.7 | 9.2 | −3.0 | ||
| 0.10 | 16.6 | 1.9 | −3.1 | 16.6 | 2.2 | 9.1 | −22.0 | |
| 0.15 | 16.8 | −5.0 | 16.6 | −5.5 | 9.3 | −33.5 | ||
| 0.20 | 16.9 | −6.1 | 16.9 | −6.1 | 9.5 | −30.4 | ||
| 0.25 | 16.0 | −7.0 | −5.0 | 17.1 | −6.5 | 9.9 | −31.8 | |
| 0.30 | 17.2 | −6.6 | 16.3 | −7.5 | 10.0 | −29.8 | ||
| 0.40 | 17.7 | −6.4 | 17.8 | −6.3 | 10.6 | −30.9 | ||
| 0.50 | 18.2 | −5.4 | −7.0 | 18.2 | −5.4 | 11.2 | −26.8 | |
| 0.60 | 18.8 | −4.5 | 18.8 | −4.5 | 11.8 | −29.5 | ||
| 0.70 | 19.5 | −2.9 | −4.0 | 19.5 | −3.0 | 12.6 | −28.3 | 10.0 |
| 0.75 | 19.6 | −0.9 | 18.9 | −2.9 | 12.1 | −25.8 | 10.0 | |
| 0.80 | 20.3 | −1.0 | −5.3 | 20.3 | −1.0 | 13.5 | −28.3 | 11.0 |
| 0.90 | 21.2 | 4.5 | −3.0 | 20.2 | 3.4 | 14.2 | −23.3 | 12.0 |
| 0.95 | 21.5 | 6.0 | 21.6 | 7.7 | 14.7 | −17.8 | 13.0 | |
| 1.00 | 21.9 | 11.1 | 22.0 | 10.9 | 15.0 | −12.5 | 13.0–14.0 | |
Phase behaviour of C16–C17 system in the bulk and in CPG (300 nm)
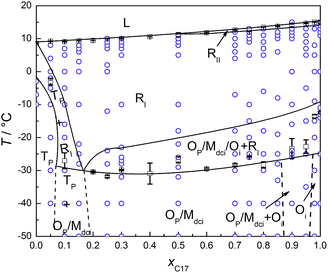
In Fig. 2, the phase transition temperatures of C16–C17 binary system in the bulk, and confined in CPG (300 nm) are plotted as a function of mole fraction of C17, xC17. The circles over each composition are the temperature points where the diffraction patterns of the corresponding solid phases are recorded as partly shown in Fig. 3. As a well-established method, phase boundaries between liquid and solid phase (e.g. L ↔ RI) and among the high and low temperature domain (e.g. RI ↔ Op, Mdci, Oi) are determined by fitting the transition temperatures from the DSC analysis, which is consistent with the literature in the bulk system.28 In low temperature range, the phase boundaries among different phase regions (e.g. Tp, Op, Mdci, and Oi) of the bulk in dashed lines (left) are drawn from results in the ref. 28. Those in CPG (300 nm) (right) are estimated from the XRD measurements. For example, at T < −10 °C the diffraction patterns of the mixture of xC17 = 0.25 indicate an Op crystal in referred to the bulk; the mixture of xC17 = 0.3 is a mixture of Op and Mdci phase. Thus, the Op one-phase region and the [Op + Mdci] two-phase region is separated between xC17 = 0.25 and 0.3 with a max uncertainty of 0.05 unit, where the boundary shifts a bit to the C16 side compared to the bulk system of xC17 > 0.3. Similarly, the boundary between the Mdci one-phase region and the [Op + Mdci] two-phase region in CPG (300 nm) is marked between xC17 = 0.65 and 0.7 with a max uncertainty of 0.05 unit, which moves a bit closer to the C17 side in reference with the bulk. The other boundaries related to Tp and Op phase, and Oi and Mdci phase are not so accurate. The changing in of the Op, and Mdci one-phase region in the phase boundary indicates a variation in the packing of the alkane molecules in CPG (300 nm), also as seen from the diffraction patterns in the following and discussion.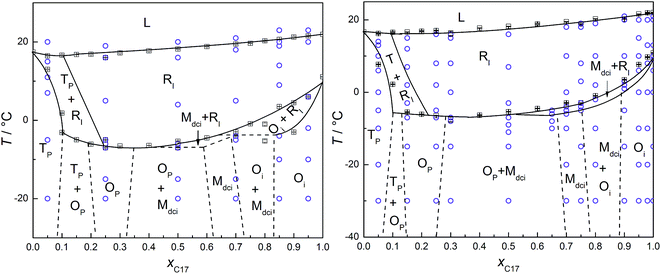 | ||
| Fig. 2 (Left) Solid–liquid phase diagram of C16–C17 binary system. The dotted lines are drawn according to the ref. 28. (Right) Phase transition temperature of C16–C17 system confined in CPG (300 nm) as a function of mole fraction of heptadecane xC17, determined using DSC (solid line, □) in the heating processes. Error bars are the average deviations of the corresponding transition temperatures. The circles (○) are the successive temperature points of the XRD scans. The dotted lines were estimated from the diffraction results. | ||
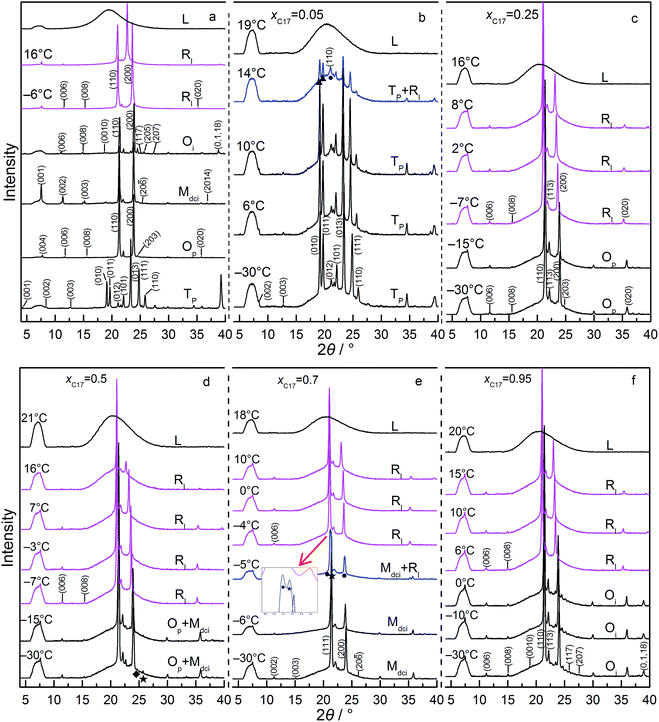
In Fig. 3 panel a, diffraction patterns of Tp, Op, Mdci, Oi, and RI phase of several bulk mixtures are displayed. The (00l) reflections from the layered arrangements of the alkane molecules are in the angle range of 2θ < 18°. Other reflections, for example from ab in-plane lattice, are in angles 2θ > 18°. The low temperature domain Tp, Op, Mdci, and Oi change little in diffraction positions with the increasing temperature, indexed according to lattice parameters in literature26,31 and the standard PDF cards.24,32 Here, the solid solution with Tp structure has the characteristic (010), (011), (013) and (111) planes, Op structure with (110), (200), (203) and (020) planes, Mdci structure with (111), (200), (20−6) and (2014) planes, and Oi structure with (110), (200), (205), (207) and (0,1,18) planes. The RI rotator phase shows its typical in-plane reflections of (110) and (200) lines, where the latter moves to lower angle on heating because of expansion of the lattice as the molecular chains rotate around the long axes.33
Fig. 3 panels (b–f) show the diffractions of five mixtures (xC17 = 0.05–0.95) confined in CPG (300 nm) in the heating processes. The solid phases with Tp, Op, Mdci, and Oi structure in each composition can be recognized from their reflections of in-plane lattice and mixed indexes at 2θ > 18° in referred to the bulk. The RI phase exhibits in-plane reflections of (110) at 2θ = 21.04–21.08° and (200) at 2θ = 23.55–23.10° at T = −7 to 16 °C, the same as in the bulk mixtures. Also, the (200) reflection peak shifts to lower angles with the increasing temperature. These diffraction peaks are fairly strong, in most cases not reduced much. In the case, the lateral ordering of the chain molecules in the alkane solids are well kept to produce strong reflections from the regular lattices. The layered ordering is also observed as evidenced from the (00l) reflections, but with much weakened intensities.
From Fig. 2, the phase regions of C16–C17 system in the bulk and confined in CPG (300 nm) are similar in the composition and temperature ranges, only that in CPG (300 nm) the [Op + Mdci] two-phase region expands some in composition and the RI one-phase region extends a bit to lower temperatures in the compositions of xC17 ≥ 0.75. The similarity in their phase behaviours is understandable since the alkane solids in the nanopores still possess the lateral and lamellar ordering, the sign of complete crystals, as observed from the diffractions. Meanwhile, the expansion of the RI and [Op + Mdci] phase regions suggests an extra disordering in the molecular arrangements, mainly end-gauche defects, induced from the pore confinement in reference with the well-established knowledge on the bulk system behaviours. The phenomena were also found previously in other nanoconfined binary systems.22 and will be discussed later from the changing in the (00l) reflection intensities especially those larger l. Following this, the enlarged [Op + Mdci] region in CPG (300 nm) simply reflects the influence of this additional disordered packing gathering at the interlayer area among the alkane layers. This is because in the nanopores a part of the mixtures with higher xC17 of the Op one-phase region becomes unstable due to enough disturbance in the packing of the chain-ends by the defects and turns into its competitive species, the Mdci phase. As a result, the Op solid phase ends inevitably in smaller xC17 composition and some of the Op phase original in the bulk changes into a coexistence with the Mdci phase. In the other side, the [Op + Mdci] two-phase region finishes in higher xC17 in CPG (300 nm) to meet the Mdci one-phase region. The reason is maintenance of the Mdci one-phase region in the pores needs more portion of C17 (less C16) molecules and thus less end-gauche defects due to the mismatch in the chain length of the two components, so as to counteract the defects in the chain-ends introduced by the confinement. Thus, the defects in the layer surface of the alkane molecules due to the inherent movements of the chains and the exterior confinement (molecule to pore wall) is balanced to obtain or keep the stability of a phase. In addition, the expansion of the RI region in higher xC17 composition under the confinement again can be ascribed to the influence of the increased disordering in the layer stacking. The extra defects in the layer surface just satisfy the conditions for the formation or stabilization of the rotator phase as found in the bulk and the other nano-sized alkane systems.34
Phase behaviour of C16–C17 binary system confined in CPG (8.1 nm)
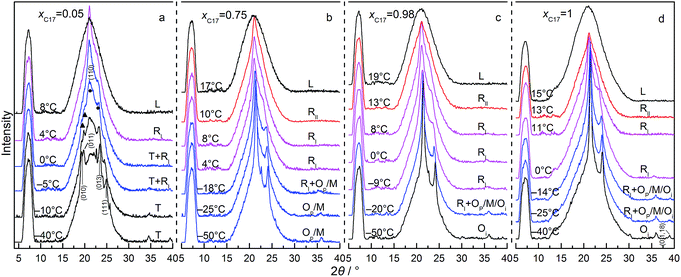
Fig. 4 shows the s–l and s–s phase transition temperatures of C16–C17 binary mixtures in CPG (8.1 nm) as a function of xC17, determined from DSC and XRD measurements in the heating processes. The circles along each composition are the temperatures for the reflection patterns scanned, as partly shown in Fig. 5. The phase boundaries of the s–l transition at around 10 °C and the s–s transition at about −30 °C are obtained by fitting the transition temperatures from DSC analysis. Just before melting, there appears a new rotator phase RII in a narrow temperature range in the composition range of xC17 = 0.50–1.00, found in the diffractions. The solid line between the rotator RII and RI is the fitting among the phase transition temperatures identified through the reflection patterns. For example, the alkane solid of xC17 = 0.5 is in the rotator RI phase at 9 °C, while changing into a rotator RII on heating up to 10 °C. A mid-point of 9.5 °C is chosen as the transition point with an uncertainty of 0.5 °C. Similarly, another solid line between the RI phase and the low temperature domain is decided in the range of xC17 ≈ 0.15–1.00 at around −20 °C. The boundary lines in vertical direction are drawn according to the diffraction results, but sometimes with a bit larger uncertainties. Here, the reflection patterns of the mixture of xC17 = 0.05 shows a Tp structure, mixed [Tp + Op] phases in composition of xC17 = 0.10 and 0.15. Thus the two regions is divided between xC17 = 0.10 and 0.05 with an uncertainty of 0.03 unit. On increasing to xC17 = 0.25, the reflection patterns show no the Tp phase but the Op or Mdci, or their mixture (designated as [Op+ or Mdci]), the details given later. Likewise, the boundary lines are marked in between xC17 = 0.85 and 0.90 for separation of the [Op+ or Mdci] and this region mixed with Oi phase, in between xC17 = 0.95 and 0.98 for the Oi one-phase region, with uncertainties no larger than 0.03.The reflection patterns of the representative solid mixtures of xC17 = 0.05, 0.75, 0.98, and 1.00 are presented in Fig. 5. It is found the (00l) reflections at 2θ < 18° disappear in the patterns. The diffraction peaks appear at angles 2θ > 18°, mostly in 2θ = 18–25°, but much widened and even vanished. Here, the Tp solid solution is found by the (010) and (011) planes at 2θ = 19.2° and 19.7°, respectively, the same as in the bulk. The solid solution with the Op, Mdci, or Oi structure show the relatively strong reflections of (110) and (200) planes at the same angles of 2θ ≈ 21° and 23°, respectively, while these are not enough other lines for distinguishing them. Different to the Op phase, the Oi phase has a weak (0,1,18) peak at 2θ = 39° and the Mdci phase sees an even weak peak at 2θ = 36°. The rotator RI is recognized from the typical reflections of (110) (2θ = 20.8–20.9°) and (200) (2θ = 22.7–24.0°) planes, the latter still movable as the temperature increases as in the bulk and in CPG (300 nm). Moreover, a new phase rotator RII characterized by one (110) peak appears in the mixtures of xC17 > 0.5 in a narrow temperature span <2 °C before melting of the solid phases. With the increasing temperature, the low temperature Op, Mdci, or Oi phase change into the RI phase, and then some to the RII phase when the (200) plane moves to and merges with the (110) plane finishing a transformation from orthorhombic to hexagonal lattice.
Comparing with the bulk, the melting line of the C16–C17 mixtures in CPG (8.1 nm) is depressed to lower temperatures by about 10 °C. The rotator phase region covers a temperature range of ∼22 °C in the bulk and in CPG (300 nm), whereas being an average ∼30 °C in CPG (8.1 nm). The Tp one-phase region is similar with that in the bulk and in CPG (300 nm). The low temperature domain the Op, Mdci and Oi phase in CPG (8.1 nm) locates at temperatures ∼25 °C below the bulk. The Oi one-phase region shrinks ∼0.1 mole fraction unit to the C17 side. In a large composition between the Tp and the Oi one-phase region, there exist the Op or Mdci phase or their mixture, which is difficult to discern them due to the same reflection patterns in the small pores. At T = −(20–30) °C and xC17 > 0.15, there is a transition region of the RI phase mixed with the Op, Mdci phase or their mixture, also indistinguishable. The pore C17 has a sequence [Oi] → [RI + Oi] → [RI] → [RII] → L, different with the bulk behaviour. The pore C16 experiences a phase sequence [T16] → [RI + T16] → L on heating.
Clearly, there is a significant changing in the phase behaviour of the C16–C17 system in CPG (8.1 nm) in reference with the bulk. From the absence of (00l) reflections in the high and low temperature domains, the layered ordering of the arrangements of the alkane molecules in CPG (8.1 nm) has been heavily perturbed. This indicates a more extent of the longitudinal diffuse of the chains and the defects of end-gauche or kinks than in the bulk and in CPG (300 nm), which rightly favours the formation of the rotator phase as found in the bulk and the nano-sized systems.34 The growth of the RI region in the temperature span of ∼8 °C manifests this increased disordering in the layer interface. At elevated temperatures, the appearance of the new rotator RII phase is favoured by the weakened lamellar coupling due to the disordered or random positions of the end groups of the chains.35 The RII phase comes up in the mixtures of higher C17 concentrations of xC17 ≥ 0.5 with average chain length ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ≥ = 16.5, where
≥ = 16.5, where ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is defined as sum of the products of carbon number and mole fraction of the composition, (xnn + xn′n′), with n = 16 and n′ = 17. Meanwhile, the phase regions in the low temperature domain also change significantly in the compositions. Taking an example, the obvious shrinking of the Oi one-phase region can be ascribed to the increased defects of the alkane molecules in the nanopores, which disrupt the stability of the Oi phase with some compositions originally in the bulk. In the case, a part of the mixtures change into another competitive phase, e.g., possibly the Mdci phase. Again, this C17-dominated one-phase region could maintain its specific molecular arrangements by discarding some “impurity”, C16 molecules, to compensate for the extra disordering in the alkane molecules from the nanoconfinement.
is defined as sum of the products of carbon number and mole fraction of the composition, (xnn + xn′n′), with n = 16 and n′ = 17. Meanwhile, the phase regions in the low temperature domain also change significantly in the compositions. Taking an example, the obvious shrinking of the Oi one-phase region can be ascribed to the increased defects of the alkane molecules in the nanopores, which disrupt the stability of the Oi phase with some compositions originally in the bulk. In the case, a part of the mixtures change into another competitive phase, e.g., possibly the Mdci phase. Again, this C17-dominated one-phase region could maintain its specific molecular arrangements by discarding some “impurity”, C16 molecules, to compensate for the extra disordering in the alkane molecules from the nanoconfinement.
Structural consideration of the confinement effect on phase behaviour of C16–C17 binary system
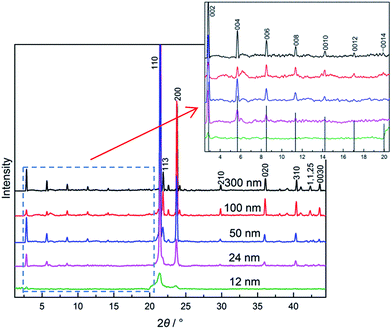
In the above sections, C16–C17 system shows size-dependent phase behaviour under confinement. From the bulk to that in CPG (300 nm) and in CPG (8.1 nm), the phase behaviour indicates an increased disordering in the molecular arrangements since the lamellar structure is clear in bulk phases in the low and high temperatures while absence in the smallest pores. As a crucial rule, the extra disordering or defects in the lamellar packing with the variation of the pore size should be tracked more detailed in the evolution of the phase behaviours.Actually, some information of the confinement effect on the layer stacking of the alkane molecules may be obtained from a qualitative consideration of the (00l) reflections in different pore size. The estimation is on the basis of findings in the bulk alkanes: a roughening of layer interface of alkane solids (e.g., C23) due to longitudinal diffuse of the chains and defects such as end-gauche, kinks can lead to a steep decrease in intensity of (00l) peaks with increasing l, and even disappearance of higher-order (00l) lines in rotator phase.36 Then, could the (00l) reflections still be such a probe for alkane interlayer area in nanopores? In Fig. 6, diffractions of tricosane C23 in CPG (nominal d = 12–300 nm) are recorded at room temperature (∼24 °C) well below the corresponding transition point, where it is in the low temperature phase (orthorhombic Oi, O23) except in 12 nm-pore with the rotator RI or RII or both of them. The layered reflections of (00l) lines at 2θ < 20° in the nanopores are present, together with those vertical lines from the PDF card of bulk C23. From the bulk to that in CPG (12 nm), their intensities (height) of the diffraction peaks show a decreasing trend with the decreasing size. However, they vary differently in lamellar and lateral packings: the (00l) lines for the layered ordering decreases largely as the pore diameter decreases; the others, e.g. (110) and (200) reflections from ab in-plane lattice, do not change too much in d = 24–300 nm. Some higher-order (00l) lines are widened to become weak: 0014 line is barely visible in C23/CPG (300 nm), 0014 line invisible in CPG (100 nm), 0014 and 0012 line invisible in CPG (50 nm), 0014 and 0012 line invisible and 0010 hardly visible in CPG (24 nm), 004 to 0014 line all invisible in CPG (12 nm). In comparison with those vertical lines of the bulk, the (00l) lines of C23 at each size decrease steeply with the increasing l and this trend is more tense with the decreasing pore size. Considering other lines (in d = 24–300 nm) at 2θ > 20° without large changing, the steep decrease in the intensities of the (00l) lines should be attributed mainly to influence of the disordering of the molecular packing in the interlayer regions in relative to the bulk. And this disorder in lamellar stacking is intensified as the pore size decreases. Accordingly, the intensities of the (00l) lines under the confinement can reflect the orderliness of the methyl layer at the interface of alkane solids. In contrast to an ordered packing of the molecules of the bulk, the above analysis indicates that the O23 phase in the pores contains some defects, which should be the same in the low temperature stable phases of other alkanes so that to bring about a significant change in their phase behaviours. The diffraction analysis of the lamellar ordering now turns to the present system. In the bulk C16–C17 system, the (00l) reflections in each composition are clear in both the low and high temperature domains, which do not show sharp decrease in the intensities, as seen in Fig. 3 panel (a). Among them, the highest-order l line (the smallest) has a ratio of signal to noise in height of s/n = 6 (Tp) and 13 (RI) in xC17 = 0.05, and 15–20 in xC17 ≥ 0.25, where the noise n is the standard deviation of base line in several degrees of angles around the peak. In contrast, the (00l) reflections for the counterparts in CPG (300 nm) are weak, especially in the highest-order l lines that are listed in the following,
• xC17 = 0.05, 003 line almost invisible (s/n = 2.6) in Tp one-phase region (T < −10 °C), and then weak (s/n ≈ 8) in RI one-phase region (T > −10 °C);
• xC17 = 0.25, 008 line almost invisible (s/n ≈ 5) in Op, and then RI one-phase region;
• xC17 = 0.5, 008 line almost invisible (s/n ≈ 4) in [Op + Mdci] mixed two-phase region, and then invisible (s/n ≈ 1.6) in RI one-phase region;
• xC17 = 0.7, 003 line almost invisible (s/n = 2.6) in Mdci one-phase region (T < −10 °C), and then weak (s/n ≈ 8) in RI two-phase region (T > −10 °C);
• xC17 = 0.95, 0010 line weak (s/n ≈ 10) in Oi, and then RI one-phase region;
• xC17 = 1, 0010 line obvious (s/n = 9.3) in Oi, and then obvious (s/n = 6.7) in RI phase.
Here pure C17 and the mixture of xC17 = 0.95 in CPG (300 nm) have larger intensities than the others in the highest-order l line. All the mixtures in CPG (300 nm) display much reduced intensity in the highest-order l line in referred to the bulk, actually almost invisible in most cases. In the meantime, the lateral arrangements of the alkane molecules are still well kept to show comparable intensities with the bulk. In the case, the steep reduction in the intensities of the (00l) lines can be attributed to a more roughened layer interface generated from the confinement than the bulk through longitudinal diffuse and twisting of the alkane chains.35 The changing in molecule packing is important for understanding the phase behaviours of the C16–C17 mixtures in the nanopores.
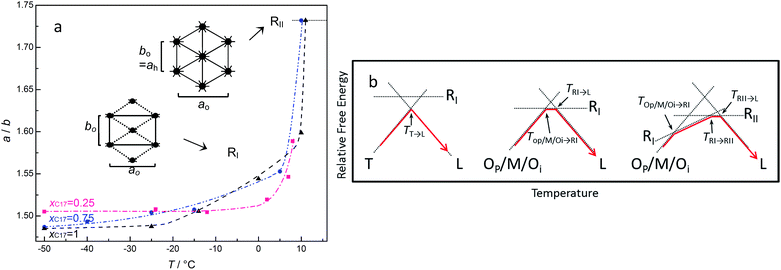
Moreover, the occurrence of the rotator RII in the mixtures and C17 is also the evidence for the increased defects in the packing of the alkane molecules otherwise only the rotator RI exists as in the bulk. The rotator RII is limited to pure C17 or the mixtures with enough long or average chain lengths. With the increasing temperature, the transformation from low to high temperature domain is accompanied by the expansion of the ab plane with the rotating of the alkane chains around their long axes, as shown in Fig. 7 panel (a) of three compositions of x17 = 0.25 (Op/Mdci/Oi), 0.75 (Op/Mdci/Oi), and 1 (Oi) in CPG (8.1 nm). The ratio of a/b changes slightly in the low temperature domain and the orientational ordering is kept in the alkane molecules. The a/b value increases with the transition to RI phase as the molecular chains rotate partly in limited angles and lose orientational ordering. Then it reaches a maximum value 31/2 on coming up of the rotator RII with fully rotating chains. Panel (b) shows the schemes of relative free energies versus temperature of the representative transitions, involving the bulk C16 (left),16 the rotator RI (middle), and the rotator RII (right) respectively.
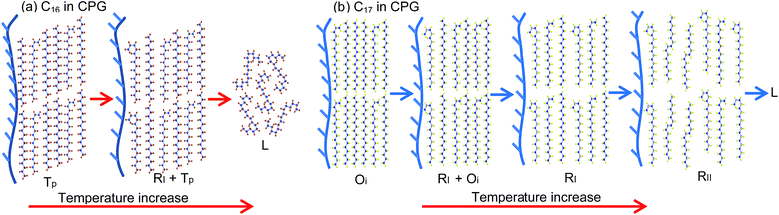
In most cases, the pore confinement seems simply to bring about more defects and chain diffuse in the layer surface, which results in the changing of the existing temperatures and compositions of the alkane solids. While one may see the phase behaviour reflecting directly the confinement effect, for example the mixed RI with Tp or Oi phase appeared in the two pure components C16 and C17 in CPG (8.1 nm) but not in the bulk. These unique behaviours suggest an inhomogeneous existence of these alkane phases in the very small pores, very likely a radial distribution of the phases in the pores.37 In a reasonable consideration, the alkane molecules near the pore surface correspond to the RI phase where they are in the scope of the effective pore wall attractions. The rest of the alkane molecules around the core are in the packing of the low temperature domain Tp or Oi phase, which is much less influenced by the wall attractions in a space “far” away from the pore surface. As discussed in the previous work, formation of RI phase near the pore wall may be favoured by the irregular adsorption of the chain molecules on the rough surface of the glass, where the defects in the chain ends or amidst the chains can be compensated by the interface interactions.38,39 In other words, it is reasonable to assume the molecules near the pore wall contain some more defects such as end gauche. This part of the Tp or Oi phase becomes unstable and turns into its competitive RI phase at elevated temperatures when the total defects in the chain ends disrupt the dense packing of the low temperature domain. As a result, a coexistence of mixed RI with Tp or Oi phase is formed as a binary for the pure C16 and C17 in CPG (8.1 nm). With increased temperatures, the transformation of the mixed phase to melt (C16), or RI and RII phase (C17) can be understood from thermal energy excitation, schemed in Fig. 8 panels (a–b). However, it is not time for a consideration of the distribution of the two-phase region of C16–C17 mixtures because of the same number of (two) phases in the nanopores with the bulk, and insufficient experimental facts available.40
It should be noted the chain length of pure alkane or the average chain length of mixtures also plays an important role in their phase behaviours. In the pure alkanes, new phases the rotators appear in C16 (RI), C17 (RII), C18 (RI and RII) and C19 (RII) in the nanopores of CPG (8.1 nm). Here, the odd–even effect fails in even-numbered alkane C16 and C18 in CPG (8.1 nm) in the knowledge of the bulk systems. With more types of the rotators, the longer chain member C18 shows more complicated phase behaviour than the shorter C16. Although with the same phase sequence, the longer member C19 has a larger temperature range of the RII phase than C17, which means the stability of the rotators is strengthened in the longer chain members.20 In the alkane mixtures, both C16–C17 and C16–C18 binary system in CPG (8.1 nm) exhibit a new RII phase region. While latter system contains a wider composition range and a larger temperature scope than the former. The difference in their phase behaviours can also be attributed to the difference of the chain length or flexibility of the chains where longer (average) chains can generate more defects in the chains so as to favour the formation of RI or even RII rotator.
Conclusions
The confinement of the glass pores with diameter d = (8.1, and 300) nm changes the phase behaviour of C16–C17 binary system. In CPG (300 nm), the binary system has the same types of the phase regions with the bulk, coming up in close positions. The high temperature domain of the RI one-phase region expands a little in the mixtures of high C17 component. In the low temperatures, the one-phase regions with Tp and Oi structure tend to shrink slightly and the two-phase region [Op + Mdci] become larger in composition. In CPG (8.1 nm), the high and low temperature domains shift to lower temperature range, reaching a difference of about 25 °C in referred to the bulk. The RI one-phase region covers a wider temperature range than the bulk and that in CPG (300 nm). The one-phase regions with Tp and Oi structure become even smaller in composition coverage, the latter being very narrow. Meanwhile, a new RII phase comes out in the mixtures with high C17 concentrations. In diffraction analysis, the confinement gives rise to additional disordering in the packing of the chain molecules, as evidenced by steep decrease in the intensities of (00l) reflections especially in the high order l, which is intensified with the decreasing pore size. Meanwhile, the ab in-plane packing is well kept in the alkane molecules. The phase behaviour of the C16–C17 mixtures can be understood from the point of defects in the chains in nanopores as in the bulk system, besides the influence of the composition, the chain length and temperature. The results may also help in elucidation of crystallization in early stages of bulk materials, and new physical phenomena of nano-sized soft mater.Acknowledgements
We thank the financial support from National Natural Science Foundation of China (No. 21273138, 23173215).References
- C. Alba-Simionesco, B. Coasne, G. Dudziak, K. E. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, J. Phys.: Condens. Matter, 2006, 18, R15 CrossRef CAS PubMed.
- M. Beiner, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 1556–1561 CrossRef CAS.
- G. Dosseh, Y. Xia and C. Alba-Simonesco, J. Phys. Chem. B, 2003, 107, 6445–6453 CrossRef CAS.
- P. Huber, J. Phys.: Condens. Matter, 2015, 27, 103102 CrossRef PubMed.
- K. C. Hugo, J. Phys.: Condens. Matter, 2001, 13, R95 CrossRef.
- Q. Jiang and M. D. Ward, Chem. Soc. Rev., 2014, 43, 2066–2079 RSC.
- Y. Long, J. C. Palmer, B. Coasne, M. Sliwinska-Bartkowiak and K. E. Gubbins, Phys. Chem. Chem. Phys., 2011, 13, 17163–17170 RSC.
- J. Haddad, H. G. Steinuck, H. Hlaing, S. Kewalramani, D. Pontoni, H. Reichert, B. M. Murphy, S. Festersen, B. Runge, O. M. Magnussen, A. Magerl, M. Deutsch and B. M. Ocko, J. Phys. Chem. C, 2015, 119, 17648–17654 CAS.
- C. L. Jackson and G. B. Mckenna, J. Chem. Phys., 1990, 93, 9002–9011 CrossRef CAS.
- D. Morineau, G. Dosseh, C. Alba-Simionesco and P. Llewellyn, Philosophical Magazine Part B: Physics of Condensed Matter. Electronics, Optical and Magnetic Properties, 1999, 79, 1847–1855 CAS.
- M. Sliwinska-Bartkowiak, G. Dudziak, R. Sikorski, R. Gras, R. Radhakrishnan and K. E. Gubbins, J. Chem. Phys., 2001, 114, 950–962 CrossRef CAS.
- F. Kleitz, F. Berube, R. Guillet-Nicolas, C. M. Yang and M. Thommes, J. Phys. Chem. C, 2010, 114, 9344–9355 CAS.
- R. Radhakrishnan, K. E. Gubbins and M. Sliwenska-Bartkowiak, J. Chem. Phys., 2000, 112, 11048–11057 CrossRef CAS.
- M. Sliwenska-Bartkowiak, G. Dudziak, R. Gras, R. Sikorski, R. Radhakrishnan and K. E. Gubbins, Colloids Surf., A, 2001, 187–188, 523–529 CrossRef.
- H. Duran, M. Steinhart, H. J. Butt and G. Floudas, Nano Lett., 2011, 11, 1671–1675 CrossRef CAS PubMed.
- E. B. Sirota and A. B. Herhold, Science, 1999, 283, 529–532 CrossRef CAS PubMed.
- E. B. Sirota, Langmuir, 1998, 14, 3133–3136 CrossRef CAS.
- G. Graubner, G. T. Rengarajan, N. Anders, N. Sonnenberger, D. Enke, M. Beiner and M. Steinhart, Cryst. Growth Des., 2014, 14, 78–86 CAS.
- P. Huber, V. P. Soprunyuk and K. Knorr, Phys. Rev. E, 2006, 74, 031610 CrossRef CAS PubMed.
- P. Huber, D. Wallacher, J. Albers and K. Knorr, Europhys. Lett., 2004, 65, 351 CrossRef CAS.
- L. P. Wang, J. Sui, M. Zhai, F. Tian and X. Z. Lan, J. Phys. Chem. C, 2015, 119, 18697–18706 CAS.
- L. P. Wang, Q. F. Li, C. Wang and X. Z. Lan, J. Phys. Chem. C, 2014, 118, 18177–18186 CAS.
- W. R. Turner, Product Research and Development, 1971, 10, 238–260 CrossRef CAS.
- S. C. Nyberg, F. M. Pickard and N. Norman, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 2289–2293 CrossRef.
- S. R. Craig, G. P. Hastie, K. J. Roberts and J. N. Sherwood, J. Mater. Chem., 1994, 4, 977–981 RSC.
- D. Mondieig, F. Rajabalee, V. Metivaud, H. A. J. Oonk and M. A. Cuevas-Diarte, Chem. Mater., 2004, 16, 786–798 CrossRef CAS.
- A. Mataz and B. M. Gregory, J. Phys.: Condens. Matter, 2005, 17, R461 CrossRef.
- A. Wurflinger, D. Mondieig, F. Rajabalee and M. A. Cuevas-Diarte, Z. Naturforsch., 2001, 626–634 CAS.
- J. M. Ha, B. D. Hamilton, M. A. Hillmyer and M. D. Ward, Cryst. Growth Des., 2009, 9, 4766–4777 CAS.
- D. Fu, Y. Su, X. Gao, Y. Liu and D. Wang, J. Phys. Chem. B, 2013, 117, 6323–6329 CrossRef CAS PubMed.
- R. D. Heyding, K. E. Russell, T. L. Varty and D. St-Cyr, Powder Diffr., 1990, 5, 93–100 CrossRef CAS.
- A. ller, Proc. R. Soc. London, Ser. A, 1932, 138, 514–530 CrossRef.
- S. R. Craig, G. P. Hastie, K. J. Roberts, J. N. Sherwood, R. D. Tack and R. J. Cernik, J. Mater. Chem., 1999, 9, 2385–2392 RSC.
- X. Gao, D. Fu, B. Xie, Y. Su and D. Wang, J. Phys. Chem. B, 2014, 118, 12549–12555 CrossRef CAS PubMed.
- M. Maroncelli, H. L. Strauss and R. G. Snyder, J. Phys. Chem., 1985, 89, 5260–5267 CrossRef CAS.
- J. Doucet, I. Denicolo, A. Craievich and A. Collet, J. Chem. Phys., 1981, 75, 5125–5127 CrossRef CAS.
- R. Montenegro, M. Antonietti, Y. Mastai and K. Landfester, J. Phys. Chem. B, 2003, 107, 5088–5094 CrossRef CAS.
- E. B. Sirota, H. E. King Jr, H. H. Shao and D. M. Singer, J. Phys. Chem., 1995, 99, 798–804 CrossRef CAS.
- Y. V. Mnyukh, J. Struct. Chem., 1960, 1, 346–365 CrossRef.
- S. Całus, B. Jabłońska, M. Busch, D. Rau, P. Huber and A. V. Kityk, Phys. Rev. E, 2014, 89, 062501 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |