Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unusual H/D isotope effect in isomerization and keto–enol tautomerism reactions of pyruvic acid: nuclear quantum effect restricts some rotational isomerization reactions†
Taro Udagawa *a,
Keita Sugiuraa,
Kimichi Suzukib and
Masanori Tachikawa*b
*a,
Keita Sugiuraa,
Kimichi Suzukib and
Masanori Tachikawa*b
aDepartment of Chemistry and Biomolecular Science, Faculty of Engineering, Gifu University, Yanagido 1-1, Gifu 501-1193, Japan. E-mail: udagawa@gifu-u.ac.jp
bQuantum Chemistry Division, Graduate School of Science, Yokohama City University, Seto 22-2, Kanazawa-ku, Yokohama, 236-0027, Japan. E-mail: tachi@yokohama-cu.ac.jp
First published on 31st January 2017
Abstract
Isomerization and keto–enol tautomerism reactions of the pyruvic acid molecule have been investigated using the multicomponent B3LYP (MC_B3LYP) methods, which can take account of the nuclear quantum effect (NQE) of a light nucleus, such as a proton and a deuteron. While the conventional harmonic zero point vibrational energy (ZPVE) correction makes the activation energies of all the reactions in this system lower, a contrasting behavior is found in our MC_B3LYP results for several rotational reactions. In such cases, the H/D isotope effect on the activation energy is also completely opposite between harmonic ZPVE-corrected B3LYP and MC_B3LYP calculations. In our MC_B3LYP calculation, the activation energies of several C–C or O–H rotational reactions of H species are slightly higher than those of D species, since the NQE of a hydrogen-bonded proton strengthens the hydrogen-bonded interaction more than that of a deuteron, and, thus, the rotational motion of H species is restricted. Such an “unusual” H/D isotope effect on the activation energies can be observed only in the MC_B3LYP results. Our MC_B3LYP calculations clearly demonstrate that direct inclusion of NQE is indispensable to analyze H/D isotope effects on activation energies of not only hydrogen transfer reactions but also C–C and O–H rotational reactions in the isomerization and keto–enol tautomerism of pyruvic acid molecule.
Introduction
Pyruvic acid is an important molecule in biochemistry. It has important roles in the Krebs cycle and is a precursor of various chemical compounds, such as lactic acid, acetyl-coenzyme A, and so on. Pyruvic acid is also known to show isomerization and keto–enol tautomerism reactions. To reveal the properties of pyruvic acid and reaction mechanism of these isomerization and tautomerism reactions in detail, many experimental and theoretical studies on the pyruvic acid molecule have been published to date.1–6 Kakkar and coworkers studied the solution phase chemistry of pyruvic acid by means of B3LYP calculations. Their calculated proton affinity and basicity values in the gas phase, and pKa value are in good agreement with experimental values. They advocated the importance of dihydrate and concluded the solution phase chemistry of pyruvic acid is completely different from its gas phase chemistry.5 Recently, Valadbeigi and Farrokhpour analyzed isomerization and keto–enol tautomerism reactions in pyruvic acid isomers with the aid of B3LYP and MP2 methods.6 They reported the harmonic zero point vibrational energy (ZPVE) corrected activation energies, imaginary frequencies, and Gibbs free energies of the reactions. They also investigated the effect of hydration on these isomerization and tautomerism reactions, and concluded that the activation energies of hydrogen transfer reactions drastically decrease by the catalytic effect of water molecule. Therefore, hydrogen-bonded interaction and hydrogen transfer reactions take important roles for isomerization and keto–enol tautomerism reactions.On the other hand, importance of nuclear quantum effect (NQE) of hydrogen nucleus has been recognized in various fields. For example, difference between NQE of proton and deuteron induces interesting chemical and physical phenomena (known as H/D isotope effect), such as the drastic change of phase transition temperature,7–9 H/D isotope effect on rate constant,10 and so on. It is also known that NQEs sometimes cause interesting, unusual H/D isotope effects. For example, the decay rate of CD3 radicals is twice higher than that of CH3 radicals in mixtures of ethanol isotopomers xC2H5OH + (1 − x)C2D5OH with a low content of H component (x < 0.02).11 In such case, heavier CD3 radical reacts faster than lighter CH3 one.
Such NQE is, however, basically ignored in the conventional quantum mechanical (QM) methods based on the Born–Oppenheimer (BO) approximation.12 To reflect NQE on electronic structure within BO framework, we have to construct BO potential energy hypersurface (PES) first, and then nuclear Schrödinger equation should be solved on the constructed electronic PES to reflect the NQE. These procedures require enormous computational costs. On the other hand, we have recently developed multicomponent QM (MC_QM) method, which can take into account NQE of light nuclei.13,14 MC_QM calculations provide the effective PES, which is directly corrected by the NQEs. Therefore, we can analyze chemical reactions taking into account NQE with the aid of MC_QM method. However, it is difficult to find transition state (TS) structures on the MC_QM effective PES (“effective” TS) using MC_MO method, since the vibrational modes involving quantum nuclei cannot be obtained by means of conventional vibrational analysis with the MC_QM method.15 To overcome this difficulty, we recently proposed the MC_QM-climbing image-nudged elastic band (CI-NEB) method16 by combining CI-NEB approach17,18 with our MC_QM method. Using MC_QM and MC_QM-CI-NEB methods, we have successfully analyzed H/D isotope effects on the activation energies of chemical reactions (H/D kinetic isotope effect (KIE))16,19,20 and molecular geometries (H/D geometrical isotope effect: (GIE)).21–25 Several groups have also developed their own MC_QM methods and analyzed various interesting chemical and physical phenomena.26–34 We should mention here that there are several computational methods to directly take account of NQE of light particles in addition to MC_QM method. Path integral molecular dynamics (PIMD) simulation is one of the powerful and useful methods for not only NQE but also temperature effect. PIMD simulation is, however, really time-consuming. In addition, NQEs are evaluated on the BO PES obtained by the standard QM calculations, in the PIMD simulation. In contrast, our MC_QM method provides the effective PES, which is directly corrected by NQE of light nuclei, since our MC_QM method is based on the multicomponent fashion. Consequently, our MC_QM provides the difference effective PES for each isotopologue.
We have already demonstrated that NQE strengthens the hydrogen-bonded interactions22,23,25 and significantly lowers the activation energy of hydrogen transfer reactions16,20 with the aid of our MC_QM method. Since some isomerization reactions and keto–enol tautomerism reactions of pyruvic acid molecule involve hydrogen transfer process, we would like to revisit these reactions directly including NQE of hydrogen nuclei. The remaining isomerization reactions involve C–C of O–H rotation. These isomerization reactions are also fruitful target for MC_QM method, because we have not investigated NQEs on chemical reactions except for hydrogen transfer ones, yet. We, thus, would like to investigate H/D isotope effects on the activation energies of isomerization and keto–enol tautomerism reactions in pyruvic acid isomers with the aid of our MC_QM method in this paper.
Theory
Multicomponent quantum mechanics method
Here, we would like to introduce our MC_QM approach briefly. More detailed information of MC_QM method can be found in elsewhere.13,14 In MC_QM method, the total Hamiltonian for a system containing Ne-electrons, M-classical nuclei, and Np-quantum nuclei is expressed as
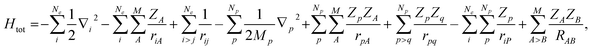 | (1) |
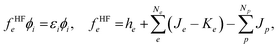 | (2) |
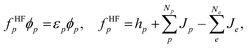 | (3) |
To improve the accuracy of the QM calculations, we have to evaluate correlation effects between quantum particles. In MC_QM calculations, we have to evaluate new types of correlation effects, such as electron-quantum nucleus and quantum nucleus-quantum nucleus correlation effects. However, we evaluate only electron–electron correlation effect in the present MC_QM calculations using the conventional B3LYP exchange–correlation functional for electrons,22,36 since the contributions from electron–quantum nucleus and quantum nucleus–quantum nucleus correlations are much smaller than that from electron–electron correlation for typical molecular systems, and we have already demonstrated that H/D isotope effect in various systems and reactions can be analyzed evaluating only electron–electron correlation effect in MC_QM calculations.20,22–25
Multicomponent quantum mechanics-climbing image-nudged elastic band method
Here, we briefly introduce CI-NEB method. To perform CI-NEB calculations, we first optimize the reactant and product molecules of the target reaction. Then we perform CI-NEB calculations to obtain minimum energy path (MEP) and TS structure. In the NEB calculations, the total force on an image is represented as the sum of the spring force along the tangent and the true force perpendicular to the tangent| Fi = Fsi|∥ − ∇V(Ri)|⊥, | (4) |
| ∇V(Ri)|⊥ = ∇V(Ri) − ∇(Ri)τi. | (5) |
We used Henkelman's revised tangent,17
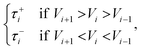 | (6) |
| Fsi|∥ = k(|Ri+1 − Ri| − |Ri − Ri−1|)τi, | (7) |
| FiTS = −∇V(RiTS) + 2∇V(RiTS)τiTSτiTS. | (8) |
It should be noted here that we can obtain both MEP and transition state structure on the MC_QM effective PES (“effective” MEP and “effective” TS structure) by minimizing energies and forces in eqn (4)–(8) using our MC_QM method. We have already demonstrated that MC_QM-CI-NEB approach adequately provides effective TS structure on the MC_QM effective PES for hydrogen transfer reactions,16,20 and we successfully analyzed H/D isotope effects on these reactions using the MC_QM-CI-NEB approach.
Computational detail
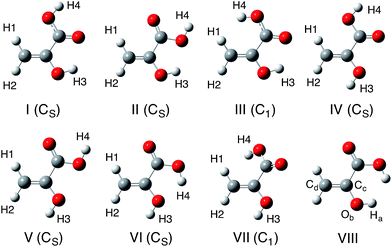
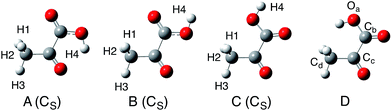
In this study, we calculated 12 isomers (8 enol and 4 keto forms) of pyruvic acid, according to the Valadbeigi's previous study.6 The structures of these 12 isomers are shown in Fig. 1 and 2. Geometrical parameters of these 12 isomers were optimized by B3LYP/6-311++G(d,p) level of calculation. To characterize these optimized structures, we also performed normal mode analysis on the optimized structures, and confirmed that all structures have no imaginary frequencies except for structures VIII and D.Next, we performed multicomponent B3LYP (MC_B3LYP) geometry optimization from the B3LYP optimized geometries. In MC_B3LYP calculations, only hydrogen nuclei were treated as quantum wavefunction. To discuss the small geometrical differences between H and D species, geometry optimization calculations were performed with tight keyword. Only electron–electron correlation contribution was evaluated by B3LYP hybrid exchange-correlation functional, and electron-nucleus and nucleus–nucleus correlations were ignored in this study, due to their small contributions. The 6-311++G(d,p) basis set and single s-type GTF, exp{−α(r − R)2} were adopted as electronic and nuclear basis sets, respectively. The α value in nuclear basis function is the orbital exponent value and determines the spatial distribution of nuclear wavefunction. We used average α values (αave, 24.1825 for H and 35.6214 for D) for geometry optimization.37–39 To refine the total energy and the spatial distribution of nuclear wavefunctions, we optimized α values at MC_B3LYP optimized geometries.39 To find out the effective TS structure on MC_B3LYP effective PES, we performed MC_B3LYP-climbing image-nudged elastic band (CI-NEB) calculations.16
All MC_B3LYP calculations were performed with the aid of modified version of GAUSSIAN 09 program,40 and CI-NEB calculations were performed with our homemade program.16
Results and discussion
Relative energies and optimized geometrical parameters of keto and enol structures
First, we performed geometry optimization of 12 isomers (I–VIII and A–D) using B3LYP/6-311++G(d,p) method. Although structure VIII and D were found in the previous study,6 we could not find these structures without CS-constraint. We note here that these CS-optimized structures have two and one imaginary frequencies, respectively. To investigate these structures in detail, we calculated the potential energy curves (PECs) for Ha–Ob–Cc–Cd rotation and Oa–Cb–Cc–Cd rotation (Fig. 3). These PECs do not show multiple minima for the Ha–Ob–Cc–Cd rotation and Oa–Cb–Cc–Cd rotation. The minimum in Ha–Ob–Cc–Cd PEC corresponds to structure VI, and that in Oa–Cb–Cc–Cd PEC to structure A. We also confirmed that structures VIII and D were not found as stable structures, even with the same methods as used in the previous study (MP2/6-311++G(2df,p) and B3LYP/6-311++G(2df,p)).6 Quite recently, Reva and coworkers also studied isomerization reactions in keto form pyruvic acid molecule both experimentally and theoretically.41 They investigated the ground state potential energy surface (PES) of keto form pyruvic acid molecule with the aid of B3LYP/6-311++G(d,p) method, and pointed out that structure D does not correspond a local minimum but correspond a first-order saddle point. Our calculation supports Reva's opinion. Therefore, we would like to focus on only 10 isomers (except for structures VIII and D) for further analysis.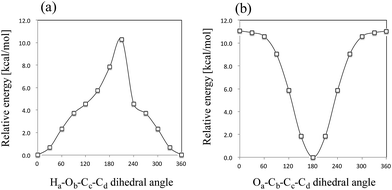 | ||
| Fig. 3 Calculated potential energy curves for (a) Ha–Ob–Cc–Cd rotation (structure VIII) and (b) Oa–Cb–Cc–Cd rotation (structure D). | ||
Table 1 lists the energy of each isomer relative to the energy of the most stable form, A. Table 1 also lists the B3LYP/6-311++G(2df,p) results6 for comparison. The notations ZPVE-H and ZPVE-D are B3LYP total energies corrected for protonic and deuteronic harmonic zero point vibrational energy (ZPVE), respectively. In ZPVE-D, all hydrogen nuclei in each molecule are regarded as deuterons. It should be mentioned here that ZPVE-H and ZPVE-D energies only differ in harmonic ZPVE. Geometries and electronic energies are the same for ZPVE-H and ZPVE-D. We can see that B3LYP/6-311++G(d,p) calculation almost reproduced the results obtained with larger 6-311++G(2df,p) basis set. Therefore, we confirmed that 6-311++G(d,p) electronic basis set is large enough for further analysis. Obviously, keto form structures are more stable than enol form structures. Our B3LYP relative energies of keto form structures are in agreement with those obtained in Reva's previous study.41 The most stable isomer of structure A is 2.1–2.3 kcal mol−1 more stable than the second most stable form of structure B in B3LYP relative energies. This energy difference is enough to conclude that structure A is expected to have a significant population,41 although Valadbeigi insisted that all 12 isomers have the same population of 8.3%.6 The difference between ZPVE-H and ZPVE-D energies are smaller than 0.2 kcal mol−1. Since the harmonic ZPVE correction only slightly changes the relative energies, H/D isotope effects on relative energies are actually small.
| B3LYP | MC_B3LYP | B3LYP/6-311++G(2df,p)6 | ||||
|---|---|---|---|---|---|---|
| Electronic energy | ZPVE-H | ZPVE-D | H species | D species | ZPVE-H | |
| I | 6.1 | 6.7 | 6.5 | 5.8 | 5.9 | 6.2 |
| II | 8.4 | 8.7 | 8.6 | 8.3 | 8.3 | 8.7 |
| III | 11.5 | 11.7 | 11.6 | 11.3 | 11.4 | 10.7 |
| IV | 11.6 | 11.9 | 11.8 | 11.9 | 11.8 | 11.8 |
| V | 11.3 | 11.6 | 11.5 | 11.5 | 11.4 | 11.4 |
| VI | 11.5 | 11.6 | 11.6 | 11.3 | 11.4 | 11.5 |
| VII | 17.7 | 17.8 | 17.8 | 18.1 | 18.0 | 17.3 |
| VIII | 20.1 | |||||
| A | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| B | 2.3 | 2.1 | 2.1 | 2.8 | 2.6 | 2.6 |
| C | 3.6 | 3.4 | 3.4 | 4.1 | 4.0 | 4.1 |
| D | 10.9 | |||||
Next, we would like to focus on the results obtained by MC_B3LYP calculations. We should mention here that MC_B3LYP calculation do not require calculating the second-order derivative of the energy to consider nuclear kinetic energy, since nuclear kinetic operator is directly included in the Hamiltonian used in MC_QM method. Consequently, MC_B3LYP calculations are less time-consuming than the ZPVE-corrected B3LYP ones. The nuclear quantum effect (NQE) of proton (or deuteron) slightly changes the relative energies of isomers. Interestingly, the opposite effects on relative energies for several structures are found between harmonic ZPVE correction and multicomponent treatment. It should be noted that Tachikawa also observed such opposite effect in interaction energies of water clusters, (H2O)n and (D2O)n (n = 2–5), by using Hartree–Fock/6-31G** level of multicomponent molecular orbital method.42 We speculate that the intramolecular hydrogen-bonded interaction is important to determine relative stability of pyruvic acid isomers. Structures IV, V, VII, B, and C become relatively unstable by taking account of NQE of hydrogen nuclei. Since NQE of hydrogen nucleus strengthens the hydrogen-bonded interaction22,23,25,42 and the most stable structure A has an intramolecular hydrogen bond, structures IV, V, VII, B, and C, which have no intramolecular hydrogen bonds in their optimized structures, become relatively unstable. Larger changes from conventional B3LYP results are found in H species results rather than D species results, due to larger NQE of proton compared to deuteron.
Table 2 lists the optimized exponent α (αopt) values for each isomer. The optimum αopt values for protons are always smaller than those for deuterons; in other words, protonic wavefunctions are always more delocalized than deuteronic ones. In addition, the optimum αopt values for protons bonded to oxygen atom are slightly smaller than those bonded to carbon atom, reflecting the larger electronegativity of oxygen atom compared to carbon atom.38 It should be noted that structures VIII and D were also not obtained in MC_B3LYP calculations as shown above.
| αopt values for H species | αopt values for D species | |||||||
|---|---|---|---|---|---|---|---|---|
| H1 | H2 | H3 | H4 | D1 | D2 | D3 | D4 | |
| I | 24.2 | 24.1 | 23.1 | 23.2 | 35.8 | 35.7 | 34.3 | 34.5 |
| II | 24.1 | 24.1 | 23.3 | 23.2 | 35.7 | 35.7 | 34.6 | 34.4 |
| III | 24.3 | 24.1 | 22.9 | 23.4 | 36.0 | 35.6 | 34.1 | 34.8 |
| IV | 24.1 | 24.2 | 23.6 | 23.3 | 35.7 | 35.8 | 35.0 | 34.6 |
| V | 24.0 | 24.2 | 23.6 | 23.3 | 35.6 | 35.8 | 35.0 | 34.6 |
| VI | 24.0 | 24.2 | 23.4 | 23.1 | 35.6 | 35.8 | 34.8 | 34.4 |
| VII | 24.2 | 24.1 | 23.5 | 23.4 | 35.8 | 35.8 | 34.9 | 34.8 |
| A | 23.9 | 23.9 | 24.2 | 22.8 | 35.4 | 35.4 | 35.8 | 34.0 |
| B | 24.0 | 24.0 | 24.2 | 23.2 | 35.5 | 35.5 | 35.9 | 34.5 |
| C | 24.0 | 24.0 | 24.2 | 23.2 | 35.6 | 35.6 | 35.8 | 34.4 |
Nuclear quantum effect and H/D isotope effects on isomerization and keto–enol tautomerism reactions in gas-phase
Table 3 lists the activation energies of 14 isomerization reactions. Transition state structures of these reactions are shown in Fig. S1 (see, ESI Fig. S1†). First, we would like to discuss about hydrogen transfer reactions of I–II, IV–V, and B–C. It is found that activation energies corrected for ZPVE are smaller than those without correction (electronic energy). This means that nuclear zero point vibrational motion slightly reduces the activation energies. Furthermore, by directly taking account of NQEs, the activation energies of MC_B3LYP calculations are more than 1.6 kcal mol−1 lower than those of ZPVE-corrected ones. Thus, NQE provides significant effect on the activation energies, and including of nuclear quantum effect is important to discuss about energetics for the hydrogen transfer reactions.| Direction | B3LYP | MC_B3LYP | |||||
|---|---|---|---|---|---|---|---|
| Electronic energy | ZPVE-H | ZPVE-D | H species | D species | |||
| Hydrogen transfer reaction | I–II | Forward | 37.9 | 34.7 | 35.5 | 32.3 | 33.9 |
| Reverse | 35.5 | 32.6 | 33.5 | 29.9 | 31.5 | ||
| IV–V | Forward | 36.0 | 33.0 | 33.8 | 30.4 | 32.0 | |
| Reverse | 36.3 | 33.3 | 34.1 | 30.7 | 32.3 | ||
| B–C | Forward | 38.7 | 35.6 | 36.4 | 33.0 | 34.6 | |
| Reverse | 37.3 | 34.3 | 35.1 | 31.6 | 33.2 | ||
| O–H rotational reaction | I–III | Forward | 11.6 | 10.5 | 10.7 | 11.6 | 11.6 |
| Reverse | 6.2 | 5.5 | 5.6 | 6.0 | 6.1 | ||
| I–IV | Forward | 8.7 | 7.9 | 8.0 | 9.2 | 9.1 | |
| Reverse | 3.2 | 2.7 | 2.8 | 3.1 | 3.1 | ||
| II–V | Forward | 6.3 | 5.8 | 5.9 | 6.6 | 6.5 | |
| Reverse | 3.5 | 2.9 | 3.0 | 3.4 | 3.4 | ||
| III–VII | Forward | 9.2 | 8.5 | 8.7 | 9.6 | 9.5 | |
| Reverse | 3.0 | 2.4 | 2.5 | 2.9 | 2.9 | ||
| IV–VII | Forward | 11.6 | 10.6 | 10.8 | 11.6 | 11.6 | |
| Reverse | 5.6 | 4.6 | 4.8 | 5.4 | 5.5 | ||
| V–VI | Forward | 11.8 | 10.6 | 10.9 | 11.6 | 11.7 | |
| Reverse | 11.6 | 10.6 | 10.8 | 11.8 | 11.7 | ||
| A–B | Forward | 13.4 | 12.0 | 12.3 | 13.6 | 13.6 | |
| Reverse | 11.1 | 9.9 | 10.2 | 10.9 | 10.9 | ||
| C–C rotational reaction | I–II | Forward | 11.9 | 11.1 | 11.2 | 12.3 | 12.2 |
| Reverse | 9.5 | 9.0 | 9.1 | 9.8 | 9.7 | ||
| IV–V | Forward | 5.0 | 4.7 | 4.8 | 4.9 | 4.9 | |
| Reverse | 5.3 | 5.0 | 5.1 | 5.2 | 5.3 | ||
| VI–VII | Forward | 8.5 | 8.3 | 8.3 | 9.0 | 8.8 | |
| Reverse | 2.3 | 2.1 | 2.1 | 2.2 | 2.2 | ||
| B–C | Forward | 1.8 | 1.5 | 1.5 | 1.6 | 1.7 | |
| Reverse | 0.4 | 0.2 | 0.2 | 0.3 | 0.3 | ||
Regarding H/D isotope effect, activation energies of H species are smaller than those of D species, because the magnitude of NQE is inversely proportional to nuclear mass. It should be noted here that geometrical differences between H and D species, which are induced by the difference between NQEs of proton and deuteron (H/D geometrical isotope effect: GIE), can be observed in MC_B3LYP calculations. We have already demonstrated that such GIEs are important to analyze H/D isotope effects on the activation energies of hydrogen transfer reactions, on the basis of “multicomponent” treatment.16,20 To analyze the difference between the behavior of protonic and deuteronic wavefunctions, Table 4 lists the optimized exponent α (αopt) values of quantum protons and deuterons in effective transition state structures of H and D species, respectively. The αopt values of migrating protons (deuterons) are 18.0, 18.1, and 18.0 (26.9, 27.1, and 26.9) in reactions I–II, IV–V, and B–C, respectively, which are obviously smaller than those for other protons (deuterons). This means that a migrating proton (or deuteron) becomes drastically delocalized wavefunction in effective transition state structure.
| αopt values for H species | αopt values for D species | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| H1 | H2 | H3 | H4 | D1 | D2 | D3 | D4 | ||
| Hydrogen transfer reaction | I–II | 24.1 | 24.1 | 23.2 | 18.0 | 35.7 | 35.7 | 34.5 | 26.9 |
| IV–V | 24.0 | 24.2 | 23.5 | 18.1 | 35.6 | 35.8 | 34.9 | 27.1 | |
| B–C | 23.9 | 24.0 | 24.2 | 18.0 | 35.5 | 35.5 | 35.8 | 26.9 | |
| O–H rotational reaction | I–III | 24.2 | 24.1 | 23.1 | 23.2 | 35.8 | 35.7 | 34.3 | 34.4 |
| I–IV | 24.1 | 24.2 | 23.5 | 23.3 | 35.7 | 35.8 | 34.9 | 34.6 | |
| II–V | 24.1 | 24.2 | 23.5 | 23.3 | 35.7 | 35.8 | 34.9 | 34.6 | |
| III–VII | 24.2 | 24.1 | 23.4 | 23.5 | 35.8 | 35.7 | 34.7 | 34.8 | |
| IV–VII | 24.1 | 24.2 | 23.6 | 23.3 | 35.7 | 35.8 | 35.0 | 34.6 | |
| V–VI | 24.1 | 24.2 | 23.6 | 23.2 | 35.6 | 35.8 | 35.0 | 34.4 | |
| A–B | 24.0 | 24.0 | 24.2 | 23.0 | 35.5 | 35.5 | 35.8 | 34.2 | |
| C–C rotational reaction | I–II | 24.2 | 24.1 | 23.5 | 23.2 | 35.8 | 35.7 | 34.9 | 34.5 |
| IV–V | 24.1 | 24.1 | 23.5 | 23.2 | 35.7 | 35.8 | 34.9 | 34.5 | |
| VI–VII | 24.1 | 24.1 | 23.5 | 23.4 | 35.7 | 35.7 | 34.9 | 34.8 | |
| B–C | 24.0 | 24.0 | 24.1 | 23.1 | 35.5 | 35.5 | 35.8 | 34.4 | |
Next, we would like to focus on isomerization reactions, accompanying with O–H rotation. The activation energies of these isomerization reactions are smaller than those of hydrogen transfer ones, since O–H rotational reactions do not involve covalent bond cleavage in contrast to hydrogen transfer reactions. The largest ZPVE-uncorrected B3LYP activation energy is 13.4 kcal mol−1, found in forward direction of A–B isomerization reaction. The harmonic ZPVE correction lowers the activation energies of all the O–H rotational reactions, and larger reductions are again found in ZPVE-H results rather than in ZPVE-D ones. For the cases of reaction I–III, I–IV, II–V, III–VII, and IV–VII, the activation energies of forward direction of the reactions are obviously larger than those of reverse direction, since these forward reactions involve intramolecular O–H⋯O hydrogen bond cleavage.
From Table 3, two different tendencies between rotational and hydrogen transfer reactions can be observed in MC_B3LYP results. One is that NQE hardly reduces the activation energies of O–H rotational reactions, but instead, the activation energies of several rotational reactions become larger by taking account of NQEs (“reverse” NQE). Second is that the activation energies of H species in such rotational reactions are higher than that of D species (“unusual” H/D isotope effect). For instance, the activation energy of H species of forward direction of reactions I–IV (9.2 kcal mol−1), II–V (6.6 kcal mol−1), III–VII (9.6 kcal mol−1), and A–B (13.6 kcal mol−1), and reverse direction of reaction V–VI (11.8 kcal mol−1) become 0.5 kcal mol−1, 0.3 kcal mol−1, 0.4 kcal mol−1, 0.2 kcal mol−1, and 0.2 kcal mol−1 higher, respectively, compared to those of ZPVE-uncorrected B3LYP activation energies.
To interpret the aforementioned interesting two differences on O–H rotational reactions, we again focused on the intramolecular hydrogen-bonded interactions in each optimized structure. An intramolecular O–H⋯O hydrogen-bonded interaction is found in structures I, II, III, VI, and A. Since hydrogen-bonded interaction is enhanced by taking account of NQE of hydrogen nucleus,22,23,25,42 the activation energies of the O–H rotational reactions from structures I, II, III, VI, and A become large in MC_B3LYP results. For instance, the strengths of the intramolecular hydrogen-bonded interactions in structure I are 6.1 kcal mol−1 for H species, 5.9 kcal mol−1 for D species, and 5.5 kcal mol−1 for B3LYP result, which are estimated as the difference between energies of structures I and IV (Table 1). The intramolecular hydrogen-bonded interaction is, indeed, enhanced by including NQE. From geometric point of view, this result implies that OH rotational motion in MC_B3LYP is restricted by strong intramolecular hydrogen-bonded interaction. On the other hand, the activation energy of I–III reaction does not change in the shown digit by including NQE despite the existence of an intramolecular hydrogen-bonded interaction in structures I and III, because the intramolecular hydrogen-bonded interaction is kept during O–H rotational isomerization reaction of I–III.
To see this enhancement in detail, Fig. 4 shows the optimized geometrical parameters of structure I. The optimized geometrical parameters of other structures (II–VII and A–C) are shown in Fig. S2 and S3 (see, ESI Fig. S2 and S3†). NQEs of proton and deuteron provide significant effect on covalent O–H and C–H bond lengths. These bond lengths of H species are about 0.025 Å longer than those obtained in B3LYP calculation, due to the direct inclusion of the anharmonicity of the potential energy curve along the covalent bond direction. On the other hand, C–C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C–O, and C
C, C–O, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond lengths are almost unchanged between MC_B3LYP and B3LYP results, as well as bond angles. These NQEs on geometrical parameters lead to the differences in hydrogen-bonded distances that hydrogen-bonded distances become short in the order of H species (2.061 Å) < D species (2.071 Å) < that obtained by B3LYP (2.095 Å). Furthermore, the optimum αopt values of H3 and D3 atoms, which act as the hydrogen donor atoms in the intramolecular hydrogen-bonded interaction, are 23.1 and 34.3, respectively. Since the delocalized protonic wavefunction less attracts surrounding electrons than relatively more localized deuteronic one, H3 atom in H species is expected to be the most positive. As shown in Fig. 4, the Mulliken atomic charge of H3 atom in H species is, indeed, the most positive. Therefore, H3 atom acts as the strongest hydrogen donor, and the hydrogen-bonded interaction is the strongest in H species.
O bond lengths are almost unchanged between MC_B3LYP and B3LYP results, as well as bond angles. These NQEs on geometrical parameters lead to the differences in hydrogen-bonded distances that hydrogen-bonded distances become short in the order of H species (2.061 Å) < D species (2.071 Å) < that obtained by B3LYP (2.095 Å). Furthermore, the optimum αopt values of H3 and D3 atoms, which act as the hydrogen donor atoms in the intramolecular hydrogen-bonded interaction, are 23.1 and 34.3, respectively. Since the delocalized protonic wavefunction less attracts surrounding electrons than relatively more localized deuteronic one, H3 atom in H species is expected to be the most positive. As shown in Fig. 4, the Mulliken atomic charge of H3 atom in H species is, indeed, the most positive. Therefore, H3 atom acts as the strongest hydrogen donor, and the hydrogen-bonded interaction is the strongest in H species.
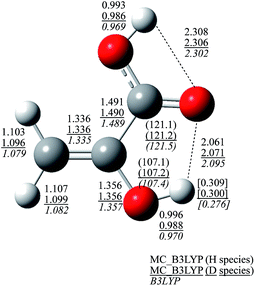 | ||
| Fig. 4 Optimized geometrical parameters of structure I. Values without brackets are atomic distances [Å], values in parenthesis are bond angle [degree], and values in brackets are Mulliken charges. | ||
According to our analysis, OH rotation from structure I to IV in B3LYP calculations is easier to occur than that in MC_B3LYP ones, since the strength of the intramolecular hydrogen-bonded interaction in structure I by B3LYP calculations is weaker than that by MC_B3LYP. Several activation energies of OH rotational reactions corrected for harmonic ZPVE are more than 1 kcal mol−1 lower than those obtained in MC_B3LYP calculations. The intramolecular hydrogen-bonded interaction in MC_B3LYP calculations is stronger than that in B3LYP ones and then, restricts OH rotation. The same idea can be used to explain the unusual H/D isotope effect on rotational reactions. The activation energies of H species are larger than those of D species, since the hydrogen-bonded interaction in H species is stronger than that in D species, and the OH rotational motion is restricted more than OD one due to stronger hydrogen-bonded interaction. Thus, we clearly revealed here that the enhancement of intramolecular hydrogen-bonded interaction by including NQE is the main reason why reverse NQEs and unusual H/D isotope effect on the activation energies are observed in several O–H rotational isomerization reactions.
Ishimoto and coworkers have also observed more facile CD3 group rotation in CD3CDO molecule rather than CH3 group rotation in CH3CHO.43 They concluded that such more facile CD3 group rotation is due to the shorter C–D bond length compared to C–H one in CH3CHO and localized electrons surrounding CD3 group. Although these changes are also induced by the difference between NQEs of proton and deuteron, the main reason of the unusual H/D isotope effect in several O–H rotational isomerization reactions of pyruvic acid isomer is enhancement of the intramolecular hydrogen-bonded interaction, as mentioned above.
In addition, significant delocalization of nuclear wavefunction is not observed even in the effective transition state structure (Table 4) of all the O–H rotational isomerization reactions, since hydrogen atom does not migrate during the reactions.
The activation energies of C–C rotational reactions of I–II and VI–VII also become larger by taking account of protonic and deuteronic quantum effect. Since structures I, II, and VI have an intramolecular hydrogen-bonded interaction and these C–C rotational reactions involve hydrogen bond cleavage, activation energies of both directions of I–II and forward direction of VI–VII increase by NQE, as well as the aforementioned O–H rotational reactions. Reverse NQE and unusual H/D isotope effect on the activation energies are also found in these C–C rotational reactions.
Table 5 lists the calculated activation energies of keto–enol tautomerism reactions. Transition state structures of these tautomerism reactions are shown in Fig. S4 (see, ESI Fig. S4†). Since these keto–enol tautomerism reactions involve hydrogen transfer process, activation energies of these tautomerism reactions are clearly larger than O–H and C–C rotational isomerization reactions. In particular, the activation energies of keto–enol tautomerism reactions are larger than the aforementioned hydrogen transfer isomerization ones, which are interconversion of enol or keto forms themselves. These larger activation energies of keto–enol tautomerism reactions can be interpreted by the geometrical relaxation, accompanying with hydrogen transfer reaction from CH3 group to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O. Unlike the hydrogen transfer reactions in interconversion reactions of enol or keto forms themselves, hydrogen transfer reaction from CH3 group to C
O. Unlike the hydrogen transfer reactions in interconversion reactions of enol or keto forms themselves, hydrogen transfer reaction from CH3 group to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O induces the overall change in geometrical parameters.6 Thus, the activation energies of hydrogen transfer reactions in keto–enol tautomerism reactions are larger than those in interconversion reactions of enol or keto forms themselves. The differences between the activation energies of H and D species (ZPVE-H and ZPVE-D) are 1.8–1.9 kcal mol−1 (0.9–1.1 kcal mol−1), thus, almost constant for all keto–enol tautomerism reactions. The reason of this accidental coincidence is the fact that the geometrical changes occurred in the reactions (hydrogen migration from CH3 to C
O induces the overall change in geometrical parameters.6 Thus, the activation energies of hydrogen transfer reactions in keto–enol tautomerism reactions are larger than those in interconversion reactions of enol or keto forms themselves. The differences between the activation energies of H and D species (ZPVE-H and ZPVE-D) are 1.8–1.9 kcal mol−1 (0.9–1.1 kcal mol−1), thus, almost constant for all keto–enol tautomerism reactions. The reason of this accidental coincidence is the fact that the geometrical changes occurred in the reactions (hydrogen migration from CH3 to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) are similar between these keto–enol tautomerism reactions. For these keto–enol tautomerism reactions, both harmonic ZPVE corrections and direct inclusion of NQEs lower the barrier of the reactions. Larger reductions are found in MC_B3LYP results, since relaxation of both the geometries and distribution of nuclear wavefunction are represented in MC_B3LYP results. Table 6 lists the optimized exponent αopt values of quantum protons and deuterons in effective transition state structures of keto–enol tautomerism reaction of H and D species, respectively. Only αopt values of migrating protons and deuterons (H3 and D3) are obviously smaller than those of other protons and deuterons. Therefore, nuclear wavefunction of migrating hydrogen nucleus becomes drastically delocalized in transition state structures of keto–enol tautomerism reactions.
O) are similar between these keto–enol tautomerism reactions. For these keto–enol tautomerism reactions, both harmonic ZPVE corrections and direct inclusion of NQEs lower the barrier of the reactions. Larger reductions are found in MC_B3LYP results, since relaxation of both the geometries and distribution of nuclear wavefunction are represented in MC_B3LYP results. Table 6 lists the optimized exponent αopt values of quantum protons and deuterons in effective transition state structures of keto–enol tautomerism reaction of H and D species, respectively. Only αopt values of migrating protons and deuterons (H3 and D3) are obviously smaller than those of other protons and deuterons. Therefore, nuclear wavefunction of migrating hydrogen nucleus becomes drastically delocalized in transition state structures of keto–enol tautomerism reactions.
| Direction | B3LYP | MC_B3LYP | |||||
|---|---|---|---|---|---|---|---|
| Electronic energy | ZPVE-H | ZPVE-D | H species | D species | |||
| Keto–enol tautomerism reaction | A–VI | Forward | 73.0 | 69.2 | 70.1 | 66.4 | 68.3 |
| Reverse | 61.5 | 57.5 | 58.6 | 55.1 | 57.0 | ||
| B–V | Forward | 70.4 | 66.7 | 67.6 | 63.8 | 65.7 | |
| Reverse | 61.4 | 57.2 | 58.3 | 55.1 | 56.9 | ||
| C–IV | Forward | 69.3 | 65.7 | 66.7 | 62.8 | 64.7 | |
| Reverse | 61.4 | 57.3 | 58.3 | 55.0 | 56.9 | ||
| αopt values for H species | αopt values for D species | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| H1 | H2 | H3 | H4 | D1 | D2 | D3 | D4 | ||
| Keto–enol tautomerism reaction | A–VI | 24.0 | 23.6 | 18.1 | 23.0 | 35.5 | 35.0 | 27.1 | 34.1 |
| B–V | 24.0 | 23.6 | 18.3 | 23.1 | 35.6 | 35.0 | 27.4 | 34.4 | |
| C–IV | 24.0 | 23.6 | 18.4 | 23.1 | 35.6 | 35.0 | 27.5 | 34.4 | |
Let us summarize the NQEs of hydrogen nuclei on isomerization reactions and keto–enol tautomerism reactions of pyruvic acid molecule in gas-phase. The activation energies of hydrogen transfer reactions are obviously larger than those of O–H and C–C rotational reactions, because only hydrogen transfer reactions involve covalent bond cleavage. In addition, since a hydrogen (or deuterium) atom itself migrates in hydrogen transfer reactions, protonic (or deuteronic) wavefunction becomes drastically delocalized in effective transition state structures. Directly taking account of the relaxation effect on the distribution of nuclear wavefunction and geometries by multicomponent treatment, MC_B3LYP activation energies of hydrogen transfer reactions are significantly smaller than those obtained in conventional B3LYP calculations. On the other hand, NQE provides significant effects on the activation energies of O–H and C–C rotational reactions via intramolecular hydrogen bond. Since NQE enhances the intramolecular hydrogen-bonded interaction in reactant or product molecules, several O–H and C–C rotational motions are restricted by stronger intramolecular hydrogen bond. Consequently, unusual H/D isotope effects on the activation energies are observed in several rotational reactions. Therefore, direct inclusion of NQE is indispensable to analyze the H/D isotope effect on not only hydrogen transfer reactions but also O–H or C–C rotational reactions, in which hydrogen atom itself does not migrate during the reaction.
Nuclear quantum effect and H/D isotope effects on isomerization and keto–enol tautomerism reactions catalyzed by a single water molecule
To investigate the effect of hydration on the activation energies, we have also analyzed the mono hydrated isomerization and keto–enol tautomerism reactions. Table 7 lists the calculated activation energies obtained by B3LYP/6-311++G(d,p) and MC_B3LYP/6-311++G(d,p) methods. Table 7 also lists the B3LYP/6-311++G(2df,p) values6 for a comparison. Optimized structures of reactant, transition state, and product of mono hydrated interconversion reactions and keto–enol tautomerism reactions are shown in Fig. S5 and S6,† respectively (see, ESI Fig. S5 and S6†). It should be noted here that the reactions of mono hydrated systems are hydrogen transfer reactions between the pyruvic acid and additional water molecules. In all methods, the hydrogen atom migration from carboxyl group to water molecule and that from water molecule to carboxyl group proceed through one-step concerted mechanism. A water molecule drastically lowers the activation energies of the hydrogen transfer-isomerization and keto–enol tautomerism reactions. Our B3LYP/6-311++G(d,p) results are about 10 kcal mol−1 higher than B3LYP/6-311++G(2df,p) ones. Although the catalytic effect of a single water molecule can be observed in our B3LYP/6-311++G(d,p) results, B3LYP/6-311++G(2df,p) activation energies,6 especially those for interconversion reactions, seem to be too low. Activation energies of interconversion reactions and keto–enol tautomerism reactions of H species (D species) become less than 7.9 kcal mol−1 (9.7 kcal mol−1) and 32.2 kcal mol−1 (34.8 kcal mol−1), respectively, by including both catalytic hydration effect and NQE of protons or deuterons.| Direction | B3LYP | MC_B3LYP | B3LYP/6-311++G(2df,p)6 | ||||
|---|---|---|---|---|---|---|---|
| Electronic energy | ZPVE-H | ZPVE-D | H species | D species | ZPVE-H | ||
| I–II | Forward | 14.5 | 11.5 | 12.5 | 7.8 | 9.6 | 1.9 |
| Reverse | 12.7 | 9.8 | 10.8 | 6.0 | 7.8 | 0.6 | |
| IV–V | Forward | 14.1 | 11.0 | 12.1 | 7.2 | 9.1 | 1.3 |
| Reverse | 14.2 | 11.0 | 12.1 | 7.3 | 9.2 | 1.6 | |
| B–C | Forward | 14.7 | 11.8 | 12.8 | 7.9 | 9.7 | 2.4 |
| Reverse | 13.9 | 11.0 | 12.0 | 7.2 | 9.0 | 0.8 | |
| A–VI | Forward | 39.3 | 37.2 | 38.0 | 30.8 | 33.4 | 32.8 |
| Reverse | 32.4 | 29.7 | 30.7 | 25.0 | 27.2 | 21.3 | |
| B–V | Forward | 41.3 | 38.9 | 39.8 | 32.2 | 34.8 | 32.8 |
| Reverse | 35.1 | 31.9 | 33.0 | 26.8 | 29.1 | 23.9 | |
| C–IV | Forward | 41.0 | 38.5 | 39.4 | 31.9 | 34.5 | |
| Reverse | 35.7 | 32.5 | 33.5 | 27.3 | 29.7 | ||
Table 8 lists the optimized α values for quantum protons and deuterons in effective transition state structures of mono hydrated isomerization and keto–enol tautomerism reactions. The optimum α values for two migrating protons (or deuterons) are clearly smaller than those for other quantum nuclei. Therefore, nuclear wavefunctions of two migrating protons (or deuterons) become prominently more delocalized ones than those of other hydrogen nuclei in effective transition state structures.
| αopt values for H species | αopt values for D species | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H1 | H2 | H3 | H4 | H5 | H6 | D1 | D2 | D3 | D4 | D5 | D6 | |
| I–II | 24.1 | 24.1 | 23.1 | 19.2 | 23.4 | 19.4 | 35.7 | 35.7 | 34.4 | 28.7 | 34.7 | 28.9 |
| IV–V | 24.1 | 24.2 | 23.6 | 19.3 | 23.5 | 19.3 | 35.6 | 35.8 | 35.0 | 28.7 | 34.8 | 28.7 |
| B–C | 24.0 | 24.0 | 24.2 | 19.3 | 23.4 | 19.3 | 35.6 | 35.5 | 35.9 | 28.8 | 34.7 | 28.8 |
| A–VI | 23.3 | 23.9 | 19.2 | 23.3 | 19.7 | 22.7 | 35.7 | 35.5 | 28.7 | 34.6 | 29.4 | 33.9 |
| B–V | 24.1 | 23.9 | 19.2 | 23.4 | 19.4 | 23.2 | 35.7 | 35.5 | 28.7 | 34.8 | 29.0 | 34.5 |
| C–IV | 24.2 | 23.9 | 19.3 | 23.4 | 19.4 | 23.2 | 35.8 | 35.5 | 28.7 | 34.8 | 29.0 | 34.4 |
In summary, a single water molecule catalyzes the isomerization and tautomerism reactions of pyruvic acid molecule. The catalytic effects of a water molecule seems to be overestimated in the previous study,6 since these activation energies, which are only corrected for harmonic ZPVE, are even smaller than MC_B3LYP ones. In the MC_B3LYP calculations, the activation energies become drastically small by both the catalytic effect of a water molecule and NQEs (relaxation of distribution of nuclear wavefunction and geometries). For instance, the activation energies of H species of hydrogen transfer reactions obtained in MC_B3LYP calculations are smaller than half of ZPVE-H ones. Therefore, direct inclusion of NQE is also important to analyze mono hydrated isomerization and tautomerism reactions and H/D isotope effects on these reactions.
Conclusions
We have analyzed nuclear quantum effects (NQEs) and H/D isotope effects on isomerization and keto–enol tautomerism reactions in pyruvic acid molecule with the aid of multicomponent B3LYP (MC_B3LYP) calculations, which can take account of protonic and deuteronic quantum effects. For hydrogen transfer isomerization and tautomerism reactions, NQEs of proton and deuteron lower the activation energies as in the case with the other hydrogen transfer reactions.14,19 On the other hand, the activation energies of several O–H and C–C rotational isomerization reactions become slightly large by taking account of NQEs of proton and deuteron, although harmonic ZPVE correction lowers them due to underestimation of intramolecular hydrogen-bonded interaction. Thus, “reverse” NQE and “unusual” H/D isotope effect on the activation energies of these rotational reactions are observed in MC_B3LYP results in contrast to the harmonic ZPVE-corrected B3LYP results (ZPVE-H and ZPVE-D).Our study clearly demonstrates that the direct treatment of NQEs of proton and deuteron is indispensable to analyze H/D isotope effect. The harmonic ZPVE correction sometimes shows an opposite trend of H/D isotope effect to multicomponent treatment. We, thus, believe that our MC_QM and MC_DFT-CI-NEB approaches are one of the powerful and suitable methods to efficiently analyze NQE and H/D isotope effects on chemical reactions.
Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers 16K17851 (to T. U.), 15KT0067 (to M. T. and T. U.). Portion of these computations were performed at Research center for Computational Science (RCCS), Okazaki.References
- E. D. Raczyńska, K. Duczmal and M. Darowska, Vib. Spectrosc., 2005, 39, 37 CrossRef.
- Y. Huang, X. Zhang, L. Xu, H. Chen and G. Chen, J. Sep. Sci., 2009, 32, 4155 CrossRef CAS PubMed.
- G. da Silva, J. Phys. Chem. A, 2016, 120, 276 CrossRef CAS PubMed.
- R. Kakkar, M. Pathak and N. P. Radhika, Org. Biomol. Chem., 2006, 4, 886 CAS.
- R. Kakkar, M. Pathak and P. Gahlot, J. Phys. Org. Chem., 2008, 21, 23 CrossRef CAS.
- Y. Valadbeigi and H. Farrokhpour, Int. J. Quantum Chem., 2013, 113, 2372 CrossRef CAS.
- N. Dalal, A. Klymachyov and A. Bussmann-Holder, Phys. Rev. Lett., 1998, 81, 5924 CrossRef CAS.
- T. Ishimoto and M. Tachikawa, Solid State Phenom., 2012, 189, 169 CrossRef CAS.
- T. Ishimoto and M. Tachikawa, Ferroelectrics, 2012, 433, 170 CrossRef CAS.
- L. Malander and W. H. Saunders, Reaction Rates of Isotopic Molecules, Wiley, New York, 1980 Search PubMed.
- V. L. Byazovkin and V. A. Tolkatchev, Phys. Chem. Chem. Phys., 2000, 2, 3797 RSC.
- M. Born and J. R. Oppenheimer, Ann. Phys., 1927, 389, 457 CrossRef.
- M. Tachikawa, K. Mori, H. Nakai and K. Iguchi, Chem. Phys. Lett., 1998, 290, 437 CrossRef CAS.
- T. Udagawa and M. Tachikawa, in Progress in Quantum Chemistry Research, ed. E. O. Hoffmann, NOVA Science Publishers, New York, 2007, ch. 3, pp. 123–162 Search PubMed.
- T. Iodanov and S. Hammes-Schiffer, J. Chem. Phys., 2003, 118, 9489 CrossRef.
- T. Udagawa, K. Suzuki and M. Tachikawa, ChemPhysChem, 2015, 15, 3156 CrossRef PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónnson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS.
- Y. Itou, S. Mori, T. Udagawa, M. Tachikawa, T. Ishimoto and U. Nagashima, J. Phys. Chem. A, 2007, 111, 261 CrossRef CAS PubMed.
- T. Udagawa and M. Tachikawa, J. Chem. Phys., 2016, 145, 164310 CrossRef PubMed.
- T. Udagawa, T. Ishimoto, H. Tokiwa, M. Tachikawa and U. Nagashima, J. Phys. Chem. A, 2006, 110, 7279 CrossRef CAS PubMed.
- T. Udagawa and M. Tachikawa, J. Chem. Phys., 2006, 125, 244105 CrossRef PubMed.
- T. Udagawa and M. Tachikawa, J. Comput. Chem., 2014, 35, 271 CrossRef CAS PubMed.
- T. Udagawa and M. Tachikawa, Theor. Chem. Acc., 2015, 134, 24 CrossRef.
- T. Udagawa and M. Tachikawa, J. Comput. Chem., 2015, 36, 1647 CrossRef CAS PubMed.
- H. Nishizawa, Y. Imamura, Y. Ikabata and H. Nakai, Chem. Phys. Lett., 2012, 533, 100 CrossRef CAS.
- Y. Ikabata, Y. Imamura and H. Nakai, J. Phys. Chem. A, 2011, 115, 1433 CrossRef CAS PubMed.
- Y. Imamura, H. Kiryu and H. Nakai, J. Comput. Chem., 2008, 29, 735 CrossRef CAS PubMed.
- K. R. Brorsen, A. Sirjoosingh, M. V. Pak and S. Hammes-Schiffer, J. Chem. Phys., 2015, 142, 214108 CrossRef PubMed.
- A. Sirjoosingh, M. V. Pak, K. R. Brorsen and S. Hammes-Schiffer, J. Chem. Phys., 2015, 142, 214107 CrossRef PubMed.
- A. Sirioosingh, M. V. Pak and S. Hammes-Schiffer, J. Chem. Phys., 2012, 136, 174114 CrossRef PubMed.
- T. Kreibich, R. van Leeuwen and E. K. U. Gross, Phys. Rev. A, 2008, 78, 022501 CrossRef.
- T. Kreibich and E. K. U. Gross, Phys. Rev. Lett., 2001, 86, 2984 CrossRef CAS PubMed.
- J. Charry, J. Romero, M. T. D. N. Varella and A. Reyes, Phys. Rev. A, 2014, 89, 052709 CrossRef.
- H. Nakai, Int. J. Quantum Chem., 2002, 86, 511 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- T. Ishimoto, M. Tachikawa and U. Nagashima, Int. J. Quantum Chem., 2006, 106, 1465 CrossRef CAS.
- T. Ishimoto, M. Tachikawa and U. Nagashima, J. Chem. Phys., 2006, 125, 144103 CrossRef PubMed.
- M. Hashimoto, T. Ishimoto, M. Tachikawa and T. Udagawa, Int. J. Quantum Chem., 2016, 116, 961 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmnn, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- I. Reva, C. M. Nunes, M. Biczysko and R. Fausto, J. Phys. Chem. A, 2015, 119, 2614 CrossRef CAS PubMed.
- M. Tachikawa, Mol. Phys., 2002, 100, 881 CrossRef CAS.
- T. Ishimoto, Y. Ishihara, H. Teramae, M. Baba and U. Nagashima, J. Chem. Phys., 2008, 128, 184309 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra28271g |
| This journal is © The Royal Society of Chemistry 2017 |