DOI:
10.1039/C6RA28286E
(Paper)
RSC Adv., 2017,
7, 15149-15157
Electronic and spatial control over the formation of transient ion pairs during photoinduced electron transfer between proflavine–amine systems in a subpicosecond time regime
Received
16th December 2016
, Accepted 20th February 2017
First published on 7th March 2017
Abstract
Probing photoinduced electron transfer (PET) in solution in terms of rate of reaction and reaction free energy is a great challenge in physical chemistry. Several factors such as solvent polarity, viscosity, and electronic coupling between reacting species control the overall rate of the reaction. However, the unambiguous reaction mechanism is still an important area of research. Earlier, our studies on proflavine–DMA and proflavine–TEA electron donor–acceptor systems revealed the dynamics of the diffusion controlled aspect of PET. Herein, we have extended our investigation in a higher time resolution i.e. in the femtosecond–picosecond timescale to decipher the incidents occurring at the time regime associated with PET. Our present contribution sheds light on the controlling factors of polarity, viscosity, and microheterogeneity, leading to the confinement of reactants at the molecular level. We also tried to qualitatively as well as quantitatively probe these factors. Our present investigation reveals that electron transfer in these two systems is dependent on several factors. In the case of alcoholic solvents, the fastest fluorescence decay components are the result of the formation of a contact ion pair (CIP) as well as direct electron transfer and therefore depend on the dielectric of the medium. On the other hand, in a heterogeneous medium, compartmentalization of reactants and interaction between the components with head groups and tail parts of micelles, depending on the overall charge of a particular micelle, are the controlling factors for the reaction dynamics.
Introduction
Nature exhibits numerous chemical reactions in living as well as non-living systems. Life processes are sustained through these reactions. Charge transfer (CT), or more precisely, charge separation (CS) is the key step of all these complex chemical reactions. This step is crucial for all the reactions occurring in solution, condensed matter, as well as in rigid and linked biological macromolecules. Since the 1960s, when Weller and co-workers started their pioneering experiments involving CT, which supported the theoretical model by Marcus on the exact kinetics of CT in solution, it has become the most studied reaction type investigated by physical chemists to date, both in homogeneous and heterogeneous media. In 1956, Marcus first theoretically correlated the rate constant of the reaction with reaction exergonicity, i.e. the driving force.1–3 The rate constant is a direct measure of the activation energy, which is composed of both nuclear and solvent reorganization energy. According to Marcus, both the probability of crossing the activation energy barrier and the height of the activation barrier are the deciding factors for the rate constant of the PET reaction. The former depends on the electronic coupling and the mutual distance and orientation between the donor and acceptor, whereas the latter is a function of solvent dielectric. These two factors have been enormously studied till date to be the reason for the change in the rate constant of PET reaction in a particular donor–acceptor couple. Marcus formulated the rate constant of the PET reaction with reaction exergonicity in the following manner:| |
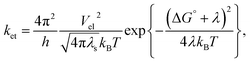 | (1) |
where the rate constant of the bimolecular ET reaction (ket) is written in terms of the electronic coupling matrix element (Vel), reorganization energy (λ: where λ is the sum of intramolecular (λi) and solvent reorganization (λs) contributions), and free energy change (ΔG°) of the ET reaction.26 Marcus first used the non-equilibrium dielectric polarization theory to calculate the free energy of activation for a system with rigid inner coordination shells.4
In the late 1960s, Rehm and Weller first expressed their serious doubt on the validity of the Marcus theory, which was the most accepted theory for the description of PET reactions, through their experiments.5,6 In practice, the rate constant of bimolecular photoinduced CT reactions increases with the driving force of the reaction up to a value correlating the diffusion of the reactants and remains diffusion limited at the driving forces more than this value, where inversion of the rate is theoretically expected. The Marcus inverted region (MIR) was first experimentally observed in the mid-1980s for intramolecular CS reactions.7,8 Since then, for several ET processes such as intramolecular charge recombination,9 intermolecular charge recombination,10–12 intermolecular charge shift,13,14 intramolecular CS,15 and CS in hydrogen-bonded complexes,16 it has been experimentally reported.
After this, many researchers worked on this particular problem of the reaction kinetics of bimolecular PET to experimentally prove the Marcus theorem. Many of them raised a debate about the results that experimentally showed MIR. Vauthey et al. used the differential encounter theory (DET) that combines a diffusion equation to determine the reactant pair distribution, n(r, t), and the Marcus theory and calculated the reaction probability at variable distances. They determined the quenching rate constant (k(t)) using this theory and showed that the quenching rate is independent of viscosity and is equal to the intrinsic ET rate constant, k0 (static quenching rate constant). At later times of a particular bimolecular PET reaction, quenching takes place between pairs at short-distance. This is why some diffusive motion is required for ET to occur. According to them, this non-stationary (transient) regime exists until the rate at which the pairs react is equal to the rate at which new reactive pairs are created by diffusion. During the stationary stage, quenching is diffusion controlled and its rate constant is equal to k∞ (stationary quenching rate constant). In the non-stationary stage, the quenching rate decreases from k0 to k∞. They also showed that the difference between k0 and k∞ increases with the viscosity of the medium. Quencher concentration is another factor that also controls the relative contributions of these three regimes to fluorescence quenching. However, both the static and non-stationary regimes dominate at high quencher concentrations. On the other hand, the Stern–Volmer (SV) equation is only valid when the electron transfer step itself is significantly slower than diffusion. Therefore, quenching is dominated by the stationary regime, that is, in low viscosity solvents and at low quencher concentration. In these cases, the quenching rate constant obtained from the SV analysis is close to k∞.17
Several times, the absence of an MIR in the Rehm–Weller-type experiment was depicted due to the masking of the intrinsic ET dynamics by diffusion in a straightforward manner.18 After this, several groups made effort on explaining the lack of observation of an MIR. In their pioneering study, Rehm and Weller postulated that the absence of an MIR could originate from the existence of additional CS pathways, leading to an ionic product in an electronic excited state.5 Vauthey et al. obtained direct experimental evidence of this CS to an excited product for several donor/acceptor pairs, whose CS to the ground-state product was expected to be in the inverted regime.19 However, on a different note, Mataga and co-workers suggested dielectric saturation, which is the breakdown of the linear dielectric response approximation, as a controlling factor. Several other groups have reported distance dependence of solvent reorganization energies as a controlling factor for that particular reaction.20
Although several groups are involved in the controversy about the experimental evidence of MIR, all have unambiguously accounted the importance of diffusion control over the rate constant of the ET reaction in homogeneous as well as heterogeneous media. Apart from this, the ease of formation of primary radical ion pairs (RIPs) due to ET, i.e., contact ion pair (CIP) and solvent separated ion pair (SSIP), is sufficiently influenced by solvent polarity in the case of homogeneous medium and accessibility of the quencher molecule in heterogeneous medium. The formation of CIP prevails in non-polar medium, whereas SSIP formation enhances with an increase in the polarity of the medium due to further solvation of the individual ions of the geminate ion pair by the solvent.
Our previous studies on the riboflavin–TEA donor–acceptor system in homogeneous and heterogeneous systems already showed the modulation of formation of geminate CIP and SSIP as well as non-geminate RIPs in the femtosecond–picosecond and nanosecond time regimes, respectively.21 These steps of formation of different types of ion pairs could be related to the static, non-stationary, and stationary regime of electron transfer, as proposed by Vauthey et al. Earlier, we studied proflavine–TEA and proflavine–DMA systems in the steady state and their dynamics within the nanosecond time regime. We obtained evidence of diffusion-controlled ET, where the rate constant is governed by diffusion as the rate-determining step, in both homogeneous and heterogeneous media. In our present study, we report our results in a higher time resolution (fs–ps timescale), which are strikingly different from the trend in the diffusion-controlled time regime. From our results, we attempted to identify all the consecutive steps of ET and quantify their timescale of occurrence in media of varying heterogeneity. Since our aim was to determine the influence of the solvent structural parameters and viscosity on the initial steps of PET, for convenience, we considered our previous system, i.e. proflavine–TEA and proflavine–DMA, which have already been thoroughly studied up to the nanosecond time regime.22,23
Materials and methods
Reagents and sample preparation
All chemicals used herein were purchased from Sigma-Aldrich and used without further purification. All the solvents were purchased from Merck, Germany. The structures of proflavine, trimethylamine (TEA), and N,N-dimethylaniline (DMA) are given in Fig. 1. Water was triply distilled before use. A 100 mM SDS solution and a 50 mM CTAB solution were prepared by dissolving the required amount of SDS and CTAB in triple-distilled water. After purging argon gas into TEA and DMA, solutions were prepared in homogeneous solvents, SDS, and CTAB micelles.
 |
| | Fig. 1 Stuctures of proflavine, N,N-dimethylaniline and trimethylamine. | |
Femtosecond fluorescence upconversion measurements
The fluorescence transients were measured using a femtosecond fluorescence upconversion setup (FOG-100, CDP Corporation). The sample was excited at 400 nm with a full excitation slit width using the second harmonic of a mode-locked Ti-sapphire laser (Mai Tai, Spectra Physics), pumped by a 5 W Millennia (Spectra Physics). To generate the second harmonic, we used a nonlinear crystal (1 mm BBO, θ = 38°, φ = 90°). The fluorescence emitted from the sample was obtained under the magic angle configuration and was up-converted in another nonlinear crystal (0.5 mm BBO, θ = 38°, φ = 90°) using the fundamental beam as a gate pulse. The up-converted light was dispersed in a monochromator and detected by photon counting electronics. The femtosecond fluorescence decays were deconvoluted using a Gaussian shape for the instrument response function having an FWHM of ∼206 fs (obtained through water Raman scattering) using commercial software (IGOR Pro, Wave Metrics, USA). The decay traces were obtained at different wavelengths, which have been reported at their respective places in this study. They were also fitted and analyzed using the IGOR Pro software to obtain fluorescence decay times.
Results and discussion
From our previous reports, it is obvious that the excited state interaction of proflavine with different amine donors quite depends on the nature of the amines, whether aliphatic or aromatic, which dictates the possibility of formation of a ground state complex between the donor and acceptor prior to excitation. We employed proflavine as the acceptor molecule and DMA as the aromatic amine and TEA as the aliphatic amine donors. Our preliminary studies showed that TEA forms a ground state complex with proflavine, whereas DMA does not.22,23
We, in our present study, attempted to decipher the initial fastest time scale of PET of these two donor–acceptor systems. According to Vauthey, for any quencher concentration, there is always a particular concentration of donor molecules that can directly donate electrons to the acceptor without any considerable diffusion. This part of ET is responsible for the reduction of the first lifetime exponential.24
In all solvents, without the presence of any quencher 0.5 mM proflavine solution shows a fluorescence decay curve that fits to a triexponential decay function. In homogeneous solvent, this type of triexponential decay curve is somewhat unusual but could be supported if both the solvation dynamics and presence of more than one emitting state of proflavine are considered. Kumar et al. extensively studied the femtosecond-resolved fluorescence decay kinetics in solvents with different polarities and viscosities. Their experimental and theoretical studies postulated that the very fast timescale (τ1) of its decay profile is due to the solvation dynamics, whereas the second ultrafast decay component (τ2) is due to the internal conversion between two different emissive states of proflavine, which has been further confirmed by the presence of an isoemissive point in its time-resolved area-normalized spectra obtained using a homogeneous solvent. The second time constant τ2 varies from 50 to 215 ps depending on the solvent.27
We studied proflavine–TEA and proflavine–DMA as donor–acceptor couples in different solvents of varying dielectric constants in a femtosecond–picosecond time-resolved fluorescence set-up. Our previous studies showed that the addition of TEA to proflavine increases its lifetime from 4.45 ns to 5.00 ns in ethanol.22 Moreover, the previous steady state and nanosecond time-resolved experiments performed in our laboratory evidently showed that in the case of alcohols with varying chain lengths, the rate constants of diffusion-controlled PET varies with alcohol chain length in the case of the gradual addition of DMA. The rate constant calculated from time-correlated single photon counting data showed a gradual decrease with the increasing viscosity of the alcohol.23
All these changes in the nanosecond time region prove that alcohol chain length is a controlling factor for the diffusion of reacting species in respective solvents. Similar to the nanosecond region, we can only monitor the change in time constant of fluorescence decay after diffusion.
Fig. 2–7 show the fluorescence decay traces of proflavine with varying concentrations of TEA and DMA in MeOH, EtOH, and n-BuOH.
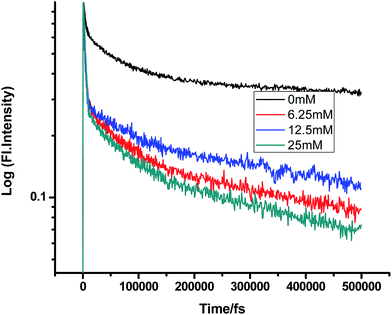 |
| | Fig. 2 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in MeOH with varying concentrations of TEA. | |
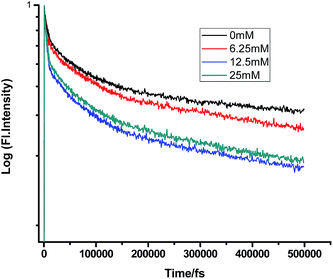 |
| | Fig. 3 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in MeOH with varying concentrations of DMA. | |
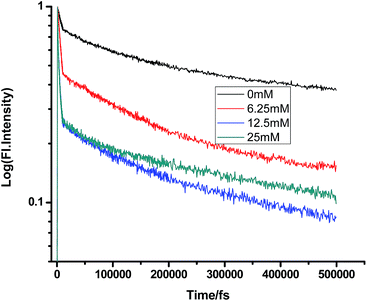 |
| | Fig. 4 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in EtOH with varying concentrations of TEA. | |
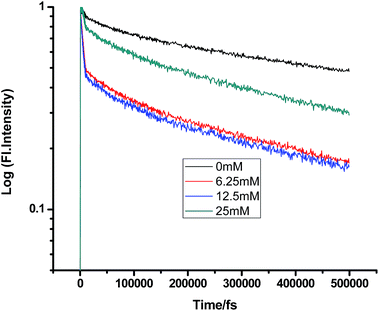 |
| | Fig. 5 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in EtOH with varying concentrations of DMA. | |
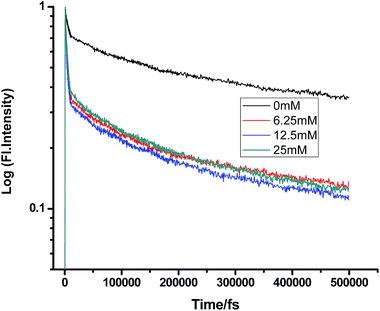 |
| | Fig. 6 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in n-BuOH with varying concentrations of TEA. | |
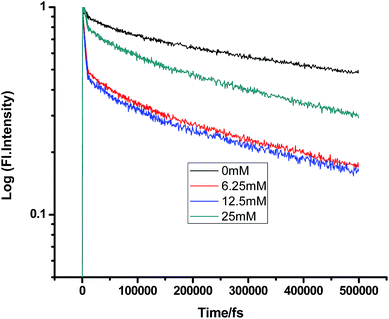 |
| | Fig. 7 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in n-BuOH with varying concentrations of DMA. | |
While monitoring the fluorescence dynamics of both systems in alcohols of varying chain lengths, it was observed that the increase in the chain length of an alcohol reduces the rate of ET in every step involving static and non-stationary regimes, as discussed earlier for both systems. However, this reduction is quite similar in different alcohols. Tables 1–6 show that the time constants associated with the fluorescence decay traces reduce with the quencher concentration but this change follows almost the same trend for both TEA and DMA. This indicates that as we monitor the change in the fluorescence lifetime due to PET in the fs–ps timescale, the extent of quenching is almost similar in all the alcohols, which in turn supports the occurrence of a direct ET in this time regime prior to considerable diffusion of the reacting species. Since diffusion occurs in a timescale longer than fs–ps, the viscosity of the alcohols, which actually controls the diffusion dynamics, does not affect the rate of reaction.
Table 1 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of TEA in MeOH (τ1, τ2, and τ3 are the femtosecond resolved decay time constants of the fluorescence decay traces of proflavine and a1, a2, and a3 are their relative contributions, respectively. The same notation holds for all the tables)
| [TEA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs)/a3 |
| 0 |
302 (0.12) |
7091 (0.26) |
254![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668 (0.61) 668 (0.61) |
| 6.25 |
163 (0.13) |
2965 (0.25) |
196![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 843 (0.61) 843 (0.61) |
| 12.5 |
251 (0.07) |
5580 (0.46) |
218![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 158 (0.46) 158 (0.46) |
| 25 |
202 (0.14) |
5807 (0.38) |
215![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 375 (0.47) 375 (0.47) |
Table 2 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of DMA in MeOH
| [DMA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs)/a3 |
| 0 |
330 (0.01) |
6781 (0.30) |
360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 (0.69) 745 (0.69) |
| 6.25 |
544 (0.29) |
3281 (0.45) |
214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 (0.25) 130 (0.25) |
| 12.5 |
784 (0.33) |
3709 (0.43) |
216![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 272 (0.24) 272 (0.24) |
| 25 |
296 (0.13) |
3805 (0.59) |
276![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 055 (0.27) 055 (0.27) |
Table 3 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of DMA in EtOH
| [DMA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs)/a3 |
| 0 |
550 (0.46) |
4511 (0.05) |
536![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 838 (0.48) 838 (0.48) |
| 6.25 |
301 (0.20) |
3925 (0.63) |
324![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 395 (0.25) 395 (0.25) |
| 12.5 |
232 (0.29) |
6887 (0.37) |
296![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 752 (0.35) 752 (0.35) |
| 25 |
202 (0.24) |
4724 (0.34) |
338![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 771 (0.40) 771 (0.40) |
Table 4 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of TEA in EtOH
| [TEA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs)/a3 |
| 0 |
225 (0.03) |
3934 (0.38) |
224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 786 (0.59) 786 (0.59) |
| 6.25 |
574 (0.28) |
3928 (0.51) |
164![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 518 (0.20) 518 (0.20) |
| 12.5 |
238 (0.21) |
3277 (0.59) |
299![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 877 (0.19) 877 (0.19) |
| 25 |
330 (0.16) |
3961 (0.63) |
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148 (0.20) 148 (0.20) |
Table 5 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of TEA in n-BuOH
| [TEA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs)/a3 |
| 0 |
225 (0.47) |
4296 (0.15) |
550![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 352 (0.38) 352 (0.38) |
| 6.25 |
188 (0.15) |
4359 (0.49) |
330![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 (0.35) 467 (0.35) |
| 12.5 |
175 (0.13) |
3907 (0.35) |
473![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368 (0.44) 368 (0.44) |
| 25 |
292 (0.25) |
4049 (0.55) |
459![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 038 (0.2) 038 (0.2) |
Table 6 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of DMA in n-BuOH
| [DMA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs)/a3 |
| 0 |
1635 (0.24) |
4900 (0.22) |
365![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535 (0.52) 535 (0.52) |
| 6.25 |
1446 (0.25) |
3893 (0.53) |
310![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184 (0.20) 184 (0.20) |
| 12.5 |
501 (0.30) |
3293 (0.54) |
227![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 471 (0.14) 471 (0.14) |
| 25 |
971 (0.32) |
3405 (0.5) |
271![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132 (0.17) 132 (0.17) |
All three alcohols used herein have dielectric constants very similar to each other. So, as viscosity is not a controlling factor here, it is evident from the very similar rate constants of ET in the fs–ps time regime that direct ET occurs from quencher molecules in the vicinity of proflavine. Therefore, it is evident that in this time regime, direct ET and CIP formation depend only on the dielectric constant of the medium, but not on its viscosity. This further supports the mechanism of direct ET in this fs–ps timescale.
On a different note, when we employed a non-polar solvent such as tetrahydrofuran with a dielectric constant of ∼7, it was observed that the rate of ET dramatically decreases for both amines (Fig. 8 and 9 and Tables 7 and 8). Both quenchers transfer electrons to the acceptor to a much smaller extent than all the reaction products, i.e. CIP, SSIP, and RIPs are much less stabilized in this non-polar solvent, resulting in the equilibrium shifting to the reactant side.
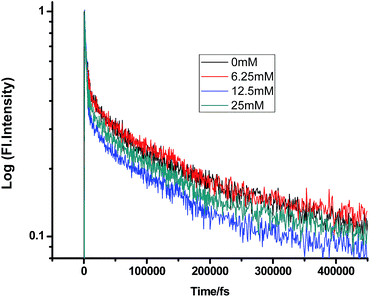 |
| | Fig. 8 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in THF with varying concentrations of TEA. | |
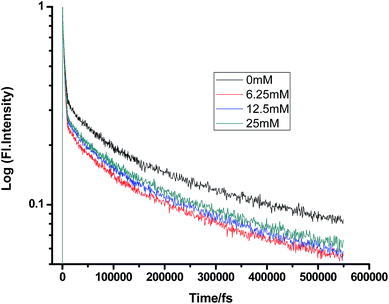 |
| | Fig. 9 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in THF with varying concentrations of DMA. | |
Table 7 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of TEA in tetrahydrofuran
| [TEA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs)/a3 |
| 0 |
458 (0.20) |
4928 (0.42) |
143![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 (0.36) 402 (0.36) |
| 6.25 |
470 (0.28) |
3987 (0.4) |
198![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654 (0.32) 654 (0.32) |
| 12.5 |
534 (0.35) |
4321 (0.41) |
169![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 (0.23) 767 (0.23) |
| 25 |
490 (0.37) |
4864 (0.13) |
209![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 865 (0.49) 865 (0.49) |
Table 8 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of DMA in THF
| [DMA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs)/a3 |
| 0 |
248 (0.18) |
3991 (0.47) |
193![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 265 (0.35) 265 (0.35) |
| 6.25 |
458 (0.1) |
3550 (0.71) |
172![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 958 (0.18) 958 (0.18) |
| 12.5 |
264 (0.15) |
3910 (0.65) |
204![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 381 (0.19) 381 (0.19) |
| 25 |
330 (0.16) |
3961 (0.63) |
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148 (0.20) 148 (0.20) |
It is quite evident from our results that homogeneous solvents of different polarities and intrinsic heterogeneity cannot differentiate between TEA and DMA, whereas heterogeneous micellar environment can differentiate between TEA and DMA due to their preferential solvation and compartmentalization ability. We used negatively charged SDS and positively charged CTAB micelles to investigate the effect of environmental constraints controlling the diffusion of the donor and acceptor (Tables 9 and 10).
Table 9 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of TEA in SDS (100 mM)
| [TEA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs)/a3 |
| 0 |
357 (0.11) |
4260 (0.49) |
480![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306 (0.39) 306 (0.39) |
| 6.25 |
280 (0.51) |
2940 (0.37) |
130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 567 (0.11) 567 (0.11) |
| 12.5 |
267 (0.48) |
2277 (0.24) |
129![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415 (0.27) 415 (0.27) |
| 25 |
320 (0.41) |
3691 (0.34) |
134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 142 (0.25) 142 (0.25) |
Table 10 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of DMA in SDS (100 mM)
| [DMA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs)/a3 |
| 0 |
252 (0.19) |
4377 (0.39) |
472![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 848 (0.40) 848 (0.40) |
| 6.25 |
433 (0.15) |
4711 (0.24) |
387![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 (0.59) 630 (0.59) |
| 12.5 |
395 (0.20) |
4399 (0.25) |
329![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415 (0.54) 415 (0.54) |
| 25 |
346 (0.17) |
4309 (0.30) |
369![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521 (0.54) 521 (0.54) |
Fig. 10 and 11 show that in the case of SDS micelles with the addition of an increasing concentration of TEA, the shortest lifetime was regularly reduced in the fs–ps timescale. This is sharply in contrast with the evidence in the ns timescale and similar to the nature of changes in the homogeneous media i.e. the increment of lifetime of PF+ due to the formation of the PF+–TEA ground state complex. This reduction of time constants in a shorter timescale could be attributed to the absence of the formation of the PF+–TEA complex in the shorter timescale in SDS. In the shorter timescale, this regular reduction of time constants of fluorescence decay traces is very much expected through direct electron transfer since both TEA and PF+ reside in the hydrophilic region of SDS.
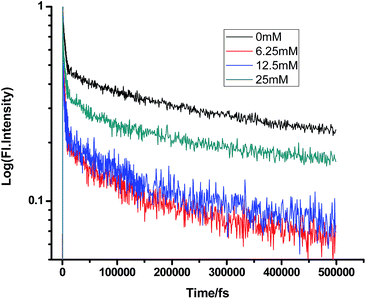 |
| | Fig. 10 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in SDS (100 mM) with varying concentrations of TEA. | |
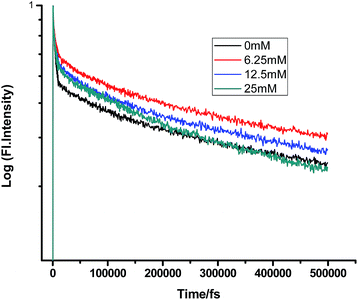 |
| | Fig. 11 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in SDS (100 mM) with varying concentrations of DMA. | |
A somewhat anomalous result was found while gradually adding DMA to PF+ in SDS micelles. Most surprisingly, the first addition of DMA (6.25 mM) increased the lifetime of PF+ instead of decreasing it. After this, the gradual addition of DMA subsequently reduced the lifetime of proflavine, both in the femtosecond and picosecond timescales. This fact could be accounted by considering the electronic as well as the steric factors of the micellar media, which control the compartmentalization of different chemical species. PF+ is a charged molecule and remains as a protonated PF+ form below pH 7 (pH of 100 mM SDS is ∼3.5). Therefore, it preferentially remains near the water phase, whereas being insoluble in water, DMA resides in the hydrophobic tail region of SDS. Still, since PF+ is positively charged, some fraction of PF+ would surely reside in the negatively charged SDS head group. Therefore, the primary addition of DMA could not quench its fluorescence lifetime. Moreover, DMA forms a structured environment with the organic chains of SDS micelles and this leads to the confinement of PF+, resulting in an increase in the fluorescence decay time constant. After further addition, some DMA molecules can transfer electron both directly as well as after diffusion to PF+ and quench the fluorescence lifetime at the fs–ps timescale.
Similarly, in the case of CTAB micelles, TEA can access proflavine and regularly reduce its fluorescence decay time constants since both TEA and proflavine remain near the micelle–water interphase (Tables 11 and 12).
Table 11 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of TEA in CTAB (50 mM)
| [TEA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs)/a3 |
| 0 |
200 (0.89) |
3336 (0.73) |
166![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565 (0.42) 565 (0.42) |
| 6.25 |
187 (0.66) |
3006 (0.91) |
157![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765 (0.33) 765 (0.33) |
| 12.5 |
152 (0.96) |
1808 (0.57) |
149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 937 (0.36) 937 (0.36) |
| 25 |
150 (0.62) |
1287 (0.72) |
132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 (0.22) 146 (0.22) |
Table 12 Femtosecond-resolved fluorescence decay time constants of proflavine (0.5 mM) with varying concentrations of DMA in CTAB (50 mM)
| [DMA]/mM |
τ1 (fs)/a1 |
τ2 (fs)/a2 |
τ3 (fs) |
| 0 |
379 (0.88) |
3871 (0.66) |
229![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 719 (0.40) 719 (0.40) |
| 6.25 |
507 (0.56) |
4989 (0.42) |
326![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 828 (0.34) 828 (0.34) |
| 12.5 |
796 (0.70) |
5607 (0.36) |
378![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 (0.52) 960 (0.52) |
| 25 |
877 (0.64) |
7973 (0.22) |
398![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 067 (0.63) 067 (0.63) |
Some very contrasting results were obtained while performing the experiment with DMA in CTAB micelles. With the gradual addition of DMA, instead of decreasing, the fluorescence decay time constant of proflavine regularly increased. This exact observation can be rationalized if we consider the energy spacing of the close lying excited states of proflavine. Theoretical calculations with this molecule show that three exponential components of its fluorescence decay curve are associated with solvation and vibrational relaxation, population transfer to another close lying singlet excited state, and relaxed excited state emission. Kumar et al. investigated the origin of these fluorescence decay time components and the plausible mechanism of the radiative and nonradiative pathways. From their study, it was found that the ultrafast time constant (τ1) of the fluorescence decay transient of proflavine varies with solvent polarity, which indicates that fluorescence originates from a different evolving excited state. The gradual increase in τ1 with the increase in solvent polarity could be attributed to the change in the characteristic solvation time of the excited state in these solvents. The other component (τ2) has a longer decay time compared to the previous component, which is 50–215 ps in different solvents. Moreover, it has been observed that the value of τ2 remains invariant with the change in emission wavelength, which in turn infers that this emitting component of the dye is not influenced by the solvation dynamics. The observed decay times are presumably due to the emission from the close lying singlet excited states (1A1 and 1B2) of proflavine in homogeneous media and the variation in τ2 is due to the variation in Stokes shift and fluorescence quantum yield of the dye with solvent polarity.27 By considering the preferential residence of DMA and PF+ molecules in different regions of the CTAB micelle, it could be inferred that the PF+ molecules are repelled by its positively charged head groups and go into the water phase and thus cannot access the DMA molecules located in the hydrophobic tail region.23 Due to the preferential residence of DMA molecules in the micellar core environment, probably the lone pair of nitrogen of this tertiary amine becomes protonated by the nearby NH4+ group of the CTAB micelle, which is impossible in the case of TEA since it easily diffuses into the water phase owing to its small size and hydrophilicity (Fig. 12 and 13). DMA has a bulky structure and cannot diffuse into PF+ molecules, but probably forms a structured environment along with the micellar structure in the vicinity of the PF+ molecules. According to Castner et al., who calculated the effective number of DMA molecules surrounding coumarin having proper orientation to directly transfer electrons without any reorientation, there should always be a particular number of quencher molecules that surround the acceptor molecule.25 These DMA molecules along with the CTAB tails block the radiative decay channels of PF+, resulting in a gradual increase in the fluorescence time constant of proflavine. This has been observed only in the fs–ps timescale. In the longer timescale (i.e. in the ns timescale), the PF+ molecules diffuse far apart from this structured core, resulting in an almost unaltered fluorescence lifetime in this micellar environment. Moreover, the gradual increase in the value of the fast component (τ1) with a change in the emission wavelength to the red side with the addition of the highest concentration of DMA further supports our assumption of slower solvation of proflavine by the surrounding DMA molecules (Fig. 14).
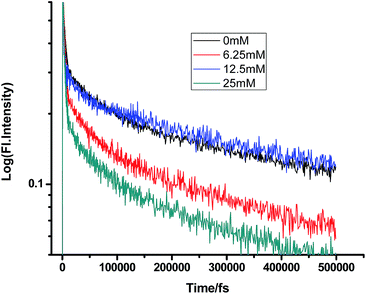 |
| | Fig. 12 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in CTAB (50 mM) with varying concentrations of TEA. | |
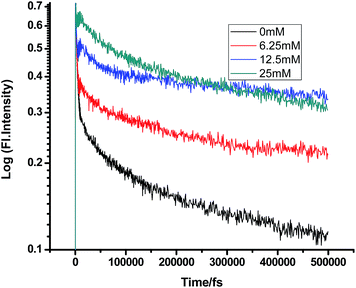 |
| | Fig. 13 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) in CTAB (50 mM) with varying concentrations of DMA. | |
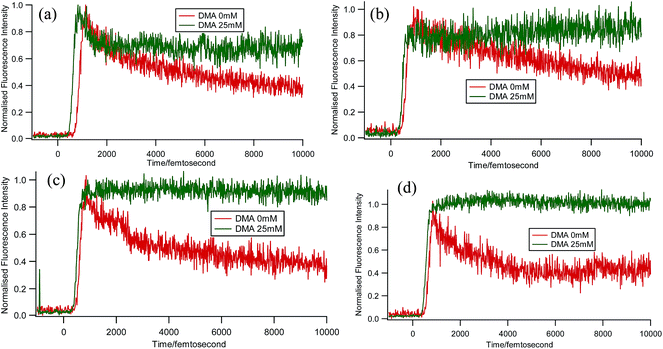 |
| | Fig. 14 Femtosecond-resolved fluorescence decay traces of proflavine (0.5 mM) with 0 and 25 mM DMA in CTAB (50 mM) at (a) 507 nm, (b) 520 nm, (c) 530 nm, and (d) 540 nm. | |
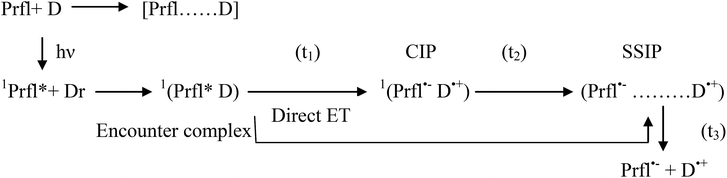
At the end of this discussion about the ET process, it could be concluded that this process can be presented by the following scheme:
The abovementioned steps are modulated by polarity, viscosity, and microheterogeneity of the medium, as we hypothesized in light of our previous nanosecond resolved experiments. Moreover, microheterogeneity leads to further compartmentalization of the reactants and also differently dictates their specific interactions with the micellar head groups and tail parts and thus determines the mode of the reaction.
Conclusion
PET in viscous media with varying homogeneity and heterogeneity has been of great interest for decades. Determination of the timescale of the occurrence of different steps of ET, such as formation of CIP, SSIP, and RIP, can lead to the possibility of modulation of the rate of the reaction. Researchers are in search of the unambiguous determination of the mechanism of ET. Herein, we showed the occurrence of hitherto unobserved events in the fs–ps timescale for proflavine–DMA and proflavine–TEA systems in solvents with varying different parameters. Our observations, along with our previous experiments on these two systems in the same media, confirm that both the kinetics of direct ET and solvation in the early (i.e. in fs–ps) timescale could be modulated by the compartmentalization of micellar media, depending upon their charge, which is almost impossible in homogeneous media. In homogeneous media, polarity is the only determining factor for the rate of ET in the fs–ps timescale. Herein, we have the growth component of the dye fluorescence decay curve in micellar media by means of blocking the specific amine donor DMA at very fast timescales (fs). This will lead to a further search for the mechanisms of PET, even beyond the diffusion-controlled steps in the future.
Acknowledgements
This work was funded by Biomolecular Assembly, Recognition and Dynamics (BARD) projects, Saha Institute of Nuclear Physics of Department of Atomic Energy (DAE), Government of India.
References
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1957, 26, 867–871 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1957, 26, 872–877 CrossRef CAS.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- D. Rehm and A. Weller, Isr. J. Chem., 1970, 8, 259 CrossRef CAS.
- D. Rehm and A. Weller, Ber. Bunsen-Ges. Phys. Chem., 1969, 73, 834 CAS.
- J. R. Miller, L. T. Calcaterra and G. L. Closs, J. Am. Chem. Soc., 1984, 106, 3047 CrossRef CAS.
- G. L. Closs and J. R. Miller, Science, 1988, 240, 440 CAS.
- M. R. Wasielewski, M. P. Niemczyk, W. A. Svec and E. B. Pewitt, J. Am. Chem. Soc., 1985, 107, 1080 CrossRef CAS.
- I. R. Gould, D. Ege, S. L. Mattes and S. Farid, J. Am. Chem. Soc., 1987, 109, 3794 CrossRef CAS.
- N. Mataga, T. Asahi, Y. Kanda, T. Okada and T. Kakitani, Chem. Phys., 1988, 127, 249 CrossRef CAS.
- E. Vauthey, P. Suppan and E. Haselbach, Helv. Chim. Acta, 1988, 71, 93 CrossRef CAS.
- D. M. Guldi and K. D. Asmus, J. Am. Chem. Soc., 1997, 119, 5744 CrossRef CAS.
- S. Fukuzumi, K. Ohkubo, H. Imahori and D. M. Guldi, Chem.–Eur. J., 2003, 9, 1585 CrossRef CAS PubMed.
- N. Mataga, H. Chosrowjan, Y. Shibata, N. Yoshida, A. Osuka, T. Kikuzawa and T. Okada, J. Am. Chem. Soc., 2001, 123, 12422 CrossRef CAS PubMed.
- M. A. Smitha, E. Prasad and K. R. Gopidas, J. Am. Chem. Soc., 2001, 123, 1159 CrossRef CAS PubMed.
- A. Rosspeintner, M. Koch, G. Angulo and E. Vauthey, J. Am. Chem. Soc., 2012, 134, 11396–11399 CrossRef CAS PubMed.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Modern Molecular Photochemistry of Organic Molecules, University Science Books, Mill Valley, CA, 2010 Search PubMed.
- M. Koch, A. Rosspeintner, K. Adamczyk, B. Lang, J. Dreyer, E. T. J. Nibbering and E. Vauthey, J. Am. Chem. Soc., 2013, 135, 9843 CrossRef CAS PubMed.
- A. Yoshimori, T. Kakitani, Y. Enomoto and N. Mataga, J. Phys. Chem., 1989, 93, 8316 CrossRef CAS.
- C. Sengupta, M. K. Sarangi, A. Sau, D. Mandal and S. Basu, J. Photochem. Photobiol., A, 2015, 29, 25–34 CrossRef.
- B. Chakraborty and S. Basu, Chem. Phys. Lett., 2009, 477(4–6), 382–387 CrossRef CAS.
- B. Chakraborty and S. Basu, Chem. Phys. Lett., 2010, 487(1–3), 51–57 CrossRef CAS.
- E. Vauthey, J. Photochem. Photobiol., A, 2006, 179, 1–12 CrossRef CAS.
- E. W. Castner Jr, D. Kennedy and R. J. Cave, J. Phys. Chem. A, 2000, 104, 2869–2885 CrossRef.
- S. Ghosh, K. Sahu, S. K. Mondal, P. Sen and K. Bhattacharyya, J. Chem. Phys., 2006, 125, 054509 CrossRef PubMed.
- K. S. Kumar, C. Selvaraju, E. J. P. Malar and P. Natarajan, J. Phys. Chem. A, 2012, 116, 37–45 CrossRef CAS PubMed.
Footnote |
| † Presently at: Eduard-Zintl Institute for Physical and Inorganic Chemistry, Darmstadt University of Technology, Alarich-Weiss-Str. 8, 64287 Darmstadt, Germany. |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a
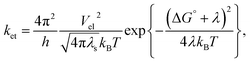






![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668 (0.61)
668 (0.61)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 843 (0.61)
843 (0.61)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 158 (0.46)
158 (0.46)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 375 (0.47)
375 (0.47)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 (0.69)
745 (0.69)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 (0.25)
130 (0.25)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 272 (0.24)
272 (0.24)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 055 (0.27)
055 (0.27)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 838 (0.48)
838 (0.48)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 395 (0.25)
395 (0.25)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 752 (0.35)
752 (0.35)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 771 (0.40)
771 (0.40)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 786 (0.59)
786 (0.59)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 518 (0.20)
518 (0.20)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 877 (0.19)
877 (0.19)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148 (0.20)
148 (0.20)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 352 (0.38)
352 (0.38)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 (0.35)
467 (0.35)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368 (0.44)
368 (0.44)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 038 (0.2)
038 (0.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535 (0.52)
535 (0.52)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184 (0.20)
184 (0.20)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 471 (0.14)
471 (0.14)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132 (0.17)
132 (0.17)

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 (0.36)
402 (0.36)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654 (0.32)
654 (0.32)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767 (0.23)
767 (0.23)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 865 (0.49)
865 (0.49)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 265 (0.35)
265 (0.35)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 958 (0.18)
958 (0.18)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 381 (0.19)
381 (0.19)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148 (0.20)
148 (0.20)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306 (0.39)
306 (0.39)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 567 (0.11)
567 (0.11)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415 (0.27)
415 (0.27)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 142 (0.25)
142 (0.25)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 848 (0.40)
848 (0.40)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 (0.59)
630 (0.59)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415 (0.54)
415 (0.54)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521 (0.54)
521 (0.54)

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565 (0.42)
565 (0.42)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765 (0.33)
765 (0.33)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 937 (0.36)
937 (0.36)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 (0.22)
146 (0.22)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 719 (0.40)
719 (0.40)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 828 (0.34)
828 (0.34)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 (0.52)
960 (0.52)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 067 (0.63)
067 (0.63)