Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bottom-up design of high-energy-density molecules (N2CO)n (n = 2–8)†
Jing-fan Xinab,
Fei-fei Hea and
Yi-hong Ding *a
*a
aLaboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, Jilin University, Changchun 130023, P. R. China. E-mail: yhdd@jlu.edu.cn
bInner Mongolia Key Laboratory of Photoelectric Functional Materials, College of Chemistry and Chemical Engineering, Chifeng University, Chifeng 024000, P. R. China
First published on 26th January 2017
Abstract
Seeking high-energy-density materials (HEDMs) with balanced huge energy release and good stability has remained quite a tough task for both experimentalists and theoreticians. The current HEDM design mostly concentrates on the chemical modification of either the skeletons or ligands. To increase the number of HEDM candidates, a novel design strategy is highly desired. In this paper, we computationally proposed a bottom-up strategy, i.e., a suitable HEDM seed (e.g., cyc-N2CO) can form novel HEDMs while retaining good stability and good performance. Starting from the experimentally known diazirinone (cyc-N2CO) as a “seed” and by considering various bond-addition channels (2 + 2/2 + 3/3 + 3 cyclo-addition at the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N/C
N/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/C–N bonds), we found that the cyc-N2CO dimer isomer 1 (i.e., (N2CO)2 containing a COCO ring with an exocyclic side-N2 at each C-atom) possess the rate-determining barrier of 29.9 kcal mol−1 and exothermicity of 168.7 kcal mol−1 into 2N2 + 2CO at the composite CBS-QB3 level. Moreover, the trimer and tetramer of cyc-N2CO each possess high rate-determining barriers of 25.8 and 30.3 kcal mol−1, respectively, at the CBS-QB3 level. Even higher oligomers with n = 5–8 have rate-determining barriers around 25 and 34 kcal mol−1. The spiral skeletons were shown to have a contribution to their good inherent kinetic stability. By comparing the detonation properties with some known HEDM compounds, the oligomers of cyc-N2CO may well deserve future synthetic trials for novel HEDMs. Our designed (N2CO)n with all the untouched N
O/C–N bonds), we found that the cyc-N2CO dimer isomer 1 (i.e., (N2CO)2 containing a COCO ring with an exocyclic side-N2 at each C-atom) possess the rate-determining barrier of 29.9 kcal mol−1 and exothermicity of 168.7 kcal mol−1 into 2N2 + 2CO at the composite CBS-QB3 level. Moreover, the trimer and tetramer of cyc-N2CO each possess high rate-determining barriers of 25.8 and 30.3 kcal mol−1, respectively, at the CBS-QB3 level. Even higher oligomers with n = 5–8 have rate-determining barriers around 25 and 34 kcal mol−1. The spiral skeletons were shown to have a contribution to their good inherent kinetic stability. By comparing the detonation properties with some known HEDM compounds, the oligomers of cyc-N2CO may well deserve future synthetic trials for novel HEDMs. Our designed (N2CO)n with all the untouched N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds differed sharply from the recently reported high-pressure polymerized forms, in which all the double bonds have been transformed into single bonds. The present bottom-up strategy from an HEDM seed (i.e., cyc-N2CO) to novel oligomeric HEDMs confirmed by the CBS-QB3 calculations seems to be quite promising and may open a new way of designing in the HEDM realm.
N bonds differed sharply from the recently reported high-pressure polymerized forms, in which all the double bonds have been transformed into single bonds. The present bottom-up strategy from an HEDM seed (i.e., cyc-N2CO) to novel oligomeric HEDMs confirmed by the CBS-QB3 calculations seems to be quite promising and may open a new way of designing in the HEDM realm.
1. Introduction
There has been considerable interest in the high-energy-density materials (HEDMs) for decades due to their potential applications in various fields, e.g., propellants, pyrotechnics, and explosives.1–8 Yet in spite of the great synthetic difficulties (e.g., suitable precursor, suitable stabilization technique, etc.), one clear obstacle in the development of energetic materials is the very limited number of HEDM targets. A well-known issue in the HEDM realm is that the designed compounds should in general satisfy two requirements, i.e., high exothermicity and a high barrier. The first requirement necessitates a large heat release upon decomposition, while the second needs a considerable rate-determining decomposition barrier to ensure good kinetic stability. Unfortunately, the two requirements seem to be quite contradictive since in many cases, a thermodynamically unstable structure would usually be kinetically unstable. Therefore, successful design of a promising HEDM is a great challenge to chemists' mental imagination.To accelerate rational design of novel molecules that could satisfy both critical HEDM requirements, clever chemists have thought out an “economic and efficient” strategy to generate new and more complex HEDMs by substituting the framework or ligands of known HEDMs9–12 In such a strategy, the inherent large exothermicity and good kinetic stability of the parent HEDM molecule can be inherited to the new HEDMs by suitable isovalent or analogous skeleton/ligand modifications. Nice examples include the tetrazole derivatives with fused energetic groups (catenated nitrogen atoms) and insensitive fragments,13 new HEDMs based on N-heterocyclic frameworks,14 high-energy metal–organic frameworks (HE-MOFs) based on various nitrogen-rich energetic ligands.15 Note that most HEDM designs concentrate on the nitrogen-content and high heat, whereas the kinetic factor that is associated with the stability has been much less studied especially for systems with larger size.
Is there any alternative designing strategy viable for novel HEDM? We propose that for some monomeric HEDMs with multiple bonds, the bond-addition might be feasible to expand the monomer into more energetic and larger-size HEDMs if good kinetic stability can be preserved. Such a strategy mimics the so-called “bottom-up” strategy, which has been hotly pursued in the cluster-assembled material science.16–18 To testify our proposal, we considered a tetra-atomic molecule N2CO, which has received considerable computational and experimental attention.19–31 Of its isomer, a three-membered ring diazirinone (cyc-N2CO) was first predicted in 1994 as a promising HEDM,19 with its definitive experimental confirmation in 2011 via the decomposition of gaseous OC(N3)2 followed by IR spectrum characterization.26 In this work, we for the first time designed a series of oligomeric HEDMs (N2CO)n only with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds transformed into single bonds, which show marked contrast to the high-pressure polymerized (N2CO)n with all multiple bonds transformed into single bonds. The good kinetic stability (around 30 kcal mol−1) of the designed (N2CO)n oligomers was confirmed by the composite CBS-QB3 calculations.
O bonds transformed into single bonds, which show marked contrast to the high-pressure polymerized (N2CO)n with all multiple bonds transformed into single bonds. The good kinetic stability (around 30 kcal mol−1) of the designed (N2CO)n oligomers was confirmed by the composite CBS-QB3 calculations.
2. Computational methods
All calculations were carried out using Gaussian03 and Gaussian09 program packages.32 The geometric optimization and frequency calculations of both the isomers and transition states were initially carried out at the B3LYP/6-31G(d) level. For structural and energy refinement, the composite CBS-QB3 method33,34 was applied, which used the B3LYP/6-311G(2d,d,p) geometries and frequencies and computes a series of high-level single-point energy calculations. The eventual energy has been designed to reach the complete basis set (CBS) limit. The connection of each transition state to associated isomers or fragments was checked by the intrinsic reaction coordinate (IRC) method at the B3LYP/6-31G(d) level. In some cases where the structure might experience significant multi-reference character, the broken symmetry strategy,35 i.e., UB3LYP/6-311G(2d,d,p) with the “guess = (mix, always) keyword, was performed for geometrical optimization (note that for such open-shell singlet calculations, the composite CBS-QB3 calculations are not available at present). To get detailed orbital information, we performed the natural bond orbital (NBO) analysis. The atom coordinate and the critical transition state coordinate of (N2CO)n (n = 2–8) are listed in ESI (see Tables S1–S7†).3. Results and discussions
The discussions are organized as follows. First, we explored the structures and relative energies of various (cyc-N2CO)2 isomers in detail, followed by the isomerization or decomposition pathways of each isomer. Second, based on the most feasible type of kinetically stabilized (cyc-N2CO)2, we discussed the heat release and kinetic stability of higher oligomeric cyc-N2CO, i.e., (cyc-N2CO)n (n = 3–8). Third, we predicted the detonation properties and impact sensitivity for (cyc-N2CO)n (n = 2–8). Finally, implications of the present work were discussed.3.1 cyc-N2CO dimer
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C–N. In principle, nine bond-addition structures can be initially designed for dimerization of cyc-N2CO at the B3LYP/6-31G(d) level (see Table 1). The N
O and C–N. In principle, nine bond-addition structures can be initially designed for dimerization of cyc-N2CO at the B3LYP/6-31G(d) level (see Table 1). The N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N/N
N/N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N addition does not lead to an N–N singly-bonded N4-ring isomer. Instead, the optimization collapses to the C–N/N–C addition isomer with a puckered six-membered-ring isomer 7 with two N
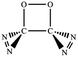
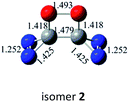
N addition does not lead to an N–N singly-bonded N4-ring isomer. Instead, the optimization collapses to the C–N/N–C addition isomer with a puckered six-membered-ring isomer 7 with two N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds at the B3LYP/6-31G(d) level. The C–N/N–C (trans) and C–N/C–N (cis) addition lead to the six-membered ring isomers 7 and 8, respectively at the B3LYP/6-31G(d) level. Yet, both isomers disappear at the B3LYP/6-311G(2d,d,p) level, resulting in the fragmentation into 2N2 + 2CO. The two four-membered-ring isomers 1 and 2 are formed by the trans- and cis-addition of two C
N bonds at the B3LYP/6-31G(d) level. The C–N/N–C (trans) and C–N/C–N (cis) addition lead to the six-membered ring isomers 7 and 8, respectively at the B3LYP/6-31G(d) level. Yet, both isomers disappear at the B3LYP/6-311G(2d,d,p) level, resulting in the fragmentation into 2N2 + 2CO. The two four-membered-ring isomers 1 and 2 are formed by the trans- and cis-addition of two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds within N2CO. Due to the strong lone pair repulsions between two neighboring O-atoms, the cis-isomer 2 is thermodynamically less stable than the trans-isomer 1 by more than 50 kcal mol−1 (higher relative energy means lower thermodynamic stability). The C
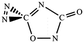
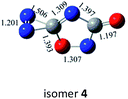
O bonds within N2CO. Due to the strong lone pair repulsions between two neighboring O-atoms, the cis-isomer 2 is thermodynamically less stable than the trans-isomer 1 by more than 50 kcal mol−1 (higher relative energy means lower thermodynamic stability). The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/N
O/N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N addition gives the five-membered-ring isomer 4, in which the additioned N
N addition gives the five-membered-ring isomer 4, in which the additioned N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond is completely broken to be non-bonding. The C
N bond is completely broken to be non-bonding. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/C–N and C
O/C–N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/N–C addition would lead to the isomers 3 and 5, respectively.
O/N–C addition would lead to the isomers 3 and 5, respectively.
| Bond-addition modes | Designed structures of (cyc-N2CO)2 | Optimized structures of (cyc-N2CO)2 | Relative energies between isomers and 2cyc-N2CO |
|---|---|---|---|
| a The structure is only a minimum at the B3LYP/6-31G(d) level. | |||
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O,O O,O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (trans-) C (trans-) |
 |
 |
−10.0 (−3.4) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O,C O,C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (cis-) O (cis-) |
 |
 |
45.9 (52.7) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O,N O,N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N N |
 |
 |
−7.3 (−5.0) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O,C–N (trans-) O,C–N (trans-) |
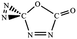 |
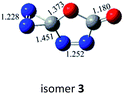 |
−61.2 (−59.5) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O,N–C (cis-) O,N–C (cis-) |
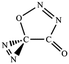 |
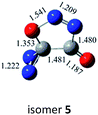 |
−34.8 (−33.4) |
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N,N N,N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N N |
 |
 |
−46.9a |
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N,C–N N,C–N |
 |
 |
−51.2a |
| C–N,N–C (trans-) | 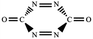 |
 |
−46.9a |
| C–N,C–N (cis-) | 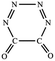 |
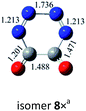 |
−35.9a |
As shown in Table 2, the isomers 4 and 5 formed by the respective C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/N
O/N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and C
N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/N–C addition have negligible kinetic stability, i.e., −1.7 and 0.96 kcal mol−1 at the CBS-QB3 level. They should be of no interest even for spectroscopic detection. The slightly negative value for isomer 4 is clearly a result of the composite CBS-QB3 calculation, in which the higher-level energy is computed based on the geometry of a different level. For the isomers 2 and 3 that are formed via the respective C
O/N–C addition have negligible kinetic stability, i.e., −1.7 and 0.96 kcal mol−1 at the CBS-QB3 level. They should be of no interest even for spectroscopic detection. The slightly negative value for isomer 4 is clearly a result of the composite CBS-QB3 calculation, in which the higher-level energy is computed based on the geometry of a different level. For the isomers 2 and 3 that are formed via the respective C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/C
O/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C
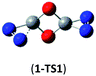
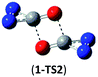
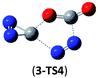
O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/C–N addition, their most feasible decomposition transition states have certain open-shell singlet characteristics. They have the barriers of 13.9 and 17.4 kcal mol−1, respectively at the UB3LYP/6-311G(2d,d,p) level. For isomer 2, the RHF → UHF energy lowering value of 7.2 kcal mol−1 is considerable, whereas that (0.5 kcal mol−1) for isomer 3 is negligible. The corresponding CBS-QB3 barriers at the restricted level are 19.8 and 22.2 kcal mol−1 for 2 and 3. We expect the rate-determining barriers of 2 and 3 to be around 15 kcal mol−1 at the correlated level, which could allow them to be detectable in future spectroscopic studies. In sharp contrast, the highly symmetric isomer 1 (D2d) have very high decomposition barriers, i.e., 29.9 (1-TS1) and 42.9 (1-TS2) kcal mol−1 at the CBS-QB3 level for the fragmentation to N2-leaving and 2cyc-N2CO, respectively (see Table 2). Clearly, isomer 1 is the most kinetically stable among all the cyc-N2CO dimers.
O/C–N addition, their most feasible decomposition transition states have certain open-shell singlet characteristics. They have the barriers of 13.9 and 17.4 kcal mol−1, respectively at the UB3LYP/6-311G(2d,d,p) level. For isomer 2, the RHF → UHF energy lowering value of 7.2 kcal mol−1 is considerable, whereas that (0.5 kcal mol−1) for isomer 3 is negligible. The corresponding CBS-QB3 barriers at the restricted level are 19.8 and 22.2 kcal mol−1 for 2 and 3. We expect the rate-determining barriers of 2 and 3 to be around 15 kcal mol−1 at the correlated level, which could allow them to be detectable in future spectroscopic studies. In sharp contrast, the highly symmetric isomer 1 (D2d) have very high decomposition barriers, i.e., 29.9 (1-TS1) and 42.9 (1-TS2) kcal mol−1 at the CBS-QB3 level for the fragmentation to N2-leaving and 2cyc-N2CO, respectively (see Table 2). Clearly, isomer 1 is the most kinetically stable among all the cyc-N2CO dimers.
It should be noted that for the associated fragments, i.e., linear CNN and O2, their triplet states are energetically more stable than the corresponding singlet ones by 28.91 and 39.02 kcal mol−1, respectively. So, possible singlet → triplet intersystem crossing (ISC) of the associated fragmentation channels needs to be considered. As examples, at the B3LYP/6-311G(2d,d,p) level, the triplet (cyc-N2CO)2 isomers 31–34 and their decomposition transition states were optimized. The rate-determining barriers of 31–34 are only 4.2, 6.8, 3.0 and 0.2 kcal mol−1, respectively. This indicates the shallowness of the triplet energy surface of (cyc-N2CO)2. Yet, more importantly, all the triplet (cyc-N2CO)2 isomers lie significantly higher than the singlet isomers and the related rate-determining transition states in square brackets, i.e., 56.9 [25.5], 53.9 [30.8], 52.9 [35.0] and 29.7 [26.9] kcal mol−1 for 1, 2, 3 and 4, respectively. So there would be no intersystem crossing prior to the singlet fragmentation transition state, and would not affect the kinetic stability of the singlet (cyc-N2CO)2 isomers. For details, see Table S8 in ESI.† We expect that the same conclusion should hold for higher oligomers of cyc-N2CO.
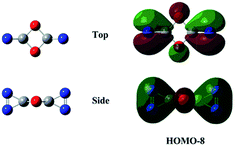
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond retained, there exists a set of π-bonding orbital within each CNN-ring. Meanwhile, there are four π-type lone-pairs at two O-atoms within the COCO-ring (see HOMO-8 in Fig. 1). Consequently, both the π-type lone-pair (COCO-ring) and N
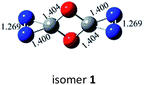
N bond retained, there exists a set of π-bonding orbital within each CNN-ring. Meanwhile, there are four π-type lone-pairs at two O-atoms within the COCO-ring (see HOMO-8 in Fig. 1). Consequently, both the π-type lone-pair (COCO-ring) and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bonding (CNN-ring) orbitals can conjugate with the exocyclic C–N (CNN-ring) and C–O (COCO-ring) σ-type bonding orbitals, respectively. As a result, the C–N and C–O bonding will be strengthened with the overlap contribution from the neighboring π-bonding orbitals. In fact, the C–O (1.404 Å) and C–N (1.400 Å) bond lengths are shorter than the respective typical single bonds (i.e., 1.421 Å in CH3OH and 1.467 Å in CH3NH2 computed at the B3LYP/6-311G(2d,d,p) level). Reasonably, the N–N bond (1.269 Å) is slightly elongated compared to the typical double bond (1.241 Å in trans-HNNH), due to the electron-delocalization.
N double bonding (CNN-ring) orbitals can conjugate with the exocyclic C–N (CNN-ring) and C–O (COCO-ring) σ-type bonding orbitals, respectively. As a result, the C–N and C–O bonding will be strengthened with the overlap contribution from the neighboring π-bonding orbitals. In fact, the C–O (1.404 Å) and C–N (1.400 Å) bond lengths are shorter than the respective typical single bonds (i.e., 1.421 Å in CH3OH and 1.467 Å in CH3NH2 computed at the B3LYP/6-311G(2d,d,p) level). Reasonably, the N–N bond (1.269 Å) is slightly elongated compared to the typical double bond (1.241 Å in trans-HNNH), due to the electron-delocalization.
From the kinetic and electronic analysis, we can infer that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/C
O/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O trans-addition to form dimer 1 with all C–O single bonds while retaining the N
O trans-addition to form dimer 1 with all C–O single bonds while retaining the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonding is a quite preferable choice. The unique spiral structure induces the effective bonding between the π orbitals (N
N bonding is a quite preferable choice. The unique spiral structure induces the effective bonding between the π orbitals (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N or O-lone pair) and the spiral σ orbitals (C–O or C–N). Besides, the energetic feature of 1 is well kept since it lies just by 3.4 kcal mol−1 below 2cyc-N2CO. The overall energy release from 1 to 2N2 + 2CO is as huge as 168.7 kcal mol−1 at the CBS-QB3 level. In light of the kinetic stability criterion threshold (30 kcal mol−1),36 the dimeric isomer 1 fully meets the two strict requirements of HEDM and has the great hope to be an energetic molecule.
N or O-lone pair) and the spiral σ orbitals (C–O or C–N). Besides, the energetic feature of 1 is well kept since it lies just by 3.4 kcal mol−1 below 2cyc-N2CO. The overall energy release from 1 to 2N2 + 2CO is as huge as 168.7 kcal mol−1 at the CBS-QB3 level. In light of the kinetic stability criterion threshold (30 kcal mol−1),36 the dimeric isomer 1 fully meets the two strict requirements of HEDM and has the great hope to be an energetic molecule.
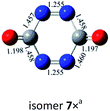
3.2 Oligomers of (cyc-N2CO)n (n = 3–8)
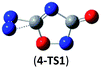
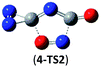
The successful assembly from cyc-N2CO monomer to the dimer 1 promptly encourages us to wonder whether higher-order oligomers in a similar mode can be feasible or not. Herein, we computed the trimer and tetramer of cyc-N2CO via the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/C
O/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond addition, i.e., (cyc-N2CO)n (n = 3, 4) with N
O bond addition, i.e., (cyc-N2CO)n (n = 3, 4) with N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond still kept. Various decomposition channels were also considered. Similar to isomer 1, the rate-determining step for trimer and tetramer is the N2-leaving with the barriers of 25.8 and 30.3 kcal mol−1 at the CBS-QB3 level, respectively. For even higher-order cyc-N2CO oligomers (n = 5, 6, 7, 8), the expensive CBS-QB3 calculations are very unlikely. Fortunately, we can find that the average deviation of the rate-determining barrier is only 1.9 kcal mol−1 between the B3LYP/6-311G(2d,d,p) and CBS-QB3 values for the small oligomers (n = 2–4) in Table 2. So for (cyc-N2CO)n (n = 5–8), we used the B3LYP/6-311G(2d,d,p) results for evaluation of the kinetic stability of the designed structures. Their respective key N2-leaving barriers are 27.2, 34.0, 24.3 and 27.0 kcal mol−1, indicative of high feasibility as molecular HEDMs.
N bond still kept. Various decomposition channels were also considered. Similar to isomer 1, the rate-determining step for trimer and tetramer is the N2-leaving with the barriers of 25.8 and 30.3 kcal mol−1 at the CBS-QB3 level, respectively. For even higher-order cyc-N2CO oligomers (n = 5, 6, 7, 8), the expensive CBS-QB3 calculations are very unlikely. Fortunately, we can find that the average deviation of the rate-determining barrier is only 1.9 kcal mol−1 between the B3LYP/6-311G(2d,d,p) and CBS-QB3 values for the small oligomers (n = 2–4) in Table 2. So for (cyc-N2CO)n (n = 5–8), we used the B3LYP/6-311G(2d,d,p) results for evaluation of the kinetic stability of the designed structures. Their respective key N2-leaving barriers are 27.2, 34.0, 24.3 and 27.0 kcal mol−1, indicative of high feasibility as molecular HEDMs.
3.3 The detonation properties and impact sensitivity for (cyc-N2CO)n (n = 2–8)
It is well known that ideal energetic materials not only require high thermal and kinetic stabilities but also exhibit an excellent detonation properties (density ρ ≈ 1.9 g cm−3, detonation velocity D ≈ 9.0 km s−1, P ≈ 40.0 GPa), and insensitivities (h50 > 12 cm).37 To provide detailed information for future experimental study, we computed various detonation properties of (cyc-N2CO)n (n = 2–8). For comparison, the properties of the known species like (N3)2CO, 1,3,5-trinitro-1,3,5-triazinane (RDX) and 1,3,5,7-tetranitro-1,3,5,7-tetrazocane (HMX) were also provided.The enthalpy of formation of (cyc-N2CO)n (n = 2–8) in the gas phase (HOFgas) was determined using the isodesmic reactions of reaction (1) and the known enthalpies of formation of NH3(g), CH4(g), H2O(g), cis-N2H2(g), CH3NH2(g), and CH3OH(g) taken from the NIST Chemistry Webbook.38
| (N2CO)m + 2mNH3 + 3mCH4 + mH2O = mN2H2 + 2mCH3NH2 + 2mCH3OH, for m = 2–8 | (1) |
Surely, to estimate the detonation performance of the title compounds, it's desirable to calculate the solid phase heats of formation (HOFsolid). According to Hess's law,39 HOFsolid can be obtained by
| HOFsolid = HOFgas − HOFsub | (2) |
| HOFsub = αA2 + β(vσtotal2)1/2 + γ | (3) |
Table 3 lists the ΔE0, ΔEZPE, ΔHT, HOFgas, HOFsub and HOFsolid of the title compounds at the B3LYP/6-311G(2d,d,p) and CBS-QB3 (when available) levels. The HOFsolid values of (cyc-N2CO)n (n = 2–8) are quite large and positive (387.58–1291.05 kJ mol−1) (see Table 3), which are much larger than the experimentally determined values for the classic energetic materials (i.e., RDX = 79.1 ± 5 kJ mol−1, HMX = 75 kJ mol−1).38
| Compound | E0 (a.u.) | EZPE (a.u.) | HT (a.u.) | HOFgas (kJ mol−1) | HOFsub (kJ mol−1) | HOFsolid (kJ mol−1) |
|---|---|---|---|---|---|---|
| N2 | −109.55593016 (−109.398445) | |||||
| CO | −113.34623537 (−113.182005) | |||||
| NH3 | −56.57603536 (−56.460190) | 0.034295 | 0.003809 | [−45.90] | ||
| CH4 | −40.53374825 (−40.409988) | 0.044604 | 0.003812 | [−74.90] | ||
| H2O | −76.44744792 (−76.337482) | 0.021325 | 0.003779 | [−241.83] | ||
| cis-N2H2 | −110.6634661 (−110.476252) | 0.027484 | 0.003805 | [212.97] | ||
| CH3NH2 | −95.88843875 (−95.668474) | 0.063803 | 0.004354 | [−23.50] | ||
| CH3OH | −115.7573935 (−115.539952) | 0.051106 | 0.004259 | [−215.00] | ||
| cyc-N2CO | −222.77096796 (−222.433774) | 0.014878 | 0.004238 | 222.44 (229.09) | 58.25 | 164.19 (170.84) |
| (cyc-N2CO)2 | −445.5473301 (−444.891981) | 0.035233 | 0.00659 | 437.67 (408.96) | 50.09 | 387.58 (358.87) |
| (cyc-N2CO)3 | −668.3643105 (−667.384038) | 0.054587 | 0.009638 | 545.45 (490.63) | 63.01 | 482.44 (427.61) |
| (cyc-N2CO)4 | −891.152937 (−889.849912) | 0.073222 | 0.012833 | 726.18 (641.42) | 75.21 | 650.97 (566.22) |
| (cyc-N2CO)5 | −1113.938994 | 0.091676 | 0.016232 | 913.71 | 90.95 | 822.76 |
| (cyc-N2CO)6 | −1336.722905 | 0.11003 | 0.019736 | 1092.02 | 109.65 | 982.37 |
| (cyc-N2CO)7 | −1559.510599 | 0.128457 | 0.023221 | 1287.80 | 129.41 | 1158.39 |
| (cyc-N2CO)8 | −1782.30456 | 0.146957 | 0.026912 | 1455.47 | 164.42 | 1291.05 |
| RDX | −897.6546332 | 0.142515 | 0.155164 | 212.72 (188.98) [192] | 94.19 [134.3] | 118.53 (94.79) [79.5 ± 5] |
| HMX | −1196.874372 | 0.190869 | 0.208291 | 282.48 [no available] | 119.17 [no available] | 163.31 [75] |
The detonation velocity (D in km s−1) and detonation pressure (P in GPa) of the title compounds are estimated by the eqn (4) and (5)43
D = 1.01(N![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 0.5Q0.5)0.5(1 + 1.3ρ) 0.5Q0.5)0.5(1 + 1.3ρ)
| (4) |
P = 1.558ρ2N![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 0.5Q0.5 0.5Q0.5
| (5) |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) is the mean molecular weight of the gaseous detonation products. Q is the heats of detonation (cal g−1). ρ is the density of the explosive (g cm−3). To obtain the theoretical density, we applied an improved equation proposed by Politzer et al.44 in which the interaction index vσtot2 is:
is the mean molecular weight of the gaseous detonation products. Q is the heats of detonation (cal g−1). ρ is the density of the explosive (g cm−3). To obtain the theoretical density, we applied an improved equation proposed by Politzer et al.44 in which the interaction index vσtot2 is:
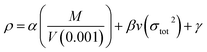 | (6) |
| Species | ρ (g cm−3) | D (km s−1) | P (GPa) | Release of heats (decomposition products of N2 + CO) (kcal mol−1) | h50 (cm) |
|---|---|---|---|---|---|
| a Ref. 6.b Ref. 2.c Ref. 46. | |||||
| cyc-N2CO | 1.58 | 7.64 (7.67) | 23.86 (24.08) | −82.3 | 50.90 |
| (cyc-N2CO)2 | 1.66 | 8.04 (7.97) | 27.30 (26.79) | −161.3 | 38.29 |
| (cyc-N2CO)3 | 1.75 | 8.15 (8.05) | 28.96 (28.21) | −214.7 | 41.55 |
| (cyc-N2CO)4 | 1.76 | 8.19 (8.07) | 29.34 (28.47) | −286.0 | 38.78 |
| (cyc-N2CO)5 | 1.76 | 8.22 | 29.55 | −358.8 | 34.30 |
| (cyc-N2CO)6 | 1.78 | 8.27 | 30.09 | −433.0 | 35.02 |
| (cyc-N2CO)7 | 1.78 | 8.28 | 30.20 | −504.9 | 33.05 |
| (cyc-N2CO)8 | 1.79 | 8.28 | 30.30 | −572.8 | 35.04 |
| (N3)2CO | [1.71]a | −116.6 | 54.62 | ||
| RDX | 1.77 [1.82]b | 8.81 (8.76) [8.75]b | 34.13 (33.73) [34.00]b | 43 [26]c | |
| HMX | 1.80 [1.91]b | 8.91 [9.10]b | 35.23 [39.00]b | 31 [29]c | |
For the characteristic height (h50), it is usually computed by dropping a given mass upon a sample of the compound and determining the height from which 50% of the drops produce evidence of reaction. The greater the value of h50, the less is the sensitivity. h50 of a compound is estimated by the eqn (7).45
| h50 = ασ+2 + βν + γ | (7) |
In eqn (7), the coefficient α, β, and γ, were estimated by Pospíšil et al. as α = −0.0064, β = 241.42, and γ = −3.43.45 σ+2 is the indicator of the strengths and variabilities of the positive surface potentials, ν is the degree of balance between positive and negative potential on the molecular surface.
The h50 values of (cyc-N2CO)n (n = 2–8) are between 33 cm and 42 cm, which are somewhat higher than those of RDX (26 cm) and HMX (29 cm)46 (see Table 4). According to ref. 5 and 6, (N3)2CO has the huge energy release (−116.6 kcal mol−1 to N2 + CO), the very high decomposition barrier (ca. 30 kcal mol−1) and the big HOF value (ca. 460 kcal mol−1), making it an ideal nitrogen-rich HEDM. In our work, we found that the monomer cyc-N2CO is inferior to (N3)2CO in view of its density (ρ = 1.58 g cm−3), detonation velocity (D = 7.64 km s−1) and detonation pressure (P = 23.86 GPa). It is ascribed to the less nitrogen-content in cyc-N2CO than in (N3)2CO. Thus, quite promisingly, with the increased oligomeric degree, the molecules (cyc-N2CO)n have much better ρ, D, P and HOF values while retaining the appreciable kinetic stability. This indicates the effectiveness of such a simple bottom-up strategy.
3.4 Implications
Overall, starting from a kinetically stable HEDM seed, i.e., cyc-N2CO, we can design novel and more complicated HEDMs (cyc-N2CO)n (n = 2–8) that contain a cross-linked (CO)n ring and n spiral CNN rings. It is worth noting that the strategy of substituting the frameworks or ligands of known HEDMs has been frequently used and shown very effectively in generation of new and more complex HEDMs. The present strategy widens the possibility of predicting new forms of HEDMs.In addition, within the presently designed HEDMs, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds within cyc-N2CO are fully transformed into the C–O single bonds, whereas the exocyclic N
O bonds within cyc-N2CO are fully transformed into the C–O single bonds, whereas the exocyclic N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds are almost untouched. These species differ much from previously reported polymeric (N2CO)n that are expected to be viable at high pressure and contain all single bonds.29 Surely, in view of the energy storage, the (N2CO)n with all single bonds are superior to our (cyc-N2CO)n with partial single bonds. Yet in view of the kinetic stability, our (cyc-N2CO)n should be quite attractive. In our model calculations of (cyc-N2CO)2, we found that activation of the N
N bonds are almost untouched. These species differ much from previously reported polymeric (N2CO)n that are expected to be viable at high pressure and contain all single bonds.29 Surely, in view of the energy storage, the (N2CO)n with all single bonds are superior to our (cyc-N2CO)n with partial single bonds. Yet in view of the kinetic stability, our (cyc-N2CO)n should be quite attractive. In our model calculations of (cyc-N2CO)2, we found that activation of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond would very easily induce the N2-extrusion. So, if the N
N bond would very easily induce the N2-extrusion. So, if the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N activation is caused one by one during the polymerization of cyc-N2CO, we believe that the polymeric forms with all single bonds could not be formed. Of course, this does not exclude the formation of polymeric cyc-N2CO in a very short time scale under extreme conditions. Our work presents the first chemically feasible (N2CO)n of HEDM interest.
N activation is caused one by one during the polymerization of cyc-N2CO, we believe that the polymeric forms with all single bonds could not be formed. Of course, this does not exclude the formation of polymeric cyc-N2CO in a very short time scale under extreme conditions. Our work presents the first chemically feasible (N2CO)n of HEDM interest.
We believe that our bottom-up assembly strategy would be general to apply to the other units with multiple bonds. For example, there have been growing molecular HEDMs that have been experimentally characterized, e.g., (N3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O,47 (N3)3P
O,47 (N3)3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O,48 and (N3)2SO2.49 Their suitably oligomerized compounds should provide new HEDM candidates. We are now studying the stability and detonation properties of their oligomers.
O,48 and (N3)2SO2.49 Their suitably oligomerized compounds should provide new HEDM candidates. We are now studying the stability and detonation properties of their oligomers.
4. Conclusion
We have presented the first theoretical design on a set of (cyc-N2CO)n (n = 2–8) as molecular HEDMs via a bottom-up strategy. The kinetically most stable isomer of each oligomer is formed via the direct C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/C
O/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O trans-addition. In these isomers, all the C
O trans-addition. In these isomers, all the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds are transformed into C–O single bonds, whereas the N
O bonds are transformed into C–O single bonds, whereas the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds are unchanged. The unique spiral structure contributes to their good kinetic stability that are around 25–30 kcal mol−1. Besides, the designed (cyc-N2CO)n (n = 2–8) possess excellent detonation properties and low impact sensitivity. Therefore, they deserve to be viewed as very promising molecular HEDMs. Our designed candidates are structurally different from the high-pressure polymerized (N2CO)n since the latter have all multiple bonds transformed into single bonds. The new HEDM molecules warmly welcome future laboratory studies.
N bonds are unchanged. The unique spiral structure contributes to their good kinetic stability that are around 25–30 kcal mol−1. Besides, the designed (cyc-N2CO)n (n = 2–8) possess excellent detonation properties and low impact sensitivity. Therefore, they deserve to be viewed as very promising molecular HEDMs. Our designed candidates are structurally different from the high-pressure polymerized (N2CO)n since the latter have all multiple bonds transformed into single bonds. The new HEDM molecules warmly welcome future laboratory studies.
Acknowledgements
This work was funded by the National Natural Science Foundation of China (No. 21273093, 21473069). The reviewers' very helpful comments and suggestions are greatly acknowledged.References
- T. M. Klapötke, High Energy Density Materials, Structure and Bonding, no. 125, New York, 2007 Search PubMed.
- M. B. Talawar, R. Sivabalan, T. Mukundan, H. Muthurajan, A. K. Sikder, B. R. Gandhe and A. Subhananda Rao, J. Hazard. Mater., 2009, 161, 589 CrossRef CAS PubMed.
- G. Bélanger-Chabot, M. Rahm, R. Haiges and K. O. Christe, Angew. Chem., Int. Ed., 2015, 54, 11730 CrossRef PubMed.
- S. Naserifar, S. Zybin, C. C. Ye and W. A. Goddard III, J. Mater. Chem. A, 2016, 4, 1264 CAS.
- D. W. Ball, Comput. Theor. Chem., 2011, 965, 176 CrossRef CAS.
- T. Yu and B. Wu, Inorg. Chem. Front., 2015, 2, 991 RSC.
- X. Y. Liu, Z. Y. Su, W. X. Ji, S. P. Chen, Q. Wei, G. Xie, X. W. Yang and S. L. Gao, J. Phys. Chem. C, 2014, 118, 23487 CAS.
- M. Tian, W. J. Chi, Q. S. Li and Z. S. Li, RSC Adv., 2016, 6, 47607 RSC.
- J. H. Zhang and J. M. Shreeve, J. Am. Chem. Soc., 2014, 136, 4437 CrossRef CAS PubMed.
- K. Hafner, T. M. Klapötke, P. C. Schmid and J. Stierstorfer, Eur. J. Inorg. Chem., 2015, 17, 2794 CrossRef.
- F. G. Li, Y. G. Bi, W. Y. Zhao, T. L. Zhang, Z. N. Zhou and L. Yang, Inorg. Chem., 2015, 54, 2050 CrossRef CAS PubMed.
- L. H. Tang, S. Y. Bao, J. H. Peng, K. Li, P. Ning, H. B. Guo, T. T. Zhu, J. J. Gua and Q. S. Li, Chem. Phys. Lett., 2015, 639, 166 CrossRef CAS.
- P. He, J. G. Zhang, K. Wang, X. Yin, X. Jin and T. L. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 5840 RSC.
- P. Yin, Q. H. Zhang and J. M. Shreeve, Acc. Chem. Res., 2016, 49, 4 CrossRef CAS PubMed.
- S. Zhang, Y. Qi, X. Y. Liu, X. N. Qu, Q. Wei, G. Xie, S. P. Chen and S. L. Gao, Coord. Chem. Rev., 2016, 307, 292 CrossRef CAS.
- L. Y. Yan, S. H. Gou, Z. B. Ye, S. H. Zhang and L. H. Ma, Chem. Commun., 2014, 50, 12847 RSC.
- L. G. Bettini, F. D. Foglia, P. Milani and P. Piseri, Int. J. Hydrogen Energy, 2015, 40, 6013 CrossRef CAS.
- J. Chen, H. L. Zhou and X. Feng, Inorg. Chem., 2016, 55, 4695 CrossRef CAS PubMed.
- A. A. Korkin, P. v. R. Schleyer and R. J. Boyd, Chem. Phys. Lett., 1994, 227, 312 CrossRef CAS.
- A. A. Korkin, J. Leszczynski and R. J. Bartlett, J. Phys. Chem., 1996, 100, 19840 CrossRef CAS.
- G. de Petris, F. Cacace, R. Cipollini, A. Cartoni, M. Rosi and A. Troiani, Angew. Chem., Int. Ed., 2005, 44, 462 CrossRef CAS PubMed.
- R. A. Moss, G. S. Chu and R. R. Sauers, J. Am. Chem. Soc., 2005, 127, 2408 CrossRef CAS PubMed.
- R. A. Moss and R. R. Sauers, Tetrahedron Lett., 2010, 51, 3266 CrossRef CAS.
- C. J. Shaffer, B. J. Esselman, R. J. McMahon, J. F. Stanton and R. C. Woods, J. Org. Chem., 2010, 75, 1815 CrossRef CAS PubMed.
- A. Perrin, X. Q. Zeng, H. Beckers and H. Willner, J. Mol. Spectrosc., 2011, 269, 30 CrossRef CAS.
- X. Q. Zeng, H. Beckers, H. Willner and J. F. Stanton, Angew. Chem., Int. Ed., 2011, 50, 1720 CrossRef CAS PubMed.
- X. Q. Zeng, H. Beckers, H. Willner and J. F. Stanton, Eur. J. Inorg. Chem., 2012, 21, 3403 CrossRef.
- Z. Raza, C. J. Pickard, C. Pinilla and A. M. Saitta, Phys. Rev. Lett., 2013, 111, 235501 CrossRef PubMed.
- C. Y. Zhu, Q. Li, Y. Y. Zhou, M. Zhang, S. T. Zhang and Q. Li, J. Phys. Chem. C, 2014, 118, 27252 CAS.
- H. M. Li, D. Q. Li, X. Q. Zeng, K. Liu, H. Beckers, H. F. Schaefer III, B. J. Esselman and R. J. McMahon, J. Phys. Chem. A, 2015, 119, 8903 CrossRef CAS PubMed.
- B. B. Xie, L. H. Liu, G. L. Cui, W. H. Fang, J. Cao, W. Feng and X. Q. Li, J. Chem. Phys., 2015, 143, 194107 CrossRef PubMed.
- (a) M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kita, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cro, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenbe, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2004 Search PubMed; (b) M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 03, Revision D.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- J. A. Montgomery Jr, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822 CrossRef.
- J. A. Montgomery Jr, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532 CrossRef.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737 CrossRef CAS.
- M. Rahm and T. Brinck, Chem.–Eur. J., 2010, 16, 6590 CrossRef CAS PubMed.
- H. M. Xiao, X. J. Xu and L. Qiu, Theoretical Design of High Energy and Density Materials, Science Press, Beijing, 2008 Search PubMed.
- http://webbook.nist.gov/chemistry/form-ser.html.
- P. W. Atkins, Physical chemistry, Oxford University Press, Oxford, 1982 Search PubMed.
- E. F. Byrd and B. M. Rice, J. Phys. Chem. A, 2006, 110, 1005 CrossRef CAS PubMed.
- F. A. Bulat, A. Toro-Labbé, T. Brinck, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679 CrossRef CAS PubMed.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
- M. J. Kamlet and S. Jacobs, J. Chem. Phys., 1968, 48, 23 CrossRef CAS.
- P. Politzer, J. Martinez, J. S. Murray, M. C. Concha and A. Toro- Labbé, Mol. Phys., 2009, 107, 2095 CrossRef CAS.
- M. Pospíšil, P. Vávra, M. C. Concha, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 895 CrossRef PubMed.
- P. Politzer and J. S. Murray, J. Mol. Model., 2015, 21, 262 CrossRef PubMed.
- X. Q. Zeng, M. Gerken, H. Beckers and H. Willner, Inorg. Chem., 2010, 49, 9694 CrossRef CAS PubMed.
- X. Q. Zeng, E. Bernhardt, H. Beckers and H. Willner, Inorg. Chem., 2011, 50, 11235 CrossRef CAS PubMed.
- X. Q. Zeng, H. Beckers, E. Bernhardt and H. Willner, Inorg. Chem., 2011, 50, 8679 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra28358f |
| This journal is © The Royal Society of Chemistry 2017 |