Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetorheology of a magnetic fluid based on Fe3O4 immobilized SiO2 core–shell nanospheres: experiments and molecular dynamics simulations
Lei Pei,
Haoming Pang,
Xiaohui Ruan,
Xinglong Gong * and
Shouhu Xuan*
* and
Shouhu Xuan*
CAS Key Laboratory of Mechanical Behavior and Design of Materials, Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230027, China. E-mail: xuansh@ustc.edu.cn; gongxl@ustc.edu.cn; Fax: +86 551 63600419; Tel: +86 551 63600419
First published on 24th January 2017
Abstract
A novel superparamagnetic magnetic fluid based on Fe3O4-immobilized-SiO2-nanospheres (MSiNPs) was developed. Both the experimental analyses and computational simulations were conducted to investigate its magnetorheology. In comparison to the pure Fe3O4 based magnetic fluid, the magnetorheological (MR) effect of the MSiNPs based magnetic fluid was about 25 times larger. To demonstrate the improving mechanical properties, a modified magnetic dipolar model was proposed to describe the magnetic interaction of two close magnetized particles. Moreover, the molecular dynamic simulations were carried out to understand the microstructure evolution under an applied magnetic field. The simulation results showed that chain-like and column-like particulate structures were formed in the stationary state and transferred into lamellar microstructures in the steady shear flow. Particle-level simulations were in good agreement with experimental data. The dramatic increase in MR effect of the MSiNPs based magnetic fluid originated from the intensity of the magnetic attractions and the size scale of the particulate structures.
Introduction
A magnetic fluid is a “solid–liquid” phase colloid solution obtained by good dispersion of magnetic particles in carrier fluids.1 By varying the size scale and magnetic characteristics of the dispersed magnetic particles, magnetic fluid could be divided into ferro-magnetic fluid and magnetorheological (MR) fluid.2 Due to their unique magnetic dipole–dipole interactions, the magnetic particles would like to assemble into chain-like microstructures under an applied magnetic field, thus the mechanical properties of the magnetic fluid critically change. Based on this typical tunable and controllable mechanical property, the magnetic fluid has been utilized in various applications such as drug targeting delivery, magnetic-thermal therapy, magnetic resonance imaging, vibration isolation, breaking, intelligent sensors, etc.3–9The magnetic forces and friction interactions of magnetic particles played the key role in the magnetorheology of the magnetic fluid.10 To improve the mechanical properties of magnetic fluid, various influence factors such as the magnetic moment, shape, density, size, roughness, and microstructures have been systematically investigated.11–15 Typically, the intrinsic structure of the magnetic particles became a hot area of the rheological properties by affecting the forming structure under applying the external magnetic field. Moreover, sedimentation was crucial for magnetic fluid due to the mismatch between the magnetic particles and carrying fluids.16 Besides the surface coating route, the size decreasing has been estimated to be an effective method to improve the stability.17,18 Based on the nano-sized Fe-alloy, the Lord Corp developed a novel MR fluid, in which the settlement problem was resolved. Similarly, the Fe, Fe-alloy, Fe@carbon nanospheres also represented both high stability and MR effects.19–21
Up to now, plenty of iron-based materials have been explored for magnetic fluid.22–24 Micron-sized carbonyl iron (CI) spheres are widely used for MR fluid due to their soft magnetic property, high magnetic permeability, proper size and common availability. However, the high density of CI causes intrinsically sedimentation problem. Another drawback of pure CI particles is the poor chemical stability in an acidic environment.25 Such drawbacks could be efficiently reduced by conventional surface coating and surface modifying methods.25,26 Fe3O4 and γ-Fe2O3 also exhibit similar magnetic properties. The biggest advantage of γ-Fe2O3 is the chemical stability. Fe3O4 particles are easy to oxidize into ferric oxyhydroxides due to the Fe2+ ions, which lead to the loss of MR effect.27 Nevertheless, the Fe3O4 microbeads have higher saturation magnetization compared to γ-Fe2O3 nanoparticles.28 Generally, Fe3O4 is used as the nano-sized magnetic material in magnetic fluid.
Fe3O4 nanoparticles have attracted increasing interests in magnetic fluids because of their easy processing and high surface compatibility. Over the past decade, intensive work has been performed to study the Fe3O4 particles' morphologies dependent MR mechanism. Therefore, cubic, octahedral, plate-like and fibrous magnetic nanoparticles based MR fluids were also reported.29–32 It was found that the unique shapes increased the friction forces and thus enhanced the MR effects. The core–shell structure is also a promising morphology to improve the MR effect and sedimentation stability, by increasing the inter-particle attraction forces and decreasing the particle density.33 To improve the magnetic particles' weight ratio, the magnetic nanoparticles were often immobilized onto the surface of the nanospherical template. Several successful examples such as the PS/Fe2O3, PMMA/Fe2O3 nanospheres were developed by Pickering emulsion polymerization.34,35 Interestingly, the static yield stress of the above suspensions displayed a linear magnetic field-dependency instead of the quadratic field-dependency of the pure Fe2O3 based MR fluid. Therefore, the study of the magnetic fluid based on the Fe3O4-immobilized particles became a pressing need in both applications and mechanism analyses.
Numerical simulation was an important method for investigating the magnetorheology of the magnetic fluid. During the past decades, many numerical simulation methods such as the finite element method, computational fluid dynamics simulation based on finite volume approach, Monte Carlo method, and molecular dynamics simulation method have been conducted to investigate the mechanical properties of the magnetic fluid.36–39 By combining experiments and simulations together, both the shear stress and the snapshots of field-induced microstructures could be obtained, which demonstrated that the molecular dynamics simulations and experimental data were in good qualitative agreement.40 The particle-level simulations have been proven to be an effective method for studying the yield behaviors of magnetic fluids. Similarly, the magnetic field dependent rheology under both steady and oscillatory shear also have been successfully cleared.41 Importantly, the simulation could also give out correct predictions for the magnetic fluids, which was finally proven by the experiments.42 To this end, it is anticipated that the particle-level simulations will present high potential in studying the magnetorheology of the magnetic fluid based on the Fe3O4-immobilized particles.
This work reported an experiment/simulation combining method to investigate the MR behavior of a novel magnetic fluid based on the Fe3O4-immobilized-SiO2-nanospheres (MSiNPs). In comparison to the pristine Fe3O4 nanoparticles, the MSiNPs based magnetic fluid exhibited higher MR effect. A particle–matrix interaction model was employed to analyze the inter-particle forces and the kinematic equation was further derived to clarify the magnetic field-dependent structural transformation in the magnetic fluid. The experimental results agreed with the simulations. Based on the above results, a possible mechanism was proposed to demonstrate the unique nanostructure dependent high MR effect, which would be also applied for discussing the origination of the magnetorheology.
Experiments
Preparation of the Fe3O4-immobilized-SiO2-nanospheres (MSiNPs)
Firstly, the SiO2 nanospheres with an average size of 200 nm which were prepared via a modified Stöber method were dispersed into an ethanol to get a 70 mg mL−1 solution. Then, 3 mL of the above solution was mixed with 40 mL triethylene glycol in the flask and heated to 95 °C to remove ethanol. After that, 320 mg Fe(acac)3 was added under sonication. 5 min later, the solution was treated in 278 °C under the protection of nitrogen. The refluxing was conducted under magnetic stirring for 30 min and then it was cooled to room temperature by adding 40 mL ethanol in the reaction solution. At last, the MSiNPs were magnetically separated and washed with ethanol for several times.The magnetic fluids based on the MSiNPs were prepared by dispersing MSiNPs into water. The total weight ratios of the MSiNPs were set as 10 wt%, 15 wt%, and 20 wt%, in which the weight fractions of Fe3O4 were 1.8 wt%, 2.7 wt%, and 3.6 wt%, respectively. As a comparison, the pure Fe3O4 nanoparticles-magnetic fluids with weight fractions 1.8 wt%, 2.7 wt%, and 3.6 wt% were also obtained.
Characterization
A transmission electron microscopy (TEM) (JEM-2100F) was employed to investigate the micro-features of MSiNPs. The elemental composition of MSiNPs was obtained on an inductively coupled plasma atomic emission spectrometer (ICP-AES) (Optima 7300 DV). Magnetic hysteresis loops figures of both MSiNPs and monodisperse Fe3O4 particles were obtained on a magnetic property measuring system (MPMS) vibrating sample magnetometer (VSM) (SQUID, Quantum Design Co., America). X-ray diffraction (XRD) patterns of the samples were measured on an intelligent XRD system (SmartLab) with Cu-Kα radiation (λ = 1.5418 Å).Rheological measurements
The rheological properties of magnetic fluid samples were studied by using a commercial rheometer (Physica MCR 301, Anton Paar Co., Austria) with a magnetic field accessory. Typically, 0.3 mL of the test sample was introduced between two parallel plates (PP 20). The distance between two plates was fixed at 1 mm. An electromagnet and a magnetic yoke generated a homogeneous magnetic field perpendicular to the plates, also perpendicular to the flow direction. Both the shear and oscillation tests were conducted under the magnetic field sweep. The temperature was maintained at 25 °C during all the experiments. Before each test, the sample was pre-sheared at a shear rate of 100 s−1 without applying any external magnetic field. Fe3O4 nanoparticles based magnetic fluid had a relatively poor sedimentation stability, ultrasonic washing processes before the experiments were applied. For the magnetic field sweep, the shear rate was chosen as 10 s−1, 25 s−1, 50 s−1, and 100 s−1. The magnetic flux density linearly increased over time until 480 mT, which had already reached the saturation area. In the oscillation test, the frequency was set as 0.5 rad s−1 and 1.0 rad s−1 while the amplitude was set at 100%.Simulation model
Characterization of the MSiNPs
In this work, the MSiNPs could be easily synthesized via a one-pot thermal decomposition method by using SiO2 nanospheres as the hard template and the Fe(acac)3 as the iron source.43 Fig. 1a shows the typical TEM image of the MSiNPs, which indicates that a lot of black Fe3O4 nanoparticles are immobilized on the surface of the spherical SiO2. The average diameter of the MSiNPs is around 200 nm with a uniform distribution. The high magnification TEM image of a single MSiNP demonstrates the surface is packaged closely by 10 nm Fe3O4 nanoparticles (Fig. 1b). Here, the Fe content of the MSiNP samples is measured to be 13.1 wt% (ICP-AES). Thus the weight fraction of Fe3O4 in a nanosphere is calculated as 18 wt%. The density of the MSiNPs is measured to be 2.6 g cm−3. Fig. 1c gives the magnetic hysteresis loops of the MSiNPs and the pristine Fe3O4 nanoparticles. The MSiNPs depict the identical superparamagnetic characteristic, in which the saturation magnetization (Ms), the coercivity and the remanence are 11 emu g−1, 31 Oe, and 0.85 emu g−1, respectively. The lower Ms than the pristine Fe3O4 nanoparticles (48 emu g−1) is responded to the presence of non-magnetic SiO2 component. Fig. 1d shows the XRD patterns of the MSiNP samples. Diffraction picks at 2θ = 30.4°, 35.4°, 43.3°, 57.4°, and 62.8° can be indexed to the (200), (311), (400), (511), and (440) crystal face, which match well with the standard Fe3O4 patterns (JCPDS card no. 10-0319). Additional peaks are not observed, which indicates the purity of the samples. The crystallite size of Fe3O4 calculated through the Scherrer equation (10 nm) is in agreement with the estimated Fe3O4 size using TEM.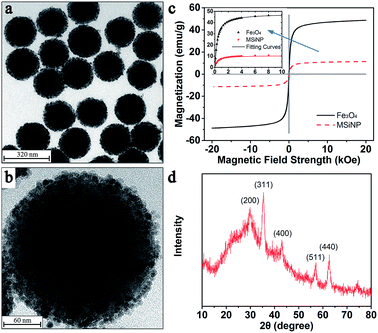 | ||
| Fig. 1 (a) and (b) TEM images of MSiNPs. (c) Magnetic hysteresis loops of MSiNPs and Fe3O4 particles (inset: nonlinear fitting results of both kinds of particles). (d) XRD patterns of MSiNPs. | ||
In order to gain an accurate view of the magnetization characteristics of MSiNPs and pristine Fe3O4 nanoparticles, the exponential nonlinear fittings of the hysteresis loops in the first quadrant was employed. The maximum magnetic field intensity didn't exceed 10 kOe in both experiments and simulations. Hence the data larger than 10 kOe from the curve was abandoned for getting more accurate results. The fitting function was:
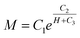 | (1) |
Particle–particle interaction
Molecular dynamics simulations based on the correctional point dipole model are carried out. Here, it is assumed that all the particles are equally magnetized under applying the magnetic field and the generated magnetic moments are paralleled to the external field. According to the exponential function:
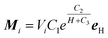 | (2) |
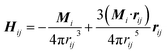 | (3) |
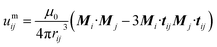 | (4) |
| uhi = −μ0Mi·H | (5) |
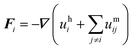 | (6) |
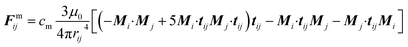 | (7) |
| FHi = μ0(Mi·∇)H | (8) |
In the presence of homogeneous magnetic field, FHi = 0. At low concentrations, the point dipole theory is an appropriate approximation. However, in the formation process, collisions among magnetic particles would continually occur. The influence of distributed magnetic moment in a single particle should be taken into account when two particles are very close to each other. Keaveny et al. theoretically investigated the magnetic interaction between two hard magnetic spheres.44 The exact solutions are quite complex. Due to the restrictions of the computational speed, a fitting factor cm is employed to correct the gap between the point dipole model and theoretical solutions.39 The inter-particle van der Waals force can be expressed as:45
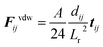 | (9) |
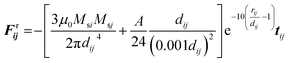 | (10) |
Kinematic equation
In both simulations and experiments, particles' motion related to the continuous Newtonian medium has an extremely low Reynolds number. Hence the Stokes' law approximates the hydrodynamic drag force as:47| Fhi = −ξiv | (11) |
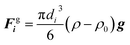 | (12) |
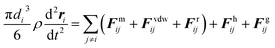 | (13) |
For both kinds of nanoparticles, the magnetic torque is so small that the magneto-induced rotation of each particle can be neglected. It is also easily accepted that the inertia of particles is negligible. In order to determine the dominated interaction in the colloidal suspension, the situation of two adjacent particles with an equal diameter of 200 nm is discussed. The particle magnetization is set as 200 kA m−1. Then we can estimate that for MSiNPs and Fe3O4 nanoparticles, |Fmij| and |Frij| are 2 to 3 orders of magnitude larger than |Fvdwij| and |Fgi|. Thus, it can be seen that the magnetic force and the exponential repulsive force are the dominant forces in the presence of an external magnetic field. In the absence of outside field, Fgi and Fvdwij will impel the particles to move while Fhi will hinder the particles' motion.
The stationary state and steady shear flow are conducted in the simulations. For MSiNPs and Fe3O4 nanoparticles, cubic regions with the edge length of 2 μm and 150 nm are respectively adopted. Periodic boundary conditions are applied to all peripheries for both cases and both kinds of particles. The simulations are composed of three steps: (1) particles are randomly distributed in the simulation box. (2) Particles are free to move in the absence of magnetic field to eliminate partial overlaps which are accidentally generated. (3) Structural formation simulations in the stationary state and steady shear flow are properly initiated, until the system reaches a self-balancing state. Once the total force imposed on a particle is calculated, its equation of motion is solved by the Euler algorithm. In the shear flow situation, considering all the approximations, the kinematic equation of a particle i can be expressed as:48
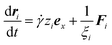 | (14) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ziex is the velocity of the ambient matrix with
ziex is the velocity of the ambient matrix with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) the shear rate. zi is the z-coordinate of the particle and ex is the unit vector of x-direction in the Cartesian coordinates. Fi is the total force acting on particle i. At each time step, the magneto-induced stress tensor is calculated as follows:
the shear rate. zi is the z-coordinate of the particle and ex is the unit vector of x-direction in the Cartesian coordinates. Fi is the total force acting on particle i. At each time step, the magneto-induced stress tensor is calculated as follows:
 | (15) |
Results and discussion
Experimental results of the MSiNPs and Fe3O4 nanoparticles based magnetic fluid
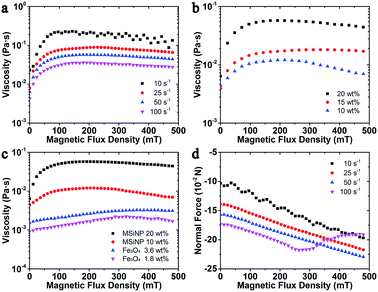
The magnetic dependent rheological properties of the magnetic fluid based on the MSiNPs (20 wt%) were firstly investigated by using the rheometer. Fig. 2a showed the variation of its viscosity under different magnetic flux densities. Typically, the viscosity firstly sharply increased with the magnetic field and then it tended to level off, which was very similar to the change phenomenon of the hysteresis loop. With increasing of the shear rate, the viscosity decreased. The weight ratio of MSiNPs played the key role in the MR effect. With increasing of the MSiNPs, more magnetic particles would present in the magnetic fluid, thus the interaction between the particles increased with the external magnetic field. As shown in Fig. 2b, the maximum viscosities of the MSiNPs based magnetic fluid reached 0.12 Pa s, 0.18 Pa s and 0.57 Pa s, as the weight fractions varied from 10 wt% to 20 wt% respectively. In the saturation region, the viscosity had a gentle decrease while the magnetic field was strengthened, which must be responded for the low weight fraction of the magnetic particles. Though the magnetic particles formed chain-like structures under the intense magnetic field, they were easily adsorbed on the testing plates. At high particle concentrations, the obstacle of other chain-like structures could resist the adsorption and lead to a relatively stable viscosity.The pure Fe3O4 nanoparticles based magnetic fluid was also investigated so as to find out the influence of the unique nanostructure. Because the weight ratio of the Fe3O4 nanoparticles in 10 wt% MSiNP magnetic fluid is 1.8 wt%, the Fe3O4 contents in 3.6 wt% Fe3O4 magnetic fluid and 20 wt% MSiNP magnetic fluid are the same. From Fig. 3c, it is very clear that the Fe3O4 magnetic fluid also presents the MR effect. The viscosity linearly increases in the region less than 300 mT, with a slope 4.1 × 10−3 Pa s T−1 and an intercept 4.9 × 10−4 Pa s. Under high magnetic field strength and low particle content, the viscosity of both kinds of magnetic fluid decreases. Clearly, the viscosities of MSiNP magnetic fluids are 4.8 times (10 wt%) and 4.2 times (20 wt%) higher than the Fe3O4 magnetic fluid under zero field. The maximum viscosities are 8 times for 10 wt% MSiNPs and 25 times for 20 wt% MSiNPs compared to the Fe3O4 magnetic fluid. On the basis of the above results, it could be concluded that the MSiNP suspension presented better MR effects than the Fe3O4 based magnetic fluid.
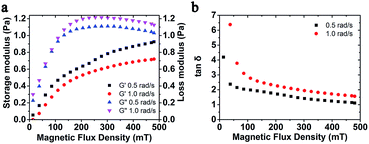 | ||
| Fig. 3 (a) Storage modulus and loss modulus; (b) loss factor versus magnetic flux density with different frequency. The weight fraction of MSiNPs is 20 wt%. | ||
The normal force as a function of magnetic flux density is shown in Fig. 3d. The MSiNP suspension imposes a drawing force to the upper plate. With increasing of the magnetic field, the particle–particle attraction was enhanced, thus the absolute value of normal force increased. Under the high shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 100 s−1), the absolute value of normal force unusually decreased because the rupture speed of chain-like structure was greater than the forming speed.
= 100 s−1), the absolute value of normal force unusually decreased because the rupture speed of chain-like structure was greater than the forming speed.
Moreover, the storage modulus and loss factor of MSiNP suspension with different frequency was studied (Fig. 3). In the absence of the magnetic field, the storage modulus was around zero, which demonstrated a Newtonian fluid feature. Upon increasing the magnetic field, the storage modulus increased while the loss modulus first increased and then decreased. The loss factor was always larger than 1, which claimed that the magnetic material always mainly possessed the fluid property. The decreasing loss factor also revealed an increasing visco-elastic character of the MSiNP suspension.
Structural evolution of the MSiNP suspension in the stationary state
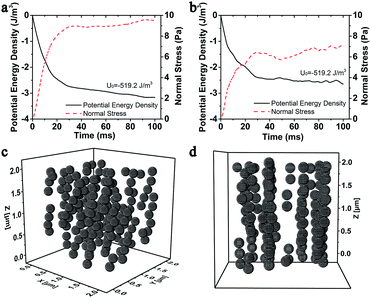
It was widely accepted that the magnetic particles assembled to form chain-like structures under applying the external magnetic field. Here, the magnetically dependent structure evolution of the MSiNPs in the magnetic fluid was investigated by the molecular dynamic simulations. Fig. 4 showed the magneto-induced microstructures of MSiNP suspension (20 wt%) in a steady magnetic field (B = 240 mT). The edge length of the simulation box was 2 μm. Firstly, the MSiNPs randomly dispersed in the initial simulation box. Then, a steady magnetic field was applied. 20 ms later, a lot of short chain-like microstructures were formed quickly. These short chains came from their neighboring particles. When the time was further prolonged, long chain-like particulate structure was formed with the particle–particle and chain–chain interaction proceeding. Finally, more stable chain-like structures and column-like structures were constructed (100 ms).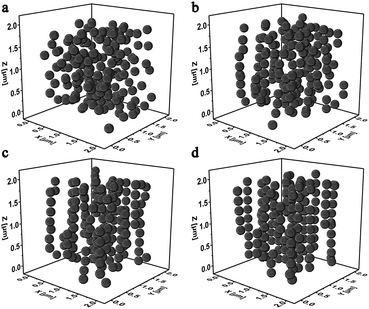 | ||
| Fig. 4 Evolution of the microstructures in 20 wt% MSiNP magnetic fluid at 0 ms (a), 20 ms (b), 50 ms (c), and 100 ms (d). | ||
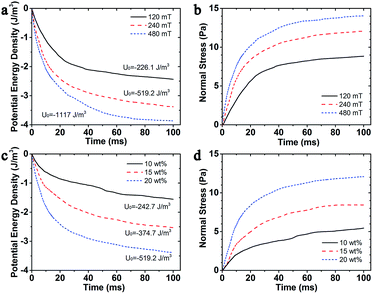
It is also significant to know the change regularity of the microstructures that depends on the magnetic potential energy and normal stress, after applying the external magnetic field. In this simulation, the magnetic fields were set as B = 120 mT, 240 mT, and 480 mT which could be achieved by adjusting the current in the electromagnetic device of the rheometer (Physica MCR 301) as 0.5 A, 1.0 A, and 2.0 A correspondingly. Fig. 5a showed the influence of magnetic field on the magnetic potential energy density of the MSiNP magnetic fluid. When the magnetic flux density B was set as 120 mT, 240 mT, and 480 mT, the initial transient values of energy density were −226.1 J m−3, −519.2 J m−3, and −1117 J m−3, respectively. In the incipient 20 ms, the energy density sharply dropped down. Meanwhile, the very complex magneto-mechanical coupling process appeared. After the simulation was launched, the magnetic potential energy gradually decreased from 20 ms to 80 ms, and more stable magneto-induced microstructures were achieved. Finally, when the time was beyond 80 ms, the energy density dropped to the steady value. The stronger the magnetic field, the larger the magnetic potential energy dropped and the lower energy was. In Fig. 5b, it can be seen that the normal stress grew fast in the earliest 20 ms and gradually approached the stable value. Clearly, the mechanical properties of the MSiNP suspension presented a typical magneto-controllable performance.
Fig. 5c and d showed the evolution of magnetic potential energy density and normal stress of MSiNP magnetic fluid with different weight fractions (B = 240 mT). It can be found that the higher weight ratio of the MSiNPs led to a lower potential energy and a larger normal force. The initial transient step drops were −242.7 J m−3, −374.7 J m−3, and −519.2 J m−3, related to weight fractions 10 wt%, 15 wt%, and 20 wt%, respectively. Furthermore, the saturated normal stress of magnetic fluid also increased with weight fraction and then reached 5.5 Pa, 8.4 Pa, and 12.1 Pa, respectively.
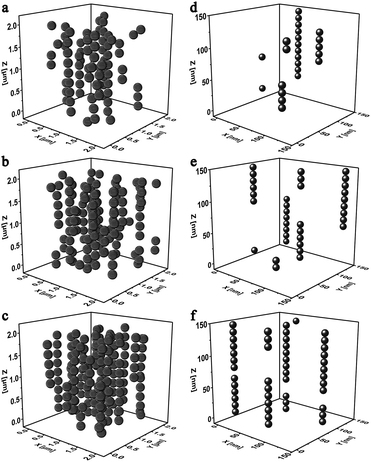
Fig. 6a–c showed the influence of the MSiNP weight fractions on the assembling microstructures in a steady magnetic field (B = 240 mT). When the particle content was 10 wt%, short and long chains both existed in the simulation box, while they were separated from each other. Meantime, some individual MSiNPs were found without attaching with each other. If the weight fraction increased to about 15 wt%, long chains were mainly presented in the particulate structures, and few isolated particles appeared in the cubic box. Finally, for 20 wt% MSiNP magnetic fluid, all the particles were within the chain structures. With increasing of the particle number, some short chains joined the long chains and formed column-like structures.
The microstructures of pure Fe3O4 magnetic fluid were also simulated (Fig. 6d–f). The computation box was shrunk into 150 nm edge length in proportion. Similarly, when the low weight fraction was low, only short and scattered chain-like structures were formed. In this case, the magnetic particles merely had weak interactions among each other. Lateral attraction among particle chains and weak friction between particles and carrier fluid led to low viscosity.
In this work, the stable MSiNPs were constructed by the inner solid SiO2 spherical core and the Fe3O4 nanoparticles shell. After imposing the external magnetic field, the MSiNPs formed chain-like structures. Because the magnetic Fe3O4 nanoparticles locate at the outer layer, they are very easily to interact with Fe3O4 nanoparticles on other MSiNPs. According to eqn (7), the attraction force is proportional to the biquadrate of rij. The Fe3O4 nanoparticles in one MSiNP also attract each other, and the attraction further guarantees the stability of the MSiNPs. Under the same Fe3O4 weight fraction, the core–shell structures of the MSiNPs reduce the separation distance among Fe3O4 particles and enlarge the average length of chain-like structures. Consequently, the friction effect between microstructures and the matrix fluid is enhanced. The above two reasons lead to the higher viscosity and MR effect of MSiNP magnetic fluid.
Structural dependent magnetorheology of the MSiNP suspension in the steady shear flow
The magneto-induced microstructures change dramatically in the incipience of a steady magnetic field. The magneto-induced microstructures under the steady shear flow become another important point in this work. Fig. 7a and b showed the normal stress and magnetic potential energy as a function of time, in which the shear rate was applied along the x-axis. Here, the weight fraction of MSiNPs was 20 wt%, the external magnetic field was set as B = 240 mT, and the shear rates were 10 s−1, 25 s−1, and 50 s−1, respectively. Different from the static occasion, after the incipient prominent change in 20 ms, both potential energy density and magneto-induced normal stress approached the stable value during an undulate process. The larger the shear rate, the smaller the variation range of magnetic potential energy and normal stress. Moreover, the evident undulate performance was found in the larger shear rates.Fig. 7c and d showed the isometric view and x-axis view of the microstructures of 20 wt% MSiNP magnetic fluid at 100 ms in which the shear rate is ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 40 s−1. Under the steady shear flow, the chain-like and column-like structures inclined towards the shear direction. Then, the internal microstructures were rapidly broke up and reformed. Finally, lamellar structures parallel to the z–x plane were formed. The inclination resulted in larger intervals among magnetic particles and finally led to smaller magneto-induced normal stresses and smaller variations of the magnetic energy densities. As the shear rate increased, the inter-particle attraction along the direction of z-axis was weakened.
= 40 s−1. Under the steady shear flow, the chain-like and column-like structures inclined towards the shear direction. Then, the internal microstructures were rapidly broke up and reformed. Finally, lamellar structures parallel to the z–x plane were formed. The inclination resulted in larger intervals among magnetic particles and finally led to smaller magneto-induced normal stresses and smaller variations of the magnetic energy densities. As the shear rate increased, the inter-particle attraction along the direction of z-axis was weakened.
Besides the structure transformation, the mechanical properties such as the magneto-induced shear stress also could be estimated by using the molecular dynamic simulations. The simulated magneto-induced shear stress of 20 wt% MSiNP suspension in the shear rate sweep was plotted in Fig. 8a. The simulated shear stress employed here was the average value from the first time shear stress declined with the increasing shear strain to the end of the simulation. After start-up of the flow, shear stress approximately linearly increased with shear strain, which manifested that the magnetic fluid had not reached the viscous flow region.2 The magneto-induced shear stresses were influenced by the magnetic attraction forces among particles and the decline angle of particle chains. The shear stress increased as the shear rate increased. Computational results were in agreement with experiments in tendency. More work will be done for the data accuracy. Fig. 8b showed the magnetic field sweep magneto-induced shear stress of 20 wt% MSiNP magnetic fluid at a shear rate of 50 s−1. Clearly, the viscosity increased with the magnetic field, which indicated a typical MR effect. The calculation results matched quite well with the experimental results. Based on the above results, it can be concluded that the present particle-level simulation was effective for describing the magnetorheology of the MSiNP suspension.
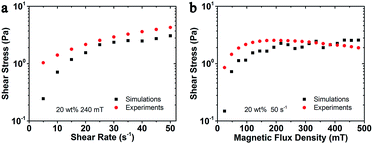 | ||
| Fig. 8 Magneto-induced shear stress comparison between simulated and experimental results of MSiNP magnetic fluid. (a) Shear rate sweep; (b) magnetic field sweep. | ||
Conclusions
In this work, the magnetorheology of a novel MSiNP suspension was systematically investigated by using a combining experimental and numerical method. Due to the unique core–shell nanostructure, the MSiNP suspension possessed a higher MR effect than the pristine Fe3O4 magnetic fluid. The oscillation shear test revealed that the MSiNP suspension transformed from Newtonian fluid to a viscoelastic material as the magnetic field exceeded the saturation value.Molecular dynamics simulations were carried out to study the relationship between the microstructures and mechanical properties of MSiNP suspension. Both the stationary flow field and steady shear flow were used in the simulation. When the magnetic fluid was placed into a uniform magnetic field, the MSiNP magnetic particles formed short chain-like structures quickly, followed by long chain-like structures along the direction of the external magnetic field. When the magnetic fluid was subjected to a steady shear flow, the magneto-induced interior microstructures tilted along the shear direction and formed a layered structure parallel to the plane consisting z-axis and x-axis. In the meantime, the magnetic potential energy and stress state varied rapidly at the inception. Then they gradually approached the stable values in the steady state while fluctuated in a dynamic balance in the steady shear flow. In comparison to the internal structures of pristine Fe3O4 magnetic fluid, the MSiNPs had larger attraction force among particles. The simulation results agreed well with the experiments, which would be favorable for predicting the mechanical properties in the application and for analyzing the MR mechanism in the fundamental research.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11572309 and 11572310). Financial supports from the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB22040502) and the Fundamental Research Funds for the Central Universities (WK2480000002) are gratefully acknowledged. This work was also supported by Collaborative Innovation Center of Suzhou Nano Science and Technology.References
- L. Vekas, Adv. Sci. Technol., 2009, 54, 127–136 CrossRef.
- J. de Vicente, D. J. Klingenberg and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 3701–3710 RSC.
- S. Kayal, D. Bandyopadhyay, T. K. Mandal and R. V. Ramanujan, RSC Adv., 2011, 1, 238–246 RSC.
- R. A. Bohara, N. D. Thorat, A. K. Chaurasia and S. H. Pawar, RSC Adv., 2015, 5, 47225–47234 RSC.
- Y. M. Wang, X. Cao, G. H. Liu, R. Y. Hong, Y. M. Chen, X. F. Chen, H. Z. Li, B. Xu and D. G. Wei, J. Magn. Magn. Mater., 2011, 323, 2953–2959 CrossRef CAS.
- W. H. Li, X. Z. Zhang and X. Y. Wang, Adv. Mater. Res., 2008, 47, 157–160 Search PubMed.
- W. H. Li and H. Du, Int. J. Adv. Manuf. Tech., 2003, 21, 508 CrossRef.
- S. Kaluvan and S. B. Choi, Smart Mater. Struct., 2014, 23, 127003 CrossRef.
- L. Rodriguez-Arco, I. A. Rodriguez, V. Carriel, A. B. Bonhome-Espinosa, F. Campos, P. Kuzhir, J. D. G. Duran and M. T. Lopez-Lopez, Nanoscale, 2016, 8, 8138–8150 RSC.
- V. Skumryev, S. Stoyanov, Y. Zhang, G. Hadjipanayis, D. Givord and J. Nogues, Nature, 2003, 423, 850–853 CrossRef CAS PubMed.
- H. T. Pu, F. J. Jiang and Z. L. Yang, Mater. Chem. Phys., 2006, 100, 10–14 CrossRef CAS.
- R. C. Bell, E. D. Miller, J. O. Karli, A. N. Vavreck and D. T. Zimmerman, Int. J. Mod. Phys. B, 2007, 21, 5018–5025 CrossRef CAS.
- S. Lee, K. Y. Shin and J. Jang, Nanoscale, 2015, 7, 9646–9654 RSC.
- F. Vereda, J. P. Segovia-Gutierrez, J. de Vicente and R. Hidalgo-Alvarez, J. Phys. D: Appl. Phys., 2015, 48, 015309 CrossRef.
- R. Q. Lv, Y. Zhao, N. Xu and H. Li, J. Magn. Magn. Mater., 2013, 337, 23–28 CrossRef.
- M. Sedlacik and V. Pavlinek, RSC Adv., 2014, 4, 58377–58385 RSC.
- A. Gómez-Ramirez, M. T. Lopez-Lopez, F. González-Caballero and J. D. G. Duran, Smart Mater. Struct., 2011, 20, 045001 CrossRef.
- K. Shah and S. B. Choi, Smart Mater. Struct., 2015, 24, 015004 CrossRef CAS.
- I. G. Kim, K. H. Song, B. O. Park, B. I. Choi and H. J. Choi, Colloid Polym. Sci., 2011, 289, 79–83 CAS.
- A. Katiyar, A. N. Singh, P. Shukla and T. Nandi, Powder Technol., 2012, 224, 86–89 CrossRef CAS.
- S. Lee, K. Y. Shin and J. Jang, Nanoscale, 2015, 7, 9646–9654 RSC.
- A. J. Margida, K. D. Weiss and J. D. Carlson, Int J Mod Phys B, 1996, 10, 3335–3341 CrossRef CAS.
- H. T. Pu and F. J. Jiang, Nanotechnology, 2005, 16, 1486–1489 CrossRef CAS.
- D. S. Jang, Y. D. Liu, J. H. Kim and H. J. Choi, Colloid Polym. Sci., 2015, 293, 641–647 CAS.
- M. Cvek, M. Mrlik, M. Ilcikova, J. Mosnacek, V. Babayan, Z. Kucekova, P. Humpolicek and V. Pavlinek, RSC Adv., 2015, 5, 72816–72824 RSC.
- F. F. Fang, Y. D. Liu and H. J. Choi, Colloids Surf., A, 2012, 412, 47–56 CrossRef CAS.
- S. A. N. Leong, P. M. Samin, A. Idris, S. A. Mazlan and A. H. A. Rahman, Smart Mater. Struct., 2016, 25, 025025 CrossRef.
- O. Gerber, B. P. Pichon, C. Ulhaq, J. M. Greneche, C. Lefevre, I. Florea, O. Ersen, D. Begin, S. Lemonnier, E. Barraud and S. Begin-Colin, J. Phys. Chem. C, 2015, 119, 24665–24673 CAS.
- I. Arief and P. K. Mukhopadhyay, J. Magn. Magn. Mater., 2014, 360, 104–108 CrossRef CAS.
- H. S. Jung and H. J. Choi, J. Appl. Phys., 2015, 117, 17E708 CrossRef.
- R. V. Upadhyay, Z. Laherisheth and K. Shah, Smart Mater. Struct., 2014, 23, 015002 CrossRef.
- K. Jain, S. Pathak and R. P. Pant, RSC Adv., 2016, 6, 70943–70946 RSC.
- H. J. Choi, W. L. Zhang, S. Kim and Y. Seo, Materials, 2014, 7, 7460–7471 CrossRef.
- Y. J. Kim, Y. D. Liu, Y. Seo and H. J. Choi, Langmuir, 2013, 29, 4959–4965 CrossRef CAS PubMed.
- W. J. Ahn, H. S. Jung and H. J. Choi, RSC Adv., 2015, 5, 23094–23100 RSC.
- W. H. Li, H. Du and N. Q. Guo, Int. J. Adv. Manuf. Tech., 2003, 21, 438–445 CrossRef.
- E. Gedik, H. Kurt, Z. Recebli and C. Balan, Comput. Fluids, 2012, 63, 128–134 CrossRef.
- M. Aoshima and A. Satoh, J. Colloid Interface Sci., 2005, 288, 475–488 CrossRef CAS PubMed.
- T. X. Liu, X. L. Gong, Y. G. Xu, S. H. Xuan and W. Q. Jiang, Soft Matter, 2013, 9, 10069–10080 RSC.
- Z. Wang, K. Shahrivar and J. de Vicente, J. Rheol., 2014, 58, 1725–1750 CrossRef CAS.
- J. C. Fernandez-Toledano, J. Rodriguez-Lopez, K. Shahrivar, R. Hidalgo-Alvarez, L. Elvira, F. M. de Espinosa and J. de Vicente, J. Rheol., 2014, 58, 1507–1534 CrossRef CAS.
- J. P. Segovia-Gutierrez, J. de Vicente, R. Hidalgo-Alvarez and A. M. Puertas, Soft Matter, 2013, 9, 6970–6977 RSC.
- Y. W. Zhang, M. Zhang, L. Ding, Y. T. Wang and J. L. Xu, Nanoscale Res. Lett., 2016, 11, 1–7 CrossRef PubMed.
- E. E. Keaveny and M. R. Maxey, J. Comput. Phys., 2008, 227, 9554–9571 CrossRef.
- D. J. Klingenberg, C. H. Olk, M. A. Golden and J. C. Ulicny, J. Phys.: Condens. Matter, 2010, 22, 324101 CrossRef CAS PubMed.
- S. Melle, O. G. Calderon, M. A. Rubio and G. G. Fuller, J. Non-Newtonian Fluid Mech., 2002, 102, 135–148 CrossRef CAS.
- H. G. Lagger, T. Breinlinger, J. G. Korvink, M. Moseler, A. Di Renzo, F. Di Maio and C. Bierwisch, J. Non-Newtonian Fluid Mech., 2015, 218, 16–26 CrossRef CAS.
- T. X. Liu, R. Gu, X. L. Gong, S. H. Xuan, H. A. Wu and Z. Zhang, Magnetohydrodynamics, 2010, 46, 257–269 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |