Open Access Article
Open Access ArticlePositron annihilation studies and complementary experimental characterization of xAg2O–(1 − x)(0.3CdO–0.7MoO3) metal oxide glass nanocomposites†
Ranadip Kundu‡
 *a,
Sanjib Bhattacharyab,
Debasish Roya and
P. M. G. Nambissanc
*a,
Sanjib Bhattacharyab,
Debasish Roya and
P. M. G. Nambissanc
aDepartment of Mechanical Engineering, Jadavpur University, Jadavpur, Kolkata 700032, India. E-mail: debasish_kr@yahoo.co.in
bDepartment of Engineering Sciences and Humanities, Siliguri Institute of Technology, Darjeeling 734009, West Bengal, India. E-mail: sanjib_ssp@yahoo.co.in
cApplied Nuclear Physics Division, Saha Institute of Nuclear Physics, Kolkata 700064, India. E-mail: pmg.nambissan@saha.ac.in
First published on 23rd January 2017
Abstract
Metal oxide nanocomposites of the composition xAg2O–(1 − x)(0.3CdO–0.7MoO3) were prepared by a melt-quenching method and were characterized by different experimental techniques like X-ray diffraction, high resolution transmission electron microscopy and optical absorption spectroscopy. X-ray diffraction showed sharp diffraction peaks indicating large crystallites but transmission electron microscope images also showed crystallites of nanometer dimensions in appreciable concentrations, which confirmed the nanocomposite structure of the samples. Although the lattice constants did not show significant changes with the increase in concentration (x) of Ag2O, there is considerable relaxation of the growth-induced strain above x = 0.2. Interestingly this is also the concentration above which the optical band gap energy showed a mild decrease. One salient feature of this study is the use of positron annihilation spectroscopy for identifying and monitoring the structural defects such as vacancies and vacancy clusters as well as the free volume cavities during the change in concentration of Ag2O. Positron lifetime measurements indicated trapping of positrons initially in the interfacial defects within the 0.3CdO–0.7MoO3 nanocrystalline ensemble and then in the free volume defects within the amorphous Ag2O matrix. At higher Ag2O concentrations, positron trapping appeared to take place within the Cd2+-monovacancies in CdO and in the divacancies of neighbouring cationic and oxygen monovacancies in the α-MoO3 and CdMoO4 nanocrystallites. At x = 0.1–0.2, the effective positron trapping centres are translocated to the tetrahedral Mo6+-monovacancies instead of the Cd2+-monovacancies. The results of coincidence Doppler broadening spectroscopic measurements, which map the electron momentum distribution and its variations, indicated increasing trapping of positrons with increasing concentration of Ag2O, which again is attributed to the trapping sites in the increasing number of nanocrystallites being formed.
1. Introduction
Metal oxide based glass nanocomposites and other similar materials have gained popular importance in recent years as the discovery of nanocrystalline properties of materials have opened up new avenues of research. Of particular interest is the tunability of such materials with the introduction of substituted elements that can enhance or modify their physical and other properties to the extent of adaptability in technological applications. Glassy systems and their nanocomposites are of special interest and focus in this context as they cater to a wide range of applications such as solid state batteries and sensors.1,2 Understanding their properties and the factors affecting their variations under different thermodynamic and experimental conditions is therefore really important. In this context, we report here the results of a very recent study on the electronic and stoichiometry-related properties of a glass nanocomposite consisting of Ag2O and 0.3CdO–0.7MoO3 in different proportions with a general nomenclature xAg2O–(1 − x)(0.3CdO–0.7MoO3). The variational parameter x had values starting from 0.0 to 0.9. Altogether seven samples have been studied and the modifications of the structure and properties have been investigated.The findings from conventional experimental techniques like Fourier transform infra-red (FTIR) and UV-Vis absorption spectroscopies are also often complemented and supported by characterization tools like X-ray diffraction (XRD) and high resolution transmission electron microscopy (HRTEM). However, there are bigger challenges like the deviation of measured electrical conductivity from the theoretically expected ones and the modifications of thermal properties which needed deeper understandings and evaluation. Of special emphasis are the defects and defects-related properties and processes that may as well undergo evolution with the variations of the concentrations of the constituents in the composition of the nanocomposites. Positron annihilation spectroscopy is a versatile non-destructive defect spectroscopic probe that has been increasingly applied in the investigation of the defects in nanomaterials and nanocomposites.3–5 Positron lifetime (PL) measurements as well as coincidence Doppler broadening spectroscopy (CDBS) were performed on the seven samples and the results are discussed.
2. Experimental details
The samples were prepared through a chemical mixing process using reagent grade chemicals AgNO3, CdO and α-MoO3. Depending upon the molar fraction x of the Ag2O part in the stoichiometric composition, calculated amounts of the reagents have been accurately weighed and taken in an alumina crucible and thoroughly mixed and preheated. (See ESI I.†) The mixtures were then melted in an electric furnace in the temperature range from 900 °C to 950 °C depending upon the composition. The melts were equilibrated for 30 minutes and then quenched between two aluminum plates. In this manner, glass-nanocomposites of thickness ∼ 1 mm have been obtained for x = 0.0 (without AgNO3)–0.9. For experiments in the powder form of the samples, the plates so formed are gently crushed in an agate mortar and filtered through a 100 μm sized mesh.X-ray diffraction (XRD) patterns of the samples were recorded using CuKα radiation (wavelength 1.54 Å) in a rotating anode Rigaku TTRAX-III X-ray diffractometer. Scanning is done from 2θ = 10° to 80° through steps of 0.02° with a scanning speed of 4° per minute. The presence and distribution of the nanocrystallites have been confirmed from the HRTEM images taken using 300 keV electrons (FEI, Tecnai, F30-ST). UV-Vis absorption studies were made in the reflection mode using PerkinElmer Lamda-750 spectrophotometer. The colloidal suspensions using ethanol as solvent for the absorption studies were prepared with the help of an ultrasonic homogenizer (Takashi SK-500F).
For positron annihilation studies, the fine powdered sample is taken in a glass tube and a radioactive isotope decaying by β+-emission is kept embedded in it at the geometrical centre of the column. The source in fact is a 22NaCl deposition on a thin (∼2 mg cm−2) Ni foil and covered by the extended portion of the foil folded along a line away from the source-deposited area. Prior to the source deposition, the Ni foil had been annealed at 1050 °C for 2 hours in good vacuum (∼10−6 mbar). The powdered sample is ensured to cover the source from all sides in thicknesses sufficient to capture and annihilate all the positrons within it and none of them reached the glass walls. Further, the glass tube is continuously evacuated to remove the air and absorbed gases from the powder column and to allow the particles to settle down under their own weight. In this way, the sample and the source assembly is made compact and maintained at dry and moisture-free conditions. The positron emission and annihilation gamma rays are captured using nuclear radiation detectors and processed by standard gamma–gamma coincidence circuits, comprising of nuclear electronic modules.4 Special mentions are to be made of the detectors used for the detection process. For positron lifetime measurements, BaF2 scintillators coupled with fast XP2020Q photomultiplier tubes were used. The slow-fast gamma–gamma coincidence spectrometer which incorporated these detectors and the associated nuclear electronic modules had a time resolution of 180 ps when measured with the nuclear gamma rays from a 60Co radioactive isotope kept under the 22Na experimental energy window settings. For CDBS studies, two high pure germanium (HPGe) detectors with energy resolutions ∼ 1.27 keV at the annihilation gamma ray energy 511 keV are used. The data were collected with sufficiently high statistics (∼106 and 107 counts or events under each PL and CDB spectra respectively) and the electronic stability had been extremely good. The positron lifetime spectra were analyzed using the program PALSfit.6 The software LAMPS developed by Pelletron Division, Tata Institute of Fundamental Research, Mumbai7 was used in the CDBS data acquisition, storage and analysis.
3. Results and discussion
3.1. X-ray diffraction
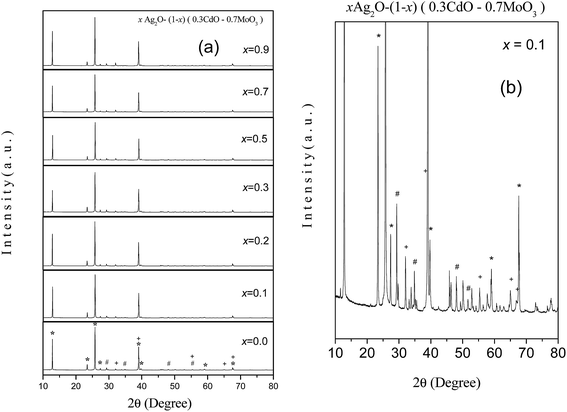
The XRD patterns of the synthesized nanocomposite samples are shown in Fig. 1(a). All the spectra displayed sharp well-defined peaks and the identification of the different diffraction peaks had been carried out by a careful comparison with the available literature data of CdO (ICDD PDF: 75-0594) and α-MoO3 (ICDD PDF: 05-0508). As reported by Usharani et al.,8 Stoyanova et al.9 and Alsaif et al.,10 the sharp peaks at 2θ = 12.85°, 27.38° and 39.05° emerge due to the diffraction from the (0 2 0), (0 4 0) and (0 6 0) planes of the large number of crystallites preferentially oriented in these planes in a lamellar configuration. Whereas, the peak of the maximum intensity corresponding to the (1 1 1) plane of CdO appears at 2θ = 32.08° and that of the (1 1 0) plane of α-MoO3 makes its presence visible at 2θ = 23.41°. There are however a number of additional diffraction peaks which lay partially hidden due to the prominent intensities of the (0 2 0), (0 4 0) and (0 6 0) peaks and they are shown magnified in Fig. 1(b). These peaks are observed at 2θ = 29.27°, 35.04°, 48.14° and 51.80° and identified as the (1 1 2), (2 0 0), (1 2 3) and (2 2 0) peaks of cadmium molybdate (CdMoO4) (ICSD #084455), having a tetragonal scheelite-type structure with space group I41/a and composed mainly of CdO8 octahedra and MoO4 tetrahedra.11,12 The procedure of synthesis adopted in this work seemed to have given favourable thermodynamic conditions for the formation of this phase, albeit unexpectedly. A still deeper scrutiny of the diffraction patterns also revealed very small peaks at 2θ = 33.82°, 55.35°, 65.03° and 77.65°, which were identified as due to the (1 1 1), (2 2 0) and (3 1 1) planes of Ag2O (ICDD PDF: 00-065-6811) and (3 1 1) plane of Ag (ICDD PDF: 00-004-0783). Since the intensities of these peaks are found extremely low, they are not considered for further discussion.The results of XRD analysis did not indicate considerable widths for the peaks and it demonstrated the coarse dimensions (dc) of the large crystallites. The Scherrer equation13
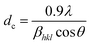 | (1) |
The lattice constants of the crystallites of CdO, α-MoO3 and CdMoO4 have also been calculated by considering the respective structure as reported in literature and the identification of the positions of the X-ray diffraction peaks from Fig. 1. The results are summarized in Table 1. No significant variations are observed in the lattice constants. This is interesting especially in the context of a number of reports on the size-dependent lattice parameter changes in a number of metal oxide nanocrystalline systems.14 The co-existence of three chemically stable metal oxides with homogenous distribution and forming a glass-like matrix could have resulted into the mutual annulment of the changes in this case.
| Concentration of Ag2O (x) | a (Å) | b (Å) | c (Å) |
|---|---|---|---|
| Crystallite: CdO; most intense peak at 2θ = 33.20°; (h k l) = (1 1 1); structure: fcc; ICDD PDF: 75-0594; reported lattice constant a = 4.686 Å | |||
| 0.0 | 4.668 | ||
| 0.1 | 4.667 | ||
| 0.2 | 4.670 | ||
| 0.3 | 4.672 | ||
| 0.5 | 4.665 | ||
| 0.7 | 4.670 | ||
| 0.9 | 4.670 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Crystallite: α-MoO3; most intense peak at 2θ = 25.79°; (h k l) = (0 4 0), structure: distorted orthorhombic; ICDD PDF: 05-0508; reported lattice constants a = 3.963 Å, b = 13.855 Å, c = 3.696 Å | |||
| 0.0 | 3.950 | 13.804 | 3.680 |
| 0.1 | 3.946 | 13.800 | 3.686 |
| 0.2 | 3.950 | 13.812 | 3.685 |
| 0.3 | 3.953 | 13.818 | 3.692 |
| 0.5 | 3.945 | 13.794 | 3.685 |
| 0.7 | 3.947 | 13.805 | 3.686 |
| 0.9 | 3.948 | 13.806 | 3.687 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Crystallite: CdMoO4; most intense peak at 2θ = 29.30°; (h k l) = (1 1 2); structure: regular orthorhombic; ICSD #084455; reported lattice constants a = 5.155 Å, c = 11.194 Å | |||
| 0.0 | 5.139 | 11.150 | |
| 0.1 | 5.138 | 11.146 | |
| 0.2 | 5.144 | 11.146 | |
| 0.3 | 5.146 | 11.160 | |
| 0.5 | 5.137 | 11.146 | |
| 0.7 | 5.139 | 11.159 | |
| 0.9 | 5.141 | 11.156 | |
We also calculated the lattice strain associated with the formation of the nanocrystallites within the glass matrix. The contribution of the strain to the broadening of the peaks in the XRD patterns of the samples due to crystal imperfections and dislocations is given by
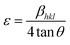 | (2) |
The basic difference between the crystallite size and the induced lattice strain is the nature of their dependency on the diffraction angle 2θ. The crystallite sizes follow 1/cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ variation whereas the strain varies as 1/4
θ variation whereas the strain varies as 1/4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. On the basis of the independent contribution of each other to the peak broadening, the strain is estimated through the Williamson–Hall (W–H) method.15 The total broadening of the peak is written as the sum of contributions of both the effects as
θ. On the basis of the independent contribution of each other to the peak broadening, the strain is estimated through the Williamson–Hall (W–H) method.15 The total broadening of the peak is written as the sum of contributions of both the effects as
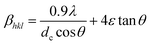 | (3) |
Rearranging the terms, we get
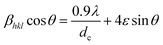 | (4) |
Eqn (4) represents the uniform deformation model where the strain induced by the nanocrystallites is assumed to be uniform. From the linear plot of βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ versus 4
θ versus 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
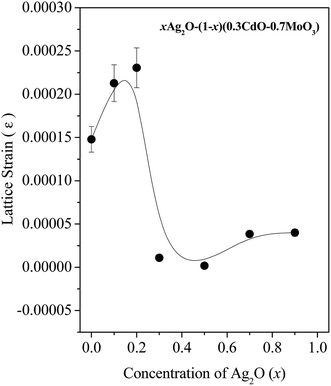
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, the strain is obtained from the slope of the line. (The y-intercept gives the sizes of the nanocrystals, as given by eqn (1).) A plot of the values of the strain thus estimated versus the concentration (x) of Ag2O of the different samples is given in Fig. 2. Although the magnitudes of the strain thus estimated are extremely small, the striking observation of an abrupt discontinuity of the strain at x = 0.2 to 0.3 is worth noting.
θ, the strain is obtained from the slope of the line. (The y-intercept gives the sizes of the nanocrystals, as given by eqn (1).) A plot of the values of the strain thus estimated versus the concentration (x) of Ag2O of the different samples is given in Fig. 2. Although the magnitudes of the strain thus estimated are extremely small, the striking observation of an abrupt discontinuity of the strain at x = 0.2 to 0.3 is worth noting.
3.2. TEM images
The X-ray diffraction peaks had been rather sharp giving doubts to the formation of very large crystallites against the nanocomposite nature that was expected. The crystallite sizes estimated from the Scherrer formula also gave the indications that the crystallites are rather large in sizes and the nanocomposition is not to be expected. For disseminating the ambiguity in this regard, we have also examined the samples through high resolution transmission electron microscopy (HRTEM). The TEM images shown in Fig. 3(a) to (c) showed rod-like structures with average diameters showing a gradual increase from 300 nm to 600 nm in samples of increasing Ag2O content (x) from 0.1 to 0.9. The diameters of these rods are indicated in the images. The corresponding selected area diffraction (SAD) patterns are shown in Fig. 3(d)–(f) respectively from regions marked by the red circles. The SAD patterns confirm the single crystalline nature of the rod-like structures. The lattice images shown in Fig. 3(g)–(i) further confirm the formation of the different solid phases discussed in the previous section. | ||
| Fig. 3 (a)–(c) TEM images of the three samples with x = 0.1, 0.5 and 0.9. (d)–(f) The SAD patterns. (g)–(i) HRTEM images of the samples showing the lattice fringes. | ||
The TEM images also demonstrated that, in addition to the large rod-like single crystals, there are innumerable nanocrystallites too (Fig. 4), the presence of which in fact should have given rise to finite line broadening for the XRD patterns, had the bulk crystallites been absent. These smaller nanocrystallites are sometimes attached to bigger crystals as, for example, reflected in Fig. 3(e) showing polycrystalline-like diffraction pattern. Further, these nanocrystallites are also single crystals and one can observe lattice plane bending etc. in the Fourier-filtered images shown in Fig. 5(a)–(c). They are also found to have defects such as stacking faults and misfit dislocations associated with them.
 | ||
| Fig. 5 (a)–(c) Fourier-filtered images of the regions marked in Fig. 4(g)–(i). | ||
3.3. UV-Vis absorption results
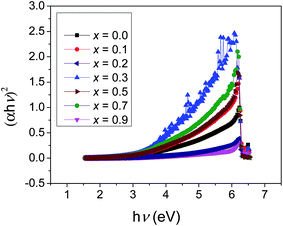
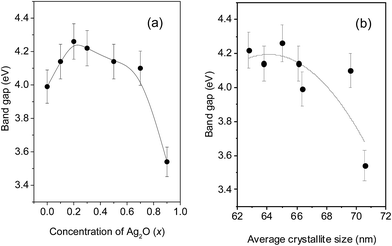
Although different solid phases are found to be formed within the nanocomposites, they also exhibited a cumulative optical behavior which could be examined and quantified in terms of the band gap energies estimated using Tauc's plots.16 The UV-visible absorption spectra of the different samples are shown in Fig. 6. The tangents to the absorption edges were linearly extrapolated to the x-axis in order to calculate the band gap energies from the relation αhν = A(hν − Eg)n where A is a constant and hν is the photon energy. The value of n depends on the nature of transition.16 In this case, n is chosen as 1/2 since both CdO and MoO3 are direct band gap semiconductors and thus the optical band gap energies of the samples are obtained by extrapolating the linear portion of the (αhν)2 vs. hν curve to 0 on the y-axis. The band gap energies thus obtained for the present samples are shown in Fig. 7(a). The initial increase followed by a decrease with increase in concentration x of Ag2O may more have to do with the actual sizes of the nanocrystallites than any compositional dependence.With this prelusion, the band gap was plotted as a function of the combined average of the sizes of the nanocrystallites of the three different phases CdO, α-MoO3 and CdMoO4 and the results are shown in Fig. 7(b). There is a gradual decrease of the band gap with the increase of the crystallite size. It is not possible here to attribute the increase of band gap with the decreasing crystallite size to quantum confinement behavior (weak, intermediate or strong) since the realm of crystallite sizes for the observation of such effects normally is much below, say ∼10 nm or below. For quantum confinement effects to manifest as an increase of the band gap, the nanocrystallite sizes need to be less than the bulk exciton Bohr radius of the material and the large crystallite sizes obtained in the present study will rule out such a possibility. For example, the exciton Bohr radius for CdO has been reported as close to 2.25 nm (ref. 17) and the values for α-MoO3 or CdMoO4, although not readily available in literature, are likely to be of the same order of magnitude. The decreasing band gap within the small range of variation of the crystallite sizes hence can be treated as an “impurity effect” in which additional energy levels are created within the band gap and weak electronic excitations are activated with photons of the corresponding wavelength getting absorbed.
3.4. Positron lifetime studies
The peak-normalized positron lifetime spectra of some of the samples are shown in Fig. 8. Notwithstanding the very small variations in the slopes of the curves, the slow decay nature indicates the presence of extended defects of the vacancy-type in the nanocomposites. In solid systems of nanocrystalline composition, the thermal diffusion of the positrons to the outer surfaces of the crystallites also will greatly influence the annihilation characteristics. In the present case, this may not be a serious issue since the sizes of the nanocrystallites are all well above the thermal diffusion lengths of positrons in oxide materials.18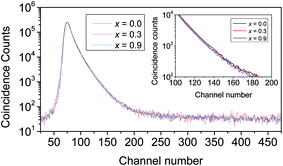 | ||
| Fig. 8 Peak-normalized positron lifetime spectra of some of the samples. The inset shows a zoomed-in portion of the decaying exponential part for the sake of clarity. | ||
The positron lifetime spectra had been analyzed using the PALSfit program to get the different positron lifetimes and their relative intensities.6 The program subtracts a linear background and deconvolutes the resolution function (fitted to a Gaussian) before the necessary source correction (23.75%) is carried out. The source component included the contributions of positrons annihilating within the supporting Ni foil (0.100 ns; 69.83%) and the 22NaCl source material (0.385 ns; 29.62%) and those getting backscattered (1.960 ns; 0.55%). These values were obtained from the analysis of the spectra earlier acquired using the same source with high pure (99.999%) and well-annealed Al single crystals. The best fit (with a reduced chi-square = 1.05 ± 0.15) for the multi exponential decay of the spectra of the glass-nanocomposite samples was obtained for three lifetime components. The longest component τ3 was of relatively small intensities (0.1–6.0%) but its presence could not be ignored for want of a reasonably good fit in the analysis. The results of the analysis are illustrated in Fig. 9(a) and (b).
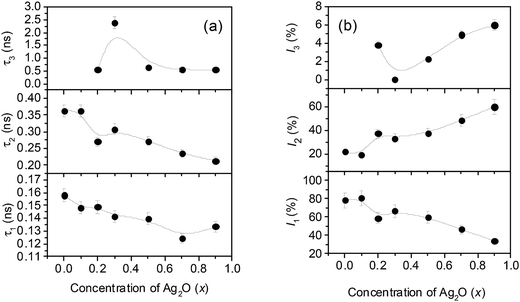 | ||
| Fig. 9 (a) The positron lifetimes and (b) the relative intensities versus the concentration of Ag2O in the samples. | ||
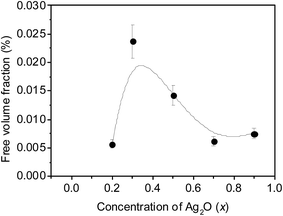
The longest component τ3 is attributed to the formation and eventual annihilation by “pick-off” process of orthopositronium (o-Ps) atoms from the free volume defects of the amorphous Ag2O matrix of the nanocomposites. The presence of this component is of special significance because it directly provides a method to calculate the size and concentration of the free volume defects.19 Also, such amorphous material systems are normally abundant with free volume cavities, whose sizes could vary over a few angstroms.
The question about the origin of the third lifetime τ3 is to be answered first. The well-known Tao–Eldrup equation20,21
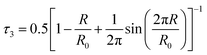 | (5) |
The free volume fraction (fV) is another quantity which is normally estimated for identical systems by using the relation
| fV = CVfI3 | (6) |
The intermediate positron lifetime component τ2 is a parameter of interest in the understanding of the defects present within the nanocomposite system under investigation. Its value 0.363 ns in the initial two samples (i.e., x = 0.0 and 0.1) is attributable only to positron trapping in very large defects like interfacial vacancy clusters within the 0.3CdO–0.7MoO3 nanocrystalline ensemble. At these two extremely low concentrations of Ag2O, strong bondage between the former and the modifier is absent. The subsequent decrease of τ2 by about 0.093 ns is significant as it signals to the formation of the nanocomposite glass due to the development of strong bonding between the α-MoO3 former and the CdO modifier mediated by the presence of Ag2O which acts as a catalyst. As the bonding intensifies, the interfaces that acted as the potential positron trapping sites disappear and positrons instead get trapped into the relatively shallow defects like the negatively charged cationic monovacancies within the nanocrystallites being formed. Thus the decrease of τ2 at x = 0.1–0.2 signifies a translocation of the positron trapping sites from the interfaces to the isolated cationic monovacancy-type defects. As already stated, we could identify from the X-ray diffraction patterns that there are crystallites of CdO, α-MoO3 and CdMoO4 but no reported values of positron lifetimes in these composite phases are available so far. On the other hand, the obtained τ2 values agree with the values available in literature for the cationic vacancies of some of the elements constituting the above mentioned nanocrystallites. For example, Seeger has reported the positron lifetime in neutral cadmium monovacancies (VCd) as 0.256 ns (ref. 23) whereas, for the negatively charged Cd2+-monovacancies 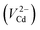 in semiconductors like CdSe and CdTe, the reported positron lifetimes varied as widely as from 0.288 ns to 0.325 ns.3 On the other hand, the positron lifetime in neutral monovacancies in silver is 0.208 ns (ref. 24) while a paper published by Wegner25 suggested 0.180–0.190 ns as the positron lifetime in a silver monovacancy associated with an oxygen ion. Identical extrapolation of these values would then suggest a positron lifetime around 0.235 ns for a Cd2+-monovacancy in CdO. It should be mentioned here that positrons are insensitive to the oxygen vacancies
in semiconductors like CdSe and CdTe, the reported positron lifetimes varied as widely as from 0.288 ns to 0.325 ns.3 On the other hand, the positron lifetime in neutral monovacancies in silver is 0.208 ns (ref. 24) while a paper published by Wegner25 suggested 0.180–0.190 ns as the positron lifetime in a silver monovacancy associated with an oxygen ion. Identical extrapolation of these values would then suggest a positron lifetime around 0.235 ns for a Cd2+-monovacancy in CdO. It should be mentioned here that positrons are insensitive to the oxygen vacancies 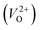 because of the positive charge associated with the latter and they normally get trapped only in neutral or negatively charged vacancies. The values reported for the positron lifetimes in other cationic defects such as Mo or Ag monovacancies are much less, 170 ps and 208 ps respectively. Interestingly, this reference by Campillo Robles and co-workers26 has also quoted the positron lifetime in neutral Cd-monovacancies as 252 ps (experimental). We therefore attribute the decreasing τ2 values in the rest of the samples (i.e., for which x > 0.2) as due to positron trapping in Cd2+-monovacancies as well as in Mo6+-monovacancies. At x = 0.9, the value of τ2 is 0.212 ns, which is close to that reported for the monovacancies in Ag2O.24 This is the sample with the highest concentration of Ag2O and it shows the presence of neutral crystalline monovacancies. Note that the X-ray diffraction data showed well-defined narrow peaks of the Ag2O phase with feeble intensities instead of a broad one, indicating small concentrations of crystalline phases within the Ag2O matrix.
because of the positive charge associated with the latter and they normally get trapped only in neutral or negatively charged vacancies. The values reported for the positron lifetimes in other cationic defects such as Mo or Ag monovacancies are much less, 170 ps and 208 ps respectively. Interestingly, this reference by Campillo Robles and co-workers26 has also quoted the positron lifetime in neutral Cd-monovacancies as 252 ps (experimental). We therefore attribute the decreasing τ2 values in the rest of the samples (i.e., for which x > 0.2) as due to positron trapping in Cd2+-monovacancies as well as in Mo6+-monovacancies. At x = 0.9, the value of τ2 is 0.212 ns, which is close to that reported for the monovacancies in Ag2O.24 This is the sample with the highest concentration of Ag2O and it shows the presence of neutral crystalline monovacancies. Note that the X-ray diffraction data showed well-defined narrow peaks of the Ag2O phase with feeble intensities instead of a broad one, indicating small concentrations of crystalline phases within the Ag2O matrix.
It is worth pointing out that metal oxide nanocrystallites are not in general free of vacancy-type defects. These defects are inherent characteristics of any metallic oxide (MmOn) system. Maintenance of an exact stoichiometry of the metal and oxygen is seldom observed and they may be actually described as Mm−aOn−b where the deviations a and b vary over a few tens to hundreds parts per million (ppm). Positrons are known to undergo saturation trapping if only the defect concentrations exceed 1020 cm−3 which, for example, is about 103 ppm in CdO.3 The unoccupied lattice sites constitute a defect concentration less than this limit and such vacancies are also responsible for the trapping and annihilation of positrons. These vacancies are perhaps inherently built up in the nanocrystallites in order to give them a certain degree of stability and such non-stoichiometric vacancies have been identified as major defect sites in several oxide nanocrystalline systems that have been investigated by a large number of research groups.27–29
It should be additionally noted that, in such ionic compounds, the vacancy type defects can have electrical charges associated with them. A metallic ion is positive and hence the vacancy generated by its absence will be negatively charged. Positrons will be effectively and efficiently trapped by them. Contrary to this, an oxygen vacancy will be having a positive charge and hence the positrons, which are positively charged particles, cannot be trapped by the oxygen vacancies. Then there is the possibility of a divacancy. In this case, the divacancy being created by the absence of a metallic ion and its immediate neighboring oxygen ion, the two opposite charges nullify each other and the divacancy becomes electrically neutral. Positrons can be still trapped and one gets a characteristic positron lifetime corresponding to it. Hence the second positron lifetime component τ2 can be safely attributed to vacancy type defects within the nanocrystallites.
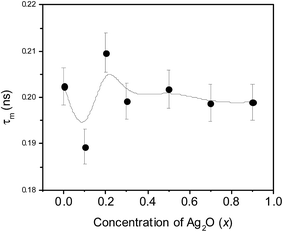
The shortest lifetime τ1 is a result of positron annihilation in bulk material and reduced by the free-state residence time of the trapped positrons.30,31 In the case of the two samples of x = 0.0 and 0.l where the positron lifetime spectra yielded only two components and in the spectra of the sample with x = 0.3, in which the intensity I3 was just 0.1%, we applied the two-state trapping model31 to calculate the positron lifetime within a possible “bulk” glass crystallite and it emerged in the range 0.170–0.180 ns. In the rest of the samples, the model did not exactly reproduce the bulk positron lifetime and hence the original scheme of analysis with a distinct τ3 and I3 is retained. Still, in all the cases, there is a contribution of the trapped positrons, whose lifetimes are defect-specific and which will vary according to their sizes and locations. In order to make this discussion complete, we are presenting in Fig. 11 the variation of the mean positron lifetime τm defined as
| τm = (τ1I1 + τ2I2 + τ3I3)/(I1 + I2 + I3) | (7) |
The features exhibited by this parameter is supportive of the previous interpretations with respect to positron trapping being translocated to the vacancy-type defects within the nanocrystallites rather than at the interfaces at higher Ag2O concentrations, especially at x > 0.3.
3.5. Coincidence Doppler broadening spectroscopic studies
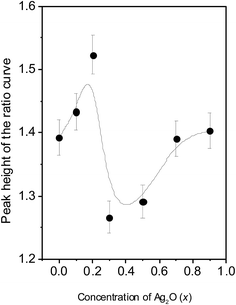
The electron momentum distributional variations reflected in the events of positrons annihilating with electrons localized at different atomic orbits are studied using the coincidence Doppler broadening measurement procedure described by Asoka-Kumar et al.32 and widely used by other researchers.33 The ratio curves generated for the different samples with respect to pure and well-annealed Al single crystals are presented in Fig. 12. The characteristic peak at the longitudinal component of the electron momentum (pL) at ∼10 × 10−3m0c comes from positron annihilation by the 2p electrons of oxygen ions. This means the annihilation events contributing to this peak are due to those positrons which are getting trapped at the vacancies created by the absence of the metallic ions at some of the lattice sites within the crystallites. To sense the changes in the cationic distribution, the positrons are to be localized at the oxygen vacancies, which however is not possible due to the Coulomb repulsion faced by positrons. The position of the peak did not show any shift with changes from sample to sample (Fig. 12), indicating that the elemental surroundings around the positron trapping defects remained oxygen throughout. However, the amplitudes (heights) of the peak shown in Fig. 13 are found to vary in a manner that exhibited a strong correlation with that of the positron lifetimes and intensities (Fig. 9(a) and (b)). Increased annihilation with the electrons of oxygen when the concentration (x) of Ag2O increased systematically is the overall trend; however, a characteristic discontinuity at x = 0.2–0.3 is remarkable and seems to indicate a sudden change of the sites of positron trapping to one with reduced number of coordinated O2− ions. As explained earlier, it comes from the annihilation of positrons in the free volume defects of the Ag2O matrix, then in the interfaces and finally in the cationic vacancies within the nanocrystallites formed.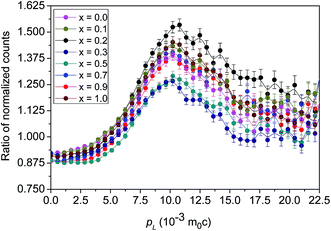 | ||
| Fig. 12 The CDBS ratio curves of the different samples with respect to single crystalline Al. The curve for pure Ag2O (x = 1.0) is also shown. | ||
In order to explain it further, we note that the gradually rising trend of the peak heights of the CDBS ratio curves is indicative of the enhancing annihilation of positrons with the 2p electrons of oxygen. This is possible with the increasing formation of the CdMoO4 phase when the concentration (x) of Ag2O is increased. Earlier, in a similar study by Bar et al. on the xCuI–(1 − x)(0.5CuO–0.5MoO3) glass-nanocomposite systems with different values of x, it had been demonstrated that the density of distribution of CuMoO4 nanoparticles increased with the increase of CuI content.34 A similar thermodynamic condition is prevalent in the present investigation too in which Ag2O is playing a strong catalytic role in the formation of the CdMoO4 nanocrystallites and these in turn happen to act as very strong trapping centres for positrons. The discontinuity manifesting as an abrupt fall at x = 0.2 is a result of translocation of the positron trapping sites from the Cd2+-monovacancies 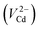 in the CdO nanocrystals35 to the Mo6+ monovacancies
in the CdO nanocrystals35 to the Mo6+ monovacancies 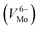 in the α-MoO3 (ref. 36 and 37) and then in the CdMoO4 (ref. 38 and 39) nanocrystallites. While a reducing influence of the 2p electrons of O2− ions results into the fall in peak height at x = 0.2, the enhanced formation of the CdMoO4 nanocrystallites as evidenced from the increasing nanocrystallite size (Fig. 2) sustains the rising trend at further concentration (x) of Ag2O.
in the α-MoO3 (ref. 36 and 37) and then in the CdMoO4 (ref. 38 and 39) nanocrystallites. While a reducing influence of the 2p electrons of O2− ions results into the fall in peak height at x = 0.2, the enhanced formation of the CdMoO4 nanocrystallites as evidenced from the increasing nanocrystallite size (Fig. 2) sustains the rising trend at further concentration (x) of Ag2O.
In this context, it may be useful to examine the structure of the different crystallites as the number and distance of the nearest neighbor O2− ions in each from a positron trapped at the metallic monovacancies may provide some more insight. Table 2 summarizes these parameters for the different crystalline phases present in the nanocomposites. CdO is essentially a face centred cubic structure and there are six neighboring O2− ions octahedrally coordinated with each Cd2+ ion. The Cd–O bond length is 2.3–2.4 Å, as reported by several authors.8,35 An oxygen density parameter is calculated as the number of coordinated O2− ions divided by the volume of the regular octahedron formed by the Cd2+ and coordinated O2− ions. Similarly, Andersson et al.36 and Li et al.37 have described α-MoO3 as a distorted orthorhombic elementary cell with the Mo6+ ion octahedrally coordinated with six O2− ions. The structure of CdMoO4 is an interesting one which crystallizes in a scheelite structure with each single crystal of CdMoO4 having eight symmetry elements and a body-centered orthorhombic primitive cell of two formula units.38,39 The Cd2+ ion is eightfold coordinated by O2− ions in the form of octahedron made up of compressed tetrahedrons of (MoO4)2−. The calculated oxygen density parameters are listed in Table 2. Although Ag2O has a simple cubic structure with each Ag1+ ion linearly coordinated with two O2− ions, one on either side,40 we have included it also in the table by considering a fictitious octahedral volume around it.
| Name of the nanocrystallite | Structure | Distance to the O2−-ion in octahedral coordination from the cation vacancy indicated in parenthesis (a/2) (Å) | Volume of octahedron v = a3/6 (Å3) | Number of coordinated O2− ions (N) | Oxygen density parameter (N/v) |
|---|---|---|---|---|---|
| CdO | Face centered cubic8,35 | 2.3–2.4 (Cd2+) | 16.854 | 6 | 0.356 |
| α-MoO3 | Orthorhombic36,37 | 1.85–2.35 (Mo6+) ≥ 2.10 (mean) | 12.348 | 6 | 0.486 |
| CdMoO4 | Body centered orthorhombic11,38,39 | 2.4–2.44 (Cd2+) (octahedral) | 18.897 | 8 | 0.423 |
| 1.75 (Mo6+) (tetrahedral) | 2.751 | 4 | 1.454 | ||
| Ag2O | Cubic40 | 2.04 (Ag1+) (linear) | 11.318 (fictitious octahedral) | 2 | 0.177 |
The results indicate the probability for increasing annihilation events with the electrons of O2− ions when the positrons are trapped in the Mo6+-monovacancies instead of Cd2+-monovacancies. The initial rise of the peak height in Fig. 13 is indicative of this. When CdMoO4 crystallites are formed, the initial trapping occurs in the Cd2+-monovacancies of it. But, in this case, the oxygen density parameter is weakened and there is an abrupt fall of the peak height. With the positron trapping in the Mo6+-monovacancies of the (MoO4)2−-tetrahedrons, the parameter increases again and the peak heights rise again. Positron trapping in Ag2O oxide could have reversed the trend at the highest concentration of x = 0.9 had the crystallites so formed been considerable in number. It should be noted further that the positron lifetime τ2 in fact had shown an abrupt fall around x = 0.1–0.2, then a small rising trend followed by a gradual decrease with increasing x (Fig. 9(a)), which clearly supported the above findings.
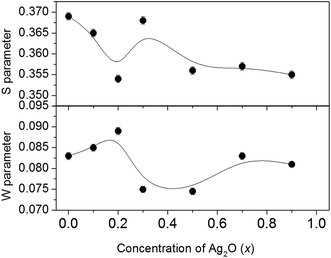
We also have calculated the S and W parameters that are popularly used in positron literature to comment on the qualitative nature of variation of the annihilation characteristics with the variational quantity chosen (x, in this case). These parameters are calculated according to their usual definitions that they respectively represent the fractions of low and high momentum electrons annihilated by the positrons. Accordingly, S is derived from the area-normalized counts within the central channels corresponding to 511 ± 0.651 keV of the one-dimensional projection of the CDB spectrum. For calculating the W parameter, equal number of channels on either side of pL = 10 × 10−3m0c have been chosen, since this corresponded to the channel where the peak due to 2p electrons of O2− ions had appeared in the CDBS ratio curves (Fig. 12). The nature of variation of these two lineshape parameters also indicated the abrupt discontinuity at x = 0.2, as had been expected (Fig. 14). Also, by definition, the value of the S parameter is also a measure of the total defect volume within the samples. In this context, the striking similarity of variations of S with that of the free volume fraction fV in Fig. 10 is notable although both positron lifetime and CDBS measurements are independent of each other and measured parameters are not directly correlated with each other.
4. Summary and conclusions
Metal oxide nanocomposites of xAg2O–(1−x)(0.3CdO–0.7MoO3) with x = 0.0 to 0.9 are investigated by, among other techniques, positron annihilation spectroscopy. The results of PAS essentially pointed towards the vacancy-type defects prevalent in the nanocomposite structure and their evolution under addition of Ag2O. The X-ray diffraction patterns were sharp indicating the presence of large crystallites but the TEM images confirmed the presence of nanocrystallites and thereby the nanocomposite nature. The optical band gaps obtained from the absorption spectra also showed systematic variation and indirectly indicated the growing influence of a new phase being formed. A distinct third positron lifetime component for samples with x > 0.3 clearly indicated the formation and annihilation of orthopositronium atoms within the free volume defects in the Ag2O amorphous matrix. Positrons were also trapped by the vacancy-type defects within the nanocrystallites, the defects being Cd2+-monovacancies in the initial stages of Ag2O incorporation and then the preferred trapping centres got successively shifted to metallic monovacancies of the other two nanocrystallites, viz., α-MoO3 and CdMoO4 at higher Ag2O concentrations. The latter inference is derived from the CDBS ratio curves in which variations of the characteristic peak heights indicated this trend. Besides, positrons also got annihilated in crystalline vacancies in the Ag2O matrix. There could be a rich concentration of oxygen vacancies, where positrons will not be trapped because of the positive charge of the vacancies.Acknowledgements
One of the authors (PMGN) wishes to thank Mr Aneesh Kumar S., Ms Drisya M. and Ms Sandhya C. of Payyanur College, Kannur, Kerala for their help in the positron annihilation experiments and data analysis during their summer project programme at Saha Institute of Nuclear Physics, Kolkata in January–February 2015. Mr Anish Karmahapatra and Ms Soma Roy of SINP, Kolkata are also gratefully acknowledged for their help in taking the XRD patterns and UV-Vis absorption spectra respectively. The authors are also grateful to Dr Biswarup Satpati of SINP, Kolkata for providing them the TEM images of the samples and some useful discussions. S. B. and R. K. wish to acknowledge Council of Scientific and Industrial Research (CSIR), New Delhi for providing financial assistance, vide Sanction No. 03(1286)/13/EMR-II.References
- B. Karmakar, Glass Nanocomposites: Synthesis, Properties and Applications, ed. Basudeb Karmakar, Klaus Rademann and Andrey Stepanov, Elsevier B.V., Amsterdam, 2016, ch. 1, pp. 3–53 Search PubMed.
- A. R. Boccaccini, M. Erol, W. J. Stark, D. Mohn, Z. Hong and J. F. Manoe, Compos. Sci. Technol., 2010, 70, 1764–1776 CrossRef CAS.
- R. Krause-Rehberg and H. S. Leipner, Positron Annihilation in Semiconductors – Defect Studies, Springer, Berlin, Germany, 1999, pp. 1–379 Search PubMed.
- P. M. G. Nambissan, Nanotechnology: Synthesis and Characterization, ed. Shishir Sinha, N. K. Navani and J. N. Govil, Studium Press LLC, Houston, U.S.A, 2013, ch. 16, vol. 2, pp. 455–491 Search PubMed.
- E. E. Assem, K. R. Mahmoud, T. Sharshar and C. Siligardi, J. Phys. D: Appl. Phys., 2006, 39, 734–739 CrossRef CAS.
- J. V. Olsen, P. Kirkegaard, N. J. Pedersen and M. Eldrup, Phys. Status Solidi C, 2007, 4, 4004–4006 CrossRef CAS.
- A. Chatterjee, K. Ramachandran, S. Singh, S. S. Pande and M. D. Ghodgaonkar, Proceedings of the DAE Symposium on Nuclear Physics, 2002, 45, 145–146 Search PubMed.
- K. Usharani, A. R. Balun, V. S. Nagarethinam and M. Suganya, Prog. Nat. Sci.: Mater. Int., 2015, 25, 251–257 CrossRef CAS.
- A. Stoyanova, R. Iordanova, M. Mancheva and Y. Dimitriev, J. Optoelectron. Adv. Mater., 2009, 11, 1127–1131 CAS.
- M. M. Y. A. Alsaif, S. Balendhran, M. R. Field, K. Latham, W. Wlodarski, J. Zhen Ou and K. Kalantar-zadeha, Sens. Actuators, B, 2014, 192, 196–204 CrossRef CAS.
- Xi-E. Wang, T.-Y. Liu, Qi-R. Zhang, H.-Y. Zhang, M. Song, X.-F. Guo and Ji-G. Yin, Chin. Phys. Lett., 2008, 25, 1042–1044 CrossRef CAS.
- M. Guzik, E. Tomaszewicz, Y. Guyot, J. Legendziewicza and G. Boulonc, J. Mater. Chem. C, 2015, 3, 4057–4069 RSC.
- A. Patterson, Phys. Rev., 1939, 56, 978–982 CrossRef CAS.
- P. Manuel Diehm, P. Ágoston and K. Albe, ChemPhysChem, 2012, 13, 2443–2454 CrossRef PubMed.
- G. K. Williamson and W. H. Hall, Acta Metall., 1953, 1, 22–31 CrossRef CAS.
- J. Tauc, Mater. Res. Bull., 1968, 3, 37–46 CrossRef CAS.
- M. Ghosh and C. N. R. Rao, Chem. Phys. Lett., 2004, 393, 493–497 CrossRef CAS.
- R. M. Nieminen and M. J. Manninen, Positrons in Solids Springer Series on Topics in Current Physics, ed. P. Hautojarvi, Springer, Berlin, Germany 1979, vol. 12, ch. 4, pp. 145–195 Search PubMed.
- Y. C. Jean, K. Venkateswaran, E. Parsai and K. L. Cheng, Appl. Phys. A, 1984, 35, 169–176 CrossRef.
- S. J. Tao, J. Chem. Phys., 1972, 56, 5499–5510 CrossRef CAS.
- M. Eldrup, D. Lightbody and J. N. Sherwood, Chem. Phys., 1981, 63, 51–58 CrossRef CAS.
- A. Uedono, R. Sadamoto, T. Kawano, S. Tanigawa and T. Uryu, J. Polym. Sci., Part B: Polym. Phys., 1995, 33, 891–897 CrossRef CAS.
- A. Seeger, J. Phys. F: Met. Phys., 1973, 3, 248–294 CrossRef CAS.
- I. K. MacKenzie, Positron Solid State Physics: International Summer School Proceedings Proceedings of the International School of Physics “Enrico Fermi”, ed. W. Brandt and A. Dupasquier, North Holland, Amsterdam, 1983, pp. 196–264 Search PubMed.
- D. Wegner, J. Phys. F: Met. Phys., 1988, 18, 2291–2302 CrossRef CAS.
- J. M. Campillo Robles, E. Ogando and F. Plazaola, J. Phys.: Condens. Matter, 2007, 19, 176222 CrossRef CAS PubMed.
- M. Fernández-Garcia and J. A. Rodriguez, Nanomaterials: Inorganic and Bioinorganic Perspectives, ed. C. M. Lukehart and R. A. Scott, Wiley, New York, 2008, pp. 453–512 Search PubMed.
- S. K. Sharma, P. K. Pujari, K. Sudarshana, D. Dutta, M. Mahapatra, S. V. Godbole, O. D. Jayakumar and A. K. Tyagi, Solid State Commun., 2009, 149, 550–554 CrossRef CAS.
- A. Das, A. Chandra Mandal, S. Roy and P. M. G. Nambissan, J. Exp. Nanosci., 2015, 10, 622–639 CrossRef CAS.
- R. N. West, Adv. Phys., 1973, 22, 263–383 CrossRef CAS.
- R. W. Siegel, Annu. Rev. Mater. Sci., 1980, 10, 393–425 CrossRef CAS.
- P. Asoka-Kumar, M. Alatalo, V. J. Ghosh, A. C. Kruseman, B. Nielsen and K. G. Lynn, Phys. Rev. Lett., 1996, 77, 2097–2100 CrossRef CAS PubMed.
- Y. Nagai, T. Nonaka, M. Hasegawa, Y. Kobayashi, C. L. Wang, W. Zheng and C. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 11863–11866 CrossRef CAS.
- A. K. Bar, D. Roy, R. Kundu, M. P. F. Graca, M. A. Valente and S. Bhattacharya, Mater. Sci. Eng. B, 2014, 189, 21–26 CrossRef CAS.
- A. Bera, R. Thapa, K. K. Chattopadhyay and B. Saha, J. Alloys Compd., 2015, 632, 343–347 CrossRef CAS.
- G. Andersson and A. Magneli, Acta Chem. Scand., 1950, 4, 793–797 CrossRef CAS.
- S. Li, W. B. Kim and J. S. Lee, Chem. Mater., 1998, 10, 1853–1862 CrossRef CAS.
- Y. Abraham, N. A. W. Holzwarth and R. T. Williams, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 1733–1741 CrossRef CAS.
- M. Daturi, G. Busca, M. Madeleine Borel, A. Leclaire and P. Piaggio, J. Phys. Chem. B, 1997, 101, 4358–4369 CrossRef CAS.
- A. Deb and A. K. Chatterjee, J. Phys.: Condens. Matter, 1998, 10, 11719–11729 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra23680d |
| ‡ Present address (RK): Department of Electrical Engineering, University of Engineering and Management, Kolkata-700156, West Bengal, E-mail: E-mail: ranadip.89@gmail.com; Fax: +91-33-23578302; Tel: +91-8902390462. |
| This journal is © The Royal Society of Chemistry 2017 |