Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Monte Carlo track chemistry simulations of the radiolysis of water induced by the recoil ions of the 10B(n,α)7Li nuclear reaction. 1. Calculation of the yields of primary species up to 350 °C
Muhammad Mainul Islama,
Phantira Lertnaisatb,
Jintana Meesungnoena,
Sunuchakan Sanguanmitha,
Jean-Paul Jay-Gerin *a,
Yosuke Katsumura†
*b,
Satoru Mukaic,
Ryuji Umeharad,
Yuichi Shimizud and
Masashi Suzukic
*a,
Yosuke Katsumura†
*b,
Satoru Mukaic,
Ryuji Umeharad,
Yuichi Shimizud and
Masashi Suzukic
aDépartement de Médecine Nucléaire et de Radiobiologie, Faculté de Médecine et des Sciences de la Santé, Université de Sherbrooke, Sherbrooke, Québec J1H 5N4, Canada. E-mail: jean-paul.jay-gerin@USherbrooke.ca
bDepartment of Nuclear Engineering and Management, School of Engineering, University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8686, Japan. E-mail: katsu@n.t.u-tokyo.ac.jp
cNuclear Chemistry Engineering, Nuclear Environment R&D Department, Nuclear Development Corporation, 622-12 Funaishikawa, Tokai-mura, Ibaraki 319-111, Japan
dWater Chemistry Technology Group, Nuclear Energy Systems Headquarters, Mitsubishi Heavy Industries Ltd., 1-1-1 Wadasaki-cho, Hyogo-ku, Kobe 652-8585, Japan
First published on 8th February 2017
Abstract
Monte Carlo track chemistry simulations were carried out to predict the yields (G-values) of all primary radical and molecular species produced in the radiolysis of pure, neutral water and 0.4 M sulfuric acid aqueous solutions by the recoil ions of the 10B(n,α)7Li nuclear reaction as a function of temperature from 25 to 350 °C. The calculations were performed individually for 1.47 MeV α-particles and 0.84 MeV lithium nuclei with “dose-average” linear energy transfer (LET) values of ∼196 and 225 eV nm−1 at 25 °C, respectively. The overall yields were calculated by summing the G-values for each recoil ion weighted by its fraction of the total energy absorbed. In the calculations, the actual effective charges carried by the two helium and lithium ions (due to charge exchange effects) were taken into account and the (small) contribution of the 0.478 MeV γ-ray, also released from the 10B(n,α)7Li reaction, was neglected. Compared with data obtained for low-LET radiation (60Co γ-rays or fast electrons), our computed yields for the 10B(n,α)7Li radiolysis of neutral deaerated water showed essentially similar temperature dependence over the range of temperatures studied, but with lower values for yields of free radicals and higher values for molecular yields. This general trend is a reflection of the high-LET character of the 10B(n,α)7Li recoil ions. Overall, the simulation results agreed well with existing estimates at 20 and 289 °C. For deaerated 0.4 M H2SO4 solutions, reasonable agreement between experiment and simulation was also found at room temperature. Nevertheless, more experimental data for both neutral and acidic solutions would be needed to better describe the dependence of radiolytic yields on temperature and to test our modeling calculations more thoroughly. Moreover, measurements of the (eaq− + eaq−) reaction rate constant in near-neutral water would help us to determine whether the predicted non-monotonic inflections above ∼150 °C in G(H2) and G(H2O2) are confirmed.
1. Introduction
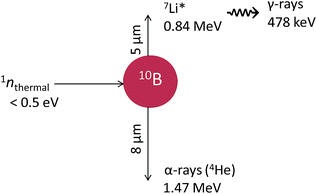
Boron-10 is one of the stable isotopes of boron with a natural abundance of ∼20%. It is known to exhibit a high propensity to absorb thermal neutrons with a neutron-capture cross-section of 3835 barns (1 barn = 10−28 m2), which is about six times greater than that of uranium-235 and three orders of magnitude greater than that of the nuclei of living tissues.1 On absorption of a slow neutron, a fission reaction occurs with the release of two energetic heavy ions: an α-particle (1.47 MeV) and, in ∼94% of all reactions, a 7Li3+ nucleus in its first excited state (0.84 MeV) which quickly returns to its ground state (half-life of ∼10−13 s) by releasing a low-energy γ-ray (478 keV).2 These heavy charged particles have path lengths in the range of ∼5–8 μm in water or biological tissues and exhibit high linear energy transfer (LET, or energy loss per unit path length −dE/dx, in units of eV nm−1) characteristics, as shown in Fig. 1.3,4 Because of this high energy deposition to the surrounding environment and the α and Li recoils' short travel distances, which are typically of the order of a cell diameter, the 10B(n,α)7Li nuclear reaction has been used in clinical studies of biochemically targeted radiotherapies for cancer treatment known as “boron neutron capture therapy” (BNCT).1,5BNCT is a potentially ideal radiotherapy modality for glioblastoma, which is a type of brain tumor that is rarely removed surgically. When a cancer cell is allowed to take up preferentially a sufficient concentration of 10B, it can be selectively irradiated by the very densely ionizing ion recoils from the 10B(n,α)7Li reaction without damaging the surrounding normal tissue. This basic idea was first proposed by Locher in 1936,6 shortly after the discovery of the neutron by Chadwick.7 Interest in BNCT was spurred by Kruger's study in 1940, who reported a low transplantation efficiency for tumors treated by BNCT in vitro and subsequently implanted in mice.8,9 Although the full clinical application of BNCT presents several difficulties, including the inadequate selectivity and toxicity of 10B delivery agents and the poor distribution of neutron flux, clinical trials of BNCT are still under way and new neutron irradiation facilities continue to be developed in Japan, the United States, Finland, and several other countries.1,5,10–12
Apart from BNCT, the unique properties of boron-10 have also been extensively applied in the field of nuclear industry. For example, boron carbide (B4C), enriched in 10B, is used as a control-rod material (neutron absorber) in boiling water reactors (BWRs). In addition, boron as boric acid (H3BO3) is generally added as a water-soluble neutron poison in the primary coolant of pressurized water reactors (PWRs) to control the neutron flux and the reactivity in the core.13–16 However, recoil ions arising from the 10B(n,α)7Li reaction act as sources of high-LET radiation in the primary coolant of PWRs, thereby leading to the formation of oxidizing species, such as hydrogen peroxide and oxygen, due to the radiolysis of water.17,18
The radiolysis of water is closely linked to the corrosion of structural materials. Water, which is used as the neutron moderator and the reactor coolant, is unavoidably exposed to extreme conditions of high temperature (∼275–325 °C), pressure (∼7–15 MPa), and intense mixed neutron and β–γ radiation fields (which have characteristically different LET values). Under these conditions, the radiolysis of water results in the formation of free radical (eaq−, H˙, ˙OH, and HO2˙/O2˙−) and molecular (H2, H2O2, and O2) species which alter the chemical environment of the coolant.18–20 The presence of the oxidizing species H2O2 and O2 can significantly increase the corrosion potential of coolant water in BWRs.16,21,22 In PWRs, the presence of boron-10 results in high-LET recoil ions and complicates the radiolytic process. Although 10B has been widely studied both in nuclear technology and clinical research, little attention has been devoted to 10B-induced reactions. In particular, data on the formation of primary products and their yields (G-values) for 10B(n,α)7Li recoil irradiation of neutral water are scarce and uncertain.15,19 In fact, the only reported measurements at room temperature were made in acid (0.4 M H2SO4) solution.23–25 Similarly, the G-values at reactor temperatures are not well known. To the best of our knowledge, there is only one report19 that estimated a complete set of water decomposition yields induced by the 10B(n,α)7Li reaction at 289 °C.
Understanding the radiation chemistry of the coolant water in reactors is important for maintaining the proper chemical environment that will minimize the degradation of materials. Recently, computer simulations have played a substantial role in evaluating the concentrations of oxidizing species produced from coolant-water radiolysis, which is difficult to observe directly because of the extreme operating conditions involved. In this current work, Monte Carlo track chemistry simulations were undertaken to predict the G-values for the various primary radical and molecular products formed from the radiolysis of pure, neutral water and 0.4 M H2SO4 aqueous solutions by the 10B(n,α)7Li reaction as a function of temperature from 25 to 350 °C.
The paper is organized as follows. The main features of our simulation approach are given in the next section. Sections 3 and 4 present, respectively, the results of our simulations of the 10B(n,α)7Li radiolysis of water at neutral pH and of 0.4 M H2SO4 aqueous solutions at 25 °C and as a function of temperature up to 350 °C, and their discussion. Conclusions are drawn in the final section.
A brief preliminary report of this work has been presented elsewhere.26
2. Monte Carlo track chemistry simulations
The entire sequence of events generated in the radiolysis of liquid water by 10B(n,α)7Li recoil ions was modeled using our Monte Carlo track chemistry simulation code called IONLYS-IRT. This computer program simulates, in a 3D geometrical environment, the highly nonhomogeneous distribution of reactive species initially produced by the absorption of incident radiation and all of the energetic secondary electrons, as well as the subsequent diffusion and chemical reactions of these species. A detailed description of the current version of the code at both ambient and elevated temperatures and under low- and high-LET irradiation conditions has been reported previously.27–30 In brief, the IONLYS step-by-step simulation program models all of the events of the early “physical” and “physicochemical” stages31 of radiation action up to ∼1 ps in the track development. The complex, highly nonhomogeneous spatial distribution of reactants formed at the end of the physicochemical stage [eaq−, H+, OH−, H˙, ˙OH, H2, H2O2, HO2˙/O2˙−, ˙O˙(3P), O(1D), O2,…], which is provided as an output of the IONLYS program, is then used directly as the starting point for the subsequent “nonhomogeneous chemical” stage31 (typically, from ∼1 ps to the μs time scale at 25 °C). This third stage, during which the different radiolytic species diffuse randomly at rates determined by their diffusion coefficients and react with one another (or with dissolved solutes, if any) until all track processes are complete, is covered by our IRT program. This program employs the “independent reaction times” (IRT) method,32–34 a computationally efficient stochastic simulation technique that is used to simulate reaction times without having to follow the trajectories of the diffusing species. The IRT method relies on the approximation that the reaction time of each pair of reactants is independent of the presence of other reactants in the system. Its ability to give accurate time-dependent chemical yields under different irradiation conditions has been well validated by comparison with full random flights (or step-by-step) Monte Carlo simulations, which do follow the reactant trajectories in detail.35,36 This IRT program can also be used to efficiently describe the reactions that occur in the bulk solution during the “homogeneous chemical” stage,31 i.e., in the time domain beyond a few microseconds. The model assumptions and procedures employed to carry out the Monte Carlo simulations of the radiolysis of aqueous 0.4 M H2SO4 solutions (pH ∼ 0.46) with IONLYS-IRT have already been given.37,38In the current version of IONLYS-IRT, we used the self-consistent radiolysis database, including rate constants and diffusion coefficients, recently compiled by Elliot and Bartels.20 This new database provides recommendations for the best values to use in high-temperature modeling of water radiolysis over the range of 20–350 °C.
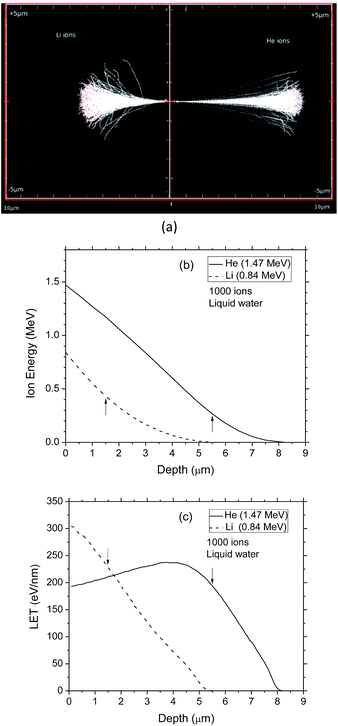
Pre-simulations were performed using the SRIM simulation program39 to calculate 1000 tracks of 1.47 MeV α-particles and 0.84 MeV lithium nuclei emitted from the 10B(n,α)7Li reaction, and the energies and LET values of the 2 recoil ions as a function of penetration depth in water (Fig. 2). As shown, the initial LETs of helium and lithium ions were ∼193 and 304 eV nm−1, respectively. The LET of 1.47 MeV 4He2+ ions calculated using our Monte Carlo simulations agreed very well with the SRIM simulation results. Since the SRIM program incorporates the change of charge state of the moving ion as it goes into and through the target (due to the effects of electron capture and loss by the ion), this agreement indicates that the helium ion, when it travels with this energy, is fully stripped of its electrons. However, for 0.84 MeV 7Li3+ ions, our calculations gave a LET which is more than twice the expected value. This difference was explained as being caused by a change in the charge state of the lithium ion, which always acts to reduce its LET relative to the LET of the bare nucleus. Our Monte Carlo simulations were used to calculate the “effective charge” (Z*) of a 0.84 MeV lithium ion in water that was required to reproduce the SRIM LET value of 304 eV nm−1. A value very close to +2 (instead of +3) was actually obtained, clearly indicating a partial neutralization of the lithium ion at this energy.
The above results confirm the importance of making charge-state calculations for each recoil ion in this study. In this work, however, to avoid complexity arising from energy-dependent charge exchange processes, simulations were performed under the simplifying approximation that the energies of the two recoil ions remained constant when passing through the water medium. These constant average energy values 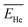 and
and 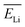 were chosen according to the following procedure: (1) Watt's compilation of quantities for radiation dosimetry in liquid water3 was first used to determine the “dose-average” LET values for both 1.47 MeV helium and 0.84 MeV lithium ions. The values thus obtained were ∼196 and 225 eV nm−1, respectively; (2) using Fig. 2(c), these two LET values were then related to the corresponding penetration depths of the two recoil ions in water, namely, ∼5.5 and 1.5 μm, respectively; and (3)
were chosen according to the following procedure: (1) Watt's compilation of quantities for radiation dosimetry in liquid water3 was first used to determine the “dose-average” LET values for both 1.47 MeV helium and 0.84 MeV lithium ions. The values thus obtained were ∼196 and 225 eV nm−1, respectively; (2) using Fig. 2(c), these two LET values were then related to the corresponding penetration depths of the two recoil ions in water, namely, ∼5.5 and 1.5 μm, respectively; and (3) 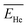 and
and 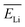 were finally deduced from Fig. 2(b) as being equal to the energies of the two ions at these penetration depths, namely, ∼0.3 and 0.4 MeV, respectively. Once these two energies known, the actual effective charges carried by the two helium and lithium ions having these energies were determined as described above by using our Monte Carlo simulations and by adjusting Z* so as to reproduce the expected LET values.
were finally deduced from Fig. 2(b) as being equal to the energies of the two ions at these penetration depths, namely, ∼0.3 and 0.4 MeV, respectively. Once these two energies known, the actual effective charges carried by the two helium and lithium ions having these energies were determined as described above by using our Monte Carlo simulations and by adjusting Z* so as to reproduce the expected LET values. 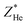 and
and 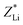 were found to be about +1.6 and +1.7, respectively.
were found to be about +1.6 and +1.7, respectively.
All calculations were performed by simulating short (typically, ∼1–5 μm) ion track segments, over which the energy and LET of the ion are well defined and remain nearly constant. Such model calculations thus gave “track segment” yields40 at a well defined LET. The number of individual ion “histories” (usually ∼2–100, depending on the irradiating ion and energy) was chosen to ensure only small statistical fluctuations in the computed averages of chemical yields, while keeping acceptable computer time limits.
Finally, the yields of primary free radical or molecular products of water radiolysis induced by the recoil ions of the nuclear reaction 10B(n,α)7Li were calculated by summing the G-values for each recoil ion (obtained from our Monte Carlo simulations) weighted by its fraction of the total energy absorbed according to38,41
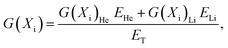 | (1) |
Absorption of the accompanying 0.478 MeV γ-ray in the aqueous solution (see Fig. 1) is small in our area of interest. Indeed, the range of an electron of this energy is ∼1 mm in liquid water at 25 °C;42 this is more than 100 times larger than the penetration ranges of the He and Li ions, which are only 5–8 μm. Thus, its contribution to the overall chemical reaction was neglected in this study.
Throughout this paper, G-values are quoted in units of molecules formed or consumed per 100 eV of radiation energy absorbed. For conversion into SI units, 1 molecule/100 eV = 0.10364 μmol J−1.
3. Results and discussion
The temperature dependences of our computed yields of eaq−, ˙OH, H˙, H2O2, and H2 in pure, deaerated liquid water irradiated by the 10B(n,α)7Li recoil ions from ambient up to 350 °C are shown in Fig. 3 along with estimated G-values at 20 °C (ref. 15) and 289 °C.19 For the sake of comparison, our G-values were calculated at two different times, namely 10−7 and 10−6 s after energy deposition at all temperatures (solid, blue and red lines shown in Fig. 3, respectively). Compared with the data obtained for low-LET radiation (γ-rays from 60Co or fast electrons), our computed yields for 10B(n,α)7Li recoil irradiation show essentially similar temperature dependences over the range of temperatures studied, but with much lower values for yields of free radicals and higher values for molecular yields. This is particularly true for the yields of eaq− and H˙ atoms, which remain extremely small at the microsecond time scale even at high temperatures [Fig. 3(a) and (c)]. This general trend is a result of the high-LET character of the 10B(n,α)7Li recoil ions. Indeed, upon increasing the LET of the radiation, there is an increased intervention of radical–radical reactions as the local concentrations of radicals along the radiation tracks are high and many radical interactions occur before the products can escape into the bulk solution. This allows fewer radicals to escape combination and recombination reactions during the expansion of tracks and in turn leads to the formation of more molecular products.28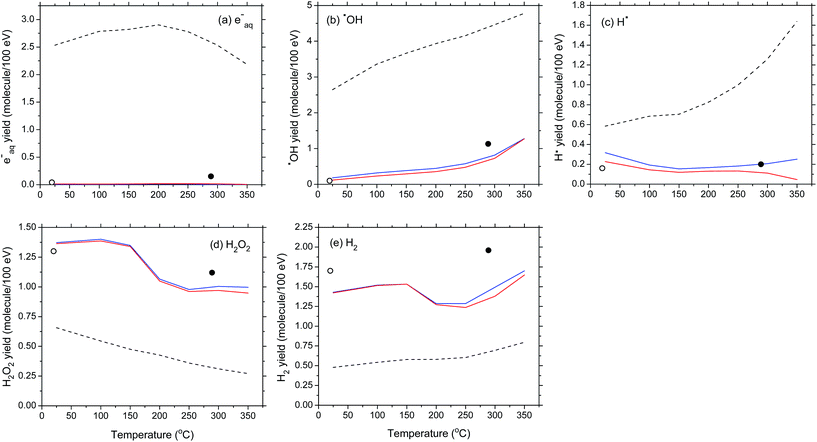 | ||
| Fig. 3 G-values (in molecule per 100 eV) for the 10B(n,α)7Li radiolysis of pure, deaerated liquid water as a function of temperature in the range of 25–350 °C: (a) G(eaq−); (b) G(˙OH); (c) G(H˙); (d) G(H2O2); and (e) G(H2). Our simulated results, obtained at 10−7 and 10−6 s, are shown as solid, blue and red lines, respectively. Symbols are the water decomposition yields induced by the 10B(n,α)7Li reaction estimated by Cohen (ref. 15) at 20 °C (based on the approximate relationship between LET and G-values given in Fig. 5.3 of Allen (ref. 43), using an average initial LET of 240 eV nm−1) (○) and by Christensen (ref. 19) at 289 °C (●). The primary (or “escape”) yields for the low-LET (∼0.3 eV nm−1) radiolysis of water (ref. 29) obtained using our previously calculated spur lifetimes between 25–350 °C (ref. 44) are also given (black dashed lines) for comparison purposes. Note that all yield curves shown in this figure were obtained under exactly the same conditions as in ref. 29 as far as the temperature dependences of the different parameters intervening in the early physicochemical stage (e.g., the electron thermalization distance – called rth in ref. 29) and in the subsequent chemical stage [e.g., the (eaq− + eaq−) reaction rate constant, represented by the non-Arrhenius black dashed line k = ka in Fig. 4(a)] of the radiolysis are concerned. | ||
A striking feature of our simulated results is the marked downward inflection that is observed above ∼150 °C in the yields of H2 and H2O2. This is in contrast to the corresponding estimates of Christensen19 at 289 °C, which seem to indicate a rather monotonic variation of G(H2) [Fig. 3(e)] and G(H2O2) [Fig. 3(d)] with temperature. Similar non-monotonic behavior in the temperature dependence of the yields of primary products in low-29,45,46 and high-47,48 LET irradiated water has already been predicted, and is due to the fact that the rate constant for the bimolecular self-reaction of the hydrated electron (k2):
| eaq− + eaq− (+2H2O) → H2 + 2OH− | (2) |
| eaq− + ˙OH → OH− (k3 = 3.34 × 1010 M−1 s−1, 20 °C), | (3) |
| ˙OH + ˙OH → H2O2 (k4 = 4.54 × 109 M−1 s−1, 20 °C), | (4) |
In connection with these predicted non-monotonic variations of G(H2) and G(H2O2), we should briefly mention here the current controversy concerning the temperature dependence of k2 (Fig. 4). In this work, we adopted the values of k2, including the drop between 150 and 200 °C, recommended by Elliot and Bartels20 as the “best values to use to model water radiolysis at temperatures up to 350 °C” [represented by the black dashed line, denoted ka, in Fig. 4(a)]. However, this drop in k2 has been measured only under alkaline conditions. Its applicability to neutral or slightly acidic (as the pH of water at 150–200 °C is about 5.7–6)15 solution remains uncertain because it could be a function of the pH of the solution.50
 | ||
| Fig. 4 (a) Rate constant for the self-reaction of two hydrated electrons as a function of temperature (ref. 49). The black dashed line (denoted ka) shows the (eaq− + eaq−) reaction rate constant measured under alkaline conditions (ref. 20). The symbols (■) are experimental data. The red solid line (denoted kb) shows the (eaq− + eaq−) reaction rate constant obtained by using an Arrhenius extrapolation procedure above ∼150 °C (ref. 50–52). (b) and (c) The red solid lines show our Monte Carlo simulation results for G(H2) and G(H2O2) (in molecule per 100 eV), at 10−6 s, as a function of temperature, when kb was used. A comparison is made with the corresponding yields of H2 and H2O2 obtained when ka was used [represented here by the black dashed lines, which are the same as the red solid lines in Fig. 3(e) and (d)]. The symbols (○) (ref. 15) and (●) (ref. 19) are the same as in Fig. 3(e) and (d). | ||
Until recently, most computer modelers of the radiolysis of water at elevated temperatures have employed, in neutral solution, an Arrhenius extrapolation of the values of k2 below 150 °C to 200–350 °C, as proposed previously by Elliot50 and Stuart et al.,51 and recently by Hatomoto et al.52 This approach assumes that such an abrupt change in k2 does not occur and that reaction (2) is diffusion controlled at temperatures greater than 150 °C. This assumption was originally justified by the good agreement between models and experiments.45,46
To show the sensitivity of G(H2) and G(H2O2) to k2, our simulations were carried out for the temperature dependence of k2 obtained by using an Arrhenius extrapolation procedure above ∼150 °C (ref. 49–52) [represented by the red solid line, denoted kb, in Fig. 4(a)]. The red solid lines in Fig. 4(b) and (c) display our calculated H2 and H2O2 yields at 10−6 s after the ionizing event over the temperature range of 25–350 °C. A comparison with our results obtained using the temperature dependence of k2 measured in alkaline water (ka) [black dashed lines in Fig. 4(b) and (c)] clearly indicates that G(H2) and G(H2O2) are strongly affected by the choice of k2. In particular, the sharp downward inflections predicted for G(H2) and G(H2O2) above ∼150 °C no longer appear. Considering the importance of the self-reaction of eaq− in high-temperature water radiolysis, further measurements of its rate constant in near-neutral water are obviously highly desirable.
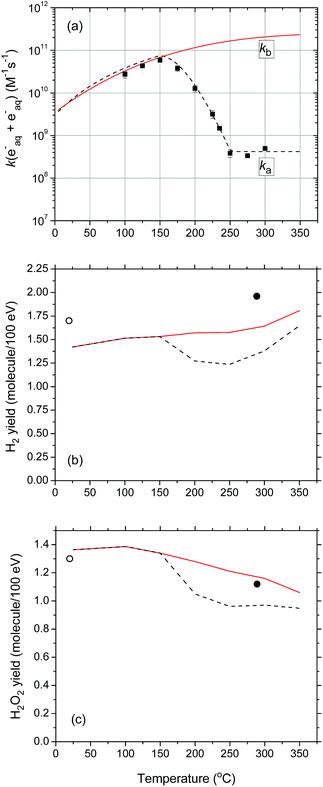
Turning now to the 10B(n,α)7Li radiolysis of deaerated 0.4 M sulfuric acid aqueous solutions, we present in Fig. 5 the results of our Monte Carlo simulations showing the variations of the G-values for H˙ (considering the conversion of eaq− to H˙ in the tracks in acidic solution),55 ˙OH, H2O2, and H2 (at 10−6 s) as a function of temperature over the range of 25–350 °C. As can be seen, the simulations agree reasonably well with the experimental data of Barr and Schuler23 at 25 °C, which are also shown in the figure for the sake of comparison. Compared with the primary (or “escape”) yield data obtained for low-LET radiation (60Co γ-rays or fast electrons) (shown as dashed lines in Fig. 5), it is seen that, as in neutral water, our computed G-values for the 10B(n,α)7Li radiolysis of deaerated 0.4 M H2SO4 aqueous solutions show essentially similar temperature dependences over the 25–350 °C temperature range studied. The same general trend is observed, but with much lower values for yields of radical species and higher values for molecular yields, reflecting again the high-LET character of the 10B(n,α)7Li recoil ions.
 | ||
| Fig. 5 G-values (in molecule per 100 eV) for the 10B(n,α)7Li radiolysis of deaerated 0.4 M H2SO4 aqueous solutions (pH 0.46 at 25 °C) as a function of temperature in the range of 25–350 °C. Note that, at this high concentration of H2SO4, the H+ ions very rapidly (<10−9 s) scavenge most, if not all, of the eaq− radicals in the tracks to form H˙ atoms (ref. 37). Note also that, in our simulations, the direct action of ionizing radiation on the sulfuric acid anions (mainly HSO4−) has been neglected. The solid curves represent the results of our Monte Carlo simulations for (a) G(H˙), (b) G(˙OH), (c) G(H2), and (d) G(H2O2) at 10−6 s after the initial energy deposition. The yields of primary species induced by the 10B(n,α)7Li reaction measured by Barr and Schuler (ref. 23) in acidic solutions at 25 °C are given by (●). The primary (or “escape”) yields for the low-LET (∼0.3 eV nm−1) radiolysis of 0.4 M H2SO4 aqueous solutions (ref. 53) obtained from our previously calculated spur lifetimes between 25–350 °C (ref. 44) are also shown (dashed lines) for the sake of comparison. Finally, in all calculations, the reaction of the H˙ atom with water: H˙ + H2O → H2 + ˙OH was assumed to follow an Arrhenius temperature dependence over the 25–350 °C range studied, with a rate constant of 4.6 × 10−5 M−1 s−1 at 25 °C and 104 M−1 s−1 at 300 °C, in agreement with recent muon spin spectroscopy experiments using muon as an analogue of a hydrogen atom (ref. 54). | ||
For the sake of completeness, we show in Fig. 6 the sensitivity of G(H2) and G(H2O2) to the temperature dependence for the (eaq− + eaq−) reaction rate constant k2 chosen in the simulations. Compared to the results obtained in near-neutral water and shown in Fig. 4(b) and (c), the choice of k2 [namely, ka or kb in Fig. 4(a)] in acidic solution is relatively unimportant. Indeed, as can be seen from Fig. 6(a) and (b), the H2 and H2O2 yield (red solid) curves obtained using k2 = ka differ only slightly from the corresponding (black dashed) curves calculated for k2 = kb and the downward inflections predicted for G(H2) and G(H2O2) above ∼150 °C are practically no longer apparent. This is easily understandable since in 0.4 M H2SO4 solutions, hydrated electrons are very rapidly (<10−9 s) transformed into H˙ atoms in the tracks,37 thereby making reaction (2) quickly inoperative in contributing to these yields whatever the temperature. Removal of this reaction thus prevents the possibility of observing any clear difference in the temperature dependence of G(H2) and G(H2O2) above ∼150 °C when either ka or kb is used for the (eaq− + eaq−) reaction rate constant.
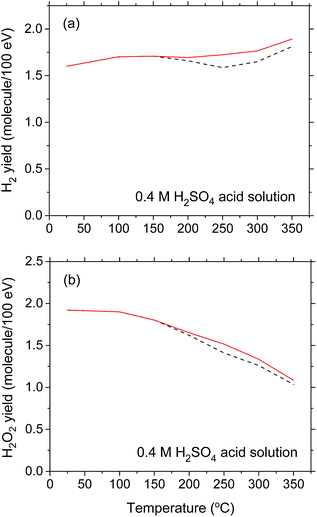 | ||
| Fig. 6 Yields of H2 (panel a) and H2O2 (panel b) (in molecule per 100 eV) formed during the 10B(n,α)7Li radiolysis of deaerated 0.4 M H2SO4 aqueous solutions as a function of temperature over the range of 25–350 °C. The black dashed lines show our Monte Carlo simulation results for G(H2) and G(H2O2) at 10−6 s when the (eaq− + eaq−) reaction rate constant k2 = ka [see Fig. 4(a)] was used (note that these curves are the same as the lines in Fig. 5(c) and (d)). A comparison is made with the corresponding yields of H2 and H2O2 obtained when k2 = kb [see Fig. 4(a)] was used (represented by the red solid lines). | ||
4. Conclusion
In this work, Monte Carlo simulations were used to calculate the G-values for the primary species of the radiolysis of neutral liquid water and 0.4 M H2SO4 aqueous solutions by the recoil ions of the 10B(n,α)7Li nuclear reaction at temperatures between 25 and 350 °C. Overall, the simulation results for neutral deaerated water agreed well with existing estimates at 20 and 289 °C. For 0.4 M H2SO4 solutions, reasonable agreement between experiment and simulation was also found at room temperature. Compared with the data obtained for low-LET radiation, our computed yields showed essentially similar temperature dependences over the range of temperatures studied, but with lower values for yields of free radicals and higher values for molecular yields, which reflect the high-LET character of the densely ionizing 10B(n,α)7Li recoil ions. More experimental data are required for both neutral and acidic solutions to better describe the dependence of radiolytic yields on temperature and to test our modeling calculations more thoroughly. Moreover, measurements of the (eaq− + eaq−) reaction rate constant in near-neutral water would help us to determine whether the predicted non-monotonic inflections above ∼150 °C in G(H2) and G(H2O2) are confirmed.Acknowledgements
The authors thank Professor Takayuki Terai, Professor Yusa Muroya, and Dr Shin-ichi Yamashita for their support and advices. They are also grateful to Professor James F. Ziegler for his helpful correspondence with regard to the use of the SRIM simulation software. M. M. I. is the recipient of a scholarship from the “Centre de Recherche Médicale de l’Université de Sherbrooke”. P. L. thanks the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan for financial support through a MEXT scholarship. The research of J.-P. J.-G. is supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) Grant No. RGPIN-2015-06100.Notes and references
- Neutron Capture Therapy. Principles and Applications, ed. W. A. G. Sauerwein, A. Wittig, R. Moss and Y. Nakagawa, Springer, Berlin, 2012 Search PubMed.
- G. F. Knoll, Radiation Detection and Measurement, Wiley, New York, 3rd edn, 2000, p. 507 Search PubMed.
- D. E. Watt, Quantities for Dosimetry of Ionizing Radiations in Liquid Water, Taylor & Francis, London, 1996 Search PubMed.
- É. Sèche, R. Sabattier, J.-C. Bajard, G. Blondiaux, N. Breteau, M. Spotheim-Maurizot and M. Charlier, Radiat. Res., 2002, 158, 292 CrossRef.
- N. S. Hosmane, J. A. Maguire, Y. Zhu and M. Takagaki, Boron and Gadolinium Neutron Capture Therapy for Cancer Treatment, World Scientific, Singapore, 2012 Search PubMed.
- G. L. Locher, Am. J. Roentgenol. Radium Ther., 1936, 36, 1 CAS.
- J. Chadwick, Proc. R. Soc. London, Ser. A, 1932, 136, 692 CrossRef CAS.
- P. G. Kruger, Proc. Natl. Acad. Sci. U. S. A., 1940, 26, 181 CrossRef CAS.
- W. Sauerwein, Strahlenther. Onkol., 1993, 169, 1 CAS.
- J. W. Hopewell, G. M. Morris, A. Schwint and J. A. Coderre, Appl. Radiat. Isot., 2011, 69, 1756 CrossRef CAS PubMed.
- R. F. Barth, M. G. H. Vicente, O. K. Harling, W. S. Kiger III, K. J. Riley, P. J. Binns, F. M. Wagner, M. Suzuki, T. Aihara, I. Kato and S. Kawabata, Radiat. Oncol., 2012, 7, 146 CrossRef PubMed.
- R. L. Moss, Appl. Radiat. Isot., 2014, 88, 2 CrossRef CAS PubMed.
- J. Pucheault, M. Lefort and M. Haïssinsky, J. Chim. Phys. Phys.–Chim. Biol., 1952, 49, 286 CAS.
- M. Koike, E. Tachikawa and T. Matsui, J. Nucl. Sci. Technol., 1969, 6, 163 CrossRef CAS.
- P. Cohen, Water Coolant Technology of Power Reactors, American Nuclear Society, La Grange Park, 1980 Search PubMed.
- J. Takagi, B. J. Mincher, M. Yamaguchi and Y. Katsumura, in Charged Particle and Photon Interactions with Matter: Recent Advances, Applications, and Interfaces, ed. Y. Hatano, Y. Katsumura and A. Mozumder, Taylor & Francis Group, Boca Raton, 2011, p. 959 Search PubMed.
- E. J. Hart, W. R. McDonell and S. Gordon, Proceedings of the International Conference on the Peaceful Uses of Atomic Energy, Geneva, 8-20 Aug. 1955, P/839, United Nations, New York, 1956, vol. 7, p. 593 Search PubMed.
- D. R. McCracken, K. T. Tsang and P. J. Laughton, Aspects of the physics and chemistry of water radiolysis by fast neutrons and fast electrons in nuclear reactors, Report AECL-11895, Atomic Energy of Canada Limited, Chalk River, Ontario, 1998 Search PubMed.
- H. Christensen, Fundamental aspects of water coolant radiolysis, SKI Report 2006:16, Swedish Nuclear Power Inspectorate, Stockholm, Sweden, April 2006 Search PubMed.
- A. J. Elliot and D. M. Bartels, The reaction set, rate constants and g-values for the simulation of the radiolysis of light water over the range 20° to 350 °C based on information available in 2008, Report AECL No. 153-127160-450-001, Atomic Energy of Canada Limited, Chalk River, Ontario, 2009 Search PubMed.
- R. L. Cowan, Water Chemistry of Nuclear Reactor Systems 7, Bournemouth, UK, 13-17 Oct. 1996, British Nuclear Energy Society, London, 1996, p. 196 Search PubMed.
- Y. Wada, A. Watanabe, M. Tachibana, K. Ishida, N. Uetake, S. Uchida, K. Akamine, M. Sambongi, S. Suzuki and K. Ishigure, J. Nucl. Sci. Technol., 2001, 38, 183 CrossRef CAS.
- N. F. Barr and R. H. Schuler, Radiat. Res., 1957, 7, 302 Search PubMed; N. F. Barr and R. H. Schuler, J. Phys. Chem., 1959, 63, 808 CrossRef CAS.
- M. Lefort, Annu. Rev. Phys. Chem., 1958, 9, 123 CrossRef CAS.
- J. Pucheault and P. Sigli, Int. J. Radiat. Phys. Chem., 1976, 8, 613 CrossRef CAS ; see also P. Sigli, Ph.D. thesis, Université Paris VI, Paris, 1972.
- P. Lertnaisat, Y. Katsumura, J. Meesungnoen, J.-P. Jay-Gerin, S. Mukai, R. Umehara, Y. Shimizu and M. Suzuki, 15th International Congress of Radiation Research, Kyoto, Japan, 25–29 May 2015, Poster 2-PS6D-06 Search PubMed.
- J. Meesungnoen and J.-P. Jay-Gerin, J. Phys. Chem. A, 2005, 109, 6406 CrossRef CAS PubMed.
- J. Meesungnoen and J.-P. Jay-Gerin, in Charged Particle and Photon Interactions with Matter: Recent Advances, Applications, and Interfaces, ed. Y. Hatano, Y. Katsumura and A. Mozumder, Taylor & Francis Group, Boca Raton, 2011, p. 355 Search PubMed; see also J. Meesungnoen, Ph.D. thesis, Université de Sherbrooke, Sherbrooke, Québec, Canada, 2007.
- S. Sanguanmith, Y. Muroya, J. Meesungnoen, M. Lin, Y. Katsumura, L. Mirsaleh Kohan, D. A. Guzonas, C. R. Stuart and J.-P. Jay-Gerin, Chem. Phys. Lett., 2011, 508, 224 CrossRef CAS.
- J. Meesungnoen, S. Sanguanmith and J.-P. Jay-Gerin, RSC Adv., 2015, 5, 76813 RSC.
- R. L. Platzman, in Radiation Biology and Medicine. Selected Reviews in the Life Sciences, ed. W. D. Claus, Addison-Wesley, Reading, 1958, p. 15 Search PubMed.
- M. Tachiya, Radiat. Phys. Chem., 1983, 21, 167 CrossRef CAS.
- S. M. Pimblott, M. J. Pilling and N. J. B. Green, Radiat. Phys. Chem., 1991, 37, 377 CrossRef CAS.
- Y. Frongillo, T. Goulet, M.-J. Fraser, V. Cobut, J. P. Patau and J.-P. Jay-Gerin, Radiat. Phys. Chem., 1998, 51, 245 CrossRef CAS.
- T. Goulet, M.-J. Fraser, Y. Frongillo and J.-P. Jay-Gerin, Radiat. Phys. Chem., 1998, 51, 85 CrossRef CAS.
- I. Plante, Ph.D. thesis, Université de Sherbrooke, Sherbrooke, Québec, Canada, 2009.
- N. Autsavapromporn, J. Meesungnoen, I. Plante and J.-P. Jay-Gerin, Can. J. Chem., 2007, 85, 214 CrossRef CAS.
- T. Tippayamontri, S. Sanguanmith, J. Meesungnoen, G. R. Sunaryo and J.-P. Jay-Gerin, Recent Res. Dev. Phys. Chem., 2009, 10, 143 CAS.
- J. F. Ziegler, J. P. Biersack and M. D. Ziegler, SRIM - The Stopping and Range of Ions in Matter, SRIM Co., Chester, MD, 2015 CrossRef CAS; see also J. F. Ziegler, M. D. Ziegler and J. P. Biersack, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818 CrossRef CAS.
- J. A. LaVerne, in Charged Particle and Photon Interactions with Matter: Chemical, Physicochemical, and Biological Consequences with Applications, ed. A. Mozumder and Y. Hatano, Marcel Dekker, New York, 2004, p. 403 Search PubMed.
- S. Gordon, K. H. Schmidt and J. R. Honekamp, Radiat. Phys. Chem., 1983, 21, 247 CrossRef CAS.
- J. Meesungnoen, J.-P. Jay-Gerin, A. Filali-Mouhim and S. Mankhetkorn, Radiat. Res., 2002, 158, 657 CrossRef CAS PubMed.
- A. O. Allen, The Radiation Chemistry of Water and Aqueous Solutions, D. Van Nostrand Co., Princeton, NJ, 1961 Search PubMed.
- S. Sanguanmith, J. Meesungnoen, Y. Muroya, M. Lin, Y. Katsumura and J.-P. Jay-Gerin, Phys. Chem. Chem. Phys., 2012, 14, 16731 RSC.
- D. Swiatla-Wojcik and G. V. Buxton, J. Phys. Chem., 1995, 99, 11464 CrossRef CAS.
- M.-A. Hervé du Penhoat, T. Goulet, Y. Frongillo, M.-J. Fraser, Ph. Bernat and J.-P. Jay-Gerin, J. Phys. Chem. A, 2000, 104, 11757 CrossRef.
- S. L. Butarbutar, Y. Muroya, L. Mirsaleh Kohan, S. Sanguanmith, J. Meesungnoen and J.-P. Jay-Gerin, At. Indones., 2013, 39, 51 CrossRef.
- S. L. Butarbutar, S. Sanguanmith, J. Meesungnoen, G. R. Sunaryo and J.-P. Jay-Gerin, Radiat. Res., 2014, 181, 659 CrossRef CAS PubMed.
- S. Sanguanmith, J. Meesungnoen, D. A. Guzonas, C. R. Stuart and J.-P. Jay-Gerin, J. Nucl. Eng. Radiat. Sci., 2016, 2, 021014 CrossRef.
- A. J. Elliot, Rate constants and g-values for the simulation of the radiolysis of light water over the range 0-300 °C, Report AECL-11073, Atomic Energy of Canada Limited, Chalk River, Ontario, 1994 Search PubMed.
- C. R. Stuart, D. C. Ouellette and A. J. Elliot, Pulse radiolysis studies of liquid heavy water at temperatures up to 250 °C, Report AECL-12107, Atomic Energy of Canada Limited, Chalk River, Ontario, 2002 Search PubMed.
- D. Hatomoto, Y. Muroya, Y. Katsumura, S. Yamashita and T. Kozawa, in Book of Abstracts, 5th Asia-Pacific Symposium on Radiation Chemistry, University of Tokyo, Tokyo, Japan, 8–11 Sept. 2014, Paper No. P08, p. 140 Search PubMed.
- S. Sanguanmith, Y. Muroya, T. Tippayamontri, J. Meesungnoen, M. Lin, Y. Katsumura and J.-P. Jay-Gerin, Phys. Chem. Chem. Phys., 2011, 13, 10690 RSC.
- C. D. Alcorn, J.-C. Brodovitch, P. W. Percival, M. Smith and K. Ghandi, Chem. Phys., 2014, 435, 29 CrossRef CAS.
- C. Ferradini and J.-P. Jay-Gerin, Res. Chem. Intermed., 2000, 26, 549 CrossRef CAS.
Footnote |
| † Present address: Japan Radioisotope Association, Honkomagome 2-28-45, Bunkyo-ku, Tokyo 113-8941, Japan. |
| This journal is © The Royal Society of Chemistry 2017 |