Photophysics of chlorin e6: from one- and two-photon absorption to fluorescence and phosphorescence

Abstract

We present the study of optical and photophysical properties of chlorin e6, a known photosensitizer producing singlet oxygen. The linear and non-linear optical properties have been studied taking into account the dynamical and vibrational effects both by using Wigner distribution or coupling with molecular dynamics. A force field correctly describing the out-of-plane vibrations has been properly parameterized. The photophysical study revealed a possible efficient population of the triplet manifold, from the S₁ minimum region. Hence, fluorescence and singlet oxygen production are shown to coexist. Two-photon absorption high cross-section and far infrared absorption also suggest the possible use of chlorin e6 as an efficient sensitizer in two-photon absorption based phototherapy.

---

1 Introduction

Photodynamic therapy,^1–6 based on photosensitization of biological targets, is an emerging therapeutic strategy used to treat a number of pathologies including infections,⁷ skin diseases,⁸ and certain types of cancers.⁹ It involves the administration of an inert drug to the patient that is subsequently activated by absorption of visible light. The selective light-activation allows a better control of its action over conventional systemic drugs, considerably reducing potential side effects. Although different drug photo-activation mechanisms have been proposed and have been observed experimentally, including electron transfer^10,11 (type I photosensitization) or energy transfer,^12,13 by far the most common mechanism consists in the activation of molecular oxygen by the photoexcited drug to produce singlet oxygen (¹O₂).^14,15 Subsequently, the highly reactive ¹O₂ will produce a considerable oxidative stress, ultimately inducing apoptosis. From a molecular point of view, different targets of ¹O₂ have been reported including proteins, lipid membranes as well as nucleic acids. Recently, novel phototherapeutic drugs operating in absence of molecular oxygen have been reported as an alternative for the treatment of solid tumors exhibiting hypoxic conditions.^16,17

Photophysically speaking, the activation of ¹O₂ involves energy transfer from the drug triplet manifold to the molecular oxygen (³O₂). Hence, it is evident that one of the most crucial aspects of a potential phototherapeutic drug is its ability to populate the triplet manifold. In that respect, relatively high spin–orbit coupling and low energy gaps between triplet and singlet states are generally required.

Furthermore, in order to assure the efficient use of the drug the absorbed wavelengths should be displaced as much as possible toward the red. Indeed, while UV and blue lights are efficiently screened by biological tissues and skin in particular, red light is far more penetrating and hence will allow the treatment of deeper lesions. In particular it is highly desirable to have significant absorption in the so-called near-infrared therapeutic window (from 650 to 1350 nm), i.e. in the spectral window in which the penetration of biological tissues is maximal.¹⁸

Recently, to further enhance the absorption in the red or infra-red windows, the use of two-photon absorption (TPA) compounds has emerged as highly promising.^16,17,19,20 Indeed, TPA being characterized by the simultaneous absorption of two photons, their energy will be divided by two and, consequently, the wavelength doubles. The use of TPA presents also a secondary advantage over one-photon absorption (OPA): since the two photons should be absorbed simultaneously its probability will be proportional to the square of the light source intensity. Hence, TPA will most likely happen only at the laser focal point decreasing much more rapidly than OPA; this will in turn allow a much better focus on the lesion and hence once again reduce side effects. Finally, the use of red emissive drugs should also be considered as an advantage since it will allow the simultaneous combination of treatment and imaging.^21,22

Apart for organometallic drugs, such as ruthenium complexes,^23,24 which can however give rise to systemic effects and cytotoxicity, one of the most widely used class of compounds are porphyrins or porphyrin-like systems.^21,25

Indeed, those molecular systems combine a good absorption in the red (Q-band) with a relatively high intersystem crossing yield, and are hence recognized as good ¹O₂ activators.

Among the different porphyrin-like systems, the chlorin e6 (Ce6, Fig. 1) has been reported as a photodynamic drug^26–30 also related to the antibacterial treatment of ocular infections.²⁷

Fig. 1 Molecular structure of chlorin e6 (Ce6) most stable isomer.

Indeed, Ce6 has an important absorption in the red,^26,29,31 has been shown to be active as TPA photodrug,³² and shows an intersystem crossing efficient enough to allow activation of ¹O₂.²⁶ Interestingly, Ce6 has also been recently reported as able to sensitize rhodopsin, hence producing an indirect cis–trans isomerization of the retinal chromophore, happening at very long wavelengths and ultimately being able to trigger night vision.^33,34

However, even though some computational studies of Ce6 exist underlining both its absorption properties from a benchmark point of view^35,36 or its interaction with polymers,³⁷ the mechanisms leading to intersystem crossing and triplet population is far less characterized.

It is noteworthy that the study of the Ce6 photophysics is not a trivial task and may allow a better comprehension of the underlining mechanism in different porphyrin-like systems. An important point that need to be highlighted is the fact that in planar conjugated systems the dynamic and vibrational effects will play an important role in modulating both the absorption and the photophysics, through the presence of low-frequency high-amplitude normal modes.^38,39 Hence, specifically tailored protocols able to efficiently tackle these effects should be taken into account.

One promising strategy in that respect is coupling excited state calculations with classical molecular dynamics (MD) simulations.^39,40 However, in this case the proper parameterization of force field is far from being trivial.^41–43 Special care is needed to the correct representation of the low-frequencies modes whose effects on the photophysics are the larger.

In this contribution we perform a detailed photophysics study of Ce6, coupled with the parameterization of a force field able to correctly reproduce optical linear and non-linear properties as compared with experimental values and also with quantum potential based protocols, such as the use of Wigner distribution extracted from molecular Hessians. The intersystem crossing pathway and mechanism are also studied in detail and clarified. Indeed, differently from most of the previous studies, a proper description of the Ce6 optical properties (especially absorption) was considered as the main criterion to establish the validity of the force field parameterization. This is particularly significant since optical properties, especially in the case of planar conjugated systems, crucially depend on the reliable representation of the chromophore geometry at Franck–Condon region and on its vibronic structure.

2 Methods

2.1 Computational strategies

In many cases it has been shown that for large conjugated planar molecules the usual approach consisting in the calculation of the absorption spectrum as vertical transition from the ground-state equilibrium geometry (Franck–Condon) is clearly insufficient. Indeed, vibrational and dynamic effects may induce a noticeable shift in the absorption wavelengths that may alter significantly the optical properties of the systems. Furthermore, a pure static approach will provide only a very low level approximation to the band shape that is often a key point in the spectrum reproduction. Obviously, exactly the same considerations hold for emission that also necessitate to go beyond the vertical approximation.

Different approaches have been proposed in order to tackle this problem, for instance Santoro's group has proposed the explicit calculation of the vibronic coupling via the Franck–Condon integrals.^44,45 Even though promising, the actual implementation based on numerical integration may fail in the case of large-scale out-of-plane vibrations.

An alternative strategy consists in coupling excited states calculations with a preliminary exploration of the conformational space. This will provide an ensemble of representative snapshots and the final spectrum will be obtained as a convolution of all the vertical transitions. Once again two different strategies can be used, one can perform classical molecular dynamics^38–40 (MD), or explore the vibrational normal modes performing a Wigner distribution based on the calculation of the harmonic vibrational frequencies at the ground-state equilibrium geometry.⁴⁶

Both methods have advantages and drawbacks, the MD based allows to explore simultaneously different conformers; furthermore it can be straightforwardly used in the case of interaction of chromophore with complex extended systems, such as biological polymers or membranes. However, the description of the normal modes is restricted at the force field level. In the case of Wigner distribution, the normal modes are calculated from the Hessian of the wavefunction, hence they do not imply any parameterization. However, only one conformation can be explored at a time, and only the chromophore in homogeneous media can be reasonably treated. On the other hand, Wigner distribution allows a straightforward extension to the study of emission (fluorescence and phosphorescence) only requiring the geometry optimization and the harmonic frequencies calculations of the first excited singlet or lowest triplet state.

As far as the environment is concerned, even though not strictly necessary, in the case of MD coupling the most straightforward approach is to use hybrid quantum mechanics/molecular mechanics (QM/MM) methods, while an implicit description of the solvent via a polarizable continuum appears more adapted for the Wigner approach.

In this contribution, the two different approaches have been tested on Ce6 in water solution. The force field parameters have also been optimized to correctly reproduce the optical properties as calculated by the Wigner approach.

2.2 Computational details

Ce6 ground state (S₀) has been optimized at density functional theory (DFT) level using the 6-31G* basis set and B3LYP functional with Gaussian09 code.⁴⁷ Solvent (water) has been represented by the polarizable continuum model (PCM).⁴⁸ Also the geometries of the lowest triplet (T₁) and first excited singlet (S₁) states have been optimized using DFT and time dependent DFT (TD-DFT), respectively. For all excited states calculations, the CAM-B3LYP/6-31+G* level of theory was applied, after benchmarking with different basis sets and functionals (see ESI†). Harmonic frequencies for all the three states minima have been calculated too.

In order to calculate the optical properties, twenty snapshots have been obtained from the Wigner distribution based on the vibrational frequencies. The absorption spectrum has been calculated as the convolution of the linear transition for all the snapshots obtained at TD-DFT level including the solvent reproduced as PCM.

More in detail, the Wigner distribution has been performed on S₀, S₁ and T₁ minima to calculate the absorption, fluorescence and phosphorescence spectra. To show that the corresponding geometries are in their local minima, a frequency calculation was performed for each of them (see ESI† for details). Phosphorescence has been calculated using Dalton2016 ^49,50 due to the possibility of calculating the singlet–triplet oscillator strengths via the inclusion of the spin–orbit coupling.^51,52

Conversely, a force field has been parameterized for Ce6 (see ESI†) based on generalized amber force field (gaff).⁵³ Charges have been obtained following the standard RESP⁵⁴ procedure while additional bonding parameters have been tuned to correctly reproduce the fused ring vibrations. Ce6 has been solvated in a truncated dodecahedron box containing 872 TIP3P⁵⁵ water molecules and a molecular dynamics of 20 ns was performed using Amber 2016.⁵⁶ Snapshots have been extracted and the absorption spectrum calculated at TD-DFT/MM level using a local modified version of the Gaussion09 code.^57,58 The performance of the force field versus Wigner approaches has been checked in terms of the maximization of the overlap between the two computed absorption spectra and minimization of the root mean square deviation (RMSD) between the Wigner and force field snapshots.

Once the force field optimized, the TPA cross section has also been calculated using the quadratic response of the single residue formalism⁵⁹ as implemented in Dalton2016.

Finally, the photophysical pathway has been obtained defining a global coordinate approximating the minimum energy path, and calculating the evolution of the involved potential energy surfaces. In particular a linear interpolation between the equilibrium S₁ and T₁ geometries has been considered. Spin–orbit couplings have been estimated with Dalton2016.

In order to better define the nature of the electronic excited state, the electronic density reorganization has been analysed in terms of natural transition orbitals (NTO)⁶⁰ obtained with the Nancy_EX code.^61–63

3 Results and discussion

3.1 Tautomeric equilibrium and force field performance

Like different non-symmetric porphyrin systems, Ce6 can exist in the form of different tautomers. The tautomerism is related to the position of the two inner hydrogen atoms (NH tautomers).⁶⁴ In the case of Ce6, six independent conformations can be realized, hence one should in principle consider six different isomers.

However it appears that only the configuration having opposite hydrogen atoms as reported in Fig. 1 (t1) has a significant Boltzmann population at room temperature. Indeed, as reported in Fig. 2, upon performing a configuration analysis, it turns out that all the other isomers lies significantly higher in energy, form 4.6 to 16.3 kcal mol⁻¹. Consequently only a population of about 0.05% can be hypothesized for the second lowest lying isomer having two adjacent hydrogen atoms (t2). The other conformers (t3–t6) having a population not exceeding 10⁻⁶% one can safely say that the photophysical properties of Ce6 can be inferred only from its dominant conformer, and as a consequence only the parameterization of one force field is needed.

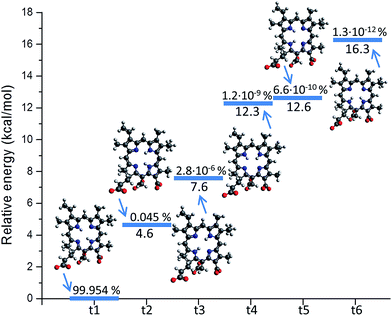Fig. 2 The six isomers of Ce6 (t1–t6) with respect to the inner hydrogen atoms position. Their relative energy and Boltzmann distribution population is shown.

Regarding the performance of the generated force field parameters, the usual procedure to test their reliability is to compute the root mean square deviation (RMSD) of the heavy atoms positions, having as reference geometry a crystal structure or, if not available as in this case, the QM optimized geometry. During the 20 ns dynamics we observed the presence of two stable conformers of the t1 tautomer, arising from the almost free rotation of the ethylene group (–CH₂–CH₃). In particular, the average RMSD values account for 0.34 when the ethylene group is coplanar with the chlorin ring, and 0.52 when out-of-plane. Our approach shows therefore an improvement when compared to previous force field parameterizations of similar compounds in vacuum.⁴³

3.2 One- and two-photon absorption spectra

The OPA absorption spectrum of Ce6 is reported in Fig. 3, calculated taking into account vibrational effects by the two approaches, MD or Wigner distribution, as detailed in the Methods section.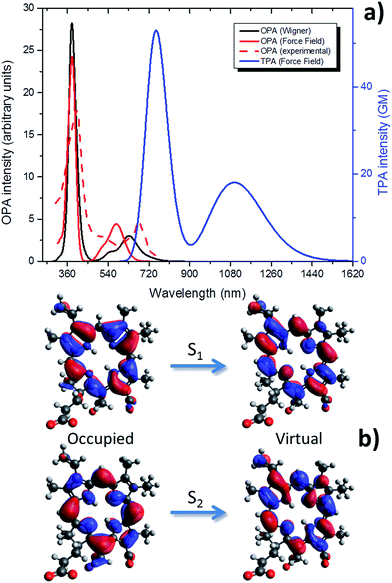

Fig. 3 Optical absorption properties of Ce6: (a) OPA calculated by Wigner distribution, considering the water environment by PCM (solid red); normalized experimental OPA in water taken from literature⁶⁵ (dashed red); OPA and TPA calculated at the QM/MM level as convolution of MD snapshots (black and blue, respectively). (b) The occupied (left) and virtual (right) NTOs describing the two lowest-lying singlet excited states (S₁ and S₂).

While the more intense Soret band is in the UVA spectral range, the Q-band covers the red portion of the spectrum.

Wigner distribution gives excitation energy at the absorption maximum of 1.97 eV (630 nm), on the other hand the force field level yields absorption maximum at 2.12 eV (585 nm). Those values compare well with the experimental absorption maximum in water of 1.92 eV (644 nm)^29,31 with even a stunning agreement with the Wigner distribution results.

Although a slightly larger difference has been found in the case of force field determination, the agreement is still in an acceptable range and however in the accuracy limit of TD-DFT calculations.

Remarkably enough, the Q-band shape is also quite well reproduced by both approaches, and in particular one can observe a shoulder at shorter wavelengths than the absorption maximum. As far as the Soret band is concerned, the agreement between our two approaches is almost perfect and the two spectra are almost completely superposable.

The critical parameterization of adequate force fields to reproduce optical properties of Ce6, and more generally porphyrin-like systems, can be easily understood by analysing the NTOs describing the S₀ → S₁ transition (Fig. 3b). Indeed the energy density reorganization involves π–π* transitions centered on the fused and conjugated rings constituting the porphyrin core. The relative energy between the ground and the excited state can change in a non-trivial way due to the out-of-plane vibrations. Indeed, from simple orbital theory one can infer that the formers will partially break conjugation; hence they will increase the energy of the ground state (π) while decreasing the energy of the excited state (π*). Only a very fine representation of those vibrational modes will then allow to correctly reproduce optical properties. This is also confirmed by the value of the RMSD between snapshots extracted from MD and Wigner distribution that is generally low, as reported in ESI.† On the other hand, tuning absorption spectra may be seen as a very precise way of obtaining force field correctly describing the complex out-of-plane vibrations of fused rings.

In Fig. 3 we also report the TPA absorption spectrum of Ce6 calculated from the force field approach. As expected the bands now lie in the red or infrared part of the spectrum. The absorption maximum for the Q-band is now around 1100 nm while the Soret band appears at more than 700 nm. Although not as high as the ones of thiophene^46,66,67 systems, TPA cross-sections are still reasonable and account for about 20 (Q-band) and 60 GM (Soret band). The available experimental TPA value at 800 nm is 33.9 GM,⁶⁸ in remarkable agreement with the simulated value (33.2 GM). Note also that the general shape of the TPA spectrum strongly resemble the OPA one, as expected by a non-symmetric molecule.²⁰ In particular, the Soret band is still much more intense than the Q-band. Due to the infrared absorption and the reasonable values of the TPA cross-section, it seems reasonable to consider Ce6 as a potentially interesting TPA absorber dye.³²

3.3 Emission pathways

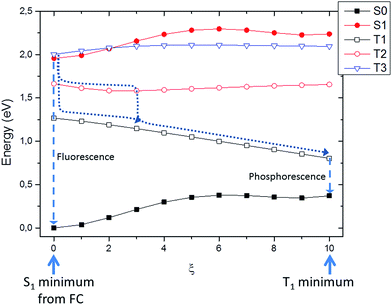
Upon excitation to the S₁ or S₂ state two different pathways leading to light emission may be considered, the first involving the singlet manifold, i.e. fluorescence; and the second leading to population of the triplet manifold and subsequent emission by phosphorescence.

Due to the Kasha's rule stipulating that emission will always take place from the lowest excited state of a given multiplicity, we optimized both S₁ and T₁ and we performed a Wigner distribution to calculate the spectra.

3.3.1 Fluorescence and phosphorescence spectra. Calculated fluorescence and phosphorescence spectra of Ce6 are reported in Fig. 4.

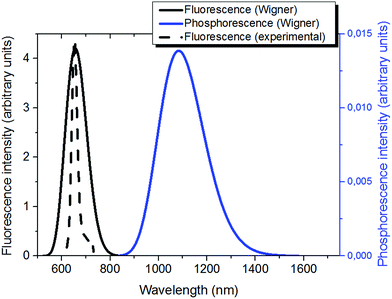Fig. 4 Emission properties of Ce6: simulated (solid black) and normalized experimental fluorescence⁶⁵ (dashed black); simulated phosphorescence (blue).

As expected, the phosphorescence spectrum is shifted to the red as compared to fluorescence. The fluorescence spectrum gives a maximum at 1.88 eV (660 nm); the Stokes shift obtained for fluorescence is globally low and accounts for about 0.3 eV. Our results agree well with the experimental findings that place the fluorescence maximum at 1.86 eV (668 nm) in a polar environment (ethanol at a temperature of 298 K).²⁹

On the other hand, simulated phosphorescence peaks at around 1.14 eV (1080 nm). Note also the recovering of the slight asymmetry of the emission spectral band with the presence of an important tail extending to the infrared region. As far as the experimental results are concerned, a direct detection of phosphorescence is not trivial, as shown by the 1.40 (886 nm) value obtained only at 77 K in ethanol.²⁹ Nevertheless, the optical properties of Ce6 were shown to be solvent independent regarding absorption and only slightly dependent concerning fluorescence (15 nm blue-shifted from ethanol to water).⁶⁵ Hence, we should conclude that a slight blue shift of ca. 0.3 eV is found by our simulations, probably due to a non-perfect description of the solvent relaxation.⁴⁰

Because of the consistent fluorescence intensity – and the difficulties in measuring phosphorescence – in biological and nanomaterials applications of Ce6 and porphyrin derivatives,^69–71 it seems unlikely that the emission is due to phosphorescence, and should rather be assigned to the emission from the singlet manifold. This aspect can be ascribed to two factors, first a non-unitary population of the triplet manifold should be taken into account, leading to a significant residual population of the singlet manifold, that can relax and lead to emission. Secondly, the presence of oxygen may lead to deactivation of the triplet state via the production of ¹O₂ and hence lower phosphorescence quantum yield.

3.3.2 Intersystem crossing pathways. In order to further rationalize the photophysical properties of Ce6 we analysed the potential energy surfaces along the path possibly leading to the triplet population.

Firstly we searched for possible singlet–triplet crossings from the Franck–Condon to the S₁ minimum. Indeed, in this region no direct crossing was found, and all the triplets lied significantly far away in energy. Hence, it is reasonable to assume that, upon excitation, Ce6 will firstly relax to the S₁ minimum, where it will be trapped for a significant amount of time. This aspect is also compatible with the hypothesized fluorescence as described in the previous section. Subsequently we studied the energy landscape along the coordinate connecting S₁ to T₁ minima. Although, once again no real crossing was observed, three triplets are sufficiently close in energy to play a photophysical role. Indeed, it has to be recalled that the system being trapped in the S₁ excited state minimum, it will be constraint to spend a significant amount of time in the same potential energy surface region. Nevertheless, the intersystem crossing rate in Ce6 is probably fast enough to compete with the radiative relaxation and internal conversion in the singlet manifold. More in detail at S₁ minimum, T₁ is lower in energy (∼0.75 eV), on the other hand T₂ is closer (0.25 eV) while a third state T₃ is higher in energy but quasi-degenerate. Along the linear interpolation coordinate S₁, T₂ and T₃ run almost parallel, while obviously T₁ is stabilized (Fig. 5).

Fig. 5 Simplified pathway (along an interpolation coordinate) between S₁ and T₁ minima structures. Fluorescence and phosphorescence emissions are represented by dashed arrows, while possible intersystem crossing mechanisms are represented by dotted arrows.

Hence, two possible mechanisms for the intersystem crossing can be hypothesized: a direct mechanism with population of the T₁ state directly from S₁, or a two-steps mechanism involving first intersystem-crossing to T₃ and secondly internal conversion to T₁ through T₂. In order to further discriminate between the two mechanisms we also estimated the spin–orbit coupling between the involved states at the S₁ minimum geometry. The coupling between S₁ and T₁ is relatively high accounting for about 30 cm⁻¹, while the ones involving T₂ and T₃ is much lower (4 and 8 cm⁻¹, respectively). Hence, even though the direct S₁ → T₁ mechanism appears as more probable the indirect one S₁ → T₃ → T₂ → T₁ can presumably compete, also due to the much smaller energy difference (Fermi's golden rule). In any case, the photophysical picture is coherent with the possible population of the triplet manifold and hence with the ability of Ce6 to act as an efficient photo-activator of singlet oxygen. Indeed, since the singlet–triplet band gap of molecular oxygen (i.e. from ³Σ_g to ¹Δ_g) is 0.97 eV, as measured by infrared emission at ∼1275 nm,^72–76 we can conclude that a feasible energy transfer can be expected from the triplet manifold of Ce6 to O₂.

Experimental findings concerning the possible intersystem crossing pathways in metal-free porphyrin derivatives, show indeed that the triplet manifold can be populated with an excited state lifetime that can reach the microsecond time scale. Moreover, a ¹O₂ quantum yield up to 0.74 can be induced, evidencing the energy transfer process feasibility.⁷⁷ Regarding ultrafast (i.e. femtosecond resolution) excited state dynamics, fluorescent-up conversion and transient absorption spectroscopy can provide useful information to compare with our simulations. Especially, experiments were conducted on tetraphenylporphyrin at room temperature (298 K) in benzene, because of solubility issues,⁷⁸ hence making possible only a qualitative comparison with our results: after illumination (i) intramolecular vibrational energy redistribution is expected in the 100–200 fs time scale, probably corresponding to the relaxation observed from Franck–Condon to S₁ minimum regions; (ii) a fast (1.4 ps) and a slow (10–20 ps) signal are addressed to vibrational and thermal redistribution (i.e. elastic collision and thermal exchange) within the solvent, hence corresponding to the expected time spent in the S₁ minimum region, giving rise to fluorescence, as experimentally observed; (iii) excited state decay of the equilibrated population on the ns time scale, due to intersystem crossing to the triplet state, as suggested by the present study. The ns nature of the excited state lifetime was also found for Ce6 in a NaCl solution.⁶⁸

Certainly, the need of further single-molecule experimental and theoretical studies attempting to reproduce more reliably the required environment (depending on the type of application), constitute a recently proposed technological challenge.⁷⁹

4 Conclusions

We have performed a detailed study of the photophysical properties of a known sensitizer, Ce6. In particular we have been able to correctly reproduce its optical linear and non-linear properties. This included comparing the strategy relying on Wigner distribution for the exploration of the conformational space with the parameterization of a tailored force field. We have shown that the two approaches give comparable results, and hence that the parameterization was successful. We remind that this aspect is a known critical point for porphyrin-like systems. Our approach allows to define a sounding method to correctly sample the out-of-plane vibrations of fused rings at force field level. The non-linear properties have been calculated too, highlighting the possible use of Ce6 as a TPA sensitizer due to its absorption in the infrared and the relatively high cross sections.

Emission properties have been calculated both taking into account fluorescence and phosphorescence. The comparison with experimental data has allowed to unambiguously assign emission to fluorescence, hence pointing to a preliminary relaxation to the S₁ minimum.

Finally, the photophysical pathways have been rationalized: although no singlet–triplet crossing has been evidenced, the population of the triplet manifold is possible starting from the S₁ minimum, due to the presence of low-lying triplets close in energy to the singlet state and presenting high or moderately high spin–orbit coupling. Two mechanisms, direct intersystem crossing to T₁ or indirect via population of T₃ and T₂, appear as the most probable paths. Those results are in agreement with both the observed fluorescence emission and the production of ¹O₂ necessitating population of the triplet manifold.

Our studies have allowed rationalizing the photophysical properties of solvated Ce6, also developing adequate tools (force fields) for its further exploration. In the future we plan the study of the photosensitization of biological systems by Ce6 including the possible photosensitization of trans-membrane proteins like rhodopsins.

Acknowledgements

We gratefully acknowledge support from the COST action “MOLIM: Molecules in Motion”. M. M. is thankful to the French and Austrian National Research Agencies (ANR and FWF, respectively) for a grant under the “DeNeTheor” project.

References

1. E. Koshi, A. Mohan, S. Rajesh and K. Philip, J. Indian Soc. Periodontol., 2011, 15, 323.
2. R. K. Pandey, J. Porphyrins Phthalocyanines, 2000, 4, 368–373.
3. Z. Huang, H. Xu, A. D. Meyers, A. I. Musani, L. Wang, R. Tagg, A. B. Barqawi and Y. K. Chen, Technol. Cancer Res. Treat., 2008, 7, 309–320.
4. R. R. Allison and C. H. Sibata, Photodiagn. Photodyn. Ther., 2010, 7, 61–75.
5. R. R. Allison and K. Moghissi, Photodiagn. Photodyn. Ther., 2013, 10, 331–341.
6. M. Yin, Z. Li, Z. Liu, J. Ren, X. Yang and X. Qu, Chem. Commun., 2012, 48, 6556–6558.
7. T. Dai, Y.-Y. Huang and M. R. Hamblin, Photodiagn. Photodyn. Ther., 2009, 6, 170–188.
8. P. Babilas, M. Landthaler and R.-M. Szeimies, Eur. J. Dermatol., 2006, 16, 340–348.
9. P. Agostinis, K. Berg, K. A. Cengel, T. H. Foster, A. W. Girotti, S. O. Gollnick, S. M. Hahn, M. R. Hamblin, A. Juzeniene, D. Kessel, M. Korbelik, J. Moan, P. Mroz, D. Nowis, J. Piette, B. C. Wilson and J. Golab, Ca-Cancer J. Clin., 2011, 61, 250–281.
10. K. Hirakawa, K. Ota, J. Hirayama, S. Oikawa and S. Kawanishi, Chem. Res. Toxicol., 2014, 27, 649–655.
11. H. Gattuso, V. Besancenot, S. Grandemange, M. Marazzi and A. Monari, Sci. Rep., 2016, 6, 28480.
12. J. Zhao, W. Wu, J. Sun and S. Guo, Chem. Soc. Rev., 2013, 42, 5323.
13. E. Bignon, H. Gattuso, C. Morell, E. Dumont and A. Monari, Chemistry, 2015, 21, 11509–11516.
14. B. W. Henderson and T. J. Dougherty, Photochem. Photobiol., 1992, 55, 145–157.
15. S. Wang, R. Gao, F. Zhou and M. Selke, J. Mater. Chem., 2004, 14, 487.
16. Y.-C. Zheng, M.-L. Zheng, K. Li, S. Chen, Z.-S. Zhao, X.-S. Wang and X.-M. Duan, RSC Adv., 2015, 5, 770–774.
17. Q. Zou, H. Zhao, Y. Zhao, Y. Fang, D. Chen, J. Ren, X. Wang, Y. Wang, Y. Gu and F. Wu, J. Med. Chem., 2015, 58, 7949–7958.
18. C.-L. Tsai, J.-C. Chen and W.-J. Wang, J. Med. Biol. Eng., 2001, 21, 7–14.
19. H. Gattuso, E. Dumont, M. Marazzi and A. Monari, Phys. Chem. Chem. Phys., 2016, 18, 18598–18606.
20. M. Pawlicki, H. A. Collins, R. G. Denning and H. L. Anderson, Angew. Chem., Int. Ed., 2009, 48, 3244–3266.
21. M. Ethirajan, Y. Chen, P. Joshi and R. K. Pandey, Chem. Soc. Rev., 2011, 40, 340–362.
22. Q. Yuan, Y. Wu, J. Wang, D. Lu, Z. Zhao, T. Liu, X. Zhang and W. Tan, Angew. Chem., Int. Ed., 2013, 52, 13965–13969.
23. E. S. Antonarakis and A. Emadi, Cancer Chemother. Pharmacol., 2010, 66, 1–9.
24. G. Suss-Fink, Dalton Trans., 2010, 39, 1673–1688.
25. R. Bonnett, Chem. Soc. Rev., 1995, 24, 19.
26. J. M. Fernandez, M. D. Bilgin and L. I. Grossweiner, J. Photochem. Photobiol., B, 1997, 37, 131–140.
27. K. Winkler, C. Simon, M. Finke, K. Bleses, M. Birke, N. Szentmáry, D. Hüttenberger, T. Eppig, T. Stachon, A. Langenbucher, H. J. Foth, M. Herrmann, B. Seitz and M. Bischoff, J. Photochem. Photobiol., B, 2016, 162, 340–347.
28. E. S. Nyman and P. H. Hynninen, J. Photochem. Photobiol., B, 2004, 73, 1–28.
29. E. Zenkevich, E. Sagun, V. Knyukshto, A. Shulga, A. Mironov, O. Efremova, R. Bonnett, S. P. Songca and M. Kassem, J. Photochem. Photobiol., B, 1996, 33, 171–180.
30. S. Paul, P. W. S. Heng and L. W. Chan, J. Fluoresc., 2013, 23, 283–291.
31. O. L. Gladkova, M. V. Parkhats, A. N. Gorbachova and S. N. Terekhov, Spectrochim. Acta, Part A, 2010, 76, 388–394.
32. A. V. Kachynski, A. Pliss, A. N. Kuzmin, T. Y. Ohulchanskyy, A. Baev, J. Qu and P. N. Prasad, Nat. Photonics, 2014, 8, 455–461.
33. I. Washington, C. Brooks, N. J. Turro and K. Nakanishi, J. Am. Chem. Soc., 2004, 126, 9892–9893.
34. I. Washington, J. Zhou, S. Jockusch, N. J. Turro, K. Nakanishi and J. R. Sparrow, Photochem. Photobiol. Sci., 2007, 6, 775–779.
35. B. Minaev and H. Ågren, Chem. Phys., 2005, 315, 215–239.
36. S. Perun, J. Tatchen and C. M. Marian, ChemPhysChem, 2008, 9, 282–292.
37. V. B. Tsvetkov, A. B. Solov'eva and N. S. Melik-Nubarov, Phys. Chem. Chem. Phys., 2014, 16, 10903–10913.
38. T. Etienne, T. Very, E. A. Perpète, A. Monari and X. Assfeld, J. Phys. Chem. B, 2013, 117, 4973–4980.
39. E. Dumont and A. Monari, J. Phys. Chem. B, 2015, 119, 410–419.
40. T. Etienne, H. Gattuso, A. Monari and X. Assfeld, Comput. Theor. Chem., 2014, 1040, 367–372.
41. F. Autenrieth, E. Tajkhorshid, J. Baudry and Z. Luthey-Schulten, J. Comput. Chem., 2004, 25, 1613–1622.
42. X. Y. Li, R. S. Czernuszewicz, J. R. Kincaid and T. G. Spiro, J. Am. Chem. Soc., 1989, 111, 7012–7023.
43. L. Zhang, D.-A. Silva, Y. Yan and X. Huang, J. Comput. Chem., 2012, 33, 1969–1980.
44. F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 84509.
45. R. Improta, V. Barone and F. Santoro, Angew. Chem., Int. Ed., 2007, 46, 405–408.
46. H. T. Turan, Y. Eken, M. Marazzi, M. Pastore, V. Aviyente and A. Monari, J. Phys. Chem. C, 2016, 120, 17916–17926.
47. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revis. D.01, Gaussian Inc., Wallingford CT, 2010.
48. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
49. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenaes, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjaergaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnaes, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284.
50. Dalton, a Mol. Electron. Struct. program. Release Dalton2016.A, see http//daltonprogram.org.
51. I. Tunell, Z. Rinkevicius, O. Vahtras, P. Sałek, T. Helgaker and H. Ågren, J. Chem. Phys., 2003, 119, 11024.
52. B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371.
53. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
54. J. Wang, P. Cieplak and P. A. Kollman, J. Comput. Chem., 2000, 21, 1049–1074.
55. P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960.
56. D. A. Case, et al., AMBER 15, University of California, San Francisco, 2015.
57. A. Monari, J.-L. Rivail and X. Assfeld, Acc. Chem. Res., 2013, 46, 596–603.
58. N. Ferré and X. Assfeld, J. Chem. Phys., 2002, 117, 4119–4125.
59. P. Sałek, O. Vahtras, T. Helgaker and H. Ågren, J. Chem. Phys., 2002, 117, 9630.
60. R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777.
61. T. Etienne, X. Assfeld and A. Monari, J. Chem. Theory Comput., 2014, 10, 3906–3914.
62. T. Etienne, X. Assfeld and A. Monari, J. Chem. Theory Comput., 2014, 10, 3906–3914.
63. T. Etienne, J. Chem. Theory Comput., 2015, 11, 1692–1699.
64. E. I. Zenkevich, A. M. Shulga, I. V Filatov, A. V Chernook and G. P. Gurinovich, Chem. Phys. Lett., 1985, 120, 63–68.
65. S. Paul, P. W. S. Heng and L. W. Chan, J. Fluoresc., 2013, 23, 283–291.
66. M. Kong, T. Wang, X. Tian, F. Wang, Y. Liu, Q. Zhang, H. Wang, H. Zhou, J. Wu and Y. Tian, J. Mater. Chem. C, 2015, 3, 5580–5588.
67. H. Zhou, F. Zhou, S. Tang, P. Wu, Y. Chen, Y. Tu, J. Wu and Y. Tian, Dyes and Pigments, 2012, 92, 633–641.
68. P. D. Zhao, P. Chen, G. Q. Tang, G. L. Zhang and W. J. Chen, Two-photon spectroscopic properties of a new chlorin derivative photosensitizer, 2004, vol. 390.
69. Y.-Y. Wang, A.-R. Ryu, S. Jin, Y.-M. Jeon and M.-Y. Lee, PLoS One, 2017, 12, e0170599.
70. L. Yan, Z. Wang, X. Chen, X. Gao, Z. Zhang, X. Zhu, M. Lan, W. Che, G. Zhu and W. Zhang, Chem. Commun., 2017 10.1039/C6CC09510K.
71. F. Cheng, X. Wu, M. Liu, Y. Lon, G. Chen and R. Zeng, Sens. Actuators, B, 2016, 228, 673–678.
72. A. Jiménez-Banzo, X. Ragàs, P. Kapusta and S. Nonell, Photochem. Photobiol. Sci., 2008, 7, 1003–1010.
73. J. W. Snyder, I. Zebger, Z. Gao, L. Poulsen, P. K. Frederiksen, E. Skovsen, S. P. McIlroy, M. Klinger, L. K. Andersen and P. R. Ogilby, Acc. Chem. Res., 2004, 37, 894–901.
74. A. U. Khan and M. Kasha, Proc. Natl. Acad. Sci. U. S. A., 1979, 76, 6047–6049.
75. P. R. Ogilby, Acc. Chem. Res., 1999, 32, 512–519.
76. A. A. Krasnovsky, Photochem. Photobiol., 1979, 29, 29–36.
77. J. Cáceres, J. Robinson-Duggon, A. Tapia, C. Paiva, M. Gómez, C. Bohne and D. Fuentealba, Phys. Chem. Chem. Phys., 2017, 19, 2574–2582.
78. J. S. Baskin, H.-Z. Yu and A. H. Zewail, J. Phys. Chem. A, 2002, 106, 9837–9844.
79. T. Kondo, W. J. Chen and G. S. Schlau-Cohen, Chem. Rev., 2017, 117, 860–898.

---

Footnote

† Electronic supplementary information (ESI) available: Details on the Wigner distribution; benchmark of the static absorption spectrum; force field and related molecular dynamics details. See DOI: 10.1039/c6ra28616j

---