Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the structure and hydrogen bonding network of (H2O)32 and (H2O)33: an improved Monte Carlo temperature basin paving (MCTBP) method and quantum theory of atoms in molecules (QTAIM) analysis†
Avijit Rakshita,
Takamasa Yamaguchib,
Toshio Asadabc and
Pradipta Bandyopadhyay *a
*a
aSchool of Computational and Integrative Sciences, Jawaharlal Nehru University, New Delhi, India 110067. E-mail: praban07@gmail.com
bDepartment of Chemistry, Graduate School of Science, Osaka Prefecture University, 1-1 Gakuen-cho, Naka-ku, Sakai 599-8531, Japan
cThe Research Institute for Molecular Electronic Devices (RIMED), Osaka Prefecture University, 1-1 Gakuen-cho, Naka-ku, Sakai 599-8531, Japan
First published on 27th March 2017
Abstract
Large water clusters are of particular interest because of their connection to liquid water and the intricate hydrogen bonding networks they possess. Generally, clusters above (H2O)25 are cage-like; however, the diversity of their hydrogen bonding can be enormous and is related to the stability of the cluster. Two main challenges for understanding hydrogen bonding networks are how to determine a few low energy minima in the extremely rugged energy surface of large water clusters and how to rationalize the relative stability of different structures of a cluster based on simple chemical concepts, particularly when they are very close in energy. In the current work, an improved version of the Monte Carlo Temperature Basin Paving (MCTBP) method has been used to find low energy structures of (H2O)32 and (H2O)33 as an answer to the first challenge. Previously, the MCTBP method has been applied to large water clusters with reasonable success. In this work, we have changed the Monte Carlo acceptance/rejection condition to make the calculation more efficient. After finding several structures at either the same or lower energy of previously known structures, the quantum theory of atoms in molecules (QTAIM) method has been applied to analyze the relationship between the stability and polarized charges on each water molecule in a cluster. Overall, an increase of the polarized charge on the oxygen atom was found to stabilize the energy of a water molecule in a cluster.
Introduction
The different forms of water have drawn significant attention from researchers for the last several decades as water influences most of the chemical and biological processes in nature. Knowledge of water clusters can be important because they bridge the properties of gas and liquid phase water. Large water clusters are characterized by their diverse hydrogen bonding (HB) network; however, how the HB network changes as a function of the size of cluster is not fully understood. A suitable strategy to understand this problem could be to find structures of water clusters as a function of their size, then rationalize their stability in terms of their HB network and electronic properties; however, because of the fluxional nature of the clusters, the number of possible structures for a particular sized water cluster is enormous. A major research thrust has been finding low energy structures of water clusters using various optimization techniques. Structural optimizations have been challenging due to the presence of a large number of stationary points on the potential energy surface of the cluster. Rationalizing the relative stability of the low energy structures can be done from a quantum mechanical (QM) approach, although for larger water clusters it is very time consuming. As part of our continuing effort to understand water clusters, we consider (H2O)32 and (H2O)33 in this work with a focus on finding low energy structures using a Monte Carlo (MC) based scheme and rationalizing the stability of a cluster with the quantum theory of atoms in molecules (QTAIM) method.1Both theoretical and experimental investigations have been done by different authors on neutral and ionized water clusters and water clusters with other molecules. As the current work is on pure water clusters, we are mostly restricting the discussion to some representative previous works related to pure water clusters. Wales et al. studied the structural and thermodynamical properties of water clusters of 8 and 20 molecules using a molecular dynamics simulation.2 Su et al. and Liu et al. carried out second-order Moller–Plesset (MP2) level of calculations on water clusters with 2–19 and 2–30 molecules, respectively.3,4 Maheshwari et al. performed Hartree–Fock (HF) and density functional theory (DFT) calculations on water clusters with 8 to 20 molecules.5 The Fragment Molecular Orbital (FMO) approach has been applied by the Gordon group on water clusters with 16, 20, 32 and 64 molecules.6 Li et al. used DFT to understand small water clusters7 and worked on large water clusters with 30 to 48 molecules with MC based scheme plus DFT calculations.8 Molecular orbital analysis and energy decomposition analysis has been done by Wang et al. at the DFT and post-HF levels to understand the HB characteristics in water dimer.9 Yang et al. have carried out vibrational frequency analysis of HB in water clusters (H2O)n (n = 6 to 21) and have shown the presence of strong HB in low energy water clusters.10 Iwata et al. used a locally-projected molecular orbital method to understand the cooperative role of charge transfer and dispersion terms in HB networks in water clusters.11 Bako et al. studied the hierarchy of cooperative effect of HB, characteristics of HB, and dipole moment in water monomer, small sized clusters, and large cage-like clusters.12 The Bandyopadhyay group examined structures of larger water clusters in several works.13–15 The Gadre group has also examined water clusters using both ab initio and molecular tailoring approaches.5,16,17 Xantheas et al. have performed high level ab initio calculations on water clusters.18–25 Anick also investigated polyhedral water clusters in several works.26,27 The Shields group looked into water cluster formation (for (H2O)n, n = 2 to 10) using a combination of molecular dynamics and MP2 calculations, and characterized anharmonicity in the vibrational frequency in water clusters of 1 to 10 molecules.28,29
Among the experimental works, the Saykally group applied tetrahertz laser vibration–rotation tunneling spectroscopy to characterize the cage forms of water hexamer and later studied the dipole moment of water molecules in clusters with 2–8 molecules using ab initio calculations and Monte Carlo simulations.30,31 Cruzan et al. used far-infrared vibration–rotation tunneling spectroscopy to study HB cooperativity of the water tetramer.32 Nauta and Miller studied water hexamer in liquid helium with infrared spectroscopy and proposed formation of a cyclic form over a cage structure of water hexamer.33 Dombrovsky et al. studied the infrared irradiation of water droplet clusters levitating over a heated water surface.34 Hamashima et al. measured infra-red spectra of phenol–water clusters to determine the variation in the free OH frequency of water as a function of cluster size.35
The complex HB network in water clusters can be described by graph theory, as used by several authors. Radhakrishnan et al. used the concept of graph theory in analyzing the HB network in water clusters.36 Later, several authors have applied a graph theoretical based method to understand topologically distinct water clusters.37–39 Brinkmann has done extensive work for generating all possible HB networks using graph theory up to a water cluster consisting of 32 molecules.40 Akase et al. analyzed graphs of water clusters in MC simulations to understand the dipole moment and HB pattern.41 Shrivastava et al. successfully applied the graph theoretical method to analyze water clusters obtained from simulations.42
Exploring the rugged potential energy surface and locating the low energy minima from the surface is a difficult optimization problem. Chill et al. have benchmarked different optimization techniques for finding local minima and transition states in different molecular clusters, including a water cluster of 20 molecules.43 Takeuchi used interior, surface, orientation, and HB arrangement operators to move water molecules in his optimization algorithm.44 Goedecker developed a minima hopping method which Kazachenko et al. further modified for water cluster optimization of (H2O)n n ≤ 37.45,46 The diffusion equation method (DEM) was applied for optimization of water clusters up to 8 molecules by Wawak et al.47 MC techniques have been widely used in many of the optimization problems. Tsai et al. and the Gordon group have applied a MC simulated annealing method in optimizing a water cluster structure with TIP4P and Effective Fragment Potential (EFP), respectively.48,49 Kemp and Gordon studied the effect of dipole moment in small and large water clusters using the EFP potential.50 Kazimirski and Buch used a molecular dynamics simulation and MC method on large water clusters.51 One of the well-known MC optimization techniques, basin hopping, was first applied to water clusters by Wales et al. on (H2O)n, n ≤ 21.52 Kabrede did vibrational modes analysis in the basin hopping technique using TIP4P potential for water cluster optimization.53 Zhan et al. combined basin hopping and the energy landscape method to develop a basin paving method.54 Bandyopadhyay applied the basin paving method on water clusters of (H2O)n, n = 20, 50.13 Shanker et al. made a modification of the basin paving method to develop the MC temperature basin paving (MCTBP) method.14 In the MCTBP method, the total energy range is divided into bins and an effective temperature is defined for each bin. The temperature of a bin depends on the number of times it is visited during MC sampling. Use of this effective temperature in the MC acceptance/rejection scheme significantly increases the efficiency of the method. Later, dissimilarity index (DSI) analysis was coupled with the MCTBP method to prohibit the system from repeatedly visiting a similar structure.15
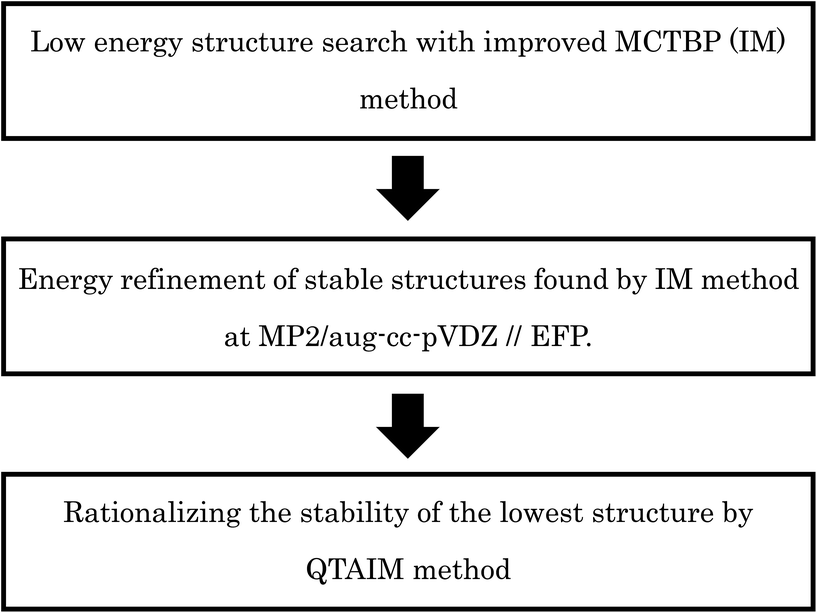
The original MCTBP method has some shortcomings; higher energy structures are more likely to be reached through a MC move due to the acceptance/rejection condition in the method. In our current work, we have improved the MCTBP method and demonstrated the new method is more efficient in locating the low energy structures for both (H2O)32 and (H2O)33. In the rest of the manuscript, the original and improved MCTBP method will be denoted by OM and IM, respectively. We have found 3 new structures lower in energy than the lowest energy structure obtained by the Hertke group for (H2O)32 (ref. 55) and we successfully located 10 new low energy structures for (H2O)33 than the lowest energy structures found by the Hertke55 and Thakkar46 groups at the EFP level of calculation. For the best 10 structures, we have performed DFT calculations with several functionals and MP2 calculations. After finding the low energy structures, we have used energy decomposition analysis using QTAIM method to rationalize the stability of the lowest energy structures we obtained for both the clusters. In particular, the stabilization energy and polarized charge of each atom for every water molecule in the cluster have been calculated using the QTAIM method. In general, larger polarized charge on an oxygen atom was found to result in more stabilization of the water compared to an isolated water molecule. The schematic illustration about the computational procedures used in this paper is given in Scheme 1.
Methodology
MCTBP method and its shortcomings
Several MC based algorithms, like basin hopping and basin paving, have been used by different authors to find low energy structures for different molecules.52,54 In these methods, after each MC move the structure is minimized to its nearest local minimum and MC acceptance/rejection is done between the minima only. One of the improvements in the basin hopping method was proposed by Shanker et al., termed as the MC temperature basin paving method (MCTBP).14 Here, the total energy range in which the structures are searched was divided into a small number of bins. An effective temperature is defined for each bin and that temperature changes as given in eqn (1).| T(E,t) = Tinitial + exp(C′′H(E,t)) | (1) |
In eqn (1), T(E,t) is the temperature of the bin with energy E at MC step t, Tinitial is the initial temperature, H(E,t) is obtained by populating the bins with each visit during the simulation, and C′′ is a scaling parameter. A new state after a MC move was accepted or rejected with the acceptance probability given in eqn (2).
| min(1,exp(−βold(Enew − Eold))) | (2) |
In eqn (2), βold = 1/kTold, k and Told are the Boltzmann constant and temperature of the old state, respectively, and Enew and Eold are the energy of new and old state, respectively. A cooling factor was also introduced to keep the temperature of the bins within a predefined value by eqn (3).
| H(E,t) = (int(H(E,t)) − CF × H(E,t)) | (3) |
In eqn (3), int converts the floating point value to the lowest integer and CF is a constant factor. The MCTBP method has been quite successful for coming out of deep potential wells in the energy surface;14,56 however, it may still visit the same state repeatedly before coming out, decreasing the efficiency of the method. In a subsequent work, Rakshit et al. introduced dissimilarity index (DSI) analysis with the MCTBP method (WDSI method).15 In the DSI method as applied by Kazimirski and Buch,51 all the oxygen–oxygen pair distances are calculated and sorted in ascending or descending order to get a vector of n(n − 1)/2 distances for n number of oxygen atoms from both structures. Then, the distance between these two vectors gives the DSI value. In the WDSI method, a DSI threshold value was set; if the new structure fell within the threshold value it was rejected immediately. This essentially eliminates finding similar structures multiple times.
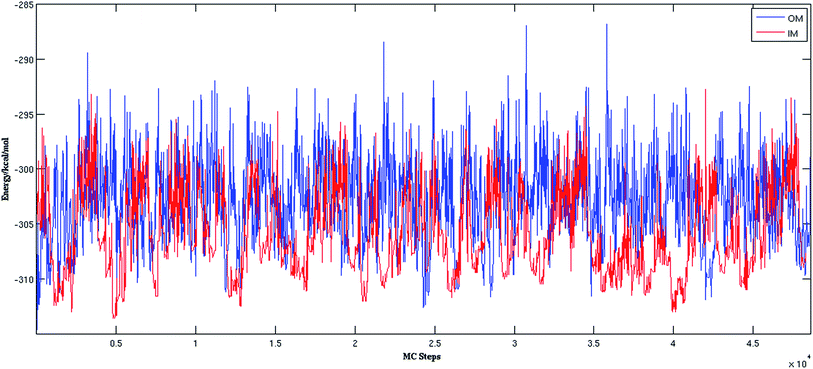
In the MCTBP method, the energy histogram takes a bell shape where energy bins in the middle are more populated than both sides, as shown in the ESI Fig. S1† for a trajectory obtained from an optimization run of (H2O)32. As a result, energy bins in the middle of the energy range have a higher temperature than the other energy bins. As the density of states of a molecular system increases sharply as a function of energy,57 a random move from a structure with an energy lower than the energy in the middle of the histogram has more probability to end up at a structure higher in energy. Moreover, because of the particular acceptance/rejection condition (eqn (2)), even a state with very high energy can be accepted as the temperature of only the old state is considered. As clearly seen in Fig. S1,† sampling a low energy structure around −310 kcal mol−1 can result in a move to the middle of the histogram above −300 kcal mol−1. This indicates that there is more chance of acceptance of higher energy states through the acceptance/rejection condition used in the MCTBP method. More frequent temperature cooling, as shown in eqn (3), may solve this problem to some extent. We have also devised two methods to circumvent this problem as described below.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. We can see from the figure that the energy of the system drops suddenly with the sudden drop in temperature. This happens because as the temperature of all the bins is small (e.g., 300 K), high energy structures are not easily accepted in the MC scheme. As mentioned before, sampling occurs mostly in bins that are more populated and in the central part of the energy histogram. We tried to incorporate the population of the energy bins in the acceptance probability so that it samples in the low energy region. For this we calculated the probability of each bin (Probi) from previous OM trajectories by normalizing the energy histogram averaged over the OM trajectories. Then, we used this in the new acceptance probability given in eqn (4).
000 K. We can see from the figure that the energy of the system drops suddenly with the sudden drop in temperature. This happens because as the temperature of all the bins is small (e.g., 300 K), high energy structures are not easily accepted in the MC scheme. As mentioned before, sampling occurs mostly in bins that are more populated and in the central part of the energy histogram. We tried to incorporate the population of the energy bins in the acceptance probability so that it samples in the low energy region. For this we calculated the probability of each bin (Probi) from previous OM trajectories by normalizing the energy histogram averaged over the OM trajectories. Then, we used this in the new acceptance probability given in eqn (4).| min(1,exp(−βold(Enew − Eold − C(Probold − Probnew)))) | (4) |
In eqn (4), C is a constant, Probold and Probnew are probabilities of the old and new energy bins, respectively, calculated from the previous trajectories, and the other symbols have same meaning as those in eqn (2).
In this improved MCTBP method (IM), structures are accepted according to the acceptance/rejection condition in eqn (4). If Probnew is greater than Probold, then the exponential becomes smaller and the acceptance probability decreases. Thus, it does not easily accept a new state in a higher energy bin which usually has high probability; it hinders the system from jumping into energy bins in the middle of the histogram with higher temperatures.
Graph theoretical representation of water clusters
Water molecules are connected through HB in water clusters and the HB network can be represented by a graph. Each water molecule can be considered to be a node and the HB between water molecules can be considered an edge in the graph.15 Almost always, a node can have a maximum of 4 connections with other water molecules in the cluster. A node can have two hydrogen bonds from the lone pair electrons on the oxygen atom to two H atoms on other nodes, and two H atoms accepting hydrogen bonds from other water molecules. As such, a water molecule has 4 degrees; two out-degrees and two in-degrees. Water clusters can be expressed as directed or undirected graphs depending on whether the directionality of the HB is considered or not, respectively. Directed graphs are called digraphs. ESI Fig. S3† shows an example of directed and undirected graphs for (H2O)4. We can predict similarity or dissimilarity between two oxygen frames of two different water clusters of the same size by checking the isomorphism between two undirected graphs. Checking the similarity in the HB pattern will require examination of the digraphs.Quantum theory of atoms in molecules
After obtaining the low energy structures we were interested to know the properties of the structures using quantum mechanical calculations. The stability of each conformation is usually determined by intermolecular interaction energies between component molecules. For these purposes, Kitaura–Morokuma energy decomposition analysis is one of the well-known methods.58 In this method, the energy of the system can be decomposed into exchange repulsion, charge transfer (CT) attraction, polarization, and electrostatic interactions based on all molecular pairs; however, there is also a term (the mixing term) that cannot be exactly classified into these components. Unfortunately, this mixing term increases with an increase in the size of the water cluster. This results in the Kitaura–Morokuma decomposition analysis (as implemented in GAMESS program package59) to fail, sometimes even for (H2O)n (n ≥ 6) in our calculations.On the other hand, the total energy of the system can be divided into atomic energies by applying the QTAIM method proposed by Bader et al., in which electron densities are divided into each atomic region by the so-called “zero-flux” interatomic surface S(r) determined by
| ∇ρ(r)·n(r) = 0 for every point on the surface S(r) | (5) |
The differences between the total energy and the sum of decomposed atomic energies were less than 0.77 kcal mol−1 for the (H2O)32 and (H2O)33 clusters (see ESI Tables ST1 and ST2†). To visualize the stabilities of each atomic energy, relative energies based on the isolated water molecule were visualized62,64 using the VMD program.65
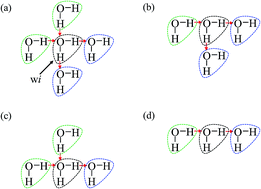
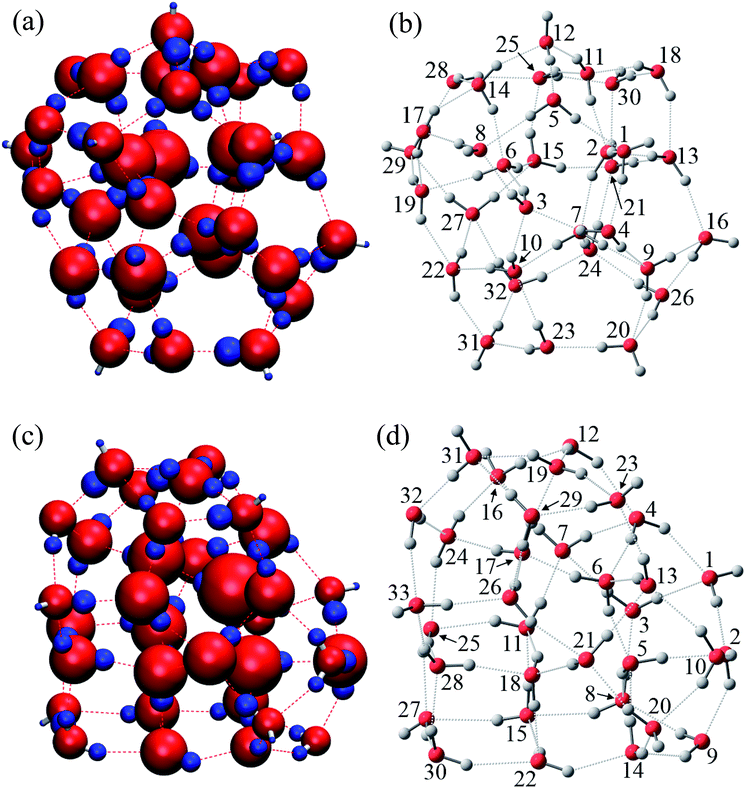
As is widely known, each water molecule can form four hydrogen bonds, except in rare cases where it may form 5 hydrogen bonds (not considered in the current work), in which two of them are hydrogen accepting (H-accepting) interactions from neighboring water molecules and two are hydrogen donating (H-donating) interactions to neighbors. Therefore, the topological index is defined in this paper so that the i-th water molecule with both NA (NA ≤ 2) H-accepting and ND (ND ≤ 2) H-donating interactions are denoted as wi(NA,ND) to distinguish water molecules with different patterns of HB networks. Some important topological indexes associated with typical HB patterns are given in Fig. 1.
Details of the simulation
We have used the Effective Fragment Potential (EFP) potential66 implemented in the GAMESS program package59 for optimization and energy calculations of water clusters. We have also re-optimized structures obtained by other groups with the EFP potential for comparison with our structures. We can divide the water molecules in large water clusters, e.g., (H2O)32 and (H2O)33, in two main groups; those near the middle of the cluster and those at the surface of the cluster. The arrangement of the HB network in the center of the cluster can be said to define the core frame of the structure. To generate a completely different structure, water molecules near the center should be moved to create a different HB network at the center of the structure. As such, in our current work, we selectively moved some randomly selected water molecules in the center and on the surface of the cluster. We moved a maximum of up to 12 water molecules at a time; at first 1 to 5 water molecules were moved near the center, then the rest were moved at the surface. Both random rotational and translational moves were given to these selected water molecules. We coupled the center and surface moves in our simulation in different ways. Translational moves were varied between 0.5 Å and 0.8 Å and rotational moves were varied between 100 and 120 degrees in different simulations. We did not see significant difference in results over this range of translational and rotational move sets.We ran 7 trajectories of (H2O)32 and 5 trajectories of (H2O)33 with the OM method. Then, in some trajectories of (H2O)32, we successively forced the system to visit some low energy structures during the simulation whenever the system sampled a high energy region for a long time. We initially choose a set of 8 structures within the range from −313.00 to −315.55 kcal mol−1 for (H2O)32; if the system's energy moved successively over a −312 kcal mol−1 energy range 20 times we moved the system to these structures. Whenever we got new low energy structures, we added them to this set. We have not run any trajectories for (H2O)33 using this method. The energy range for (H2O)32 was selected from −320 kcal mol−1 to −280 kcal mol−1 and was divided into bin sizes of 0.5 kcal mol−1.
With the IM method, we ran 15 trajectories for (H2O)33 and 9 for (H2O)32. The energy range for (H2O)32 was divided as in the OM method and for (H2O)33 it was divided from −330 kcal mol−1 to −280 kcal mol−1 with a bin size of 0.5 kcal mol−1. The constant C in eqn (4) was given a value from 100 to 130 in different simulations to increase the efficiency of the new acceptance probability. In the IM method, we reduced the temperature to the initial value whenever any bin reached the maximum temperature threshold value, which was set between 7000 K and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K in different simulations.
000 K in different simulations.
Results and discussion
Comparison between the original-MCTBP (OM) and the improved-MCTBP (IM) methods
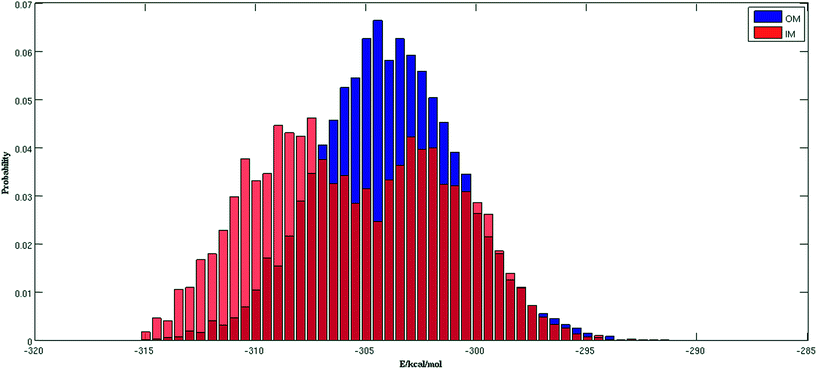
Fig. 2 shows the trajectories from the OM (in blue) and IM methods (in red) for a (H2O)32 cluster starting from the same high energy structure of −290.16 kcal mol−1. All simulation parameters, such as initial temperature, rotational, and translational movements of water molecules, were kept same for both trajectories. We can clearly see from the figure that the IM method visited the states below −310 kcal mol−1 more frequently than the OM method. Also, the OM method visited high energy states over −295 kcal mol−1 more frequently than the IM method. In rare occasions, the IM method went over the −295 kcal mol−1 energy range, suggesting the IM method tends to explore the lower energy region more frequently than the OM method. Table 1 describes how many times the system visited low energy structures within 5 kcal mol−1 and 10 kcal mol−1 of the lowest energy structure determined by the group of Thakkar (T structure) for (H2O)32 for both methods. We can see that the IM method more frequently visited structures within 5 and 10 kcal mol−1 of the T structure compared to the OM method. From all the trajectories, we found a total of 1607 structures from the OM method within 5 kcal mol−1 of the T structure, among them 95 were found to be DSI unique structures when filtered with a DSI threshold value of 1 Å. In contrast, for the IM method we found a total of 3157 structures within a 5 kcal mol−1 range of T structure, among them 300 were unique when filtered with the same way. Fig. 3 shows the histogram of energy for both the trajectories; the blue color represents the OM method and red defines the IM method. We can clearly see from this figure that the IM method samples more frequently in the low energy region compared to the OM method, as the histogram shifted towards the left side of the former method.| MC steps | OM | IM | ||
|---|---|---|---|---|
| NT5 | NT10 | NT5 | NT10 | |
| 1000 | 15 | 126 | 0 | 12 |
| 5000 | 15 | 226 | 30 | 343 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
15 | 310 | 35 | 572 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
15 | 409 | 35 | 843 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
18 | 629 | 35 | 1446 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
18 | 806 | 35 | 1970 |
45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
18 | 968 | 82 | 3280 |
Result from trajectories of (H2O)32
Our goal was to find new structures of (H2O)32 lower in energy than the structures reported by the groups of Thakkar46 and Hertke55 (T and H structures, respectively). In this part of the manuscript, we compare our results to these two structures. We obtained all the structures from all trajectories of different methods as described in the Methodology section. Table 2 describes the 10 unique lowest energy structures for (H2O)32 with their respective radii of gyration values, energies and DSI values relative to T and H structures. The radius of gyration value gives us an idea about the compactness and span of the structures. Only the oxygen frame of the structures is used for calculation of the radius of gyration for a cluster with n water molecules using the eqn 6.
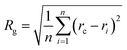 | (6) |
| Structure | EEFP (kcal mol−1) | ΔET (kcal mol−1) | DSI(T) (Å) | DSI(H) (Å) | Rg (Å) |
|---|---|---|---|---|---|
| a This structure is depicted in Fig. 4(a).b This structure is depicted in Fig. 4(b).c This structure is depicted in Fig. 4(c).d This is T structure.e This is H structure. | |||||
| 1a | −317.46 | 0.06 | 1.65 | 4.33 | 4.55 |
| 2b | −316.85 | 0.67 | 4.23 | 2.78 | 4.66 |
| 3c | −316.73 | 0.79 | 4.20 | 2.89 | 4.69 |
| 4 | −316.30 | 1.22 | 2.22 | 3.71 | 4.55 |
| 5 | −316.00 | 1.52 | 4.02 | 2.85 | 4.69 |
| 6 | −315.93 | 1.59 | 4.01 | 2.77 | 4.65 |
| 7 | −315.56 | 1.96 | 3.99 | 2.68 | 4.66 |
| 8 | −315.29 | 2.23 | 4.87 | 3.67 | 4.72 |
| 9 | −314.83 | 2.69 | 3.70 | 2.30 | 4.66 |
| 10 | −314.68 | 2.84 | 5.24 | 3.44 | 4.72 |
| 11d | −317.52 | 0.00 | 0.00 | 3.52 | 4.59 |
| 12e | −316.69 | 0.83 | 3.52 | 0.00 | 4.64 |
In eqn (6), Rg stands for the radius of gyration and rc and ri define the center of mass of the oxygen frame and position of i-th oxygen atom in the water cluster, respectively. The structures were filtered with a DSI threshold value of 1 Å. We found three structures lower in energy than the H structure, but did not observe any structures lower in energy than the T structure; however, structure number one has almost the same energy as the T structure. We can see the 10 new structures have high DSI values with both T and H structure (2 to 5 Å) but their Rg values differ only a little (∼0.1 Å). This indicates that the T and H structures reside in a very different structural space from the 10 lowest energy structures obtained. In our simulation, we have not been able to search that particular structural space when starting the trajectories from random structures. As a result, we gave a large amount of rotational and translational movement to the T and H structures and took those distorted structures as input structures for the IM method. We got back the T and H structures from those trajectories within almost 200 MC steps; however, as the simulation proceeded those structures were not located again. Table 3 gives the statistics of selected IM trajectories. Fig. 4 shows the three unique low energy structures of (H2O)32 found below the H structure. The values in the figure indicate the relative energies of those structures from the T structure. We checked the isomorphism between the undirected graphs of the 10 unique lowest energy structures obtained from simulation and found all the structures have different oxygen frames. This suggests all the low energy structures we found are unique. Water clusters with the same undirected graph can have different directed graphs. This means different water clusters can have the same oxygen frame but different HB networks. ESI Table ST3† represents the number of different HB networks found for each unique oxygen frame. We can see that structures with different HB networks correspond to the same oxygen frames of T and H structures were found; however, diversity in the HB networks found for the oxygen frames of these two structures is much less than the diversity of the HB network for the rest of the oxygen frames listed in ESI Table ST3.† The number of structures with different HB networks are greater than 20 in most of the oxygen frames. For the oxygen frame of the second lowest structure obtained in this work, the number of structures with different HB networks was found to be 193.
| Serial no. | Einitial (kcal mol−1) | Ntotal | Nacc | Emin (kcal mol−1) | Nmin | NT5 |
|---|---|---|---|---|---|---|
| 1 | H structure | 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 509 509 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054 054 |
−316.70 | 118 | 379 |
| 2 | −316.85 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184 184 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 897 897 |
−316.85 | 1 | 182 |
| 3 | H structure | 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299 299 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 216 |
−316.70 | 29 | 529 |
| 4 | T structure | 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 901 901 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 204 204 |
−317.52 | 4 | 339 |
| 5 | −314.35 | 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 930 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 683 683 |
−315.06 | 321 | 355 |
| 6 | H structure | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 631 631 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 457 457 |
−316.70 | 22 | 279 |
| 7 | T structure | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 874 874 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 325 |
−317.52 | 204 | 292 |
| 8 | −314.35 | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 792 792 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 855 855 |
−316.30 | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 197 197 |
180 |
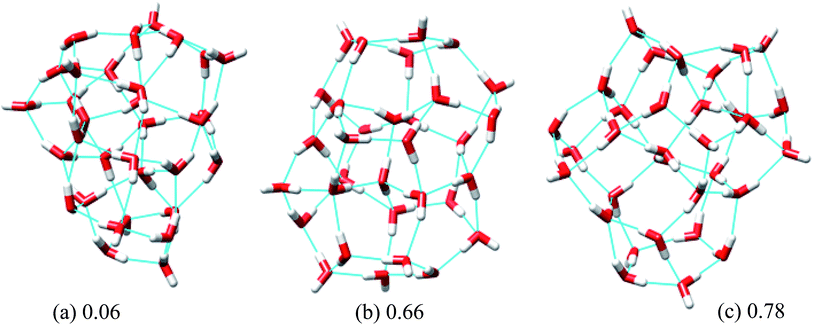 | ||
| Fig. 4 Three low energy unique structures of (H2O)32 lower in energy than the H structure. The values in the figure define the relative energy from the T structure in kcal mol−1. | ||
Result from trajectories of (H2O)33
For (H2O)33, we compared our results with the lowest energy structures reported in ref. 46 and 55. For simplicity, we are denoting these two structures T33 and H33, respectively. Table 4 shows the details of the IM trajectories for (H2O)33. We started the simulations from different low energy structures. For all the trajectories we obtained structures lower in energy than T33 and H33. We also ran a few trajectories where we gave large random rotational and translational displacements to structures T33 and H33 and took the resulting structures as initial structures for the IM trajectories. We obtained those two structures from the trajectories and also found structures lower in energy. Table 5 gives the Rg values and DSI values of the 10 lowest energy structures with the T33 and H33 structures. For (H2O)33, we observed 10 new unique DSI structures lower in energy than the T33 structure in the EFP potential. We can see that the structures have high DSI values with both T33 and H33 structures; however, their Rg values do not differ significantly. The large DSI values with T33 and H33 compared to the other structures suggests that T33 and H33 reside in a very different structural space from the rest of the structures as found for (H2O)32. Graph isomorphism analysis between the undirected graphs of these 10 lowest energy structures showed that they have different oxygen frames.| Serial no. | Einitial (kcal mol−1) | Ntotal | Nacc | Emin (kcal mol−1) | Nmin | NT5 |
|---|---|---|---|---|---|---|
| 1 | −325.17 | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 501 501 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992 992 |
−325.72 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 458 458 |
2043 |
| 2 | −325.17 | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 283 283 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 501 501 |
−325.77 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 938 |
3814 |
| 3 | −322.43 | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528 528 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 128 |
−324.75 | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 932 932 |
3158 |
| 4 | −323.59 | 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129 129 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 189 189 |
−325.17 | 2438 | 3280 |
| 5 | −318.71 | 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512 512 |
−324.89 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 729 729 |
2581 |
| 6 | H33 | 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 469 469 |
−325.36 | 5292 | 2538 |
| 7 | T33 | 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288 288 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195 195 |
−324.86 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975 975 |
2224 |
| 8 | −325.17 | 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 720 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 067 067 |
−325.17 | 34 | 2000 |
| Structure | EEFP (kcal mol−1) | ΔET (kcal mol−1) | DSI(T) (Å) | DSI(H) (Å) | Rg (Å) |
|---|---|---|---|---|---|
| a This structure is depicted in Fig. 5(a).b This structure is depicted in Fig. 5(b).c This structure is depicted in Fig. 5(c).d This structure is depicted in Fig. 5(d).e This structure is depicted in Fig. 5(e).f This is T33 structure.g This is H33 structure. | |||||
| 1a | −325.77 | −1.02 | 2.79 | 2.17 | 4.64 |
| 2b | −325.72 | −0.97 | 4.66 | 3.31 | 4.71 |
| 3c | −325.36 | −0.61 | 3.92 | 3.79 | 4.63 |
| 4d | −325.17 | −0.42 | 2.65 | 3.13 | 4.57 |
| 5e | −325.02 | −0.27 | 2.83 | 2.37 | 4.63 |
| 6 | −324.94 | −0.19 | 7.75 | 6.27 | 4.81 |
| 7 | −324.89 | −0.14 | 6.64 | 4.98 | 4.76 |
| 8 | −324.86 | −0.11 | 6.49 | 5.56 | 4.77 |
| 9 | −324.85 | −0.10 | 3.34 | 2.52 | 4.66 |
| 10 | −324.77 | −0.02 | 3.61 | 2.60 | 4.67 |
| 11f | −324.75 | 0.00 | 0.00 | 2.36 | 4.59 |
| 12g | −324.66 | 0.09 | 2.36 | 0.00 | 4.63 |
Fig. 5 shows the 5 lowest energy structures found below the lowest energy structure in the ref. 46 (T33). The ESI Table ST4† shows the statistics of the HB networks of the oxygen frames of the low energy (H2O)33 structures. From the table, we can see no other HB network with the same oxygen frames of the low energy structure H33 were found. On the other hand, we have located eight different HB networks for the oxygen frame of the structure T33. The number of structures with different HB networks for (H2O)33 corresponding to the same oxygen frame are quite smaller than in the case of (H2O)32. This may be because we have run more trajectories for (H2O)32 than (H2O)33.
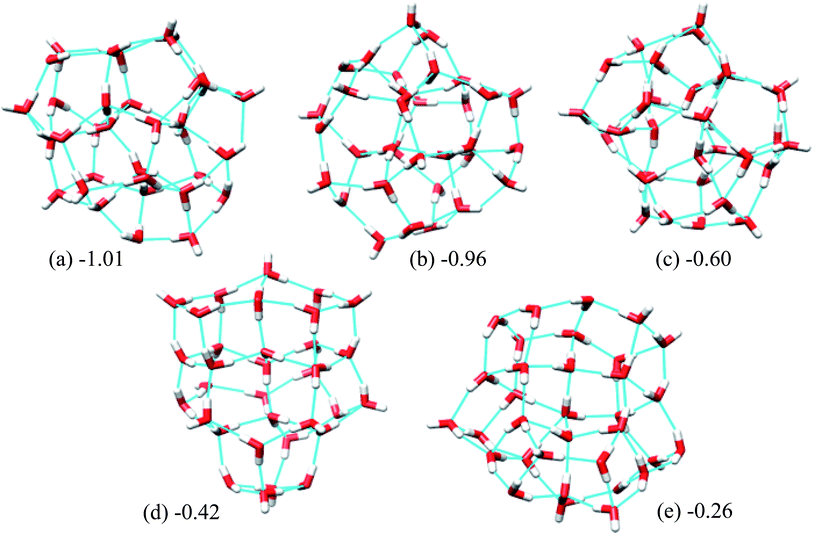 | ||
| Fig. 5 Five low energy unique structures of (H2O)33 lower in energy than the T33 structure. The values in the figure indicate their relative energies from T33 structure in kcal mol−1. | ||
We also compared the features of our structures with those obtained in ref. 8. In that work, structures of water cluster of size 30 to 48 were obtained by using Monte Carlo search and then optimized the obtained structures at the DFT level of theory. The authors found that mean adjacent oxygen–oxygen distance, RO–O varies from 2.8 Å to 2.81 Å for most favorable structures irrespective of the size of the cluster. They also reported the average H-bond distance is around 1.81 Å for different types of clusters of (H2O)33. Whereas lowest energy structure of (H2O)32 obtained by us (Fig. 4(a)) have RO–O of 2.88 Å and average H-bond distance of 1.97 Å. The average RO–O and H-bond values over 10 new lowest energy structures are found to be 2.87 Å and 1.95 Å, respectively. The lowest energy structure of (H2O)33 (Fig. 5(a)) has average RO–O and H-bond values of 2.88 Å and 1.96 Å, respectively. Averaging over 10 lowest energy structures of (H2O)33 give the same value as found for the lowest energy structure. We optimized our structures with EFP method whereas structures of ref. 8 are optimized at DFT level of theory. This may be one of the reasons of the difference in RO–O and H-bond values between their and our structures.
The topology of the structure plays a major role in stability of the structure. Ref. 8 showed the average number of water molecules with two-coordinated H-bond, three-coordinated H-bond and four-coordinated H-bond for low energy structure of (H2O)33 are 1, 22 and 10, respectively (Fig. 2 of ref. 8). The lowest energy structure of (H2O)33 obtained by us has number of water molecules with two-coordinated H-bond, three-coordinated H-bond and four-coordinated H-bond as 1, 18, and 14. And when averaged over 10 lowest energy structure of (H2O)33 the above values came as 0.7, 18.9, and 13.1. So we can clearly see that our water clusters have more water with four-coordinated H-bond than reported in ref. 8. The total number of H-bonds (56) in our lowest energy structure for (H2O)33 is two more than that for the lowest energy structure reported in ref. 8.
Rationalizing the relative stability of different structures with the QTAIM method
After locating several low energy structures for (H2O)32 and (H2O)33 we focused our attention on the details of the electronic effect on the stability of the water cluster structures. We also tried to relate stability to the HB topology indices described previously.Relative energies of the 10 lowest energy structures optimized by EFP potentials, as well as the H and T structures, are summarized in Table 6a and b using EFP, RHF/aug-cc-pVDZ, M06-2x/aug-cc-pVDZ, M06-2x/6-311G(d,p), M06-2x/6-311+G(d,p), and MP2/aug-cc-pVDZ levels of theory. Although the orders of stability are different from each other, the most stable structures are predicted as structures 1 and 11 (listed in Table 6) by MP2/aug-cc-pVDZ//EFP level for (H2O)32 and (H2O)33, respectively. Although QTAIM analysis failed at MP2/aug-cc-pVDZ and M06-2x/aug-cc-pVDZ levels due to the large number of basis sets, M06-2x/6-311+G(d,p) was successfully applied for energy decompositions. Our calculation showed that energy differences are overestimated without diffuse functions such as the M06-2x/6-311G(d,p) level, they are improved by including diffuse functions like M06-2x/6-311+G(d,p), and the most stable structures by MP2/aug-cc-pVDZ could be reproduced by M06-2x/6-311+G(d,p) calculations. Accordingly, we have decided to use the M06-2x/6-311+G(d,p) level of theory in the following QTAIM analysis.
| (a) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Structure | EFP | RHF/aug-cc-pVDZ | M06-2x/aug-cc-pVDZ | M06-2x/6-311G(d,p) | M06-2x/6-311+G(d,p) | MP2/aug-cc-pVDZ | |||||
| ΔE (kcal mol−1) | E (Hartree) | ΔE (kcal mol−1) | E (Hartree) | ΔE (kcal mol−1) | E (Hartree) | ΔE (kcal mol−1) | E (Hartree) | ΔE (kcal mol−1) | E (Hartree) | ΔE (kcal mol−1) | |
| a This structure is depicted in Fig. 4(a).b This structure is depicted in Fig. 4(b).c This structure is depicted in Fig. 4(c).d This is T structure.e This is H structure.f This structure is depicted in Fig. 5(a).g This structure is depicted in Fig. 5(b).h This structure is depicted in Fig. 5(c).i This structure is depicted in Fig. 5(d).j This structure is depicted in Fig. 5(e).k This is T33 structure.l This is H33 structure. | |||||||||||
| 1a | 0.06 | −2433.73067 | 0.83 | −2445.59726 | 0.00 | −2445.94906 | 0.00 | −2446.06700 | 0.00 | −2440.67995 | 0.00 |
| 2b | 0.67 | −2433.73200 | 0.00 | −2445.58752 | 6.11 | −2445.93454 | 9.11 | −2446.05758 | 5.91 | −2440.67489 | 3.17 |
| 3c | 0.79 | −2433.73161 | 0.24 | −2445.58941 | 4.92 | −2445.93676 | 7.71 | −2446.05899 | 5.02 | −2440.67584 | 2.58 |
| 4 | 1.22 | −2433.72810 | 2.45 | −2445.59349 | 2.36 | −2445.94407 | 3.13 | −2446.06258 | 2.77 | −2440.67817 | 1.12 |
| 5 | 1.52 | −2433.73106 | 0.58 | −2445.58874 | 5.35 | −2445.93643 | 7.92 | −2446.05857 | 5.29 | −2440.67518 | 3.00 |
| 6 | 1.59 | −2433.73065 | 0.84 | −2445.58662 | 6.67 | −2445.93246 | 10.41 | −2446.05625 | 6.74 | −2440.67390 | 3.79 |
| 7 | 1.96 | −2433.73015 | 1.16 | −2445.58597 | 7.08 | −2445.93175 | 10.86 | −2446.05539 | 7.28 | −2440.67349 | 4.05 |
| 8 | 2.23 | −2433.73058 | 0.89 | −2445.58686 | 6.52 | −2445.93304 | 10.05 | −2446.05677 | 6.42 | −2440.67332 | 4.16 |
| 9 | 2.69 | −2433.72931 | 1.68 | −2445.58495 | 7.72 | −2445.93043 | 11.69 | −2446.05482 | 7.64 | −2440.67200 | 4.99 |
| 10 | 2.84 | −2433.72927 | 1.71 | −2445.58682 | 6.55 | −2445.93280 | 10.20 | −2446.05621 | 6.77 | −2440.67248 | 4.69 |
| 11d | 0.00 | −2433.73113 | 0.54 | −2445.59644 | 0.51 | −2445.94856 | 0.31 | −2446.06659 | 0.26 | −2440.67886 | 0.69 |
| 12e | 0.82 | −2433.72968 | 1.45 | −2445.59241 | 3.04 | −2445.94409 | 3.12 | −2446.06208 | 3.08 | −2440.67725 | 1.69 |
| (b) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Structure no. | EFP | RHF/aug-cc-pVDZ | M06-2x/aug-cc-pVDZ | M06-2x/6-311G(d,p) | M06-2x/6-311+G(d,p) | MP2/aug-cc-pVDZ | |||||
| ΔE (kcal mol−1) | E (Hartree) | ΔE (kcal mol−1) | E (Hartree) | ΔE (kcal mol−1) | E (Hartree) | ΔE (kcal mol−1) | E (Hartree) | ΔE (kcal mol−1) | E (Hartree) | ΔE (kcal mol−1) | |
| 1f | 0.00 | −2509.78384 | 0.83 | −2522.01496 | 4.26 | −2522.37349 | 7.90 | −2522.49901 | 3.46 | −2516.94740 | 1.14 |
| 2g | 0.05 | −2509.78515 | 0.00 | −2522.01267 | 5.70 | −2522.37023 | 9.94 | −2522.49682 | 4.84 | −2516.94643 | 1.74 |
| 3h | 0.41 | −2509.78512 | 0.02 | −2522.01323 | 5.35 | −2522.37006 | 10.05 | −2522.49692 | 4.77 | −2516.94654 | 1.68 |
| 4i | 0.60 | −2509.78183 | 2.09 | −2522.01654 | 3.27 | −2522.37842 | 4.81 | −2522.50090 | 2.27 | −2516.94635 | 1.80 |
| 5j | 0.75 | −2509.78335 | 1.13 | −2522.01282 | 5.61 | −2522.37137 | 9.23 | −2522.49645 | 5.07 | −2516.94592 | 2.07 |
| 6 | 0.83 | −2509.78395 | 0.75 | −2522.00740 | 9.01 | −2522.36144 | 15.46 | −2522.49165 | 8.08 | −2516.94140 | 4.90 |
| 7 | 0.88 | −2509.78471 | 0.28 | −2522.01075 | 6.91 | −2522.36828 | 11.17 | −2522.49508 | 5.93 | −2516.94412 | 3.20 |
| 8 | 0.91 | −2509.78019 | 3.12 | −2522.01213 | 6.04 | −2522.37307 | 8.16 | −2522.49698 | 4.73 | −2516.94174 | 4.69 |
| 9 | 0.92 | −2509.78444 | 0.45 | −2522.01085 | 6.84 | −2522.36827 | 11.17 | −2522.49495 | 6.01 | −2516.94510 | 2.58 |
| 10 | 1.00 | −2509.78336 | 1.12 | −2522.00918 | 7.89 | −2522.36686 | 12.06 | −2522.49353 | 6.90 | −2516.94365 | 3.49 |
| 11k | 1.01 | −2509.77950 | 3.55 | −2522.02176 | 0.00 | −2522.38608 | 0.00 | −2522.50452 | 0.00 | −2516.94921 | 0.00 |
| 12l | 1.11 | −2509.78207 | 1.94 | −2522.01556 | 3.89 | −2522.37749 | 5.39 | −2522.49951 | 3.15 | −2516.94654 | 1.68 |
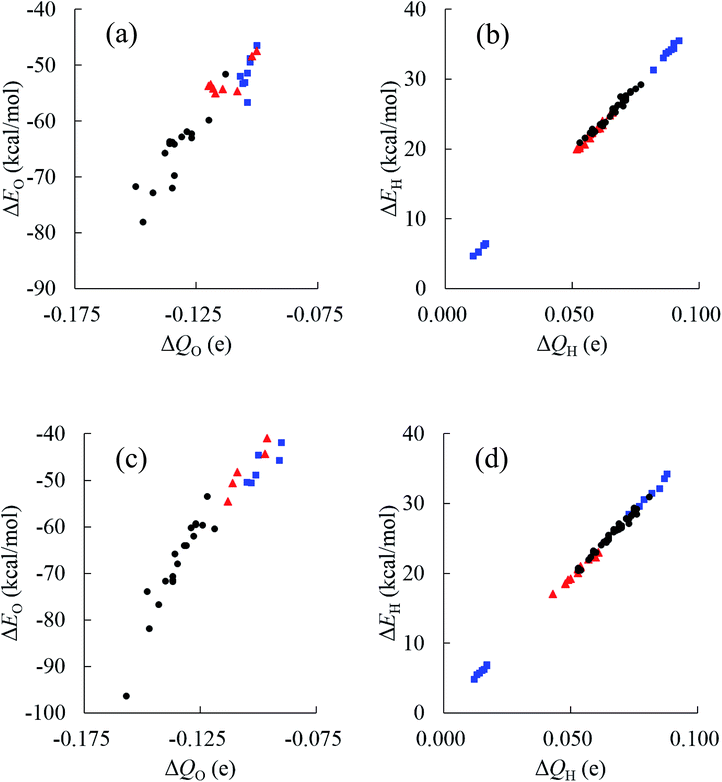
The relative energies ΔE and charges ΔQ of atoms based on isolated water are summarized in Tables 7 and 8, as calculated by the QTAIM method, as well as the topological indices of water molecules. The stability of atoms for the most stable structure are shown in Fig. 6, in which the absolute values of ΔE for each atom were indicated by the radius of the sphere and stabilized and destabilized atoms were distinguished by red and blue colors, respectively. Interestingly, Fig. 6 shows that atoms in water molecules close to the center of the cluster are particularly stabilized or destabilized relative to those outside the cluster. For example, the ΔE of an O atom in w6, w7, w10, and w15 has a large negative value below −70.0 kcal mol−1 for the (H2O)32 cluster in Table 7, illustrated by the large size of red spheres in Fig. 6(a). Similar trends were observed in the (H2O)33 cluster. From a structural point of view, although most inside water molecules have four hydrogen bonds, free dangling bonds can be detected in the surface region. Such HB networks should have influence on the electronic structures and atomic energies. The QTAIM analysis confirmed that the total polarized charge ΔQ(sum) in each water molecule was quite small, less than ca. 0.010e, as seen in Table 7. Nevertheless, the absolute value of polarized O and H atomic charges in water molecules were 0.011–0.150e, which were larger than the ΔQ(sum), representing transfer of charge between molecules. Therefore, stabilities of each molecule were related to polarized charges induced by surrounding water molecules. Of note, the CT effects were also included in the atomic energies in the QTAIM analysis, in contrast to the Kitaura–Morokuma energy decomposition scheme.
| i | NA | ND | MAa | MDb | ΔE (kcal mol−1) | ΔQ (e) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O | H1 | H2 | Sum | O | H1 | H2 | Sum | |||||
| a Counter molecules for H-accepting interaction.b Counter molecules for H-accepting interaction. | ||||||||||||
| 1 | 2 | 1 | 2, 5 | 4 | −56.59 | 34.28 | 6.24 | −16.07 | −0.104 | 0.089 | 0.015 | 0.000 |
| 2 | 2 | 2 | 11, 13 | 1, 7 | −69.66 | 26.90 | 27.55 | −15.22 | −0.134 | 0.070 | 0.069 | 0.005 |
| 3 | 2 | 2 | 4, 10 | 6, 8 | −64.01 | 26.93 | 23.91 | −13.18 | −0.136 | 0.070 | 0.063 | −0.002 |
| 4 | 1 | 2 | 1 | 3, 9 | −54.68 | 22.49 | 21.61 | −10.58 | −0.108 | 0.058 | 0.056 | 0.007 |
| 5 | 1 | 2 | 12 | 1, 8 | −54.16 | 22.97 | 22.45 | −8.74 | −0.118 | 0.061 | 0.058 | 0.001 |
| 6 | 2 | 2 | 3, 14 | 15, 19 | −72.82 | 28.68 | 25.39 | −18.75 | −0.143 | 0.075 | 0.066 | −0.003 |
| 7 | 2 | 2 | 2, 24 | 9, 10 | −71.66 | 25.31 | 28.29 | −18.07 | −0.150 | 0.067 | 0.073 | −0.010 |
| 8 | 2 | 1 | 3, 5 | 17 | −51.38 | 33.95 | 6.42 | −11.01 | −0.104 | 0.088 | 0.016 | −0.001 |
| 9 | 2 | 2 | 4, 7 | 16, 20 | −59.79 | 22.90 | 25.86 | −11.03 | −0.120 | 0.058 | 0.067 | 0.005 |
| 10 | 2 | 2 | 7, 23 | 3, 22 | −71.94 | 23.55 | 27.01 | −21.37 | −0.135 | 0.061 | 0.071 | −0.004 |
| 11 | 2 | 2 | 18, 25 | 2, 12 | −63.62 | 27.42 | 24.66 | −11.54 | −0.136 | 0.071 | 0.065 | 0.000 |
| 12 | 2 | 1 | 11, 14 | 5 | −53.05 | 34.44 | 6.18 | −12.43 | −0.105 | 0.090 | 0.015 | −0.001 |
| 13 | 2 | 2 | 18, 21 | 2, 16 | −63.69 | 26.21 | 23.81 | −13.66 | −0.135 | 0.070 | 0.062 | −0.004 |
| 14 | 2 | 2 | 17, 28 | 6, 12 | −62.76 | 25.39 | 22.56 | −14.82 | −0.131 | 0.066 | 0.059 | −0.006 |
| 15 | 2 | 2 | 6, 27 | 21, 25 | −78.06 | 27.69 | 28.20 | −22.17 | −0.147 | 0.071 | 0.073 | −0.003 |
| 16 | 2 | 1 | 9, 13 | 26 | −49.41 | 33.74 | 5.34 | −10.33 | −0.103 | 0.087 | 0.013 | −0.004 |
| 17 | 1 | 2 | 8 | 14, 19 | −48.34 | 22.16 | 20.42 | −5.76 | −0.102 | 0.057 | 0.053 | 0.008 |
| 18 | 1 | 2 | 30 | 11, 13 | −47.43 | 22.27 | 19.98 | −5.18 | −0.100 | 0.058 | 0.052 | 0.009 |
| 19 | 2 | 2 | 6, 17 | 22, 29 | −51.55 | 20.99 | 25.82 | −4.74 | −0.113 | 0.053 | 0.066 | 0.006 |
| 20 | 2 | 1 | 9, 26 | 23 | −53.21 | 35.52 | 6.50 | −11.19 | −0.106 | 0.092 | 0.016 | 0.001 |
| 21 | 2 | 2 | 15, 24 | 13, 30 | −64.06 | 28.16 | 22.38 | −13.52 | −0.134 | 0.073 | 0.057 | −0.004 |
| 22 | 2 | 2 | 10, 19 | 27, 31 | −61.87 | 27.52 | 21.60 | −12.74 | −0.129 | 0.071 | 0.055 | −0.003 |
| 23 | 1 | 2 | 20 | 10, 31 | −53.75 | 23.40 | 22.87 | −7.49 | −0.120 | 0.062 | 0.060 | 0.002 |
| 24 | 2 | 2 | 26, 32 | 7, 21 | −62.92 | 26.37 | 23.38 | −13.17 | −0.127 | 0.068 | 0.062 | 0.003 |
| 25 | 2 | 2 | 15, 28 | 11, 30 | −62.20 | 27.53 | 22.23 | −12.45 | −0.127 | 0.071 | 0.058 | 0.002 |
| 26 | 1 | 2 | 16 | 20, 24 | −55.03 | 20.65 | 24.02 | −10.36 | −0.117 | 0.055 | 0.062 | 0.000 |
| 27 | 2 | 2 | 22, 32 | 15, 29 | −65.69 | 29.24 | 22.37 | −14.08 | −0.138 | 0.077 | 0.058 | −0.002 |
| 28 | 1 | 2 | 29 | 14, 25 | −53.42 | 25.22 | 21.55 | −6.66 | −0.119 | 0.066 | 0.057 | 0.003 |
| 29 | 2 | 1 | 19, 27 | 28 | −51.90 | 35.20 | 6.51 | −10.19 | −0.107 | 0.090 | 0.016 | −0.001 |
| 30 | 2 | 1 | 21, 25 | 18 | −46.45 | 31.33 | 5.23 | −9.89 | −0.100 | 0.082 | 0.013 | −0.006 |
| 31 | 2 | 1 | 22, 23 | 32 | −48.77 | 33.07 | 4.70 | −10.99 | −0.103 | 0.086 | 0.011 | −0.006 |
| 32 | 1 | 2 | 31 | 24, 27 | −54.22 | 24.86 | 20.16 | −9.20 | −0.114 | 0.065 | 0.053 | 0.004 |
| i | NA | ND | MAa | MDb | ΔE (kcal mol−1) | ΔQ (e) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O | H1 | H2 | Sum | O | H1 | H2 | Sum | |||||
| a Counter molecules for H-accepting interaction.b Counter molecules for H-accepting interaction. | ||||||||||||
| 1 | 2 | 1 | 3, 4 | 2 | −38.47 | 30.59 | 6.96 | −0.93 | −0.091 | 0.079 | 0.017 | 0.005 |
| 2 | 2 | 2 | 1, 5 | 9, 10 | −71.69 | 27.18 | 29.03 | −15.48 | −0.137 | 0.069 | 0.075 | 0.007 |
| 3 | 1 | 2 | 8 | 1, 7 | −40.90 | 19.10 | 18.59 | −3.21 | −0.096 | 0.049 | 0.048 | 0.001 |
| 4 | 2 | 2 | 7, 12 | 1, 6 | −67.92 | 21.98 | 28.50 | −17.45 | −0.135 | 0.057 | 0.076 | −0.002 |
| 5 | 2 | 2 | 6, 14 | 2, 8 | −81.86 | 26.32 | 27.95 | −27.59 | −0.147 | 0.069 | 0.072 | −0.005 |
| 6 | 2 | 2 | 4, 13 | 5, 17 | −96.25 | 31.00 | 28.36 | −36.89 | −0.157 | 0.081 | 0.074 | −0.001 |
| 7 | 2 | 2 | 3, 11 | 4, 16 | −60.17 | 26.90 | 20.40 | −12.87 | −0.129 | 0.070 | 0.053 | −0.006 |
| 8 | 2 | 2 | 5, 9 | 3, 15 | −59.63 | 27.81 | 20.66 | −11.16 | −0.124 | 0.072 | 0.053 | 0.001 |
| 9 | 1 | 2 | 2 | 8, 14 | −37.60 | 19.25 | 17.06 | −1.29 | −0.089 | 0.050 | 0.043 | 0.004 |
| 10 | 1 | 2 | 2 | 13, 20 | −39.35 | 20.61 | 18.47 | −0.28 | −0.101 | 0.053 | 0.048 | 0.000 |
| 11 | 2 | 2 | 15, 18 | 7, 25 | −73.85 | 29.29 | 24.87 | −19.69 | −0.148 | 0.076 | 0.065 | −0.008 |
| 12 | 1 | 2 | 16 | 4, 19 | −50.60 | 21.99 | 23.01 | −5.59 | −0.111 | 0.057 | 0.061 | 0.007 |
| 13 | 2 | 2 | 10, 21 | 6, 23 | −65.73 | 27.13 | 22.39 | −16.22 | −0.136 | 0.073 | 0.058 | −0.005 |
| 14 | 2 | 2 | 9, 22 | 5, 20 | −53.41 | 23.25 | 20.53 | −9.64 | −0.122 | 0.059 | 0.054 | −0.009 |
| 15 | 2 | 2 | 8, 22 | 11, 27 | −59.52 | 26.55 | 20.84 | −12.13 | −0.127 | 0.070 | 0.053 | −0.004 |
| 16 | 2 | 1 | 7, 24 | 12 | −50.47 | 33.59 | 6.17 | −10.71 | −0.103 | 0.087 | 0.015 | −0.001 |
| 17 | 2 | 2 | 6, 26 | 19, 24 | −76.64 | 26.87 | 27.81 | −21.97 | −0.143 | 0.070 | 0.073 | 0.001 |
| 18 | 2 | 2 | 21, 28 | 11, 22 | −71.60 | 26.35 | 28.89 | −16.36 | −0.140 | 0.067 | 0.075 | 0.001 |
| 19 | 2 | 2 | 12, 17 | 23, 31 | −60.33 | 24.44 | 24.78 | −11.12 | −0.119 | 0.064 | 0.064 | 0.008 |
| 20 | 2 | 1 | 10, 14 | 21 | −41.87 | 28.50 | 5.54 | −7.83 | −0.090 | 0.073 | 0.013 | −0.004 |
| 21 | 2 | 2 | 20, 26 | 13, 18 | −70.57 | 26.00 | 26.28 | −18.29 | −0.137 | 0.067 | 0.068 | −0.002 |
| 22 | 2 | 2 | 18, 30 | 14, 15 | −61.89 | 24.07 | 25.18 | −12.65 | −0.128 | 0.062 | 0.065 | −0.001 |
| 23 | 2 | 1 | 13, 19 | 29 | −48.76 | 32.18 | 5.75 | −10.83 | −0.101 | 0.085 | 0.014 | −0.002 |
| 24 | 2 | 2 | 17, 32 | 16, 25 | −59.30 | 26.20 | 24.56 | −8.54 | −0.127 | 0.068 | 0.063 | 0.004 |
| 25 | 2 | 2 | 11, 24 | 27, 28 | −63.96 | 23.03 | 28.32 | −12.60 | −0.131 | 0.059 | 0.074 | 0.002 |
| 26 | 2 | 2 | 29, 33 | 17, 21 | −71.35 | 29.38 | 25.55 | −16.43 | −0.137 | 0.075 | 0.065 | 0.003 |
| 27 | 2 | 1 | 15, 25 | 30 | −44.58 | 31.49 | 4.85 | −8.24 | −0.100 | 0.082 | 0.012 | −0.006 |
| 28 | 2 | 2 | 25, 30 | 18, 33 | −63.95 | 26.72 | 23.07 | −14.15 | −0.132 | 0.069 | 0.060 | −0.003 |
| 29 | 1 | 2 | 23 | 26, 31 | −54.53 | 23.08 | 20.06 | −11.39 | −0.113 | 0.061 | 0.053 | 0.000 |
| 30 | 1 | 2 | 27 | 22, 48 | −44.37 | 20.65 | 20.86 | −2.86 | −0.097 | 0.053 | 0.054 | 0.010 |
| 31 | 2 | 1 | 19, 29 | 32 | −50.40 | 34.29 | 6.84 | −9.27 | −0.105 | 0.088 | 0.017 | 0.000 |
| 32 | 1 | 2 | 31 | 24, 33 | −48.20 | 22.34 | 21.06 | −4.80 | −0.109 | 0.060 | 0.054 | 0.005 |
| 33 | 2 | 1 | 28, 32 | 26 | −45.65 | 29.61 | 6.31 | −9.72 | −0.091 | 0.077 | 0.016 | 0.002 |
Relationships between stabilities and positions of atoms in the water cluster are particularly important for understanding the role of HB networks in the cluster. Since a number of polarized charges are affecting atomic energies, polarized atomic charges are plotted against atomic energies in Fig. 7. Thus, it was found that atomic energies are proportional to the polarized atomic charges for all atoms in the cluster, regardless of their different positions or orientations, especially for H atoms. Increased electron density on an atom decreases its energy. A least square fitting approach indicates that slopes of the correlation plots for O atoms were 486.4 and 492.0 kcal mol−1 e−1 in (H2O)32 and (H2O)33, respectively. For H atoms, they are 385.1 and 385.5 kcal mol−1 e−1 in (H2O)32 and (H2O)33, respectively. Applying the simplest model that ΔQ(sum) is zero, which means that the total charge of the water molecules is conserved in the cluster, ΔQ of an O atom should be exactly same as the negative sign of the sum of the ΔQ of the H atoms. Then, the polarization of water molecules causes the stabilization of water since the slope of the O atom is larger than that of the H atom, and the ΔQ of the O atom shows more important effects on molecular stabilities. Therefore, the relationships between polarized charges of the O atoms and topologies of the HB networks should be investigated.
Although an O atom in the i-th water molecule can bind to positively charged H atoms in neighboring waters via lone pairs as hydrogen bonds, directions of these hydrogen bonds are not parallel to the OH bonds, resulting in rather weak OH bond polarization. On the other hand, each H atom can also form a hydrogen bond with the negatively charged O atom on a neighbor, which is parallel to the OH bond, and a large polarization is induced in the OH bond. Therefore, the number of H-donating interactions (ND) is more efficient for the polarized charges on O atoms than the number of H-accepting interactions (NA), as seen in Fig. 7(a). Since any hydrogen bonds can increase the electron density on an O atom under the simple assumption that the amount of CT would be small enough, water molecules indicated by wi(2,2) have the most negative charges on the O atom, followed by wi(1,2), wi(2,1) and wi(1,1), consistent with the results in Fig. 7(a). As a consequence, the most stable water molecules in (H2O)32 and (H2O)33 were w10(2,2) and w31(2,2), respectively, which have two H-donating and two H-accepting interactions resulting in large negative O charges.
The environmental effects on the polarization of H atoms are somewhat different from the O atom. Charges on H atoms become more positive only if one H atom makes a hydrogen bond because the cooperative effects suppress OH polarization due to cumulative negative charges on the O atom when two H atoms form hydrogen bonds simultaneously. Similar to the discussion of the O atom, the polarized charge becomes more positive when NA is 2. This is the reason why wi(2,1) shows the most positive values on the H atoms, as seen in Fig. 7(b). In the other words, the H atom in wi(2,1) becomes the most unstable.
In addition to topological information of hydrogen bonds in a given molecule, the amount of charges on the counter molecule is important to determine the OH polarization. A H atom tends to bind with an O atom with a large negative charge density. Therefore, H atoms in the most stable water, w15(2,2) in (H2O)32, have two hydrogen bonds with O atoms in both w21(2,2) and w25(2,2), which are expected to have highly negative charges on the O atoms. The same situation was observed in the most stable water, w6(2,2) in (H2O)33, which bonds to O atoms in w5(2,2) and w17(2,2). According to these considerations, O atoms with large negative charges tend to be in water molecules with four hydrogen bonds where two H-donating interactions are formed with O atoms in w(2,2) type of water molecules. This is the reason why atoms in water molecules close to the center of the cluster are particularly stabilized or destabilized relative to those outside the cluster, as seen in Fig. 6.
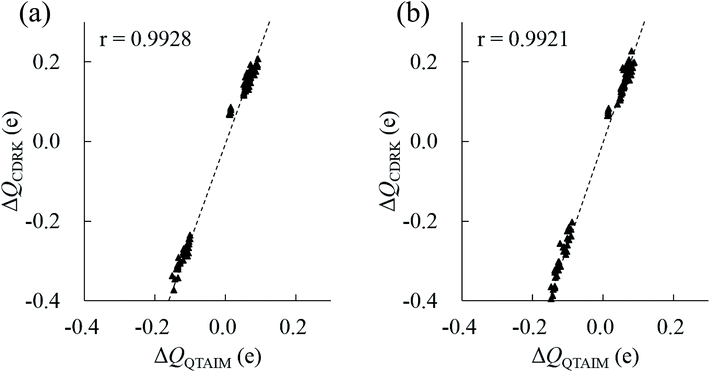
In principle, polarized atomic charges can be evaluated by the external electrostatic potential of the atoms, which include information about both environmental charges and interatomic distances associated with hydrogen bonds, as is suggested by charge response kernel (CRK) approximations by Iuchi et al.67 According to CRK approximation of a water molecule, the electron density on the H1 atom is affected by the external electrostatic potential on the H1 atom and the electrostatic potential on the H2 atom, in the amount of about 15% of the H1 potentials. Recently, the charge and dipole response kernel (CDRK) method was proposed by one of the authors,68 which can successfully evaluate the polarization of molecules in the molecular assembly where polarized atomic charges and dipoles are explicitly derived using the external electrostatic potentials and fields on atoms in the molecule. Fig. 8 shows the comparison of polarized atomic charges evaluated by the CDRK method with the QTAIM charges. The CDRK polarized charges could reasonably reproduce the QTAIM results with a good correlation coefficient of over 0.99 for both (H2O)32 and (H2O)33 clusters, although the slopes were somewhat different. In addition, the polarized charges on a given atom can be decomposed into contributions of each surrounded molecule by adapting the CDRK approach. The decomposition analyses were performed on the most stable structure for both size of clusters (see ESI Fig. S4†). In this figure, coordinated water molecules were classified into the first (0 Å ≦ ROO < 3.2 Å), second (3.2 Å ≦ ROO < 5.6 Å), and third (5.6 Å ≦ ROO) solvation shell by the interatomic distance between oxygen atoms ROO based on the radial distribution function in the liquid water.69 Coordinated molecules in the first, second, and third solvation shells influence to the target molecule by 65%, 30%, and 5%, respectively as a whole for (H2O)32 cluster. In contrast, each molecule in the first, second, and third solvation shells influence to the target molecule by 16%/molecule, 2%/molecule, and 0.4%/molecule, respectively for (H2O)32. In the same manner, water molecules in the first, second, and third shell contribute 67%, 27%, and 6%, respectively as a whole, and then each molecule in each shell contribute 17%/molecule, 1.5%/molecule, and 0.6%/molecule, respectively for (H2O)33. These results confirm that the atomic stabilization energies are dominantly stabilized by the first solvation water molecules though hydrogen bonds. Then the second hydration shell is almost as important for determining the charges on first shell of water molecules that influence the stability of atoms in the target molecule.
Conclusion
In the current work, two large water clusters (H2O)32 and (H2O)33 are investigated using MCTBP and QTAIM methods. The improved MCTBP approach successfully and efficiently found many low energy structures. We determined a structure with almost the same energy as that of ref. 46 for (H2O)32 and several structures lower in energy than that determined by Bandow et al. Rationalization of the stability of the most stable structures found in this work was carried out using the polarized charge on each water molecule in a cluster. The stability of clusters can be rationalized by the HB topology and the amount of charge on each atom (relative to that of an isolated water molecule) of the cluster. This work confirms that a combination of MCTBP and QTAIM can be an excellent tool to find important stable structures and examine the properties of large water clusters.Acknowledgements
P. B. wishes to acknowledge financial help from UPE-II grant and DST-PURSE awarded to JNU.References
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- D. J. Wales and I. Ohmine, J. Chem. Phys., 1993, 98, 7245–7256 CrossRef CAS.
- J. T. Su, X. Xu and W. A. Goddard III, J. Phys. Chem. A, 2004, 108, 10518–10526 CrossRef CAS.
- X. Liu, W. Lu, C. Z. Wang and K. M. Ho, Chem. Phys. Lett., 2011, 508, 270–275 CrossRef CAS.
- S. Maheshwari, N. Patel, N. Sathyamurthi, A. D. Kulkarni and S. R. Gadre, J. Phys. Chem. A, 2001, 105, 10525–10537 CrossRef.
- S. R. Pruitt, M. A. Addicoat, M. A. Collins and M. S. Gordon, Phys. Chem. Chem. Phys., 2012, 14, 7752–7764 RSC.
- F. Li, L. Wang, J. Zhao, J. R. H. Xie, K. E. Riley and Z. Chen, Theor. Chem. Acc., 2011, 130, 341–352 CrossRef CAS.
- F. Li, Y. Liu, L. Wang, J. Zhao and Z. Chen, Theor. Chem. Acc., 2012, 131, 1163 CrossRef.
- B. Wang, W. Jiang, X. Dai, Y. Gao, Z. Wang and R. Q. Zhang, Sci. Rep., 2016, 6, 22099 CrossRef CAS PubMed.
- H. H. Yang, Y. Song and H. S. Chen, J. Cluster Sci., 2016, 27, 775–789 CrossRef CAS.
- S. Iwata, P. Bandyopadhyay and S. S. Xantheas, J. Phys. Chem. A, 2013, 117, 6641–6651 CrossRef CAS PubMed.
- I. Bako and I. Mayer, J. Phys. Chem. A, 2016, 120, 631–638 CrossRef CAS PubMed.
- P. Bandyopadhyay, Chem. Phys. Lett., 2010, 487, 133–138 CrossRef CAS.
- S. Shanker and P. Bandyopadhyay, J. Phys. Chem. A, 2011, 115, 11866–11875 CrossRef CAS PubMed.
- A. Rakshit and P. Bandyopadhyay, Theor. Comput. Chem., 2013, 1021, 206–214 CrossRef CAS.
- J. P. Furtado, A. P. Rahalkar, S. Shanker, P. Bandyopadhyay and S. R. Gadre, J. Phys. Chem. Lett., 2012, 3, 2253–2258 CrossRef CAS PubMed.
- N. Sahu, S. S. Khire and S. R. Gadre, Mol. Phys., 2016, 113, 2970–2979 CrossRef.
- S. Yoo and S. S. Xantheas, J. Chem. Phys., 2011, 134, 121105 CrossRef PubMed.
- E. Miliordos, E. Apra and S. S. Xantheas, J. Chem. Theory Comput., 2016, 12, 4004–4014 CrossRef PubMed.
- S. Iwata, D. Akase and S. S. Xantheas, Phys. Chem. Chem. Phys., 2016, 18, 19746–19756 RSC.
- S. Yoo, E. Apra, X. C. Zengv and S. S. Xantheas, J. Phys. Chem. Lett., 2010, 1, 3122–3127 CrossRef CAS.
- S. S. Xantheas, Can. J. Chem. Eng., 2012, 90, 843–851 CrossRef CAS.
- E. Miliordos, E. Apra and S. S. Xantheas, J. Chem. Phys., 2013, 139, 114302 CrossRef PubMed.
- E. Miliordos and S. S. Xantheas, J. Chem. Phys., 2015, 142, 234303 CrossRef PubMed.
- K. R. Brorsen, S. Y. Willow, S. S. Xantheas and M. S. Gordon, J. Phys. Chem. Lett., 2015, 6, 3555–3559 CrossRef CAS PubMed.
- D. J. Anick, J. Chem. Phys., 2003, 119, 12442–12456 CrossRef CAS.
- D. J. Anick, J. Mol. Struct.: THEOCHEM, 2001, 574, 109–115 CrossRef CAS.
- R. M. Shields, B. Temelso, K. A. Archer, T. E. Morrell and G. C. Shields, J. Phys. Chem. A, 2010, 114, 11725–11735 CrossRef CAS PubMed.
- B. Temelso, K. A. Archer and G. C. Shields, J. Phys. Chem. A, 2011, 115, 12034–12046 CrossRef CAS PubMed.
- K. Liu, M. G. Brown, C. Carter, R. J. Saykally, J. K. Gregory and D. C. Clary, Nature, 1996, 381, 501–503 CrossRef CAS.
- J. K. Gregory, D. C. Clary, K. Liu, M. G. Brown and R. J. Saykally, Science, 1997, 275, 814–817 CrossRef CAS PubMed.
- J. D. Cruzan, L. B. Braly, K. Liu, M. G. Brown, J. G. Loeser and R. J. Saykally, Science, 1996, 271, 59–62 CAS.
- K. Nauta and R. E. Miller, Science, 2000, 287, 293–295 CrossRef CAS PubMed.
- L. A. Dombrovsky, A. A. Fedorates and D. N. Medvedev, Infrared Phys. Technol., 2016, 75, 124–132 CAS.
- T. Hamashima, K. Mizuse and A. Fujii, J. Phys. Chem. A, 2011, 115, 620–625 CrossRef CAS PubMed.
- T. P. Radhakrishnan and W. C. Herndon, J. Phys. Chem., 1991, 95, 10609–10617 CrossRef CAS.
- D. McDonald, L. Ojamae and S. J. Singer, J. Phys. Chem. A, 1998, 102, 2824–2832 CrossRef.
- T. Miyake and M. Aida, Chem. Phys. Lett., 2002, 363, 106–110 CrossRef CAS.
- D. Vukicevic, T. Grubesa and A. Graovac, Chem. Phys. Lett., 2005, 416, 212–214 CrossRef CAS.
- G. Brinkmann, J. Math. Chem., 2009, 46, 1112–1121 CrossRef CAS.
- D. Akase and M. Aida, J. Phys. Chem. A, 2014, 118, 7911–7924 CrossRef CAS PubMed.
- R. Shrivastava, A. Rakshit, S. Shanker, L. Vig and P. Bandyopadhyay, J. Chem. Sci., 2016, 128, 1507–1516 CrossRef CAS.
- S. T. Chill, J. Stevenson, V. Ruechle, C. Shang, P. Xiao, J. D. Farell, D. J. Wales and G. Henkelman, J. Chem. Theory Comput., 2014, 10, 5476–5482 CrossRef CAS PubMed.
- H. Takeuchi, J. Chem. Inf. Model., 2008, 48, 2226–2233 CrossRef CAS PubMed.
- S. Goedecker, J. Chem. Phys., 2004, 120, 9911–9917 CrossRef CAS PubMed.
- S. Kazachenko and A. J. Thakkar, Chem. Phys. Lett., 2009, 476, 120–124 CrossRef CAS.
- R. J. Wawak, M. M. Wimmer and H. A. Scheraga, J. Phys. Chem., 1992, 96, 5138–5145 CrossRef CAS.
- C. J. Tsai and K. D. Jordon, J. Phys. Chem., 1993, 97, 5208–5210 CrossRef CAS.
- P. N. Day, R. Patcher, M. S. Gordon and G. N. Merill, J. Chem. Phys., 2000, 112, 2063–2073 CrossRef CAS.
- D. Kemp and M. S. Gordon, J. Phys. Chem. A, 2008, 112, 4885–4894 CrossRef CAS PubMed.
- J. K. Kazimirski and V. Buch, J. Phys. Chem. A, 2003, 207, 9762–9775 CrossRef.
- D. J. Wales and M. P. Hodges, Chem. Phys. Lett., 1998, 286, 65–72 CrossRef CAS.
- H. Kabrede, Chem. Phys. Lett., 2006, 430, 336–339 CrossRef CAS.
- L. Zhan, J. Z. Y. Chen and W. Liu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 015701 CrossRef PubMed.
- B. Bandow and B. Hertke, J. Phys. Chem. A, 2006, 110, 5809–5822 CrossRef CAS PubMed.
- S. Shanker and P. Bandyopadhyay, J. Biosci., 2012, 37, 533–538 CrossRef CAS PubMed.
- F. Reif, Statistical Physics, Berkeley Physics Course, The McGraw-Hill, New Delhi, 2008 Search PubMed.
- K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340 CrossRef CAS.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- L. Albrecht and R. J. Boyd, J. Phys. Chem. A, 2012, 116, 3946–3951 CrossRef CAS PubMed.
- T. A. Keith, AIMAll (Version 15.09.27), TK Gristmill Software, Overland Park KS, USA, 2015, http://aim.tkgristmill.com Search PubMed.
- A. Taylor, J. Taylor, G. W. Watson and R. J. Boyd, J. Phys. Chem. B, 2010, 114, 9833–9839 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- M. S. Gordon, M. A. Freitag, P. Bandyopadhyay, J. H. Jensen, V. Kairys and W. J. Stevens, J. Phys. Chem. A, 2001, 105, 293–307 CrossRef CAS.
- S. Iuchi, A. Morita and S. Kato, J. Phys. Chem. B, 2002, 106, 3466–3476 CrossRef CAS.
- T. Asada, K. Ando, K. Sakurai, S. Koseki and M. Nagaoka, Phys. Chem. Chem. Phys., 2015, 17, 26955–26968 RSC.
- J. Wang, G. Román-Pérez, J. M. Soler, E. Artacho and M.-V. Fernández-Serra, J. Chem. Phys., 2011, 134, 024516 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra28688g |
| This journal is © The Royal Society of Chemistry 2017 |