Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The influence of oxygen vacancies on the linear and nonlinear optical properties of Pb7O(OH)3(CO3)3(BO3)†
A. H. Reshak *ab and
S. Auluckc
*ab and
S. Auluckc
aNew Technologies – Research Centre, University of West Bohemia, Univerzitni 8, 306 14 Pilsen, Czech Republic. E-mail: maalidph@yahoo.co.uk
bSchool of Material Engineering, University Malaysia Perlis, 01007 Kangar, Perlis, Malaysia
cCouncil of Scientific and Industrial Research, National Physical Laboratory, Dr K S Krishnan Marg, New Delhi 110012, India
First published on 7th March 2017
Abstract
We have investigated the influence of the oxygen vacancy on the linear and nonlinear optical properties and the microscopic first hyperpol of asymmetric Pb7O(OH)3(CO3)3(BO3). The O-vacancy reduces the energy gap and changes the energy band gap from indirect to direct. The calculated indirect energy band gap of Pb7O(OH)3(CO3)3(BO3) (I) of 3.56 eV is in good agreement with the experimental gap of 3.65 eV. The direct gap in O-deficient Pb7(OH)3(CO3)3(BO3) (II) is 1.61 eV. The oxygen vacancy results in a red-shifted energy band gap, making the material useful in the visible region. Calculations show that I exhibits a negative uniaxial anisotropy and birefringence, whereas II exhibits positive uniaxial anisotropy and birefringence. This shows that the O-vacancy has a significant influence on the uniaxial anisotropy and birefringence. We have calculated the second harmonic generation (SHG) for I and II at zero energy limit and at wavelength λ = 1064 nm. The calculated SHG for I at λ = 1064 nm is close to the experimental value of the well known compound KTiOPO4 (KTP), whereas for II it is about a quarter of the experimental value of the KTP. In addition, the microscopic first hyperpolarizability for I and II is calculated at the static limit and at wavelength 1064 nm.
1. Introduction
Developing highly efficient nonlinear optical (NLO) crystals for ultra-violet and deep-ultra-violet applications is important for laser spectroscopy and laser processing, including laser-tailoring of molecules and optical triggering. Borate crystals are found to be extremely useful for solid state ultra-violet lasers.1–3 The nonlinear optical properties of oxoborate materials have been reported and found to be comparable to those of β-BaB2O4 (BBO) for second harmonic generation (SHG).4 It has been reported that the B atom has two types of hybridized orbitals, the planar sp2 and the three-dimensional sp3, to coordinate three or four oxygen atoms forming BO33−, BO34− or BO45− clusters. Further, these clusters comprise several different BxOy groups, and therefore various types of borate crystals can be constructed based on these structures. Thus it is interesting to investigate the influence of BO33−, BO34− or BO45− clusters on the NLO properties of various borate crystals.4 Bian et al.5 calculated the birefringence of Pb8B9O21F, PbBiBO4, Pb3BO4F, Pb6B3O10Cl, and Pb2BO3F with different B–O networks (isolated BO3 groups). They found that PbBiBO4, Pb3BO4F, and Pb2BO3F have a birefringence greater than 0.1. Pb2BO3F is perhaps the first compound with birefringence above 0.08 among the positive uniaxial borate crystals. It has been found that the parallel arrangement of fundamental building units is not the only light anisotropy active characteristic. In further research of Pb2BO3F, polarization disproportion via a visualized model was first put forward for identifying the origin of the large birefringence, which will be helpful in the search for new optical materials with suitable birefringence. Li et al.6 have calculated the ground state properties of Pb2B5O9Cl, BaPb[B5O9(OH)]·H2O, and Ba2Pb(B3O6)2, to investigate the influence of the Pb atom on the band gap and SHG response. It has been found that BaPb[B5O9(OH)]·H2O and Ba2Pb(B3O6)2 have a small band gap red shift due to their weak distortion and stereochemical activity. The intensity of the Pb lone-pair stereochemical activity plays a major role in determining the band gap reduction. However, it is still desirable to find materials with promising NLO properties.Recently, Abudoureheman et al.7 synthesized a mixed borate and carbonate nonlinear optical material which exhibits a large SHG response. They reported the first borate carbonate ultra-violet nonlinear optical material with the chemical formula Pb7O(OH)3(CO3)3(BO3). Abudoureheman's group have reported X-ray diffraction data and find that Pb7O(OH)3(CO3)3(BO3) crystallizes in a non-centro-symmetric structure with the hexagonal space group P63mc with lattice parameters a = b = 10.519(16) Å and c = 8.900(13) Å.7 The unit cell contains of two formulas. They have reported that the measured SHG of the grinded and sieved polycrystalline Pb7O(OH)3(CO3)3(BO3) is comparable with the SHG of grinded and sieved polycrystalline KH2PO4 (KDP)7 using the Kurtz–Perry method.8 The SHG of Pb7O(OH)3(CO3)3(BO3) powder is 4.5 times larger than that of KH2PO4 (KDP) powder.7 It is important to mention that, on the basis of anionic group theory,9 the overall SHG response of a crystal is the geometrical superposition of the second-order susceptibilities. Therefore, the packing of the BO3 and CO3 structural units and stereochemically active lone pair in the Pb polyhedra may also affect the macroscopic SHG coefficients.7 The large SHG is due to the strong interactions between the stereo effect of Pb cations and co-parallel BO3 and CO3 triangle groups.7 Thus, the reported values of the SHG have been measured for a powder without taking into account the influence of the packing of the BO3 and CO3 structural units and the stereochemically active lone pair in the Pb polyhedra. Hence, we have addressed ourselves to calculating the SHG of the Pb7O(OH)3(CO3)3(BO3) crystal taking into account the influence of the packing of the BO3 and CO3 structural units and the stereochemically active lone pair in the Pb polyhedra. Abudoureheman et al. have calculated the band structure and the density of states within the generalized gradient approximation (PBE-GGA)7 using a non-full-potential method which ignores the potential in the interstitial region. Moreover, PBE-GGA10 leads to an underestimate of the band gap. We emphasize that in full-potential methods the potential and charge density are expanded into lattice harmonics inside each atomic sphere and as a Fourier series in the interstitial region. This has a profound effect on the electronic structure, linear and nonlinear optical properties and needs to be studied.
Therefore, we thought it would be worthwhile to perform full-potential calculations using the recently modified Becke–Johnson potential (mBJ)11 to calculate the linear and nonlinear optical properties and the microscopic first hyperpolarizability of Pb7O(OH)3(CO3)3(BO3). The modified Becke–Johnson potential allows the calculations with accuracy similar to the very expensive GW calculations.11 It is a local approximation to an atomic “exact-exchange” potential and a screening term. In addition, we have explored the effect of an oxygen vacancy on the electronic structure and hence on the linear and nonlinear optical properties. The prediction and discovery of new materials is always exciting for the promise of new applications and properties.12,13 This motivated us to perform comprehensive theoretical calculations to ascertain the influence of an oxygen vacancy on the linear and nonlinear optical properties. It has been reported that an oxygen vacancy adds two extra electrons to preserve charge neutrality. The O vacancy itself would release two electrons in its vicinity. The O vacancy is a natural possibility for charge compensation.14
2. Calculation methodology
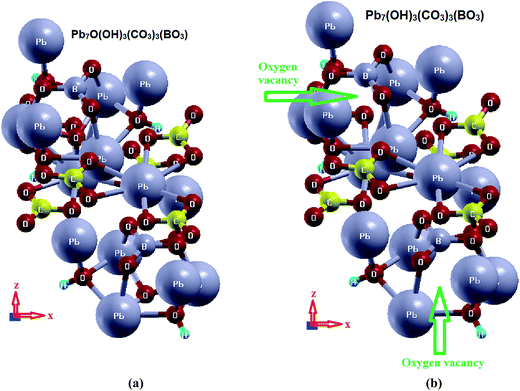
Based on the reported X-ray crystallographic data of the original compound,7 we have performed comprehensive calculations for the linear and nonlinear optical properties and the microscopic first hyperpolarizability. Using the experimental crystallographic data, we have removed two O atoms (because the unit cell has Z = 2) to investigate the influence of O-vacancy on the linear and nonlinear optical properties. We designate the original compound as I and the O-deficient compound as II. The geometrical relaxation was obtained using the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA).10 We employed the full-potential linear augmented plane wave (FP-LAPW + lo) method as embodied in the Wien2k code.15 The resulting relaxed geometry was used to calculate the electronic structure, linear and nonlinear optical properties. We have used mBJ to treat the exchange correlation.11 Fig. 1(a) and (b) depicts the relaxed crystal structures of I and II, which clearly shows the position of the O-vacancy. The muffin-tin radii (RMT) of the atoms were chosen in such a way that the spheres did not overlap. The basis functions in the interstitial region (IR) were expanded up to RMT × Kmax = 7.0 inside the atomic spheres for the wave function. The lmax was taken to be 10, and the charge density is Fourier expanded up to Gmax = 12 (a.u)−1. A mesh of 300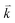 points in the irreducible Brillouin zone (IBZ) was used to achieve self-consistency. The self-consistent calculations are converged when the total energy of the system is stable within 0.00001 Ry. The linear and nonlinear optical properties and the microscopic first hyperpolarizability calculations are performed within 2500
points in the irreducible Brillouin zone (IBZ) was used to achieve self-consistency. The self-consistent calculations are converged when the total energy of the system is stable within 0.00001 Ry. The linear and nonlinear optical properties and the microscopic first hyperpolarizability calculations are performed within 2500 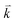 points in the IBZ.
points in the IBZ.
3. Results and discussion
3.1. Salient features of the electronic band structure
The calculation of the dielectric function involves the energy eigenvalues and electron wave functions which are natural outputs of band structure calculations. Therefore, we will first recall the salient features of the calculated electronic band structure of I and II,16 see Fig. S1 (ESI†). We set the zero of the energy at Fermi level (EF). The valence band maximum (VBM) of I and II is located at the center (Γ) of the BZ, while the conduction band minimum (CBM) of I is situated between Γ and A points of BZ, resulting in an indirect energy band gap of 3.34 eV (PBE-GGA) and 3.56 eV (mBJ). The CBM of II is located at Γ of the BZ, resulting in a direct band gap of 1.10 eV (PBE-GGA) and 1.61 eV (mBJ). The band gap reduction in II is attributed to the appearance of new energy bands within the energy gap region of I. Thus, the O-vacancy causes the reduction of the energy band gap. It also changes the gap from indirect to direct. It has been found that mBJ succeeds in bringing the calculated energy gap of I close to the experimental value (3.65 eV),7 as is expected from this approach,17–19 see Fig. S2 (ESI†). Therefore, in the following, we show only the results obtained by mBJ. A material with such an energy band gap value is expected to possess a high laser damage threshold.20,21The electronic band structures of I and II show the influence of the O-vacancy on the bands' dispersion. It is clear that in the VB of I there is a high-density state region situated between −2.5 eV and EF which belongs to the O atom. This feature vanishes from the electronic band structure of II. It has been noticed that for I the VBM is mainly formed by O3, O4, O5 and Pb2, Pb3 atoms, while for II it is clear that the O bands are absent, confirming that the O-vacancy keeps the VBM with Pb1 and Pb3 only. The O-vacancy pushes the Pb1 states which are situated below VBM towards Pb3 to form the VBM, while it pushes Pb2 and the rest of the Pb1, Pb3 states towards lower energies by around 2.0 eV. It is interesting to mention that in II, energy bands appear directly above EF in the forbidden gap, which is composed of O2-2p states. These could be called intermediate bands (IB). The appearance of new bands in II will result in new excitations. Recently, Ding et al.22 reported that the position of such local energy levels changes as a function of O-vacancy concentration.
3.2. Complex first-order linear optical dispersion
The complex first-order linear optical dielectric functions of I and II are calculated on the basis of the calculated electronic band structure. The obtained electronic band structure shows that the C–O and B–O anionic groups are the main factors which influence the band gap and hence the linear optical properties.5 Therefore, based on the calculated electronic band structure, the imaginary part of the inter-band optical dielectric function is obtained using the expression taken from ref. 23 and 24.
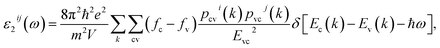 | (1) |
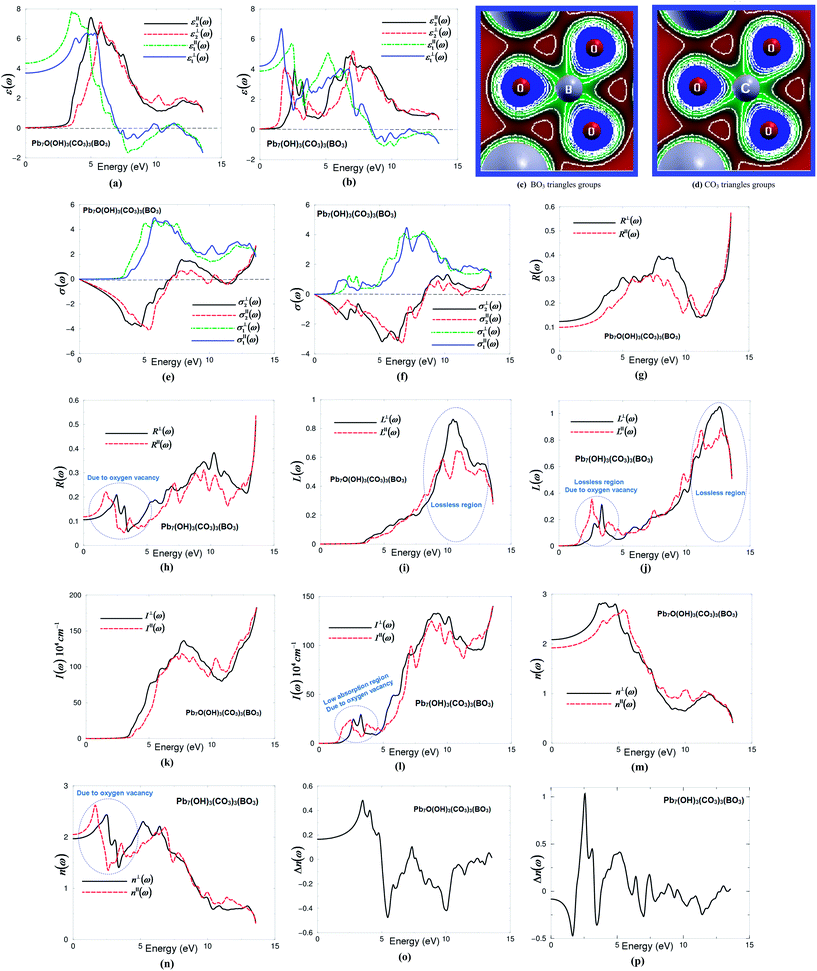
Following the expression (1), we note that the imaginary part of the optical dielectric tensor is inversely proportional to the square of the energy difference. Hence it is very important to get an accurate value of the energy gap. Therefore, the accuracy of the results will be very sensitive to the selection of the exchange–correlation potential (XC), which plays an important role in the determination of the energy gap. Based on our experience in using different XC potentials (LDA, PBE-GGA, EV-GGA, LDA-mBJ and PBE-GGA-mBJ) on several systems whose energy band gaps are known experimentally,17–19 we find that PBE-GGA-mBJ gives the best agreement with the experimental data.17–19 This motivated us to use PBE-GGA-mBJ to calculate the band structure and hence the first-order linear optical dielectric functions of I and II. These structures have a hexagonal space group; the symmetry allows only two independent tensor components. These are εxx(ω) and εzz(ω), which completely characterize the linear optical properties of the hexagonal system. In this symmetry, εxx(ω) = εyy(ω) = ε⊥(ω) and εzz(ω) = ε∥(ω); thus these are only two tensor components corresponding to an electric field perpendicular and parallel to the c-axis. The complex optical dielectric function consists of real and imaginary parts. The imaginary part can be obtained from the calculated electronic band structure, while the real part is obtained from the imaginary part by means of the Kramers–Kronig transformation.23,24 Fig. 1(a) and (b) show ε∥2(ω), ε⊥2(ω) and ε∥1(ω), ε⊥1(ω) of I and II. In order to identify the observed spectral structures, we need to look at the magnitude of the optical matrix elements. The observed spectral structures would correspond to those transitions that have large optical matrix elements.
The absorption edges of I (λ = 348.3 nm) and II (λ = 770.1 nm) are located at around 3.56 eV (I) and 1.61 eV (II). The absorption edges of I show good agreement with the experimental data, see Fig. S2 (ESI†). The edges of optical absorption give the threshold for direct optical transitions between the VBM (Pb3-6s/6p, O-2p) and the CBM (O-2s, Pb3-6p/5d) for I, while for II between the VBM (Pb3-6p/5d/4f) and the CBM (O-2s, Pb3-2s/-6p/5d/4f). It has been noticed that ε∥2(ω) and ε⊥2(ω) of I exhibit only one main structure situated between 3.0 and 7.0 eV. The strength of this structure could be explained by the fact that ε2(ω) scales as 1/ω2. For II both ε∥2(ω) and ε⊥2(ω) exhibit two main structures; the first one is located around 2.5 eV and the second one is situated around 7.0 eV. The intensity of these structures is almost half of that for I. This is due to the fact that optical transitions from Pb3-2s/5d/4f, B-2p, O-2s/2p of the VBs to B-2p, C-2p, O-2s/2p, Pb-/6p/5d/bands of the CBs for I, whereas for II it is from Pb3-2s/6p/5d/4f, B-2p, O-2p of the VBs to C-2p, O-2s/2p, Pb-6s/6p/5d/bands of the CBs. After that, a prompt reduction occurs in the spectral structure to form a tail of the spectra.
The zero frequency value in the dielectric function defines the static electronic dielectric constant by ε∞ = ε1(0). These values for both I and II are listed in Table 1. Furthermore, the calculated real part of the optical dielectric functions can give information about the energy gaps, since the calculated static electronic dielectric constant ε∞ = ε1(0) is inversely related to the energy gap as in the Penn model.26 One of the important features of the optical spectra is the plasmon oscillations ω∥p(ω) and ω⊥p(ω) (Table 1). These are associated with inter-band transitions that occur at energies where the real part of the optical spectra crosses zero. The other important feature is the uniaxial anisotropy (δε), which can be calculated from the zero frequency value (Table 1). From Table 1, it is clear that I exhibits negative uniaxial anisotropy and II shows positive uniaxial anisotropy. Following Fig. 2(a) and (b) and Table 1, we can see that structure I shows ε∥1(0) < ε⊥1(0), while for structure II it is ε⊥1(0) < ε∥1(0). Therefore, according to the expression of the uniaxial anisotropy (δε = [(ε∥0 − ε⊥0)/εtot0]) structure I exhibits a negative uniaxial anisotropy whereas structure II shows positive uniaxial anisotropy. Hence, the O-vacancy turns the uniaxial anisotropy from positive to negative, which shows the significant influence on the linear optical properties and hence on the nonlinear optical properties, as the anisotropy between the two tensor components favors an important quantity in nonlinear optical properties due to better fulfillment of phase-matching conditions.
In I and II, [BO3]− and [CO3]− groups are the main contributors to the optical anisotropy, while Pb2+ cations may also contribute to the optical anisotropy due to the repulsion interactions of the lone pairs of Pb2+ cations.5 Furthermore, the high electron density configuration and strong anisotropy of C–O and B–O groups indicates the main contribution of BO3 and CO3 groups to the optical anisotropy (Fig. 2(c) and (d)).
The complex optical conductivity consists of imaginary and real parts. It can be obtained from the complex first-order linear optical dielectric function following the expression 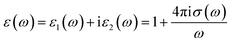 .23,24 The calculated complex optical conductivity of I and II are shown in Fig. 2(e) and (f). The complex optical conductivity of I and II show different spectral features which can be attributed to the fact that the two compounds exhibit different electronic band structures.
.23,24 The calculated complex optical conductivity of I and II are shown in Fig. 2(e) and (f). The complex optical conductivity of I and II show different spectral features which can be attributed to the fact that the two compounds exhibit different electronic band structures.
The calculated optical reflectivity spectra R∥(ω) and R⊥(ω) of I and II are shown in Fig. 2(g) and (h). At low energies both compounds exhibit low reflectivity ∼10–12%. It is clear that the O-vacancy significantly influences the reflectivity spectra, resulting in a new structure around 2.5 eV (Fig. 2(h)). This represents the first reflectivity maxima. The first reflectivity minima for I is situated around 7.0 eV, whereas for II it is located around 8.5 eV. This confirms the occurrence of a collective plasmon resonance in concordance with our observation in Fig. 2(a) and (b). Thus, the oxygen vacancy causes the shift of the first reflectivity minima towards higher energies by around 1.5 eV. At higher energies, the region around 11.0 eV (I) and 12.0 eV (II) represents the lossless region. To support this statement, we have calculated the loss function of I and II as shown in Fig. 2(i) and (j), which confirm that the lossless region occurs at 11.0 eV (I) and 12.0 eV (II). It has been found that there is a small lossless region that appears around 2.5 eV due to the oxygen vacancy (Fig. 2(j)).
The calculated absorption coefficient of I and II are shown in Fig. 2(k) and (l). It can be seen that the oxygen vacancy causes the shift of the absorption edge towards lower energies by around 2.0 eV; the absorption edge of I is located at around 3.56 eV and that of II around 1.61 eV. In addition, there is a small absorption structure (low absorption region) that appears between 1.61 eV and 3.56 eV due to the oxygen vacancy. Following Fig. 2(k) and (l), the lossless region occurs at 11.0 eV (I) and 12.0 eV (II) in concordance with our previous observations. We have compared the calculated absorption coefficient of I with the experimental data see Fig. S2 (ESI†). We have noticed that the calculated absorption edge of I (3.56 eV) is in good agreement with the measurements (3.65 eV).7
The calculated linear optical properties show a considerable anisotropy between the two tensor components. This favors an important quantity in SHG and OPO due to better fulfillment of phase-matching conditions determined by birefringence. The birefringence can be estimated from the refractive indices following the expression Δn(ω) = n∥(ω) − n⊥(ω). The refractive indices of I and II as shown in Fig. 2(m) and (n) are obtained from the calculated complex dielectric function. The calculated values of n⊥(0), n∥(0), Δn(0) and Δn(ω)λ=1064 nm are given in Table 1, and the dispersion of the calculated birefringence of I and II is illustrated in Fig. 2(o) and (p). Following Fig. 2(m) and (n), one can see that for low energies n⊥(ω) > n∥(ω) for I, while structure II n∥(ω) > n⊥(ω). Therefore, according to the birefringence expression (Δn(ω) = n∥(ω) − n⊥(ω)), structure I exhibits negative birefringence, whereas structure II shows positive birefringence, as shown in Table 1. The O-vacancy turns the birefringence from negative to positive.
According to Bian et al.5 the electron cloud of BO3 anionic groups which exhibit a planar shape with conjugated electron orbitals makes the BO3 anionic groups the main source of large birefringence in Pb2BO3F. Therefore, similar to BO3, the CO3 can be the source of the large birefringence in I and II. The electron clouds of the BO3 and CO3 anionic groups (Fig. 2(c) and (d)) exhibit a planar shape with conjugated electron orbitals. It is well known that the birefringence determines partly whether an NLO material has potential utility.5 Furthermore, Fig. 2(c) and (d) show a high electron density configuration and strong anisotropy for B–O and C–O groups (BO3 and CO3 groups) which could contribute to the optical anisotropy.
3.3. Complex second-order non-linear optical dispersion
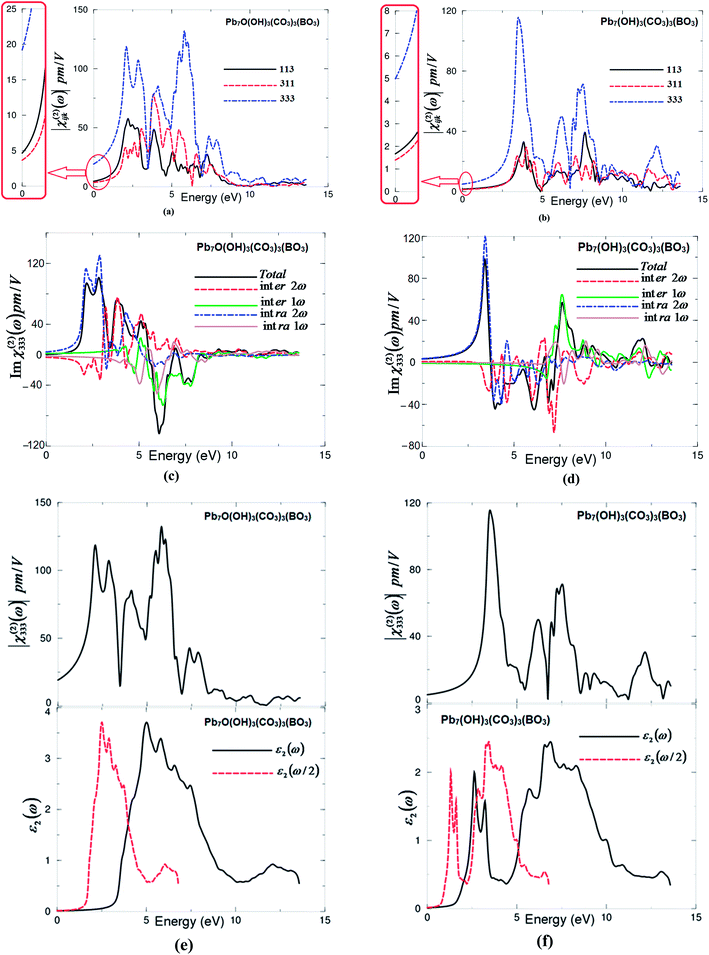
The non-centro-symmetric structure with hexagonal symmetry allows only three non-zero components of the second harmonic generation third rank tensor. These are χ(2)113(−2ω;ω;ω), χ(2)311(−2ω;ω;ω) and χ(2)333(−2ω;ω;ω). The three non-zero components are calculated based on the calculated electronic band structures. The formalism for calculating the SHG is given elsewhere.27–30 The obtained |χ(2)ijk(ω)| for I and II are shown in Fig. 3(a) and (b). It has been found that |χ(2)333(ω)| is the dominate tensor component for I and II compounds. Since mBJ succeeds in bringing the calculated energy gap (3.56 eV) of I closer to the experimental one (3.65 eV),7 therefore, we present the results obtained by mBJ only. Further, to correct the energy band gap a quasi-particle self-energy correction at the level of scissors operators is applied, which causes a rigid shift to the energy bands to bring the calculated energy gap to the exact experimental value.31 The values of all tensor components |χ(2)ijk(ω)| of I and II at the static limit and at λ = 1064 nm are presented in Tables 2 and 3.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000] the measured SHG of the grinded and sieved polycrystalline Pb7O(OH)3(CO3)3(BO3) (powder) is 4.5 times larger than that of KH2PO4 (KDP) powder7
000] the measured SHG of the grinded and sieved polycrystalline Pb7O(OH)3(CO3)3(BO3) (powder) is 4.5 times larger than that of KH2PO4 (KDP) powder7
| Tensor components | I | |||
|---|---|---|---|---|
| χ(2)ijk (0) | dijk = 0.5χ(2)ijk(ω) at static limit | χ(2)ijk(ω) at λ = 1064 nm | dijk = 0.5χ(2)ijk(ω) λ = 1064 nm | |
| |χ(2)113(ω)| | 4.82 | d15 = 2.41 | 11.19 | d15 = 5.59 |
| |χ(2)311(ω)| | 3.70 | d11 = 1.85 | 7.52 | d11 = 3.76 |
| |χ(2)333(ω)| | 19.23 | d33 = 9.62 | 35.58 | d33 = 17.79 |
| β333 | 178 × 10−30 esu | 335.2 × 10−30 esu | ||
| Tensor components | II | |||
|---|---|---|---|---|
| χ(2)ijk (0) | dijk = 0.5χ(2)ijk(ω) at static limit | χ(2)ijk(ω) at λ = 1064 nm | dijk = 0.5χ(2)ijk(ω) λ = 1064 nm | |
| |χ(2)113(ω)| | 1.67 | d15 = 0.84 | 2.46 | d15 = 1.23 |
| |χ(2)311(ω)| | 1.39 | d11 = 0.69 | 2.08 | d11 = 1.04 |
| |χ(2)333(ω)| | 5.00 | d33 = 2.5 | 7.43 | d33 = 3.72 |
| β333 | 45.80 × 10−30 esu | 68.32 × 10−30 esu | ||
The calculated value of d33 at λ = 1064 nm of I is about 17.79 pm V−1. This is close to the experimental value of the well-known KTiOPO4 (KTP) single crystal, which exhibits values of 16.9,32 13.7,33 15.4 ± 0.2,34 14.6 ± 1.0,35 17.4 ± 1.7,36 16.9 ± 3.3,37 16.9 ± 1.7,38 10.6 ± 7.5,39 16.75 (ref. 40) and 16.65 (ref. 40) at λ = 1064 nm. Abudoureheman et al.7 have reported that, by using the Kurtz–Perry method,8 the measured SHG (or d33) of the grinded and sieved polycrystalline Pb7O(OH)3(CO3)3(BO3) (powder) is 4.5 times that of KH2PO4 (KDP) powder.7 This is attributed to the fact that Abudoureheman et al. have measured the SHG for powder without taking into account the influence of the packing of the BO3 and CO3 structural units and the stereochemically active lone pair in the Pb polyhedra. According to the anionic group theory,9 the overall SHG response of crystal is the geometrical superposition of the second-order susceptibilities. Therefore, the packing of the BO3 and CO3 structural units and the stereochemically active lone pair in the Pb polyhedra may also affect the macroscopic SHG coefficients.7 The large SHG is due to the strong interactions between the stereo effect of Pb(II) cations and co-parallel BO3 and CO3 triangle groups.7 Further, the obtained value of d33 at λ = 1064 nm of II is about 3.72 pm V−1, which is about a quarter of the experimental value of KTiOPO4 (KTP).
The requirement for good SHG performance is a small band gap, which limits the transmittance in the UV region. The main point of obtaining NLO materials used in the UV region is getting the delicate balance between the SHG response and band gap.6 Therefore, based on our results we can say that I is a good NLO material that can be used in the UV region, whereas II is a good NLO material that can be used in the visible region. Thus, the oxygen vacancy tunes the material to be efficient in the visible region. The large SHG is due to the strong interactions between the stereo effect of Pb(II) cations and coparallel BO3 and CO3 triangle groups.
The imaginary part of the dominant tensor component χ(2)333(ω) for I and II are calculated. The imaginary part is further separated into 2ω/ω inter-/intra-band contributions as shown in Fig. 3(c) and (d). It is clear that the 2ω terms oscillate at the half energy gap (1.83 eV for I and 0.80 eV for II) and the ω terms start to oscillate at the value of the fundamental energy gap (3.65 eV for I and 1.61 eV for II) to associate 2ω terms, while the tail of the imaginary part originates from ω terms only. The 2ω/ω inter-/intra-band contributions oscillate around zero and exhibit a considerable anisotropy. The sum of 2ω/ω inter-/intra-band contributions gives the total value of the imaginary part of the SHG (Fig. 3(c) and (d)).
Further, to understand the origin of the large SHG, we have analyzed the spectral features of |χ(2)333(ω)| using the spectral features of the imaginary part of the optical dielectric function as a function of ω/2 and ω. This is illustrated in Fig. 3(e) and (f). Unlike the linear optical dispersion, the features in the complex second-order nonlinear optical susceptibility tensors are more difficult to identify from the band structure because of the presence of 2ω and ω terms. But we can use the linear optical dispersion to identify the different resonances leading to various features in the complex second-order nonlinear optical susceptibilities spectra. The spectral structures of ε2(ω), ε2(ω/2) and |χ(2)333(ω)| can be divided into three spectral regions. The spectral region confined between 1.83 eV (0.80 eV) I (II) (Eg/2) and 3.65 eV (1.61 eV) I (II) (Eg) is mainly formed by the 2ω resonance. The second spectral structure between 3.65 eV (1.61 eV) I (II) (Eg) and 7.5 eV is associated with interference between 2ω and ω resonances, and this is associated with the first spectral structure of ε2(ω). It is clear that in this region the ω terms start to oscillate and contribute to the spectral structure of |χ(2)333(ω)| in addition to 2ω terms. The third spectral structure from 7.5 eV and 13.5 eV is mainly due to ω resonance which is associated with the second spectral structure in ε2(ω).
3.4. Microscopic first hyperpolarizability
We can calculate the microscopic first hyperpolarizability, βijk,41 the vector component along the dipole moment direction, at the static limit and at λ = 1064 nm from the existing information about I and II and the values of χ(2)113(ω), χ(2)311(ω), χ(2)333(ω). We should emphasize that the βijk term cumulatively yields a bulk observable second order susceptibility term, χ(2)ijk(ω), which in turn is responsible for the strong SHG response.42 Since χ(2)333(ω) is the dominate component at the static limit and at λ = 1064 nm for both compounds, we have calculated the values of β333 at the static limit and at the wavelength 1064 nm (Tables 2 and 3).4. Conclusions
We have investigated the influence of the oxygen vacancy on the electronic structure, band gap, linear and nonlinear optical properties and the microscopic first hyperpolarizability of asymmetric Pb7O(OH)3(CO3)3(BO3). The all-electron full-potential calculations within the generalized gradient approximation (PBE-GGA) and the recently modified Becke–Johnson (mBJ) potentials were used to perform comprehensive theoretical calculations for acentric I and II. Using the experimental crystallographic data of I, we removed two oxygen atoms to investigate the influence of O-vacancy on the ground state properties. It has been found that mBJ brings the calculated energy band gap of I very close to the measured band gap. The oxygen vacancy causes a red shift to the energy band gap, making the material useful in the visible region. Calculations show that I exhibits negative uniaxial anisotropy and birefringence, whereas II exhibits positive uniaxial anisotropy and birefringence. We have calculated the second harmonic generation (SHG) of I and II at the zero limit and at the wavelength (λ = 1064 nm). The calculated SHG for I at λ = 1064 nm is close to the experimental value of the well-known KTiOPO4 (KTP) single crystal, whereas for II it is about a quarter of the experimental value of the KTP. Further, we have calculated the microscopic first hyperpolarizability for I and II at the static limit and at the wavelength 1064 nm.Acknowledgements
The result was developed within the CENTEM project, reg. no. CZ.1.05/2.1.00/03.0088, cofunded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI programme and, in the follow-up sustainability stage, supported through CENTEM PLUS (LO1402) by financial means from the Ministry of Education, Youth and Sports under the National Sustainability Programme I. Computational resources were provided by MetaCentrum (LM2010005) and CERIT-SC (CZ.1.05/3.2.00/08.0144) infrastructures. SA would like to thank CSIR-National Physical Laboratory for support. SA would also like to thank the High Performance Computer (HPC) facilties at Intra-University Accelerator Centre (IUAC) at New Delhi, Indian Institute of Mathematical Sciences (IMSC) at Chennai, CSIR-4PI at Bangaluru, Indian Institute of Technology at Kanpur and the University of Hyderabad at Hyderabad.References
- R. C. Ramachandra, R. Gobinathan and F. D. Gnanan, Cryst. Res. Technol., 1993, 28, 453–456 CrossRef.
- C. Chen, Y. Wang, Y. Xia, B. Wu, D. Tang, K. Wu, W. Zeng, L. Yu and L. Mei, J. Appl. Phys., 1995, 77, 2268–2272 CrossRef CAS.
- Y. Mori, I. Kuroda, S. Nakajima, T. Sasaki and S. Nakai, Appl. Phys. Lett., 1995, 67, 1818 CrossRef CAS.
- D. Xue and Z. Zhang, Appl. Phys. A: Mater. Sci. Process., 1999, 68, 57–61 CrossRef CAS.
- Q. Bian, Z. Yang, L. Dong, S. Pan, H. Zhang, H. Wu, H. Yu, W. Zhao and Q. Jing, J. Phys. Chem. C, 2014, 118, 25651–25657 CAS.
- D. Li, Q. Jing, C. Lei, S. Pan, B. Zhang and Z. Yang, RSC Adv., 2015, 97, 79882–79887 RSC.
- M. Abudoureheman, L. Wang, X. Zhang, H. Yu, Z. Yang, C. Lei, J. Han and S. Pan, Inorg. Chem., 2015, 54, 4138–4142 CrossRef CAS PubMed.
- S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813 CrossRef CAS.
- (a) N. Ye, Q. Chen, B. C. Wu and C. T. Chen, J. Appl. Phys., 1998, 84, 555–558 CrossRef CAS; (b) C. Chen, N. Ye, J. Lin, J. Jiang, W. R. Zeng and B. C. Wu, Adv. Mater., 1999, 11, 1071–1078 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- M. L. Cohen, Science, 1993, 261, 307 CAS.
- S. Serra, C. Cavazzoni, G. L. Chiarotti, S. Scandolo and E. Tosatti, Science, 1999, 284, 788 CrossRef CAS PubMed.
- R. Pentcheva and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035112 CrossRef.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Vienna University of Technology, Austria, 2001 Search PubMed.
- A. H. Reshak and S. Auluck, RSC Adv., 2016, 6, 18965 RSC.
- A. H. Reshak, RSC Adv., 2015, 5, 22044–22052 RSC.
- A. H. Reshak, H. Huang, H. Kamarudin and S. Auluck, J. Appl. Phys., 2015, 117, 085703 CrossRef.
- A. H. Reshak, RSC Adv., 2015, 5, 33632–33638 RSC.
- J. W. Lekse, M. A. Moreau, K. L. McNerny, J. Yeon, P. S. Halasyamani and J. A. Aitken, Inorg. Chem., 2009, 48, 7516–7518 CrossRef CAS PubMed.
- J. A. Brant, D. J. Clark, Y. S. Kim, J. I. Jang, J.-H. Zhang and J. A. Aitken, Chem. Mater., 2014, 26, 3045–3048 CrossRef CAS.
- B. F. Ding, H. J. Qian, C. Han and J. Y. Zhang, J. Phys. Chem. C, 2014, 118, 25633 CAS.
- F. Bassani and G. P. Parravicini, Electronic States and Optical Transitions In Solids, Pergamon Press Ltd., Oxford, 1975, pp. 149–154 Search PubMed.
- C. Ambrosch-Draxl and J. O. Sofo, Comput. Phys. Commun., 2006, 175, 1–14 CrossRef CAS.
- http://www.wien2k.at/reg_user/textbooks/usersguide.pdf.
- D. R. Penn, Phys. Rev., 1962, 128, 2093 CrossRef CAS.
- S. Sharma, J. K. Dewhurst and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 165332 CrossRef.
- A. H. Reshak, Ph.D. thesis, Indian Institute of Technology-Rookee, India, 2005.
- A. H. Reshak, J. Chem. Phys., 2006, 125, 03471 CrossRef PubMed.
- A. H. Reshak, J. Chem. Phys., 2006, 124, 104707 CrossRef PubMed.
- S. N. Rashkeev, W. R. L. Lambrecht and B. Segall, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 3905 CrossRef CAS.
- K. Zhang and X. Wang, Chin. Sci. Bull., 2001, 46, 2028–2036 CrossRef CAS.
- http://www.castech-us.com/casktp.htm.
- M. V. Pack, D. J. Armstrong and A. V. Smith, Appl. Opt., 2004, 43, 3319 CrossRef CAS PubMed.
- I. Shoji, T. Kondo, A. Kitamoto, M. Shirane and R. Ito, J. Opt. Soc. Am. B, 1997, 14, 2268–2294 CrossRef CAS.
- A. Anema and T. Rasing, Appl. Opt., 1997, 36, 5902–5904 CrossRef CAS.
- L. K. Cheng, L. T. Cheng, J. Galperin, P. A. M. Hotsenpiller and J. D. Bierlein, J. Cryst. Growth, 1994, 137, 107–115 CrossRef CAS.
- H. Vanherzeele and J. D. Bierlein, Opt. Lett., 1992, 17, 982–984 CrossRef CAS PubMed.
- B. Boulanger, J. P. Feve, G. Marnier and B. Menaert, Pure Appl. Opt., 1998, 7, 239 CrossRef CAS.
- A. H. Reshak, I. V. Kityk and S. Auluck, J. Phys. Chem. B, 2010, 114, 16705–16712 CrossRef CAS PubMed.
- R. Y. Boyd, Principles of Nonlinear Optics, Academic Press, NY, 1982, p. 420 Search PubMed.
- R. W. Boyd, Nonlinear optics, Academic Press is an imprint of Elsevier, 3rd edn, 2008, ISBN:978-0-12-369470-6 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1: calculated electronic band structure of I and II. Fig. S2: the calculated energy band gap of I in comparison with the measured one. We have used a software to extract the experimental data of the absorption and then we re-plot these data in comparison with our calculated absorption and the electronic band structure. Our calculated energy band gap show good agreement with the measured one. CIF files: the crystallographic cif files of the relaxed structures of I and II. See DOI: 10.1039/c7ra00012j |
| This journal is © The Royal Society of Chemistry 2017 |