Open Access Article
Open Access ArticleImproved electrical conductivity of PDMS/SCF composite sheets with bolting cloth prepared by a spatial confining forced network assembly method
Xiaolong Gao a,
Yao Huang*a,
Ying Liuab,
Semen Kormakova,
Xiuting Zhengac,
Dan Wua and
Daming Wu*ab
a,
Yao Huang*a,
Ying Liuab,
Semen Kormakova,
Xiuting Zhengac,
Dan Wua and
Daming Wu*ab
aCollege of Mechanical and Electrical Engineering, Beijing University of Chemical Technology, Beijing 100029, China. E-mail: wudaming@vip.163.com; hy06@163.com; Fax: +86-10-64435015; Tel: +86-10-64435231
bState Key Laboratory of Organic–Inorganic Composites, Beijing University of Chemical Technology, Beijing 100029, China
cPolymer Material Processing Equipment Engineering Research Center of the Ministry of Education, Beijing 100029, China
First published on 6th March 2017
Abstract
A novel method of Spatial Confining Forced Network Assembly (SCFNA) for preparation of high-performance electrically conductive polymeric composites was proposed in this paper. Differing from the self-assembly mechanism, as in traditional compounding processes, the SCFNA process could provide conductive fillers with an effective forced networking assembly action to get a more compacted network. High electro-conductive polydimethylsiloxane (PDMS)/short carbon fiber (SCF) binary composites with a low percolation threshold of 0.15 wt% were prepared by the SCFNA method. A rapid increase in electrical conductivity from 1.71 × 10−12 S m−1 of PDMS to 1.67 × 102 S m−1 was achieved with 4 wt% short carbon fibers. It was shown that a continuous and compact SCF network was built in a PDMS matrix. Furthermore, when the bolting cloth as a sarking was co-compressed with the mixture, a much lower percolation threshold of 0.06 wt% and a higher electrical conductivity of 3.22 × 102 S m−1 with 4 wt% of SCF were obtained due to volume exclusion. Compared with the conventional compounding method, the electro-conductive properties of the composites prepared by the above mentioned method can be enhanced up to several times, or even by orders of magnitudes. Moreover, if the mesh number of the bolting cloth is large enough, the carbon fibers will be impeded from penetrating the bolting cloth together with the polymer when they are co-compressed, thus an electrically conductive film with single or double insulating face could be prepared through this method.
Introduction
Electrically conductive polymeric composites (CPCs) have attracted great interest in many applications such as energy storage, batteries, three-dimensional printing materials, electromagnetic shielding, flexible displays and smart sensors.1–13 The theory and practice have shown that constructing a continuous and compact network of conductive fillers in a polymeric matrix is essential to prepare composites with high conductivity.14–20 It is a conventional method to construct such a network mainly by increasing the amount of conductive fillers until percolation appears.14–16,21–24 As most polymers have very low electrical conductivity, the electrically conductive fillers are incorporated into polymers to fabricate CPCs. Many efforts have been focused on how to build conductive networks in polymer matrixes using electrically conductive fillers with high aspect ratio, including carbon black particles, carbon fiber, graphite flake, carbon nanotubes (CNTs) and graphene.14,15,17,25–33Generally, there are mainly three approaches to obtain a continual conductive network. A widely adopted processing technology is to increase the fraction of the conductive fillers to a certain value until the percolation threshold appears.13–16 Another method is to adopt a system of two immiscible polymers and conductive fillers.34,35 With suitable fraction ratio of the two polymers and thermodynamic conditions, a co-continuous two-phase structure with selected location of the fillers in one polymer could be obtained, which serves as continuous conductive network. Recently, Yan et al.35 reported improved electrical conductivity of polyamide 12/graphene nanocomposites with maleated polyethylene-octene rubber prepared by melt compounding, both higher electrical conductivity and storage modulus were obtained when most graphene sheets were located in PA12 matrix rather than that in POE-g-MA phase. The third method is to form a segregated structure in the composites by compressing a mixture of polymer granules decorated with conductive fillers via dry or solution mixing to construct the segregated conductive networks.16,36,37 In spite of a notable increase in electrical conductivity at percolation loading, the composites still demonstrate much lower electrical conductivity than theoretically predicted.20,38–40
PDMS has been widely used as the elastomeric substrate for stretchable electronics. Recently, many researchers use PDMS or other Si-elastomers as the matrix of high performance conductive stretchable composites. Kato et al.41 prepared a highly conductive elastomer by loading a low content (1 wt%) of a long single-walled carbon-nanotube into conductive silicone rubber, and this material has a higher mechanical strength than commercialized generic stocking. It indicated that the rubbers would become brittle to lose its mechanical properties when incorporating the conductive fillers at high loading levels, therefore a high conductive network with a low content of fillers is necessary for a highly conductive elastomer. Han et al.42 reported an efficient and simple method to fabricate lightweight and flexible composites composed of a reduced graphene oxide aerogel film (rGO-AF) and PDMS. Single and multilayer rGO-AF/PDMS composites were fabricated by liquid PDMS infiltrating and curing. Zhu et al.43 reported a simple route for preparation of cotton–AgNWs–PDMS stretchable conductor was explored through the dip-coating method. Both excellent electrical and mechanical properties were obtained as the combination of an interconnected porous structure of cotton as skeleton with supported 2D AgNWs networks. But conductivity of this material seems to be difficult to control and the filler of AgNWs is too expensive despite its high conductivity.
In this paper, a novel method of Spatial Confining Forced Network Assembly (SCFNA) was used to prepare PDMS/SCF CPCs, which was focused on constructing a more compacted electrically conductive network to enhance the electrical conductivity of polymer composites significantly. The main idea of SCFNA was introducing a mechanical delivered additional interaction to carry out a forced assembly of conductive network. Furthermore, the addition of high-strength bolting cloth and carbon fibers leads composites to excellent mechanical properties. As PDMS could penetrate through the bolting cloth and carbon fibers could not when they are co-compressed, the volume exclusion effect was achieved. Thus a higher electrically conductive film with single or double insulating face can be prepared in this way. This method is not only suitable for the preparation of thermosetting resin conductive composite sheets, but also effective on the preparation of other polymer-based conductive composite sheets, such as thermoplastic polypropylene, nylon, etc. As to thermal conductive composites, reinforcing and toughening composites, it may provide some valuable reference. However, it must be pointed out that just sheet samples were obtained from early experiments. Although we have try many times to prepare highly electrical conductive composites with a certain thickness by laminating and it achieved good results, but if you want to use this method to prepare different shapes and dimension products, it need further research.
Experimental
Materials used
PDMS with a trade name of SYLGARD 184 SILICONE ELASTOMER was obtained from DOW CORNING, USA. Its density and curing temperature are 1.03 g cm−3 at 25°C and on range of 25–150 °C. Short carbon fibers with 7 μm diameter and 4 mm length were provided by Toray, Japan. Its electrical conductivity is 2.6 × 104 S m−1. Bolting cloth with different meshes was bought from Shanghai Xinhua Filter Development Trade Co., Ltd (China).Composite preparation
The experimental hot embossing device was designed, which could provide a pressing force up to 50 kN with a pressing speed of 0.005 mm s−1 to 0.5 mm s−1. The servo motor of this embossing device was accurately controlled by a PLC system and the position accuracy of ±3 μm for the up platen was guaranteed. The compressing mold was made of two flat plates with electrical heaters and the surface of the plates can be smooth or micro/nano structured on both or one of their surfaces. The temperature of the molds can be controlled from ambient temperature to 220 °C with a control accuracy of ±1 °C. The effective working area was 160 × 80 mm.Prior to internal mixing, SCF was dried at 100 °C under vacuum for 1 h. PDMS and SCF were mixed to get a homogeneously dispersed mixture in a HAAKE MiniLab conical twin-screw mixer at 25 °C with a rotational speed of 50 rpm for 15 min. Then the vacuum pump was used to remove the air bubbles from the homogeneously dispersed mixture. In order to investigate the SCF location and dispersion in PDMS matrix and its effect on electrical and mechanical properties, the CPCs prepared by compounding process, SCFNA process and SCFNA with bolting cloth process were designated as P1, P2 and P3, respectively.
Characterizations
Results and discussion
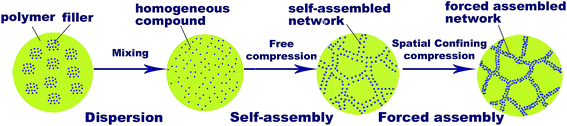
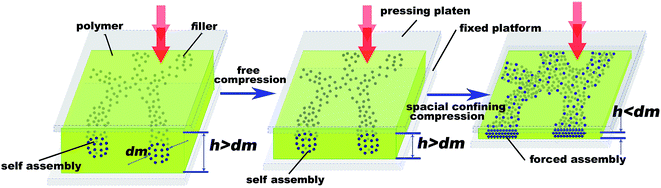
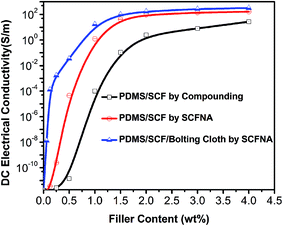
For convenience, we defined the thickness of average diameter of the network threads as a characteristic diameter (dm). The procedure of SCFNA involves three steps, as shown in Fig. 1. Firstly, the polymer and conductive fillers were mixed by melt compounding or solution mixing to get a homogeneously dispersed mixture. Secondly, the homogeneously dispersed mixture was compressed by a pressing mold to initiate and finish the networking of the conductive filler by normal self-assembly mechanism. Thirdly, the sample was further compressed after forming a self-assembled network until to the thickness less than characteristic diameter. When the thickness of samples is much large than characteristic diameter (h > dm), it is called free compression which could only cause the self-assembly network wiggling in polymer matrix without estimable densification of the network threads. When the sample was compressed to a thickness less than characteristic diameter (h < dm), a noteworthy densification of the network threads could be come into being by spatial confining compression, as shown in Fig. 2. Simultaneously an array anchoring action is applied to the conductive network with the help of micro–nano structured array on the surface of pressing mold, which provides additional enhancement in compactness of the network at anchoring locations. It's important to note that the mixture of polymer and fillers needs to be kept as flow state in the whole process of compression.Fig. 3 shows the relationships between direct current (DC) electrical conductivity and filler content of PDMS/SCF composite sheets by different processes of P1, P2 and P3, which follows the conductive percolation theory.21–24 When the filler content is low, the change of the composites conductivity is not obvious. With the filler content increasing to a certain degree, a dramatic improvement of magnitude in the conductivity of composites happens, which changes the polymer from insulator to conductor. Then a small change of the filler content will cause a large fluctuation in the conductivity of the composites. Above the percolation area, conductivity of the composites changes little again with increase of filler content. An integrated conductive network is built in polymer matrix, which brings high conductivity. The percolation threshold values of the composites prepared by different processes of P1, P2 and P3 are 0.45 wt%, 0.15 wt%, 0.06 wt%, respectively. As shown in the curve, the PDMS/SCF composite sheets prepared by the SCFNA process (P2) exhibit a rapid transition from electrically insulating to conducting with a low percolation threshold of 0.15 wt%, implying the formation of a continuous and compact SCF network for electrons transport in the matrix. The addition of bolting cloth further improved the electrical conductivity of the PDMS/SCF composite sheets with a lower percolation threshold of 0.06 wt%, which is much lower than PA12/MWNT nanocomposites prepared by melt compounding (0.9 wt%) reported by Socher et al.,44 and polyamide 12/graphene nanocomposites with maleated polyethylene-octene rubber (0.65 wt%) reported by Yan et al.,35 The electrical conductivity (σ) follows the power law at loadings near the percolation threshold (φc).45
| σ ∝ σ0(φ − φc)n | (1) |
The average gap of the conducting fillers in the network plays a crucial role in all of parameters and conditions affecting the level of conductivity of the composites. The transmission mechanism of electrons between adjacent particles of conductive fillers in polymeric matrix is explained as an ohmic conduction with an average gap between adjacent particles less than or equal to 10 Å on the basis of Franckel's theory, and non-ohmic transmission of tunneling effect or electron emission from one particle to the next with an average gap beyond 10 Å.31,38 Up to now rare morphology of conductive network of either microscale fillers or nanoscale fillers with average gap of less than or equal to 10 Å between adjacent particles prepared by existing compounding methods was reported. Adequate theoretical and experiment investigations had quantitatively proven the conclusive effect of the gap between adjacent particles on the conductivity of the composites.15–18,38–40,44,46 Nevertheless, it is so disappointed that the existing prediction models avoided the most important parameter of average gap between conducting fillers. However, in this paper, many efforts have been focused on how to decrease the average gap of the conducting fillers to build a continuous and compact network in a polymer matrix. According to the SEM micrographs of PDMS/4 wt% SCF composites section by P1, P2, P3, respectively (Fig. 4a–c), the distribution states of carbon fibers in PDMS matrix and the average gap of adjacent fibers are different in the composites. Fig. 4a reveals that carbon fibers are homogeneously dispersed in PDMS. The average gap of adjacent carbon fibers in the network is greater than 20 μm, implying the SCF conductive network in the PDMS matrix by P1 process is not compact enough. Because the possible aggregation force of the filler, including van der Waals force, liquid bridge, electrostatic force, hydrogen bond, is not large enough to repel all polymer away in between. The network by such a self-assembly mechanism could not be very compacted, which is the main reason of limited conductivity of the polymeric composites by present compounding technology. While for P2, differing from self-assembly mechanism, as in traditional compounding process (P1), Fig. 4b reveals that carbon fibers are dispersed regularly in PDMS with obvious reunion phenomenon in certain spacing and carbon fibers agglomerate into a circle like the section of network cable as shown in the inset of three circles on Fig. 4b. The average gap of adjacent carbon fibers in the network is less than 5 μm by statistical calculation of fibers in the circles. Moreover, it provided an additional enhancement in compactness of the network at anchoring locations with the help of micro–nano structured array on the surface of compressing mold, which left grooves on the surface of materials. In this way the self-assembly network is assembled more tightly to form a forced-assembly network with enhanced electric conductivity. Furthermore, an insulating surface layer composed of bolting cloth was co-compressed with the composite (P3). The adjacent fillers at the network were forced to be more closely at the salient points of the bolting cloth to provide additional anchoring act with the help of the bolting cloth under the plate. The average gap of adjacent carbon fibers in the network is less than 1 μm, implying a more compact SCF conductive network was built in PDMS matrix compared with the composites by P2 without bolting cloth. As PDMS could penetrate through the bolting cloth and carbon fibers could not (Fig. 4c). The PDMS/SCF composite sheets with a higher electrical conductivity were prepared due to volume exclusion.
 | ||
| Fig. 4 (a–c) SEM micrographs of PDMS/4 wt% SCF composites section by P1, P2, P3, respectively. BC is bolting cloth. | ||
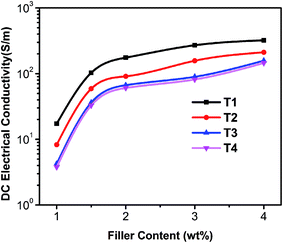
Fig. 5 shows the relationships between direct current (DC) electrical conductivity and SCF content for PDMS/SCF composite sheets of T1, T2, T3 and T4 by the SCFNA with bolting cloth process, which follow the same change rule of P3 in Fig. 3 under the condition of invariable in thickness. Table 1 makes a list of the conductivity values of that compared with the compounding method. Known from the curve in Fig. 5 and the values in Table 1, the conductivity increased with the decrease of thickness of the composite sheets under the condition of same filler concentration. In detail, when the thickness of samples is 350 μm or 450 μm, the conductivities of the samples change little and for 250 μm its conductivity double improves, continue to 150 μm its conductivity increases several times. Fig. 6a–c are the micrographs of PDMS/4 wt% SCF composite sheets surface by P3 of T4, T3 and T1, respectively, which show the whole situation of SCF conductive network. The characteristic diameters of the network are about 580 μm, 440 μm and 156 μm marked on the figures, implying the SCF conductive network in PDMS was getting more and more compact and fine-grained as the samples were compressed to a thickness from 450 μm to 150 μm.
| Filler content (wt%) | DC electrical conductivity (S m−1) | |||||
|---|---|---|---|---|---|---|
| T1 | T2 | T3 | T4 | P1 | Increase | |
| 1 | 17.28 | 8.28 | 4.24 | 3.78 | 0.0001 | 173000 |
| 1.5 | 103.2 | 59 | 36.2 | 32.8 | 0.11 | 938.2 |
| 2 | 175.2 | 91 | 66.8 | 60.6 | 2.5 | 70.1 |
| 3 | 271 | 157.4 | 89.8 | 81.6 | 8.1 | 33.5 |
| 4 | 322 | 211 | 157.6 | 145.4 | 2.7 | 11.6 |
 | ||
| Fig. 6 (a–c) Micrographs of PDMS/4 wt% SCF composite sheets surface by P3 of T4, T3 and T1, respectively. | ||
The dispersion and location of the carbon fibers in PDMS and the average gap between adjacent carbon fibers in the network was used to explain this rule (Fig. 7a–d). In T3 and T4, the compression of the sample could only cause the self-assembly network wiggling in polymer matrix without estimable densification of the network threads as the thickness of the samples is much large than characteristic diameter. The carbon fibers are self-assembly in PDMS with mild reunion phenomenon in certain spacing and the average gap of adjacent carbon fibers in the network is about 5 μm (T3) and 10 μm (T4). In contrast, for T1 and T2, when the sample was compressed to a thickness less than characteristic diameter, a noteworthy densification of the network threads could be come into being by forced compression of the mold to the network. The average gap of adjacent carbon fibers in the network is less than 1 μm (T2) and less than 100 nm (T1). In process of forced compression, the carbon fibers at the threads will tend to be more closely and exceeded polymer between the fillers at the threads will be squeezed out (Fig. 7a and b) because the wiggling freedom of the network has been restricted and the aggregate force between the fillers at the threads can prevent fillers from disaggregation.
 | ||
| Fig. 7 (a–d) SEM micrographs of PDMS/4 wt% SCF composites section of T1, T2, T3 and T4, respectively. | ||
In the practical engineering application, electro-conductive polymeric composites with surface insulation are usually needed. In this work, PDMS/SCF functional composite sheets with one insulating surface layer or double insulating surface layers were prepared by the SCFNA method with bolting cloth (Fig. 8a and b). And Table 2 shows the surface resistivity of PDMS/4 wt% SCF composite sheets with 0, 1 and 2 layers of insulating surface. In addition, different range of surface resistivity of composites could also be prepared by using different size of conductive fillers or different mesh number of bolting cloth.
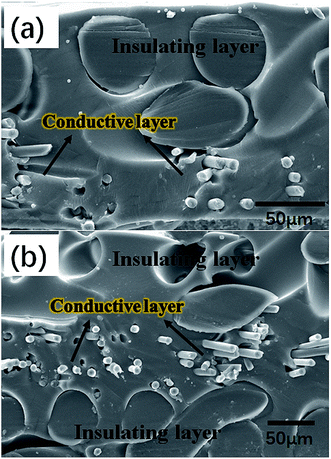 | ||
| Fig. 8 (a and b) SEM micrographs of PDMS/4 wt% SCF composites section of single insulating surface layer and double insulating surface layers by P3. | ||
| Layers of BC | Surface resistivity(Ω) | ||
|---|---|---|---|
| 0 | 1 | 2 | |
| Surface 1 | 45.0 | 21.1 | 8.59 × 106 |
| Surface 2 | 43.2 | 3.35 × 106 | 9.78 × 106 |
The high electro-conductive PDMS/SCF composite sheets with bolting cloth prepared by the SCFNA method are not only high flexible because of high elastic PDMS, but also have excellent mechanical properties, as the addition of high-strength bolting cloth and carbon fibers. The tensile curve of samples (150 mm × 20 mm × 0.3 mm) reveal that the bolting cloth greatly improved the mechanical properties of materials (Fig. 9), especially for the PDMS/SCF composite sheets with 2 layers of bolting cloth, which tensile strength is several times higher than that of sheets without bolting cloth. The yield stress of samples with 0, 1 and 2 layers of insulating surface are 2.82 MPa, 7.03 MPa, 23.06 MPa, respectively. As a result, both high electrical conductivity and mechanical properties were obtained by the SCFNA method with bolting cloth.
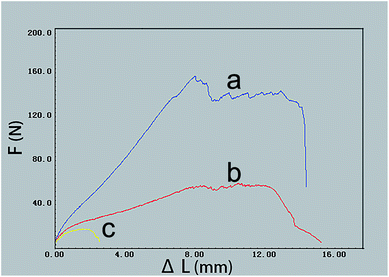 | ||
| Fig. 9 The tensile curve of PDMS/4 wt% SCF samples (150 mm × 20 mm × 0.3 mm) with 0, 1 and 2 layers of insulating surface by P3, marked with (c), (b), (a), respectively. | ||
Conclusions
High electro-conductive polydimethylsiloxane(PDMS)/short carbon fiber (SCF) binary composites with a low percolation threshold of 0.15 wt% were prepared by a Spatial Confining Forced Network Assembly (SCFNA) method. The addition of bolting cloth further improved the electrical conductivity and the mechanical property of the composite sheets. A much lower percolation threshold of 0.06 wt% and a higher electrical conductivity of 3.22 × 102 S m−1 with 4 wt% of SCF were obtained due to the volume exclusion effect. The analysis of dispersion and location of the carbon fibers in PDMS, the average gap between adjacent carbon fibers in the network and the micrographs of the SCF conductive network on the composite sheets surface were used to verify the effectiveness of the forced assembly. Compared with conventional compounding method, the electro-conductive properties of the composites prepared by above mentioned method can be enhanced up to several times, or even orders of magnitudes as a result of the action of forced assembly. Moreover, if the mesh number of the bolting cloth is large enough, the carbon fibers will be impeded from penetrating the bolting cloth together with the polymer when they are co-compressed, thus an electrically conductive film with single or double insulating face can be prepared through this method.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 51673020) and China Postdoctoral Science Foundation (Grant No. 2016M600032).References
- Y. Q. Sun and G. Q. Shi, J. Polym. Sci., Part B: Polym. Phys., 2012, 51, 231–253 CrossRef.
- H. L. Wang, Q. L. Hao, X. J. Yang, L. D. Lu and X. Wang, Nanoscale, 2010, 2, 2164–2170 RSC.
- S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney and E. A. Stach, et al., Nature, 2006, 442, 282–286 CrossRef CAS PubMed.
- Z. Y. Cao and B. Q. Wei, ACS Nano, 2014, 8, 3049–3059 CrossRef CAS PubMed.
- A. E. Jakus, E. B. Secor, A. L. Rutz, S. W. Jordan, M. C. Hersam and R. N. Shah, ACS Nano, 2015, 9, 4636–4648 CrossRef CAS PubMed.
- J. J. Liang, Y. Wang, Y. Huang, Y. F. Ma, Z. F. Liu and J. M. Cai, et al., Carbon, 2009, 47, 922–925 CrossRef CAS.
- Y. F. Xu, Y. Wang, J. J. Liang, Y. Huang, Y. F. Ma, X. J. Wan and Y. S. Chen, Nano Res., 2009, 2, 343–348 CrossRef CAS.
- L. Lin, S. Y. Liu, Q. Zhang, X. Y. Li, M. Z. Ji, H. Deng and Q. Fu, ACS Appl. Mater. Interfaces, 2013, 5, 5815–5824 CAS.
- K. Suzuki, K. Yataka, Y. Okumiya, S. Sakakibara, K. Sako, H. Mimura and Y. Inoue, ACS Sens., 2016, 1, 817–825 CrossRef CAS.
- E. Roh, B. U. Hwang, D. Kim, B. Y. Kim and N. E. Lee, ACS Nano, 2015, 9, 6252–6261 CrossRef CAS PubMed.
- F. B. Madsen, A. E. Daugaard, S. Hvilsted and A. L. Skov, Macromol. Rapid Commun., 2016, 37, 378–413 CrossRef CAS PubMed.
- L. X. Wang, H. L. Peng, X. L. Wang, X. Chen, C. S. Yang, B. Yang and J. Q. Liu, Microsyst. Nanoeng., 2016, 2, 16065 CrossRef CAS.
- S. S. Hassouneh, L. Y. Yu, A. L. Skov and A. E. Daugaard, J. Appl. Polym. Sci., 2017, 134, 44767–44775 CrossRef.
- Y. L. Ma, D. M. Wu, Y. Liu, X. F. Li, H. Qiao and Z. Z. Yu, Composites, Part B, 2014, 56, 384–391 CrossRef CAS.
- H. Deng, L. Lin, M. Z. Ji, S. M. Zhang, M. B. Yang and Q. Fu, Prog. Polym. Sci., 2014, 39, 627–655 CrossRef CAS.
- H. Pang, L. Xu, D. X. Yan and Z. M. Li, Prog. Polym. Sci., 2014, 39, 1908–1933 CrossRef CAS.
- R. Balint, N. J. Cassidy and S. H. Cartmell, Acta Biomater., 2014, 10, 2341–2353 CrossRef CAS PubMed.
- K. K. József, M. Haroon and P. Alessandro, Prog. Mater. Sci., 2015, 73, 1–43 CrossRef.
- E. Bekyarova, E. T. Thostenson, A. Yu, H. Kim, J. Gao, J. Tang, H. T. Hahn, T. W. Chou, M. E. Itkis and R. C. Haddon, Langmuir, 2007, 23, 3970–3974 CrossRef CAS PubMed.
- H. Qian, A. R. Kucernak, E. S. Greenhalgh, A. Bismarck and M. S. P. Shaffer, ACS Appl. Mater. Interfaces, 2013, 5, 6113–6122 CAS.
- M. Shtein, R. Nadiv, M. Buzaglo, K. Kahil and O. Regev, Chem. Mater., 2015, 27, 2100–2106 CrossRef CAS.
- E. Tkalya, M. Ghislandi, W. Thielemans, P. V. D. Schoot, G. D. With and C. Koning, ACS Macro Lett., 2013, 2, 157–163 CrossRef CAS.
- E. Tkalya, M. Ghislandi, R. Otten, M. Lotya, A. Alekseev and P. V. D. Schoot, et al., ACS Appl. Mater. Interfaces, 2014, 6, 15113–15121 CAS.
- S. M. Zhang, H. Deng, Q. Zhang and Q. Fu, ACS Appl. Mater. Interfaces, 2014, 6, 6835–6844 CAS.
- H. Simzar, M. R. Sayed, V. F. Ebrahim, M. Matin, Z. Soheila and S. Masoud, Polymer, 2016, 97, 205–216 CrossRef.
- F. M. AL-Oqla, S. M. Sapuan, T. Anwer, M. Jawaid and M. E. Hoque, Synth. Met., 2015, 206, 42–54 CrossRef CAS.
- Z. L. Hou, W. L. Song, P. Wang, M. J. Meziani, C. Y. Kong and A. Anderson, et al., ACS Appl. Mater. Interfaces, 2014, 6, 15026–15032 CAS.
- X. Q. Ji, Y. H. Xu, W. L. Zhang, L. Cui and J. Q. Liu, Composites, Part A, 2016, 87, 29–45 CrossRef CAS.
- V. C. Lokhande, A. C. Lokhande, C. D. Lokhande, J. H. Kim and T. Ji, J. Alloys Compd., 2016, 682, 381–403 CrossRef CAS.
- Z. Stary, J. Krückel, C. Weck and D. W. Schubert, Compos. Sci. Technol., 2013, 85, 58–64 CrossRef CAS.
- N. J. S. Sohi, S. Bhadra and D. Khastgir, Carbon, 2011, 49, 1349–1361 CrossRef CAS.
- K. Alper, D. Akın and D. Ali, Composites, Part B, 2014, 62, 113–120 CrossRef.
- T. Wiriya, R. J. Spontak and C. M. Balik, Polymer, 2002, 43, 3717–3725 CrossRef.
- X. Y. Qi, D. Yan, Z. G. Jiang, Y. K. Cao, Z. Z. Yu, F. Yavari and N. Koratkar, ACS Appl. Mater. Interfaces, 2011, 3, 3130–3133 CAS.
- D. Yan, H. B. Zhang, Y. Jia, J. Hu, X. Y. Qi, Z. Zhang and Z. Z. Yu, ACS Appl. Mater. Interfaces, 2012, 4, 4740–4745 CAS.
- C. Mao, Y. T. Zhu and W. Jiang, ACS Appl. Mater. Interfaces, 2012, 4, 5281–5286 CAS.
- G. Q. Tang, Z. G. Jiang, X. F. Li and Z. Z. Yu, Carbon, 2014, 77, 592–599 CrossRef CAS.
- R. Haggenmueller, C. Guthy, J. R. Lukes, J. E. Fischer and K. I. Winey, Macromolecules, 2007, 40, 2417–2421 CrossRef CAS.
- E. Y. Li and N. Marzari, ACS Nano, 2011, 5, 9726–9736 CrossRef CAS PubMed.
- C. M. Chang and Y. L. Liu, ACS Appl. Mater. Interfaces, 2011, 3, 2204–2208 CAS.
- Y. Kato, M. Horibe, S. Ata, T. Yamada and K. Hata, RSC Adv., 2017, 7, 10841–10847 RSC.
- D. Han, Y. H. Zhao, S. L. Bai and W. C. Ping, RSC Adv., 2016, 6, 92168–92174 RSC.
- C. H. Zhu, L. M. Li, J. H. Wang, Y. P. Wu and Y. Liu, RSC Adv., 2017, 7, 51–57 RSC.
- R. Socher, B. Krause, S. Hermasch, R. Wursche and P. Pötschke, Compos. Sci. Technol., 2011, 71, 1053–1059 CrossRef CAS.
- S. Kirkpatrick, Rev. Mod. Phys., 1973, 45, 574–588 CrossRef.
- I. Chakraborty, K. J. Bodurtha, N. J. Heeder, M. P. Godfrin, A. Tripathi, R. H. Hurt, A. Shukla and A. Bose, ACS Appl. Mater. Interfaces, 2014, 6, 16472–16475 CAS.
| This journal is © The Royal Society of Chemistry 2017 |