Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Matrix-assisted diffusion-ordered NMR spectroscopy with an invisible, tuneable matrix
A. Hernandez-Cid a,
M. Piekarskaa,
R. W. Adams
a,
M. Piekarskaa,
R. W. Adams a,
M. Nilsson
a,
M. Nilsson a,
R. Evans
a,
R. Evans b and
G. A. Morris
b and
G. A. Morris *a
*a
aSchool of Chemistry, University of Manchester, Manchester M13 9PL, UK. E-mail: g.a.morris@manchester.ac.uk
bAston Institute of Materials Research, School of Engineering and Applied Science, Aston University, Birmingham, B4 7ET, UK
First published on 8th February 2017
Abstract
Mixtures of species of similar sizes can be analysed with 1H NMR using diffusion-ordered spectroscopy (DOSY), by adding a co-solute with which different analytes interact to different extents (“matrix-assisted DOSY”). A matrix containing aqueous perfluorooctanoate micelles has the dual advantages of invisibility to 1H NMR, and interactions tuneable by adjusting the pH.
Introduction
Diffusion-ordered spectroscopy1–3 is a powerful tool for the analysis of intact mixtures by NMR, but has two significant limitations: the signals of different species can normally only be resolved if the species differ significantly in size, and hence in rate of diffusion; and then only if the individual NMR signals do not overlap. The requirement that species have different sizes can be circumvented by adding a co-solute to which different analytes bind to different extents, so that their average diffusion coefficients in the matrix of solvent and co-solute are different. This matrix-assisted DOSY approach (MAD, also known as chromatographic DOSY) has been widely applied,4–10 but suffers from the disadvantage that the NMR signals of the co-solute can overlap with and obscure analyte signals. This is a particular problem with one of the most successful classes of MAD co-solute, micellar surfactants.4,9,11,12 These typically have long alkyl chains and hence have wide footprints in the aliphatic region of the 1H spectrum. Perfluorinated microemulsions have been successfully used previously for MAD/NMR chromatography.9 Here it is shown that perfluorinated micelles, which are also invisible to 1H NMR, can be very effective at resolving the signals of test mixtures of amino acids, and that the versatility of MAD can be greatly enhanced by varying pH to modulate charge–charge interactions between analytes and co-solute.A variety of different types of species have been used to modify the diffusion matrix in MAD. Some of the earliest experiments used solids,13–16 either in slurries or as suspensions. These have the advantage of comparative invisibility, with little if any 1H signal visible in DOSY experiments, but suffer from poor resolution (even when magic angle spinning is used) and/or sample instability (because of slow sedimentation). Polymer co-solutes can be chosen to have few signals,17 but in general the most successful and versatile co-solutes, such as micellar surfactants and cyclodextrins, tend to have big spectral footprints. One way to avoid this problem is to use a high level of deuteriation,18 but this tends to be prohibitively expensive.
Perfluorosurfactants such as sodium perfluorooctanoate (PFO) are an attractive alternative, as they are cheap and readily available, and having no 1H signal provide an “invisible” matrix9,19 (just as the signals of conventional hydrogenated surfactants are invisible in 19F matrix-assisted DOSY20,21). A less obvious advantage is that the forces that drive analyte–matrix association can be both more predictable and easier to control than is often the case with alkyl chain surfactants. Common surfactants such as sodium dodecyl sulfate (SDS) and cetyl trimethylammonium bromide (CTAB),22,23 and nonionic surfactants such as the Brij family,23 have been extensively used in matrix-assisted DOSY for the separation of species on the basis of differences in hydrophobicity and amphiphilicity. Very recently, it has been shown that very high ionic strength CTAB solutions can be used as invisible matrices if strong T2 weighting is used in DOSY experiments.24 However, analytes such as the dihydroxybenzenes, that show strong differential interactions with SDS and CTAB micelles, show negligible binding to PFO under similar conditions. Because perfluorosurfactant micelles have lower affinity for hydrophobic species than alkyl chain surfactants,25 their binding of analytes with ionisable groups tends to be dominated by charge–charge interactions. Adjusting the pH then allows this binding to be varied, tuning the matrix to achieve the separation required.
Here the use of PFO micelles at different pHs to separate the signals of aqueous mixtures of amino acids is demonstrated, and the relevant equilibria are analysed to rationalise the binding seen. PFO micelles should allow charge-based separation of the signals of a wide range of ionic analytes, and those separations will be tuneable in just the same way for other amphiprotic analytes.
Results and discussion
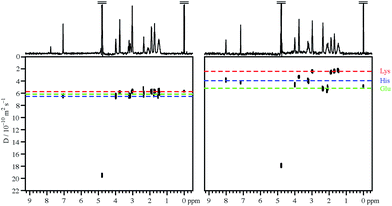
Fig. 1 compares the DOSY spectrum of an approximately neutral aqueous (D2O) mixture of three amino acids with the spectrum measured in the presence of 100 mM sodium PFO at similar pH. As expected, all three amino acids show similar diffusion coefficients in the absence of PFO, and the DOSY spectrum is unresolved in the diffusion dimension. This remains the case over a wide pH range. The diffusion dimension is also unresolved in the presence of PFO at high pH, but as the pH is reduced each amino acid in turn shows a fall in measured diffusion coefficient, as it begins to bind to the PFO micelles, until at very low pH all three diffuse more slowly. For this mixture good resolution in the diffusion domain, with the signals of the three different amino acids clearly separated, is obtained around neutral pH, as shown in Fig. 1.This behaviour can be rationalised quite straightforwardly in terms of the Coulomb interaction. At high pH the net charge on all the amino acid species is negative, and the charge–charge interactions between these species and the negatively charged PFO micelles tend to discourage binding. As the pH is lowered, the charge on the amino acids reduces and they become neutral zwitterions, but binding remains weak. Only when the net charge on the amino acid species is positive do the charge–charge interactions with the negative micelles become favourable and lead to substantial binding. The sequence in which the individual amino acids begin to bind as the pH is lowered is governed by the ordering of the individual pKas, notably those of the side chains.
The effect of charge–charge driven binding on amino acid diffusion and speciation can be modelled quantitatively, given reasonable approximations, by solving the interlocking equilibria between free amino acid species, aqueous protons, and micelle-bound species to determine the fraction xb of a given amino acid that is bound to micelles. The observed amino acid diffusion coefficient Dav is then given by Lindman's law26
| Dav = Df(1 − xb) + Dbxb | (1) |
| Dm = (DS[PFO] − DPFOcmc)/([PFO] − cmc) | (2) |
An amino acid with n protonation equilibria will have n + 1 different net charge states, e.g. −1, 0 and +1 for valine, which has only amino and carboxylic protonation equilibria. The bound and free concentrations cb and cf for a given charge state i are linked as follows:
| Kai = cfi[D+]/cfi+1 | (3) |
| Kbi = cbi/([Sm]cfi) | (4) |
| xbi = cbi/ctot | (5) |
Using the measured amino acid diffusion coefficients in the absence of PFO, the experimental micellar diffusion coefficient from eqn (2), and literature values for the pKas of all the ionisable groups, it is possible to fit measured amino acid diffusion coefficients in the presence of PFO to obtain estimates of the binding constants of the individual charged states of the different amino acids. A number of simplifying assumptions are needed. These include ideal behaviour, a single binding constant for each amino acid species that is independent of the amount bound and of any other species that may be bound, only one significant species per charge state, a Dm that is unaffected by pH or by amino acid binding, a Dfree that is substantially independent of pH, and pH measurement that is unaffected by the solutes present.
The effect of using D2O rather than H2O may be allowed for by using the apparent pH measured in D2O solution using a standard glass electrode, pH*, in place of the deuterio analogue of pH, pD, and adjusting the apparent pKa to allow for the change in solvent.28
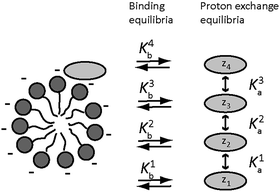
In an amino acid solution containing PFO micelles, three types of equilibria occur simultaneously, see Fig. 2. The first is amino acid protonation. Depending on the type of side chain, one amino acid may have up to four different protonation states of net charge zi, with up to three corresponding equilibrium constants Kai. The second set of up to four equilibria, with constants Kbi, is between the free and the micelle-bound forms of the individual amino acid charge states. The third and final equilibrium is that between free and micellar NaPFO, which requires that the concentration of NaPFO be greater than its critical micelle concentration (cmc, 31 mM at 25 °C (ref. 29)).
To investigate the nature and extent of the binding of different amino acid species to PFO micelles as a function of pH, two different mixtures were studied, containing respectively 1 mM each of histidine (His), glutamic acid (Glu) and lysine (Lys) (mixture 1), and 1 mM each of phenylalanine (Phe), tyrosine (Tyr) and valine (Val) (mixture 2). Samples of mixtures 1 and 2 were made up in D2O containing 1 mM sodium trimethylsilylpropanoate-d4 (TMSP) as reference, with and without 100 mM sodium perfluorooctanoate (NaPFO). The choice of amino acid concentration here is a compromise between the need for sufficient signal-to-noise ratio to allow the determination of diffusion coefficients in a reasonable time, and the need to keep the ratio of PFO to total amino acid concentration high to minimise any effect of amino acid binding on the binding constants Kbi and on the micellar diffusion coefficient Dm. Similarly, the number of amino acids per mixture is a compromise between the need to resolve sufficient signals of individual amino acids to allow reliable determination of diffusion coefficients, and the need to minimise the number of samples and the duration of the experiments required.
Fig. 3 summarises the results of measurements of diffusion coefficients as a function of pH for the four samples studied. For each amino acid the experimental diffusion coefficient in the presence and in the absence of PFO is plotted as a function of pH, together with solid lines showing the results Dfree of averaging the diffusion coefficients measured in the absence of PFO, and the results of fitting the diffusion coefficients measured in the presence of PFO to Lindman's law (eqn (1)) using bound fractions calculated from the equilibria of Fig. 2 using literature values for the protonation constants, experimental values for Dm and Dfree, and treating the three or four binding constants Kbi as variable parameters. Free amino acid diffusion coefficients in the presence of 100 mM NaPFO were estimated from the averages Dfree measured in the absence of PFO by scaling down by a factor 1 + φ/2, where φ is the estimated volume fraction of the surfactant in the solution.30 The binding constants obtained in the fitting and the literature acid dissociation constants used are summarised in Table 1. The actual values obtained for Kbi should be treated with caution given the approximations required in the analysis. Where two pKa values are similar, as for example in the case of tyrosine, the experimental data can be insufficient to allow a binding constant to be estimated.
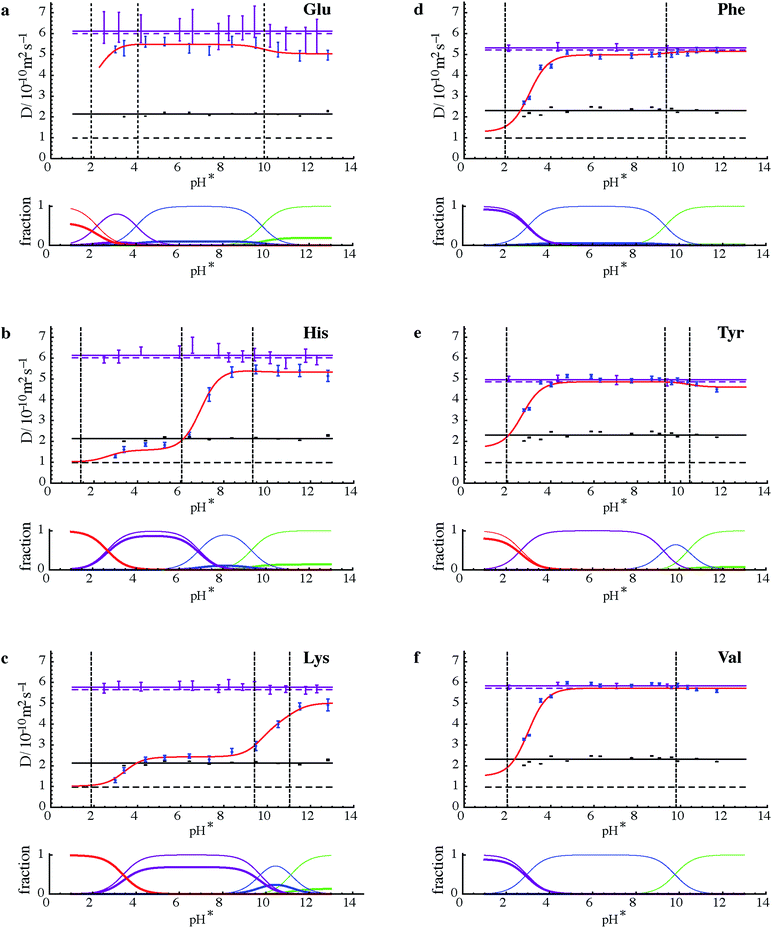 | ||
| Fig. 3 (Upper parts of a to f) Experimental results for measurements of diffusion coefficient D (dots with vertical error bars) as a function of measured pH (pH*) for the six amino acids shown in samples of mixtures 1 and 2 with (blue) and without (purple) 100 mM NaPFO. Solid horizontal purple lines show the averages of D measurements in the absence of NaPFO, and dashed horizontal purple lines those averages corrected for the estimated effects of the obstruction caused by surfactant in the samples containing NaPFO. Black dots with vertical error bars indicate the diffusion coefficients measured by 19F NMR for PFO, with their averages shown by solid horizontal black lines, and the micellar diffusion coefficients Dm calculated from eqn (2) indicated by dashed horizontal black lines. Error bars indicate plus and minus twice the standard error estimated in fitting, and do not take into account systematic errors. Literature values for pKa (ref. 27) are shown by dashed vertical black lines. The results of fitting the experimental amino acid diffusion coefficients D to eqns (A1) and (A2) for the equilibria shown in Fig. 1, using literature values for pKa corrected for D2O solvent28 and treating the binding constants Kbi as variable parameters, are shown as solid red lines. (Lower parts of a to f) Speciation plots showing bound (thick lines) and total (thin lines) mole fractions for the three or four different protonation states of each amino acid, with net charge becoming more positive in the order green, blue, purple, red, calculated using the fitted values for Kbi. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kb) obtained by fitting, and literature dissociation constants,27 for the components of samples 1 and 2. Error ranges quoted are twice the standard errors estimated in the least squares fitting, and do not take into account systematic errors
Kb) obtained by fitting, and literature dissociation constants,27 for the components of samples 1 and 2. Error ranges quoted are twice the standard errors estimated in the least squares fitting, and do not take into account systematic errors
| Sample | Species | pKa1 | pKa2 | pKa3 | pKb1 | pKb2 | pKb3 | pKb4 |
|---|---|---|---|---|---|---|---|---|
| a No statistically significant binding constant estimate found (estimated standard error > 0.5). | ||||||||
| 1 | Glu | 9.58 | 4.15 | 2.16 | −0.53 ± 0.13 | −0.22 ± 0.18 | −0.18 ± 0.82 | a |
| 1 | His | 9.09 | 6.04 | 1.70 | −0.36 ± 0.14 | −0.28 ± 0.30 | −2.03 ± 0.11 | a |
| 1 | Lys | 10.67 | 9.16 | 2.15 | −0.36 ± 0.16 | −0.86 ± 0.13 | −1.51 ± 0.04 | −3.21 ± 0.20 |
| 2 | Phe | 9.09 | 2.18 | a | 0.09 ± 0.24 | −2.23 ± 0.08 | ||
| 2 | Tyr | 10.10 | 9.04 | 2.24 | −0.02 ± 0.6 | a | a | −1.80 ± 0.15 |
| 2 | Val | 9.52 | 2.27 | a | a | −2.07 ± 0.10 | ||
The common pattern for each amino acid in Fig. 3 is that strong binding is only seen where the net charge on the amino acid species is positive, confirming that the dominant factor in binding is the Coulomb interaction. This is in contrast to the behaviour of alkyl chain surfactants, where hydrophobic interactions also play a major part. The speciation plots show that binding of amino acid species in the +2 charge state (for histidine and lysine, Fig. 3b and c, at low pH) is almost complete under the conditions used. In contrast, glutamate shows relatively little binding over the whole range studied (although it would be expected to bind strongly at even lower pH were PFO micelles still present; unfortunately, below about pH 2.5 NaPFO drops out of solution).
The need to keep amino acid concentrations low to avoid competition for binding limits the signal-to-noise ratio of the experimental measurements and hence the precision of the diffusion coefficients obtained. This in turn means that some features of the fits (red lines in Fig. 3) are at the borderline of statistical significance. It is interesting to note that there is some evidence for a role for hydrophobic effects; for example in the case of tyrosine (Fig. 2e), binding appears to increase in strength when the dianion is formed. Conversely, the reference material TMSP binds significantly in its neutral form, presumably because of the highly hydrophobic trimethylsilyl group. Signal-to-noise ratio is a particular problem for glutamic acid, since the only resolved signals are complex side chain multiplets, leading to large uncertainties in diffusion coefficient. Valine on the other hand has two strong methyl resonances that allow very good diffusion coefficient estimates to be made at this concentration.
The effect of binding to the PFO micelles on the protonation equilibria of the different amino acids31 can be seen when comparing the pH dependence of their diffusion with the literature values27 for acid dissociation constants. If the equilibria were unperturbed by the binding, the points of inflection in the red curves would coincide with the pKa values. Where the binding is weak, at high pH, this is a good approximation (see e.g. Fig. 3d and e). However where a significant fraction of the amino acid is bound, as at low pH in all the species studied except glutamic acid and tyrosine, the removal of much of the more protonated species from free solution shifts the overall equilibrium, so that the points of inflection lie to the right (to higher pH) of the pKa values.
The results of Fig. 3 provide significant reassurance about the approximations used and the probity of the model. The experimental diffusion coefficients measured for PFO show little variation with pH, confirming that within the pH range studied the micellisation is substantially unperturbed either by pH, or by amino acid binding at the low concentrations used. Indeed the quality of the fits seen in Fig. 3 is remarkably good given the small number of variable parameters used (just the three or four binding constants, not all of which are significant), and the assumptions and approximations involved.
One of the most significant of these qualifications is the assumption that the amino acid ionisation equilibria can be approximated by using pH* values as a proxy for [D+] with appropriate adjustments to the H2O solution values for the acid dissociation constants Ka. The adjustment used is based on extensive measurements made at 0.1 molal ionic strength.28 At first sight this seems a good match to the experimental conditions used (dominated by the 0.1 mol dm−3 NaPFO), but the effective ionic strength here is rather lower because two thirds of the NaPFO is in micellar form. This, and the potential for the surfactant to perturb the performance of the standard glass membrane pH electrode used, does introduce significant uncertainty and it is gratifying that only one dataset, that for histidine, shows significant systematic deviations between experimental data and fitted line, and that even these deviations disappear if the histidine side chain pKa is changed by 0.4 of a unit.
The two groups of amino acids used here were chosen because their similar sizes mean that they have very similar diffusion coefficients in free neutral solution, and hence pose a particular challenge for DOSY separation. The ability to achieve good diffusion separation by controlling the pH in PFO solution depends on the existence of a significant difference in pKa. Thus Phe and Tyr above are more difficult to separate than His and Lys.
Experimental
All materials were available commercially and used as received from Sigma Aldrich and Cambridge Isotopes Laboratories, Inc. pH was adjusted by sequential addition of NaOD/DCl in D2O. Diffusion coefficient measurements for 1H and 19F were carried out on a Varian INOVA 400 spectrometer at 298 K, using the Oneshot DOSY pulse sequence.30,32 Data were acquired with an array of 16 nominal gradient amplitudes, ranging from 3.0 to 27.0 G cm−1, using 16 transients, 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768 complex data points, a total diffusion-encoding gradient duration δ of 2 ms and a diffusion time Δ of 0.25 s. Reference deconvolution33,34 with a Gaussian target line shape, 5 or 6 Hz wide as appropriate, was chosen to give the best compromise between sensitivity and spectral resolution for 1H measurements. DOSY spectra were constructed using correction for the effects of pulse field gradient non-uniformity.35 Diffusion coefficients were determined using weighted averages of the fitted values obtained for well-resolved signals for each amino acid.
768 complex data points, a total diffusion-encoding gradient duration δ of 2 ms and a diffusion time Δ of 0.25 s. Reference deconvolution33,34 with a Gaussian target line shape, 5 or 6 Hz wide as appropriate, was chosen to give the best compromise between sensitivity and spectral resolution for 1H measurements. DOSY spectra were constructed using correction for the effects of pulse field gradient non-uniformity.35 Diffusion coefficients were determined using weighted averages of the fitted values obtained for well-resolved signals for each amino acid.
Fitting was carried out using a Mathematica 9 notebook which can be downloaded, along with all raw experimental data and parameters, from DOI: 10.15127/1.306019.
Conclusions
In matrix-assisted DOSY, sodium perfluorooctanoate micelles provide an “invisible” matrix that can be tuned by adjusting the pH to allow the signals of amphiprotic analytes such as amino acids to be separated. The binding of the amino acids studied is dominated by the Coulomb interaction, suggesting that it should be possible to predict in advance the conditions required to allow the separation of signals of ionic species in a given mixture.Appendix
Analytical expressions for amino acid diffusion coefficients
Eqns (1)–(5) can be assembled to yield analytical expressions for average amino acid diffusion coefficient Dav in the presence of a total surfactant concentration S and a deuterium ion concentration D+. For the cases where there are two and three ionization constants respectively these are
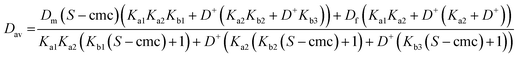 | (A1) |
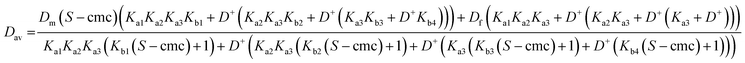 | (A2) |
Acknowledgements
This work was supported by the EPSRC (grant numbers EP/E05899X/1 and EP/H024336/1). AH thanks the Mexican Scientific and Technology Council (CONACyT) for financial support. MP thanks the Analytical Chemistry Trust Fund for a summer studentship (ACSS 12/012).Notes and references
- C. S. Johnson Jr, Prog. Nucl. Magn. Reson. Spectrosc., 1999, 34, 203 CrossRef.
- Y. Cohen, L. Avram and L. Frish, Angew. Chem., Int. Ed., 2005, 44, 520 CrossRef CAS PubMed.
- G. A. Morris, Diffusion-ordered spectroscopy, in eMagRes, John Wiley & Sons, Ltd, 2007, DOI:10.1002/9780470034590.emrstm0119.pub2.
- R. Evans, S. Haiber, M. Nilsson and G. A. Morris, Anal. Chem., 2009, 81, 4548 CrossRef CAS PubMed.
- S. R. Chaudhari, Srinivasa and N. Suryaprakash, J. Mol. Struct., 2013, 1033, 75 CrossRef CAS.
- C. Carrara, C. Lopez and S. Caldarelli, J. Chromatogr. A, 2012, 1257, 204 CrossRef CAS PubMed.
- A. K. Rogerson, J. A. Aguilar, M. Nilsson and G. A. Morris, Chem. Commun., 2011, 47, 7063 RSC.
- R. W. Adams, J. A. Aguilar, J. Cassani, G. A. Morris and M. Nilsson, Org. Biomol. Chem., 2011, 9, 7062 CAS.
- C. Pemberton, R. E. Hoffman, A. Aserin and N. Garti, Langmuir, 2011, 27, 4497 CrossRef CAS PubMed.
- R. Evans and I. J. Day, RSC Adv., 2016, 6, 47010 RSC.
- J. Cassani, M. Nilsson and G. A. Morris, J. Nat. Prod., 2012, 75, 131 CrossRef CAS PubMed.
- C. F. Tormena, R. Evans, S. Haiber, M. Nilsson and G. A. Morris, Magn. Reson. Chem., 2012, 50, 458 CrossRef CAS PubMed.
- S. Viel, F. Ziarelli and S. Caldarelli, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 9696 CrossRef CAS PubMed.
- G. Pages, C. Delaurent and S. Caldarelli, Anal. Chem., 2006, 78, 561 CrossRef CAS PubMed.
- S. Caldarelli, Magn. Reson. Chem., 2007, 45, 48 CrossRef PubMed.
- C. Pemberton, R. Hoffman, A. Aserin and N. Garti, J. Magn. Reson., 2011, 208, 262 CrossRef CAS PubMed.
- S. Huang, J. Gao, R. Wu, S. Li and Z. Bai, Angew. Chem., Int. Ed., 2014, 53, 11592 CrossRef CAS PubMed.
- M. E. Zielinski and K. F. Morris, Magn. Reson. Chem., 2009, 47, 53 CrossRef CAS PubMed.
- US Pat., 8,633,691, 2014 Search PubMed.
- G. Dal Poggetto, D. C. Favaro, M. Nilsson, G. A. Morris and C. F. Tormena, Magn. Reson. Chem., 2014, 52, 172–177 CrossRef CAS PubMed.
- G. Dal Poggetto, V. U. Antunes, M. Nilsson, G. A. Morris and C. F. Tormena, Magn. Reson. Chem., 2016 DOI:10.1002/mrc.4534.
- C. Tormena, R. Evans, S. Haiber, M. Nilsson and G. A. Morris, Magn. Reson. Chem., 2010, 48, 550 CrossRef CAS PubMed.
- N. V. Gramosa, N. M. S. P. Ricardo, R. W. Adams, G. A. Morris and M. Nilsson, Magn. Reson. Chem., 2016, 54, 815 CrossRef PubMed.
- R. Evans, A. Hernandez-Cid, G. Dal Poggetto, A. Vesty, S. Haiber, G. A. Morris and M. Nilsson, RSC Adv., 2017, 7, 449–452 RSC.
- S. Y. Yang and M. G. Khaledi, Anal. Chem., 1995, 67, 499–510 CrossRef CAS PubMed.
- P. Stilbs, Magn. Reson. Chem., 2016 DOI:10.1002/mrc.4365.
- CRC Handbook of Chemistry and Physics, Internet Version, CRC Press/Taylor & Francis, Boca Raton, FL, USA, 97th edn, 2017 Search PubMed.
- A. Krężel and W. Bal, J. Inorg. Biochem., 2004, 98, 161 CrossRef.
- N. Muller and H. Simsohn, J. Phys. Chem., 1971, 75, 942 CrossRef CAS.
- R. Bai, P. J. Basser, R. M. Briber and F. Horkay, J. Appl. Polym. Sci., 2014, 131, 40001 Search PubMed.
- M. G. Khaledi and A. H. Rodgers, Anal. Chim. Acta, 1990, 239, 121–128 CrossRef CAS.
- A. Botana, J. A. Aguilar, M. Nilsson and G. A. Morris, J. Magn. Reson., 2011, 208, 270–278 CrossRef CAS PubMed.
- G. A. Morris, H. Barjat and T. J. Horne, Prog. Nucl. Magn. Reson. Spectrosc., 1997, 31, 197 CrossRef CAS.
- P. Ebrahimi, M. Nilsson, G. A. Morris, H. M. Jensen and S. B. Engelsen, J. Chemom., 2014, 28, 656–662 CrossRef CAS.
- P. Damberg, J. Jarvet and A. Gräslund, J. Magn. Reson., 2001, 148, 343 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |