Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Experimental and predicted mechanical properties of Cr1−xAIxN thin films, at high temperatures, incorporating in situ synchrotron radiation X-ray diffraction and computational modelling†
Ehsan Mohammadpoura,
Zhong-Tao Jiang *a,
Mohmmednoor Altarawneh
*a,
Mohmmednoor Altarawneh b,
Nicholas Mondinosa,
M. Mahbubur Rahmana,
H. N. Limc,
N. M. Huang
b,
Nicholas Mondinosa,
M. Mahbubur Rahmana,
H. N. Limc,
N. M. Huang d,
Zonghan Xiee,
Zhi-feng Zhouf and
Bogdan Z. Dlugogorskib
d,
Zonghan Xiee,
Zhi-feng Zhouf and
Bogdan Z. Dlugogorskib
aSurface Analysis and Materials Engineering Research Group, School of Engineering & Information Technology, Murdoch University, Murdoch, WA 6150, Australia. E-mail: Z.Jiang@murdoch.edu.au; Tel: +61 8 9360 2867
bSchool of Engineering & Information Technology, Murdoch University, Murdoch, WA 6150, Australia
cDepartment of Chemistry, Faculty of Science, University Putra Malaysia, 43400 UPM Serdang, Selangor, Malaysia
dFaculty of Engineering, Xiamen University of Malaysia, Jalan Sunsuria, Bandar Sunsuria, 43900 Sepang, Selangor Darul Ehsan, Malaysia
eSchool of Mechanical Engineering, University of Adelaide, SA 5005, Australia
fDepartment of Mechanical and Biomedical Engineering, City University of Hong Kong, Kowloon, Hong Kong, China
First published on 20th April 2017
Abstract
Cr1−xAlxN coatings, synthesised by an unbalanced magnetic sputtering system, showed improved microstructure and mechanical properties for ∼14–21% Al content. In situ SR-XRD analysis indicated various crystalline phases in the coatings that included: CrN, AlN, α-Cr with small amounts of AlO2 and Al2O3 over the 25–700 °C range. Al doping improves resistance to crystal growth, stress release and oxidation resistance of the coatings. Al doping also enhances the coating hardness (H) from 29 to 42 GPa, elastic modulus (E) from 378 to 438 GPa and increased the resistance to deformation. First-principles and quasi-harmonic approximation (QHA) studies on bulk CrN and AlN were incorporated to predict the thermo-elastic properties of Cr1−xAlxN thin film coatings in the temperature range of 0–1500 °C. The simulated results at T = 1500 °C give a predicted hardness of H = ∼41.5 GPa for a ∼21% Al doped Cr1−xAlxN coating.
1. Introduction
3-d transition metal nitrides, such as CrN and TiN, combine attractive physico-chemical, electronic, optical, magnetic, mechanical and thermal properties.1 These composite materials have shown a wide range of technical applications in various key industrial areas. For example, due to their extreme hardness, high melting point and superior chemical stabilities, nitride-based ceramic coatings have been used for high-speed machining,2 cold forming, moulding dies,3 sliding parts and rocket nozzles.4 It is noted that CrN has significant superiority over TiN in wear, corrosion resistance,5 and anti-oxidative properties at temperatures up to 700 °C.6Vacuum sputtering technique is an outstanding method for synthesising high quality CrN ceramic thin film coatings with superior structural, mechanical and tribological properties.3,4 These studies have been extended to ternary combinations of CrN with doping of other elements, e.g., Al,7 Si,8,9 Ti,10 V,11 Nb12 or Cu.13 The doping elements mainly distribute in the amorphous layers which surrounds the columnar structured nanocrystalline (nc-) CrN grains. These amorphous layers can effectively enhance many mechanical properties of such thin film coatings. In particular, Al has shown great potential in improving the hardness14 as well as corrosion and oxidation resistances.15,16 This Cr–Al–N framework is of particular interest as they can form aluminium oxides on the top surface layers which suppress the diffusion of oxygen into the coating film. Analysis indicated the thin film coatings have enhanced chemical stability, good mechanical properties, good tribological properties, high temperature stability (up to 1000 °C) and exhibit excellent oxidation resistance.3,11,17
Characterisation at room temperature indicated that Al significantly affected the preferred grain orientation of the thin films.18 TEM and XPS studies indicated that amorphous AlN existed at the columnar CrN grain boundaries. The incorporation of Al introduced compressive residual stress to the coating material lattice. Moreover, the mechanical properties such as hardness, elastic strain and plastic deformation resistance of the coatings showed significant improvement over non doped CrN coating. These clearly indicated the crucial role of Al in producing a combination of superior hardness and excellent damage resistance in nc-CrN frameworks.18
In the present work, in situ synchrotron radiation powder diffraction (SR-XRD) beamline was employed to quantitatively investigate the changes in phase composition and microstructure of Cr1−xAlxN thin film coatings as a function of Al content at different measurement temperatures in an atmospheric environment. Rietveld analysis of high resolution SR-XRD data and nanoindentation measurements will provide quantitative results, hence making a connection between microstate phases and mechanical properties of the coating. Density Functional Theory (DFT) calculations and Quasi-Harmonic Approximation (QHA) are employed to estimate the cell-volume, thermal expansion and hardness of Cr1−xAlxN system at temperatures up to 1500 °C.
2. Experimental
2.1 Thin film coatings preparation
Cr1−xAlxN coatings with a total film thickness of 2 μm were deposited on M2 high speed steel substrates at 550 °C using a closed field unbalanced magnetron sputtering system (Teer Coatings Ltd, UK) with a four-target configuration. The coating process were described in detail by Li et al.18 and Wo et al.192.2 In situ SR-XRD characterizations
In situ SR-XRD experiments were performed on the Powder Diffraction beamline at the Australian Synchrotron with monochromatic X-rays, λ = 0.827 Å, verified by standard reference material (LaB6 660b) as supplied by the USA National Institute of Standards and Technology (NIST). The incidence angles of the X-ray beam (ω) were in range of 4.1 to 5.9°. The diffraction data were collected by a Mythen microstrip detector over the range of 10° ≤ 2θ ≤ 89° in flat-plate asymmetric reflection geometry. The coated substrates were mounted on a Pt heating stage in an Anton Paar HTK-2000 high temperature furnace and aligned to the centre of rotation on the diffractometer. The heating rate was 10 °C min−1 from ambient temperature up to 700 °C in air atmosphere.20 The temperature difference between the sample surface and Anton Parr furnace was calibrated manually before the in situ experiments carried out. Diffraction patterns were obtained at three temperatures (25, 200 and 500 °C) below and two temperatures (600 and 700 °C) above the deposition temperature of 550 °C due to time constrains at the synchrotron facilities. Each data acquisition at designated temperature was 120 s.The diffraction patterns were analysed with the TOPAS v5 academic software21 using the Rietveld method.22 The atomic positions for the structural models, based on the main identified phases of the coating, were extracted from Crystallography Open Database.23 Modelled peak shapes were used to determine the volume-weighted mean crystallite sizes (Lvol) and microstrain (e0). An accurate description of the peak shapes, in all of the diffraction patterns, was obtained by applying correctional functions for a flat plate in fixed incident beam geometry.24–26 The initial parameters for the refinement, as well as phase determination, were obtained from the JCPDS cards.
2.3 Nanoindentation measurements
Young's modulus and hardness of the coatings were measured, at room temperature (∼25 °C), by a calibrated Ultra-Micro Indentation System, UMIS-2000 equipped with a Berkovich indenter. A maximum load of 20 mN was applied in 10 increments. The loading rate used was 2.5 mN s−1 and represented the static response of the materials. The area function of the indenter tip was calibrated using a standard fused silica specimen. Load control method with a maximum loading of 5 mN was employed for calibration. The peak loading is based on the considerations that the maximum displacement during indentation should be no more than 10% of the coating thickness. For better resolutions, the number of test points were 20 for loading and 20 for unloading.2.4 DFT computational simulations
All structural optimizations and calculations were performed with the generalized gradient approximations (GGA) using the PW91 functional27 as implemented in the VASP package.28 Energy cut-off for plane waves included in the expansion of wave functions was 500 eV. Pseudo-atomic calculations were performed for Cr: 3d54s1, Al 3s23p1 and N 2s22p3. k-Point sampling for reciprocal space integration was optimised and adopted a 21 × 21 × 21 Gamma scheme for cubic structures. CrN in contrast to other early transition metal (Ti, Sc, V, …) nitrides, needed additional effort due to the local magnetic moments of the Cr atoms in CrN structure. The calculations for bulk CrN was carried out for both paramagnetic (CrN-m) and non-magnetic (CrN-nm) structures.The thermodynamic properties of cubic phases were explored using the quasi-harmonic Debye–Slater model as implemented in Gibbs2 code.29 In all temperature dependent property calculations, the Vinet's equation of state was adopted to fit the energy–volume curves.30 To calculate the elastic constants and determine the second derivatives, we used a finite differences method as implemented in VASP package (IBRION = 6).
3. Results and discussion
3.1 Structural analysis via in situ synchrotron radiation XRD technique
The surface elemental composition and chemical bonding state, obtained from previous XPS analysis and full discussion of the coatings by Li et al.18 indicated the existence of CrN, Cr2O3, AlN and Al2O3 phases in the coating surface region, are summarised in Table 1.| Coating notation | Element (at%) | |||
|---|---|---|---|---|
| Cr | Al | N | O | |
| C1 | 33.4 | 0 | 34.9 | 31.7 |
| C2-14% Al | 27.5 | 14.2 | 31.8 | 26.6 |
| C3-17% Al | 16.6 | 17.2 | 29.4 | 36.8 |
| C4-21% Al | 19.1 | 21.4 | 30.4 | 29.0 |
The JCPDS cards used for phase identification in the SR-XRD spectra: 00-076-2494 (CrN), 00-025-1495 (AlN), 00-901-4565 (AlO2), 00-900-9676 (Al2O3), 00-035-0803 (Cr2N), 00-901-3484 (α-Fe) and 00-041-1351 (Fe3W3C). The atomic positions for Fe3W3C were taken from.31 The in situ full patterns of all samples, for all temperatures, are included in the ESI section (Fig. S1–S4†). For clarity the spectra for each temperature are combined in one plot for each sample.
The Rietveld refinement of the diffraction spectra resulted in R-weighted pattern (Rwp) values in the range of 15–20. The largest errors in the refinement models are mainly due to the incomplete crystallographic data for the substrate. An example of a typical fitted spectrum is indicated by Fig. 1, which shows the Rietveld refinement for the C1 sample at 700 °C with Rwp = 15. The allowed hkl values for each phase are indicated by the small vertical bars. The difference between experimental and modelled results is indicated by the difference plot above the hkl bars.
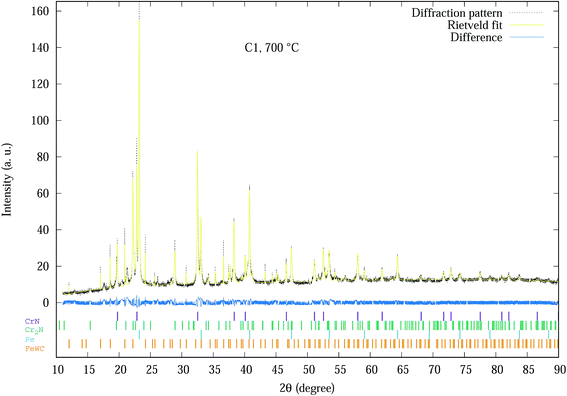 | ||
| Fig. 1 Experimental SR-XRD and Rietveld refinement profile of C1 coating at 700 °C. The allowed hkl values for each phase are indicated by the small vertical bars. | ||
Basically all 20 spectra shown in Fig. S1–S4 of the ESI† section were analysed by Rietveld analysis with similar plots as Fig. 1 producing data used for further analysis as indicated in Fig. 2–6. The phases of the C1 sample at different temperatures was similar to the sample (denoted as CrN-M2ST) recorded in Mohammadpour et al.20
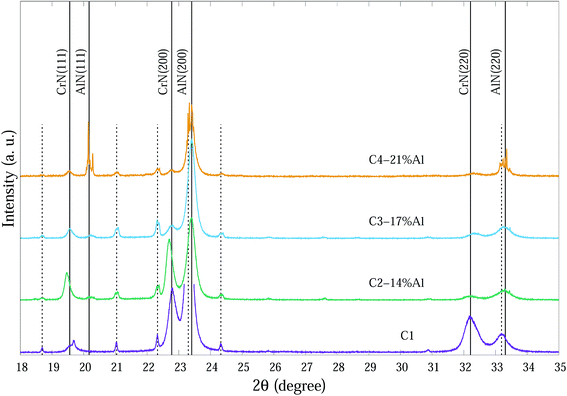 | ||
| Fig. 2 SR-XRD diffraction patterns at ∼25 °C of as-deposited Cr1−xAlxN coatings with various Al contents. The dashed vertical lines indicate substrate peaks. | ||
SR-XRD diffraction patterns at ∼25 °C of as-deposited Cr1−xAlxN coatings are depicted in Fig. 2. For clarity the 2θ range in Fig. 2 is from 18° to 35° 2θ consisting of the main peaks for each individual phase.
The compositions of the main phase in as-deposited CrAlN thin film coatings were determined to be CrN and AlN phases. Thin film coating C1 showed strong intensity in (200), (220) directions at ∼22.8° and ∼32.4° 2θ, respectively for the CrN phase. In the Al doped samples the dominant orientations of the CrN phase are in the (200) and (111) planes. These diffraction peaks became broader and of lower intensity as the Al content increased (C3-17% Al and C4-21% Al) indicating a combination of small grain size and high concentration of possible amorphous nature. The peaks at 20.2°, 23.4° and 33.3° 2θ in the C4-21% Al sample are identified as diffractions from c-AlN (111), (200) and (220) planes, with some overlap with substrate (α-Fe) diffraction peaks. The confirmation of the AlN phase in SR-XRD pattern agrees with the NEXAFS results by Mahbubur et al.32 and XPS analysis by Li et al.18 from similar coatings. All samples in as-deposited condition (∼25°) had Al2O3 and Cr2O3 phases detected by XPS but SR-XRD did not show any noticeable peaks related to those oxides. This could be due to (i) most of oxygen accumulate in the top surface layers of thin films, and (ii) possible amorphous state of the oxide phases. However, at temperatures >500 °C minor amounts of Al2O3 and metastable AlO2 were observed from the diffraction patterns (Fig. 3).
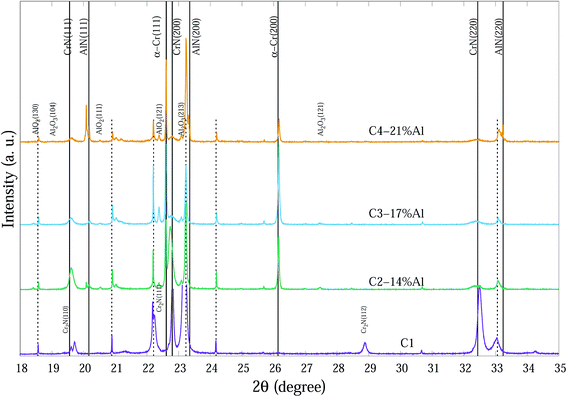 | ||
| Fig. 3 SR-XRD diffraction patterns at 700 °C of Cr1−xAlxN coatings with various Al contents. The dashed vertical lines indicate substrate peaks. | ||
Fig. 3 indicates the main phases of these coatings at 700 °C. Diffraction spectra of CrAlN coatings at 700 °C show α-Cr, AlO2 and Al2O3 phases. Peaks at 22.60°, 26.16° and 37.33° 2θ can be determined as α-Cr (111), (200) and (220), respectively. Agouram et al.33 concluded that the phase content of CrNx-based coatings is strongly influenced by deposition processes. The presence of α-Cr in CrNx coatings can reduce the hardness; however, it may improve the coating toughness or as a metallic source which diffuse outward and contribute in the formation of surface oxidation layers. Although hexagonal-structured Cr2N (h-Cr2N) exhibits higher hardness than cubic CrN, it is more susceptible to oxidation which can deteriorate the thermal stability of the C1 thin film with considerable h-Cr2N content especially at high temperatures.20 It seems Al doping successfully prevents the formation of h-Cr2N in the CrAlN coatings even at lowest Al percentage (C2-14% Al) in the temperature range of study. Our observations did not confirm any possible existence of Cr2O3 crystalline phases in the column structure of coatings; that may indicate (i) small amorphous structures distributing in grain boundary regions, and (ii) either amorphous or crystalline phase structure in the very top surface layers of thin films where normal XRD cannot fully determine the phases (Grazing incidence SR-XRD would be able to provide more precise surface crystalline information). The shifts of diffraction peaks from substrate, especially for Fe (111) at 23.8° is probably due to the thermal expansion of the unit cells at elevated temperatures. Peaks related to CrN and AlN phases exhibited some sharpening with increasing temperature.
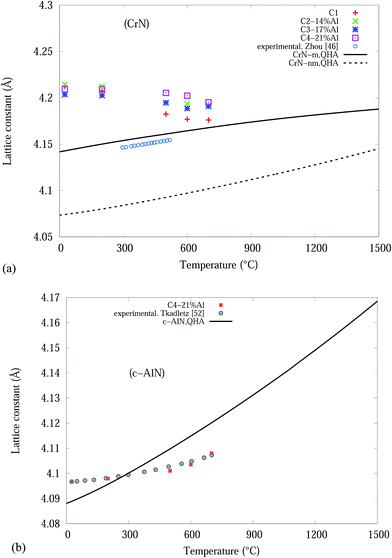
From the Rietveld refined SR-XRD data, the lattice constants of the CrN and c-AlN phases in the Cr1−xAlxN coatings were calculated and plotted as a function of temperature in Fig. 4. The lattice constant of CrN decreases continuously from 4.21 Å to 4.17 Å for C1 and to 4.19 Å for the Al doped samples. The overall changes of the lattice constant for the CrN phase are slightly smaller in the samples with Al doping than without doping. Overall, the lattice parameter values agree with the experimental values from other sources, such as Barshilia et al.34 (4.09 to 4.16 Å) and Elangovan et al.35 (4.15 to 4.17 Å). Lattice constants of c-AlN (in sample C4-21% Al) increased steadily from approximately 4.09 Å at room temperature to 4.1 Å at 700 °C indicating unit cell expansion by 0.5%. The lattice constant of α-Cr phase, in all samples at 700 °C, were 3.65 Å ± 10%.
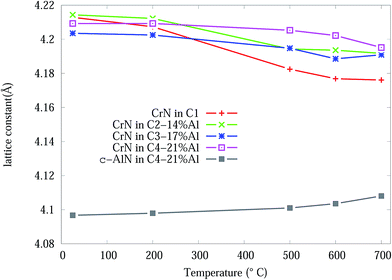 | ||
| Fig. 4 CrN and c-AlN lattice constants, from Rietveld analysis, in Cr1−xAlxN coatings as a function of the in situ experiment temperature. | ||
The crystallite size and microstrain as a function of temperature, from Rietveld analysis, for the CrN phase are shown in Fig. 5. The Effect of adding Al onto the microstructure of the as-deposited coatings is more pronounced in C3-17% Al and C4-21% Al coatings exhibiting about 30% smaller crystallite sizes compared to Al free and C2-14% Al samples. The crystallite sizes in all samples gradually increased in the temperature range 25 to 600 °C and then abruptly increased from 600 to 700 °C. C1 and C2-14% Al show the highest crystallite size growth by ∼100% and ∼67%, respectively. The higher Al content in C3-17% Al and C4-21% Al effectively prevented the crystallite growth of CrN during heating below 700 °C. Above, 600 °C the CrN crystallite size in C4-21% Al increases by ∼34%. The most stable crystallite size for CrN is exhibited by C3-17% Al with an 8% crystallite growth. The crystallite sizes of the α-Cr phase are 1832 (C2-14% Al), 1780 (C3-17% Al) and 828 (C4-21% Al) nm in the 700 °C Cr1−xAlxN samples.
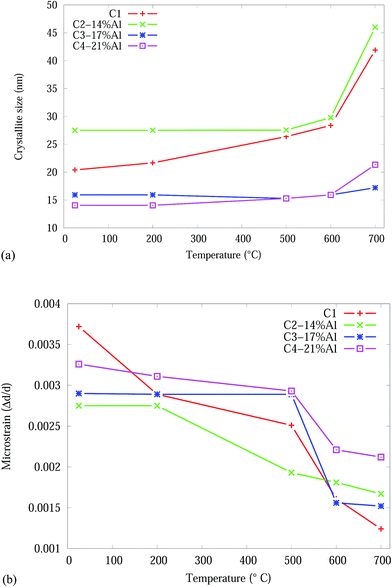 | ||
| Fig. 5 Effect of temperature on the CrN phase in the Cr1−xAlxN coatings, from Rietveld analysis: (a) crystallite size (b) microstrain. | ||
Our observations showed that microstrain in C1 sample decreased by ∼67% during heating which is almost ∼1.7× of the microstrain release in samples with Al contents. The residual stress in these types of coatings could be due to two mechanisms (1) thermal stress and/or (2) accumulation of defects (dislocations, vacancies, etc.) in the coating layer. Thermal stress is a resultant of the difference in the coefficient of thermal expansion (CTE) value for coating and substrate. The decline of internal stress in the coatings could be a result of absorption and annihilation of defects during annealing. It allows the defects to diffuse through the lattice and to be absorbed at grain boundaries and dislocation cores. This seems to be more pronounced in the binary CrN coating case. The presence of amorphous content in Cr1−xAlxN coatings at grain boundaries hinders stress release in the coatings which resist against coating softening.
The stress in the coating structure, from the changes in d space for CrN (220), is shown in Fig. 6. Similar plots for the (111), (200) and (311) planes of CrN phase are included in Fig. S5–S7 of the ESI section.† The stress (σ) in the coating were calculated based on eqn (1) using the elastic properties of CrN (elastic modulus, E = 300 GPa and Poisson ratio, ν = 0.28).36
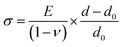 | (1) |
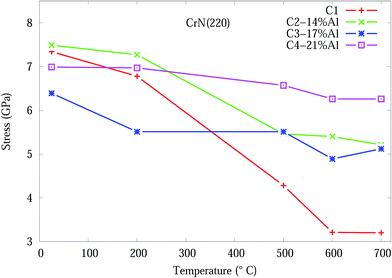 | ||
| Fig. 6 Effect of temperature on the residual stress, from eqn (1), for CrN (200) orientation in Cr1−xAlxN coating. | ||
3.2 Experimental mechanical properties of CrAlN coatings
Nano-indentation tests, for Cr1−xAlxN coatings at as-deposited conditions and after the completion of the in situ SR-XRD experiment (heated samples), were undertaken at room temperature. The hardness (H) and elastic modulus (E) for these coatings are set out in Table 2 and Fig. S8 and S9 of the ESI section.† Analysis of Table 2 and the plots clearly indicate that there is no difference in H and E, within the experimental errors, between the as-deposited and heated sample. The resistance to deformation is indicated by H3/E2 and plotted in Fig. S10 of the ESI section.† The coatings with smaller crystallite size/higher microstrain present greater hardness (C3-17% Al and C4-21% Al samples) in as deposited condition. Improvement in coating hardness confirms the microstructure refining effect of Al dopants.| Sample | As-deposited | Heated | ||
|---|---|---|---|---|
| H (GPa) | E (GPa) | H (GPa) | E (GPa) | |
| C1 | 29 ± 2 | 378 ± 21 | 28 ± 2 | 376 ± 22 |
| C2-14% Al | 35 ± 3 | 401 ± 27 | 35 ± 3 | 396 ± 25 |
| C3-17% Al | 39 ± 3 | 421 ± 38 | 39 ± 3 | 421 ± 30 |
| C4-21% Al | 42 ± 3 | 438 ± 32 | 42 ± 3 | 436 ± 32 |
These findings are consistent with the quantitative SR-XRD measurements of crystallite size and micro strains in the Al doped coatings that exhibited very little hardness drop after heating. The calculated ratio of H3/E2 improved significantly in samples containing Al compared to the reference sample (C1). However, there is no change in resistance to deformation between as deposited and heated conditions of the samples. The combination of microstructure and nanoindentation studies indicate that the hardness of the as-deposited nanocrystalline coatings can be controlled by several parameters such as phase composition, crystallographic directions, crystallite size and residual stress/microstrain.37
3.3 Density functional theory modelling
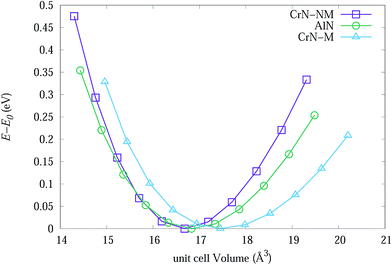 | ||
| Fig. 7 The change in energy of primitive unit cells for bulk CrN-nm, CrN-m and c-AlN as a function of cell volume. | ||
Table 3 lists experimental lattice parameter values from SR-XRD data and DFT calculations from present work and available literature. The calculated lattice parameter for CrN-m (spin-polarised) is closer to SR-XRD results. The magnetic moment for each Cr atoms in CrM-m structure converged to 2.044 μB which is within range of 1.9 to 2.28 μB from calculations of Filippetti et al.38
The QHA method (Debye model) was used to predict the thermal expansion of the studied bulk structures as a function of temperatures. Fig. 8(a) and (b) are plots of the experimental and theoretical lattice parameters, with respect to temperature, for bulk CrN and c-AlN phases in the temperature range 0–1500 °C, respectively. Fig. 8(a) also includes lattice constant calculated from the experimental thermal expansion coefficient, α(T), of Zhou et al.46 with a0 = 4.14 Å (standard CrN phase) at room temperature. Fig. 8(a) clearly shows the CrN-m model is highly compatible to the experimentally obtained data. The CrN lattice constant at room temperature for all samples differ from the simulation values within ∼1.6%. Interestingly these converge to the simulated results with increasing temperature resulting in a ∼0.4% difference at 700 °C. The most significant drop in lattice constant values of CrN occurs to C1 sample which is very close to QHA model at 700 °C.
Quasi-binary systems like Cr1−xAlxN coatings with a mixture of NaCl-structured CrN/AlN phases can form (Cr,Al)N solid solutions up to x = 0.75.47 Phase segregation during deposition results in a mixture of fcc-structured Cr-rich (Cr,Al)N and AlN28,48 which will increase the coating hardness due to activation of solid-solution hardening mechanism. Theoretical49 and experimental47,50 studies show that substitution of Cr atoms (r = 1.4 Å) with Al atoms (r = 1.25 Å) can progressively decrease lattice constant of CrN phase as Al content increases. However, smaller Al atoms can incorporate into interstitial positions in CrN structure which can expand the lattice constant as observed for CrSiN coating.19,51
The c-AlN lattice parameter in C4-21% Al are in good agreement with experimental data from Tkadletz et al.52 as indicated in Fig. 8(b). The experimental results are within ∼±0.3%, of the simulated QHA results up to 700 °C.
Overall the differences between the simulated and experimental results is due to the use of pure homogeneous bulk material in the Debye (QHA) model calculations, and the solid solution of different nitride phases of the thin film coatings.
| C11 + 2C12 > 0, C11 − C12 > 0, C44 > 0, C11 > 0, C11 > B > C12 | (2) |
| Phase | C11 | C12 | C44 | B (GPa) | G (GPa) | E (GPa) | ν |
|---|---|---|---|---|---|---|---|
| CrN-nm | 588.0 | 215.1 | 5.9 | 340 | 44 | 126 | 0.43 |
| 526c,42 | 226c,42 | 5c,42 | 326c,42 | 35c,42 | 101c,42 | 0.43c,42 | |
| 502c,54 | 214c,54 | 4.1c,54 | 310c,54 | 58c,58 | 163c,58 | 0.41c,58 | |
| 580c,46 | 210c,46 | 8c,46 | 327c,58 | 100–250e,36 | |||
| 546c,58 | 184c,58 | 20c,58 | 340c,59 | ||||
| CrN-m | 352 | 88.7 | 61.0 | 176.4 | 93.9 | 239.0 | 0.27 |
| 369c,42 | 125c,42 | 114c,42 | 192c,42 | 111c,25 | 279c,42 | 0.25c,42 | |
| 348c,46 | 117c,46 | 74c,46 | |||||
| c-AlN | 387 | 149 | 305 | 254.3 | 209 | 303 | 0.2788 |
| 423c,45 | 167c,45 | 306c,45 | 251c,45 | ||||
| 221e,60 |
All of these conditions were satisfied by the CrN and c-AlN phases indicating the mechanical stability of these structures. The overview of available literature as shown in Table 4 indicates that the reported calculated values for elastic constants and modulus are widely scattered and depend on the choice of k-points, cut-off energies, functional (s) and simulation packages. As an example, Yan et al.42 and Brik et al.54 used the CASTEP module of Materials Studio package with different settings of k points grids and cut off energies for CrN-nm analysis. With 8 × 8 × 8 (400 eV) and 10 × 10 × 10 (320 eV) k points grids the authors calculated C11 values of 526 and 546 GPa, respectively.
ESI section Tables S2 and S3† show the influence of k-points grids selection on the elastic constants of CrN-m and CrN-nm for the present project. To calculate the elastic constants for CrN-m and CrN-nm, k-point grids of 21 × 21 × 21 and 31 × 31 × 31 were chosen for the simulations. The results of these analyses are tabulated in Table 4. The calculated elastic constants for CrN-nm in present study are comparable (∼2%) with calculations of Zhou46 who used similar approach via VASP package and projector-augmented wave (PAW) method. The values of C11 and C12 for c-AlN underestimate by ∼9% the calculations of Wang et al.45 carried out by VASP package and PAW method.
The positive difference between C11 and C44 (C11 − C44 = 582 for CrN-nm), known as Cauchy pressure, indicates the metallic bonding nature of Cr-N structure55 which is comparable to much smaller difference for AlN (C11 − C44 = 83). Cauchy pressure is also a sign of the ductility of materials, since it indicates the angular character of atomic bonding in metals. A positive Cauchy pressure reveals ductility of crystal, while a brittle material exhibits a negative value.56 Bulk modulus (B), shear modulus (G) and Young's modulus (E) for each phase were estimated by applying Voigt–Reuss equations57 and compared with available literature.
The calculated results, at 0 K, from Table 4 are spread out but have similar magnitudes including the 2 experimental values at ∼25 °C. The k-point grids that optimised the calculation of the elastic constants and unit cell volumes will be used in the DFT and QHA simulations.
QHA method for CrN and c-AlN are used to predict the hardness of two binary compounds (CrN and c-AlN) in a wide temperature range (25–1500 °C). The method for calculating the hardness of materials is based on atomic potentials and bond strength developed by Šimůnek and Vackář61 for single crystals and then extended to binary compounds. The hardness of a crystal can be calculated by introducing its bond strength (Sij):
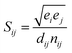 | (3) |
For binary compounds, the difference between atomic potentials is:
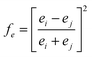 | (4) |
The hardness of such a system with volume (V) is defined as:
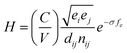 | (5) |
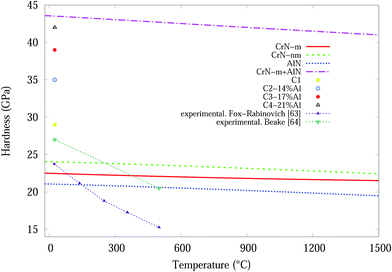
Temperature dependent variations in unit cell volume for each structure were obtained from QHA modelling up to 1500 °C (Fig. 8). Subsequently the bond length, dij, as a function of temperature was deduced from the cell volumes and by use of eqn (5) the hardness values for CrN (CrN-nm and CrN-m) and c-AlN phases. The results of hardness over a wide range of temperatures are shown in Fig. 9. Also plotted in Fig. 9 are the high temperature (25–500 °C) in situ nanoindentation data for commercially available Al0.7Cr0.3N coatings studied by Fox-Rabinovich et al.63 and Beake et al.64 Room temperature nanoindentation results for the current projects' Cr1−xAlxN coatings are also incorporated in Fig. 9.
Based on predicted material behaviours, hardness values for both phases reduced constantly at elevated temperatures. However, there are considerable differences in the reduction slopes depending on the phase type. Hardness values for CrN-nm structure showed the highest resistance to temperature while AlN was more susceptible to temperature. Experimental hardness in Table 2 of Cr1−xAlxN samples showed that nanocomposites of CrN in amorphous AlN matrix can effectively improve the resistance to grain boundary sliding65 which makes these samples harder than C1 sample. In addition, the deposition process and doping significantly distorts the lattice of CrN/AlN mixture, as is evident in microstrain and residual stress plots, which can also contribute to improve the deformation resistance of doped samples. According to Šimůnek and Vackář61 the hardness of multicomponent compound systems is expected to be a geometrical sum of the values of hardness of all binary systems in the solid (given by their eqn (6)). Interestingly for the current multicomponent system (at 25 °C), consisting of CrN and AlN phases, H = H1 + H2 = 22.5 + 21 = 43.5 GPa (H1 for CrN-m and H2 for AlN) compares remarkably well with the experimental value of 42 GPa for the C4 sample. Here the values correspond to a numerical sum of eqn (5) as opposed to a geometric sum. To show this point more clearly, the simulated data for CrN-m and AlN are added and the plot included in Fig. 9.
The experimental results of Fox-Rabinovich et al.,63 are in some agreement with the simulated CrN-m, CrN-nm and AlN results for temperatures up to ∼150 °C while they deviate significantly for higher temperatures up to ∼500 °C, whilst Beake et al.64 results are in agreement over the same temperature range. It should be noted that the materials in Beake's investigation has a high percentage Al content (∼70%) whilst our materials have a maximum of ∼21% Al content (C4). The hardness of experimental result from C4 and computational modelling from the summation of the CrN-m and AlN components are very similar at room temperature, see Fig. 9. If this is a real relationship, then the magnetic properties of the Cr are important for the formation of stable and hard Cr1−xAlxN coatings.
Based on the results from both experiments and computational calculation, the temperature dependent hardness of the synthesized CrN/AlN thin film nanocomposites can be predicted in the temperature range from 25 °C to 1500 °C, refer to Fig. 9. Furthermore a numeric sum for the hardness of the 2 components, at T = 1500 °C give a predicted hardness H ∼ 41.5 GPa. Only real experimental measurements at the 200–1500 °C range will show if the hardness of the CrN/AlN multicomponent thin film has the predicted direct sum values.
4. Conclusions
Synthesised Cr1−xAlxN coatings, with a maximum Al content of ∼21%, by unbalanced magnetic sputtering system showed improved microstructure and mechanical properties compared to undoped CrN coating. Analysis of in situ synchrotron X-ray diffraction at temperatures range of 200–700 °C established: (i) remarkable resistance to crystal growth and stress release up to 700 °C for coatings with Al doping greater than ∼14%. (ii) Al-dopants improve oxidation resistance of the coatings by preventing the formation of Cr2N at high temperatures.Nano indentation results at ∼25 °C show: (i) Al doping improved the coating hardness (H) and elastic modulus (E) from 29 to 42 GPa and 378 to 438 GPa respectively, and (ii) resistance to deformation increased as the Al content increased.
First-principles and quasi-harmonic approximations (QHA) studies for bulk magnetic and non-magnetic CrN (CrN-m and CrN-nm) and AlN over the temperature range of 0–1500 °C were undertaken to calculate elastic constants (Cij) and hardness (H). Comparison of DFT-QHA models and the nanoindentation results indicate that hardness of Cr1−xAlxN coating with ∼21% Al content may be the sum of values from CrN-m and AlN phase. Our computational modelling predicts that the hardness (H) of Cr1−xAlxN coating with the Al content of ∼21% can reach to about 41.5 GPa at T = 1500 °C.
Acknowledgements
Ehsan Mohammadpour is highly grateful to the Murdoch University for the awarded scholarship (MIPS). The authors wish to acknowledge the support provided by the Australian Synchrotron with the beamline proposal AS141/PD/7582. The study has also been supported by grants of computing time from the National Computational Infrastructure (NCI), Canberra, Australia and the Pawsey Supercomputing Centre, Perth, Australia. We acknowledge the support from Dr M. Rowles (Curtain University) for invaluable discussions.References
- S. Zhang, Y. Li, T. Zhao and Q. Wang, Sci. Rep., 2014, 4(5241), 1–7 Search PubMed.
- J. Y. Cheong, X. Z. Ding, B. K. Tay and X. T. Zeng, Key Eng. Mater., 2010, 447–448, 725–729 CrossRef CAS.
- S. R. Pulugurtha, D. G. Bhat, M. H. Gordon, J. Shultz, M. Staia, S. V. Joshi and S. Govindarajan, Surf. Coatings Technol., 2007, 202, 1160–1166 CrossRef CAS.
- J. Musil, Surf. Coatings Technol., 2012, 207, 50–65 CrossRef.
- X. Guan, Y. Wang, G. Zhang, J. Xin, L. Wang and Q. Xue, RSC Adv., 2016, 6, 87003–87012 RSC.
- P. Z. Shi, J. Wang, C. X. Tian, Z. G. Li, G. D. Zhang, D. J. Fu and B. Yang, Surf. Coatings Technol., 2013, 228, S534–S537 CrossRef CAS.
- N. Bagcivan, K. Bobzin and S. Theiß, Thin Solid Films, 2013, 528, 180–186 CrossRef CAS.
- H. N. Shah, R. Jayaganthan and A. C. Pandey, Mater. Des., 2011, 32, 2628–2634 CrossRef CAS.
- Z. Wu, F. Zhou, Q. Ma, Q. Wang, Z. Zhou and L. Kwok-Yan Li, RSC Adv., 2016, 6, 76724–76735 RSC.
- L. Lu, Q. M. Wang, B. Z. Chen, Y. C. Ao, D. H. Yu, C. Y. Wang, S. H. Wu and K. H. Kim, Trans. Nonferrous Met. Soc. China, 2014, 24, 1800–1806 CrossRef CAS.
- P. Panjan, A. Drnovšek, J. Kovač, P. Gselman, T. Bončina, S. Paskvale, M. Čekada, D. Kek Merl and M. Panjan, Thin Solid Films, 2015, 591, 323–329 CrossRef CAS.
- E. Bemporad, C. Pecchio, S. De Rossi and F. Carassiti, Surf. Coatings Technol., 2004, 188–189, 319–330 CrossRef CAS.
- S. Tan, X. Zhang, X. Wu, F. Fang and J. Jiang, Appl. Surf. Sci., 2011, 257, 5595–5600 CrossRef CAS.
- Q. Luo, S. C. Wang, Z. Zhou and L. Chen, J. Mater. Chem., 2011, 21, 9746–9756 RSC.
- J. Xu, L. Liu, P. Munroe, Z. Xie and Z. Jiang, J. Mater. Chem. A, 2013, 1, 10281–10291 CAS.
- J. Xu, D. Lai, Z. Xie, P. Munroe and Z.-T. Jiang, J. Mater. Chem., 2012, 22, 2596–2606 RSC.
- Y. Long, J. Zeng, D. Yu and S. Wu, Ceram. Int., 2014, 40, 9889–9894 CrossRef CAS.
- Z. Li, P. Munroe, Z. Jiang, X. Zhao, J. Xu, Z. Zhou, J. Jiang, F. Fang and Z. Xie, Acta Mater., 2012, 60, 5735–5744 CrossRef CAS.
- P. C. Wo, P. R. Munroe, Z. Li, Z.-T. Jiang, Z. H. Xie, Z. F. Zhou and K. Y. Li, Mater. Sci. Eng. A, 2012, 534, 297–308 CrossRef CAS.
- E. Mohammadpour, Z.-T. Jiang, M. Altarawneh, Z. Xie, Z. Zhou, N. Mondinos, J. Kimpton and B. Z. Dlugogorski, Thin Solid Films, 2015, 599, 98–103 CrossRef.
- A. A. Coelho, J. Appl. Crystallogr., 2003, 36, 86–95 CAS.
- R. W. Cheary, A. a. Coelho and J. P. Cline, J. Res. Natl. Inst. Stand. Technol., 2004, 109, 1–25 CrossRef CAS PubMed.
- S. Gražulis, A. Daškevič, A. Merkys, D. Chateigner, L. Lutterotti, M. Quirós, N. R. Serebryanaya, P. Moeck, R. T. Downs and A. Le Bail, Nucleic Acids Res., 2012, 40, 420–427 CrossRef PubMed.
- H. Toraya, T. C. Huang and Y. Wu, J. Appl. Crystallogr., 1993, 26, 774–777 CrossRef CAS.
- O. Masson, R. Guinebretière and A. Dauger, J. Appl. Crystallogr., 1996, 29, 540–546 CrossRef CAS.
- M. R. Rowles and I. C. Madsen, J. Appl. Crystallogr., 2010, 43, 632–634 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Rev. B, 1992, 45, 13244–13249 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558–561 CrossRef CAS.
- A. Otero-De-La-Roza and V. Luaña, Comput. Phys. Commun., 2011, 182, 1708–1720 CrossRef CAS.
- P. Vinett, J. H. Rose, J. Ferrante and J. R. Smith, Phys. Rev. B, 1996, 53, 5252–5258 CrossRef.
- Pierre Villars, PAULING FILE, in Inorganic Solid Phases, SpringerMaterials (online database), Springer, Heidelberg Springer Materials Fe3W3C (W3Fe3C) Crystal Structure http://materials.springer.com/isp/crystallographic/docs/sd_1707470.
- M. Mahbubur Rahman, A. Duan, Z.-T. Jiang, Z. Xie, A. Wu, A. Amri, B. Cowie and C.-Y. Yin, J. Alloys Compd., 2013, 578, 362–368 CrossRef CAS.
- S. Agouram, F. Bodart and G. Terwagne, Surf. Coatings Technol., 2004, 180–181, 164–168 CrossRef CAS.
- H. C. Barshilia, N. Selvakumar, B. Deepthi and K. S. Rajam, Surf. Coat. Technol., 2006, 201, 2193–2201 CrossRef CAS.
- T. Elangovan, P. Kuppusami, R. Thirumurugesan, V. Ganesan, E. Mohandas and D. Mangalaraj, Mater. Sci. Eng. B, 2010, 167, 17–25 CrossRef CAS.
- L. Cunha, M. Andritschky, K. Pischow and Z. Wang, Thin Solid Films, 1999, 355–356, 465–471 CrossRef CAS.
- D. Rafaja, C. Wüstefeld, C. Baehtz, V. Klemm, M. Dopita, M. Motylenko, C. Michotte and M. Kathrein, Metall. Mater. Trans. A, 2011, 42, 559–569 CrossRef CAS.
- A. Filippetti, W. E. Pickett and B. M. Klein, Phys. Rev. B, 1999, 59, 7043–7050 CrossRef CAS.
- Z. G. Zhang, O. Rapaud, N. Bonasso, D. Mercs, C. Dong and C. Coddet, Vacuum, 2008, 82, 501–509 CrossRef CAS.
- S. Yang, E. Wiemann and D. G. Teer, Surf. Coatings Technol., 2004, 188–189, 662–668 CrossRef CAS.
- F. Sanchette, C. Ducros, T. Schmitt, P. Steyer and a. Billard, Surf. Coatings Technol., 2011, 205, 5444–5453 CrossRef CAS.
- M. F. Yan and H. T. Chen, Comput. Mater. Sci., 2014, 88, 81–85 CrossRef CAS.
- I. Scanavino and M. Prencipe, RSC Adv., 2013, 3, 17813–17821 RSC.
- B. Alling, T. Marten and I. A. Abrikosov, Phys. Rev. B, 2010, 82, 1–9 Search PubMed.
- A. J. Wang, S. L. Shang, Y. Du, Y. Kong, L. J. Zhang, L. Chen, D. D. Zhao and Z. K. Liu, Comput. Mater. Sci., 2010, 48, 705–709 CrossRef CAS.
- L. Zhou, F. Körmann, D. Holec, M. Bartosik, B. Grabowski, J. Neugebauer and P. H. Mayrhofer, Phys. Rev. B, 2014, 90, 184102 CrossRef.
- Y. Makino and K. Nogi, Surf. Coatings Technol., 1998, 98, 1008–1012 CrossRef CAS.
- S.-K. Tien and J.-G. Duh, Thin Solid Films, 2006, 494, 173–178 CrossRef CAS.
- B. Alling, T. Marten, I. a. Abrikosov and A. Karimi, J. Appl. Phys., 2007, 102, 1–8 CrossRef.
- A. Sugishima, H. Kajioka and Y. Makino, Surf. Coat. Technol., 1997, 97, 590–594 CrossRef CAS.
- F. L. E. Martinez, R. Sanjines and O. Banakh, Thin Solid Films, 2004, 446, 18–22 CrossRef.
- M. Tkadletz, N. Schalk, R. Daniel, J. Keckes, C. Czettl and C. Mitterer, Surf. Coatings Technol., 2016, 285, 31–46 CrossRef CAS.
- B. Kocak, Y. O. Ciftci, K. Colakoglu and E. Deligoz, Phys. B Condens. Matter, 2012, 407, 316–323 CrossRef CAS.
- M. G. Brik and C.-G. Ma, Comput. Mater. Sci., 2012, 51, 380–388 CrossRef CAS.
- M. E. Eberhart and T. E. Jones, Phys. Rev. B - Condens. Matter Mater. Phys., 2012, 86, 1–7 CrossRef.
- D. Wu, H. Wang, L. Wei, R. Pan and B. Tang, J. Magnes. Alloy., 2014, 2, 165–174 CrossRef CAS.
- A. Lesar, M. Hodos and I. Introduction, Chem. Phys., 1998, 109, 9410–9416 CAS.
- Y. Liang, X. Yuan and W. Zhang, Solid State Commun., 2010, 150, 2045–2048 CrossRef CAS.
- F. Rivadulla, M. Bañobre-López, C. X. Quintela, A. Piñeiro, V. Pardo, D. Baldomir, M. A. López-Quintela, J. Rivas, C. a. Ramos, H. Salva, J.-S. Zhou and J. B. Goodenough, Nat. Mater., 2009, 8, 947–951 CrossRef CAS PubMed.
- Q. Xia, H. Xia and A. L. Ruoff, J. Appl. Phys., 1993, 73, 8198–8200 CrossRef CAS.
- A. Šimůnek and J. Vackář, Phys. Rev. Lett., 2006, 96, 1–4 CrossRef PubMed.
- H. Ichimura and I. Ando, Surf. Coatings Technol., 2001, 145, 88–93 CrossRef CAS.
- G. S. Fox-Rabinovich, B. D. Beake, J. L. Endrino, S. C. Veldhuis, R. Parkinson, L. S. Shuster and M. S. Migranov, Surf. Coatings Technol., 2006, 200, 5738–5742 CrossRef CAS.
- B. D. Beake, G. S. Fox-Rabinovich, S. C. Veldhuis and S. R. Goodes, Surf. Coatings Technol., 2009, 203, 1919–1925 CrossRef CAS.
- S. Veprek and A. S. Argon, Surf. Coatings Technol., 2001, 146–147, 175–182 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra00342k |
| This journal is © The Royal Society of Chemistry 2017 |