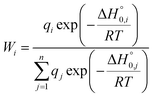Dimetallofullerene M₂@C₁₀₀ or carbide cluster fullerene M₂C₂@C₉₈ (M = La, Y, and Sc): which ones are more stable?

Abstract

The geometric and thermodynamic stability of the M₂C₁₀₀ (M = La, Y, and Sc) series was systematically investigated using density functional theory calculations on the level of B3LYP/6-31G(d) ∼ Lanl2dz. In all the cases, M₂@D₅(285913)-C₁₀₀ isomers are the lowest-energy species. However, carbide endohedral fullerenes M₂C₂@C₁(230933)-C₉₈ present excellent thermodynamic stabilities, except for those with La metal. The main product in electric arc experiments at temperatures lower than 3500 K for La₂C₁₀₀ should be La₂@D₅(285913)-C₁₀₀, which was successfully synthesized previously; for Y and Sc, the predicted main products in these experiments should be M₂C₂@C₁(230933)-C₉₈. Further analysis of the geometric structures of the M₂C₁₀₀ series showed that the dimetallofullerenes M₂@C₁₀₀ have greater effects on the shapes of cages than M₂C₂@C₉₈. These results provide some valuable guidance for the synthesis and characterization of large endohedral fullerenes including La, Y or Sc.

---

Introduction

Endohedral dimetallofullerenes were firstly considered to exist in the form of M₂@C_2n.^1–9 However, based on ¹³C NMR spectroscopic studies, Wang et al. found that the previously suggested endohedral metallofullerene (EMF) of Sc₂@C₈₆ was in fact, Sc₂C₂@C₈₄.¹⁰ Since then, many types of carbide cluster fullerenes have been widely reported. It is well known that EMFs of M₂C_2n may exist in two distinguished forms: classical dimetallofullerenes, M₂@C_2n, or carbide cluster fullerenes M₂C₂@C_2n−2.^11–16 Among the reported carbide cluster fullerenes, Sc plays a very important role; for example, the reported carbide cluster fullerenes with two Sc atoms include Sc₂C₂@C₈₄,^8,10,17 Sc₂C₂@C₈₂,^12,18 Sc₂C₂@C₈₀ (ref. 4 and 11) and Sc₂C₂@C₆₈.¹⁵ Recently, a family of Y₂C₂@C_2n was isolated by Dorn et al., and some of them were determined by ¹³C NMR spectroscopy,⁹ whereas the isolation and crystallographic characterization of La₂C₂@C_2n is less reported.^19,20 On the other hand, many dimetallofullerenes of M₂@C_2n have also been identified; for example, structures of Sc₂@C₆₆,²¹ Sc₂@C₈₂ (ref. 22) and Y₂@C₈₂ (ref. 23) have been determined by ¹³C NMR spectroscopy. Dimetallofullerenes of La₂@C_2n including La₂@C₇₂,²⁴ La₂@C₇₈ (ref. 25) and La₂@C₈₀ (ref. 26) have also been synthesized and characterized.

Recently, endohedral fullerenes with large cage sizes (n > 90) have attracted significant research interest;^27–30 for example, the largest fullerene cage that has been identified by X-ray is Sm₂@D_3d(822)-C₁₀₄, which shows a nanotubular shape,²⁷ and a series of EMFs containing two gadolinium atoms with cages from C₉₀ to C₁₂₄ have been observed by Yang et al.²⁸ However, the effective isolation and structural characterization of these EMFs are still very challenging; for example, Christine M. Beavers et al. discovered an extensive series of soluble dilanthanum endohedral fullerenes from La₂C₉₀ to La₂C₁₃₈, but only a very few of them have been isolated in pure form and characterized by single-crystal X-ray diffraction.²⁹

Due to the difficulty in synthesis, separation and structural assignment of these species, theoretical study has been widely performed to help to predict or determine the structure, stability and properties of these species.^31–36 There are at least two challenges in these calculations that should be mentioned. First, the number of different cage isomers for a particular cage size quickly increases with the cage size. Since the non-IPR cages can be greatly stabilized by the encaged metal atoms in EMFs, they should be considered in many cases. Yang et al. performed a systematic investigation on the structures of Dy₂@C₁₀₀ including IPR and non-IPR isomers (with a total number of 24 755) and found that the D₅(285913)-C₁₀₀ cage was the most promising candidate for encapsulation.³¹ Second, for EMFs having the form of M₂C_2n, both dimetallofullerenes M₂@C_2n and carbide cluster fullerenes M₂C₂@C_2n−2 should be considered and compared. For example, in order to deduce the most stable isomers of M₂C₉₈ (M = Sc, Y, La, Gd, Lu), Zheng et al. performed systematic studies on the series by density functional theory (DFT) methods, and found that the metal-carbide endohedral fullerenes are more stable.³⁴

In order to better understand the structures of large-sized EMFs, herein, we conduct a comprehensive analysis on M₂C₁₀₀ (M = La, Y, Sc) with DFT methods. The geometric structure and thermodynamic stability of M₂C₁₀₀ species, including dimetallofullerenes of M₂@C₁₀₀ (based on the full screening of 285913 C₁₀₀ cages) and carbide cluster fullerenes of M₂C₂@C₉₈ (based on full screening of 231017 C₉₈ cages), have been systematically investigated. Interestingly, our results show that compared with the previous results of M₂C₉₈ obtained by Zheng et al.,³⁴ the increase in the cage by only a single unit of C₂ does affect their energy priorities for corresponding dimetallofullerenes and carbide cluster fullerenes, implying the difficulty in predicting their structures and energies for EMFs with larger cages.

Computational details

It is known that each encapsulated metal atom of La, Y or Sc will donate three electrons to the fullerene cage in M₂@C_2n isomers;^34–36 thus, the geometry optimization of M₂@C_2n isomers (M = La, Y, Sc) was set based on the optimization results of C₁₀₀⁶⁻. Since non-IPR fullerenes can be stabilized by the inside metal ions, the total of 24 755 isomers, including all 450 IPR (isolated-pentagon-rule) isomers and 24 305 non-IPR isomers with less than two adjacent pentagons, were considered here. The 5 most stable isomers of C₁₀₀⁶⁻ were taken from the previous results reported by Yang et al.³¹ For M₂C₂@C₉₈ (M = La, Y, Sc), the encapsulated M₂C₂ clusters maintain a + 4 valence state and thus, their geometry optimizations were performed based on the optimization results of C₉₈⁴⁻. A total of 17 941 carbon cages, including all 259 IPR and 17 232 non-IPR cages with less than two adjacent pentagons, were first calculated at the AM1 level (Table S1†). Then, the ten lowest-energy C₉₈⁴⁻ (Table S2†) cages and five lowest-energy C₁₀₀⁶⁻ cages were further optimized at the level of B3LYP/6-31G. After that, optimized metalloclusters M₂ (M = La, Y, Sc) or M₂C₂ (M = La, Y, Sc) were put into the corresponding C₁₀₀⁶⁻ and C₉₈⁴⁻ cages in different directions. All these isomers of M₂@C₁₀₀ and the six most stable isomers of M₂C₂@C₉₈ were at last optimized at the B3LYP/6-31G(d) ∼ Lanl2dz level and further verified by vibrational analysis on the same level. For all these species, electronic energies were calculated at 0 K with zero-point energy corrections and free energies were calculated at 298 K. All DFT calculations were carried out using the Gaussian 09 program package.³⁷

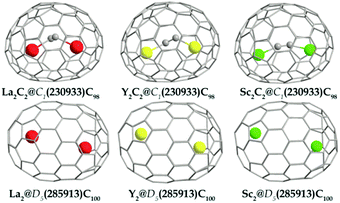
Relative concentrations (W_i) of the ith isomer at different temperatures were calculated using the following equation:³⁸

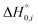where R is the gas constant, T is the absolute temperature, q_i and are the partition function and the relative heat of formation at absolute zero temperature of the ith isomer, respectively. Chirality contributions were also taken into account by doubling their partition functions for enantiomeric pairs, and rotational–vibrational partition functions were calculated from the optimized structural and vibrational data obtained at the level of B3LYP/6-31G(d) ∼ Lanl2dz without frequency scaling.

Results and discussion

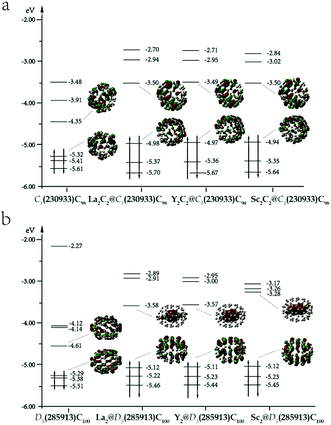
Table 1 shows the relative energies and HOMO–LUMO gaps of M₂C₁₀₀ isomers (M = La, Y, Sc) optimized at the level of B3LYP/6-31G(d) ∼ Lanl2dz. All the isomers were calculated based on closed-shell electron configurations. The results show that for La, the two isomers with lowest energies are La₂@D₅(285913)-C₁₀₀ and La₂@C₂(285864)-C₁₀₀, in which the latter has an energy of 17.9 kcal mol⁻¹ higher than that of the former. Among the carbide cluster fullerenes, the isomer with the lowest energy is La₂C₂@C₁(230933)-C₉₈, which is 34.6 kcal mol⁻¹ higher in energy than La₂@D₅(285913)-C₁₀₀. A comparison among their relative energies is also shown in Fig. S1a,† where it can be seen that the energies of the La₂@C₁₀₀ isomers are generally lower, compared to those of La₂C₂@C₉₈. It is also revealed in Table 1 that the isomer La₂@D₅(285913)-C₁₀₀ has a considerably large HOMO–LUMO gap (1.54 eV), indicating its prominent chemical stability. For the IPR-violating fullerene of La₂@C₁(230600)-C₉₈, its relative energy is found to be much higher, compared to those of IPR. To further confirm the results, a different pseudopotential of ECP46MHF was also applied,³⁹ and the results were similar. The energy of La₂C₂@C₁(230933)-C₉₈ is 40.2 kcal mol⁻¹ higher than that of La₂@D₅(285913)-C₁₀₀ and their gaps are 0.1 eV and 0.02 eV lower than the results obtained with the pseudopotential of Lanl2dz for the two species, respectively.

Table 1 Relative energies and HOMO–LUMO gaps of M₂C₁₀₀ isomers (M = La, Y, and Sc)^a,b

Spiral ID^c	IPR ID^d	PA^e	Sym.^f	ΔE^g (La)	Gap^h (La)	ΔE^g (Y)	Gap^h (Y)	ΔE^g (Sc)	Gap^h (Sc)
a Optimization was performed on the basis of B3LYP/6-31G(d) ∼ Lanl2dz.b Optimization of the isomers of M2@C98-230925 (M = La, Y) failed.c Based on IUPAC standards to encode all of the carbon cages.d Based on IUPAC standards to encode the carbon cages abiding by IPR rules.e The number of adjacent pentagons.f Symmetry of the original empty carbon cage, which is also applied in the nomenclature of the EMFs (after the symbol of @).g Relative energy units in kcal mol^−1.h Units in eV.
C98-230924	166	0	C2	45.0	1.05	18.4	1.16	9.6	1.13
C98-230925	167	0	C2v	—	—	—	—	10.5	1.57
C98-230926	168	0	C1	45.2	1.25	17.9	1.25	8.2	1.26
C98-230933	175	0	C1	34.6	1.48	10.7	1.48	0.9	0.90
C98-230979	221	0	C2	52.0	1.50	24.0	1.36	13.9	1.38
C98-230600		1	C1	63.8	1.04	31.0	1.05	15.2	1.44
C100-285793	330	0	C2	21.8	1.08	17.0	1.19	14.4	1.41
C100-285858	395	0	D2d	22.8	1.26	18.6	1.34	13.9	1.61
C100-285864	401	0	C2	17.9	0.88	19.6	1.10	19.6	1.22
C100-285868	405	0	C1	26.4	0.84	20.7	0.89	14.8	1.32
C100-285913	450	0	D5	0	1.54	0	1.54	0	1.85

---

To evaluate the overall thermodynamic stability of these EMFs at relatively high temperatures, their temperature-relative concentration curves were calculated and are shown in Fig. 1a. All thermodynamic properties were evaluated using the harmonic approximation to calculate the partition function. Errors caused by anharmonicity are not considered here. Under temperatures lower than 2000 K, the relative concentration of La₂@D₅(285913)-C₁₀₀ dominates the distribution. With increasing temperature, the concentration decreases and is surpassed by the isomer of La₂C₂@C₁(230933)-C₉₈ at 3500 K. At about 3500 K, the relative concentration of La₂C₂@C₁(230933)-C₉₈ ascends to 35% and prevails with the increase in temperature. As a result, dimetallofullerenes display distinct stability at low temperature, but carbide cluster fullerenes are more stable when the temperature is higher than 3500 K. The result suggests that the isomer of La₂@D₅(285913)-C₁₀₀ may exist and accounts for an important component in the synthesis, which matches well with the experimental results reported by Beavers et al.²⁹ In their electric arc experiments, a series of EMFs from La₂C₉₀ to La₂C₁₃₈ was discovered, and the most abundant product was found to be La₂@D₅(285913)-C₁₀₀, which was isolated in pure form and characterized by X-ray diffraction. The consistent results also prove that our theoretical calculation results performed here are reliable and credible.

Fig. 1 Relative concentrations of low-energy isomers of (a) La₂C₁₀₀, (b) Y₂C₁₀₀ and (c) Sc₂C₁₀₀.

Based on a similar calculation strategy, further studies with Y and Sc atoms were also carried out. These results are also shown in Table 1. Y₂@D₅(285913)-C₁₀₀ and Sc₂@D₅(285913)-C₁₀₀ are the lowest-energy isomers of Y₂@C₁₀₀ and Sc₂@C₁₀₀, respectively. For carbide cluster fullerenes, the isomers with the lowest energies still have the IPR cages of C₁(230933)-C₉₈. However, the energy differences between pure EMFs and metal carbide EMFs for different metal atoms are different. The energy of Y₂C₂@C₁(230933)-C₉₈ was found to be 10.7 kcal mol⁻¹ higher than that of Y₂@D₅(285913)-C₁₀₀, and the value decreases to 0.90 kcal mol⁻¹ in the case of Sc₂C₁₀₀. A comparison among the relative energies of all calculated isomers of M₂@C₁₀₀ and M₂C₂@C₉₈ (M = Y, Sc) is shown in Table S4,† where their differences are clearly reflected. For Y₂C₁₀₀, the energies of Y₂@C₁₀₀ isomers and those of Y₂C₂@C₉₈ are very close, and they change their energy orders sequentially. However, the energies for corresponding Sc₂C₂@C₉₈ isomers are generally lower than those of Sc₂@C₁₀₀, except for the most stable isomer of Sc₂@D₅(285913)-C₁₀₀. Triplet states of some isomers are also considered (Table S4†) and their energies are obviously higher than those of singlet states.

Relative concentrations of M₂C₁₀₀ (M = Y, Sc) isomers under different temperatures are shown in Fig. 1b and c, respectively. Y₂@D₅(285913)-C₁₀₀, the lowest-energy structure in the Y₂C₁₀₀ series is prevalent under low temperature below 500 K. With temperature increasing, its relative concentration descends sharply and is surpassed by Y₂C₂@C₁(230933)-C₉₈ at 1100 K. At about 1700 K, the relative concentration of Y₂C₂@C₁(230933)-C₉₈ ascends to its maximum yield of 65%. Though its concentration decreases after 1700 K, it still occupied the main fraction. Y₂C₂@C₁(230933)-C₉₈ together with the other three carbide cluster fullerenes share the largest contributions when the temperature is higher than 3500 K. For the Sc₂C₁₀₀ system (Fig. 1c), the relative concentration of Sc₂@D₅(285913)-C₁₀₀, which is the lowest-energy structure at 0 K, can be totally neglected under general temperature. In contrast, the relative concentration of Sc₂C₂@C₁(230933)-C₉₈ decreases to about 55% at 2000 K and keeping declining with increasing temperature, but is still significantly higher than other isomers. Like the Y₂C₁₀₀ system, carbide cluster fullerene isomers are dominant in the high temperature region. The results reflect a similar trend to the M₂C₉₈ (M = Y, Sc) series, in which M₂C₂@C₂(230933)-C₉₈ are the most stable isomers because of their thermodynamic and kinetic stabilities.

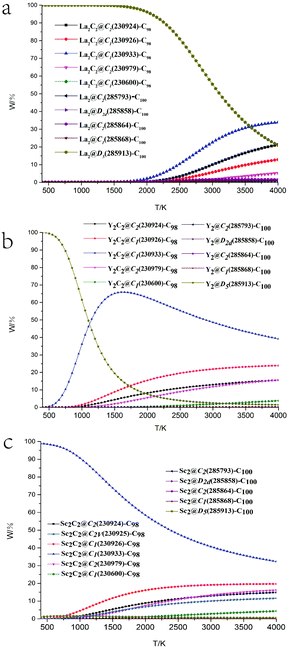
Chen et al. and Deng et al. discussed the possible geometric shapes of carbide clusters with different M–M distances,^43,44 and revealed that Sc₂C₂ was a planar, twisted unit. The structures of the most stable isomers of M₂C₂@C₉₈ and M₂@C₁₀₀ (M = La, Y, Sc) are shown in Fig. 2, and some of their structural parameters are listed in Table 2. For M₂C₂@C₉₈ isomers, the Sc₂C₂ cluster tends to retain a linear structure, while La₂C₂ tends to form a butterfly-shaped structure. As shown in Table 2, the average La–C–C angle is about 83°, while that of Sc–C–C is about 162°, and the d_M-cage values for La and Sc are 2.65 Å and 2.29 Å, respectively. They all have very similar C–C distances (∼1.26 Å) in the cages, indicating the existence of a triple bond between the two carbon atoms, which is also consistent with the NBO bonding analysis (Table S8†). These results are very similar to the previous results of M₂C₂@C₉₆ (M = La, Y, Sc) reported by Zheng et al.³⁴ On the other hand, the longest distances of the surfaces of three cages are 9.71, 9.70 and 9.69 Å, which are all very close to the corresponding value for the empty cage (9.71 Å), showing that the encapsulation of M₂C₂ has an insignificant effect on the shape of the cage. For M₂@C₁₀₀ isomers, the d_M–M values are much larger than those in M₂C₂@C₉₈ isomers. The metal atoms are oriented with the longest metal–metal distances to minimize the electrostatic repulsion between them. The calculated d_La-cage and d_La–La are 2.50 and 5.63 Å, respectively, which are very close to the experimentally reported values of 2.45 and 5.74 Å.³⁵ However, for Y and Sc, their d_M-cage values decrease and d_M–M values increase correspondingly, suggesting that the interactions between the Sc atoms and the nearby hexagons are the strongest, compared to the cases of Y and La. The longest distances between the two carbon atoms along the axis are 10.59 Å for La, 10.44 Å for Y and 10.43 Å for Sc, respectively. These distances are all much longer than that of the empty cage (10.28 Å), indicating that the cages are elongated after the metal clusters of M₂ are encapsulated.

Fig. 2 Geometric structures of the most stable isomers of M₂@C₁₀₀ and M₂C₂@C₉₈ (M = La, Y, and Sc).

Table 2 Structural parameters of M₂ or M₂C₂ clusters in some important M₂C₁₀₀ species

	M–C–C angle (deg)	dM–M^a (Å)	dC–C^b (Å)	dM–C^c (Å)	dM–cage^d (Å)	L^e (Å)
a Distance between two metal atoms.b Distance between carbide atoms.c Distance between metal atoms and neighbouring carbon atoms of carbine fragment.d Distance between metal atoms and the nearest carbon atoms of the fullerene cage.e Maximum distance of two carbon atoms on the cage. Values of L for the empty cages of C98 and C100 are 9.71 Å and 10.28 Å, respectively.
La2C2@C1(230933)-C98	84.4, 82.5	4.58	1.26	2.54, 2.55	2.65	9.71
Y2C2@C1(230933)-C98	108.2, 131.4	4.95	1.26	2.28, 2.30	2.47	9.70
Sc2C2@C1(230933)-C98	158.8, 164.2	5.32	1.25	2.14, 2.15	2.29	9.69
La2@D5(285913)-C100	—	5.63	—	—	2.50	10.59
Y2@D5(285913)-C100	—	6.05	—	—	2.34	10.44
Sc2@D5(285913)-C100	—	6.41	—	—	2.18	10.43

---

NBO charge distributions of M₂C₂ or M₂ entrapped in cages C₁(230933)-C₉₈ or D₅(285913)-C₁₀₀ were employed and are shown in Fig. S2.† For all structures, carbon cages and encapsulated carbon atoms present negative charge states and metal atoms present positive charge states. The carbon atoms in carbide clusters are much more negatively charged than those on cages. It has also been found that the electrons are more centralized at the adjacent pentagon pole. The strong electronic interaction between the metal ion and the pentagon also helps to significantly stabilize the whole EMF.

In order to investigate the electronic structures of the thermodynamically favorable isomers, frontier molecular orbitals of M₂C₂@C₉₈ and M₂@C₁₀₀ (M = La, Y, Sc) are presented in Fig. 3. In M₂C₂@C₁(230933)-C₉₈ isomers, all HOMO and LUMO orbitals have similar energy levels. The HOMO–LUMO gap of the C₁(230933)-C₉₈ empty cage is enlarged when the cage encapsulates M₂C₂ clusters. In other words, entrapping M₂C₂ clusters can obviously make the C₁(230933)-C₉₈ cage more stable, and the type of metal element is independent of electronic structures. Similar results have been found for the isomers of M₂@D₅(285913)-C₁₀₀ (Fig. 3b). In these species, the HOMO is mainly localized on the carbon cage. However, the LUMO is completely localized on the two encaged metals. It shows a very unique situation in these isomers, in which the metal ions with 3+ oxidation state undergoing strongly repulsive Coulomb interaction might still have metallic interactions over a very long distance of 5–6 Å. The results also indicate that such structures might have a very stable and less reactive carbon cage.

Fig. 3 Main frontier molecular orbitals of the most stable isomers of M₂@C₁₀₀ (bottom) and M₂C₂@C₉₈ (top) (M = La, Y, and Sc) and corresponding cages.

These results can be compared with the previous results of M₂C₉₈ (M = La, Y. Sc) reported by Zheng et al.³⁴ Table 3 shows the relative energies of the most stable isomers at 0 K. It is revealed that for M₂C₉₈ and M₂C₁₀₀ species, the classical dimetallofullerenes have a lower energy for La, but a higher energy for Sc. On the other hand, with the size of the carbon cage increasing, the advantage of the dimetallofullerene gradually increases. In order to make the results more reliable, the method of M06-2X/6-31G(d) ∼ Lanl2dz^40–42 was also applied to the lowest-energy isomers of M₂@C₁₀₀ and M₂C₂@C₉₈ (Tables S6–S8†). Although the energy values are different, the tendency remains the same. However, considering the temperature effect on the distribution of all possible isomers, it should be noticed that the most stable species at higher temperatures, such as 3500 K, are still governed by metal-carbide EMFs, except in the case of La₂C₁₀₀. The result also implies that dimetallofullerenes might be more readily synthesized experimentally for carbon cages with larger sizes (n > 100). A systematic calculation on M₂C₁₀₂ may help us to see if the suggestion is correct. The relevant work is ongoing in our lab.

Table 3 Comparison of the relative energies of the most stable isomers of M₂C₁₀₀ and M₂C₉₈ (M = La, Y, and Sc) at 0 K^a

M2C2@C2n−2	M2@C2n	ΔE^b
a Energies of M2C98 species were taken directly from ref. 33.b Relative energies (in kcal mol^−1) were calculated by ΔE = E(M2@C2n) − E(M2C2@C2n−2).
La2C2@C96-191809	La2@C98-168785	−4.8
Y2C2@C96-191809	Y2@C98-168785	17.1
Sc2C2@C96-191809	Sc2@C98-230924	19.7
La2C2@C98-230933	La2@C100-285913	−34.6
Y2C2@C98-230933	Y2@C100-285913	−10.7
Sc2C2@C98-230933	Sc2@C100-285913	−0.9

---

Conclusions

Theoretical investigations have been performed on EMFs of M₂C₁₀₀ (M = La, Y, Sc) by DFT calculation. In all cases, isomers of M₂@D₅(285913)-C₁₀₀ are the lowest-energy species. However, statistical thermodynamic analysis shows that the most stable isomers under high temperatures (for example, T = 3000 K) should be metal-carbide endohedral fullerenes, except for La metal. Based on these results, the main product in electric arc experiments for La₂C₁₀₀ should be La₂@D₅(285913)-C₁₀₀, which has been proven by the successful synthesis and X-ray crystallographic characterization conducted by Christine M. Beavers et al. in 2011.²⁹ For Sc₂C₁₀₀, the main products should be Sc₂C₂@C₁(230933)-C₉₈, and for Y₂C₁₀₀, the main products should be Y₂C₂@C₁(230933)-C₉₈, although some classical dimetallofullerenes might also be synthesized in the process. Further analysis on the geometric structures of M₂C₂@C₉₈ and M₂@C₁₀₀ showed that the positions of M₂ or M₂C₂ clusters rely very much on metal atoms. The effects of the encaged clusters on energies and shapes of the cages are also compared. Although both M₂ and M₂C₂ clusters can make outside cages more stable, the M₂C₂ clusters have a lesser effect on the shapes of the cages than M₂ clusters. The analyses on NBO charge distributions and frontier molecular orbitals reveal a strong electrostatic interaction between metal atoms and cages. It is also revealed that the LUMO orbital is mainly distributed on the metal atoms in the species of M₂@C₁₀₀. Simulated IR spectra of main M₂C₁₀₀ isomers are shown in Fig. S4.† These results not only provide some valuable information for the experimental characterization and synthesis of large EMF species of M₂C₁₀₀, but can also help us to determine structures of larger EMFs of M₂C_2n (2n > 100, M = La, Y, Sc).

Acknowledgements

Financial support from the National Natural Science Foundation of China (No. 21475065, 21627801) is gratefully acknowledged.

Notes and references

1. A. A. Popov, S. F. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113.
2. X. Lu, L. Feng, T. Akasaka and S. Nagase, Chem. Soc. Rev., 2012, 41, 7723–7760.
3. H. Zheng, X. Zhao, W. W. Wang, T. Yang and S. Nagase, J. Chem. Phys., 2012, 137, 14308.
4. H. Kurihara, X. Lu, Y. Iiduka, N. Mizorogi, Z. Slanina, T. Tsuchiya, T. Akasaka and S. Nagase, J. Am. Chem. Soc., 2011, 133, 2382–2385.
5. X. Lu, K. Nakajima, Y. Iiduka, H. Nikawa, N. Mizorogi, Z. Slanina, T. Tsuchiya, S. Nagase and T. Akasaka, J. Am. Chem. Soc., 2011, 133, 19553.
6. X. Lu, K. Nakajima, Y. Iiduka, H. Nikawa, T. Tsuchiya, N. Mizorogi, Z. Slanina, S. Nagase and T. Akasaka, Angew. Chem., Int. Ed., 2012, 51, 5889.
7. B. Cao, M. Hasegawa, K. Okada, T. Tomiyama, T. Okazaki, K. Suenaga and H. Shinohara, J. Am. Chem. Soc., 2001, 123, 9679–9680.
8. H. Kurihara, X. Lu, Y. Iiduka, H. Nikawa, M. Hachiya, N. Mizorogi, Z. Slanina, T. Tsuchiya, S. Nagase and T. Akasaka, Inorg. Chem., 2012, 51, 746.
9. J. Zhang, T. Fuhrer, W. Fu, J. Ge, D. W. Bearden, J. L. Dallas, J. C. Duchamp, K. L. Walker, H. Champion, H. F. Azurmendi, K. Harich and H. C. Dorn, J. Am. Chem. Soc., 2012, 134, 8487–8493.
10. C. R. Wang, T. Kai, T. Tomiyama, T. Yoshida, Y. Kobayashi, E. Nishibori, M. Takata, M. Sakata and H. Shinohara, Angew. Chem., Int. Ed., 2001, 40, 397.
11. H. Kurihara, X. Lu, Y. Iiduka, H. Nikawa, N. Mizorogi, Z. Slanina, T. Tsuchiya, S. Nagase and T. Akasaka, J. Am. Chem. Soc., 2012, 134, 3139.
12. Y. Yamazaki, K. Nakajima, T. Wakahara, T. Tsuchiya, M. O. Ishitsuka, Y. Maeda, T. Akasaka, M. Waelchli, N. Mizorogi and H. Nagase, Angew. Chem., Int. Ed. Engl., 2008, 47, 7905.
13. T. Yumura, Y. Sato, K. Suenaga and S. Iijima, J. Phys. Chem. B, 2005, 109, 20251.
14. Y. Iiduka, T. Wakahara, K. Nakajima, T. Nakahodo, T. Tsuchiya, Y. Maeda, T. Akasaka, K. Yoza, M. T. H. Liu, N. Mizorogi and S. Nagase, Angew. Chem., Int. Ed., 2007, 46, 5562.
15. Z. Q. Shi, X. Wu, C. R. Wang, X. Lu and H. Shinohara, Angew. Chem., Int. Ed., 2006, 45, 2107.
16. K. Tan and X. Lu, Chem. Commun., 2005, 4444.
17. M. Krause, M. Hulman, H. Kuzmany, O. Dubay, G. Kresse, K. Vietze, G. Seifert, C. Wang and H. Shinohara, Phys. Rev. Lett., 2004, 93, 137403.
18. Y. Iiduka, T. Wakahara, K. Nakajima, T. Tsuchiya, T. Nakahodo, Y. Maeda, T. Akasaka, N. Mizorogi and S. Nagase, Chem. Commun., 2006, 2057.
19. W. Cai, L. Bao, S. Zhao, Y. Xie, T. Akasaka and X. Lu, J. Am. Chem. Soc., 2015, 137, 10292.
20. W. Cai, F. Li, L. Bao, Y. Xie and X. Lu, J. Am. Chem. Soc., 2016, 138, 6670.
21. C. R. Wang, T. Kai, T. Tomiyama, T. Yoshida, Y. Kobayashi, E. Nishibori, M. Takata, M. Sakata and H. Shinohara, Nature, 2000, 408, 426.
22. H. Kurihara, X. Lu, Y. Iiduka, N. Mizorogi, Z. Slanina, T. Tsuchiya, S. Nagase and T. Akasaka, Chem. Commun., 2012, 48, 1290.
23. T. Inoue, T. Tomiyama, T. Sugai, T. Okazaki, T. Suematsu, N. Fujii, H. Utsumi, K. Nojima and H. Shinohara, J. Phys. Chem. B, 2004, 108, 7573.
24. H. Kato, A. Taninaka, T. Sugai and H. Shinohara, J. Am. Chem. Soc., 2003, 125, 7782.
25. B. P. Cao, T. Wakahara, T. Tsuchiya, M. Kondo, Y. Maeda, G. M. A. Rahman, T. Akasaka, K. Kobayashi, S. Nagase and K. Yamamoto, J. Am. Chem. Soc., 2004, 126, 9164.
26. T. Akasaka, S. Nagase, K. Kobayashi, M. Walchli, K. Yamamoto, H. Funasaka, M. Kako, T. Hoshino and T. Erata, Angew. Chem., Int. Ed. Engl., 1997, 36, 1643.
27. B. Q. Mercado, A. Jiang, H. Yang, Z. Wang, H. Jin, Z. Liu, M. M. Olmstead and A. L. Balch, Angew. Chem., Int. Ed. Engl., 2009, 48, 9114.
28. H. Yang, C. Lu, Z. Liu, H. Jin, Y. Che, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2008, 130, 17296.
29. C. M. Beavers, H. Jin, H. Yang, Z. Wang, X. Wang, H. Ge, Z. Liu, B. Q. Mercado, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2011, 133, 15338.
30. S. F. Yang and L. Dunsch, Angew. Chem., Int. Ed., 2006, 45, 1299.
31. T. Yang, X. Zhao and S. Nagase, Phys. Chem. Chem. Phys., 2011, 13, 5034.
32. A. A. Popov and L. Dunsch, J. Am. Chem. Soc., 2007, 129, 11835.
33. R. Valencia, A. Rodríguez-Fortea and J. M. Poblet, J. Phys. Chem. A, 2008, 112, 4550.
34. H. Zheng, X. Zhao, W. W. Wang, J. S. Dang and S. Nagase, J. Phys. Chem. C, 2013, 117, 25195.
35. X. Zhao, W. Y. Gao, T. Yang, J. J. Zheng, L. S. Li, L. He, R. J. Cao and S. Nagase, Inorg. Chem., 2012, 51, 2039.
36. Y. Guo, T. Yang, S. Nagase and X. Zhao, Inorg. Chem., 2014, 53, 2012.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. J. Rendell, C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.01, Gaussian, Inc., Wallingford, CT, 2009.
38. Z. Slanina, Int. Rev. Phys. Chem., 1987, 6, 251.
39. A. Nicklass, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1995, 102, 8942.
40. R. S. Zhao, Y. J. Guo, P. Zhao, M. Ehara, S. Nagase and X. Zhao, J. Phys. Chem. C, 2016, 120, 1275–1283.
41. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
42. A. Dreuw and M. Headgordon, Chem. Rev., 2005, 105, 4009–4037.
43. C. H. Chen, K. B. Ghiassi, M. R. Ceron, M. A. G. Ayala, L. Echegoyen, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2015, 137, 10116.
44. Q. Deng and A. A. Popov, J. Am. Chem. Soc., 2014, 136, 4257.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra00717e

---